«Применение информационных технологий при решении задач высшей алгебры»
| Вид материала | Реферат |
- «Применение методов информатики для решения химических задач», 200.25kb.
- Факультативные занятия по физике «Решение творческих задач», 54.67kb.
- Элективный курс «Методы решения физических задач», 47.45kb.
- Графический метод при решении задач с параметрами, 32.34kb.
- «Применение современных информационных технологий при изучении вопросов нетарифного, 316.46kb.
- Идеи В. К. Иванова об использовании априорной информации при решении некорректно поставленных, 84.46kb.
- Алгебра и теория чисел, 52.79kb.
- «Применение информационных технологий в преподавании литературы», 318.23kb.
- Применение информационных технологий в исторических исследованиях, 413.67kb.
- Педагогические технологии обучения географии, 40.66kb.
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Выпускная работа по
«Основам информационных технологий»
Магистрант
кафедры теории функций
Сыричев Вадим Викторович
Руководители:
доцент кафедры теории функций
Васильев Игорь Леонидович
ст. преподаватель Кожич Павел Павлович
Минск – 2008 г.
Оглавление
Оглавление 3
Список обозначений ко всей выпускной работе 4
Реферат на тему «Применение информационных технологий при решении задач высшей алгебры» 5
Интернет ресурсы в предметной области исследования 18
Действующий личный сайт в WWW 19
Граф научных интересов 20
Презентация магистерской диссертации 21
Список литературы к выпускной работе 22
Приложение А 23
Приложение Б 27
Список обозначений ко всей выпускной работе
ИТ Информационные технологии
СЛУ Система линейных уравнений
Реферат на тему «Применение информационных технологий при решении задач высшей алгебры»
Введение
Новые ИТ прошли несколько этапов, смена которых определилась развитием научно-технического прогресса, проявлением новых технических средств переработки информации. Основным средством переработки информации является компьютер, который существенно повлиял на использование технических процессов и на качество результатов переработки информации.
Большинство пользователей заинтересовано в том, чтобы правильно выполнить конкретные аналитические преобразования, вычислить в символьном виде производную или первообразную заданной функции, разложить ее в ряд Тейлора или Фурье, провести аппроксимацию и т. д., а вовсе не в детальном и сложном математическом и логическом описании того, как это делается компьютером (или, точнее, его программистом). Словом, большинству пользователей нужны системы компьютерной алгебры в качестве простого и удобного инструмента для работы. Этим инструментом являются многие широко известные математические пакеты, такие как Maple, Mathematica, Matlab, MathCad и другие. В данной работе конкретнее рассмотрим
Целью данной работы поиск ответов на ряд актуальных вопросов, связанных с применением ИТ при решении задач алгебры:
- какие компьютерные математические пакеты лучше всего использовать при решении алгебраических задач;
- как правильно использовать возможности математических пакетов.
Глава 1 (Обзор литературы)
1. «Информационные технологии в математике» Ю.Ю. Тарасевич. В книге рассматриваются вопросы, касающиеся решения математических задач с использованием пакетов Maple и Mathcad, подготовки математических и естественнонаучных текстов с использованием издательской системы LaTeX.
2. «Mathcad 8-12 для студентов» В. П. Дьяконов. Содержит полное описание самых популярных версий системы Mathcad (от Mathcad 8 до новейшей Mathcad 12), ориентированное на студентов и преподавателей вузов, а также инженеров и научных работников. Особое внимание уделено наглядности описания, вмзуализации результатов вычислений и примерам применения систем в практике математических, научно-технических и учебных расчетов. В книге описаны многие сотни примеров применения систем класса Mathcad. Для всех пользователей системами Mathcad. Может служить описанием систем, руководством пользователя по ним и самоучителем.
3. «Mathcad для студента» Ю. М. Бидасюк. Книга предназначена для самостоятельного изучения последней версии популярной системы математических расчетов Mathcad 12. Основная ее цель - помочь в освоении современных средств компьютерной математики для выполнения математических расчетов. В книге рассматривается применение MathCAD для решения задач из различных областей математики: линейной алгебры, математического анализа, математической статистики, а также для таких целей, как построение графиков, импорт и экспорт данных и т.д. Материал книги изложен так, что будет понятен и полезен как для читателей, уже знакомых с предыдущими версиями MathCAD, так и для читателей, еще не знакомых с компьютерной математикой и даже не овладевших в достаточной мегТе работой на компьютере в среде Windows. Однако материал требует обязательного знания хотя бы основ высшей математики. Это означает, что книга ориентирована, в первую очередь, на студентов высших учебных заведений, научных и технических работников.
4. Электронное учебное пособие по высшей математике на базе системы MATHEMATICA. Авторы: Кулешов А.А., Земсков С В., Позняк Ю.В.
5. «Практическое введение в пакет MATHEMATICA» В. Муравьев, Д. Бурланкова. Учебное пособие предназначено для изучения языка символьной математики "MATHEMATICA". На практических примерах показаны аналитические, численные и графические возможности пакета. Изложены принципы программирования в системе "MATHEMATICA". Даны рекомендации по работе в среде пакета. Приведены примеры программ, освоив которые, студент сможет работать далее самостоятельно.
Задачами реферата являются:
- Показать возможность применения математических пакетов Mathcad и Mathematica для решения задач высшей алгебры.
- Анализ математических пакетов
- Привести примеры алгоритмов решения задач
Глава 2 (Методика исследований)
При написании реферата использовались следующие методаы теории познания:
Индукция;
Дедукция;
Анализ;
Синтез;
Кроме того использовались классические методы линейной алгебры.
Глава 3 (Основные результаты)
Возможности Mathcad
Mathcad - универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Основное преимущество пакета - естественный математический язык, на котором формируются решаемые задачи.
Объединение текстового редактора с возможностью использования общепринятого математического языка позволяет пользователю получить готовый итоговый документ. Пакет обладает широкими графическими возможностями, расширяемыми от версии к версии. Практическое применение пакета существенно повышает эффективность интеллектуального труда.
Приведем пример решения системы линейных уравнений с помощью Mathcad матричным способом.
Отметим также, что системы линейных уравнений удобно решать с помощью функции lsolve.
lsolve(А, b)
Возвращается вектор решения x такой, что Ах = b.
Аргументы:
А - квадратная, не сингулярная матрица.
b - вектор, имеющий столько же рядов, сколько рядов в матрице А.
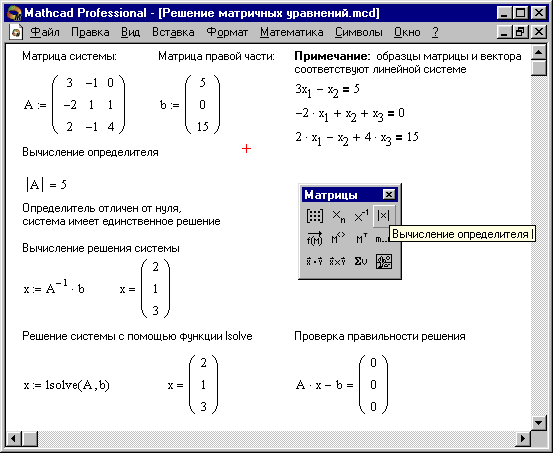
Теперь решим ту же систему линейных уравнений методом Гаусса.
В Mathcad прямой и обратный ходы метода Гаусса выполняет функция rref(A).
На рисунке показано решение системы линейных уравнений методом Гаусса, в котором используются следующие функции:
(A)
Возвращается ступенчатая форма матрицы А.
augment(A, В)
Возвращается массив, сформированный расположением A и В бок о бок. Массивы A и В должны иметь одинаковое число строк.
submatrix(A, ir, jr, ic, jc)
Возвращается субматрица, состоящая из всех элементов с ir по jr и столбцах с ic по jc. Удостоверьтесь, что ir jr и ic jc, иначе порядок строк и (или) столбцов будет обращен.
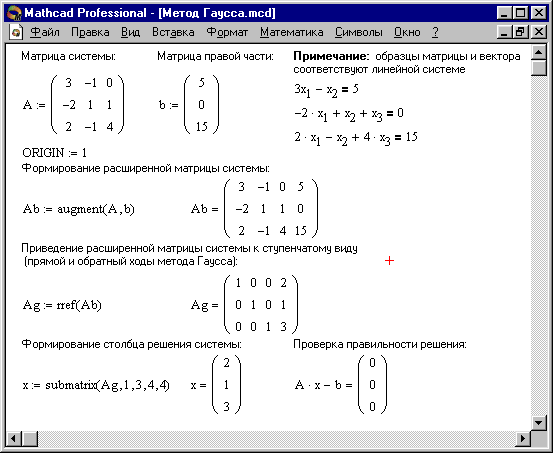
Возможности Mathematica.
Этот пакет является более мощным по сравнению с Mathcad, так как Mathematica отличается охватом широкого круга задач и ее разработчики задались целью объединить все известные математические методы, использующиеся для решения научных задач, в унифицированном и согласованном виде, включая аналитические и численные расчеты. Mathematicа дает возможность специалистам решать большое количество достаточно сложных задач, не вдаваясь в тонкости программирования. Благодаря этому программа получила широкое распространение в таких областях, как физика, биология, экономика. Программа также применяется как для выполнения, так и для оформления инженерных проектов.
Кроме того следует отметить, что Mathematica содержит стандартные дополнения, включающих подпрограммы (пакеты), значительно расширяющие функциональные возможности в различных областях. В частности, в дополнения для алгебры входят пакеты, позволяющие задавать различные алгебраические поля и оперировать в них, а также несколько пакетов, расширяющих функциональность программы при оперировании с полиномами и нахождении их корней. В новой версии оно пополнилось пакетами для решения некоторых типов алгебраических неравенств и симметричных полиномов и, кроме того, добавлена Гамильтонова алгебра кватернионов и элементы полей Пигуа.
В рамках данного реферата приведем пример решения предыдущей задачи с помощью пакета Mathematica.
Метод Гаусса для СЛУ, состоящей из трех уравнений с тремя неизвестными
Приведем пример решения той же системы, что была решена посредством Mathcad.
Исходный код:

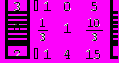
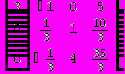
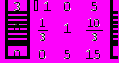
{{x1=2,x2=1,x3=3}}
Теперь перейдем к построению более сложного алгоритма. Поставим цель решить СЛУ для произвольного числа уравнений и произвольного числа неизвестных методом Крамера.
Исходный код:



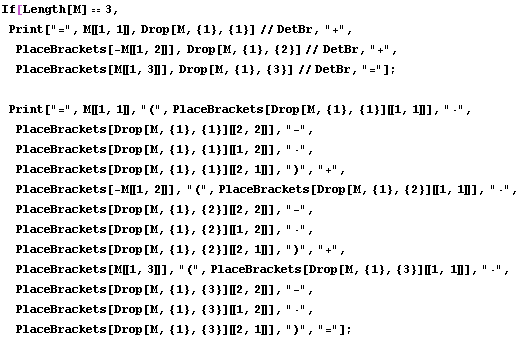


Решим с помощью этого алгоритма предыдущую задачу.
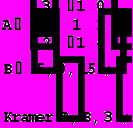
Решим систему методом Крамера:
= A = 5
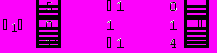

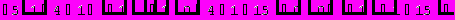
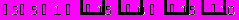
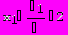
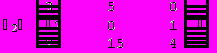
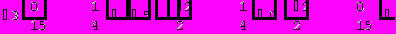
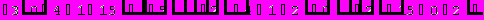

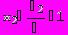
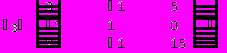

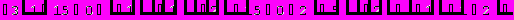
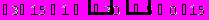
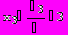
Отметим, что приведенные в качестве примера алгоритмы решения задач в пакете Mathematica, показывают весь ход решения, а не только окончательный ответ.
Применение данного алгоритма для решения СЛУ , состоящей из четырех уравнений находится в приложении.
Глава 4 (Обсуждение результатов)
Рассматривая различные математические пакеты (в данном случае Mathematica и Mathcad), следует отметить, что сравнение систем не совсем уместно, так как у каждой программы есть свои достоинства и недостатки, свои приверженцы. Создатели Mathematica и Mathcad, ставили перед собой разные цели. Для разработчиков Mathematica – это возможность решения специфических, узконаправленных, серьезных, с большими вычислениями задач. Для разработчиков Mathcad – это простота в использовании, наглядность, ориентация на широкую аудиторию, включая и тех, кто не очень ориентируется в математике и программировании. Поэтому каждый сам для себя выбирает, какой пакет использовать в силу своих потребностей, знаний, умений разбираться в новом. Конечно, тем, кто всерьез применяет системы компьютерной математики, совсем неплохо работать с несколькими системами.
Заключение
Применение ИТ в математических исследованиях открыло перед математиками огромные возможности.
С помощью описываемых пакетов можно сэкономить массу времени и избежать многих ошибок при математических вычислениях. Естественно, системы не ограничиваются только этими возможностями. Спектр задач, решаемых подобными системами, очень широк.
Одновременно эти системы является уникальными по своей полноте «живыми» справочниками по различным математическим понятиям, алгоритмам и функциям. Они обеспечивает высочайшую степень визуализации вычислений, начиная от представления исходных данных и кончая выводом промежуточных и конечных результатов вычислений. Таким образом, главным для систем становится предоставление пользователю самых серьезных и, порой, новых знаний в столь почетной и древней области человеческого интеллекта, как математика.
Список литературы к реферату.
1. «Информационные технологии в математике» Ю.Ю. Тарасевич. - М.: СОЛОН-Пресс, 2003. – 144 с.
2. «Mathcad 8-12 для студентов» В. П. Дьяконов. М.: СОЛОН-Пресс, 2005. - 632 с.
3. «Mathcad для студента» Ю. М. Бидасюк. Вильямс, 2006.
4. Электронное учебное пособие по высшей математике на базе системы MATHEMATICA. Авторы: Кулешов А.А., Земсков С В., Позняк Ю.В.
5. «Практическое введение в пакет MATHEMATICA» В. Муравьев, Д. Бурланкова. Издательство Нижегородского университета, 2000. - 124 с.
6.– Режим доступа: ссылка скрыта. – Дата доступа: 11.12.2008.
7.– Режим доступа: ссылка скрыта. – Дата доступа: 11.12.2008.
Предметный указатель к реферату.
Maple 5
Mathcad 6, 7, 8, 9, 10, 14, 16
MathCAD 5, 14
Mathematica 5, 14, 18
Matlab 5
Интернет ресурсы в предметной области исследования
- ссылка скрыта - здесь представлены различные пособия в формате ноутбук для начинающих. Здесь всегда можно выбрать наиболее подходящее для Вас. Также здесь собраны примеры использования программы Mathematica во взаимодействии с другими программами. Примеры разбиты на группы по областям применения.
- ссылка скрыта – полезный сайт для математиков. На сайте можно найти электронные книги, статьи по популярным математическим пакетам, ознакомиться с примерами их применения, получит новую информацию. Если вы пользователь одного из математических пакетов, вы можете обсудить свои проблемы на форуме, посвящённом этому пакету.
- ссылка скрыта - здесь собраны материалы по всем конференциям, посвященным системе Mathematica.
- ссылка скрыта - здесь представлены различные двумерные, трехмерные графики, анимации, диаграммы и многое другое.
- ссылка скрыта – научная электронная библиотека. Один из наиболее полезнейших источников информации.
- ссылка скрыта – общероссийский математический портал, предоставляющий российским и зарубежным математикам различные возможности в поиске информации о математической жизни в России.
- ссылка скрыта – в этом разделе можно посмотреть аннотации на различные книги, журналы и статьи. Существуют форумы по разным естественным дисциплинам, в том числе и по механике. На форуме можно обсудить имеющиеся у вас проблемы, посмотреть ссылки на литературу по интересующей теме. Сайт постоянно снабжается свежими новостями из мира науки.
- ссылка скрыта – здесь представлены исследования и разработки в естественных науках и образовательных технологиях. Решение типовых задач по различным разделам высшей и элементарной математики с помощью пакета Mathematica.
- ссылка скрыта – cайт Высшей аттестационной комиссии Республики Беларусь. Здесь собраны все нормативные акты, касающиеся оформления и защиты диссертаций.
- ссылка скрыта – информационные технологии в образовании. Этот сайт посвящен информатике и информационным технологиям.
Действующий личный сайт в WWW
ссылка скрыта
Граф научных интересов
магистранта Сыричева В.В.
Механико-математический факультет
Специальность «Математика»
| Смежные специальности
| Основная специальность
| Сопутствующие специальности Нет |
Презентация магистерской диссертации
Тема магистерской диссертации: «Бесконечные матрицы и пространство последовательностей».
Перечень слайдов находится в приложении Б.
Для просмотра презентации локально:
Список литературы к выпускной работе
- «Бесконечные матрицы и пространство последовательностей», Р. Кук Издательство: Государственное издательство физико-математической литературы 472 страниц; 1960 г.
- «Информационные технологии в математике» Ю.Ю. Тарасевич. - М.: СОЛОН-Пресс, 2003. – 144 с.
- Электронное учебное пособие по высшей математике на базе системы MATHEMATICA. Авторы: Кулешов А.А., Земсков С В., Позняк Ю.В.
- Режим доступа: ссылка скрыта. – Дата доступа: 22.11.2008.
- Режим доступа: ссылка скрыта. – Дата доступа: 11.12.2008.
Приложение А
Решим СЛУ, состоящую из четырех уравнений с четырьмя неизвестными.
Последняя часть алгоритма будет иметь следующий вид:

Вводим данные:

Решим систему методом Крамера:
= A = 6
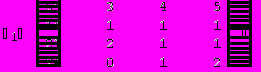
Для вычисления определителя преобразуем матрицу.
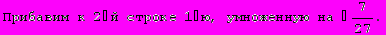
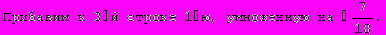
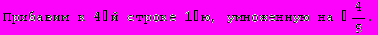

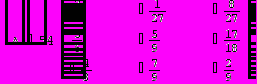
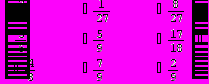

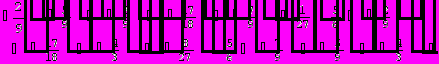
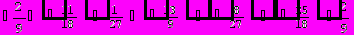
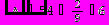
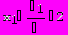
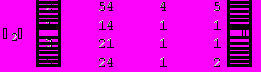
Для вычисления определителя преобразуем матрицу.
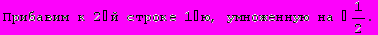
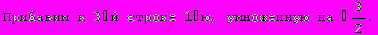
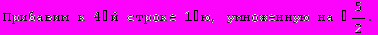

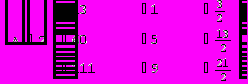
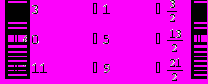

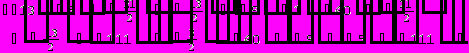
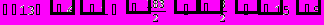
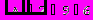
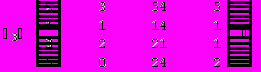
Для вычисления определителя преобразуем матрицу.
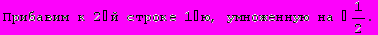
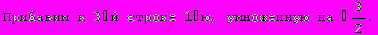
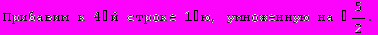
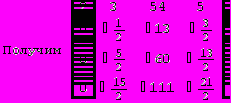
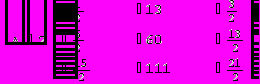
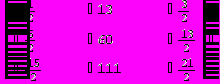


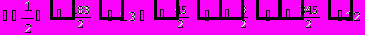
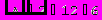
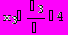
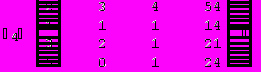
Для вычисления определителя преобразуем матрицу.
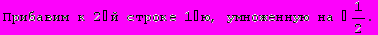
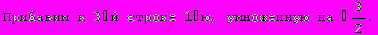
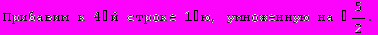
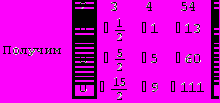
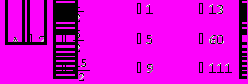
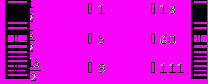
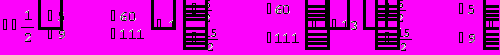

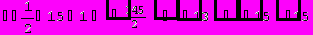
Не составляет труда убедиться в правильности решения.
Приложение Б
Презентация магистерской диссертации.
 |  |
 |  |
 |  |
 |  |
 |  |
 | |
