Идеи В. К. Иванова об использовании априорной информации при решении некорректно поставленных задач и их практическое применение Аннотация

Вид материала

Документы

Содержание Некорректные задачи на компактах. A задан с погрешностью, то понятие квазирешения вводится, как и выше, заменой оператора A Некорректные задачи в случае истокопредставимости решения. Практические приложения.

Подобный материал:

• Об одном способе регуляризации некорректно поставленных задач распознавания образов, 40.68kb.
• «Применение информационных технологий при решении задач высшей алгебры», 159.09kb.
• Факультативные занятия по физике «Решение творческих задач», 54.67kb.
• Роль априорной информации в творческом процессе, 515.3kb.
• Аннотация рабочей программы дисциплины молекулярная биология клетки цель дисциплины, 48.5kb.
• Урок по теме «Применение производной в различных областях науки», 150.03kb.
• Аннотация программы учебной дисциплины 01. 01 «Решение инженерных задач на пэвм», 50.18kb.
• Аннотация дисциплины, 1371.94kb.
• К. Д. Ушинского Обучение младших школьников решению сюжетных математических задач одна, 79.12kb.
• Примерная программа дисциплины учебно-исследовательская работа направление подготовки, 183.34kb.

А. Г. Ягола, д-р физ.-мат. наук

Физический факультет МГУ

им. М.В. Ломоносова

(Россия, 119991, Москва, Ленинские горы, 1, стр. 2

тел.(495) 9391033, Е-mail: yagola@yahoo.com )


Идеи В.К.Иванова об использовании априорной информации при решении некорректно поставленных задач и их практическое применение

Аннотация. В работах В.К.Иванова дано строгое математическое обоснование двух методов решения некорректно поставленных задач при условии, что имеется дополнительная априорная информация об искомом решении. Если известно, что решение является элементом заданного компакта, им был разработан метод квазирешений. В этом случае возможна и оценка погрешности приближенного решения. В случае, если искомое решение истокопредставимо с помощью вполне непрерывного оператора, устойчивое приближенное решение может быть найдено с помощью предложенного В.К.Ивановым метода расширяющихся компактов. При этом возможна так называемая апостериорная оценка погрешности. Показаны практические применения данных методов.


Некорректные задачи на компактах. Пусть дано операторное уравнение:

,

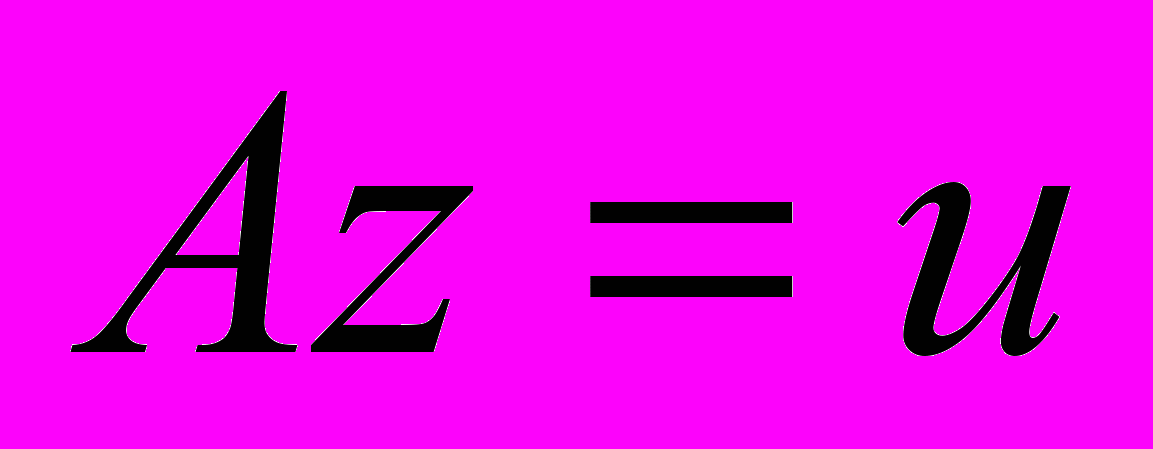где - линейный инъективный оператор, действующий из нормированного пространства Z в нормированное пространство U. Пусть - точное решение операторного уравнения, , u -точная правая часть и задана приближенная правая часть 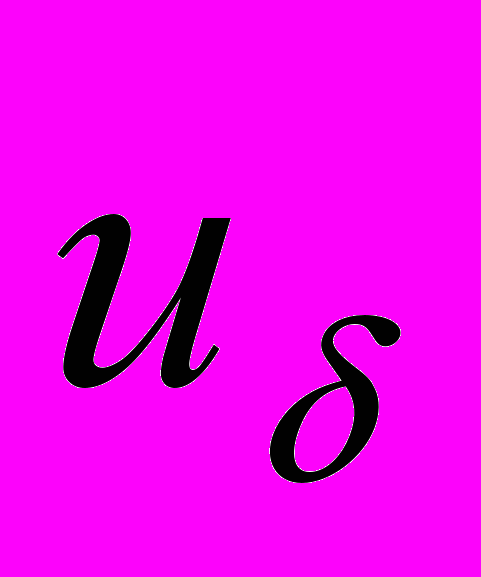такая, что .

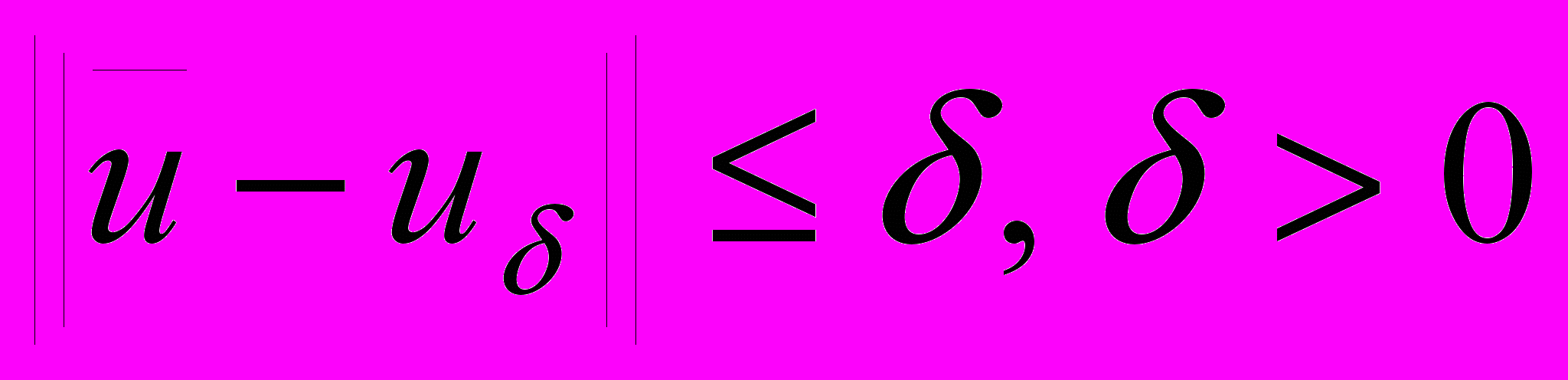Множество является множеством приближенных решений операторного уравнения. Для линейных некорректных задач 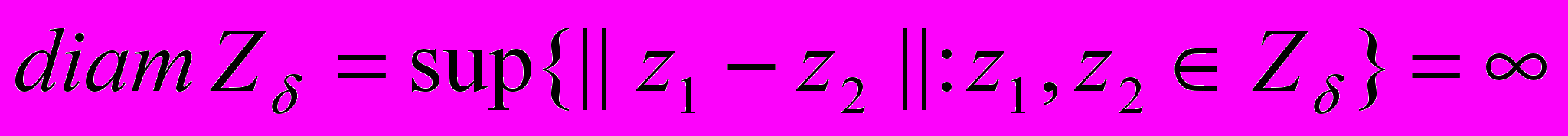для любого 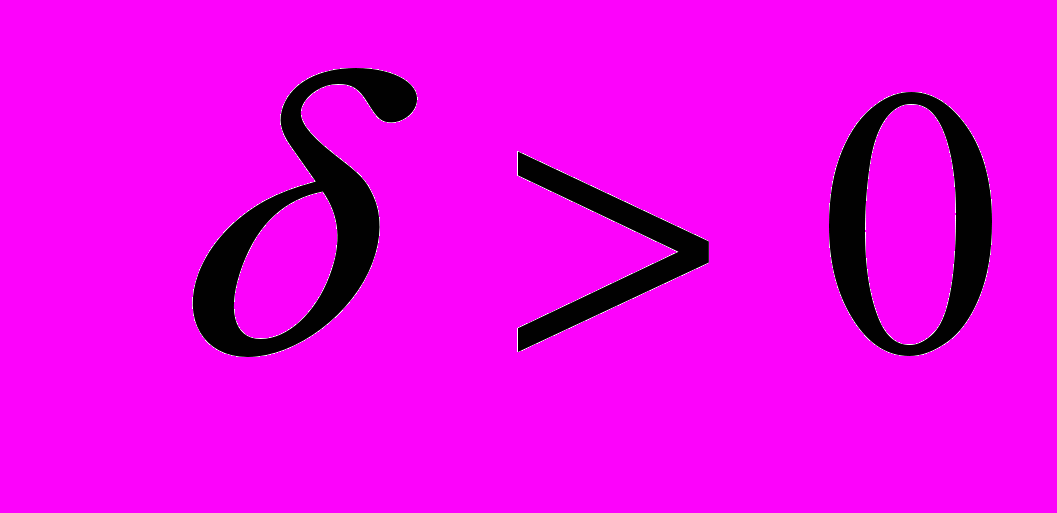, поскольку обратный оператор не ограничен.

Возникает вопрос: нельзя ли использовать дополнительную априорную информацию для того, чтобы сузить множество приближенных решений, а еще лучше получить корректную задачу. А.Н.Тихонову принадлежит следующая идея: если известно, что множество решений является компактом, то задача решения операторного уравнения корректна при условии, что приближенная правая часть операторного уравнения также принадлежит образу компакта. Для доказательства этого утверждения А.Н.Тихонов применил следующую теорему.

Теорема. Пусть инъективный непрерывный оператор действует: 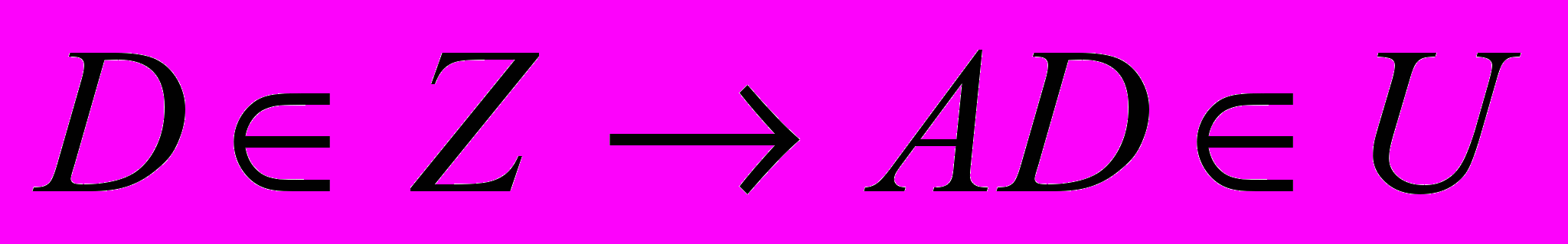, где 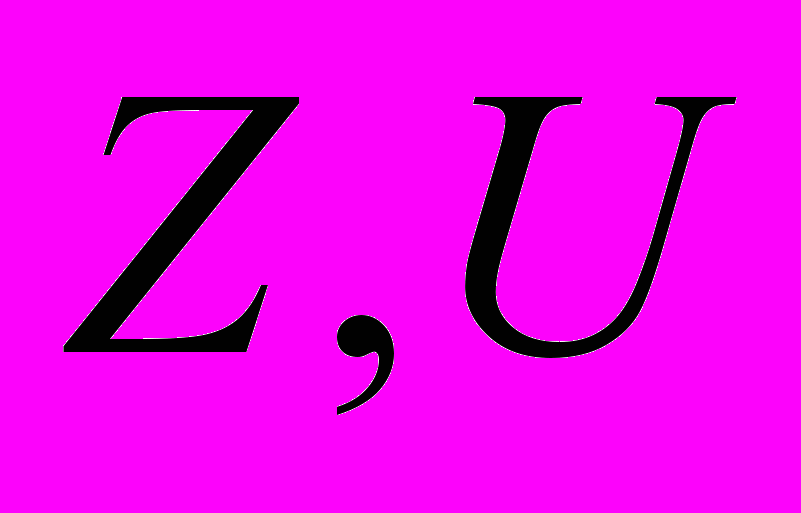- нормированные пространства, - компакт. Тогда обратный оператор непрерывен на .

Теорема верна и для нелинейных операторов. Таким образом, решение операторного уравнения на компакте является корректной задачей при условии, что приближенная правая часть принадлежит . Эта идея позволила М.М.Лаврентьеву ввести понятие задачи, корректной по Тихонову (предполагается существование множества корректности, на котором задача становится корректной), а В.К.Иванову дать определение квазирешения некорректной задачи.

Приведенная выше теорема неприменима, если 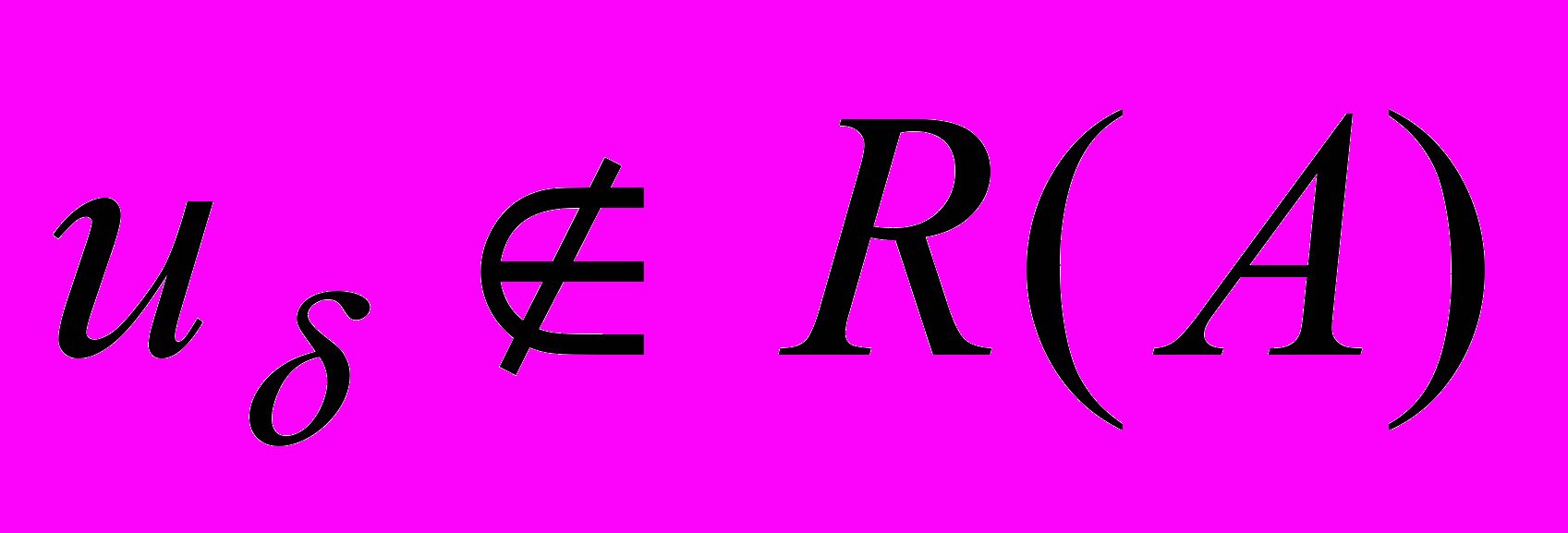. Поэтому необходимо ее обобщить.

Определение. Элемент 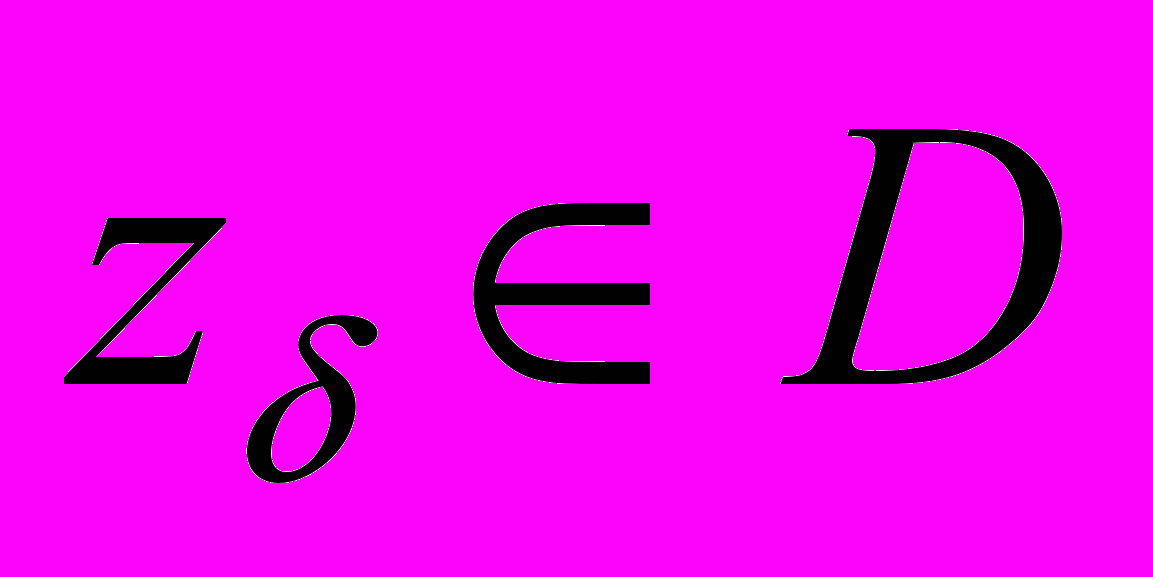такой, что 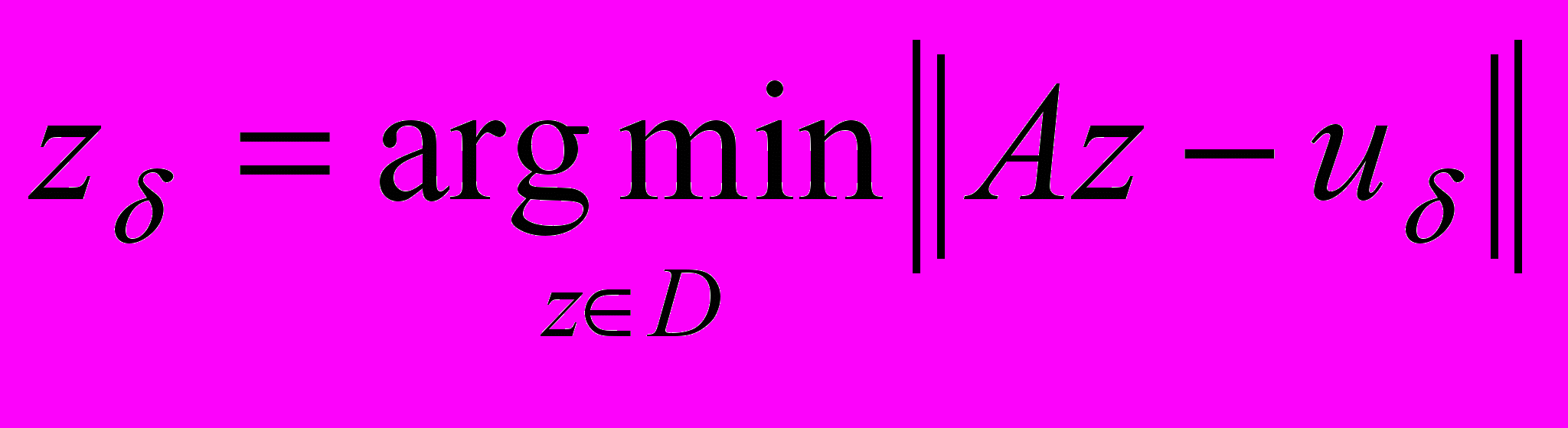, называется квазирешением операторного уравнения на компакте D ( 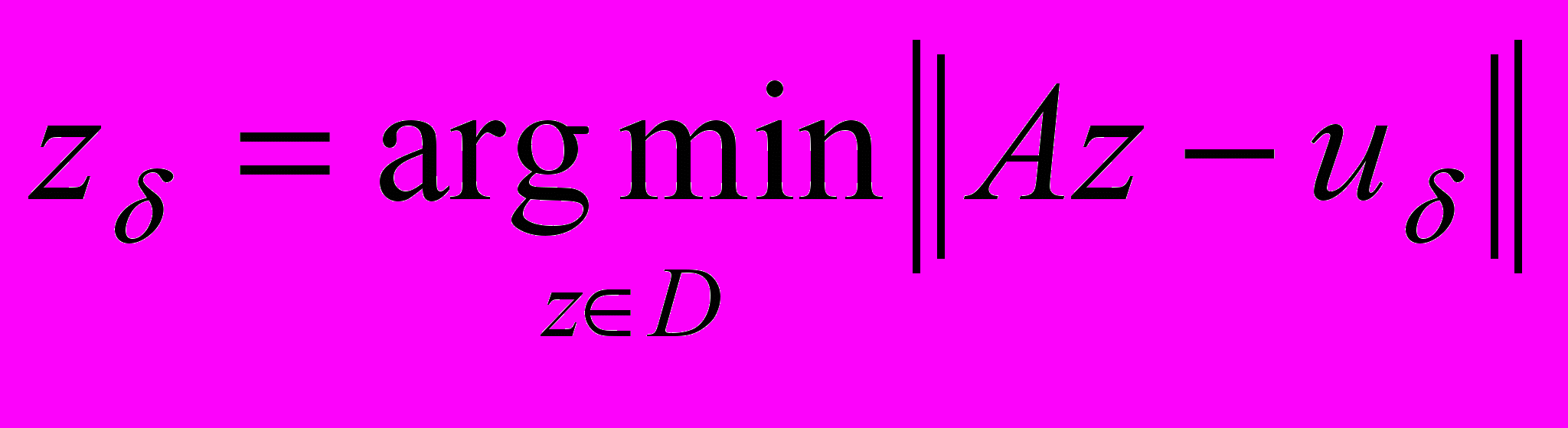означает, что ).

Квазирешение существует, но возможно не единственно. Тем не менее, для любого квазирешения имеет место сходимость к точному решению: 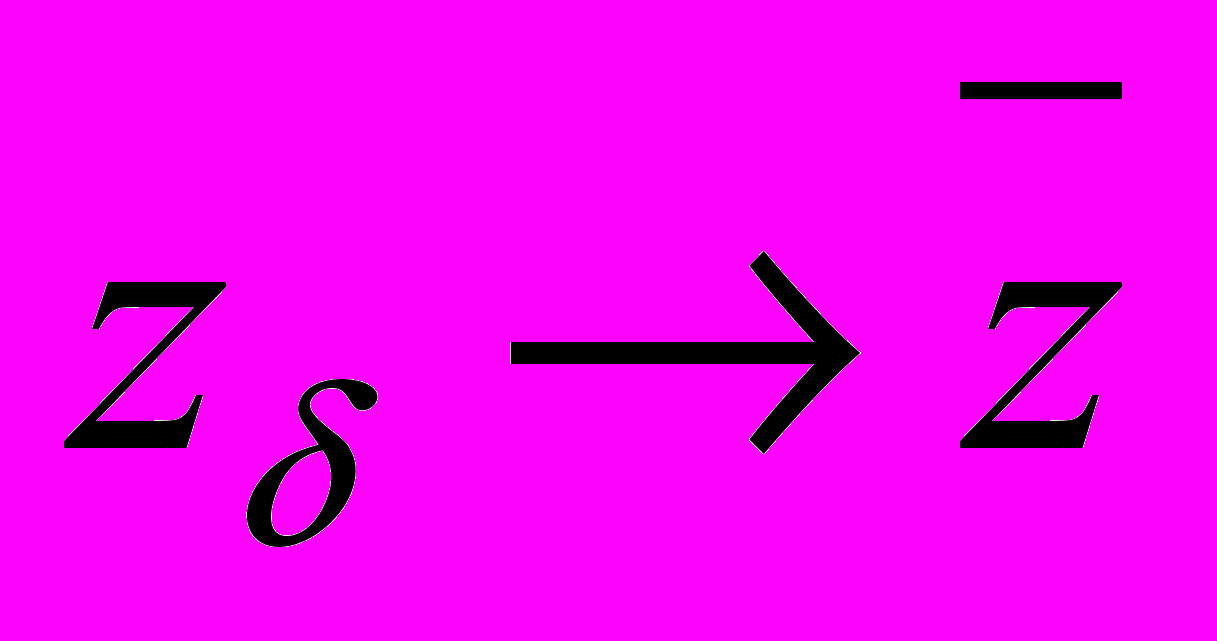при . При этом знание не обязательно. Если же погрешность δ известна, то

1) в качестве приближенного решения может быть взят любой элемент 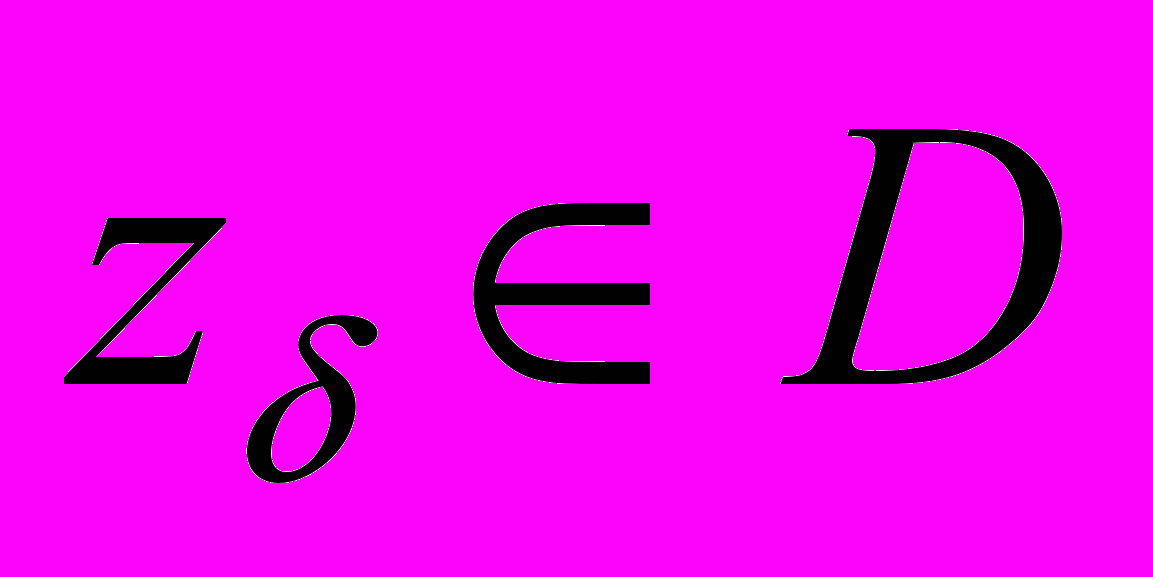, удовлетворяющий неравенству: 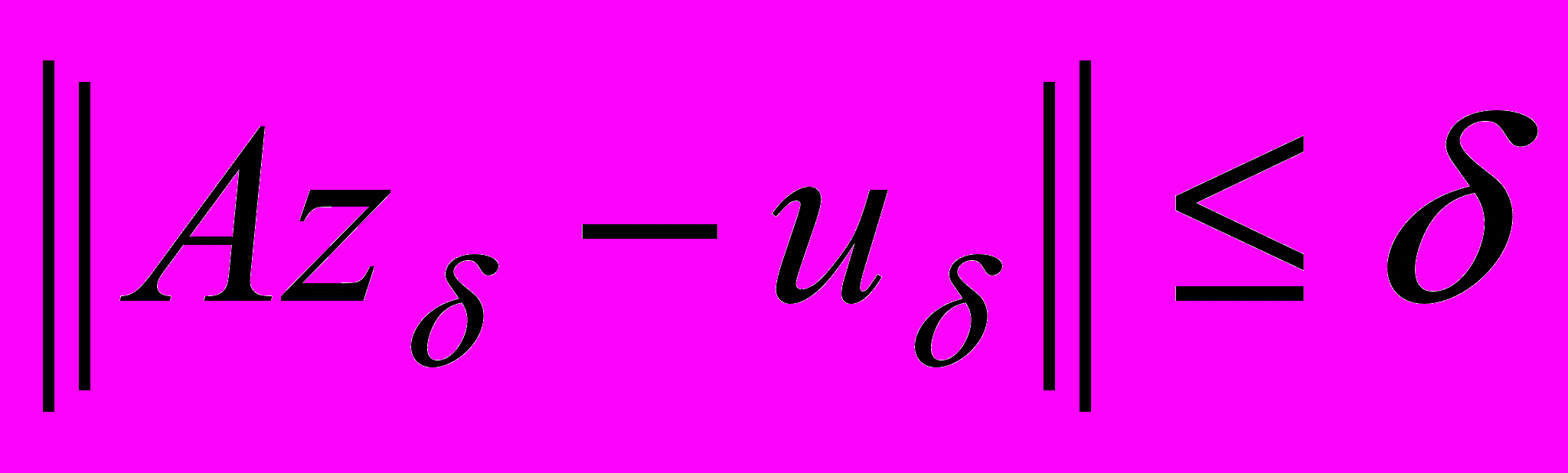(δ-квазирешение);

2) можно найти погрешность приближенного решения, решив экстремальную задачу:

найти max||z-z_δ|| по всем 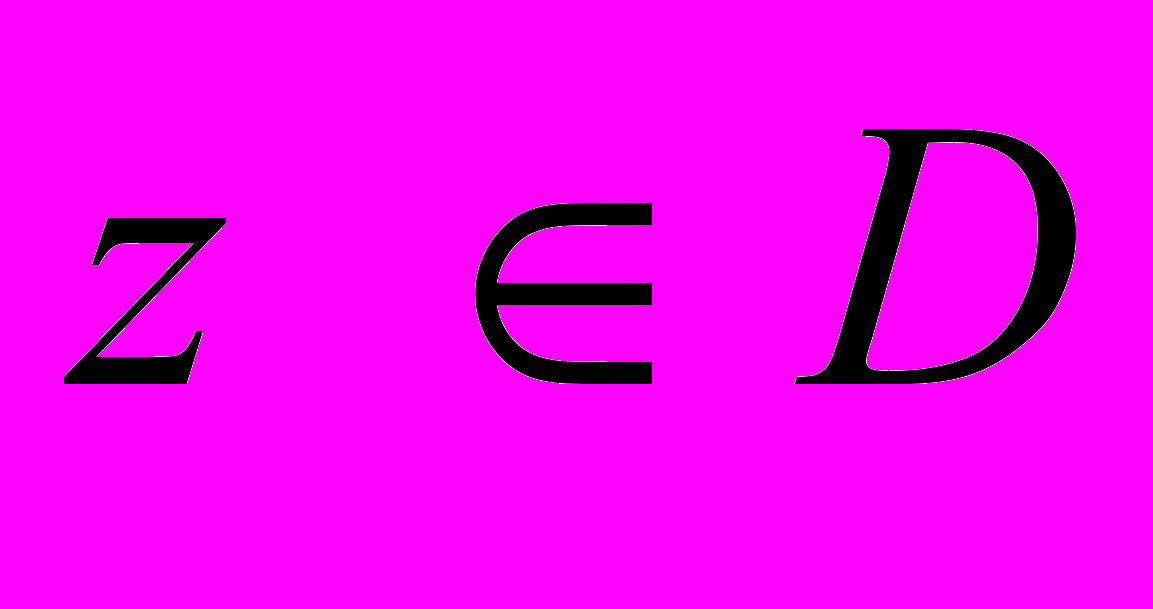, удовлетворяющим неравенству: 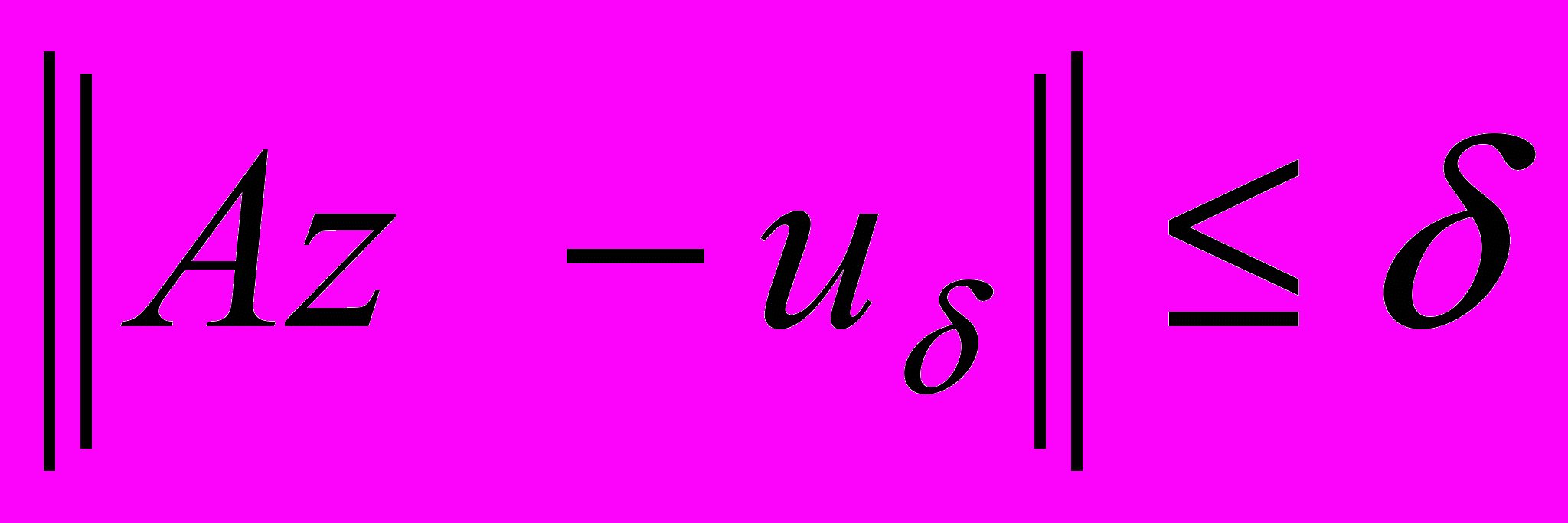(очевидно, что точное решение удовлетворяет данному неравенству).

Таким образом, задача отыскания квазирешения практически не отличается от корректной. Не выполняется, вообще говоря, только условие единственности квазирешения.

Если же и оператор A задан с погрешностью, то понятие квазирешения вводится, как и выше, заменой оператора A на оператор A_h.

Определение. Элемент 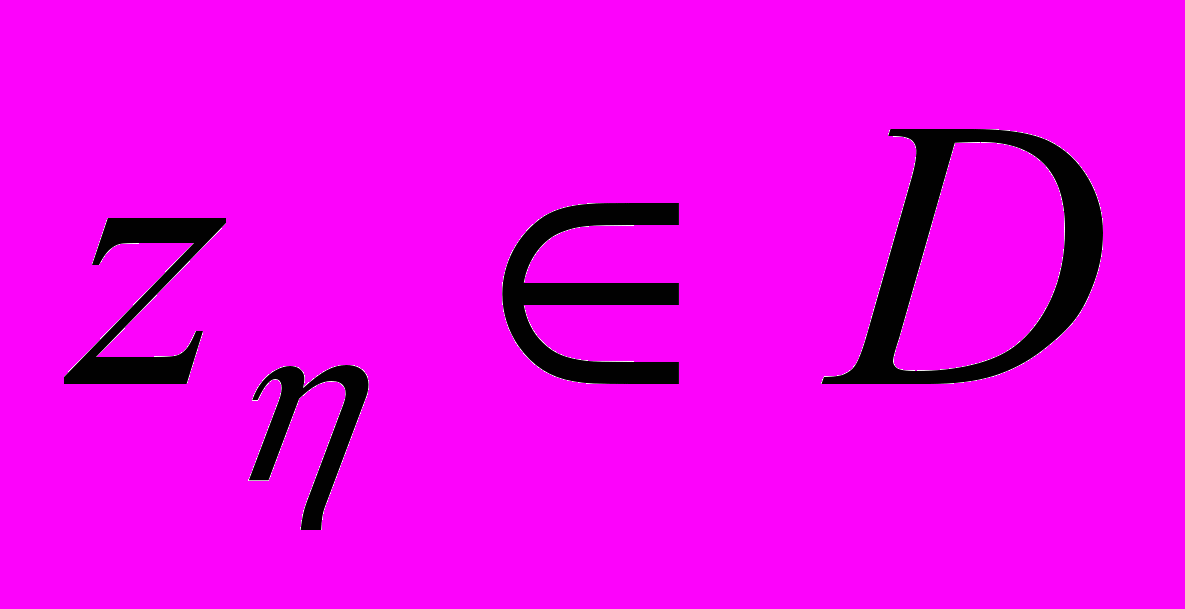такой, что , называется квазирешением операторного уравнения на компакте D.

В качестве же приближенного решения может быть выбран любой элемент 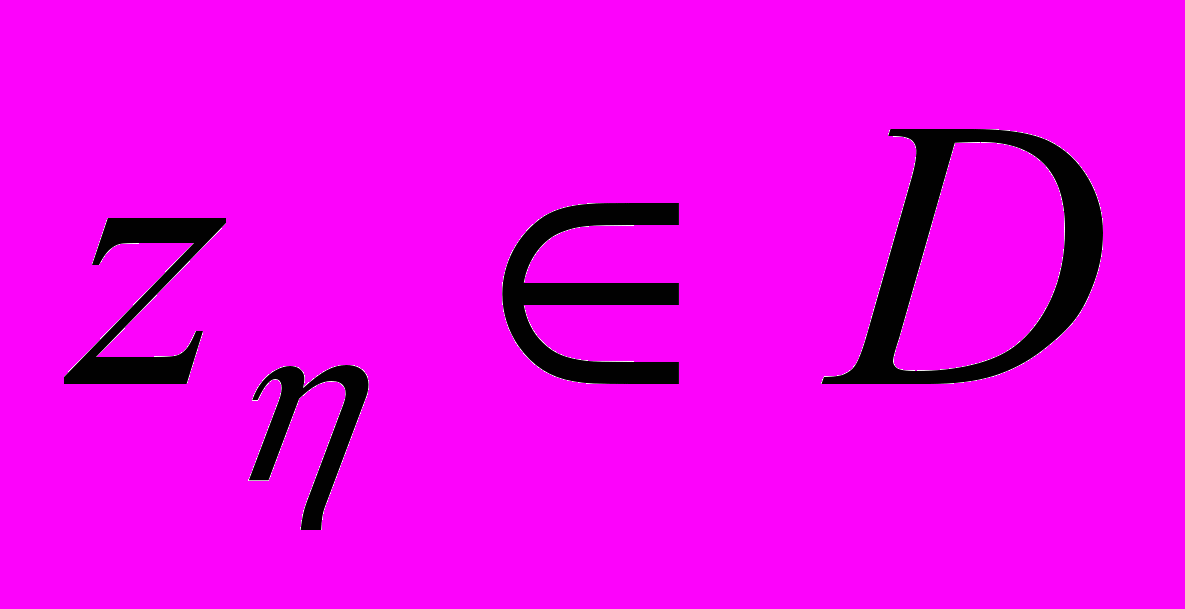, удовлетворяющий неравенству: (η-квазирешение).

Если Z и U – гильбертовы пространства, то многие численные методы отыскания квазирешений для линейных операторных уравнений основаны на том, что функционал невязки 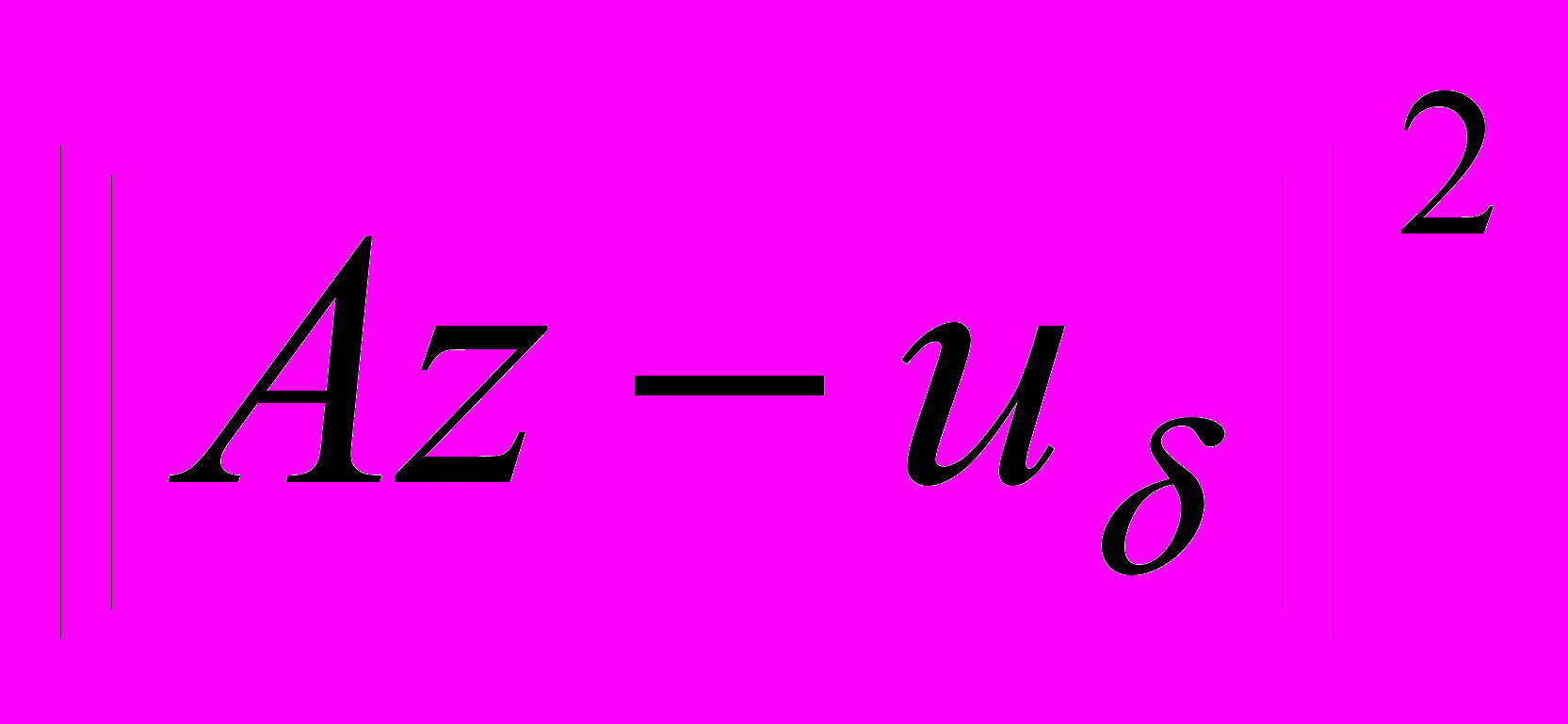является выпуклым и дифференцируемым. Если - выпуклый компакт, то нахождение квазирешения - задача выпуклого программирования. Записанные выше неравенства, определяющие приближенные решения на компактах, могут быть использованы в качестве критериев остановки минимизации функционала невязки. Задача отыскания погрешности найденного приближенного решения является нестандартной задачей выпуклого программирования, поскольку при решении этой задачи требуется найти максимум, а не минимум выпуклого функционала.

Хорошо известны множества корректности, которые часто встречаются в прикладных задачах. Прежде всего, если известно, что точное решение принадлежит конечно-параметрическому семейству функций, то ставится задача отыскания параметров, которая может быть корректной и в том случае, если задача без этой априорной информации является некорректной.

Если в операторном уравнении неизвестной является функция z(s), s[a, b], о которой известно, что она является монотонной и ограниченной, то этой информации оказывается достаточно для выделения компакта в пространстве L₂[a, b]. Для отыскания квазирешения после перехода к конечно-разностной аппроксимации могут быть применены известные методы квадратичного программирования, например, метод проекции сопряженных градиентов или метод условного градиента. Аналогичный подход применим и при наличии априорной информации о том, что точное решение является ограниченной и выпуклой, или монотонной и выпуклой, или имеющей заданное число максимумов и минимумов функцией. В этих случаях возможно отыскание и погрешности приближенного решения.


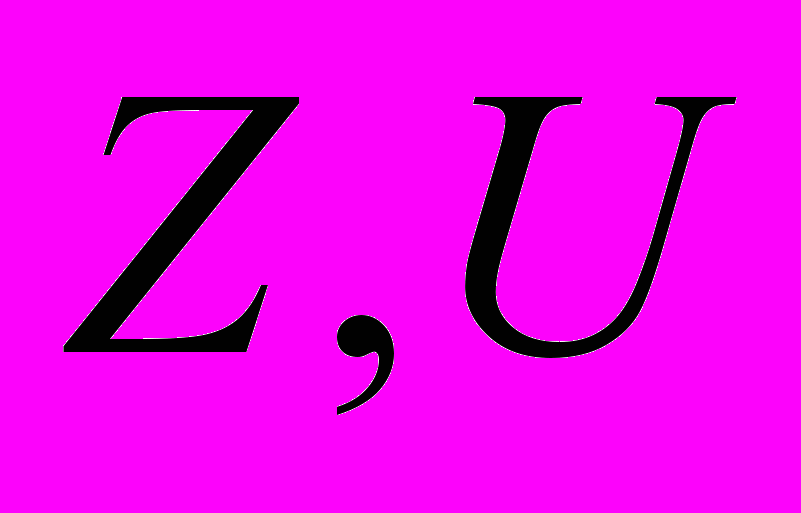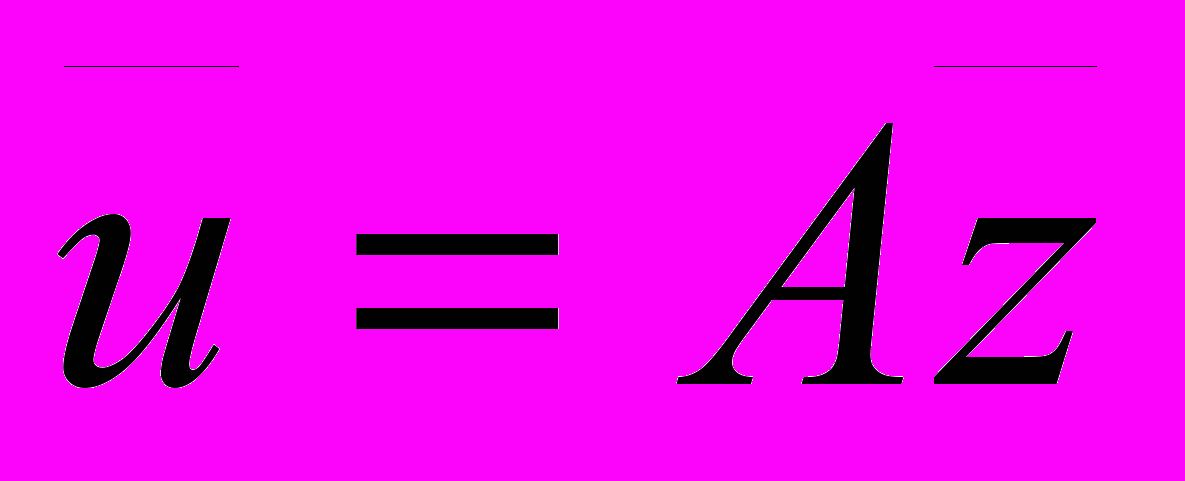Некорректные задачи в случае истокопредставимости решения. Пусть линейный оператор инъективный, непрерывный и отображает ; - нормированные пространства. Пусть также имеется следующая априорная информация, которая встречается при решении многих физических задач. Известно, что точное решение для уравнения представимо в виде 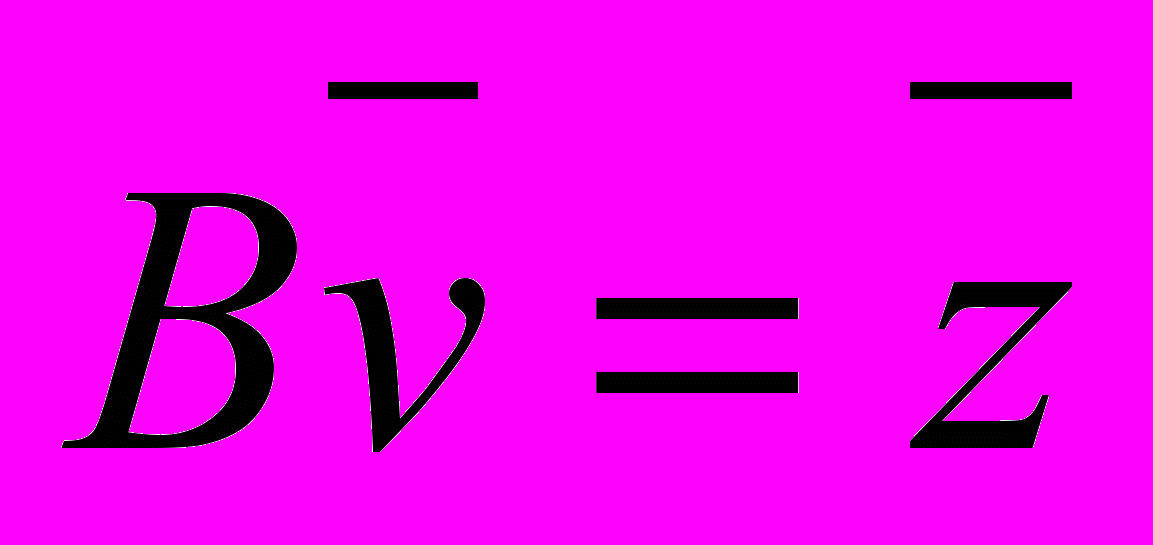, 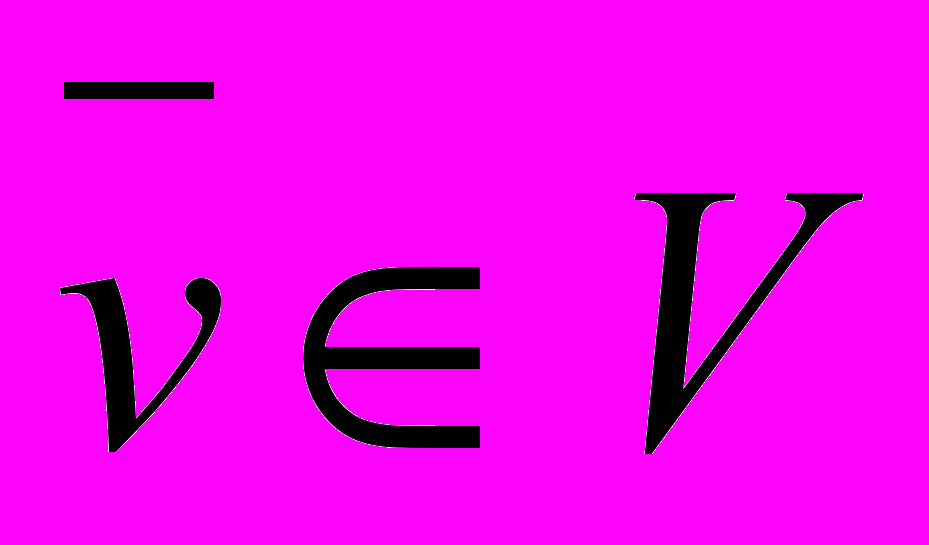; ; - инъективный, вполне непрерывный оператор; V –гильбертово пространство. Предполагается, что известны 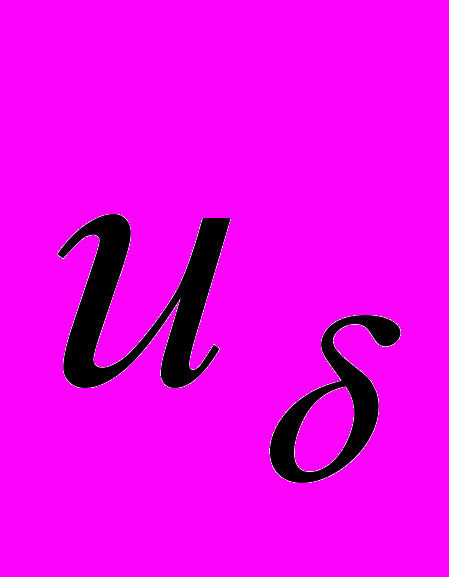- неточная правая часть такая, что 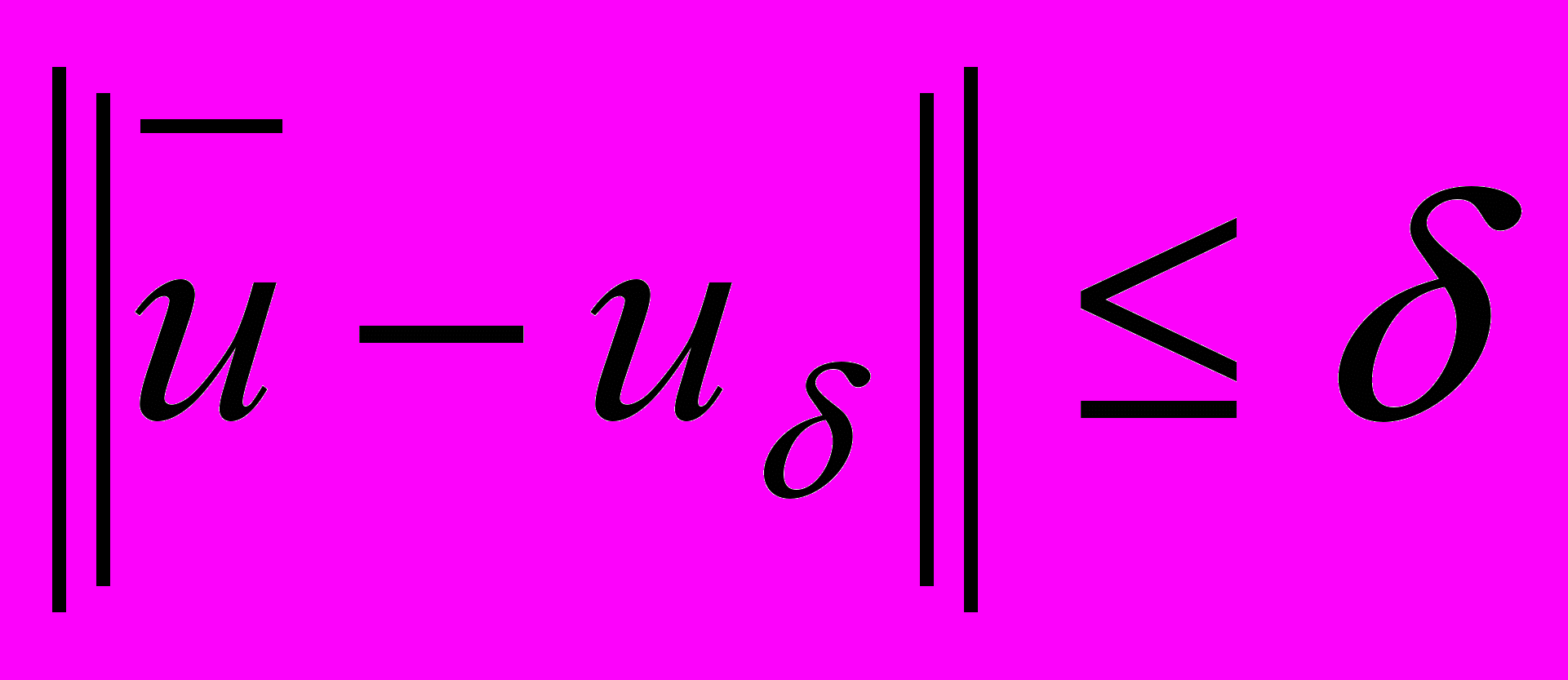, и ее погрешность .

Ниже рассматривается метод расширяющихся компактов, идея и обоснование которого принадлежит В.К.Иванову и И.Н.Домбровской.

Сначала номер итерации полагается n=1 и определяется замкнутый шар в пространстве V: 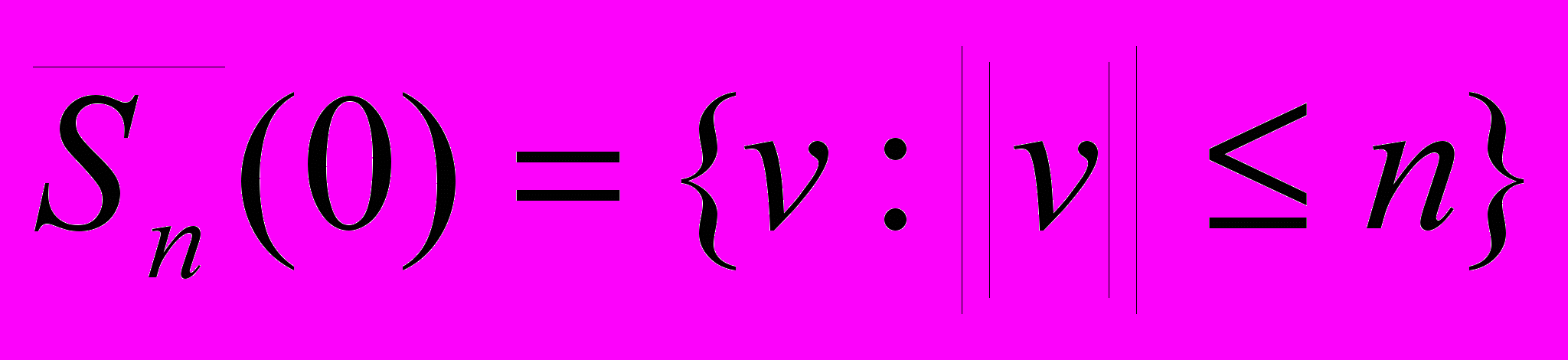. Его образ при действии оператора B 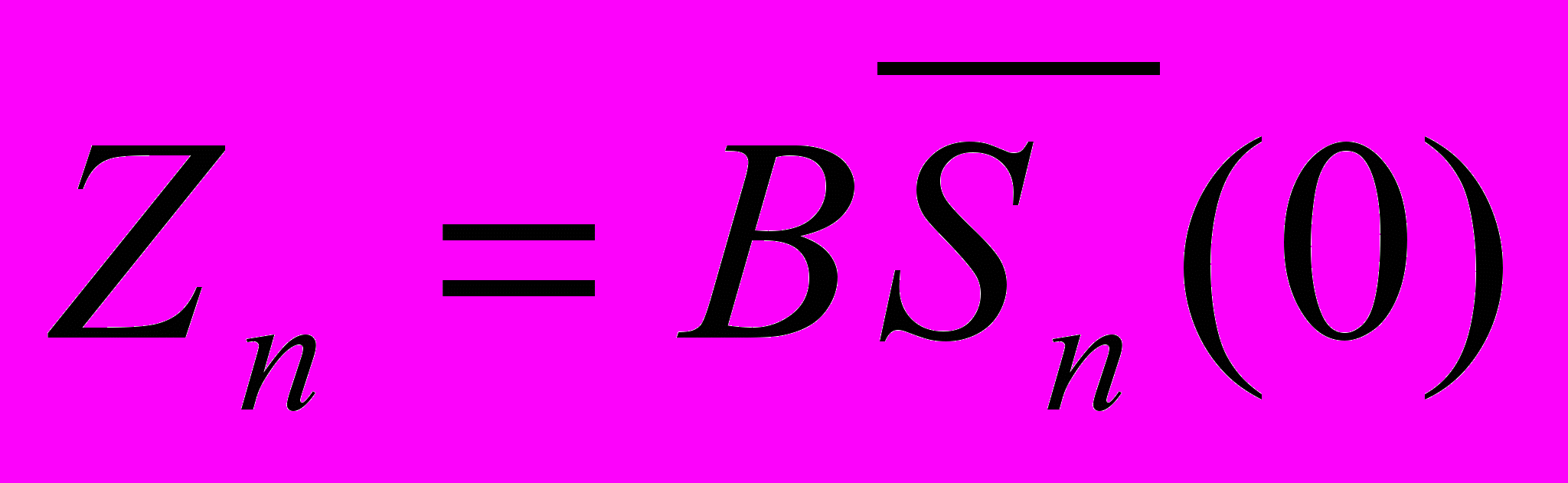является компактом, поскольку - вполне непрерывный оператор, а V –гильбертово пространство. Далее отыскивается 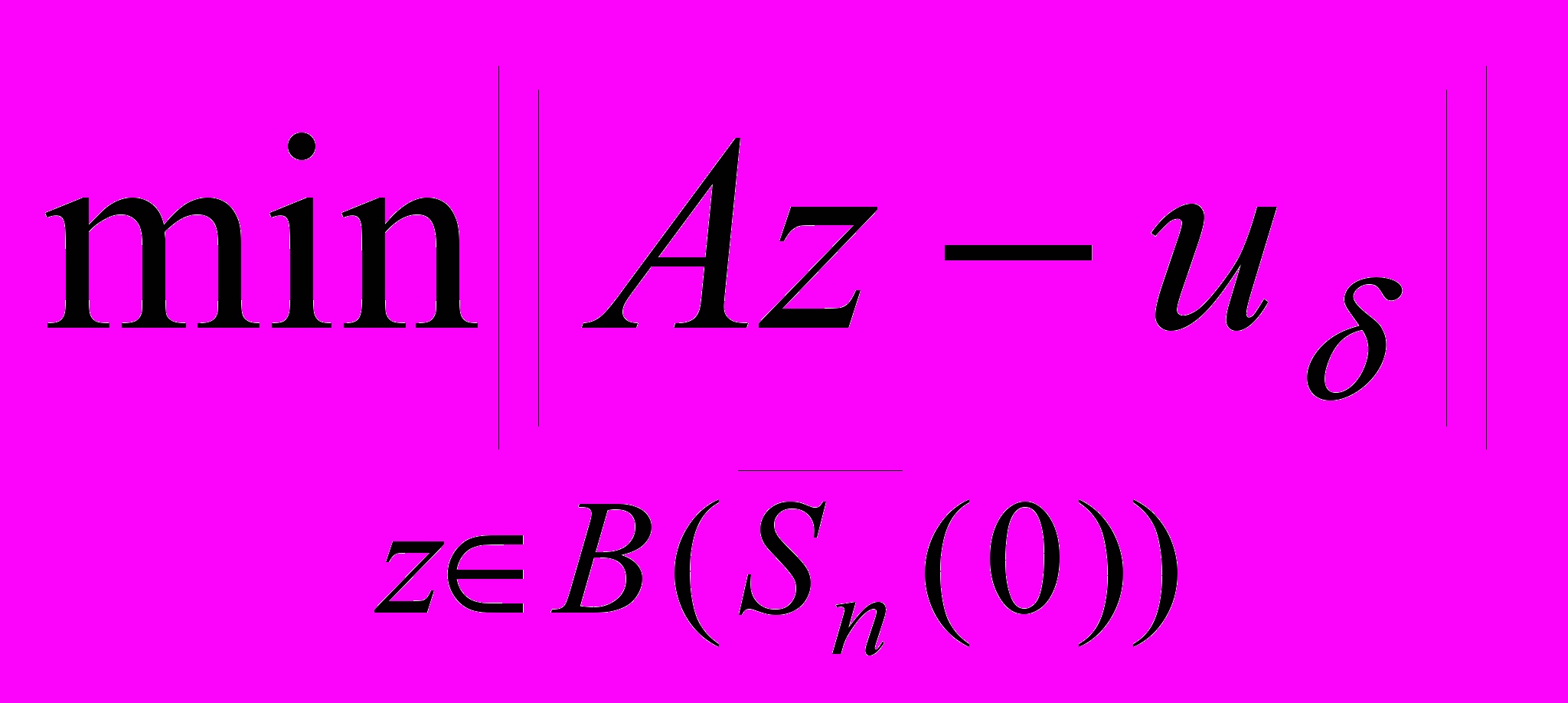, где 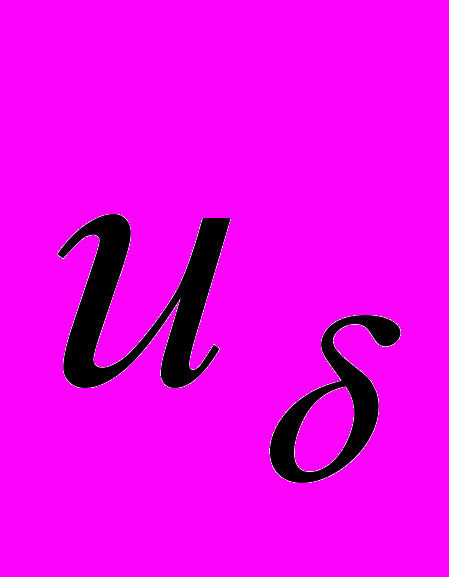- заданная неточная правая часть 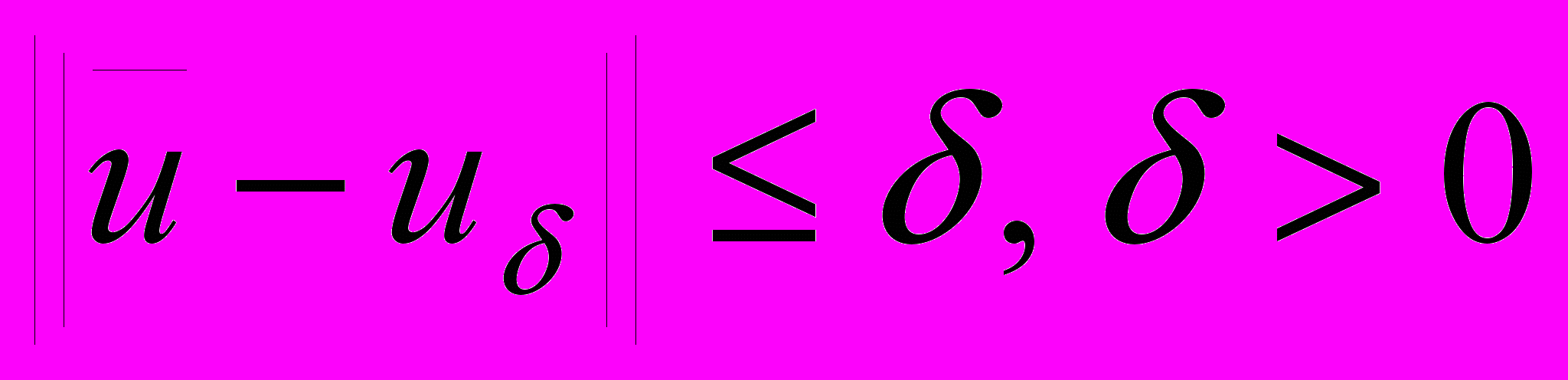. Существование минимума гарантируется постановкой задачи – компактностью 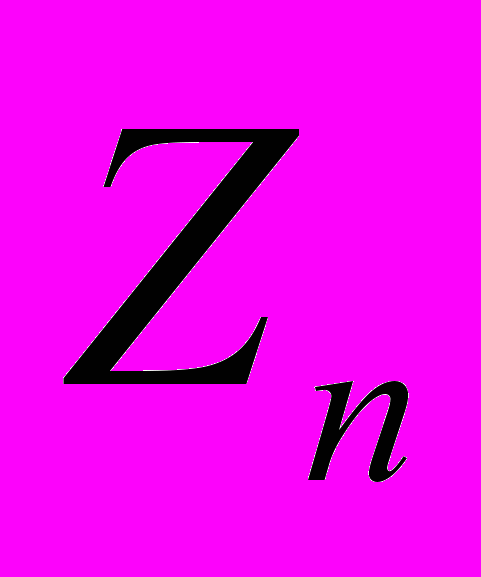и непрерывностью A. Если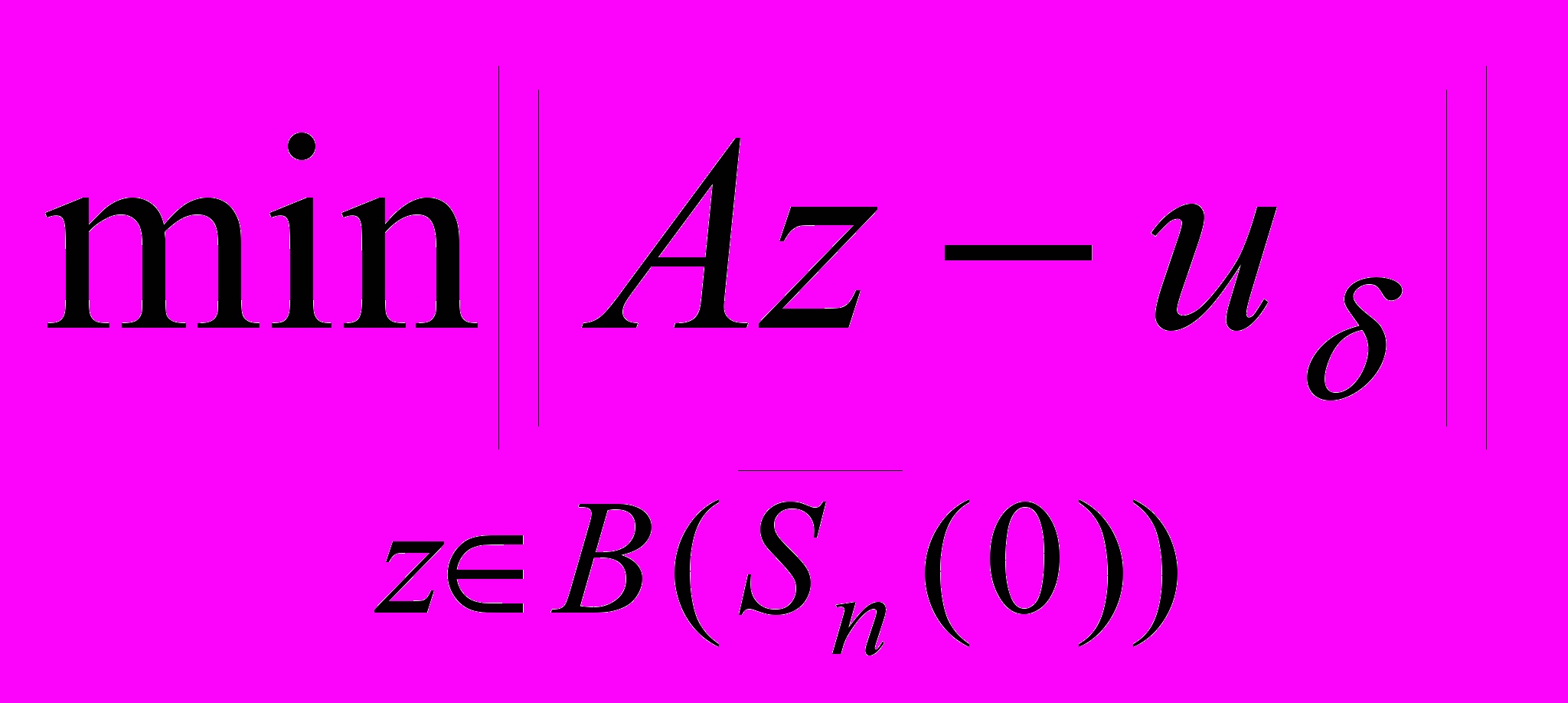 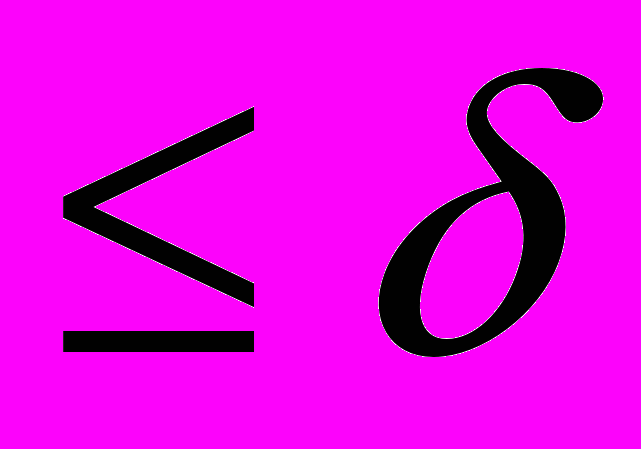, тогда процесс прекращается, полагается 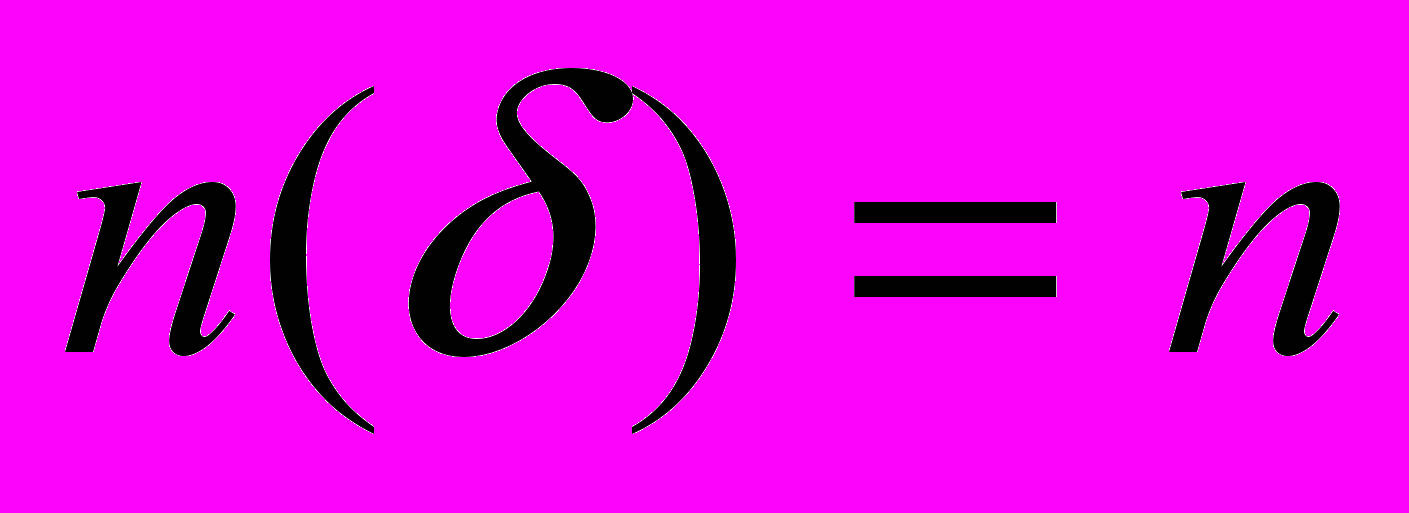, а в качестве приближенного решения выбирается любой элемент и . Если же , то нужно расширять компакт, для чего n увеличивается на единицу, процесс повторяется.

Теорема. Описанный выше процесс сходится: 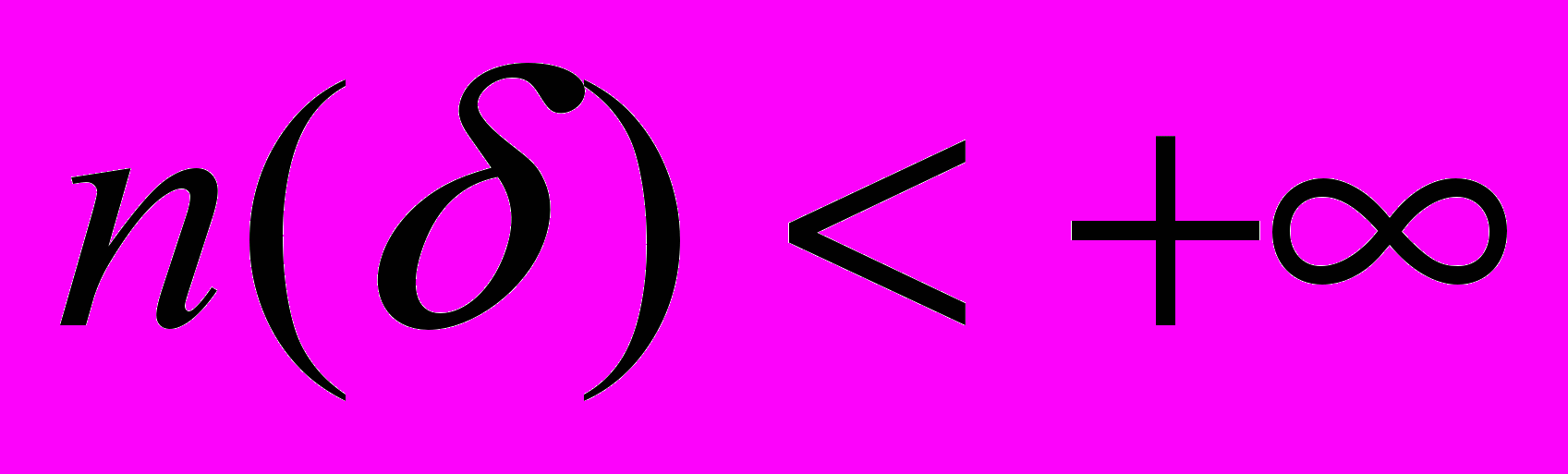. Существует 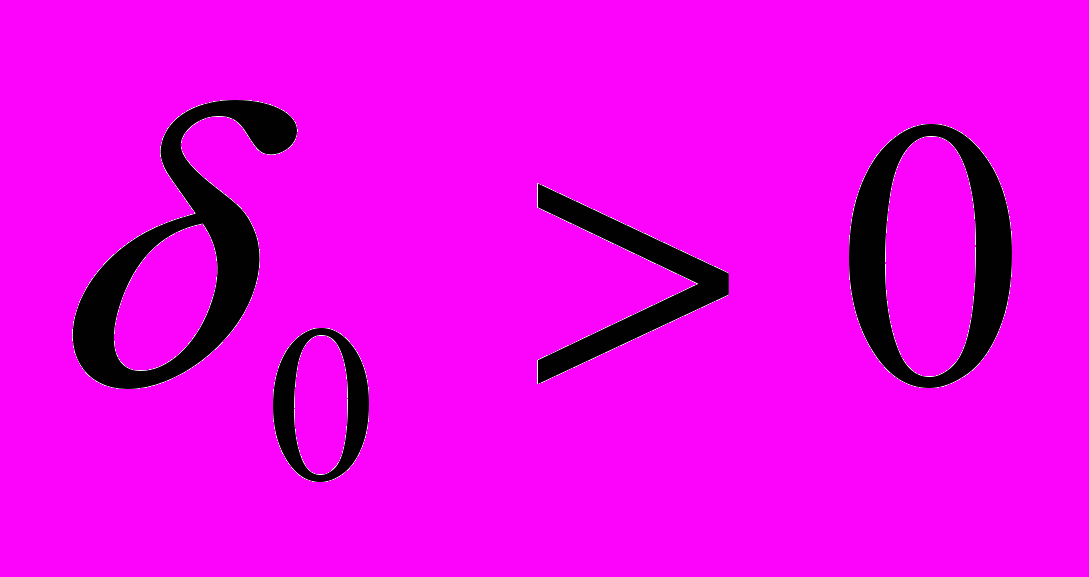(которое, вообще говоря, зависит от ) такое, что 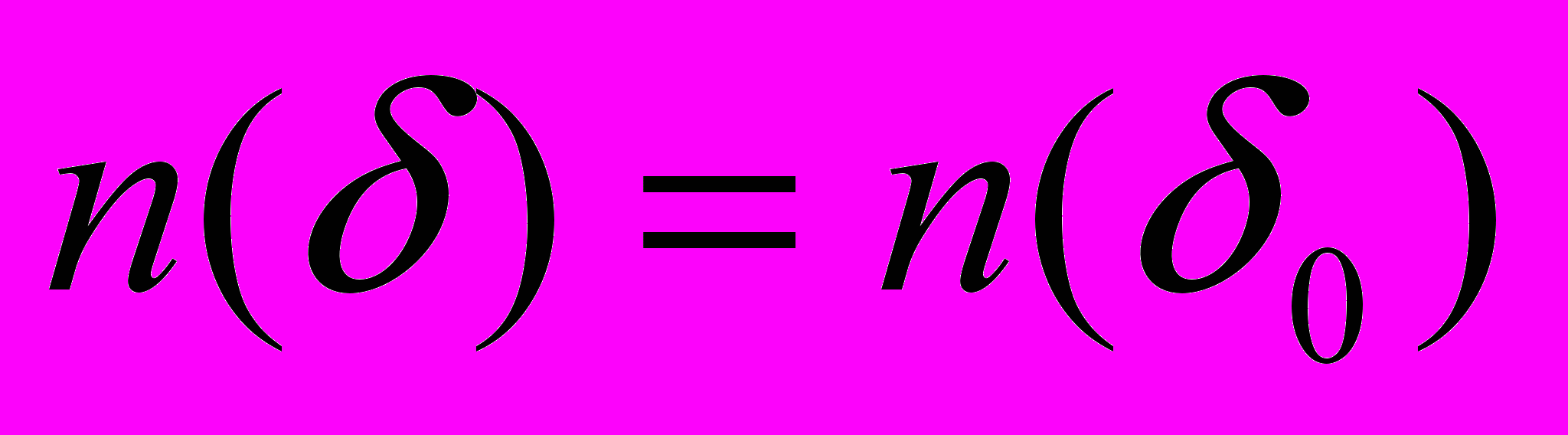. Приближенное решение сходится к точному решению при .

Из сказанного выше понятно название метода. Оказывается, этот метод допускает возможность построения так называемой апостериорной оценки погрешности, т.е. существует функция 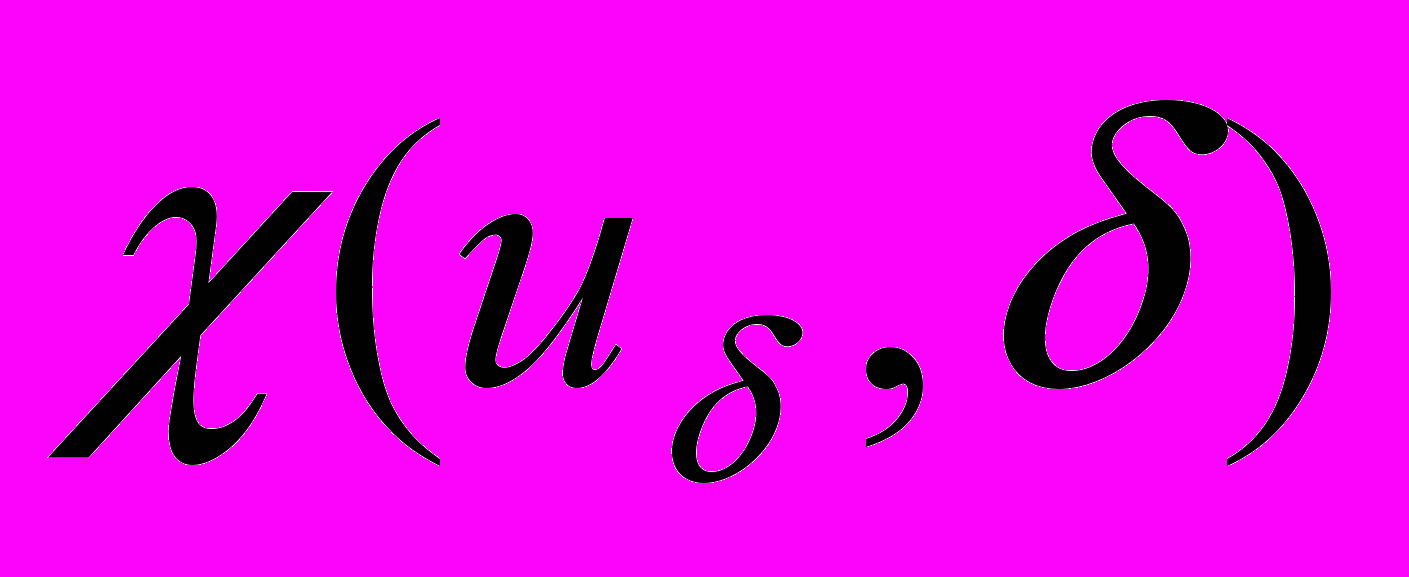такая, что 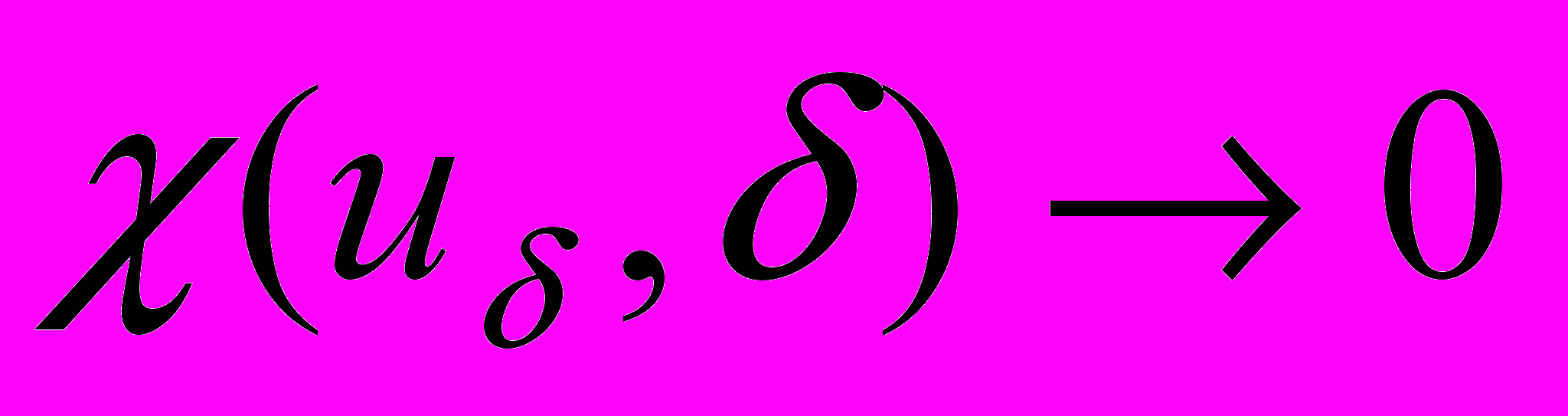при , и по крайней мере, при достаточно малых . В качестве апостериорной оценки погрешности можно взять .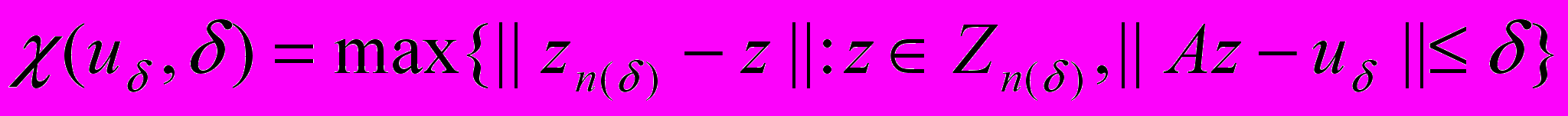

Апостериорная оценка погрешности не является оценкой погрешности в полном смысле слова, построение оценки погрешности решений некорректно поставленных задач невозможно. Однако при достаточно малых (а именно ) апостериорная оценка погрешности является оценкой погрешности решения некорректной задачи при наличии априорной информации об истокопредставимости.

Данный подход легко обобщается на случаи, когда операторы A и B заданы с погрешностями, а также на нелинейные некорректные задачи с условием истокопредставимости.

Разработаны численные методы решения линейных некорректных задач при условии истокопредставимости, в том числе и построения апостериорной оценки погрешности. Использование последовательности натуральных чисел в качестве радиусов шаров в пространстве V не обязательно. Может быть взята любая монотонно возрастающая неограниченная последовательность положительных чисел.


Практические приложения. Методы решения некорректных задач на компактных множествах специальной структуры (монотонных функций, выпуклых функций, монотонных выпуклых функций), а также при условии истокопредставимости, были эффективно применены для решения некорректных задач астрофизики, физической химии, электронной микроскопии и др. Эти методы могут применяться в геофизике, например, для решения обратной задачи гравиметрии на множестве выпуклых тел.

На рисунке приведен пример решения обратной задачи для двумерного уравнения теплопроводности при условии, что начальная температура является двумерной вогнутой функцией. В этом случае можно не только найти приближенное решение, но и функции, определяющие погрешность этого решения в соответствии с погрешностью входных данных и разностной аппроксимацией. Функция, ограничивающая решение сверху и показана на рисунке.




Работа выполнена при поддержке РФФИ, проекты 08-01-00160-а, 07-01-92103-ГФЕН_а.

Список литературы

1. Иванов В. К., Васин В. В., Танана В. П. Теория линейных некорректных задач и ее приложения. М.: Наука, 1978.
   
2. Тихонов А. Н., Гончарский А. В., Степанов В. В., Ягола А. Г. Численные методы решения некорректных задач. М.: Наука, 1990.
   
3. Dorofeev K. Yu., Nikolaeva N. N., Titarenko V. N., Yagola A. G. New approaches to error estimation to ill-posed problems with application to inverse problem of heat conductivity// Journal of Inverse and ill-posed Problems. 2002, Vol. 10, pp. 155-170.
   
4. Николаева Н.Н., Титаренко В.Н., Ягола А.Г. Оценка погрешности решения уравнения Абеля на множествах монотонных и выпуклых функций// Сибирский журнал вычислительной математики, 2003, т. 6, № 2, с. 171-180.
   
5. Titarenko V., Yagola A. Linear ill-posed problems on sets of convex functions on two-dimensional sets//J. of Inverse and Ill-Posed Problems, 2006, v. 14, No 7, pp. 735-750.
   
6. Yagola A., Titarenko V. Using a priori information about a solution of an ill-posed problem for constructing regularizing algorithms and their applications//Inverse Problems in Science and Engineering, 2007, v. 15, No 1, pp. 3 – 17.