Варианты заданий 37 Контрольные вопросы к защите ргр: 39

Вид материала

Контрольные вопросы

Содержание

Порядок выполнения работы
ПРИМЕР выполнения расчетно-графической РАБОТЫ

Подобный материал:

1 2 3 4 5 6 7 8

Порядок выполнения работы

Содержание работы (с указанием страниц).
Задание на расчетно-графическую работу.
Теоретическая часть. Основные понятия методов сортировки, их назначение, определение эффективности сортировки.
Практическая часть работы (все этапы работы выполняются для обоих методов сортировки):
1. Словесное описание алгоритма сортировки.
2. Блок-схема алгоритма.
3. Подпрограмма, реализующая данный алгоритм сортировки.
4. Анализ эффективности сортировки (по количеству сравнений и перестановок).
5. Протокол выполнения подпрограммы, который включает в себя, входной массив и упорядоченный массив;
График зависимости количества сравнений от длины массива (20, 40, 60, … 200 элементов) для обоих методов сортировки, в том числе для модифицированной сортировки построить график исходного метода.
Анализ эффективности обоих методов и модифицированного метода с исходным по графическим результатам.
Приложение (листинг программы).

ПРИМЕР выполнения расчетно-графической РАБОТЫ

Содержание:

	Задание	2
	Понятие сортировки, ее назначение, эффективность	2
	Сортировка подсчетом	3
	Пузырьковая сортировка	6
	График зависимости от длины массива	8
	Анализ эффективности методов сортировки	8
	Листинг программы	9

Задание:

Изучить основные методы сортировки. Разработать алгоритмы сортировки подсчетом и пузырьковой сортировки. Оценить эффективность метода в зависимости от длины массива. Построить график зависимости от длины массива (20,40,60,80,…200 элементов).

Сортировка подсчетом (по неубыванию)

Алгоритм сортировки подсчетом состоит в следующем:

У нас имеется массив некоторых чисел. Начинаем сравнение первого элемента с остальными и подсчитываем количество тех элементов, которых он больше или равен. Записываем этот элемент в новый массив по адресу: количество + 1. Затем переходим на следующий элемент и так далее.

Блок-схема сортировки подсчетом:

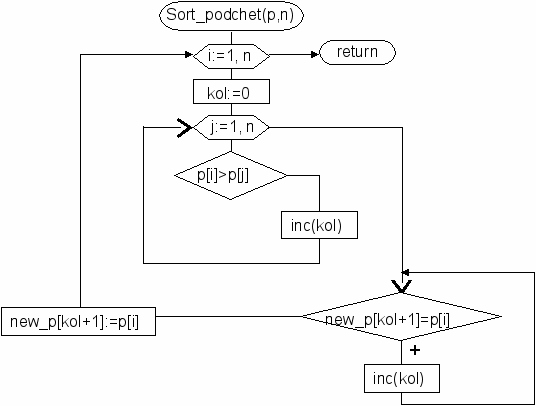
Процедура сортировки подсчетом:

procedure sort_podchet(p:mas; n:integer);

var i,j,kol:integer; new_p:mas;

begin

for i:=1 to n do

begin

kol:=0;

for j:=1 to n do

if p[i]>=p[j] then inc(kol);

while new_p[kol+1]=p[i] do

inc(kol);

new_p[kol+1]:=p[i];

end;

end;

Протокол выполнения подпрограммы:

Массив чисел:

-14 21 -13 -12 -12 22 8 -15 12 -15 4 -18 -21 -16 -4 0 -11 6 13 9

Упорядоченный по неубыванию массив:

-21 -18 -16 -15 -15 -14 -13 -12 -12 -11 -4 0 4 6 8 9 12 13 21 22

Эффективность сортировки подсчетом:

Эффективность сортировки подсчетом по количеству сравнений имеет квадратичный порядок, так как для каждого из N элементов выполняется N сравнений, C=N*N=Θ(N²). При этом и в худшем и в лучшем случае, когда все элементы уже упорядочены, количество сравнений неизменно – N² .

Количество перестановок и в худшем и в лучшем случае равно длине массива N, то есть эффективность алгоритма по перестановкам имеет линейную сложность.

Пузырьковая сортировка (по неубыванию)

Пузырьковая сортировка является одной из основных методов квадратичных сортировок. В основе этого метода лежит последовательное сравнение двух соседних элементов и их перестановке по необходимости. Поэтому эта сортировка называется сортировкой простым обменом. При первом обходе в конец массива переместится наибольший элемент массива. Сократив длину массива на 1 элемент с конца, повторяем процедуру обхода. В итоге в конец переместится следующий элемент и т.д. Повторение процедуры обхода продолжается до тех пор, пока длина массива не будет равна 2 элементам.

Блок-схема пузырьковой сортировки:

+

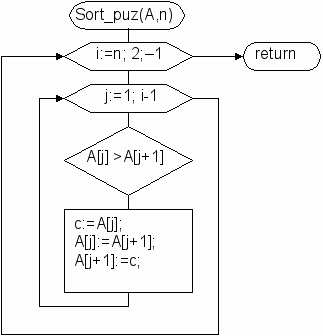
Процедура пузырьковой сортировки:

procedure sort_puz(A:mas; n:integer);

var

c,i,j:integer;

begin

for i:=n downto 2 do

for j:=1 to i-1 do

if A[j]>=A[j+1] then

begin

c:=A[j];

A[j]:=A[j+1];

A[j+1]:=c;

end;

end;

Протокол выполнения подпрограммы

Массив чисел:

-22 -19 17 -25 -18 23 24 3 -4 3 -11 -2 19 13 -20 -21 -15 -16 15 -16

Упорядоченный по неубыванию массив:

-25 -22 -21 -20 -19 -18 -16 -16 -15 -11 -4 -2 3 3 13 15 17 19 23 24

Эффективность пузырьковой сортировки:

При сортировке методом «пузырька» выполняется (N-1) просмотров, на каждом i-ом просмотре производится (N-1) сравнений. Общее количество C=N*(N-1)/2= Θ(N²).

Количество перестановок в худшем случае равно

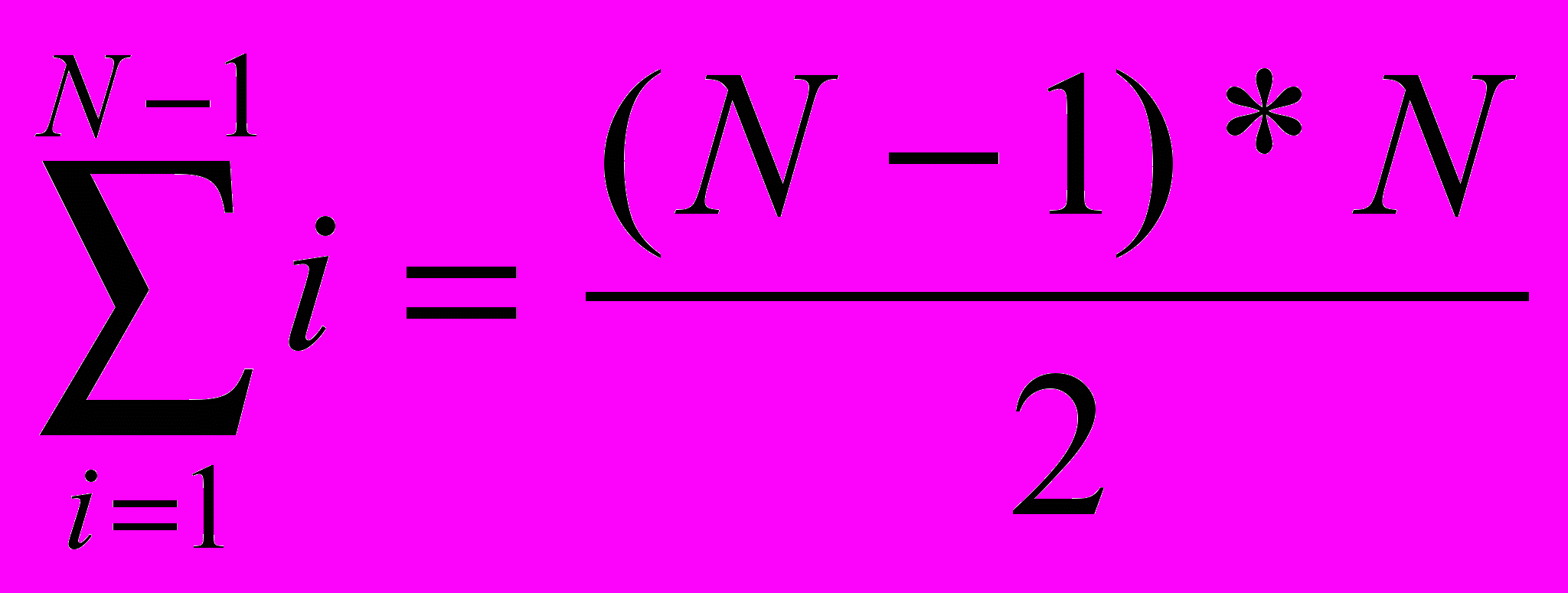=N², в лучшем – 0. Таким образом, сортировка и по перестановкам имеет квадратичную сложность.

График зависимости количества сравнений от длины массива:

Массив сравнений сортировки подсчетом:

400 1600 3600 6400 10000 14400 19600 25600 32400

Массив сравнений пузырьковой сортировки:

190 780 1770 3160 4950 7140 9730 12720 16110

------------------------------------------------

Press any key...

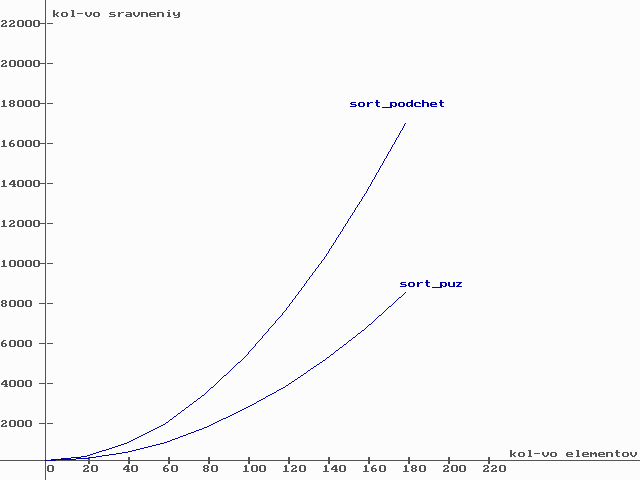
Анализ эффективности:

График подтверждает квадратичную сложность обеих сортировок от количества сравнений. Из графика видно, что количество сравнений при одинаковом количестве элементов массива при пузырьковой сортировке меньше, чем при сортировке подсчетом. Причем, с ростом длины массива, количество сравнений пузырьковой сортировки меньше почти в два раза. Следовательно, пузырьковая сортировка значительно эффективнее, нежели сортировка подсчетом.

Листинг программы:

program rgr_past;

uses crt,graph;

type mas=array[1..200] of integer;

var y1,y2,z:mas;

n,i,dr,mode,x,y,k,l:integer;

st:string;

srav:longint;

procedure next_list;

var key:char;

begin

writeln;

writeln('Press any key...');

key:=readkey;

if key<>' ' then clrscr;

end;

procedure zapoln(var z:mas; n:integer);

var i:integer;

begin

randomize;

for i:=1 to n do

z[i]:=random(100)-25;

end;

function sort_podchet(p:mas; n:integer):longint;

var i,j,kol:integer; new_p:mas; sr:longint;

begin

sr:=0;

for i:=1 to n do begin

kol:=0;

for j:=1 to n do

begin

inc(sr);

if p[i]>=p[j] then inc(kol);

end;

while new_p[kol+1]=p[i] do inc(kol);

new_p[kol+1]:=p[i];

end;

sort_podchet:=sr;

end;

function sort_puz(A:mas; n:integer):longint;

var c,i,j:integer; sravn:longint;

begin

sravn:=0;

for i:=n downto 2 do

for j:=1 to i-1 do

begin

inc(sravn);

if A[j]>=A[j+1] then begin

c:=A[j];

A[j]:=A[j+1];

A[j+1]:=c;

end;

sort_puz:=sravn;

end;

procedure Graphik (var m:Mas;st:string);

begin

n:=40;

setcolor(1);

moveto(45,460);

for i:=1 to 9 do begin

x:=45+n;

y:=round(460-m[i]/96);

lineto(x,y);

n:=n+40;

end;

outtext(st);

end;

BEGIN

clrscr;

n:=0;

for i:=1 to 9 do

begin

n:=n+20;

zapoln(z,n);

y1[i]:= sort_podchet(z,n);{заполнение массива сравнений при сортировке подсчетом}

y2[i]:= sort_puz(z,n); {заполнение массива сравнений при пузырьковой сортировке }

end;

writeln('Массив сравнений сортировки подсчетом:':60);

writeln;

for i:=1 to 9 do write(y1[i]:4,' ');

writeln;

writeln;

writeln('Массив сравнений пузырьковой сортировки:':60);

writeln;

for i:=1 to 9 do write(y2[i]:4,' ');

writeln;

write('------------------------------------------------');

next_list;

{подключение графического режима}

dr:=detect;

initgraph(dr,mode,'C:\BP\BGI');

if GraphResult<>0 then halt;

{вывод координатных осей }

setcolor(8);

setbkcolor(15);

line(45,0,45,getmaxY);

line(0,460,getmaxX,460);

OutTextXY(53,10,'kol-vo sravneniy');

OutTextXY(510,450,'kol-vo elementov');

moveto(47,465);

OutText('0');

x:=45+40;

y:=460-40;

k:=0;

{ отметка координатных точек осей}

while x<=520 do begin

OutTextXY(x,457,'|');

k:=k+20;

str(k,st);

outtextxy(x-2,465,st);

x:=x+40;

end;

k:=0;

while y<=520 do begin

OutTextXy(39,y,’—’);

k:=k+2000;

str(k,st);

OutTextXY(1,y,st);

y:=y-40;

end;

{построение графика сравнений подсчетом}

Graphik(y1,'sort_podchet');

{построение графика сравнений пузырька}

Graphik (y2, 'sort_puz');

readln;

closegraph;

readkey;

end.

Blog

Варианты заданий 37 Контрольные вопросы к защите ргр: 39

Содержание

Порядок выполнения работы

ПРИМЕР выполнения расчетно-графической РАБОТЫ