Geum.ru

Варианты заданий 37 Контрольные вопросы к защите ргр: 39

Вид материалаКонтрольные вопросы

Содержание


Сортировка простым выбором
Подобный материал:
1   2   3   4   5   6   7   8

Сортировка простым выбором


Идея сортировки выбором заключается в поиске максимального элемента и вставки его в конец массива. Затем длина массива уменьшается на один элемент («водворенный на свое место» исключается) и процедура повторяется снова. Алгоритм сортировки выполняется до тех пор, пока длина сортируемого массива не станет равна двум элементам.

Пример 2

Пример сортировки по возрастанию массива чисел М={5, 13, 7, 9, 18, 16}.

1 шаг. Длина массива N=6. Найдем максимальный элемент массива:

5
13
7
2
1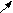8
16

max

Он находится на 5-ой позиции и равен 18. Поменяем местами максимальный элемент с последним элементом массива.

5
13
7
2
16
18

В результате число 18 встало на «свое место».


2 шаг. Рассмотрим часть массива без последнего, стоящего на своем месте элемента, то есть длина массива (N-1)=5. И снова найдем максимальный элемент.

5
13
7
2
1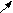6
18

max

16 уже стоит на своем месте. Его меняем с самим с собой.


3 шаг.

5
1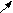3
7
2
16
18

max

5
2
7
13
16
18



4 шаг.

5
2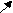
7
13
16
18

max

5
2
7
13
16
18


5 шаг.

5
2
7
13
16
18

max

2
5
7
13
16
18

Если учитывать тот факт, что максимальный элемент в некоторых случаях уже стоит на «своем месте» и не выполнять перестановку элемента с самим собой, то эффективность и быстродействие сортировки улучшится. Для этого сравним индекс максимального элемента с индексом текущего «последнего» элемента.


Блок-схема сортировки простым выбором:




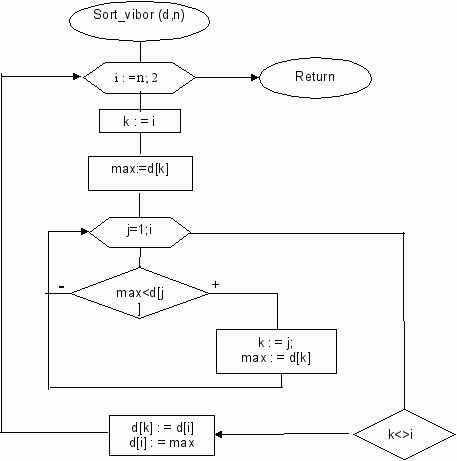
Процедура сортировки простым выбором:


procedure sort_vibor (var d:array of integer; n:integer);

var k,max:integer;

begin

for i:=n downto 2 do {регулируется длина массива}

begin

k:=i; max:=d[k]; {последний элемент объявляется максимальным}

for j:=1 to i-1 do {в цикле все остальные элементы массива

if maxсравниваются с максимальным}

k:=j;

max:=d[k];

end;

{проверка необходимости перестановки}

if k<>i then begin

d[k]:=d[i];

d[i]:=max;

end;

end;

end;


Алгоритм содержит N-1 шагов. На каждом шаге производится поиск максимального значения посредством сравнения каждого элемента с максимумом, то есть (N-i) сравнений. Всего количество сравнений 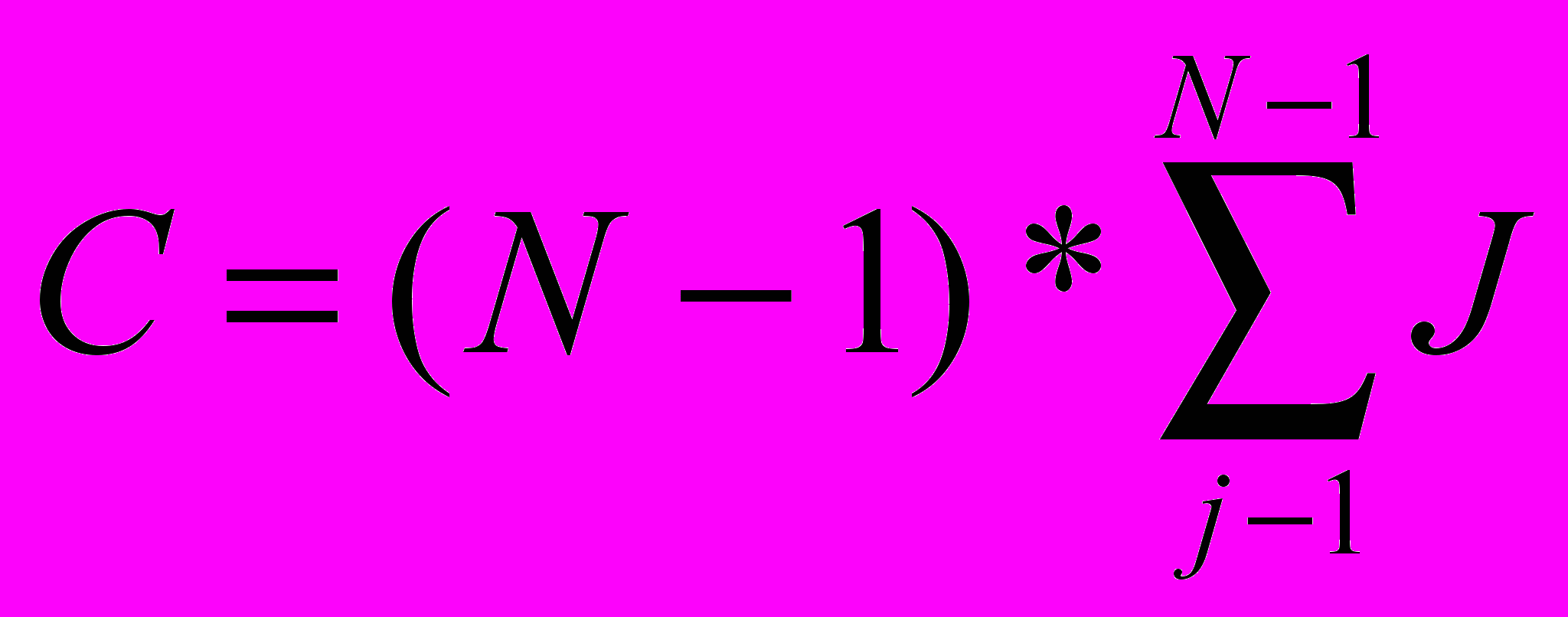. Так как сумма чисел от 1 до N определяется по формуле 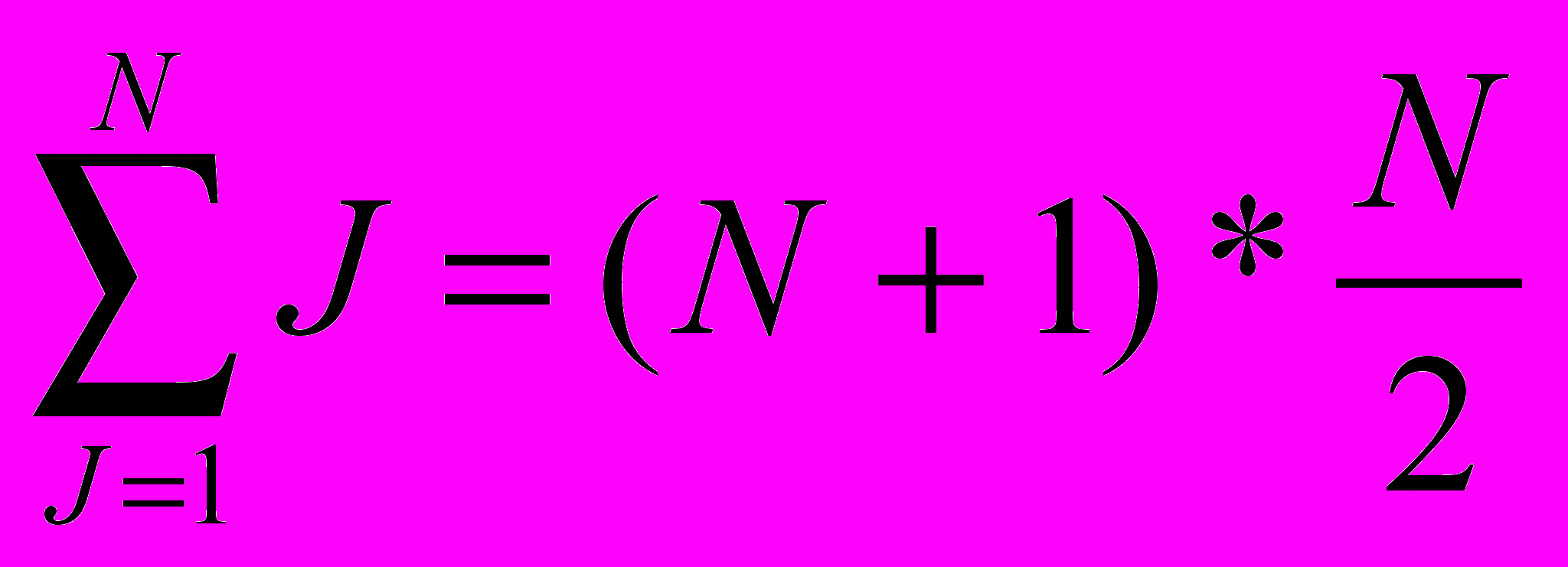, то C=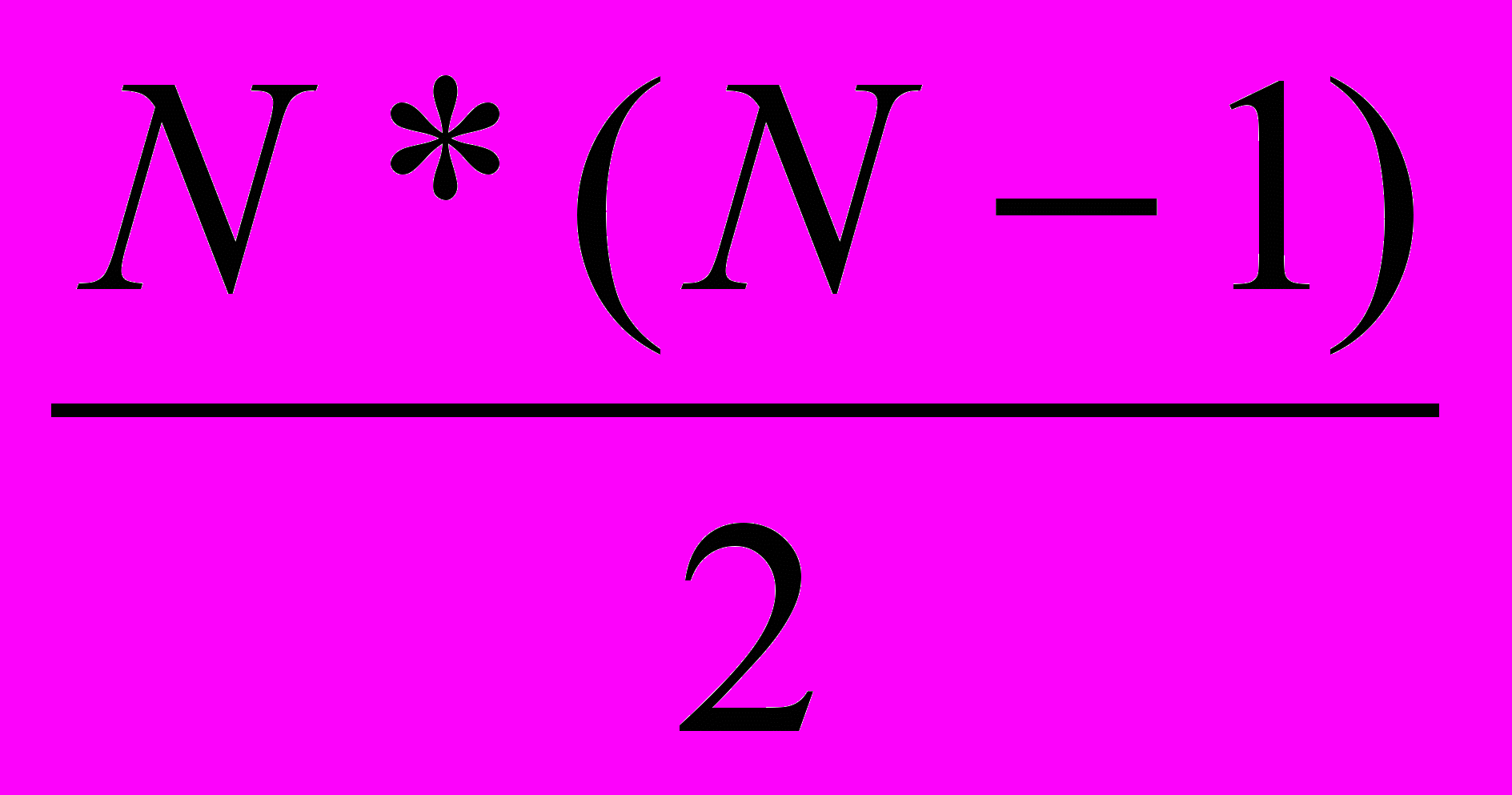= Θ (N2).

Эффективность по количеству перестановок в худшем случае равна N-1, в лучшем случае – 0.