Geum.ru

Варианты заданий 37 Контрольные вопросы к защите ргр: 39

Вид материалаКонтрольные вопросы

Содержание


Сортировка простым обменом («Пузырьковая сортировка»)
Шейкерная сортировка
Быстрая сортировка
Сортировка слиянием
Подобный материал:
1   2   3   4   5   6   7   8

Сортировка простым обменом («Пузырьковая сортировка»)


Сортировка обменом основана на многократном обходе массива чисел a1, a2,… an. При каждом обходе сравниваются два соседних элемента ai и ai+1. Если элементы неупорядочены, то они меняются местами. В следствие последовательных перестановок, например, при упорядочивании массива по возрастанию, постепенно продвигается вправо и становится на свое место максимальный элемент массива. При втором обходе – длина массива уменьшается на 1 (исключается последний элемент) и процесс повторяется. Последний обход выполняется для массива из 2 элементов.

Пример 5

Отсортировать массив чисел M={5, 4, 8, 2, 9} по возрастанию.


1-ый просмотр. Рассматривается весь массив.

{i - номер первого элемента проверяемой (сравниваемой) пары}.

i=1
5
>
4



8



2



9

меняем местами

i=2
4



5
<
8



2



9

не меняем

i=3
4



5



8
>
2



9

меняем

i=4
4



5



2



8
<
9

не меняем

Число 9 встало на свое место и в последующих просмотрах его можно не рассматривать.


2-ой просмотр. Рассматривается весь массив, с первого элемента до предпоследнего.

i=1
4
<
5



2



8



9

не меняем

i=2
4



5
>
2



8



9

меняем

i=3
4



2



5
<
8



9

не меняем

Число 8 также встало на свое место. Говорят, «всплыл» еще один «пузырек».


3-ий просмотр. Рассматривается часть массива без последних двух элементов.

i=1
4
>
2



5



8



9

меняем

i=2
2



4
<
5



8



9

не меняем

Число 5 встало на свое место.


4-ый просмотр. Рассматривается последняя пара элементов.

i=1
2
<
4



5



8



9

не меняем

В итоге имеем отсортированный массив:

2



4



5



8



9


Блок-схема сортировки простым обменом:




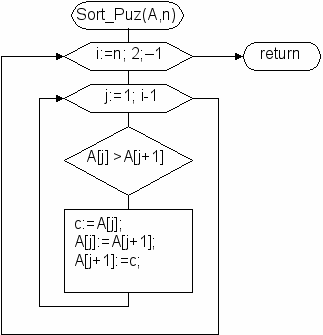
Процедура сортировки простым обменом:


procedure sort_puz(A:array of integer; n:integer);

var c,i,j:integer;

begin

for i:=n downto 2 do

for j:=1 to i-1 do

if A[j]>A[j+1] then begin

c:=A[j];

A[j]:=A[j+1];

A[j+1]:=c;

end;

end;


При сортировке методом «пузырька» выполняется (N-1) просмотров, на каждом i-ом просмотре производится (N-1) сравнений. Общее количество C=N*(N-1)/2= Θ(N2).

Сортировку простым обменом можно усовершенствовать, если фиксировать перестановки на каждом проходе и, если на очередном проходе не было ни одной перестановки (массив уже отсортирован и последующие проходы со сравнениями будут “холостыми”), сортировку прекратить. Например, массив чисел 6, 5, 1, 14, 3, 7 при сортировке по возрастанию методом простого обмена будет упорядочен уже после 3-го прохода.

Шейкерная сортировка


Шейкерная сортировка является модификацией пузырьковой сортировки. Она заключается в чередовании последовательных просмотров слева направо и наоборот, справа налево, при этом фиксируется количество перестановок. Если количество перестановок на очередном просмотре равно 0, массив упорядочен и, следовательно, процесс сортировки можно закончить.

Пример 6

Сортировка по возрастанию массива чисел М ={13,2,6,66,51,19,3,11,34,20}.

1 проход (прямой, ).

1
2
3
4
5
6
7
8
9
10

13
2
6
66
51
19
3
11
34
20



При первом обходе (слева направо) как при обычной «пузырьковой сортировке» встанет на «свое» место максимальный элемент массива.

1
2
3
4
5
6
7
8
9
10

2
6
13
51
19
3
11
34
20
66

Количество перестановок k=8.


2 проход (обратный, ). Уменьшив длину массива, выполним проход в обратном направлении.

1
2
3
4
5
6
7
8
9

2
6
13
51
19
3
11
34
20


В результате перестановок «всплывет» еще один «пузырек».

1
2
3
4
5
6
7
8
9

2
3
6
13
51
19
11
20
34

Количество перестановок k=5.


3 проход (). Продолжаем обход слева направо без 1–го элемента (он уже стоит на «своем месте»).

2
3
4
5
6
7
8
9

3
6
13
51
19
11
20
34




На выходе:

2
3
4
5
6
7
8
9

3
6
13
19
11
20
34
51

K=4.

4 проход ( ).

2
3
4
5
6
7
8

3
6
11
13
19
20
34

К=2

5 проход ().

3
4
5
6
7
8

6
11
13
19
20
34

Количество перестановок k = 0, значит, массив упорядочен и процесс можно прекратить.

Быстрая сортировка


Реализация данного метода сортировки основывается на рекурсивном вызове процедуры упорядочивания. Она была разработана в 1962 году профессором Оксфордского университета К.Хоаром.

Быстрая сортировка основывается на принципе «разделяй и властвуй» и является улучшенной модификацией пузырьковой сортировки. Сначала берется весь массив и частично упорядочивается особенным образом: выбирается серединный элемент, назовем его ключом, а остальные элементы упорядочиваются относительно этого ключа так, чтобы слева располагались элементы меньшие ключа (если массив сортируется по возрастанию), а справа – большие. В итоге ключевой элемент встает на «свое место». Затем к левой и правой частям (относительно ключа) применяется этот же метод, то есть выбирается новый ключ и упорядочивание подмассива относительно его. И так до тех до тех пор, пока каждая из частей не будет содержать ровно один элемент.

Пример 7

Рассмотрим работу данного метода на примере сортировки массива А={6, 23, 17, 8, 14, 25, 6, 3, 30, 7} по возрастанию.


Выбирается серединный элемент массива – key=A[5]=14. Просматривая левую часть массива (слева направо) найдем элемент, больший key, а в правой части ищем элемент (двигаясь справа налево), меньший key. Затем эти элементы меняем местами.

(i,j- индексы левой и правой половины соответственно)

i=2 j=10

6 23 17 8 14 25 6 3 30 7


Продолжаем поиск элементов для перестановки:

i=3 j=8

6 7 17 8 14 25 6 3 30 23


i=5 j=7

6 7 3 8 14 25 6 17 30 23




i=6 j=7

6 7 3 8 6 25 14 17 30 23


i=j=6

6 7 3 8 6 25 17 30 23


В итоге ключевой элемент стоит на «своем месте», т.е. всплыл первый «пузырек». Слева (с 1-го по 5-ый элемент) и справа (с 7-го по 10-ый) от ключа элементы еще не упорядочены, применим к ним тот же метод, вызвав процедуру быстрой сортировки. Это уже будет второй уровень рекурсии.

Блок-схема быстрой сортировки:





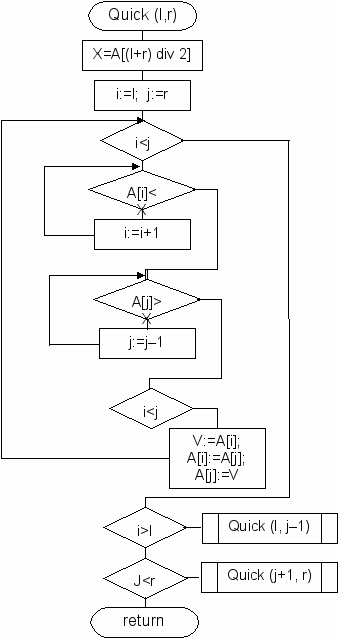
Процедура быстрой сортировки:


procedure quick(var A:array of integer; l,r:integer);

var X,i,j, V:integer;

begin

X:=A[(l+r)div 2];

i:=l; j:=r;

while (i
begin

while A[i]
while A[j]>X do dec(j);

If i
V:=A[i];

A[i]:=A[j];

A[j]:=V;

end;

end;

if i>l then quick(A,l,j-1);

if j
end;


Оценим эффективность метода быстрой сортировки. На каждом шаге делим массив на две части, для каждой из этих частей – N/2 сравнений (всего – 2*N/2=N), затем на 2-ом шаге снова делим, получаем N/4 сравнений (4*N/4=N) и т.д. Так как глубина рекурсии (количество разбиений) равна Log2N, а количество сравнений на каждом уровне – N, то сложность алгоритма С = Θ (N*logN).

Сортировка слиянием


Сортировка слиянием основывается на рекурсивном делении массива пополам на два подмассива до тех пор пока каждый подмассив не будет состоять из одного элемента и затем постепенном объединении (слиянии) подмассивов в один упорядоченный.

Для слияния двух (упорядоченных на предыдущих рекурсивных итерациях) подмассивов понадобится новый массив, в который элементы из двух подмассивов будут «сливаться» уже в отсортированном виде. Слияние осуществляется следующим образом. Сравниваются два элемента из «левого» и «правого» подмассивов. Тот элемент, который удовлетворяет признаку упорядочивания (т.е. меньший, если сортируем по возрастанию) записывается в новый упорядоченный массив. Затем снова сравниваются элементы из подмассивов и так до тех пор, пока в одном из подмассивов не останется выбранных элементов. Тогда из другого подмассива оставшиеся элементы переписываем в порядке их следования (они уже упорядочены).

Пример 8

Пример слияния двух упорядоченных по неубыванию массивов А={3, 5,12, 23} и B={2, 6, 9} в один массив.


(i,j- индексы массивов А и В соответственно)

i












j






3
5
12
23



2
6
9

Сравниваем первые элементы массивов: A[1]>B[1], следовательно в результирующий массив запишем элемент массива В: C[1]=B[1]:

С:
2



















Индекс массива В j наращивается и продолжается сравнение элементов двух подмассивов:

i















j



3
5
12
23



2
6
9




С:
2
3















Наращивается индекс i:
i












j



3
5
12
23



2
6
9




С:
2
3
5












Продолжая процесс, сравниваем следующие элементы массивов. Элемент 5 идет в новый массив и снова наращивается индекс i.



i









j



3
5
12
23



2
6
9




С:
2
3
5
6









Следующее сравнение:



i












j

3
5
12
23



2
6
9




С:
2
3
5
6
9







Из правого массива выбраны все элементы, значит из левого массива по порядку переписываем оставшиеся элементы. В итоге имеем упорядоченный по возрастанию массив.

С:
2
3
5
6
9
12
23


Процедура сортировки слиянием рекурсивно делит массив на подмассивы до тех пор, пока каждый подмассив не будет содержать только один элемент, а затем вызывается процедура слияния двух подмассивов, в которую передаются левый и правый подмассивы.


Б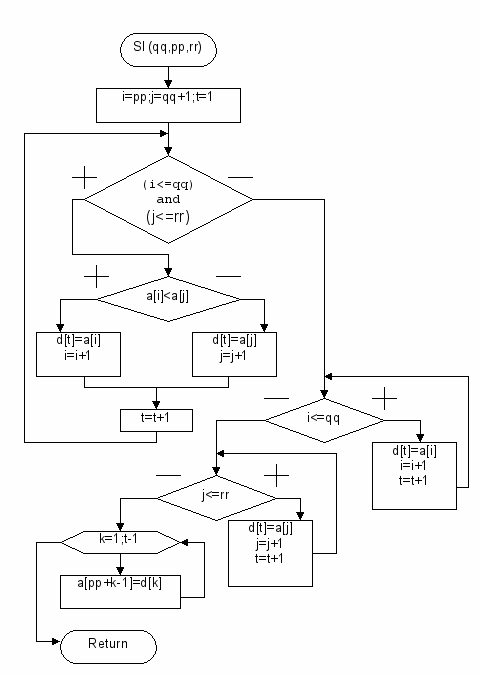лок-схема процедуры слияния двух подмассивов:


Процедура сортировки слиянием:


procedure sort_slij(var a:array of integer; p,r:integer);

var q:integer;

d:array[1..r]of integer;


{в процедуру слияния передаем начало и конец левого массива, конец правого}

procedure sl(pp,qq,rr:integer);

var t,i,j,k:integer;

begin

i:=pp;j:=qq+1;t:=1; {передача значений индексам массивов }

{i – индекс левого массива}

{j – индекс правого массива}

{t – индекс нового массива}

while (i<=qq)and(j<=rr)do

begin

if a[i]
d[t]:=a[i];

inc(i);

end

else begin

d[t]:=a[j];

inc(j);

end;

inc(t);

end;

{Запись оставшихся элементов в новый массив}

while i<=qq do begin d[t]:=a[i];inc(i);inc(t) end;

while j<=rr do begin d[t]:=a[j];inc(j);inc(t) end;

{копирование элементов массива d в исходный массив а}

for k:=1 to t-1 do a[pp+k-1]:=d[k];

end;

{основная программа сортировки слиянием}

begin

if p
q:=(p+r) div 2;{деление пополам}

sort_slij(A,p,q); {вызов процедуры сортировки }

{для левой половины}

sort_slij(A,q+1,r); {вызов для правой половины}

sl(p,q,r); {вызов процедуры слияния}

end;

end;


В следствие того, что процедура вызывается для каждой половины при каждом рекурсивном вызове, эффективность сортировки, как и в быстрой сортировке имеет сложность порядка С= Θ (N*logN).