Geum.ru

Варианты заданий 37 Контрольные вопросы к защите ргр: 39

Вид материалаКонтрольные вопросы

Содержание


Сортировка простыми вставками
Подобный материал:
1   2   3   4   5   6   7   8

Сортировка простыми вставками


Сортировка вставками наиболее эффективна при частично отсортированном массиве. Пусть k первых элементов массива уже упорядочены по неубыванию. Берется (k+1)-ый элемент и размещается среди k первых элементов так, чтобы упорядоченность не нарушилась.

Пример 3

Пример сортировки массива М ={3, 6, 13, 1, 7, 0, 2} по возрастанию.


Для начала определим длину отсортированной части массива. Для этого будем сравнивать два соседних элемента.

1 п. К =1;

2 п. Пока m[k] < m[k+1] увеличиваем k на 1;


В результате имеем к=3, т.е. отсортированная по возрастанию часть массива состоит из трех элементов.

3
6
13
1
7
0
2


Упорядочим остальные элементы, последовательно вставляя их в отсортированную часть массива.


1 шаг. Вставим 4-ый элемент, назовем его ключом, в отсортированную часть массива, не нарушая упорядоченности. Поиск подходящего места осуществляется путем сравнивания ключа с соседом слева и постепенным продвижением ключа влево до тех пор, пока он не встанет на «нужное место». При этом элементы, которые больше ключа, постепенно сдвигаются вправо на одну позицию.

3
6
13
1
7
0
2




1
3
6
13
7
0
2

Ключ вставлен в отсортированную часть массива, при этом все 3 элемента отсортированной части сместились вправо на 1. Теперь отсортированная часть массива состоит из 4-х элементов.


2 шаг. Вставим 5-ый элемент в упорядоченную часть массива, key=M[5].

1
3
6
13
7
0
2




Число 13 сместилось вправо на 1, а число 7 встало на ”свое” место.

1
3
6
7
13
0
2


3..4 шаг. Отсортированная часть массива состоит из 5-ти элементов, вставим 6-ой и 7-ой элементы.

key=M[6].

1
3
6
7
13
0
2


key=M[7].

0
1
3
6
7
13
2





0
1
2
3
6
7
13

Массив упорядочен возрастанию.


Блок-схема сортировки простыми вставками:





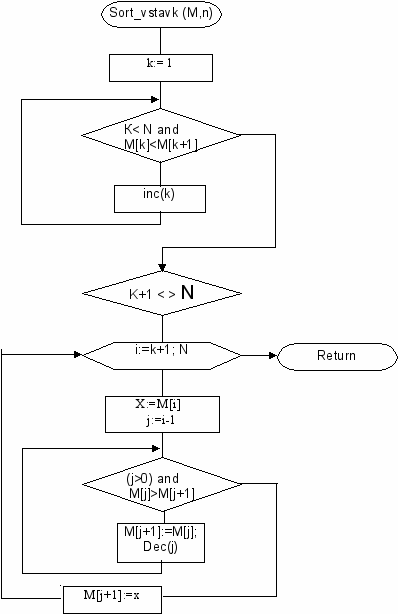
Процедура сортировки простыми вставками:

Procedure Sort_Vstavk (var M:array of integer; n:integer);

Var K,I,j:integer;

Begin

k:=1;

while (k
if k+1<>N then begin

for i:=k+1 to N do

begin

X:=M[i];

j:=i-1;

while (j>0)and(M[j]>X) do

begin

M[j+1]:=M[j];

dec(j);

end;

M[j+1]:=X;

end;

end;

end;


Проанализируем эффективность алгоритма. Имеем N–(k+1) шагов, на каждом шаге сравнений не более чем i-1, где i– номер вставляемого элемента. Таким образом, эффективность имеет квадратичный порядок C=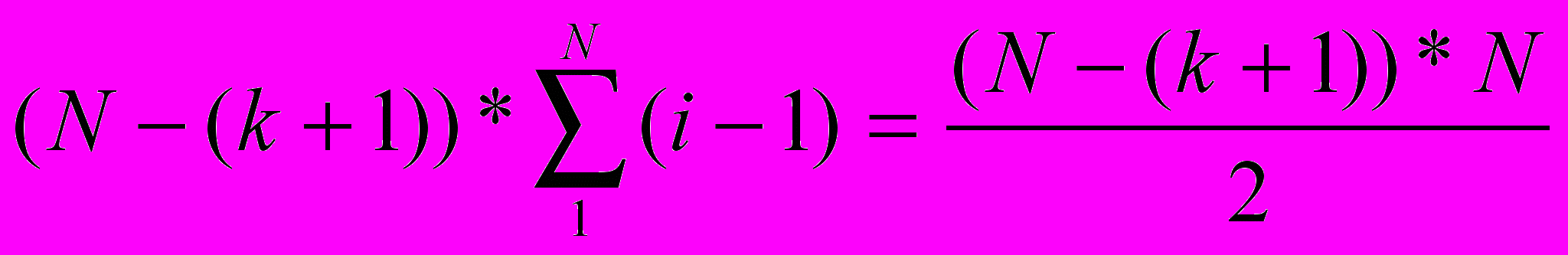=Θ(N2).

Количество перестановок в худшем случае 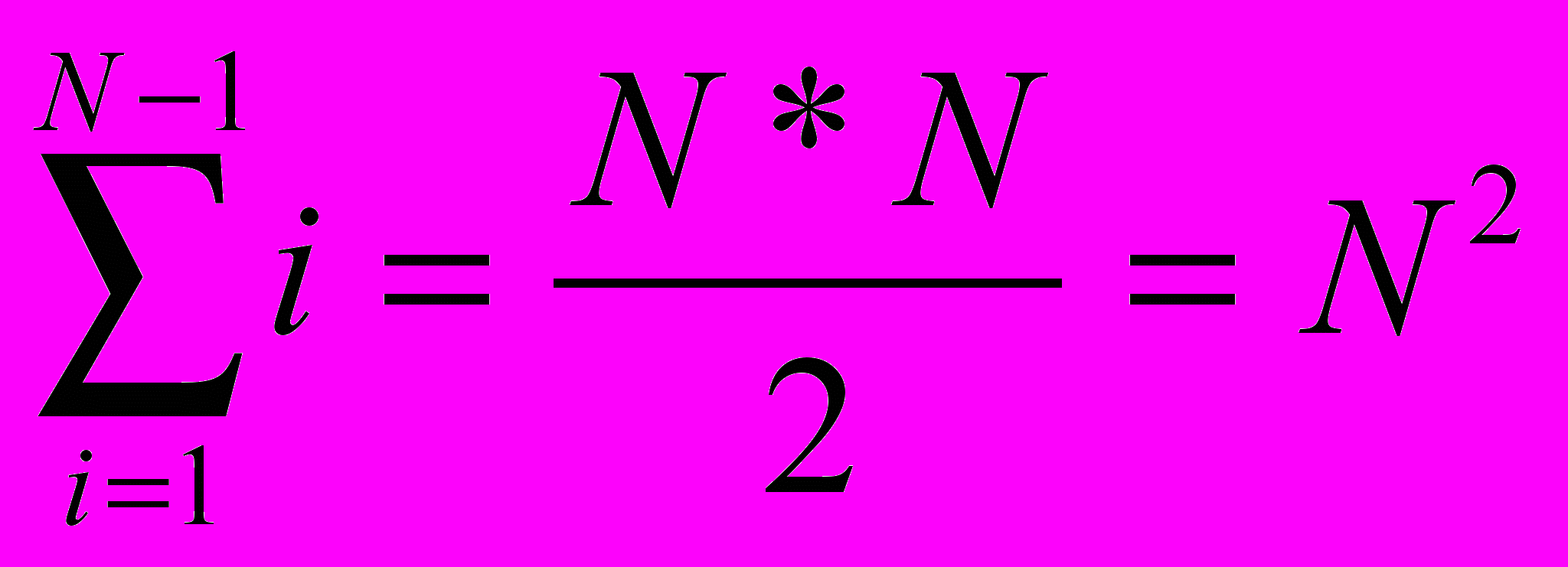, в лучшем случае - 0.