Содержание
| Вид материала | Документы |
Содержание2.6. Алгоритм симплекс-метода Вторая итерация |
- Содержание дисциплины наименование тем, их содержание, объем в часах лекционных занятий, 200.99kb.
- Содержание рабочей программы Содержание обучения по профессиональному модулю (ПМ) Наименование, 139.63kb.
- Заключительный отчет июль 2010 содержание содержание 1 список аббревиатур 3 введение, 6029.85kb.
- 5. Содержание родительского правоотношения Содержание правоотношения, 110.97kb.
- Содержание введение, 1420.36kb.
- Сборник статей Содержание, 1251.1kb.
- Сборник статей Содержание, 1248.25kb.
- Анонсы ведущих периодических изданий содержание выпуска, 806.18kb.
- Вопросы к экзамену по дисциплине «Коммерческая деятельность», 28.08kb.
- Конспект лекций содержание содержание 3 налог на прибыль организаций 5 Плательщики, 795.2kb.
2.6. Алгоритм симплекс-метода
Теперь мы в состоянии сформулировать алгоритм симплекс-метода для решения задач линейного программирования, заданных в канонической форме. Обычно он реализуется в виде так называемой симплекс-таблицы, изображенной на следующей странице.
В первом столбце этой таблицы располагаются обозначения векторов, входящих в базис.
Второй столбец коэффициенты
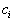 целевой функции, соответствующие векторам, входящим в базис.
целевой функции, соответствующие векторам, входящим в базис.Третий столбец компоненты опорного плана. В дополнительной строке в этом столбце пишется величина
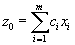 . Её легко вычислить перемножая числа из второго столбца и третьего столбца и складывая их.
. Её легко вычислить перемножая числа из второго столбца и третьего столбца и складывая их.Далее идут столбцы, соответствующие всем векторам
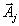 , и в этих столбцах записываются координаты этих векторов в рассматриваемом базисе. Заметим, что для векторов, входящих в базис, эти координаты имеют вид (0,0, ... ,0,1,0, ..., 0), где единица стоит в той строке, где находится сам этот базисный вектор.
, и в этих столбцах записываются координаты этих векторов в рассматриваемом базисе. Заметим, что для векторов, входящих в базис, эти координаты имеют вид (0,0, ... ,0,1,0, ..., 0), где единица стоит в той строке, где находится сам этот базисный вектор.В дополнительной строке сверху обычно выписывают коэффициенты
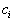 , соответствующие этим векторам.
, соответствующие этим векторам.В дополнительной строке снизу пишутся величины
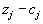 , вычисляемые по формулам:
, вычисляемые по формулам: .
.Заметим, что для векторов, входящих в базис, эти разности всегда равны нулю.
Далее идут следующие этапы, связанные с преобразованием этой таблицы. При ручном счете каждый раз эту таблицу лучше переписывать заново, при счете на ЭВМ (который, естественно, всегда используется при решении практических, а не учебных задач), эта таблица просто преобразуется в памяти ЭВМ.
Этап 1
Просматривается дополнительная строка снизу, где записаны разности .
| Если все эти разности 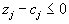 , , | то план является оптимальным |
Этап 2
Если есть столбцы, где
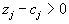 , то выбирается столбец с максимальным значением этой разности. Индекс j определит вектор, вводимый в базис.
, то выбирается столбец с максимальным значением этой разности. Индекс j определит вектор, вводимый в базис.Пусть
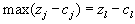 , то есть в базис надо вводить вектор
, то есть в базис надо вводить вектор 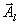 . Назовем столбец, соответствующий этому вектору, направляющим столбцом. В дальнейшем мы будем направляющий столбец помечать символом
. Назовем столбец, соответствующий этому вектору, направляющим столбцом. В дальнейшем мы будем направляющий столбец помечать символом 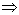 .
.Этап 3
Просматривается столбец, соответствующий этому вектору. Если все
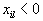 , то значения целевой функции неограничены снизу. Если есть
, то значения целевой функции неограничены снизу. Если есть 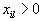 , то находятся
, то находятся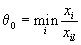
| где просматриваются лишь те дроби 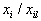 , , | для которых 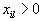 |
Пусть этот минимум достигается для вектора
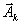 . Тогда именно вектор
. Тогда именно вектор 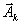 подлежит выводу из базиса. Строка, соответствующая этому вектору, называется направляющей строкой. В дальнейшем в примерах мы будем
подлежит выводу из базиса. Строка, соответствующая этому вектору, называется направляющей строкой. В дальнейшем в примерах мы будем| помечать ее символом 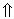 . . |
Этап 4
После того, как определены направляющие столбец и строка, начинает заполняться новая симплекс-таблица, в которой на месте направляющей
| строки будет стоять вектор 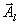 . . | |
Обычно заполнение этой новой таблицы начинается именно с направляющей строки. В качестве компоненты опорного плана туда
| пишется величина 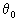 , то есть , то есть | |
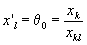 .
.Остальные элементы этой строки заполняются величинами
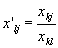 .
.Обратите внимание на особую роль элемента
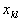 , стоящего на пересечении направляющей строки и направляющего столбца. Именно на него делятся все бывшие элементы направляющей строки. На месте бывшего элемента
, стоящего на пересечении направляющей строки и направляющего столбца. Именно на него делятся все бывшие элементы направляющей строки. На месте бывшего элемента 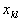 автоматически появляется единица.
автоматически появляется единица.Написанные выше формулы для пересчета элементов направляющей строки можно записать следующим правилом:
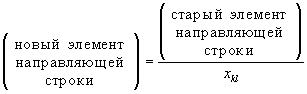 .
.Этап 5
Далее начинается пересчет всех остальных строк таблицы, включая и дополнительную нижнюю строку по формулам: для компонент плана
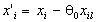 ;
;для координат разложения по базису
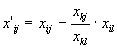 ;
;для дополнительной строки
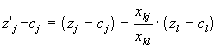 .
.Обратите внимание на то, что все эти формулы по сути дела строятся по одному правилу
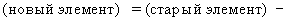
 .
.Это правило применимо и к компонентам плана, и к величинам
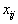 , и к разностям
, и к разностям 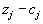 . Его даже можно использовать для пересчета элементов самого направляющего столбца, хотя проще заполнить его нулями, оставив
. Его даже можно использовать для пересчета элементов самого направляющего столбца, хотя проще заполнить его нулями, оставив| 1 на месте бывшего элемента 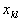 . . |
Далее итерации продолжаются.
Пример
Решить задачу линейного программирования
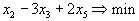
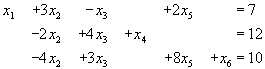
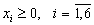
В данном случае вектор
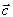 равен (0,1,-3,0,2,0), а в векторной форме ограничения могут быть записаны в виде
равен (0,1,-3,0,2,0), а в векторной форме ограничения могут быть записаны в виде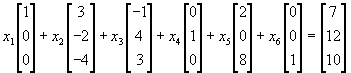 .
.Заполним исходную симплекс-таблицу, взяв в качестве исходного базиса
| вектора 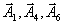 , , | что удобно из-за их вида. |
Исходная симплекс-таблица
| | Ба- | 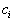 | План | 0 | 1 | -3 | 0 | 2 | 0 |
| | зис | | | 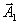 | 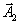 | 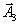 | 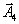 | 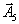 | 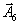 |
| | 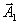 | 0 | 7 | 1 | 3 | -1 | 0 | 2 | 0 |
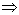 | 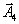 | 0 | 12 | 0 | -2 | 4 | 1 | 0 | 0 |
| | 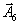 | 0 | 10 | 0 | -4 | 3 | 0 | 8 | 1 |
| | | | 0 | 0 | -1 | 3 | 0 | -2 | 0 |
| | | | | | | 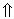 | | | |
Обратите внимание на то, что из-за специфического вида векторов
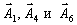 в столбец "план" просто переписался вектор
в столбец "план" просто переписался вектор 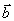 , а в качестве координат векторов в нашем базисе стоят просто сами векторы.
, а в качестве координат векторов в нашем базисе стоят просто сами векторы.Ну, а величины
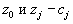 приходится считать:
приходится считать: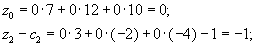
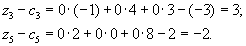
Первая итерация
Просматривая дополнительную строку мы видим, что в ней всего один положительный элемент в столбце, соответствующем вектору
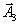 . Следовательно, этот вектор надо вводить в базис и этот столбец и будет направляющим столбцом.
. Следовательно, этот вектор надо вводить в базис и этот столбец и будет направляющим столбцом.В этом направляющем столбце есть два положительных числа 4 и 3. Поэтому нужно рассмотреть два частных
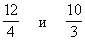
и выбрать из них наименьшее. Так как
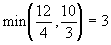
и он достигается на векторе
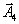 , то этот вектор подлежит выводу из базиса и соответствующая ему строка и будет направляющей строкой.
, то этот вектор подлежит выводу из базиса и соответствующая ему строка и будет направляющей строкой.| | Ба- | 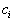 | План | 0 | 1 | -3 | 0 | 2 | 0 |
| | зис | | | 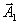 | 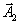 | 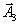 | 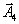 | 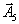 | 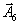 |
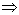 | 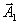 | 0 | 10 | 1 | 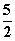 | 0 | 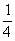 | 2 | 0 |
| | 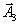 | -3 | 3 | 0 | 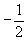 | 1 | 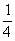 | 0 | 0 |
| | 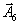 | 0 | 1 | 0 | 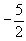 | 0 | 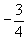 | 8 | 1 |
| | | | -9 | 0 | 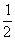 | 0 | 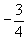 | -2 | 0 |
| | | | | | 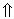 | | | | |
Заполним теперь новую симплекс-таблицу, следуя сформулированным выше правилам.
Начинается заполнение, естественно, со второй строки (так как она была направляющей), а затем пересчитываются все остальные строки.
Вторая итерация
Просматривая дополнительную строку мы вновь видим в ней всего один положительный элемент это 1/2, стоящая в столбце вектора
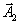 . Следовательно, этот вектор надо ввести в базис и этот столбец будет направляющим.
. Следовательно, этот вектор надо ввести в базис и этот столбец будет направляющим.В столбце, соответствующем вектору
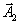 , всего один положительный элемент это 5/2, которая стоит в первой строке. Поэтому первая строка будет
, всего один положительный элемент это 5/2, которая стоит в первой строке. Поэтому первая строка будет| направляющей и вектор 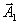 | должен быть выведен из базиса. |
| | Ба- | 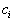 | План | 0 | 1 | -3 | 0 | 2 | 0 |
| | зис | | | 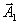 | 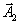 | 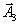 | 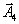 | 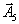 | 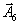 |
| | 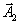 | 1 | 4 | 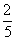 | 1 | 0 | 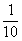 | 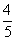 | 0 |
| | 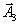 | -3 | 5 | 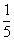 | 0 | 1 | 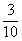 | 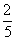 | 0 |
| | 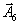 | 0 | | 1 | 0 | 0 | 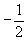 | 10 | 1 |
| | | | -11 | 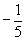 | 0 | 0 |  |  | 0 |
Запишем новую симплекс-таблицу, следуя сформулированным выше правилам.
В получившейся таблице в дополнительной строке стоят лишь отрицательные числа и нули. Поэтому получившийся план является оптимальным.
Итак, оптимальный план имеет вид
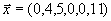
то есть
 , а все остальные Ему соответствует значение целевой функции, равное -11
, а все остальные Ему соответствует значение целевой функции, равное -11