Geum.ru

Содержание

Вид материалаДокументы

Содержание


4.6. Снятие вырожденности
Построение исходного опорного плана.
Первая итерация
Вторая итерация
Третья итерация
Подобный материал:
1   ...   9   10   11   12   13   14   15   16   17

4.6. Снятие вырожденности

4.6.1. Эпсилон-прием


К сожалению, при решении транспортных задач, особенно тогда, когда 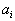и 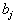 целые числа, часто приходится сталкиваться с вырожденными опорными планами, то есть с планами, число положительных компонент которых меньше 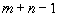. Это бывает тогда, когда, как уже указывалось выше, какое-то подмножество складов удовлетворяет потребности какого-то подмножества пунктов потребления.

Для борьбы с этим неприятным явлением существует очень простой прием, который, в качестве профилактики, рекомендуется применять всегда, когда запасы продукта на складах и потребности пунктов потребления  целые числа.

Он состоит в следующем: пусть запасы продукта есть ,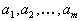
а




потребности пунктов потребления есть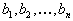

. Рассмотрим новую




задачу с теми же самыми ,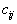
для которой



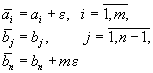
с некоторым  >0. Можно взять  конкретным, но достаточно малым числом, а можно просто оставить в алгебраическом виде как букву. Затем транспортная задача решается обычным путем, а в ответе просто полагается  =0, (или полученный результат округляется, если  было взято конкретным малым числом).

Проиллюстрируем этот прием на конкретном примере.

Пример

Пусть матрица стоимостей перевозок имеет вид:

1

2

3

4

4

3

2

1

1

2

2

1



Запасы складов равны .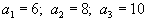

Потребности пунктов








потребления равны .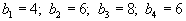
 

Заметьте, что в данном случае 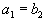, или 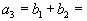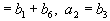, то есть имеются подгруппы складов, полностью удовлетворяющие потребности некоторых пунктов потребления.

Чтобы снять намечающееся вырождение, будем решать задачу с теми же

самыми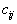

, но с



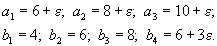
Дальнейшее дается с минимальными пояснениями.

Построение исходного опорного плана.

Используя метод северо-западного угла, получим следующий исходный опорный план

4

2+

 
 

 
4-

4+2

 

 
 
4-2

6+3

Для этого плана значение функции потерь равно



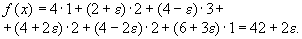
Первая итерация

Этап 1
Определение потенциалов и проверка оптимальности плана.

 
1

2

1

0

0

1

2

1

0

1

1

3

2

1

1

2

3

2

1

План не является оптимальным. Отмечены те элементы, для которых

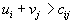. Для ввода в базис выбран вектор .



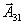Этап 2

Строим цикл, находим  и переходим к новому опорному плану.



4-

2+ +

 
 
 
2

6-

 
 



4- -

4+2 +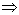

 


 


8

 





 
4-2 -

6+3

 
4-2

 
 
6+3

В данном случае 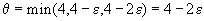. Обратите внимание на то, что если бы было  =0, то построенный план имел бы всего 4 положительных компоненты, то есть он был бы вырожденным.

Вторая итерация

Этап 1

Находим потенциалы и проверяем оптимальность плана.

 
1

2

1

1



0
1

2

1

1



1
2

3

2

2



0
1

2

1

1

Полученный план снова не является оптимальным. Условие 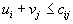нарушается на элементе с i =2, j =4.

Цикл нарисован заранее.

Этап 2



2 -

6- +

 
 
 


6

 
 



 -

8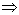





 
 
8





4-2 +

 
 
6+3 -

 
4-

 
 
6+2

В данном случае 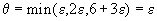. Опять-таки, если бы было  =0, то план был бы вырожденным.

Третья итерация

Этап 1

Нахождение потенциалов и проверка на оптимальность.

Соответствующая таблица приведена ниже.

 
1

2

2

1

0

1

2

2

1

0

1

2

2

1

0

1

2

2

1

В данном случае для всех клеток таблицы выполнено условие 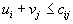, так что построенный план является оптимальным.

Чтобы получить решение исходной задачи, надо положить  =0. Тогда мы получим:
6

 
 
 
 
6

 
 

 
 
8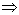





 
 
8

 

4-

 
 
6+2

 
4

 
 
6

Найденный оптимальный план имеет всего 4 компоненты, то есть он является вырожденным. Для него значение транспортных потерь равно



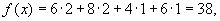
то есть значение транспортных издержек уменьшилось по сравнению с планом, построенным по методу северо-западного угла , на 4 единицы. или на 9.5%