Содержание
| Вид материала | Документы |
Содержание2.7. Метод искусственного базиса Первая итерация Вторая итерация Третья итерация |
- Содержание дисциплины наименование тем, их содержание, объем в часах лекционных занятий, 200.99kb.
- Содержание рабочей программы Содержание обучения по профессиональному модулю (ПМ) Наименование, 139.63kb.
- Заключительный отчет июль 2010 содержание содержание 1 список аббревиатур 3 введение, 6029.85kb.
- 5. Содержание родительского правоотношения Содержание правоотношения, 110.97kb.
- Содержание введение, 1420.36kb.
- Сборник статей Содержание, 1251.1kb.
- Сборник статей Содержание, 1248.25kb.
- Анонсы ведущих периодических изданий содержание выпуска, 806.18kb.
- Вопросы к экзамену по дисциплине «Коммерческая деятельность», 28.08kb.
- Конспект лекций содержание содержание 3 налог на прибыль организаций 5 Плательщики, 795.2kb.
2.7. Метод искусственного базиса
Последняя трудность, которую осталось преодолеть это определение исходного опорного плана и исходной симплекс-таблицы, с которой начинаются все итерации.
За счет чего мы так легко составили исходную симплекс-таблицу в предыдущем примере? Легко видеть, что это произошло потому, что среди
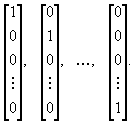
| векторов 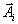 | были векторы вида |
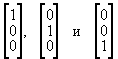,так как искать координаты в этом базисе очень просто.
На искусственном введении этих векторов и основан метод искусственного базиса.
Итак, пусть мы имеем задачу линейного программирования в канонической форме
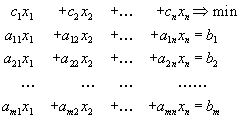
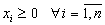.| Можно считать, что все 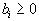 , | так как умножением соответствующего |
| ограничения на -1 у  | всегда можно сменить знак. |
Возьмем ну очень большое число M и будем решать следующую вспомогательную задачу:
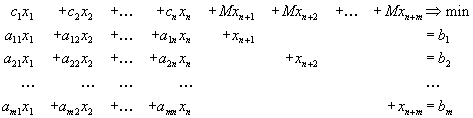
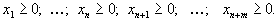
В этой задаче сразу ясен исходный базис в качестве него надо взять
| векторы, стоящие при 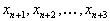 , | ведь они имеют вид |
В качестве исходного опорного плана надо взять план
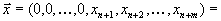
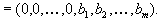
Коэффициенты разложения векторов
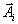. Исходная симплекс-таблица приобретает тогда вид: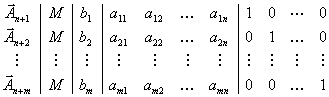
Надо лишь сосчитать дополнительную строку, где стоят числа
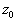и
:
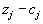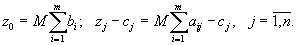
Заметим, что в матричных обозначениях исходная симплекс-таблица выглядит так:
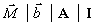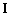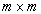,| где  единичная матрица размерности  | , а  . |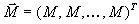
А теперь начнем преобразования симплекс-таблицы, стараясь выводить из базиса векторы, соответствующие введенным дополнительным переменным. Так как M очень большое, то среди разностей
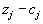будет много положительных и будет много претендентов на введение в базис из| векторов  . | |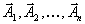
Заметим, что если какой-то вектор, соответствующий какой-то дополнительной переменной
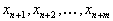выведен из базиса, то соответствующий столбец симплекс-таблицы можно просто вычеркнуть и больше к нему не возвращаться.В конце концов возможны два варианта.
Вариант 1
Все векторы, соответствующие введенным дополнительным переменным, будут выведены из базиса. В этом случае мы просто вернемся к исходной задаче, попав в какую-то вершину допустимой области. Все столбцы симплекс-таблицы, соответствующие дополнительным переменным, тогда исчезнут и дальше будет решаться исходная задача.
Вариант 2
Несмотря на то, что M очень велико, получающийся оптимальный план будет все-таки содержать какую-то из дополнительных перем енных. Это означает, что допустимая область исходной задачи пуста, то есть ограничения исходной задачи противоречивы и поэтому исходная задача вообще не имеет решений.
Заметим в заключение, что величина M вообще не конкретизируется и так и остается в виде буквы M. При решении учебных задач в дополнительную строку пишут алгебраические выражения, содержащие M, а при счете на ЭВМ вводится еще одна дополнительная строка, куда пишутся коэффициенты при M.
Проиллюстрируем это примером.
Пример
Решить задачу линейного программирования
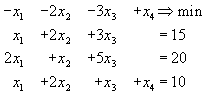
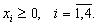
Заметим, что у нас уже есть один подходящий вектор это вектор
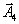при переменной 
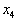. Поэтому вводим лишь две дополнительные переменные 
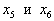, заменяя исходную задачу следующей: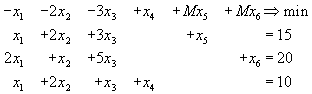
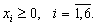
Исходная симплекс-таблица примет тогда вид:
| | Ба- | с | План | -1 | -2 | -3 | 1 | М | М |
| | зис | | |  |  |  | |  |  |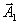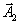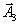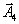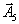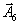
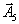| | | M | 15 | 1 | 2 | 3 | 0 | 1 | 0 |
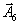 | | M | 20 | 2 | 1 | 5 | 0 | 0 | 1 |
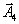| | | 1 | 10 | 1 | 2 | 1 | 1 | 0 | 0 |
| | | | 10+ 35M | 2+ 3M | 4+ 3M | 4+ 8M | 0 | 0 | 0 |
| | | | | | |  | | | |
Дальнейшие итерации приводятся без особых пояснений.
Первая итерация
Так как из базиса выводится вектор
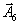, то в получающейся симплекс-таблице соответствующий столбец сразу удаляется.| | Ба- | с | План | -1 | -2 | -3 | 1 | М |
| | зис | | | | | | | |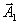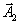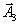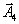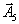
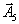| | | M | 3 | 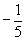 | 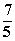 | 0 | 0 | 1 |
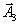| | | -3 | 4 | 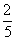 | 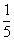 | 1 | 0 | 0 |
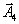| | | 1 | 6 |  | 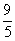 | 0 | 1 | 0 |
| | | | -6+ 3M | 2/5- -1/5M | 16/5+ +1/5M | 0 | 0 | 0 |
| | | | | | | | | |
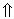Вторая итерация
На этой итерации из базиса выводится вектор
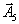. Соответственно из симплекс-таблицы удаляется столбец, соответствующий этому вектору, и все введенные дополнительные переменные исчезают. | | Ба- | с | План | -1 | -2 | -3 | 1 |
| | зис | | | | | | |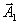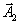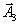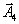
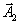| | | -2 | 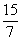 | 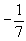 | 1 | 0 | 0 |
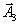| | | -3 | 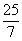 | 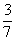 | 0 | 1 | 0 |
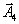| | | 1 | 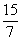| 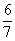 | 0 | 0 | 1 |
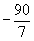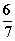| | | |  |  | 0 | 0 | 0 |
| | | | | | | | |
Третья итерация
Мы вернулись к исходной задаче и продолжаем решать ее по стандартной схеме.
| Ба- | с | План | -1 | -2 | -3 | 1 |
| зис | | | | | | |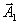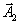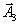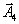
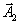| | -2 | 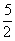 | 0 | 1 | 0 |  |
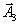| | -3 | 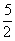| 0 | 0 | 1 |  |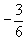
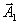| | -1 | 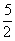| 0 | 1 | 0 |  |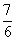
| | | -15 | 0 | 0 | 0 | -1 |
Таким образом, задача решилась и оптимальный план имеет вид:
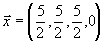.Минимальное значение целевой функции равно 15.
Отметим в заключение, что если первоначальная задача линейного программирования имела ограничения вида
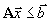и все компоненты вектора 
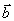неотрицательны, то, приводя её к канонической форме, мы сразу будем иметь единичную матрицу порядка m которую и можно брать в качестве исходного базиса