Содержание
| Вид материала | Документы |
- Содержание дисциплины наименование тем, их содержание, объем в часах лекционных занятий, 200.99kb.
- Содержание рабочей программы Содержание обучения по профессиональному модулю (ПМ) Наименование, 139.63kb.
- Заключительный отчет июль 2010 содержание содержание 1 список аббревиатур 3 введение, 6029.85kb.
- 5. Содержание родительского правоотношения Содержание правоотношения, 110.97kb.
- Содержание введение, 1420.36kb.
- Сборник статей Содержание, 1251.1kb.
- Сборник статей Содержание, 1248.25kb.
- Анонсы ведущих периодических изданий содержание выпуска, 806.18kb.
- Вопросы к экзамену по дисциплине «Коммерческая деятельность», 28.08kb.
- Конспект лекций содержание содержание 3 налог на прибыль организаций 5 Плательщики, 795.2kb.
Линейное программирование
Часть I
Содержание:
Линейное программирование 1
Содержание: 2
1. Основные понятия 3
1.1. Примеры моделей, приводящих к задачам линейного программирования 3
1.2. Стандартная и каноническая формы задачи линейного программирования 8
1.3. Геометрическая интерпретация задач линейного программирования 16
2. Симплекс-метод 24
2.1. Выпуклые множества и многогранники 24
2.2. Вершины выпуклого многогранника 29
2.3. Переход от вершины к вершине 35
2.4. Переход к новому базису 38
2.5. Отыскание оптимального плана 40
2.6. Алгоритм симплекс-метода 44
2.7. Метод искусственного базиса 51
3. Двойственные задачи 56
3.1. Постановка двойственных задач 56
3.2. Свойства двойственных задач 59
3.3. Двойственный симплекс-метод 66
4. Транспортная задача 67
4.1. Постановка задачи 67
4.2. Простейшие свойства транспортной задачи 69
4.3. Методы определения первоначального опорного плана 71
4.3.1. Построение исходного опорного плана (метод северо-западного угла) 71
4.3.2. Метод минимального (максимального) элемента 76
4.3.3. Метод аппроксимации Фогеля 78
4.3.4. Метод двойного предпочтения 80
4.4. Методы проверки опорного плана на оптимальность 82
4.4.1. Потенциалы. Критерий оптимальности плана 82
4.4.2. Дельта-метод 87
4.5. Алгоритм улучшения плана 89
4.6. Снятие вырожденности 95
4.6.1. Эпсилон-прием 95
4.6.2. 0-подстановка 100
1. Основные понятия
1.1. Примеры моделей, приводящих к задачам линейного программирования
Линейное программирование является одной из основных частей того раздела современной математики, который получил название математического программирования. В общей постановке задачи этого раздела выглядят следующим образом.
Имеются какие-то переменные
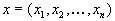 и функция этих переменных
и функция этих переменных 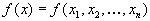 , которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции
, которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции 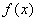 при условии, что переменные x принадлежат некоторой области G:
при условии, что переменные x принадлежат некоторой области G: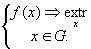
В зависимости от вида функции
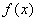 и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Подробнее об этом будет сказано в заключении.
и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Подробнее об этом будет сказано в заключении.Линейное программирование характеризуется тем, что
| а) функция 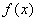 | является линейной функцией переменных 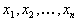 ; ; | |
б) область G определяется системой линейных равенств или неравенств.
Чтобы понять, откуда берутся задачи линейного программирования, рассмотрим некоторые, уже ставшие классическими, примеры подобных задач.
Задача о диете
Задача о диете возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям.
Предположим, что в нашем распоряжении имеется n продуктов питания (сено, зерно, комбикорм, соль и т.д.). Обозначим эти продукты через
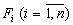 . Предположим, что . Предположим, что 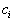 | есть стоимость единицы веса (например, |
| стоимость одного килограмма) продукта 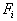 . . |
Рациональная диета должна доставлять животному определенные компоненты (белки, жиры, углеводы, витамины, микроэлементы и т.д.). Обозначим эти компоненты через
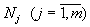 . Тогда можно составить таблицу - справочник, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта.
. Тогда можно составить таблицу - справочник, указывающую, какое количество каждого компонента имеется в единице веса каждого продукта.| | 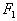 |  | ... |  | ... |  |
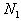 |  | 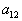 | ... | 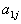 | ... | 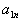 |
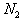 | 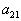 | 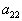 | ... | 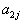 | ... |  |
| ... | ... | ... | ... | ... | ... | ... |
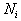 |  | 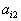 | ... | 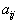 | ... | 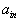 |
| ... | ... | ... | ... | ... | ... | ... |
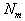 | 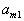 | 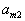 | ... | 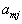 | ... |  |
Таким образом, величина
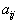 есть количество i-го компонента, содержащегося в единице веса j-го продукта. Матрица
есть количество i-го компонента, содержащегося в единице веса j-го продукта. Матрица 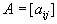 называется матрицей питательности.
называется матрицей питательности.Рацион кормления должен указать, какое количество
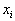 i-го продукта должно быть скормлено животному за определенный срок (скажем, за месяц). Он означает, что за этот срок животное должно получить единиц первого
i-го продукта должно быть скормлено животному за определенный срок (скажем, за месяц). Он означает, что за этот срок животное должно получить единиц первого 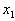
| продукта, 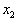 | единиц второго, ... ,  | единиц n-го продукта. |
Что же требуется от рациона? Во-первых, должны быть выполнены определенные медицинские требования, которые заключаются в том, что за указанный срок животное должно получить не менее определенного количества каждого компонента (не менее определенного количества белков, жиров, витаминов и т.д.). Обозначим через
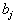 то минимальное количество j-го компонента, которое должно получить животное. Тогда рацион кормления должен удовлетворять ограничениям
то минимальное количество j-го компонента, которое должно получить животное. Тогда рацион кормления должен удовлетворять ограничениям 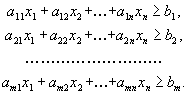 | (1.1) |
| Кроме того очевидно, что все переменные 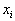 | неотрицательны, т.е. |
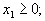 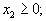 | ... 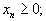 | | (1.2) |
| Пусть стоимость единицы веса i-го продукта равна 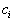 . . | Тогда весь наш |
Мы, естественно, хотели бы понести минимальные затраты на содержание животных. Поэтому задача приобретает вид: найти рацион минимальной стоимости при выполнении медицинских ограничений (1.1) и естественных ограничений (1.2). Математически это выглядит так:
Обратите внимание на полученный результат. Во-первых, достаточно реальная задача приобрела строгую математическую форму. Во-вторых, целевая функция (стоимость рациона) является линейной функцией переменных 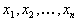 .В третьих, сами ограничения на значения переменных .В третьих, сами ограничения на значения переменных 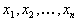 имеют вид линейных неравенств. Всё это и определило название этого класса задач - задачи линейного программирования. имеют вид линейных неравенств. Всё это и определило название этого класса задач - задачи линейного программирования.Рассмотрим теперь другую классическую задачу.  Задача о составление плана производства Рассмотрим деятельность некоторой производственной единицы (цеха, отдела и т.д.). Пусть наша производственная единица может производить |
| некоторые товары  | |
| Для производства этих товаров приходится использовать некоторые сырьевые ресурсы. Пусть число этих ресурсов есть m; обозначим их через 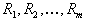 . .Tехнологией производства товара  назовем набор чисел назовем набор чисел  , показывающий, какое количество i-го ресурса необходимо для производства единицы товара , показывающий, какое количество i-го ресурса необходимо для производства единицы товара  . Это можно записать в виде технологической матрицы, которая полностью описывает технологические потребности . Это можно записать в виде технологической матрицы, которая полностью описывает технологические потребности |
| производства и элементами которой являются числа 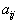 . . |
| | 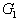 | 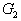 | ... |  | ... | 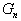 |
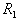 |  | 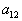 | ... | 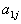 | ... | 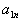 |
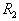 | 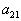 | 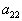 | ... | 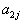 | ... |  |
| ... | ... | ... | ... | ... | ... | ... |
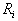 |  | 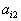 | ... | 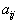 | ... | 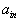 |
| ... | ... | ... | ... | ... | ... | ... |
 | 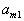 | 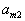 | ... | 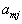 | ... |  |
Пусть у нас имеется
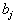 запасов каждого ресурса и мы планируем произвести
запасов каждого ресурса и мы планируем произвести 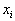 единиц i-го товара. Так как мы не можем выскочить за пределы имеющихся у нас ресурсов, то наш план производства
единиц i-го товара. Так как мы не можем выскочить за пределы имеющихся у нас ресурсов, то наш план производства 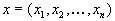 должен удовлетворять ограничениям
должен удовлетворять ограничениям 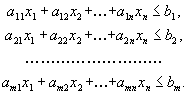 | (1.5) |
| при очевидных условиях не отрицательности переменных 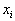 : : | |
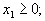 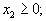 | ... | 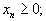 . . |
Естественно, мы стремимся получить за нашу продукцию возможно больше. Поэтому стоящая перед нами задача составления плана производства приобретает вид:
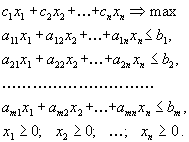 | (1.6) |
У нас снова получилась линейная целевая функция, и ограничения снова имеют характер линейных неравенств. Таким образом, мы снова имеем дело с задачей линейного программирования.
Мы не будем рассматривать примеры других задач линейного программирования. Отметим лишь, что они встречаются очень часто при оптимизации самых разнообразных производственных и экономических задач