Содержание
| Вид материала | Документы |
Содержание4.2. Простейшие свойства транспортной задачи 4.3.2. Метод минимального (максимального) элемента Пример № 2 4.3.3. Метод аппроксимации Фогеля 4.3.4. Метод двойного предпочтения |
- Содержание дисциплины наименование тем, их содержание, объем в часах лекционных занятий, 200.99kb.
- Содержание рабочей программы Содержание обучения по профессиональному модулю (ПМ) Наименование, 139.63kb.
- Заключительный отчет июль 2010 содержание содержание 1 список аббревиатур 3 введение, 6029.85kb.
- 5. Содержание родительского правоотношения Содержание правоотношения, 110.97kb.
- Содержание введение, 1420.36kb.
- Сборник статей Содержание, 1251.1kb.
- Сборник статей Содержание, 1248.25kb.
- Анонсы ведущих периодических изданий содержание выпуска, 806.18kb.
- Вопросы к экзамену по дисциплине «Коммерческая деятельность», 28.08kb.
- Конспект лекций содержание содержание 3 налог на прибыль организаций 5 Плательщики, 795.2kb.
4.2. Простейшие свойства транспортной задачи
Теорема 1. Для любой транспортной задачи существует план (то есть для любой транспортной задачи допустимая область не пуста).
Доказательство
Действительно, по смыслу задачи,
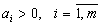
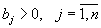 .
.| Так как 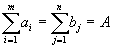 , , | то возьмем план в виде |
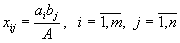 .
.| Величины 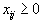 . . | Далее |
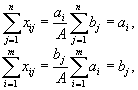
то есть ограничения выполняются. Поэтому
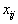 составляют план. Теорема доказана.
составляют план. Теорема доказана. Теорема 2. Транспортная задача всегда имеет оптимальный план.
Доказательство
Действительно, допустимая область не пуста. Далее, так как по смыслу
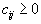 , то для любого плана перевозок
, то для любого плана перевозок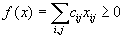 .
.В силу того, что значения целевой функции ограничены снизу, транспортная задача всегда имеет решение. Теорема доказана.
| Теорема 3. Любой опорный план имеет не более 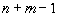 | |
положительных компонент.
Доказательство
Действительно, исходная система содержит всего
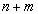 ограничений типа равенств:
ограничений типа равенств: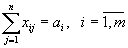 , то есть m ограничений;
, то есть m ограничений;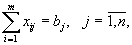 то есть n ограничений.
то есть n ограничений.Однако в силу соотношения
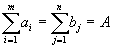 одно из этих ограничений является следствием всех остальных. Действительно, сложим все первые m ограничений
одно из этих ограничений является следствием всех остальных. Действительно, сложим все первые m ограничений 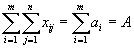 | (1) |
а из второй группы сложим первые n 1 ограничение
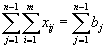 | (2) |
Вычитая теперь (2) из (1), получим:
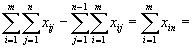
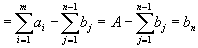 ,
,и мы получили последнее, n-ое ограничение второй группы.
Таким образом, независимых ограничений всего не более
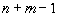 . Поэтому
. Поэтому| каждый опорный план имеет не более 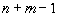 | компонент. |
Следствие. Оптимальный план содержит не более, чем
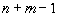 перевозку.
перевозку.4.3. Методы определения первоначального опорного плана
4.3.1. Построение исходного опорного плана (метод северо-западного угла)
Для начала решения транспортной задачи необходимо иметь какой-то исходный опорный план, то есть оказаться в какой-то вершине допустимой области. Приведем конструктивный прием построения такого опорного плана, получивший название "метод северо-западного угла".
| Итак, пусть имеется m складов с запасами 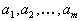 | и n пунктов |
| потребления с потребностями 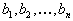 . . | Пусть запасы и потребности |
| сбалансированы, то есть 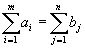 . . | |
Представим это в виде таблицы,
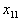 | | | | | 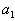 |
| | | | | |  |
| | | | | | 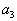 |
| | | | | | 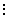 |
| | | | | | 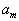 |
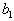 | 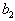 | 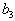 | ... | 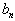 | |
где в столбце справа указаны запасы, в строке снизу потребности, а пустые клетки оставлены для будущего плана перевозок.
Начнем заполнение с клетки, расположенной вверху слева, то есть с "северо-западного угла". Вместо
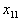 впишем число
впишем число 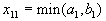 . Возможны два варианта.
. Возможны два варианта.-
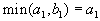 , то есть
, то есть 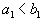 . Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме
. Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме 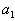 мы полностью опустошим первый склад и там ничего не останется. Поэтому все остальные перевозки из первого склада могут быть только нулевые.
мы полностью опустошим первый склад и там ничего не останется. Поэтому все остальные перевозки из первого склада могут быть только нулевые.
Ну, а потребность в первом пункте потребления останется в объеме
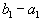 . Наша таблица примет вид:
. Наша таблица примет вид: 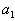 | 0 | 0 | ... | 0 | 0 |
| | | | | |  |
| | | | | | 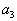 |
| | | | | | 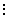 |
| | | | | | 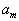 |
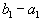 | 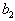 | 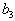 | ... | 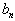 | |
Обратите внимание на то, что оставшаяся незаполненной часть таблицы вновь по структуре та же, что и исходная таблица, только в ней на одну строку меньше.
-
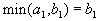 , то есть
, то есть 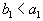 . Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме
. Тогда, запланировав перевозку из первого склада в первый пункт потребления в объеме 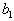 , мы полностью удовлетворим его потребности. Перевозить туда больше будет ничего не надо, поэтому остальные перевозки туда будут равны нулю.
, мы полностью удовлетворим его потребности. Перевозить туда больше будет ничего не надо, поэтому остальные перевозки туда будут равны нулю.
Ну, а в первом складе еще останется
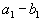 запасов продукта. Наша таблица примет вид:
запасов продукта. Наша таблица примет вид: 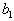 | | | | | 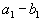 |
| 0 | | | | |  |
| 0 | | | | | 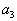 |
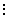 | | | | | 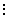 |
| 0 | | | | | 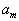 |
| 0 | 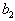 | 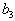 | ... | 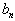 | |
Обратите внимание на то, что оставшаяся незаполненной часть таблицы вновь по структуре та же, что и исходная таблица, только в ней на один столбец меньше.
Ну, а дальше все можно повторить, продолжая заполнять оставшуюся часть таблицы перевозок начиная с левого верхнего, "северо-западного" угла, пока не будут исчерпаны запасы всех складов и не удовлетворены потребности всех пунктов потребления.
У нас всего в таблице m строк и n столбцов. Каждый раз исчезает, как минимум, либо строка, либо столбец (могут исчезнуть сразу и строка, и столбец, если запасы какого-то подмножества складов полностью удовлетворят потребности какого-то подмножества пунктов потребления). Однако при последней перевозке исчезает сразу и последняя строка, и последний столбец. Поэтому получающийся план перевозок содержит не
| более 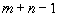 | компонент. |
Мы не будем доказывать, что план, полученный методом северо-западного угла, является опорным. Заметим лишь, что если получающийся план содержит ровно
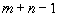 компоненту, то он называется невырожденным. Если число положительных компонент плана перевозок меньше
компоненту, то он называется невырожденным. Если число положительных компонент плана перевозок меньше 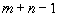 , то он называется вырожденным.
, то он называется вырожденным.Рассмотрим два примера. С целью экономии места, вся таблица не переписывается, а лишь приписываются последние строки и столбцы.
Пример 1
Пусть
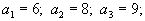
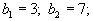
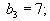
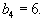
| 3 | 3 | 0 | 0 | 6 | 3 | 0 | 0 | 0 | 0 | 0 |
| 0 | 4 | 4 | 0 | 8 | 8 | 8 | 4 | 0 | 0 | 0 |
| 0 | 0 | 3 | 6 | 9 | 9 | 9 | 9 | 9 | 6 | 0 |
| 3 | 7 | 7 | 6 | В данном случае число | ||||||
| 0 | 7 | 7 | 6 | складов m =3, число пунктов | ||||||
| 0 | 4 | 7 | 6 | потребления n =4, так что | ||||||
| 0 | 0 | 7 | 6 | m+n-1=6. Получившийся | ||||||
| 0 | 0 | 3 | 6 | опорный план содержит ровно | ||||||
| 0 | 0 | 0 | 6 | 6 компонент, и поэтому являет- | ||||||
| 0 | 0 | 0 | 0 | ся невырожденным. |
Пример 2
Пусть
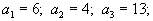
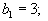
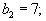
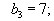
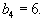 Аналогичная процедура приводит к таблице, изображенной ниже.
Аналогичная процедура приводит к таблице, изображенной ниже.В этом случае получившийся опорный план имеет всего 5 компонент, то есть является вырожденным. Это
| 3 | 3 | 0 | 0 | 6 | 3 | 0 | 0 | 0 | 0 | |
| 0 | 4 | 0 | 0 | 4 | 4 | 4 | 0 | 0 | 0 | |
| 0 | 0 | 7 | 6 | 13 | 13 | 13 | 13 | 6 | 0 | |
| 3 | 7 | 7 | 6 | В данном случае число скла- | ||||||
| 0 | 7 | 7 | 6 | дов m =3, число пунктов потре- | ||||||
| 0 | 4 | 7 | 6 | бления n =4, так что m+n-1=6. | ||||||
| 0 | 0 | 7 | 6 | Получившийся опорный план | ||||||
| 0 | 0 | 0 | 6 | содержит 5 компонент, и поэтому | ||||||
| 0 | 0 | 0 | 0 | является вырожденным. |
произошло потому, что запасы складов
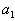 и
и 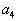 полностью удовлетворили потребности пунктов потребления
полностью удовлетворили потребности пунктов потребления 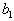 и
и 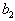 и поэтому в тот момент, когда эти сбалансированные потребности удовлетворились (
и поэтому в тот момент, когда эти сбалансированные потребности удовлетворились (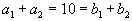 ), обнулились сразу и строка, и столбец.
), обнулились сразу и строка, и столбец.Ниже вся теория будет строится для случая, когда все опорные планы невырожденные, то есть все они имеют
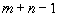 компоненту. Как бороться с явлением вырождения, которое в транспортных задачах встречается достаточно часто будет рассказано в самом конце
компоненту. Как бороться с явлением вырождения, которое в транспортных задачах встречается достаточно часто будет рассказано в самом конце4.3.2. Метод минимального (максимального) элемента
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел
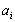 и
и 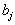 . Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.Пример № 2
Составить первоначальный опорный план методом минимального элемента для транспортной задачи вида:
| 2 | 3 | 4 | 15 |
| 11 | 6 | 10 | 1 |
| 8 | 9 | 3 | 3 |
| 4 | 1 | 2 | 21 |
| 10 | 20 | 10 | |
Решение:
Задача сбалансирована.
Строим первоначальный опорный план методом минимального элемента.
- Выясним минимальную стоимость перевозок.
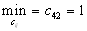 Первая перевозка будет осуществляться с пункта производства
Первая перевозка будет осуществляться с пункта производства 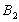 в пункт потребления,
в пункт потребления, 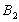 и она составит максимально возможное число единиц продукта
и она составит максимально возможное число единиц продукта 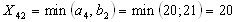 :В этом случае, потребности пункта потребления
:В этом случае, потребности пункта потребления 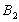 будут удовлетворены полностью. Значит, стоимости столбца 2 можно больше не рассматривать, так как перевозки
будут удовлетворены полностью. Значит, стоимости столбца 2 можно больше не рассматривать, так как перевозки 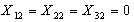 .Выясним минимальную стоимость перевозок (без учета столбца № 2).
.Выясним минимальную стоимость перевозок (без учета столбца № 2).
-
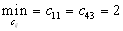 Вторая и третья перевозки будут осуществляться с пункта производства
Вторая и третья перевозки будут осуществляться с пункта производства 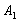 и
и 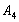 в пункт потребления
в пункт потребления 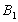 и
и 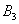 соответственно и составят максимально возможное число единиц продукта :
соответственно и составят максимально возможное число единиц продукта : 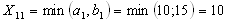 ,
, 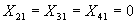 ;
;
-
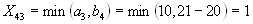
- Четвертая перевозка осуществляется с пункта
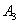 в пункт потребления
в пункт потребления 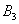 , т.к.
, т.к. 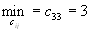 (без учета первого, второго столбца и четвертой строки).
(без учета первого, второго столбца и четвертой строки). 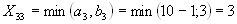 .
.
- Пятая перевозка осуществляется с пункта
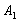 в пункт потребления
в пункт потребления 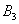 , т.к.
, т.к. 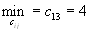 (без учета первого, второго столбца, третьей и четвертой строки).
(без учета первого, второго столбца, третьей и четвертой строки). 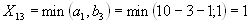 .
.
- Шестая перевозка осуществляется с пункта
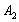 в пункт потребления
в пункт потребления 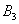 т.к.
т.к. 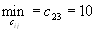 (без учета первого, второго столбца, первой, третьей и четвертой строки).
(без учета первого, второго столбца, первой, третьей и четвертой строки). 
Опорный план имеет вид;
| 10 | 5 | 0 |
| 0 | 1 | 0 |
| 0 | 3 | 0 |
| 0 | 11 | 10 |
4.3.3. Метод аппроксимации Фогеля
При определении опорного плана транспортной задачи методом аппроксимации Фогеля находят разность по всем столбцам и по всем строкам между двумя записанными в них минимальными тарифами. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают минимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальная стоимость.
Если минимальная стоимость одинакова для нескольких клеток столбца (строки), то для заполнения выбирают ту клетку, которая расположена в столбце (строке, соответсующем наибольшей разности между двумя минимальными стоимостями, находящимися в данном столбце (строке).
Пример
Найти методом аппроксимации Фогеля первоначальный опорный план транспортной задачи:
(Здесь мы перенесли потребности в верхнюю строку для удобства построения плана). Рассмотрим задачу, приведенную для методов северо-западного угла и минимального элемента
Решение:
| 10 | 20 | 10 | | | | |
| 2 7 | 3 0 | 4 8 | 15 | 1 | 1 | 1 |
| 11 0 | 6 1 | 10 0 | 1 | 4 | 4 | - |
| 8 3 | 9 0 | 3 0 | 3 | 5 | - | - |
| 4 0 | 1 19 | 2 2 | 21 | 1 | 1 | - |
| 2 | 2 | 1 | ||||
| 2 | 2 | 2 | ||||
| 2 | 2 | 2 | ||||
| 2 | - | 2 | ||||
| - | - | 2 | ||||
| - | - | - |
| 7 | 0 | 8 |
| 0 | 1 | 0 |
| 3 | 0 | 0 |
| 0 | 19 | 2 |
4.3.4. Метод двойного предпочтения
В случае больших размерностей, эффективен способ определения первоначального опорного плана с помощью метода двойного предпочтения.
В каждом столбце отмечают знаком клетку с наименьшей стоимостью. Затем тоже проделывают в каждой строке. В результате некоторые клетки имеют двойную отметку. В них находится минимальная стоимость как по столбцу, так и по строке. В эти клетки помещают максимально возможные объемы перевозок, каждый раз исключая и рассмотрения соответствующие столбцы или строки. Затем распределяют перевозки по клеткам с единичной отметкой. Остальные перевозки распределяют по наименьшей стоимости.
Пример
| 10 | 20 | 10 | |
| 2** | 3 | 4 | 15 |
| 11 | 6* | 10 | 1 |
| 8 | 9 | 3* | 3 |
| 4 | 1* | 2* | 21 |
- Заполняем клетки с двойным предпочтением :
10
20
10
10
15
0
1
0
3
0
21
- Заполняем клетки с простым предпочтением, начиная с наименьшей стоимости.
| 10 | 20 | 10 | |
| 10 | 0 | | 15 |
| 0 | 0 | | 1 |
| 0 | 0 | 3 | 3 |
| 0 | 20 | 1 | 21 |
3. Заполняем оставшиеся пустыми клетки.
| 10 | 20 | 10 | |
| 10 | 0 | 5 | 15 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 3 | 3 |
| 0 | 20 | 1 | 21 |
Это опорный план составленный методом двойного предпочтения
