Программа «Методы принятия решений». Гу-вшэ, 2010 г. Министерство экономического развития и торговли Российской Федерации Национальный исследовательский университет 

Вид материала

Программа

Содержание R =  является единственным примером транзитивного антирефлексивного отношения, для которого R R на конечном множестве множество мажорант Ω X множество Парето непусто.Привести пример множества X 5. Михайлова Елена 6. Морозова Мария 7. Перепечаева Арина 8. Полищук Наталья 9. Сафронова Екатерина 10. Старкова Елена 11. Фандеев Валерий 12. Широков Кирилл

Подобный материал:

• Российской Федерации Министерство образования и науки Российской Федерации Государственный, 343.55kb.
• Министерство экономического развития и торговли российской федерации государственный, 5460.46kb.
• Министерство экономического развития и торговли российской федерации государственный, 5459.19kb.
• Министерство экономического развития и торговли российской федерации государственный, 5458.65kb.
• Министерство экономического развития и торговли российской федерации государственный, 5753.09kb.
• Государственная программа Российской Федерации «Доступная среда» на 2011 2015 годы, 1560.95kb.
• Правительство Российской Федерации, а после утверждения направляется в Федеральное, 11.35kb.
• Приказ «о едином учёте преступлений», 767.93kb.
• 1. 10. Министерство экономического развития и торговли Российской Федерации, 198.8kb.
• Правительство Российской Федерации Национальный исследовательский университет Высшая, 299.13kb.

ЗАДАЧА 4. Доказать, что если yP^ijzP⁰u, то или yP⁰u, или существует векторная оценка v такая, что yP⁰vP^iju.

Вопросы для оценки качества усвоения дисциплины

Дайте определения следующих ключевых понятий:

Принятие решений

Лицо, принимающее решения (ЛПР)

Роли людей в процессах принятия решений

Активные группы

Индивидуальный выбор

Альтернативы

Критерии

Шкалы критериев

Процесс принятия решений, его этапы

Доминирующие и доминируемые альтернативы

Множество Эджворта-Парето (Э-П)

Типовые задачи принятия решений


Привести примеры классификации множества альтернатив


Привести примеры стратификации множества альтернатив


Привести примеры ранжирования множества альтернатив


Привести примеры целостного представления множества альтернатив


Привести примеры критериального представления множества альтернатив


Рассмотреть различные методы выбора на основе голосования


Какие решения приходилось Вам принимать? Привести примеры удачных и неудачных решений. В чём причина неудач?


Что такое оптимум Парето, граница Парето, множество Эджворта-Парето?


Сформулируйте и докажите необходимые и достаточные условия Парето-оптимальности для общего случая, поясните их смысл.


Сформулируйте и докажите теорему Гермейера, поясните её смысл


Сформулируйте и докажите условия Парето-оптимальности для вогнутых задач, поясните их смысл.


Сформулируйте и докажите необходимые и достаточные условия Парето-оптимальности для линейных задач, поясните их смысл.


Как построить множество Парето-Эджворта?


Доказать, что для любых отношений R₁ и R₂ верно, что

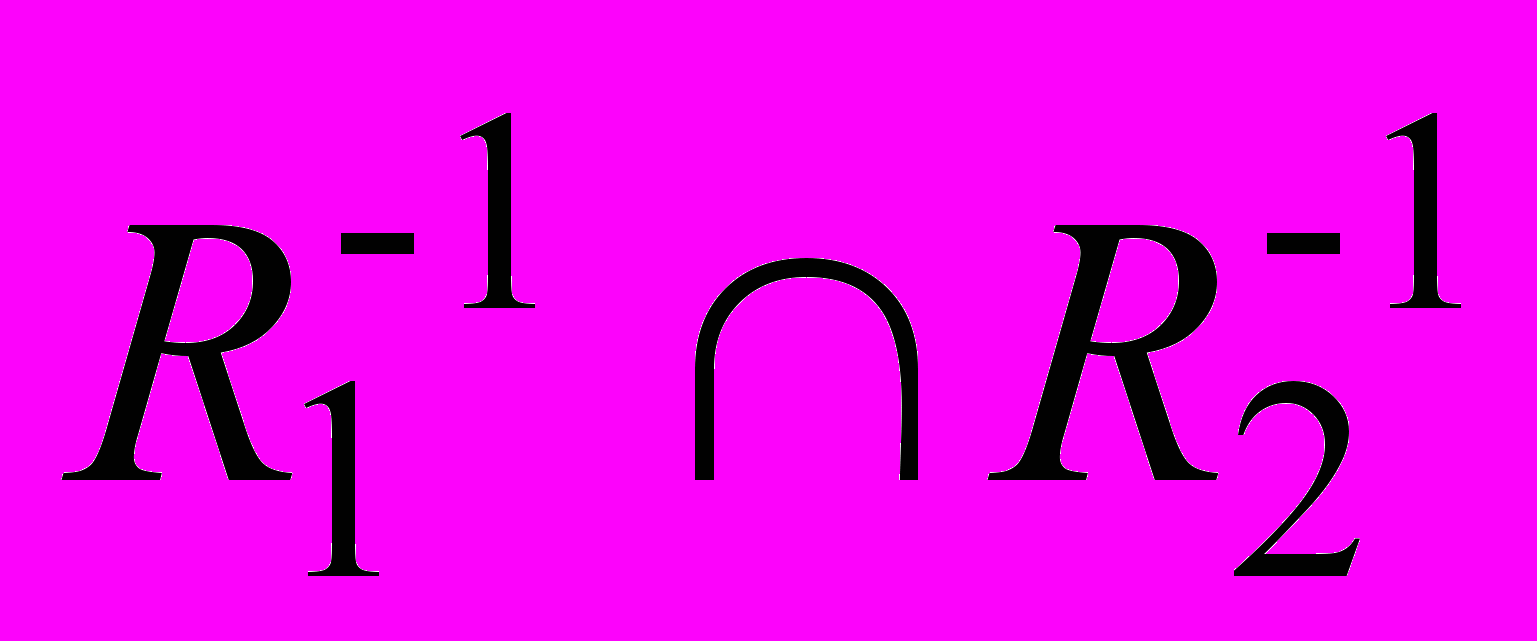(R₁ R₂)^-1 = ,

()^-1 =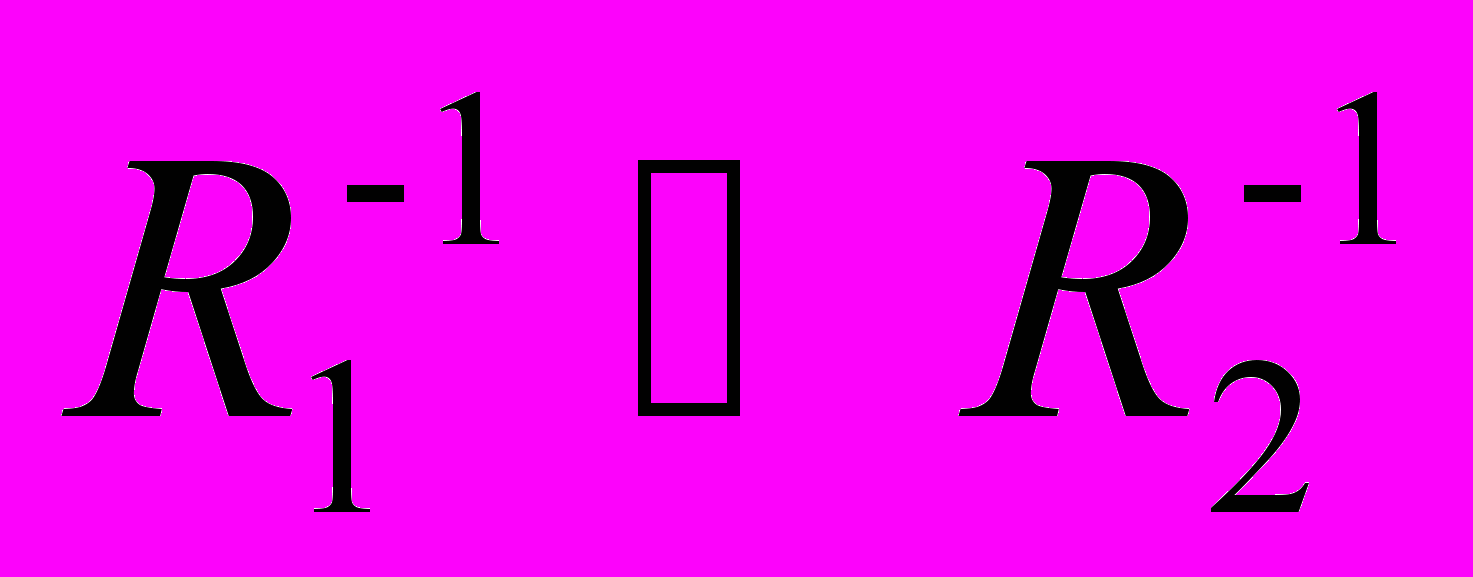


Доказать, что 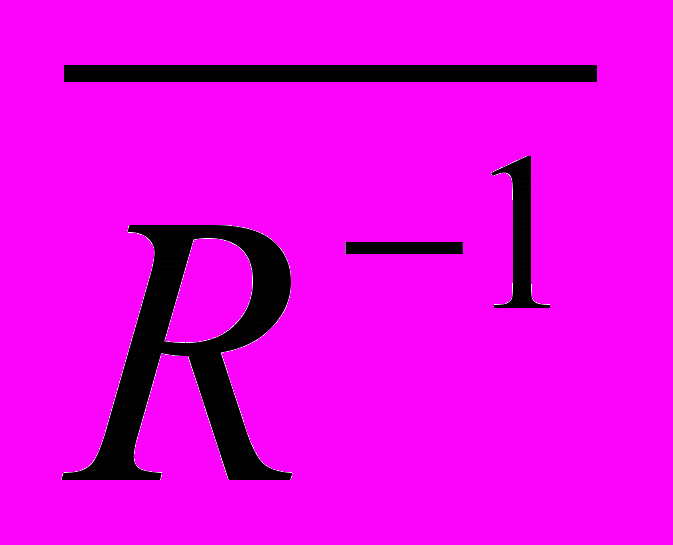= ()^-1 (т.е. операции дополнения и обращения перестановочны)


Доказать соотношения двойственности:

(R^d)^d = R,

(R₁R₂)^d = ,

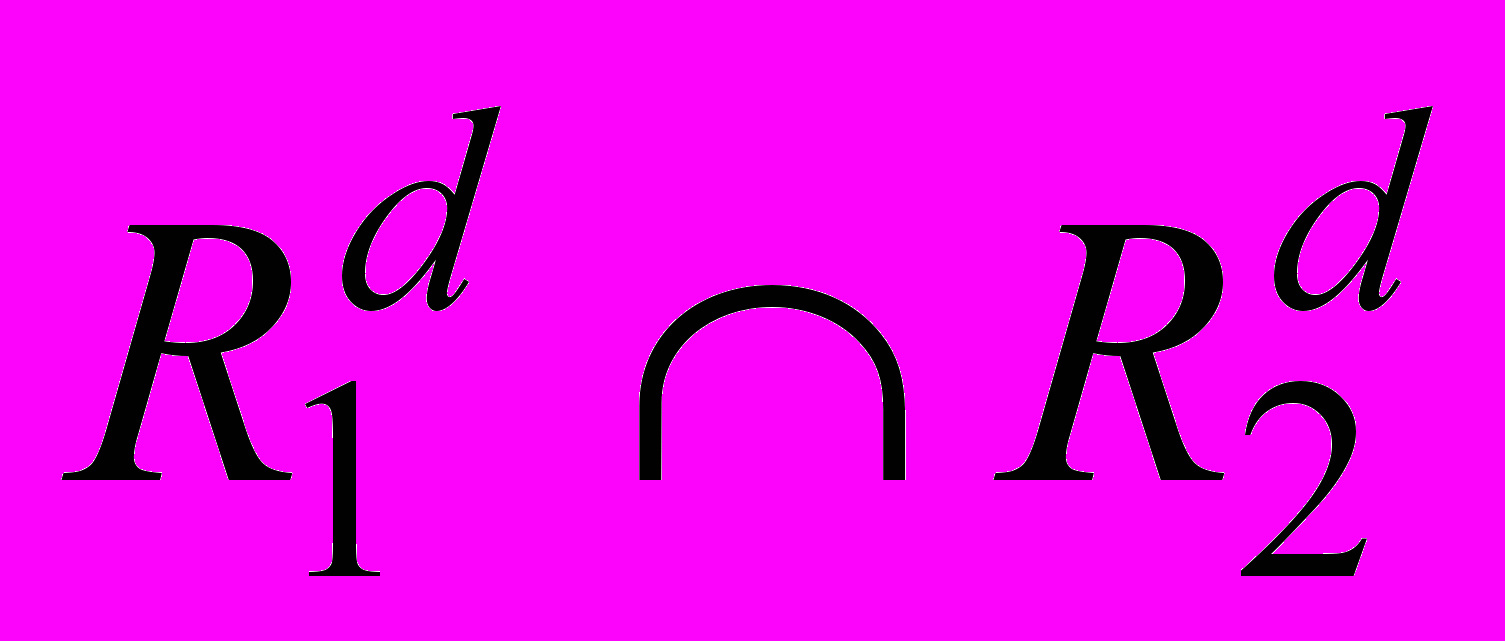(R₁R₂)^d =


Какой вид имеет отношение RR, если R – отношение «меньше» на множестве действи-тельных чисел? На множестве целых чисел?


Доказать, что для произведения отношений выполняется ассоциативный (сочетательный) закон: (AB)C = A(BC).


Привести пример двух отношений R₁ и R₂, таких, что R₁R₂ ≠ R₂R₁


Привести пример двух разных отношений R₁ и R₂, таких, что R₁R₂ = R₂R₁


Доказать, что отношение R симметрично тогда и только тогда, когда R = R^-1


Доказать, что если R асимметрично, то оно антирефлексивно.


Привести пример антисимметричного отношения, которое не является ни симметричным, ни асимметричным.


Описать все отношения, являющееся одновременно симметричными и антисимметрич-ными.

Доказать, что пустое отношение транзитивно.


Доказать, что для рефлексивного отношения транзитивность эквивалентна условию R² = R


Привести пример транзитивного отношения, для которого R²  R (содержится и не совпа-дает).


Доказать, что R =  является единственным примером транзитивного антирефлексивного отношения, для которого R² = R.


Доказать, что ацикличность эквивалентна условию: из x₁Rx₂, x₂Rx₃, …, x_{k – 1}Rx_k следует, что x_kx₁ для любого k.


Доказать, что любое ацикличное отношение асимметрично.


Доказать, что любое антирефлексивное транзитивное отношение ациклично.


Привести пример транзитивного не ацикличного отношения.


Привести примеры отношений, обладающими в точности одним, двумя, тремя и четырьмя свойствами из числа следующих: рефлективность, симметричность, транзитивность, анти-симметричность.


Сколько отношений эквивалентности существует на множествах из 2, 3 и 4 элементов?


Привести пример отношения, являющегося одновременно частичным порядком и эквивалентностью.


Сколько частичных порядков существует на множествах из 2, 3 и 4 элементов?


Доказать, что максимум по частичному порядку единственен.


Верно ли утверждение предыдущей задачи для произвольного отношения?


Доказать, что максимум не является мажорантой.


Доказать, что для любого ацикличного отношения R на конечном множестве множество мажорант Ω^R непусто.


Верно ли утверждение предыдущей задачи для произвольных множеств?


Пусть R – отношение частичного порядка на конечном множестве Ω. Доказать, что Ω^R непусто.


Могут ли одновре­менно существовать максимумы и мажоранты, не являющиеся максиму-мами, по одному отношению?


Проверить, что для множества альтернатив {(3,7,0), (4,5,1), (2,3,0), (3,7,3), (2,6,3), (4,5,2)} множество Парето состоит из альтернатив (3,7,3) и (4,5,2).


Пусть исходное множество альтернатив состоит из 100 элементов. Может ли множество Парето состоять из: 1 элемента; 100 элементов; 43 элементов; 99 элементов?


Доказать, что для любого конечного множества X множество Парето непусто.


Привести пример множества X, для которого множество Парето пусто.


Пусть 12 школьников имеют следующие оценки:

Школьник	Алгебра	Геометрия	Литерату- ра	Английс-кий	Физика	История	Физкуль- тура
1. Aрсенкова Александра	5	4	4	5	4	5	4
2. Баранникова Елена	3	4	4	3	4	3	4
3. Василенко Владимир	4	5	5	4	3	4	5
4. Кулакова Екатерина	3	3	4	3	3	4	3
5. Михайлова Елена	3	3	4	4	4	5	3
6. Морозова Мария	5	4	3	5	4	3	3
7. Перепечаева Арина	4	3	5	4	5	4	5
8. Полищук Наталья	3	5	3	3	3	3	4
9. Сафронова Екатерина	4	4	4	3	4	5	5
10. Старкова Елена	4	5	3	4	3	4	4
11. Фандеев Валерий	4	4	4	5	5	4	4
12. Широков Кирилл	5	3	5	4	4	3	3