Программа «Методы принятия решений». Гу-вшэ, 2010 г. Министерство экономического развития и торговли Российской Федерации Национальный исследовательский университет
| Вид материала | Программа |
Содержание4. Михайлова Елена 6. Перепечаева Арина |
- Российской Федерации Министерство образования и науки Российской Федерации Государственный, 343.55kb.
- Министерство экономического развития и торговли российской федерации государственный, 5460.46kb.
- Министерство экономического развития и торговли российской федерации государственный, 5459.19kb.
- Министерство экономического развития и торговли российской федерации государственный, 5458.65kb.
- Министерство экономического развития и торговли российской федерации государственный, 5753.09kb.
- Государственная программа Российской Федерации «Доступная среда» на 2011 2015 годы, 1560.95kb.
- Правительство Российской Федерации, а после утверждения направляется в Федеральное, 11.35kb.
- Приказ «о едином учёте преступлений», 767.93kb.
- 1. 10. Министерство экономического развития и торговли Российской Федерации, 198.8kb.
- Правительство Российской Федерации Национальный исследовательский университет Высшая, 299.13kb.
Однако аналитик-консультант, опираясь на данные о значениях трех критериев, хочет предложить для выбора инвестору не два первых фонда из таблицы, а бóльшее их число. Раскрыть соображения аналитика.
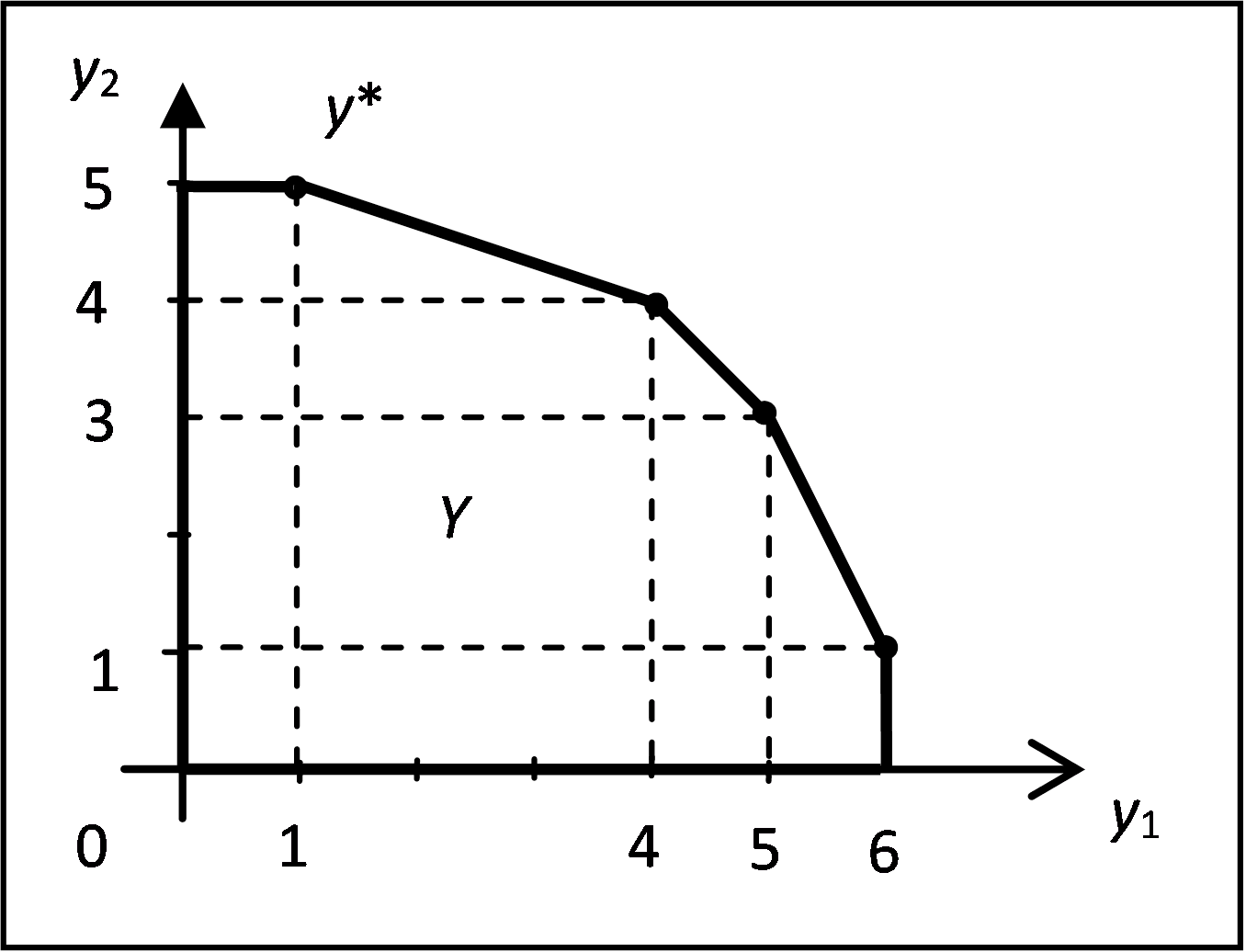
ЗАДАЧА 2. Множество достижимых векторных оценок Y представлено на рисунке. Выделить (жирными линиями и точками на рисунке) паретову границу. Указать, при каких значениях компоненты w1 вектора w = (w1, w2) с положительными компонентами, в сумме равными 1, точка y* будет выделена при максимизации на Y функций
L
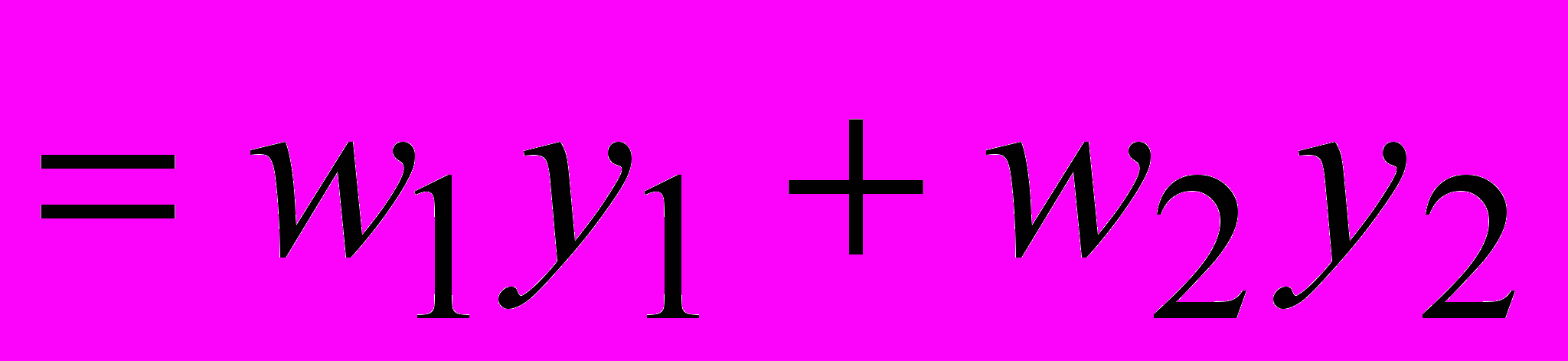 и G
и G 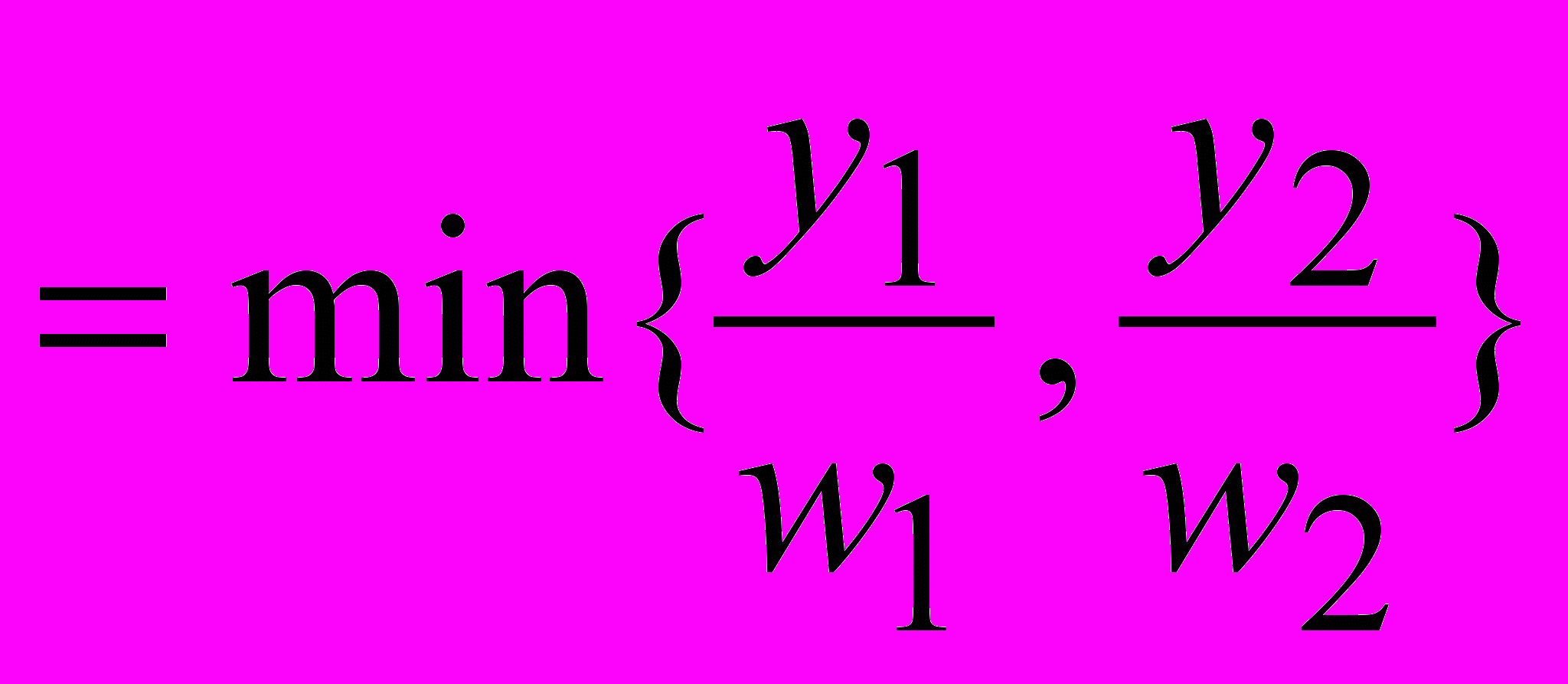 .
.
ЗАДАЧА 3. При каких условиях (свойствах множества вариантов и критериев) можно га-рантировать, что в что в трехкритериальной задаче максимизация на X функции

выделит Парето-оптимальный вариант? Ответ обосновать.
ЗАДАЧА 4. Пусть на множестве Ω = {a, b, c, d} заданы два бинарных отношения: aR1b, aR1c; bR2b, dR2a. Найти R1R2.
Вариант экзаменационной работы
ЗАДАЧА 1. Отметки 7 школьников по 4 предметам даны в таблице:
| Школьник | Алгебра | Геометрия | Литература | Английский |
| 1. Aрсенкова Александра лександра | 5 | 4 | 4 | 5 |
| 2. Баранникова Елена | 3 | 4 | 4 | 3 |
| 3. Кулакова Екатерина | 3 | 3 | 4 | 3 |
4. Михайлова Елена | 3 | 3 | 4 | 4 |
5. Морозова Мария | 5 | 4 | 3 | 5 |
6. Перепечаева Арина | 4 | 3 | 5 | 4 |
7. Полищук Наталья | 3 | 5 | 3 | 3 |
Найти и нарисовать паретовские уровни (со всеми дугами, соединяющими соседние уровни) по данным этой таблицы.
ЗАДАЧА 2. На конкурс представлены пять проектов новой системы, оцениваемой по че-тырём критериям. Оценки проектов по этим критериям с четырёхбалльной шкалой предс-тавлены таблицей. Требуется ранжировать все проекты по предпочтению, последователь-но применяя решающие правила, использующие следующую информацию о важности критериев (их шкала полагается порядковой):
1) (информации о важности нет);
2) качественная важность = {2 3 1 4};
3) количественная важность: 2 2 3 1,5 1 4.
На основании результатов проведенных расчетов для каждого из шагов 1) – 3) выделить множество претендентов на лучший проект. Для этапов 2 и 3 построить объясняющие цепочки для доминируемых вариантов.
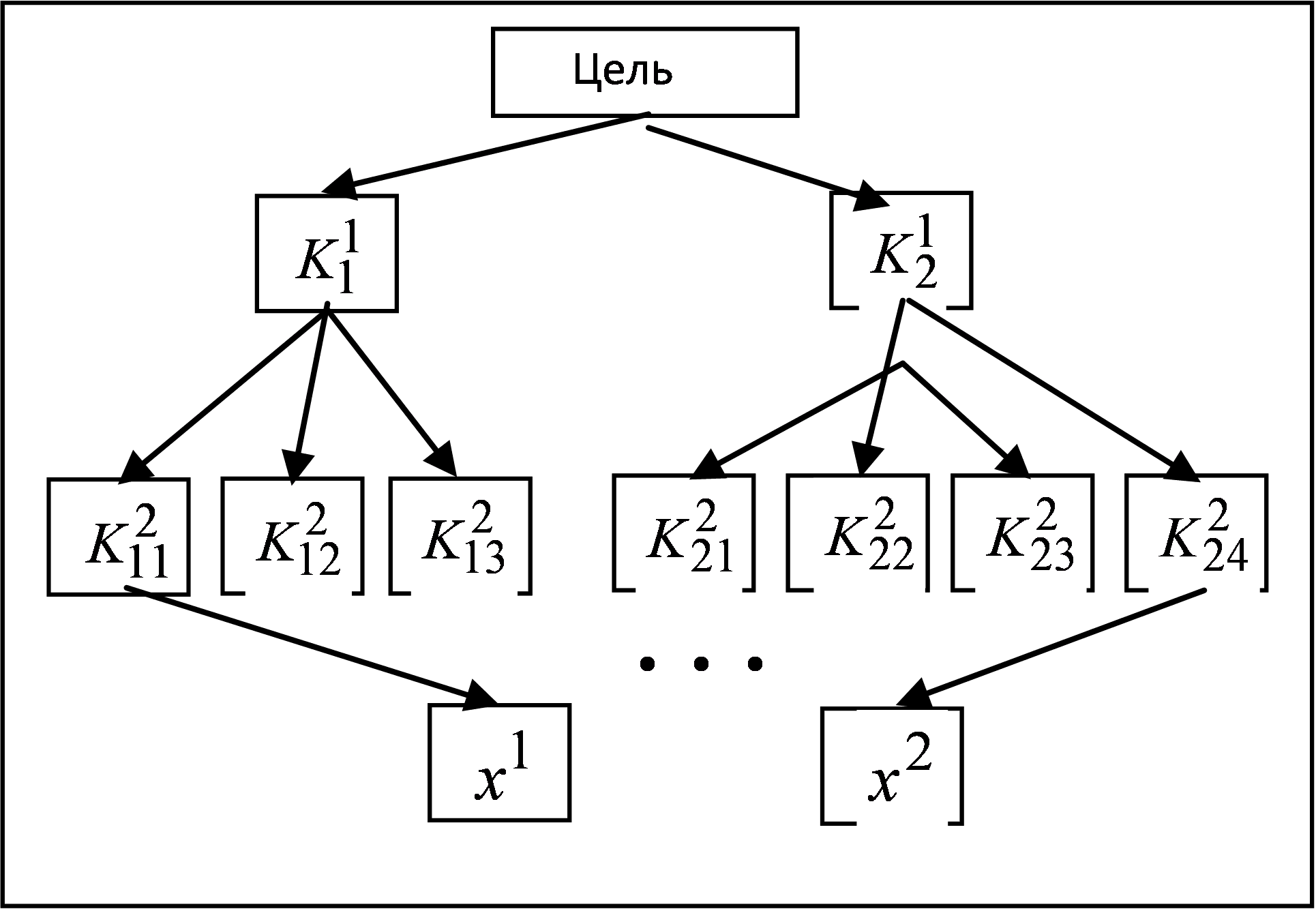
ЗАДАЧА 3. Для заданной иерархической структуры задачи выбора одного из двух воз-можных вариантов размещения нового производства найти методом анализа иерархий лучший вариант. Результаты парных сравнений критериев по важности и вариантов по ценности заданы таблицами:
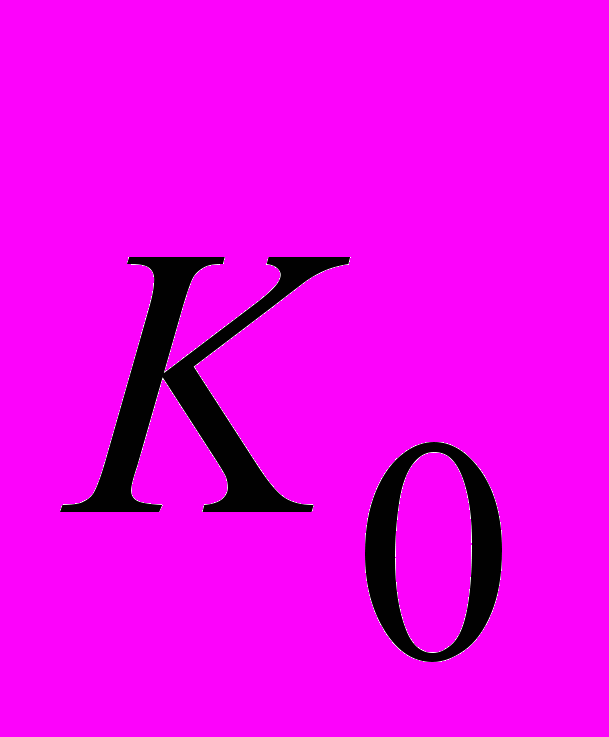 | 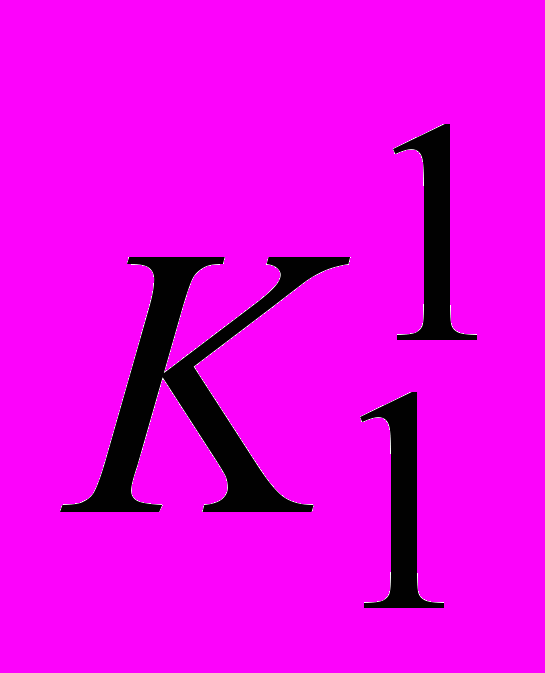 | 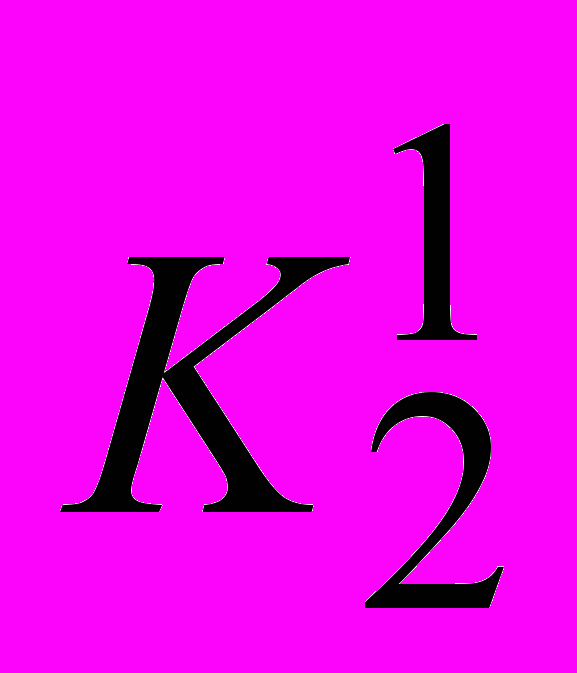 | | 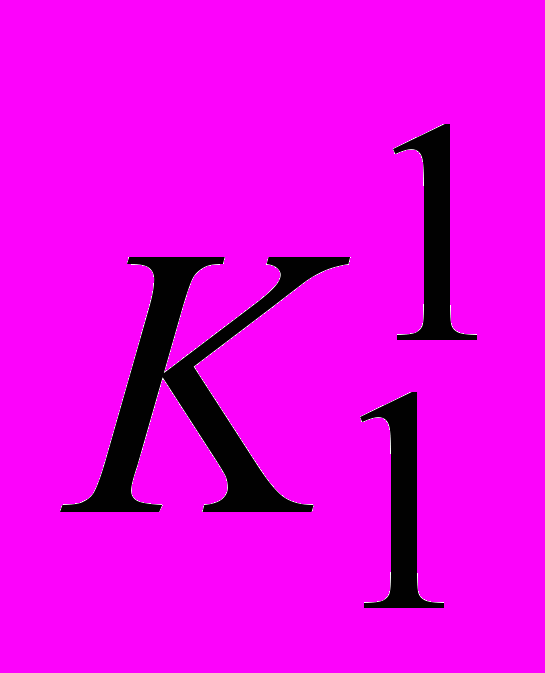 |  | 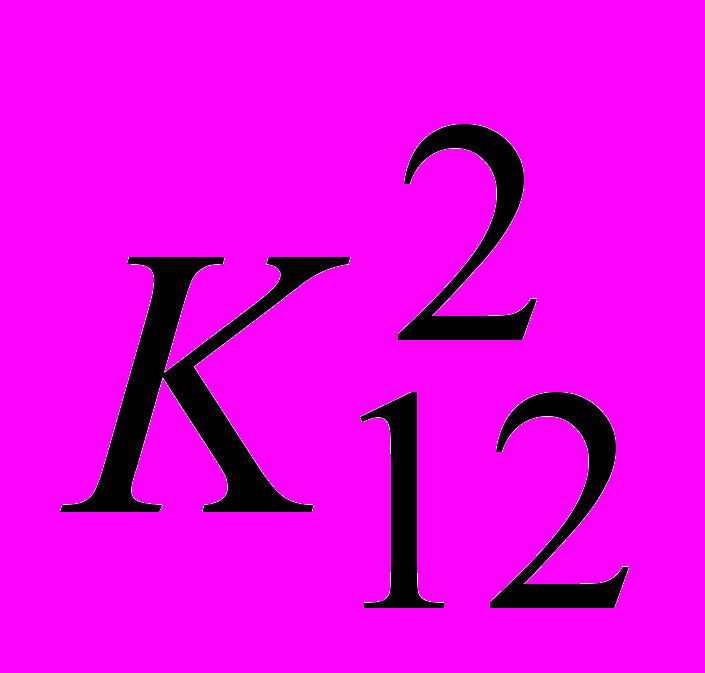 | 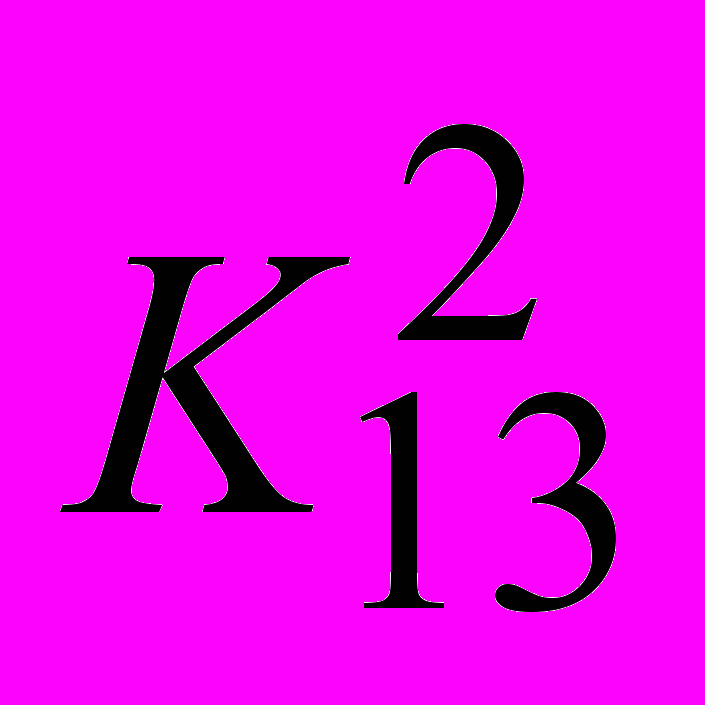 | | 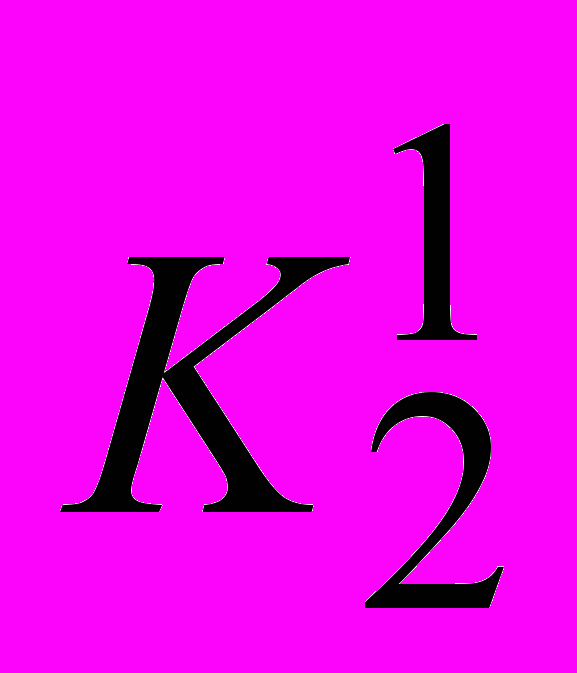 | 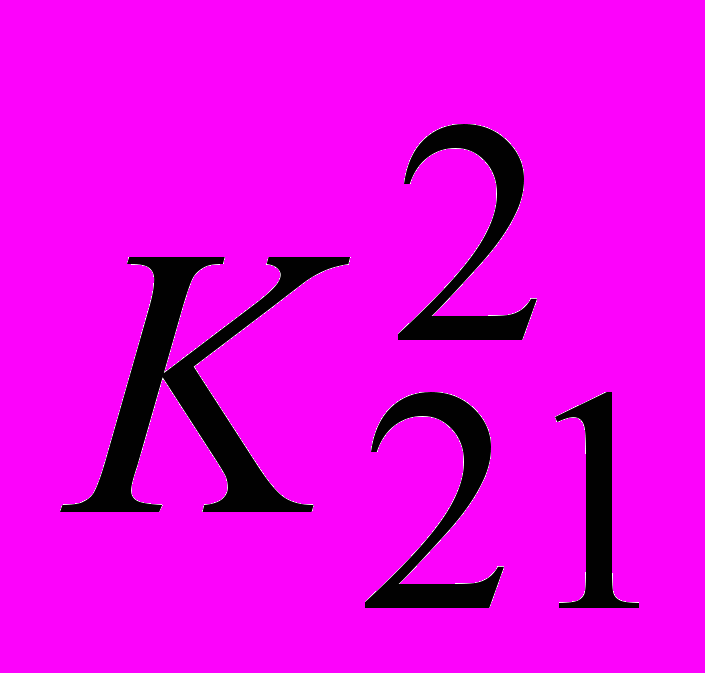 | 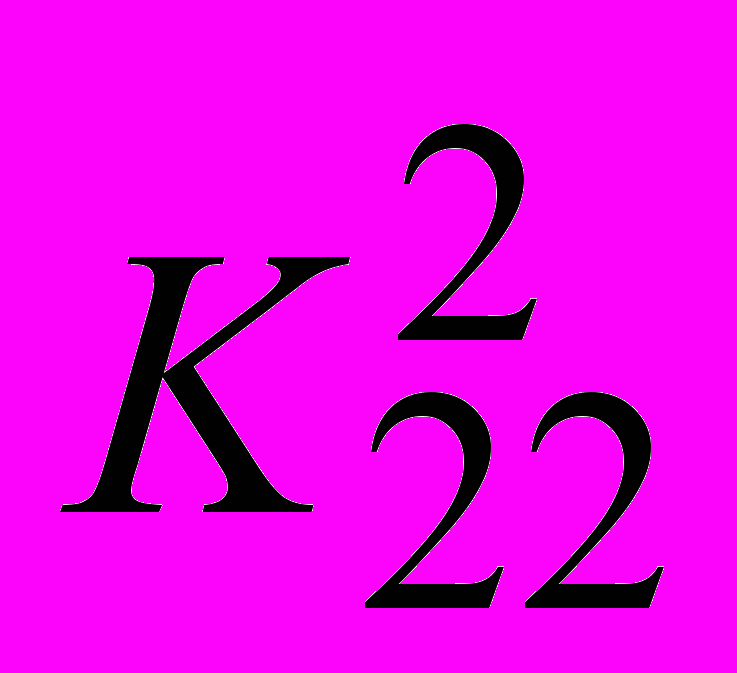 | 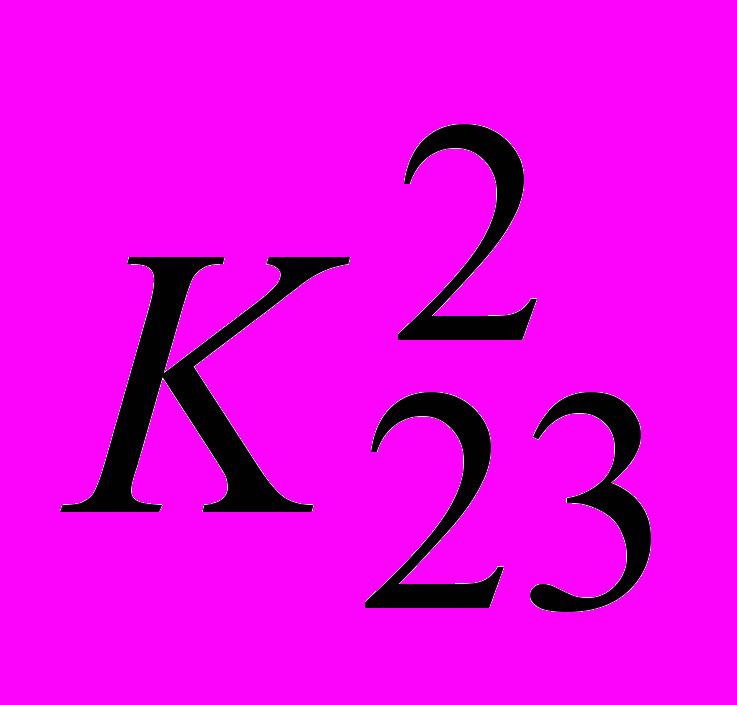 |  | |
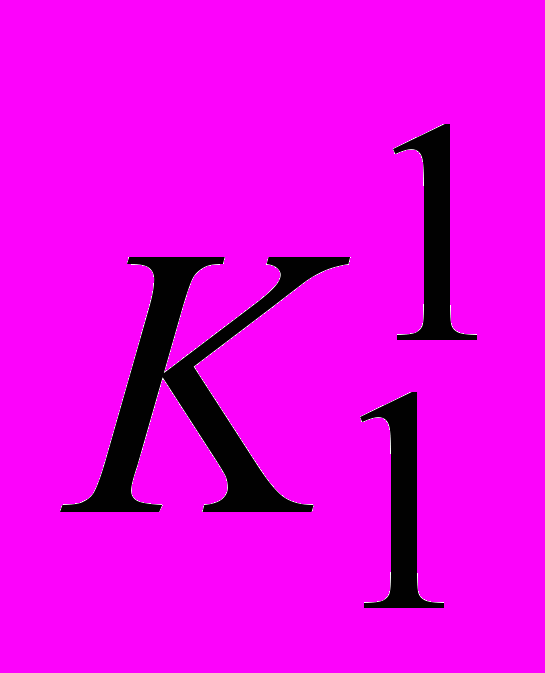 | 1 | ½ | |  | 1 | 3 | 5 | | 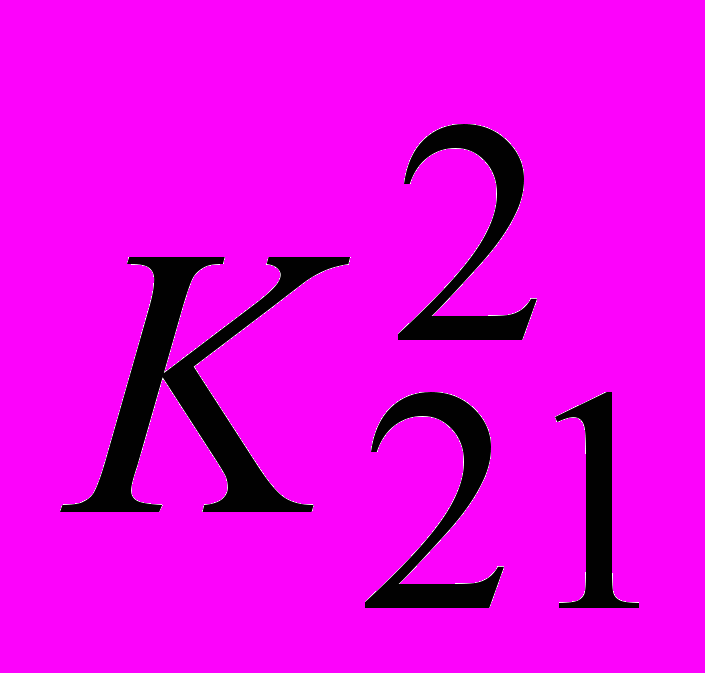 | 1 | 2 | 1/5 | ⅓ | |
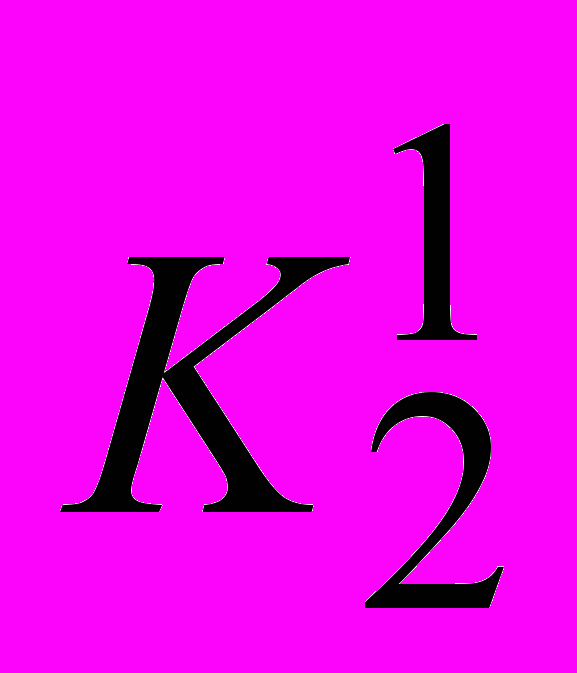 | 2 | 1 | | 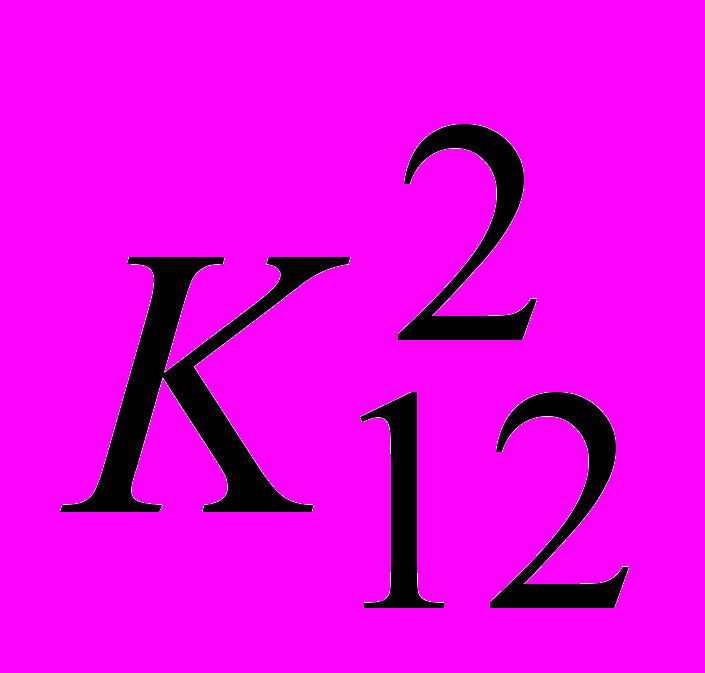 | ⅓ | 1 | 2 | | 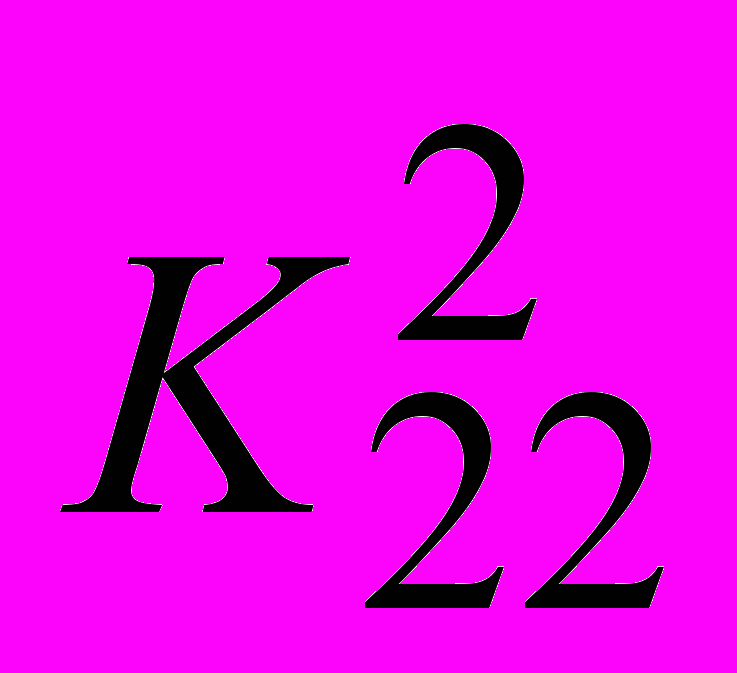 | ½ | 1 | ¼ | ¼ | |
| | | | | 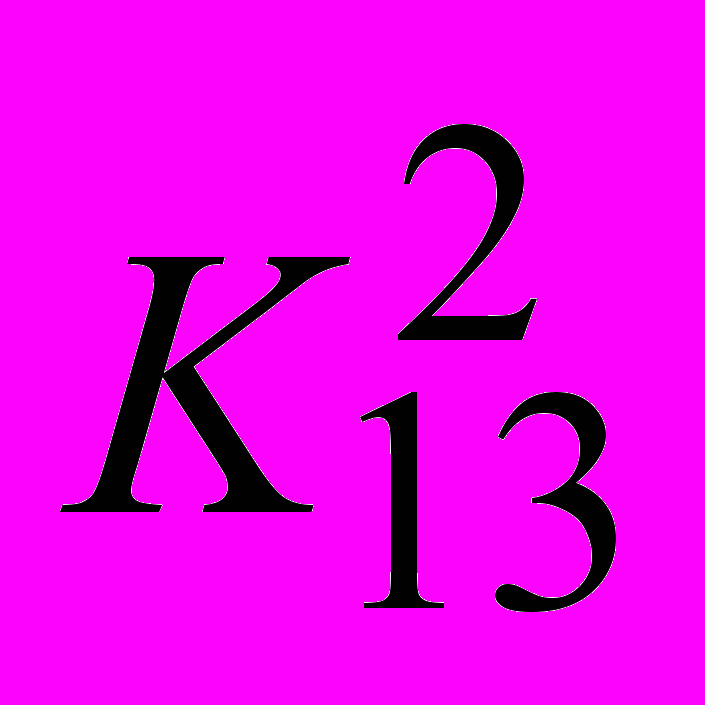 | 1/5 | ½ | 1 | | 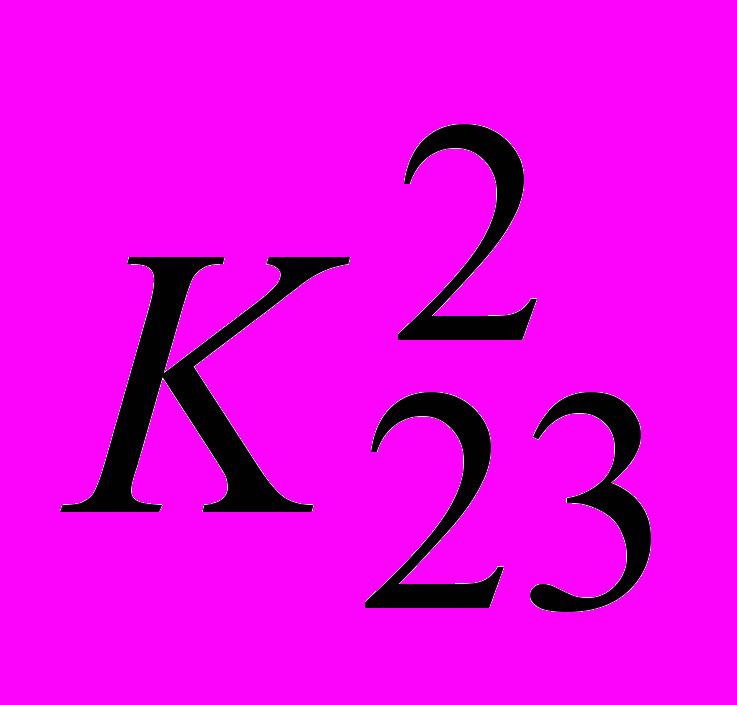 | 5 | 4 | 1 | 3 | |
| | | | | | | | | |  | 3 | 4 | ⅓ | 1 | |
| | | | | | | | | | | | | | | |
 | x1 | x2 | | 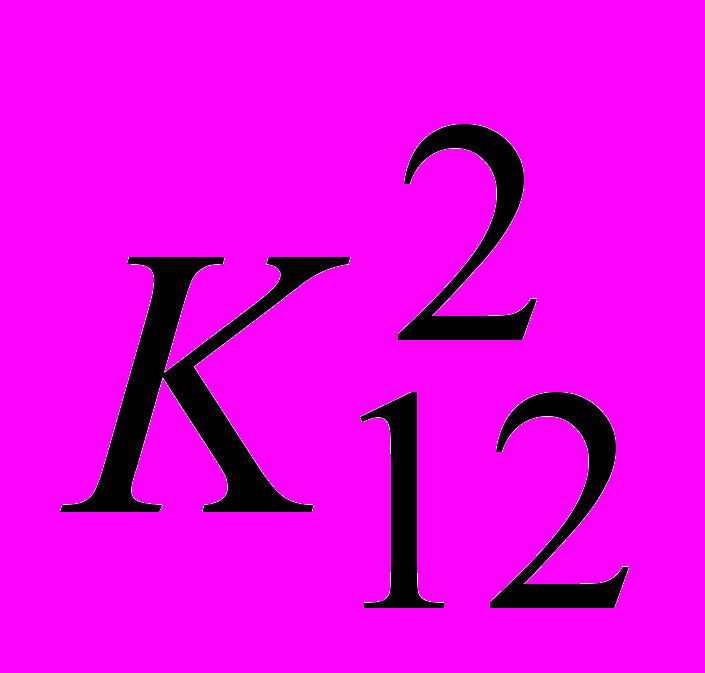 | x1 | x2 | | 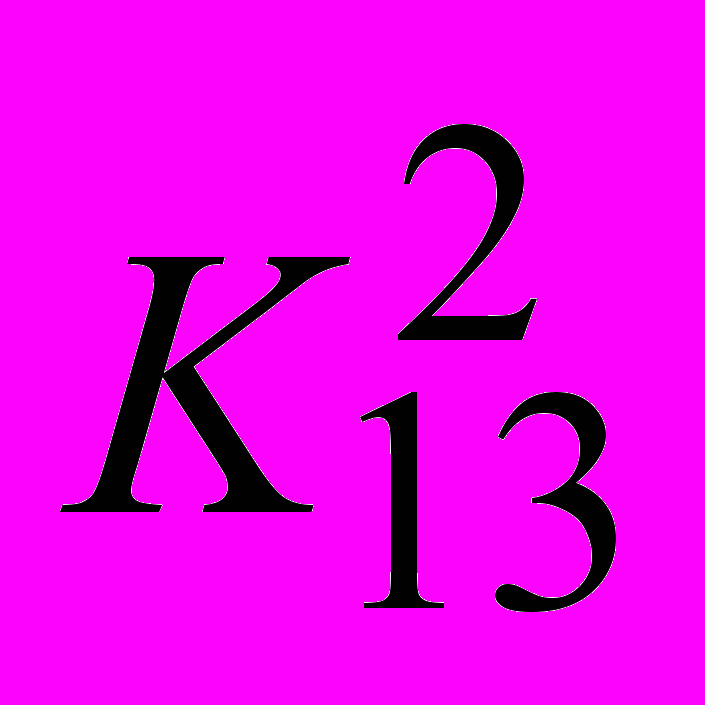 | x1 | x2 | | | | |
| x1 | 1 | 2 | | x1 | 1 | ⅓ | | x1 | 1 | 4 | | | | |
| x2 | ½ | 1 | | x2 | 3 | 1 | | x2 | ¼ | 1 | | | | |
| | | | | | | | | | | | | | | |
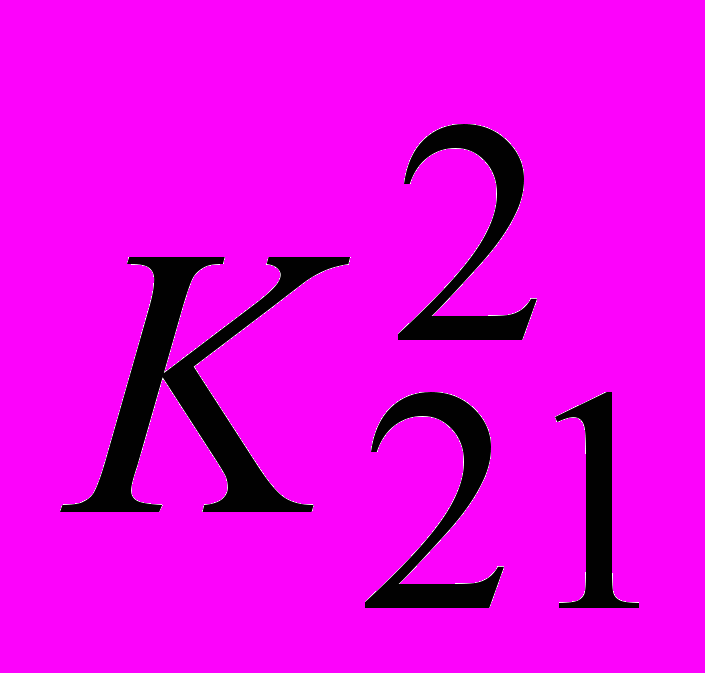 | x1 | x2 | | 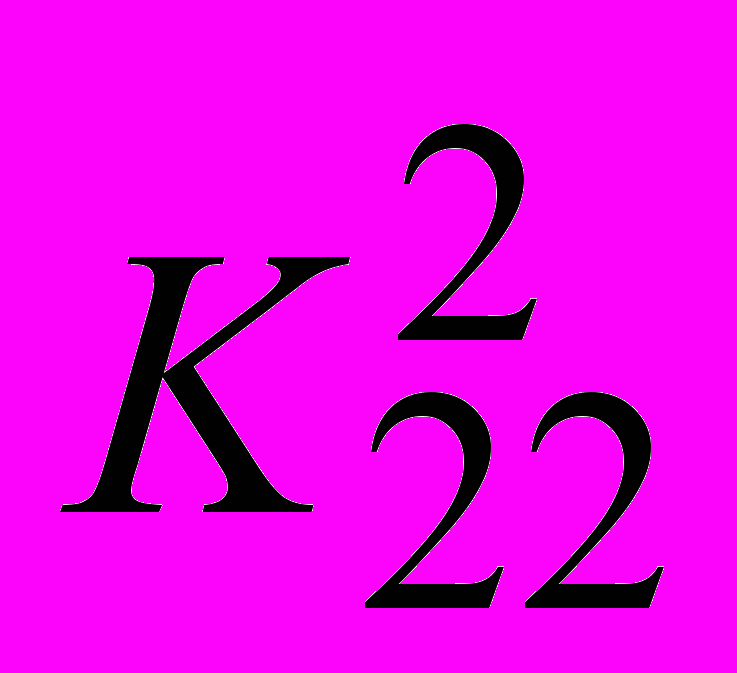 | x1 | x2 | | 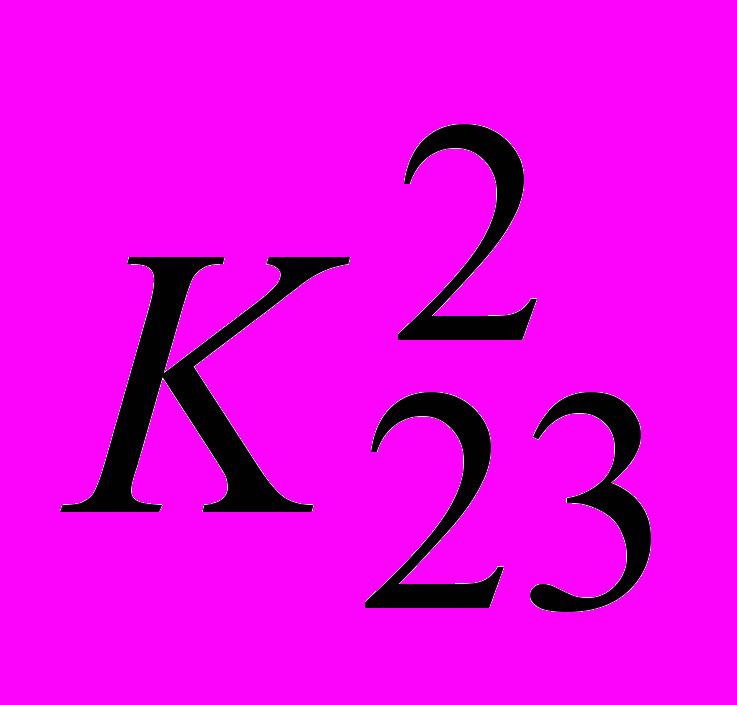 | x1 | x2 | |  | x1 | x2 |
| x1 | 1 | 3 | | x1 | 1 | 8 | | x1 | 1 | 1/5 | | x1 | 1 | ⅓ |
| x2 | ⅓ | 1 | | x2 | ⅛ | 1 | | x2 | 5 | 1 | | x2 | 3 | 1 |
