Методические указания по выполнению индивидуальных заданий по курсу «основы электроники» Для студентов Iкурса

Вид материала

Методические указания

Содержание Метод, основанный на применении законов Кирхгофа J в проводнике сопротивлением R Метод контурных токов. NК обычно меньше общего числа N NК уравнений на основе второго закона Кирхгофа: для контура A J Метод узловых потенциалов. Ii с использованием формулы преобразования: I Метод наложения. E1 оказываются подключенными последовательно соединенные сопротивления r1 и R Метод эквивалентного генератора. J сводится к определению ЭДС Е J1, протекающий через источник E Jэ2 рассчитывается любым из рассмотренных ранее методов. Определить сопротивление r Индивидуальное задание №2.

Подобный материал:

• Пособие предназначено для студентов дневного и вечернего отделений. Указани, 502.9kb.
• Методические указания к выполнению индивидуальных заданий для студентов дневного, 229.08kb.
• Методические указания по выполнению контрольных работ и домашних заданий (рефератов), 314.07kb.
• Методические указания по выполнению контрольной работы Для студентов Iкурса, обучающихся, 344.05kb.
• Физические основы электроники, 499.24kb.
• Методические указания к выполнению курсовой работы по курсу «Основы климатологии, 417.3kb.
• Программа и методические указания к выполнению курсовой работы и контрольных работ, 146.23kb.
• Методические указания к выполнению курсовой работы «Разработка приложений, предназначенных, 348.71kb.
• Методические указания по выполнению курсовой работы по общепрофессиональным дисциплинам, 245.54kb.
• Методические указания по выполнению семестровой контрольной работы с комплектом заданий, 701.46kb.

Рассмотрим решение задачи каждым из упомянутых методов.

Метод, основанный на применении законов Кирхгофа

Свойства любой электрической цепи можно установить из уравнений, составленных на основе известных физических законов: закона Ома, первом и втором законах Кирхгофа.

Согласно закону Ома сила тока J в проводнике сопротивлением R пропорциональна напряжению U на его концах:

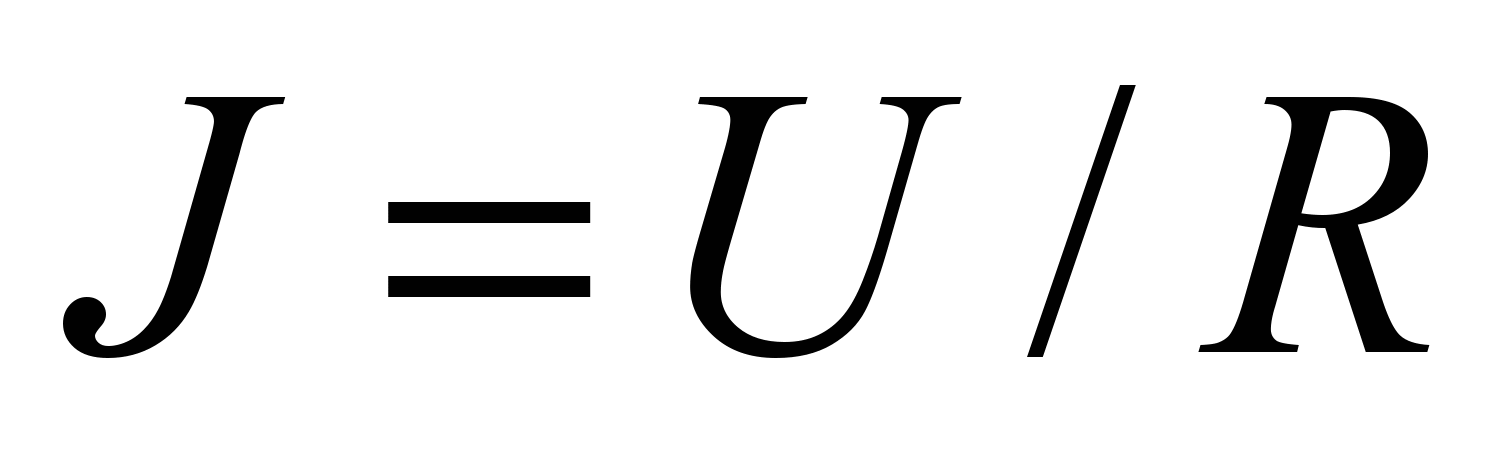(1)

Расчет токов, напряжений и ЭДС в разветвленной цепи производится на основе законов Кирхгофа.

Первый закон: алгебраическая сумма сил токов на участках цепи, сходящихся в любой точке разветвления, равна нулю

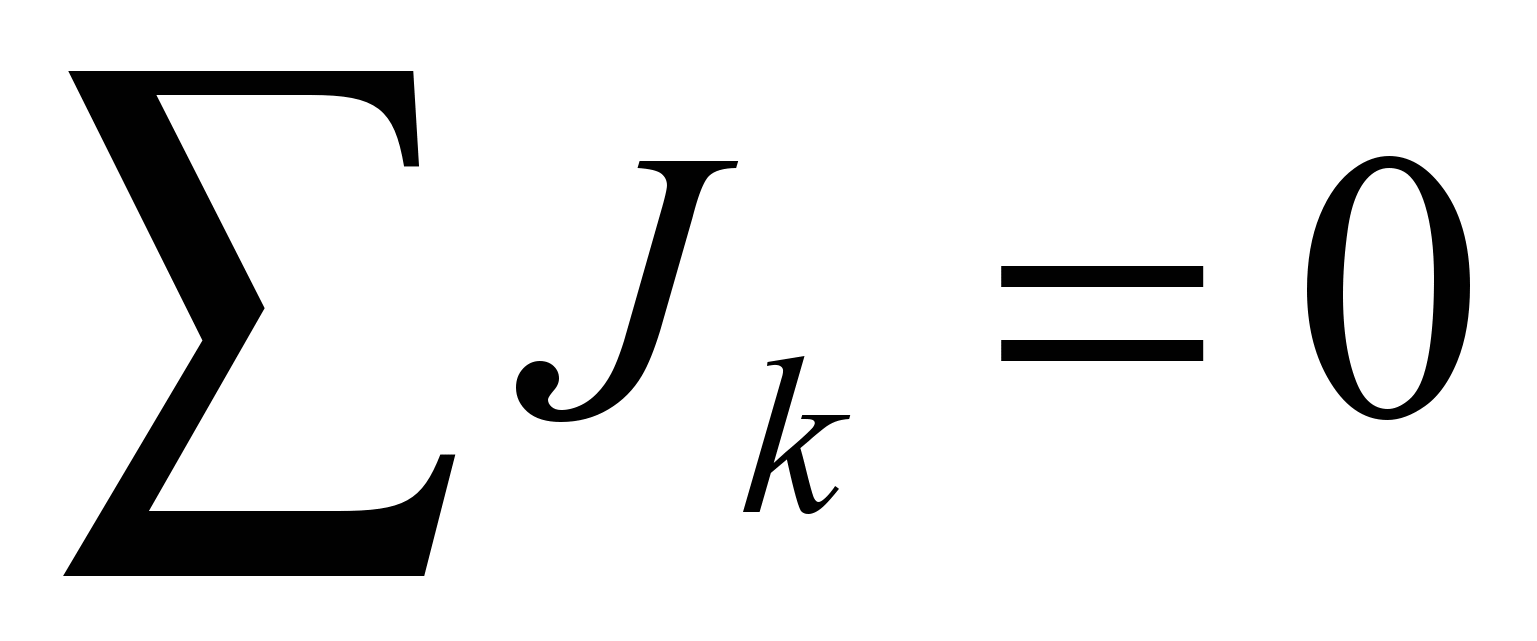(2)

Перед составлением уравнений по первому закону Кирхгофа нуж­но сначала в каждой ветви задаться условно-положительным направлением тока. Токам, направленным к узлу, приписывают знак «плюс», а токам, направленным от узла, — знак «минус».

Второй закон: для любого замкнутого контура, выделенного из разветвленной цепи, алгебраическая сумма произведений сил токов на соответствующие сопротивления равна алгебраической сумме всех электродвижущих сил в этом контуре

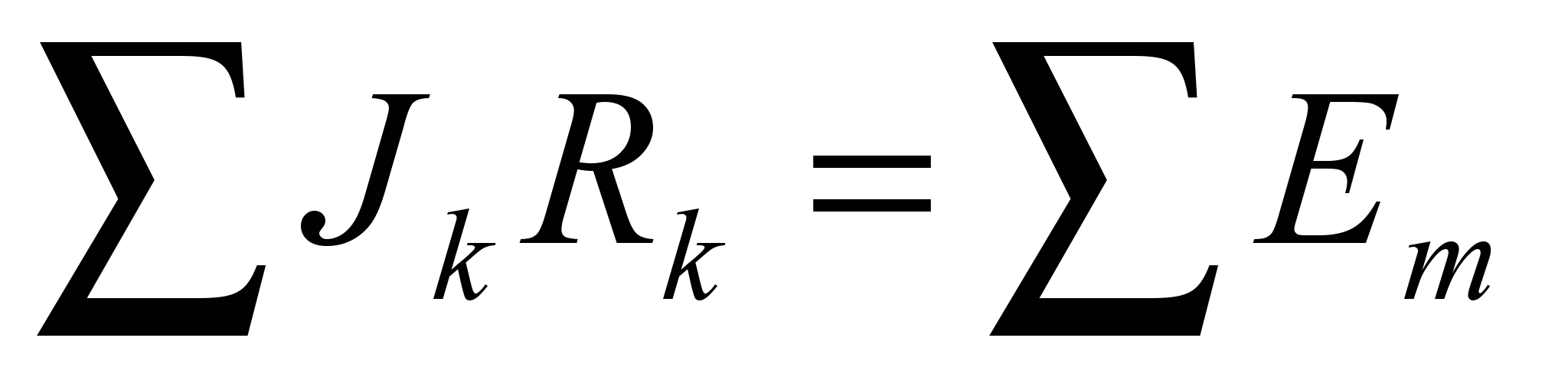(3)

При этом, если условно-положительные направления токов через пассивные элементы совпадают с направлением обхода контура, падение напряжения на соответствующем элементе за­писывают со знаком «плюс», если же направление тока через пассивный элемент противоположно направлению обхода контура — со зна­ком «минус». ЭДС соответствующего источника энергии записывают со знаком «плюс», если направление обхода контура совпадает с­ направле­нием стрелки ЭДС, и со знаком «минус» — в противоположном случае.

Зададимся предполагаемыми направлениями токов J_k и направлением обхода (пунктирные стрелки) как это показано на рис. 2.



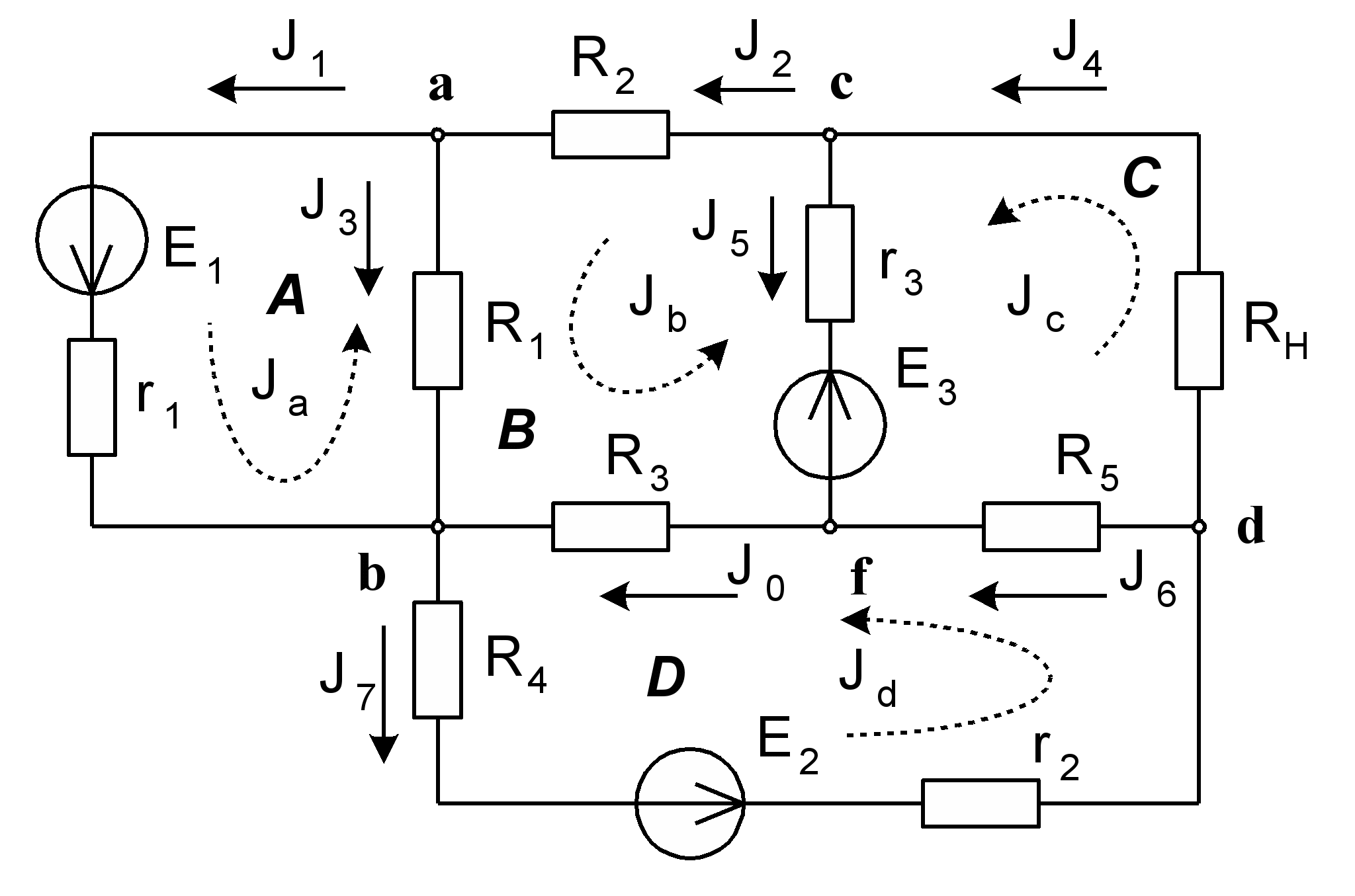
Рис. 2. Принципиальная схема с предполагаемыми направлениями токов и направлениями обхода контуров.

Далее составим N_У–1 уравнений по первому закону Кирхгофа:

для узла a –J₁ + J₂ – J₃=0

для узла c –J₂ + I₄ – J₅=0

для узла d –J₄ – J₆ + J₇=0

для узла f J₅ + J₆ – J₀=0

Составим N_К уравнений по второму закону Кирхгофа:

для контура A J₁r₁ – J₃R₁ = E₁

для контура B J₃R₁+J₂R₂ – J₅r₃–J₀R₃ = E₃

для контура C J₅r₃+J₄R_H –J₆R₅ = – E₃

для контура D J₇(r₂+R₄)+ J₆R₅+J₀R₃ = E₂

Объединим эти уравнения в одну систему, подставим соответствующие значения E_i, r_i, R_j и решим систему одним из известных методов. Решение задачи в MathCAD приведено на листинге №1.

Следует обратить внимание на знаки полученных значений токов. Если значение тока отрицательное, то его направление противоположно тому, что указано на схеме.

Далее следует провести проверку полученных значений токов. Для этого необходимо проверить баланс мощностей: для любой замкнутой электрической цепи сумма мощностей Р_e, развиваемая источниками электрической энергии, должна быть равна сумме мощностей Р_r, расходуемых в приемниках этой энергии.

Мощность, выделяющаяся в резистивном элементе, всегда положительна и равна RJ².

Знак мощности источников энергии зависит от режима их работы. Если направление тока в цепи совпадает с направлением ЭДС, то источник отдает мощность и Р_е > 0. В противном случае источник потребляет мощность и Р_е < 0.

Общий вид уравнения баланса мощностей:

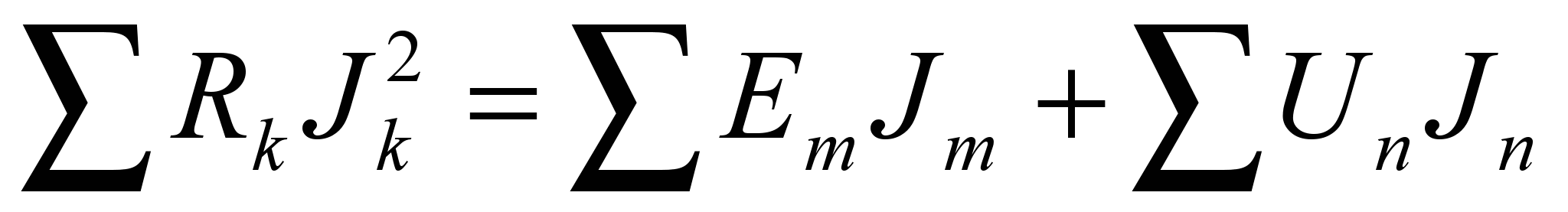(4)

В нашей схеме источники тока отсутствуют, поэтому второе слагаемое в правой части выражения (4) равно нулю.

Для расчета падений напряжения на элементах электрической цепи следует воспользоваться законом Ома (1).



Метод контурных токов.

При использовании метода контурных токов расчет сложной разветвленной схемы проводят в два этапа.

На первом этапе вводят и рассчитывают вспомогательные контурные токи, число которых N_К обычно меньше общего числа N_В неизвестных токов. На втором этапе путем простого алгебраического суммирования находят искомые токи.

Для решения нашей задачи зададимся направлениями контурных токов J_a, J_b, J_c и J_d в замкнутых контурах A, B, C и D соответственно (на пример, как это показано на рис. 2, пунктирными линиями против часовой стрелке). По любой ветви должен протекать хотя бы один контурный ток.

Для расчета контурных токов составим систему из N_К уравнений на основе второго закона Кирхгофа:

для контура A J_a (r₁+R₁) – J_b R₁= E₁

для контура B J_b (R₁+R₂+ R₃+r₃) – J_a R₁– J_c r₃ – J_d R₃= E₃

для контура C J_c (r₃+R_H+R₅) – J_b r₃ – J_d R₅= – E₃

для контура D J_d (r₂+R₃+R₄+R₅) – J_c R₅ – J_b R₃ = E₂

Действительные токи в ветвях определяются наложением контурных токов. Для определения истинных значений токов, протекающих в схеме, запишем соотношения, связывающие их с контурными токами:

J₀ = J_d – J_b ; J₁ = J_a ; J₂ = J_b ;

J₃ = J_b– J_a ; J₄ = J_c ; (5)

J₅ = J_c – J_b ; J₆ = J_d – J_c ; J₇ = J_d

Если какое-нибудь значение тока получится отрицательным, то его направление противоположно тому, что указано в схеме.

Правильность расчета значений токов в схеме, как и в предыдущем случае, проверяется путем проверки выполнения баланса мощностей (4).

Для расчета падений напряжения на элементах электрической цепи следует воспользоваться законом Ома (1).

Решение задачи методом контурных токов с помощью программы MathCAD приведено на листинге №2.



Метод узловых потенциалов.


Этим методом рекомендуется пользоваться в тех случаях, когда число уравнений в системе меньше числа уравнений, составленных по методу контурных токов. Число уравнений в системе при использовании метода узловых потенциалов равно n = N_У–1.

Расчет разветвленной схемы методом узловых потенциалов проводят в несколько этапов.

Если в схеме имеются источники ЭДС, их сначала преобразуют в эквивалентные источники тока I_i с использованием формулы преобразования:

I_i = E_i g_i (6)

где g_i = 1 / r_i есть внутренняя проводимость источника i.

Далее выбирают опорный, базисный узел и принимают его потенциал равным нулю. В качестве такого узла целесообразно выбрать узел, в котором сходится наибольшее число ветвей. Потенциалы в остальных узлах схемы отсчитываются от базисного узла.

Затем составляют и решают систему уравнений относительно узловых потенциалов V_i:

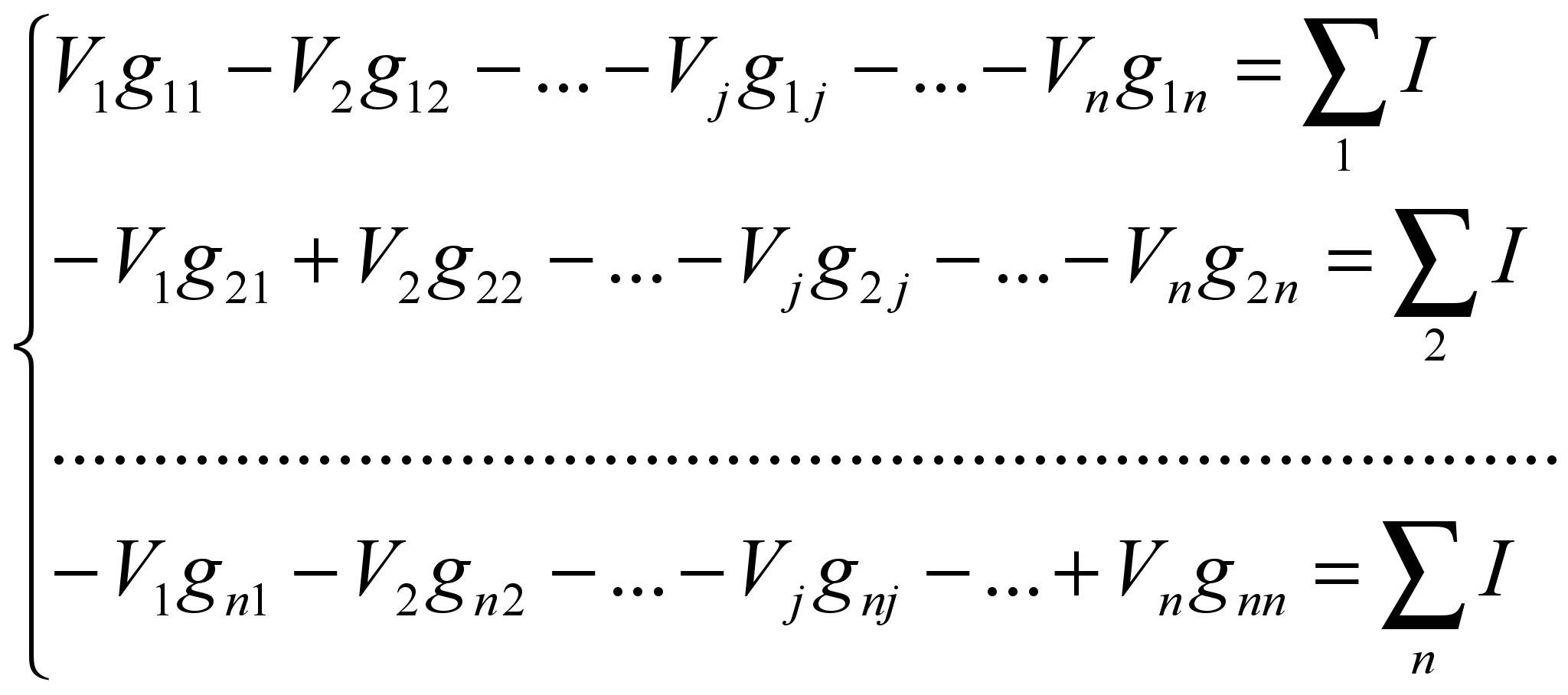(7)

где g_ii - сумма проводимостей ветвей, присоединенных к узлу i;

g_ij - сумма проводимостей ветвей, непосредственно соединяющих узел i с узлом j;

å I_i - алгебраическая сумма токов источников тока, присоединенных к узлу i, при этом со знаком плюс берутся те токи, которые направлены к узлу, и со знаком минус – в направлении от узла.

На последнем этапе по найденным узловым потенциалам находят искомые токи в ветвях с помощью закона Ома (1).

Преобразуем нашу схему в соответствии с изложенными выше правилами к виду, показанному на рис. 3.



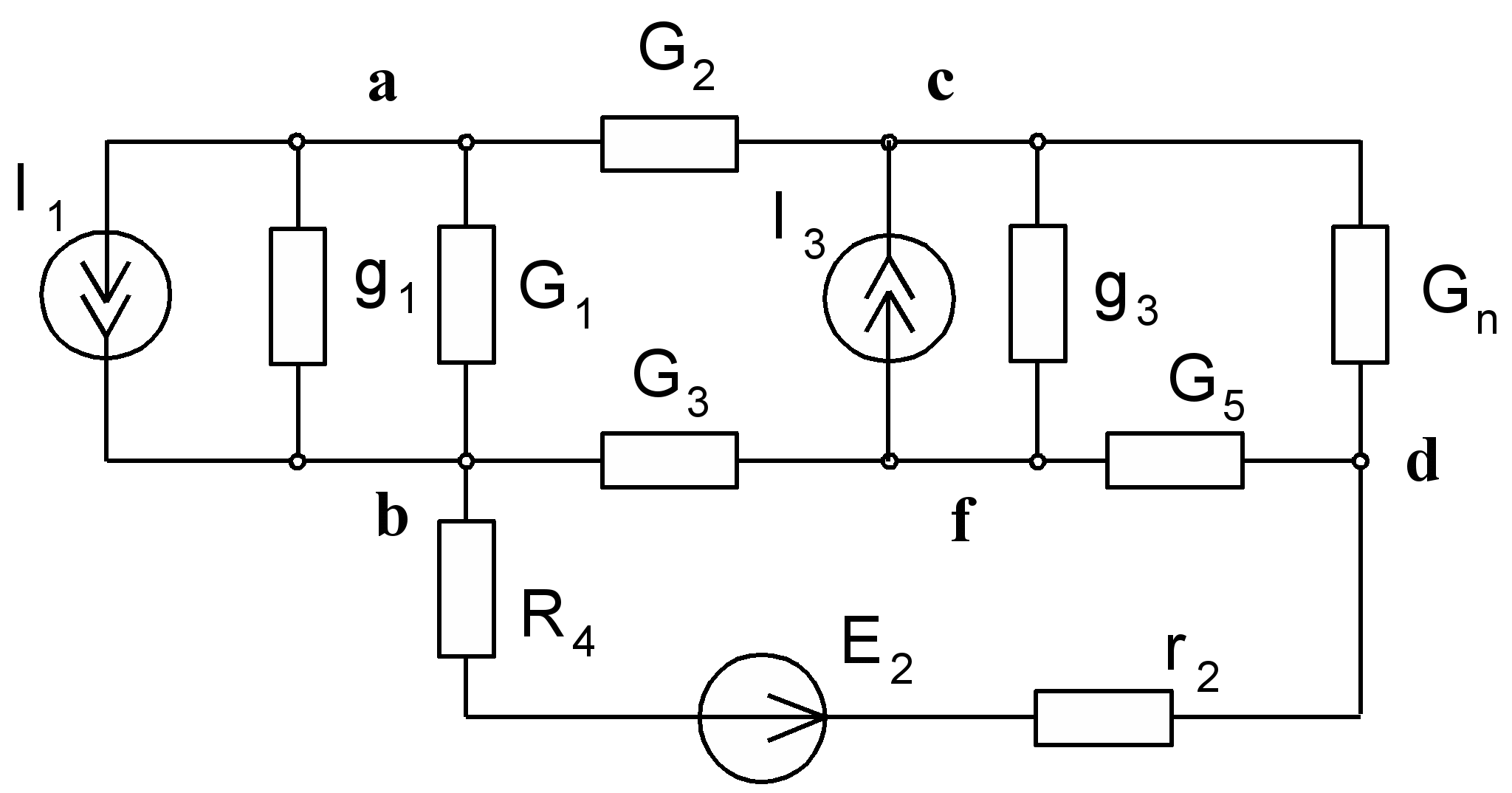
Рис. 3. Эквивалентная схема разветвленной цепи.


Выберем в качестве опорного базисного узла узел (b). Примем его потенциал равным нулю и составим систему уравнений относительно остальных узловых потенциалов:

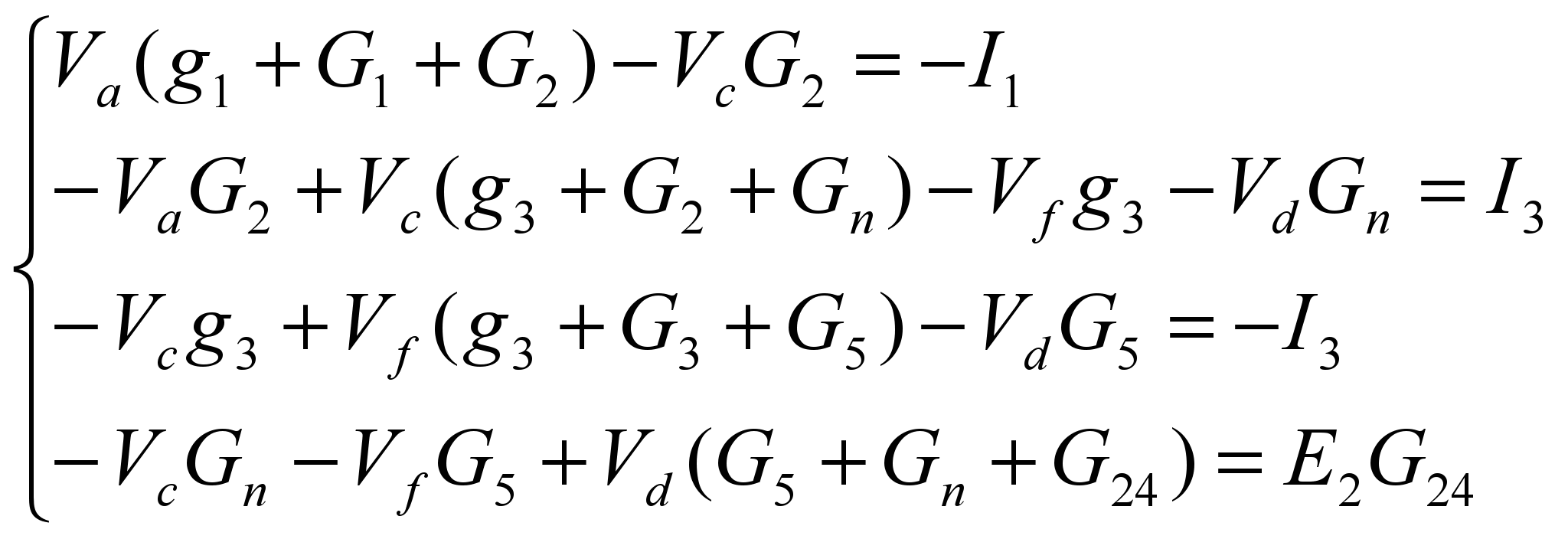(8)

где G₂₄ = 1/(r₂+R₄).

Определив значения потенциалов V_a, V_c, V_d и V_f соответственно для узлов a, c, d и f, воспользуемся законом Ома (2) и рассчитаем значения токов в ветвях нашей схемы:

J₀ = V_f G₃ ; J₁ = (E₁ + V_a) g₁ ; J₂ = (V_c - V_a) G₂ ;

J₃ = V_a G₁ ; J₄ = (V_d - V_c) G_n ; J₅ = (V_c - V_f - E₃ ) g₃ ;

J₆ = (V_d - V_f) G₅ ; J₇ = (E₂ - V_d ) G₂₄

Решение задачи по определению значений токов в схеме методом узловых потенциалов с использованием программы MathCAD приведено на листинге №3.

Правильность расчета проверяется путем проверки выполнения баланса мощностей (4).

Для расчета падений напряжения на элементах электрической цепи следует воспользоваться законом Ома (1).




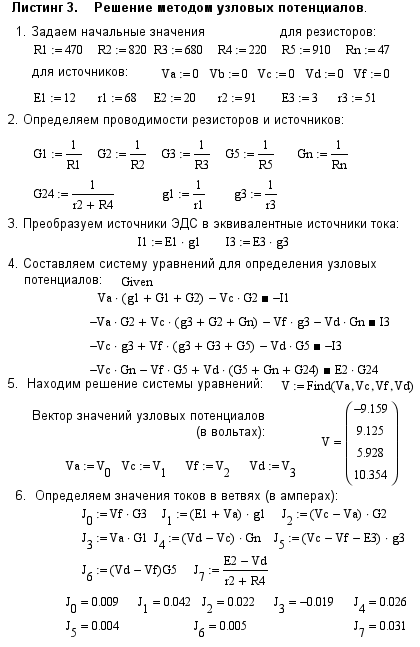
Метод наложения.


В основе метода наложения лежит принцип суперпозиции, заключающийся в том, что ток в любой ветви электрической цепи можно рассчитать как алгебраическую сумму токов, вызываемых в ней от каждого источника в отдельности. Ток от отдельно взятого источника называется частным. При расчете частного тока все остальные источники ЭДС заменяются короткозамкнутыми перемычками, а ветви с источниками тока размыкаются. Поскольку в этом случае в рассматриваемых цепях остается только по одному источнику, расчеты производят не решением системы уравнений, а последовательным упрощением цепей путем использования правил для последовательного и параллельного соединения элементов, преобразования звезды в треугольник или треугольника в эквивалентную звезду и т. д.

Напомним основные правила и закономерности эквивалентного преобразования схем.

1. Эквивалентное сопротивление цепи, состоящей из последовательно соединенных сопротивлений, равно сумме этих сопротивлений. Падения напряжений на этих сопротивлениях прямо пропорционально этим сопротивлениям.

2. Эквивалентная проводимость цепи, состоящей из параллельно соединенных сопротивлений, равна сумме проводимостей этих сопротивлений. Протекающие через сопротивления токи прямо пропорциональны их проводимостям или обратно пропорциональны их сопротивлениям.

3. Звезду сопротивлений можно преобразовать в эквивалентный треугольник сопротивлений, как это показано на рис. 4, и наоборот.



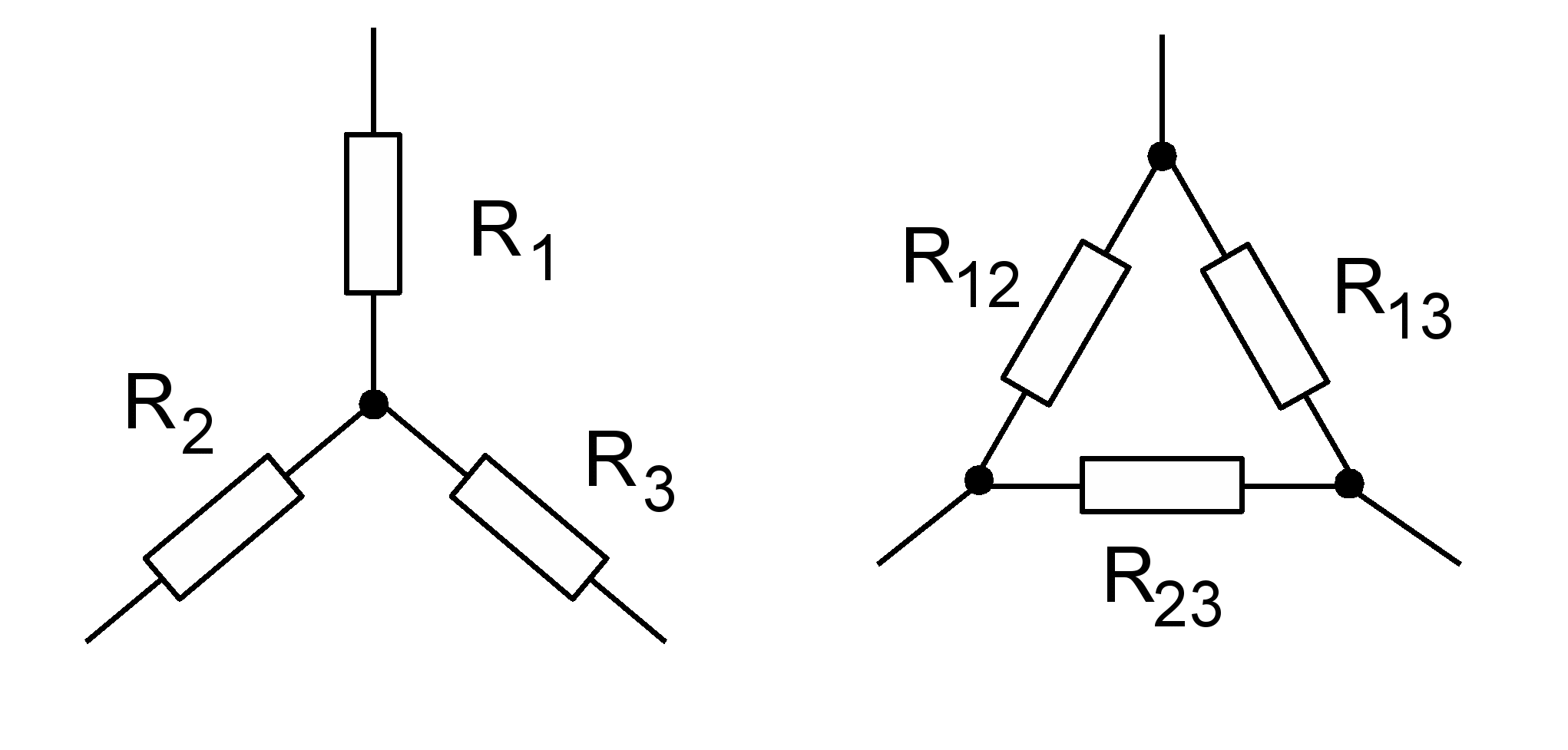
Рис. 4 Эквивалентные звезда и треугольник сопротивлений.

Формулы преобразования звезды сопротивлений в эквивалентный треугольник сопротивлений имеют вид:

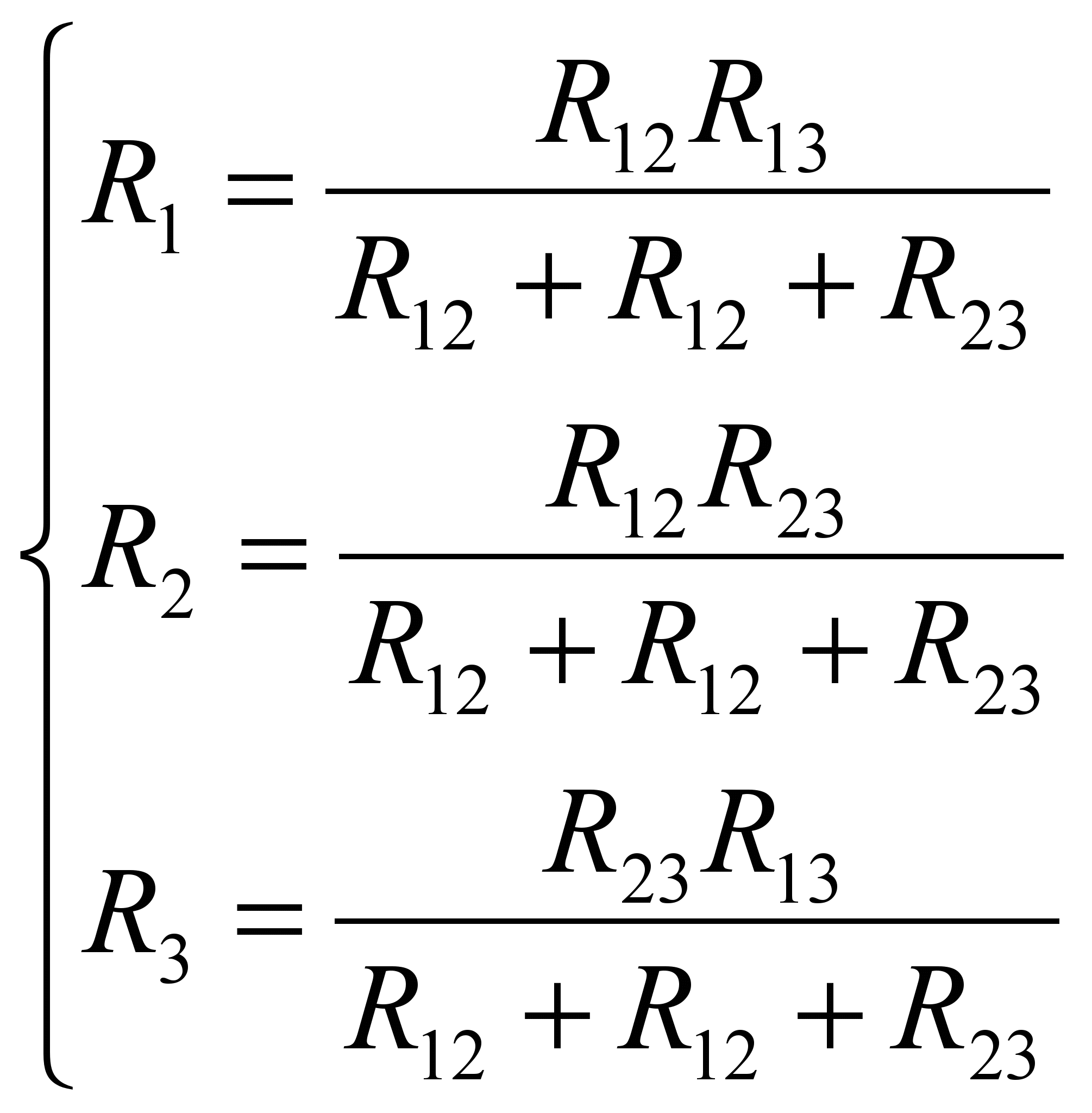(8)

Для обратного преобразования можно использовать следующие выражения:

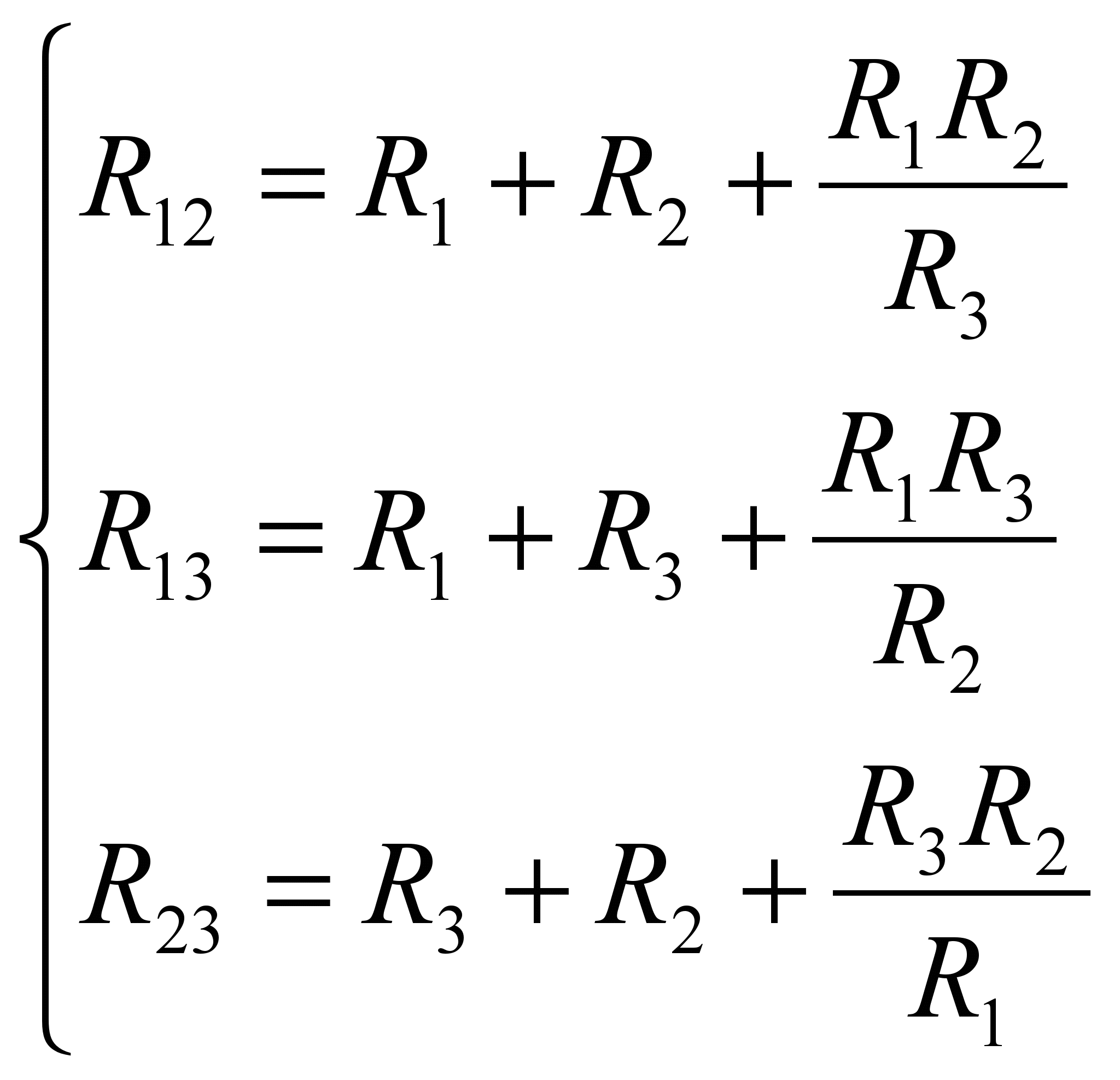(9)

Во всех случаях преобразования замена одних схем на другие, им эквивалентные, не должна привести к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.

Для расчета нашей схемы методом наложения на первом этапе исключим из нее все источники кроме E₁, а затем упростим ее. Все стадии упрощения приведены на рис. 5.

При эквивалентном преобразовании схемы (А) к схеме (Б) звезду сопротивлений r₃R₃R₅ преобразуем в треугольник сопротивлений R_1bcR_1bdR_1cd. Далее при преобразовании к схеме (В) учтем, что сопротивления R_H и R_1cd, а также сопротивления r₂R₄ и R_1bd соединены параллельно. Аналогичным образом осуществим переход к схемам (Г) и (Д).

Таким образом, к источнику E₁ оказываются подключенными последовательно соединенные сопротивления r₁ и R_ab. Отсюда ток

J₁₁ = E₁ / ( r₁+ R_ab) (10)



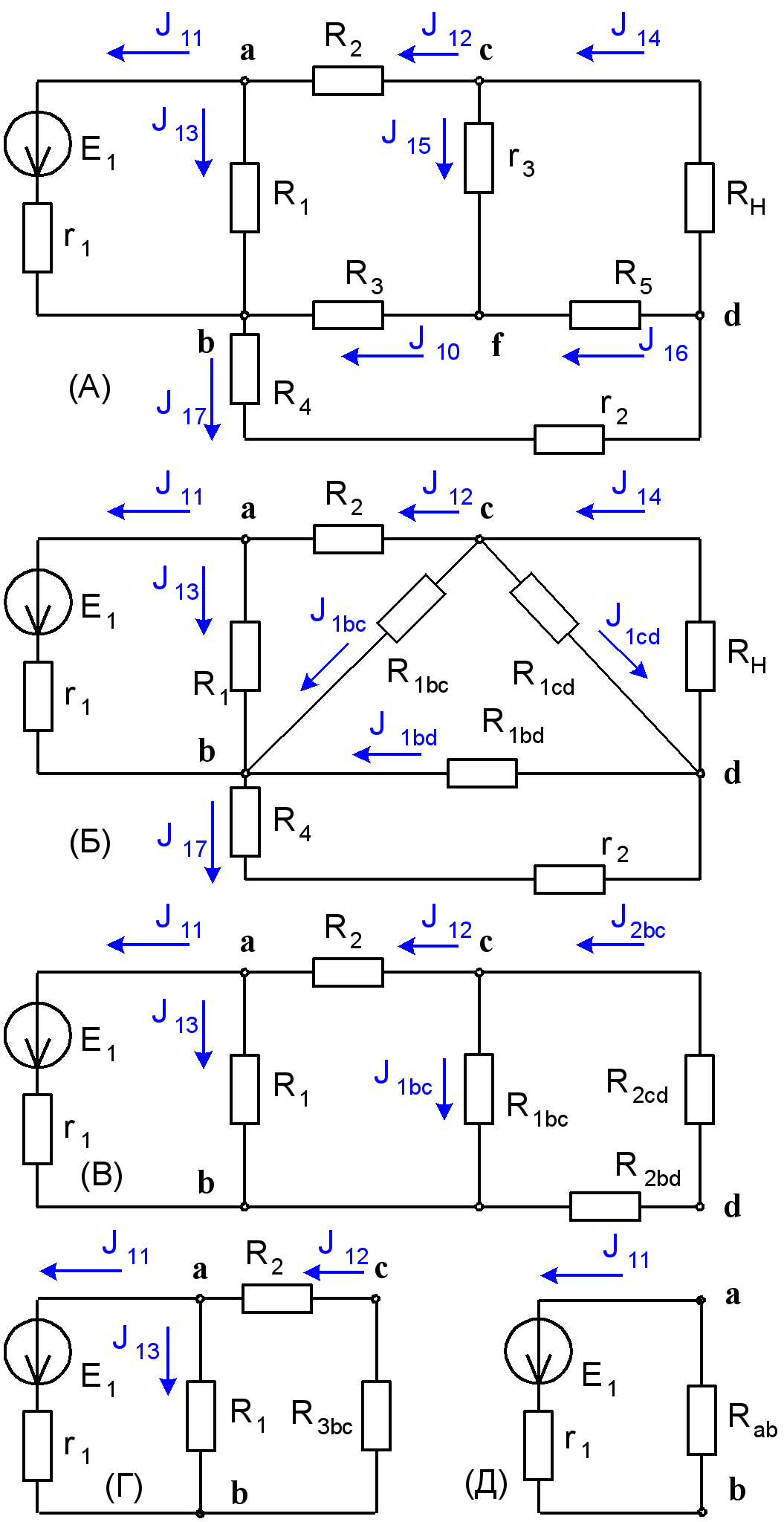
Рис. 5. Последовательное эквивалентное упрощение схемы.

Для определения значения токов J₁₂ и J₁₃ перейдем к схеме (Г) и учтем, что параллельно соединенные сопротивления образуют делитель тока. Следовательно:

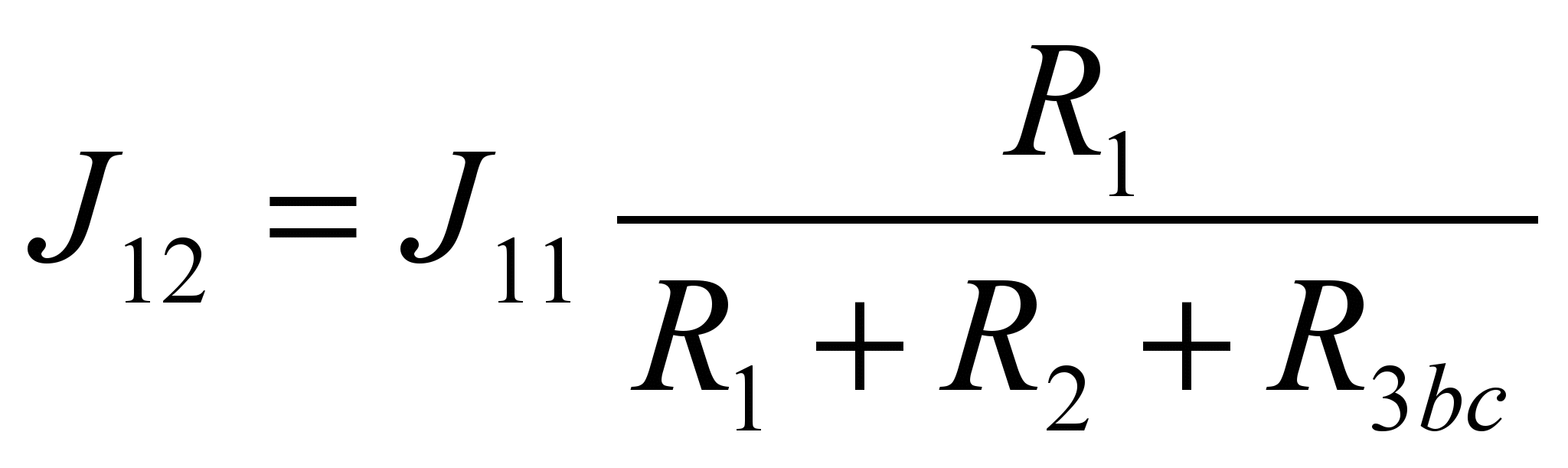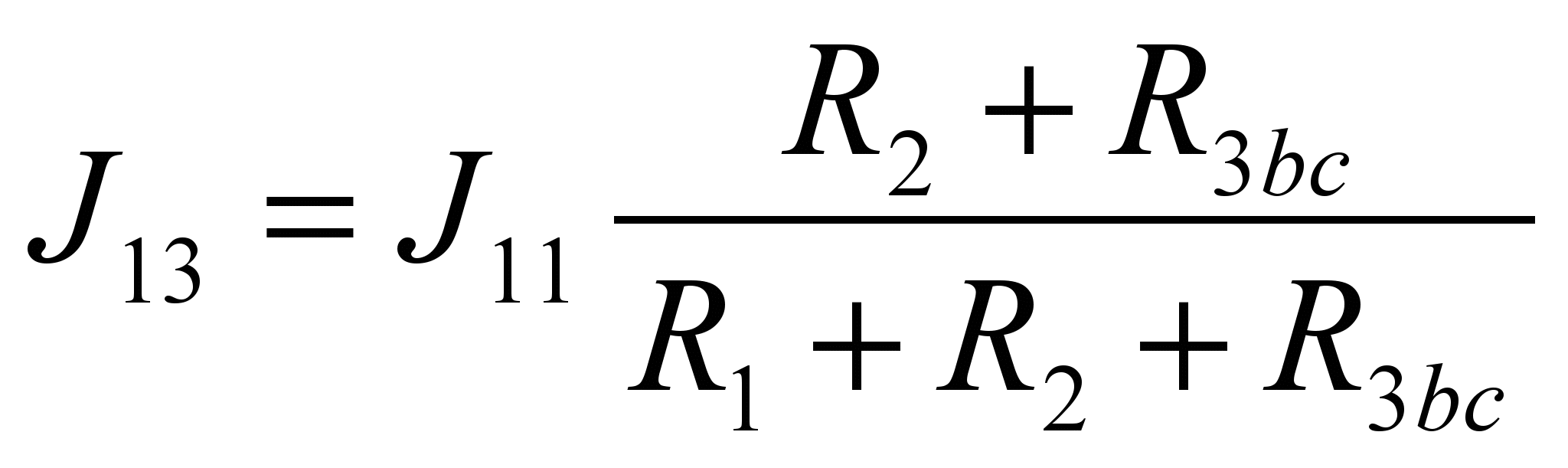; (11)

Анализируя схему (В), не трудно заметить, что сопротивления R_1bc и R_2bdR_2cd так же образуют делитель тока. Соответственно

;

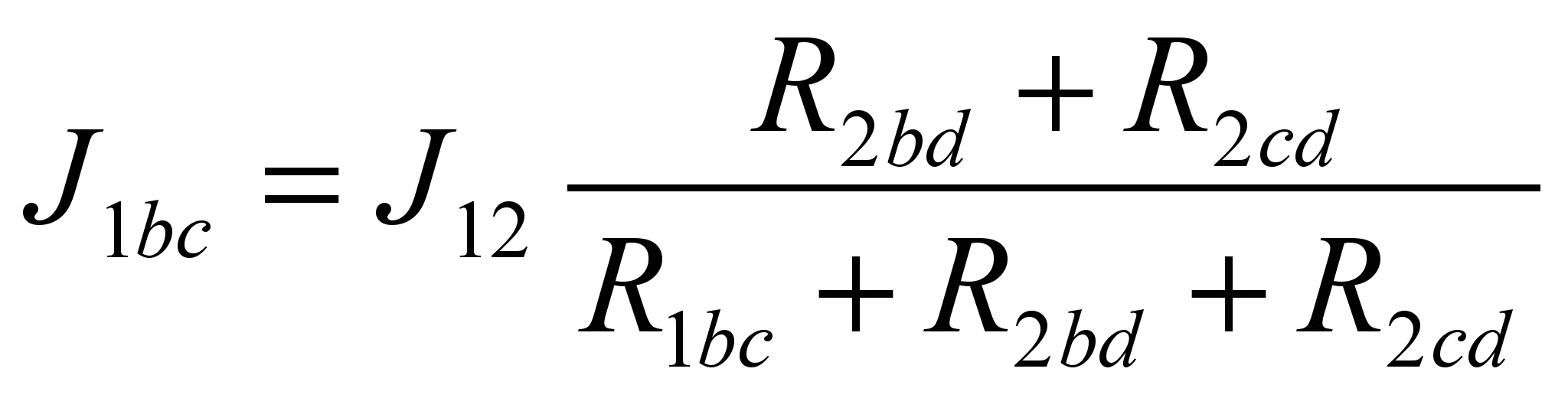
На основе анализа схем (А) и (Б), найдем токи

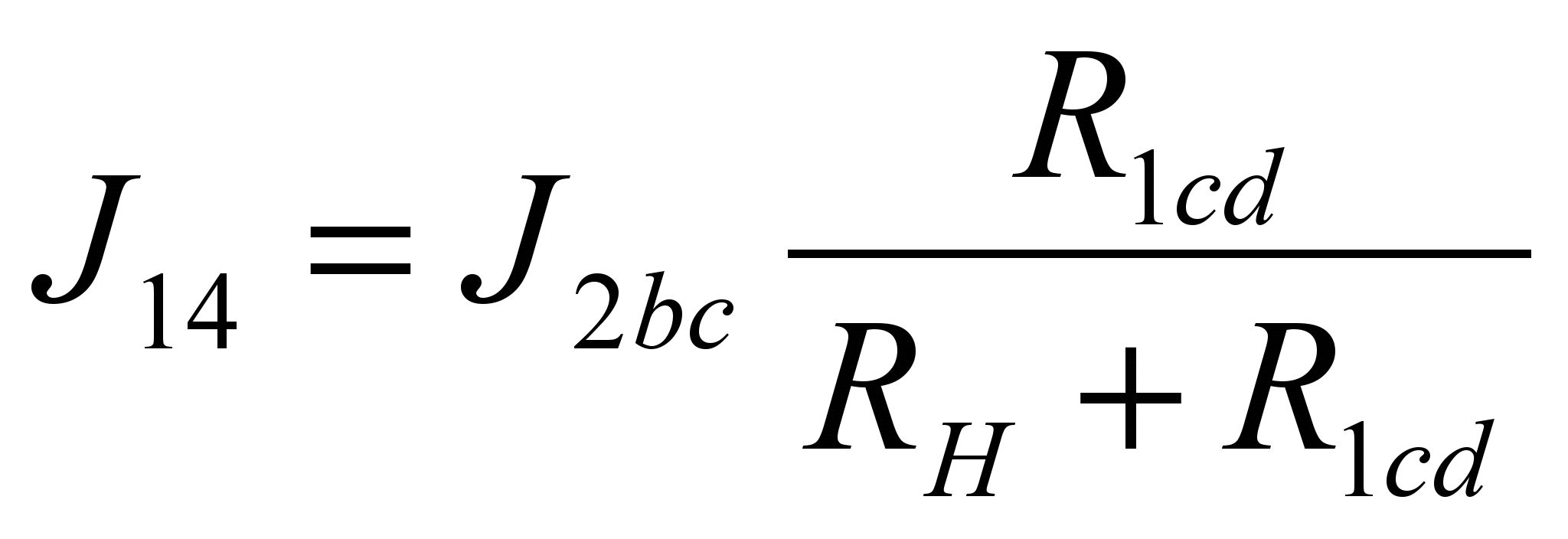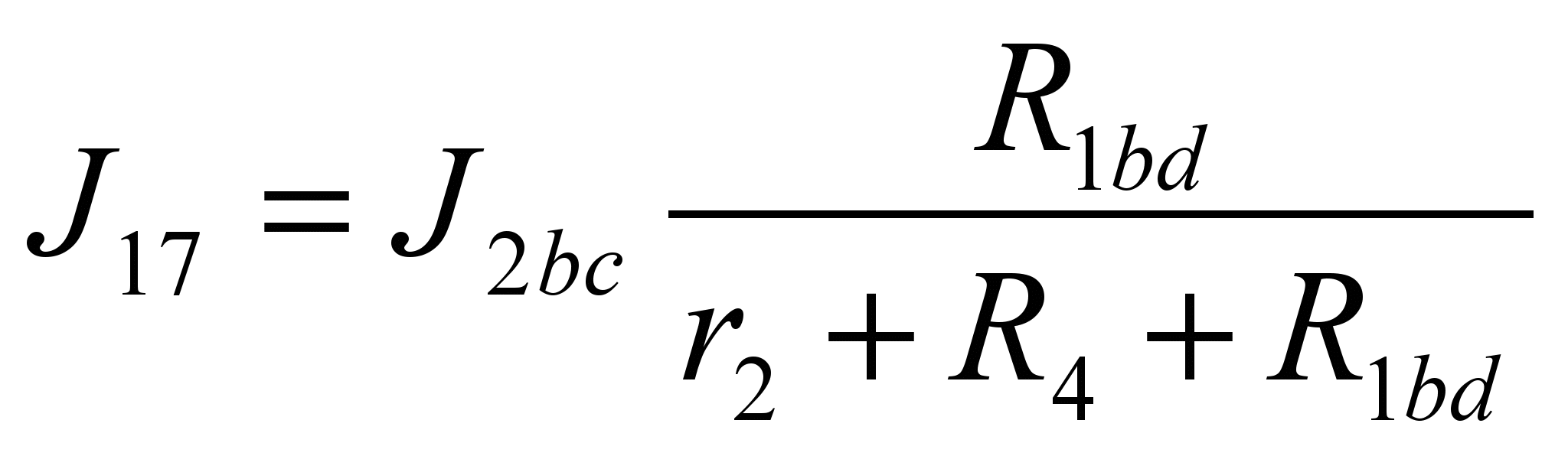; (12)

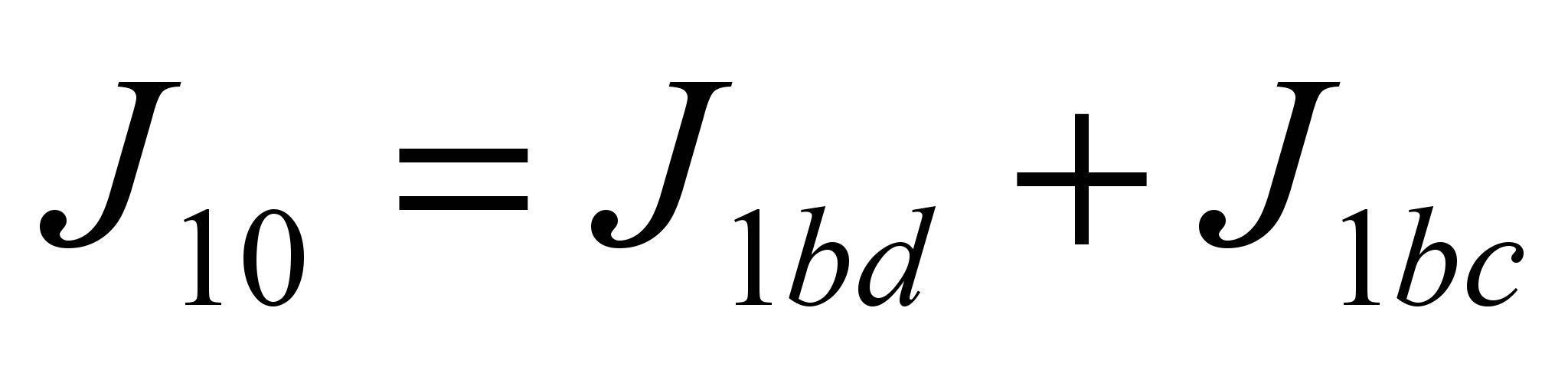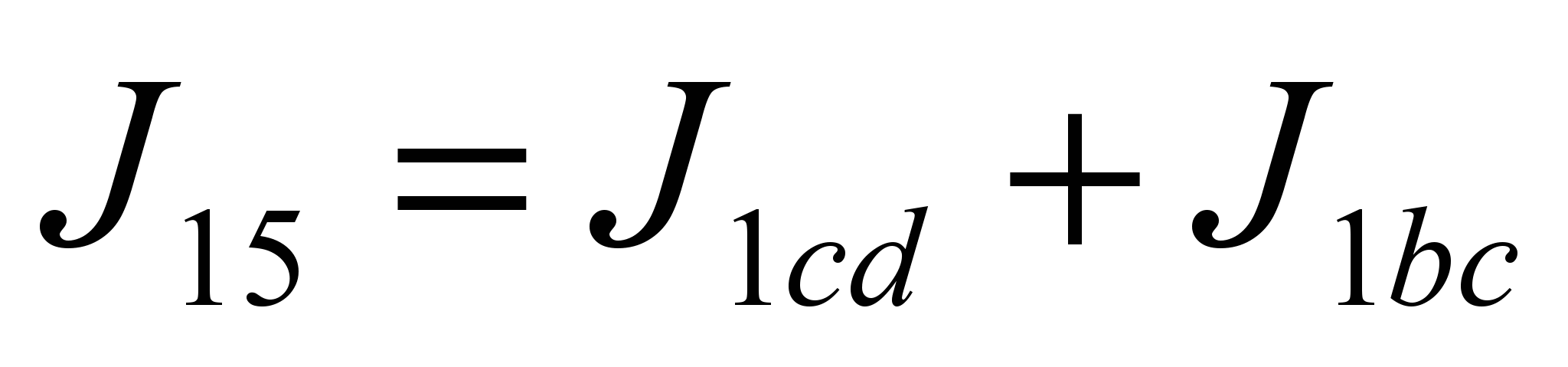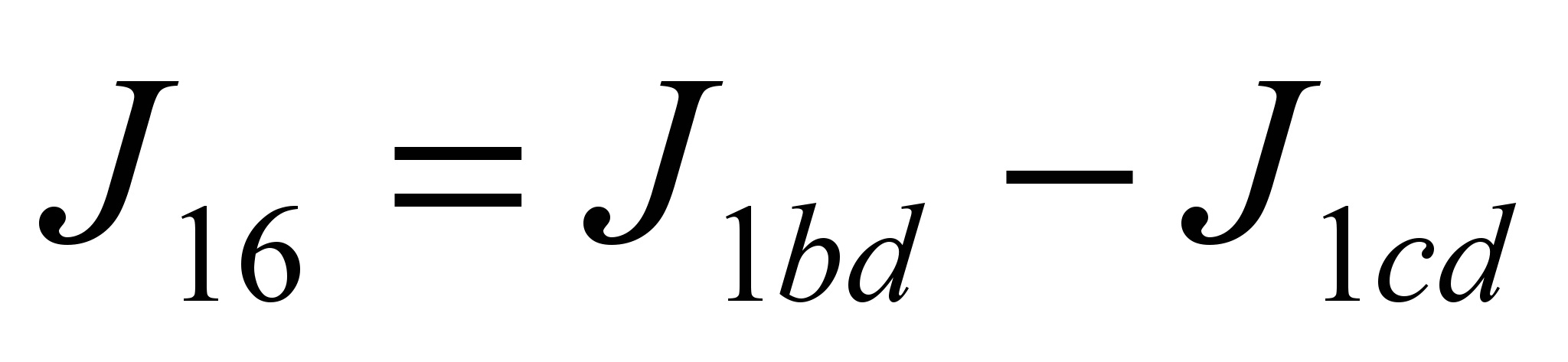; ; (13)

Таким же образом, сначала упростив схему, определяются частные токи от источников Е₂ и Е₃.

После этого действительные токи в ветвях находят путем векторного, т.е. с учетом знаков, суммирования частных токов:

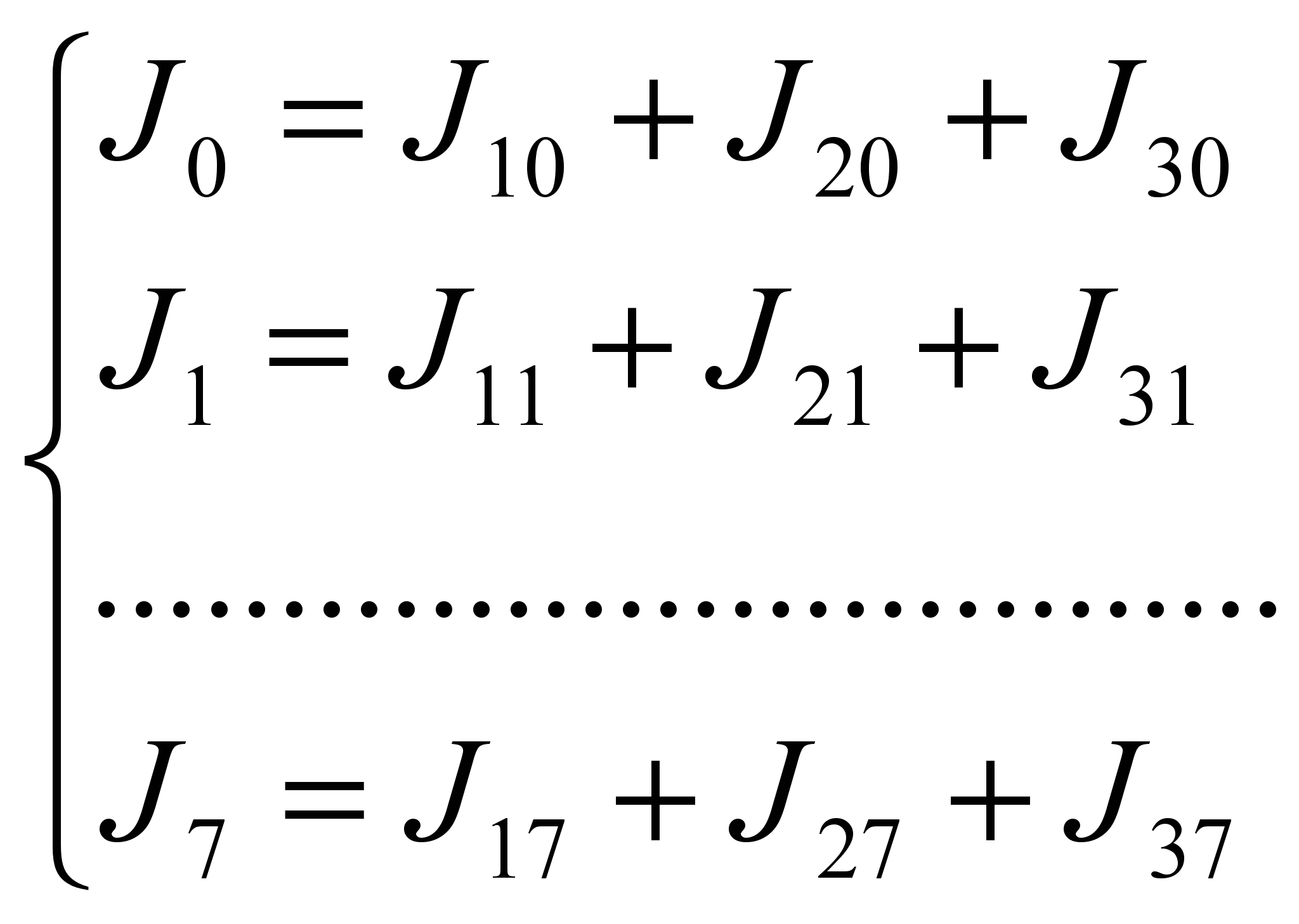(14)

Правильность расчетов, как обычно, проверяется с помощью проверки энергетического баланса мощностей.


Метод эквивалентного генератора.


Метод эквивалентного генератора обычно используется тогда, когда требуется рассчитать ток в одной ветви цепи. В этом случае следует предположить, что выбранная ветвь подключена к некоторому источнику с ЭДС равному Е_экв и внутренним сопротивлением r_экв. Если выбранная ветвь представляет собой последовательно включенный источник E и сопротивление R, то ток в этой ветви можно найти по формуле:

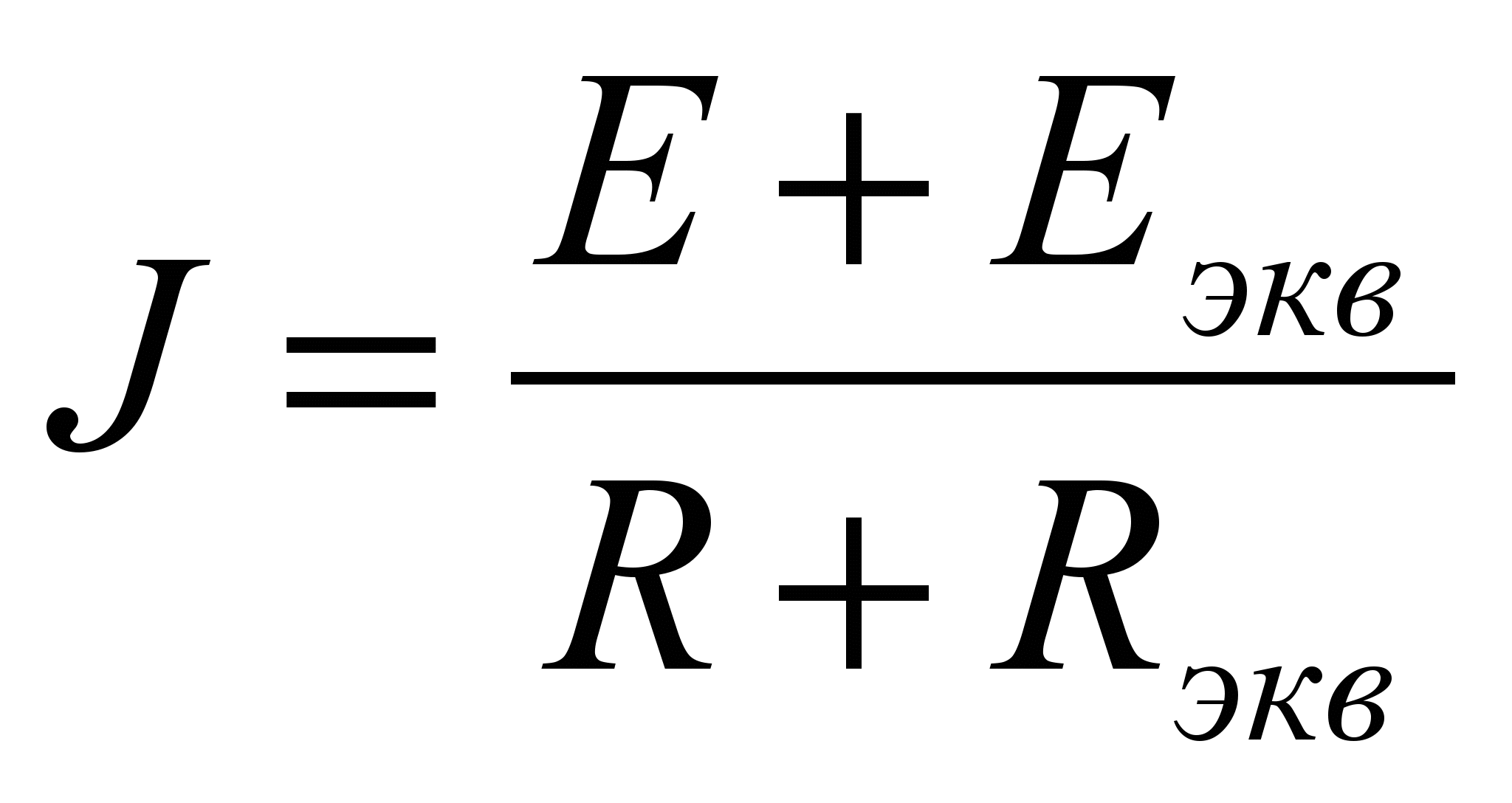(15)

Таким образом, решение задачи по определению тока J сводится к определению ЭДС Е_экв эквивалентного генератора и его внутреннего сопротивления r_экв.

Предположим, что в рассматриваемой схеме, изображенной на рис. 2, нам необходимо определить ток J₁, протекающий через источник E₁ и сопротивление r₁. Для решения задачи методом эквивалентного генератора сначала вычленим из рассматриваемой схемы выбранную ветвь, как это показано на рис. 6. Тогда правая часть схемы будет представлять собой схему эквивалентного генератора.



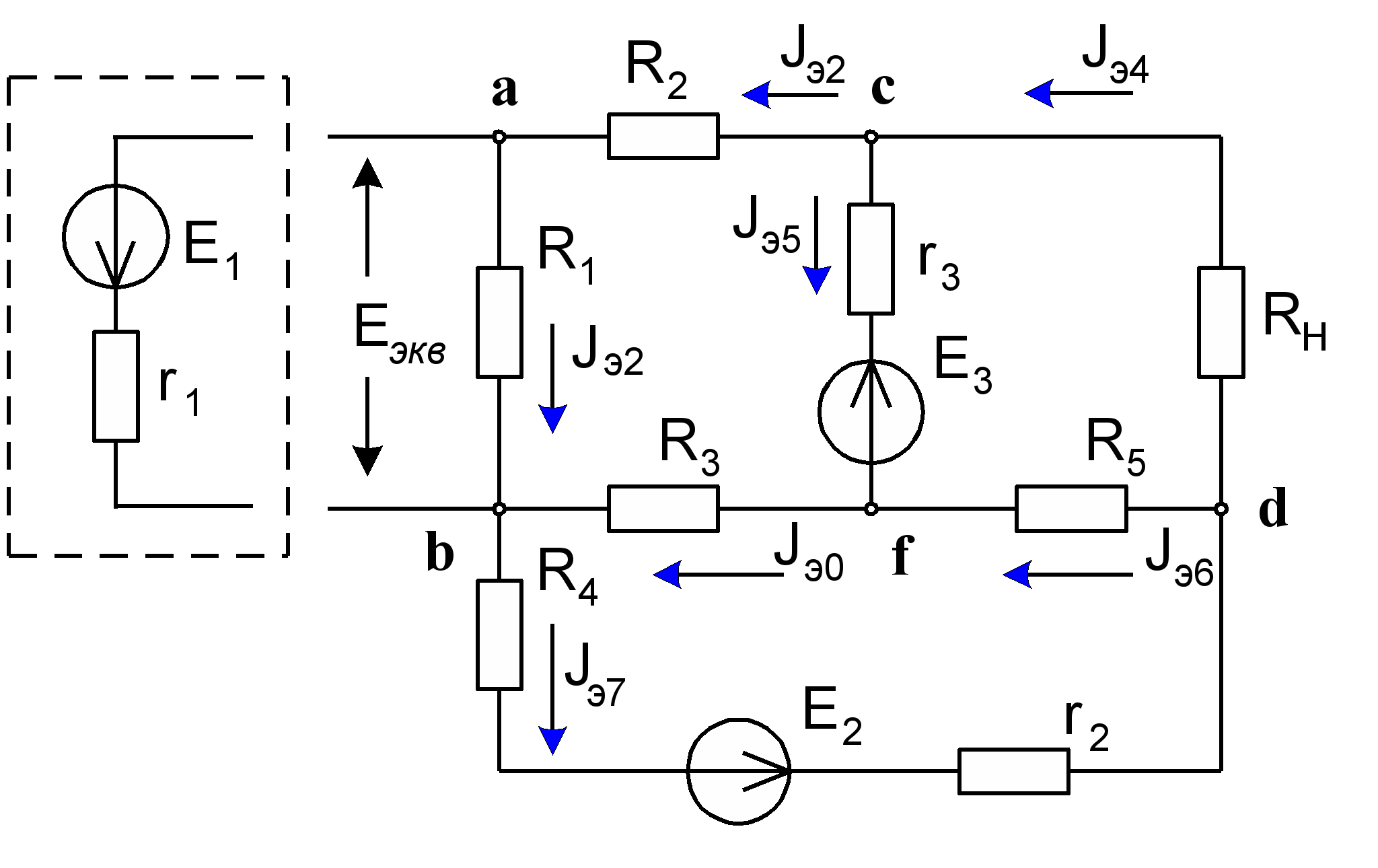
Рис. 6. Преобразование схемы при использовании метода эквивалентного генератора.


Не трудно заметить, что ЭДС Е_экв генератора в данном случае численно равна

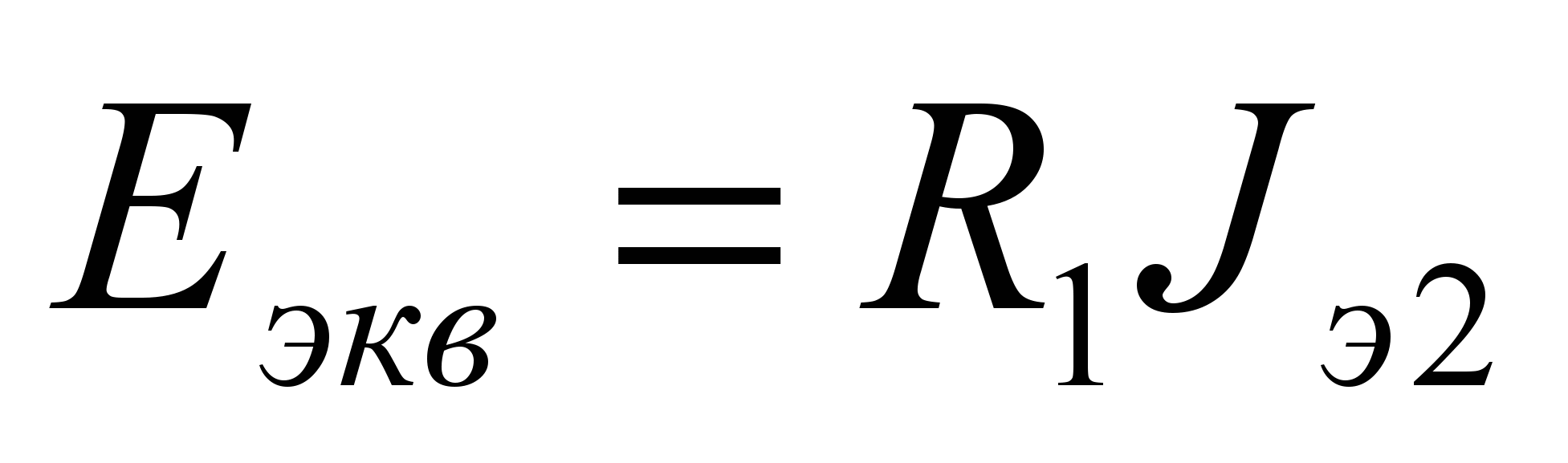(16)

Величина тока J_э2 рассчитывается любым из рассмотренных ранее методов.

Определить сопротивление r_экв можно двумя способами.

Во-первых, можно закоротить выход эквивалентного генератора, то есть положить R₁ =0 и заново пересчитать J_э2. Новое значение J_э2 будет соответствовать току короткого замыкания J_кз. Тогда

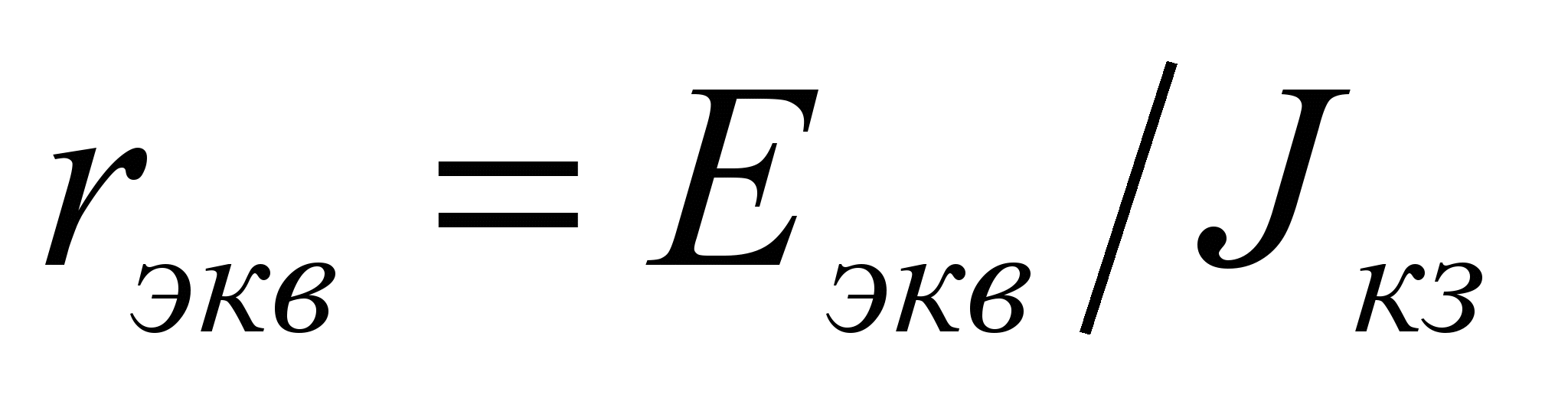(16)

Второй способ – это исключить из схемы все источники ЭДС, заменив их коротко замкнутыми перемычками и рассчитать сопротивление на выходе схемы, в данном случае в точках (ab). Очевидно, при расчетах потребуется провести преобразования аналогичные тем, что показаны на рис. 5.

Замечание: Следует напомнить, что в вашем индивидуальном задании необходимо определить все токи, протекающие в схеме. Поэтому для их расчета вам придется применить метод эквивалентного генератора соответствующее число раз.


Индивидуальное задание №2.

Расчет разветвленной электрической цепи переменного тока с использованием закона Ома.


Целью данного задания является научиться применять закон Ома при расчетах электрических цепей переменного тока. При выполнении задания необходимо уметь пользоваться различными формами записи комплексных величин, описывающих электрическую цепь, а также применять эти записи для вычисления токов, падений напряжений на отдельных элементах электрической цепи и построении векторных диаграмм.

В соответствии с вариантом индивидуального задания необходимо рассчитать параметры электрической цепи, представленной на рис. 7. Выполнение задания подразумевает определение номинальных значений элементов схемы, а также добротности реактивных элементов. Кроме того, необходимо рассчитать значения токов во всех ветвях электрической цепи и падение напряжения на всех ее элементах, вычислить действующие значения всех токов и приложенного к электрической цепи напряжения, построить векторную диаграмму и найти фазовый сдвиг между входным током и приложенным к электрической цепи напряжением.




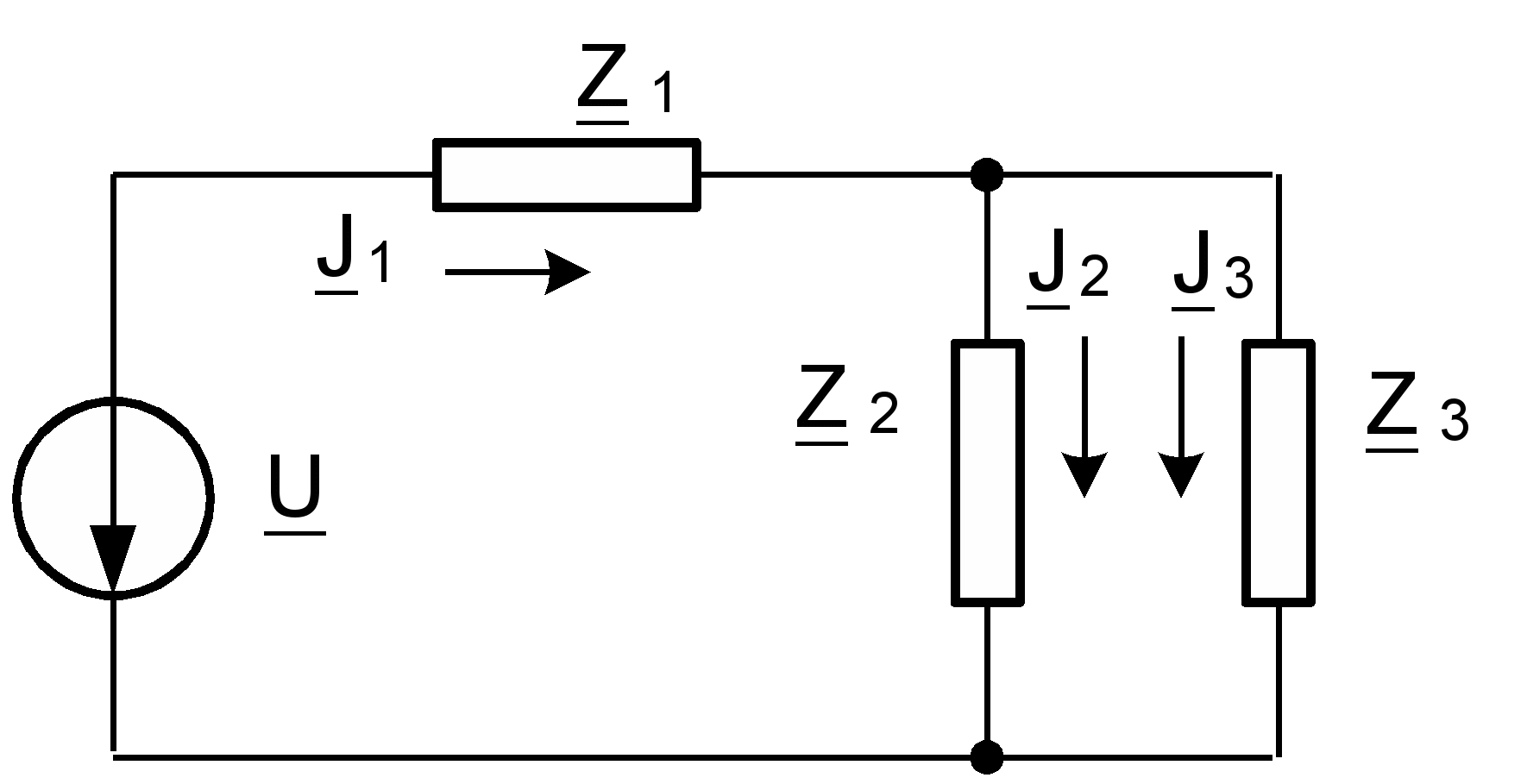
Рис. 7. Схема электрической цепи переменного тока.


Предположим, что имеются следующие исходные данные к расчету:

U	Z1	Z2	Z3
f, Гц	Um, B	Ф, о	R1, Ом	X1, Ом	R2, Ом	X2, Ом	R3, Ом	X3, Ом
50	120	240	48	24	12	-40	30	6