Методические указания по выполнению индивидуальных заданий по курсу «основы электроники» Для студентов Iкурса
| Вид материала | Методические указания |
- Пособие предназначено для студентов дневного и вечернего отделений. Указани, 502.9kb.
- Методические указания к выполнению индивидуальных заданий для студентов дневного, 229.08kb.
- Методические указания по выполнению контрольных работ и домашних заданий (рефератов), 314.07kb.
- Методические указания по выполнению контрольной работы Для студентов Iкурса, обучающихся, 344.05kb.
- Физические основы электроники, 499.24kb.
- Методические указания к выполнению курсовой работы по курсу «Основы климатологии, 417.3kb.
- Программа и методические указания к выполнению курсовой работы и контрольных работ, 146.23kb.
- Методические указания к выполнению курсовой работы «Разработка приложений, предназначенных, 348.71kb.
- Методические указания по выполнению курсовой работы по общепрофессиональным дисциплинам, 245.54kb.
- Методические указания по выполнению семестровой контрольной работы с комплектом заданий, 701.46kb.
Для определения реальных компонент электрической цепи учтем знаки при мнимых составляющих комплексных сопротивлений: если знак положительный, то сопротивление имеет индуктивный характер, если знак отрицательный, то сопротивление имеет емкостной характер. В нашем случае комплексные сопротивления Z1 и Z3 имеют индуктивный, а Z2 - емкостной характер. Следовательно, нашу схему следует преобразовать к виду:
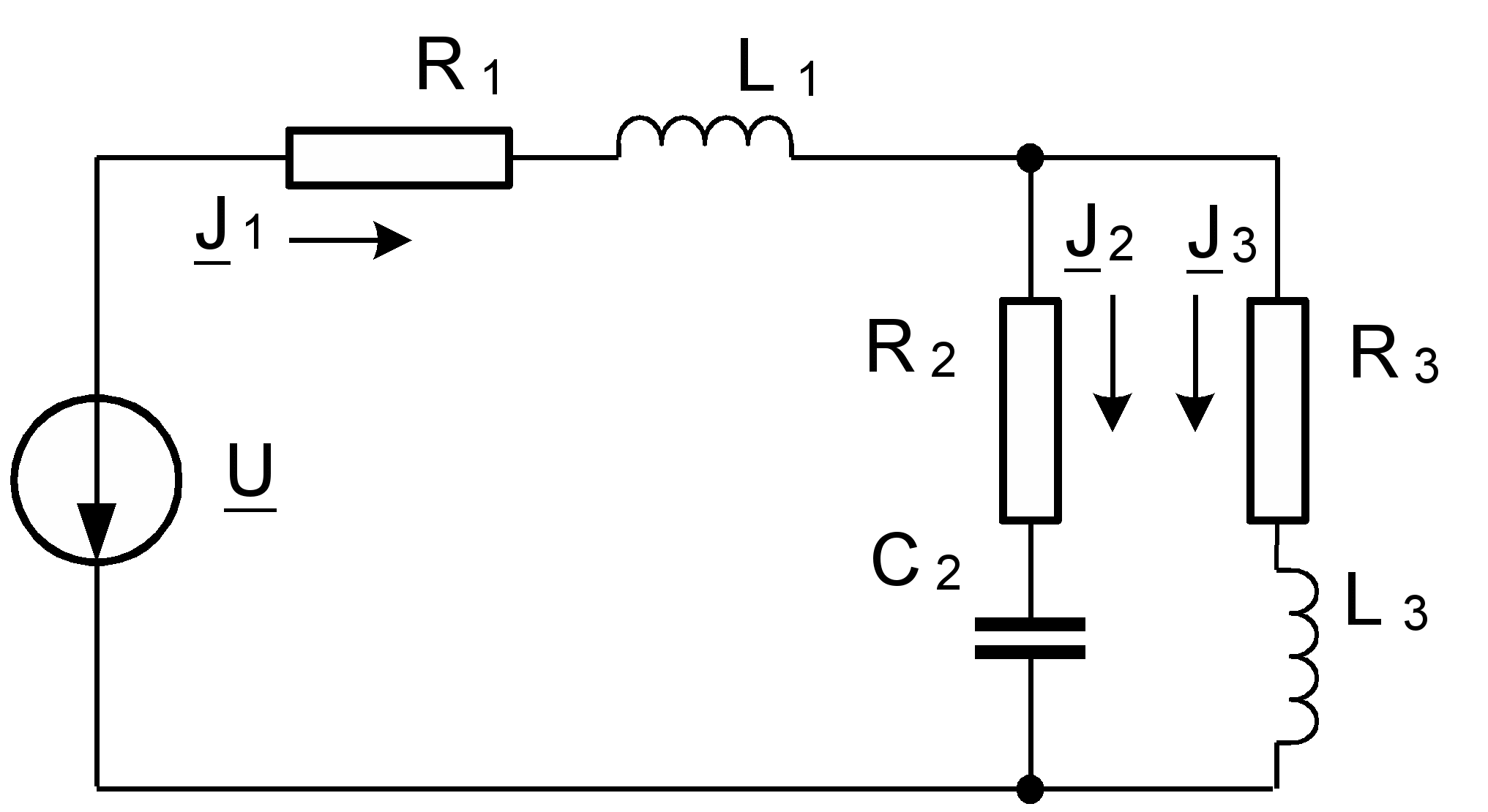
Рис. 8. Принципиальная схема разветвленной электрической цепи переменного тока.
Номинальные значения индуктивности и емкости определяются с помощью выражений:
; 
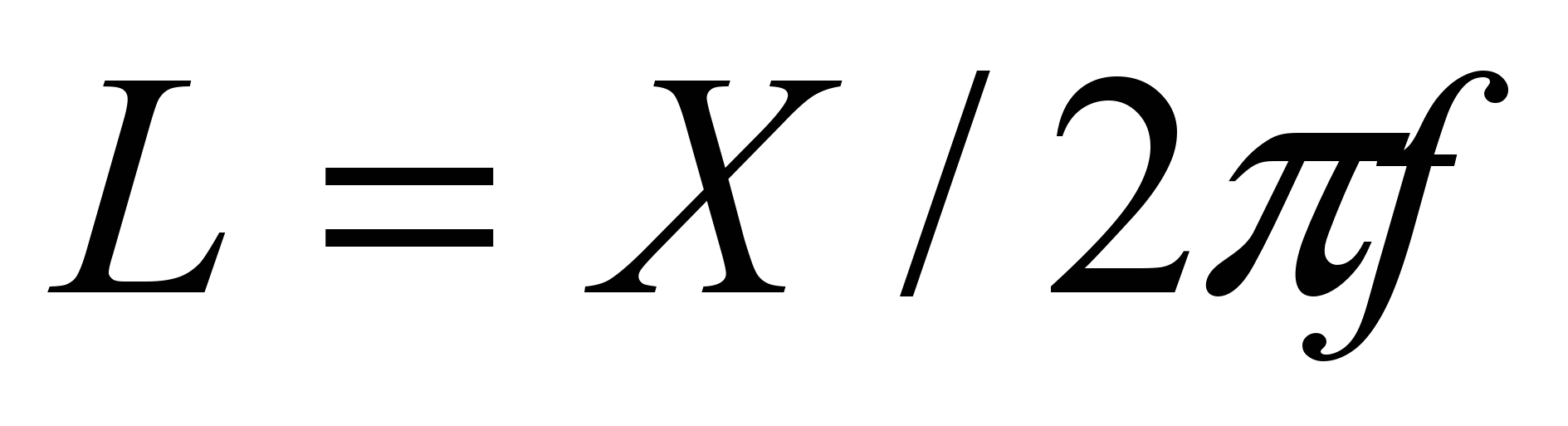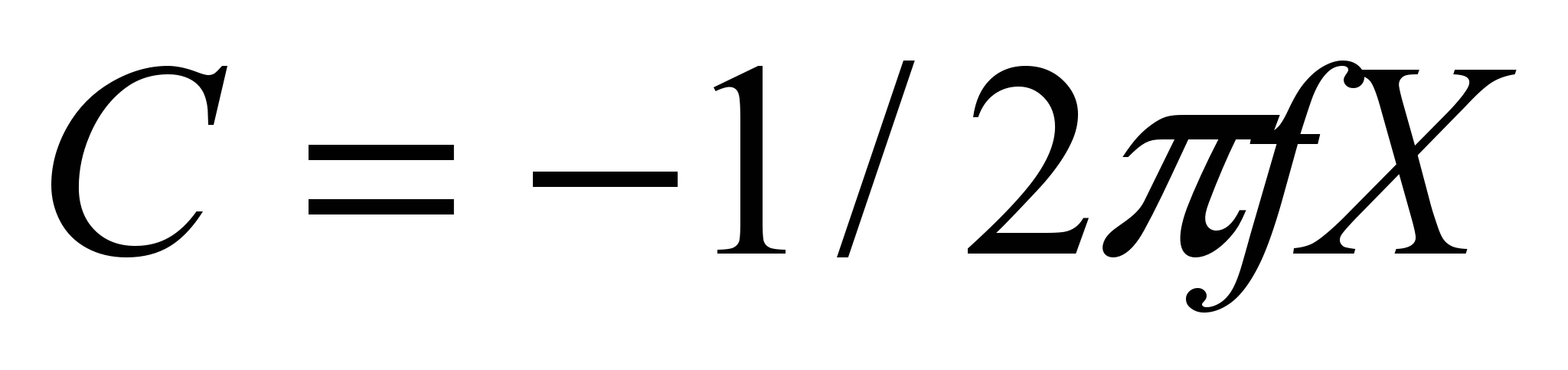(17)Для определения добротности элементов следует воспользоваться выражением:
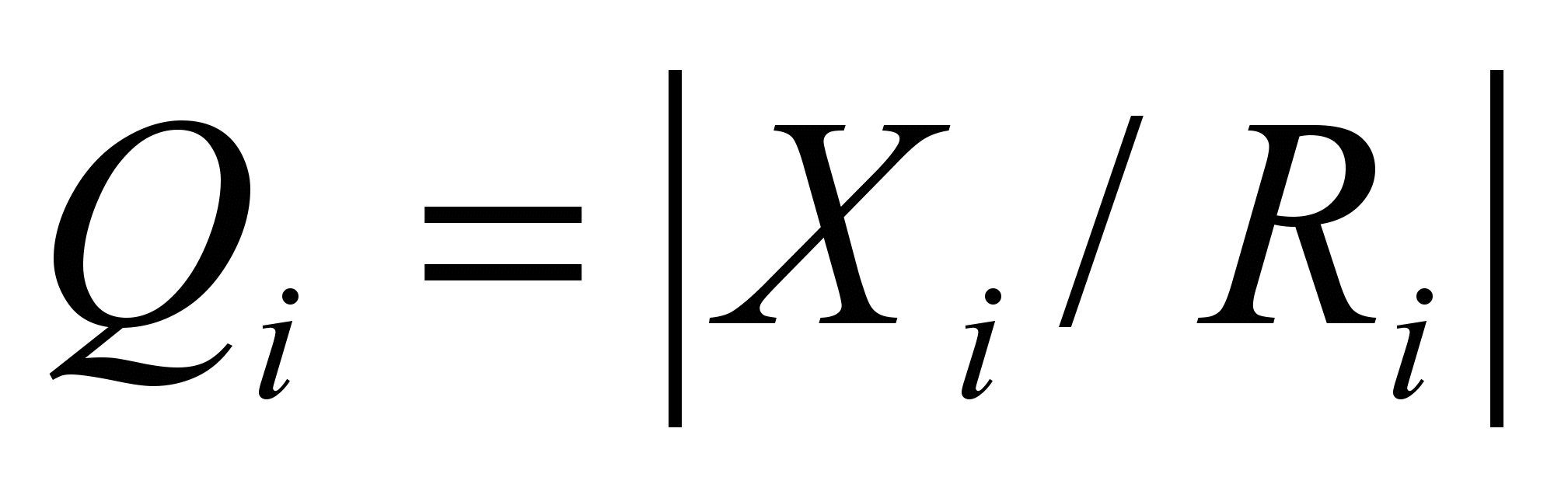(18)Результаты вычислений номинальных значений элементов для выбранного варианта задания приведены в таблице:
| Z1 | Z2 | Z3 | ||||||
| R1, Ом | L1, мГн | Q1 | R2, Ом | С2, мкФ | Q2 | R3, Ом | L3, мГн | Q3 |
| 48 | 76 | 0,5 | 12 | 80 | 3,33 | 30 | 19 | 0,2 |
Для определения токов в цепи следует воспользоваться законами Ома и Кирхгофа, но с учетом того, что все входящие величины являются комплексными.
Существует три формы записи комплексного числа. В алгебраической форме комплексное число А представляют в виде алгебраической суммы двух составляющих – вещественной
и мнимой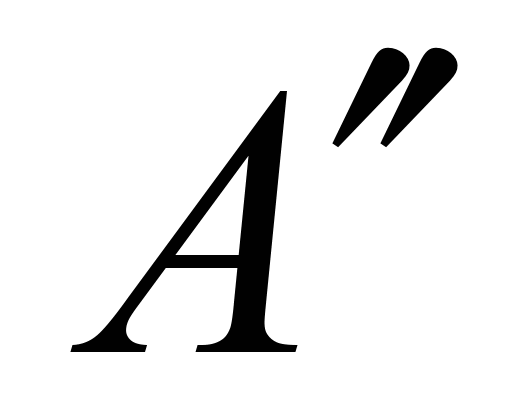 
:
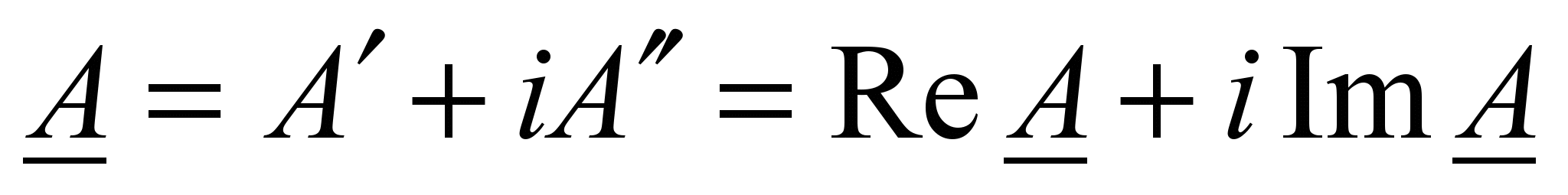(19)где
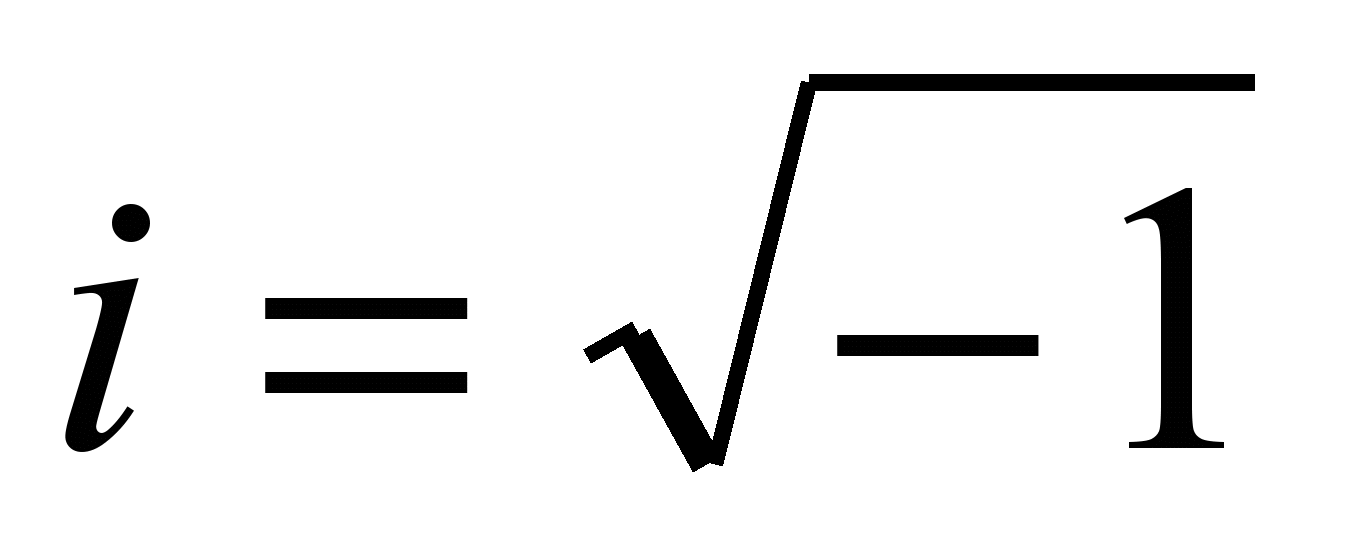обозначает мнимую единицу.Число А можно изобразить в виде вектора на комплексной плоскости, у которой горизонтальная ось совпадает с осью вещественных составляющих, а вертикальная ось совпадает с осью мнимых составляющих комплексных чисел. По отношению к горизонтальной оси вектор А будет направлен под углом Ф. Положительное значение угла отсчитывается по часовой, отрицательное – против часовой стрелки.
Геометрическое рассмотрение вектора А на комплексной плоскости приводит к тригонометрической и экспоненциальной формам записи комплексного числа:
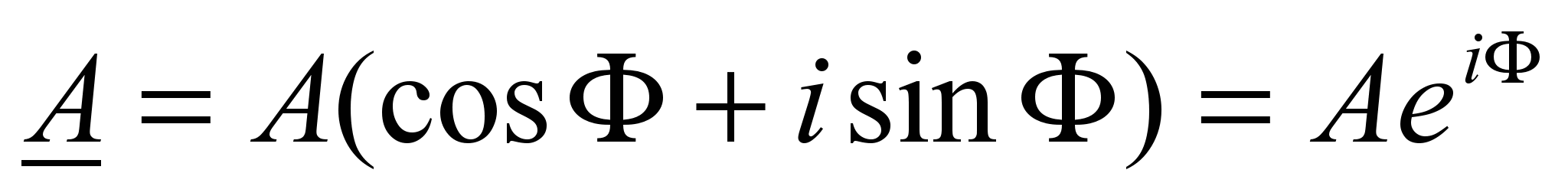(20)где
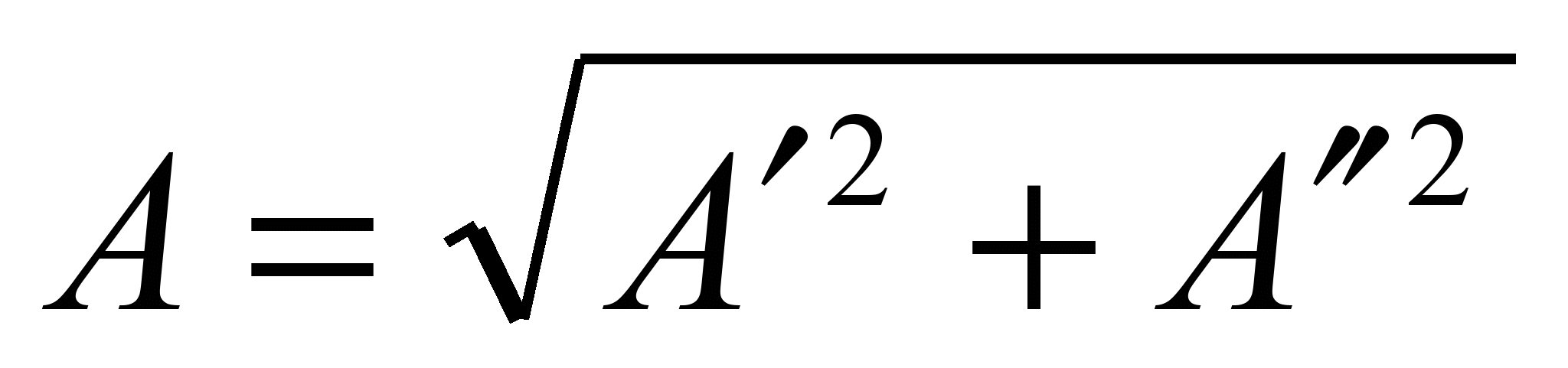- модуль, 
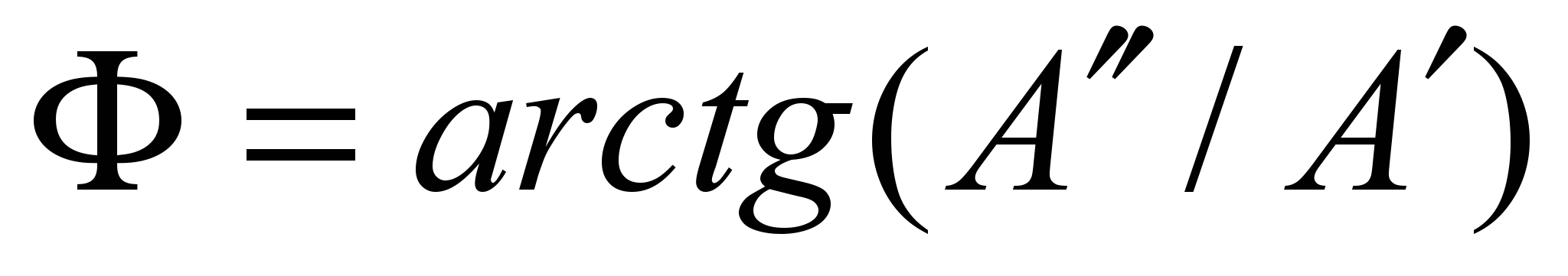- фаза (аргумент) комплексного числа А. Алгебраическую форму записи удобно применять при сложении и вычитании, а экспоненциальную – при умножении и делении комплексных чисел.
Вернемся к рассмотрению схемы, изображенной на рис. 7.
Сопротивление участка цепи с параллельно соединенными элементами Z2 и Z3 равно:
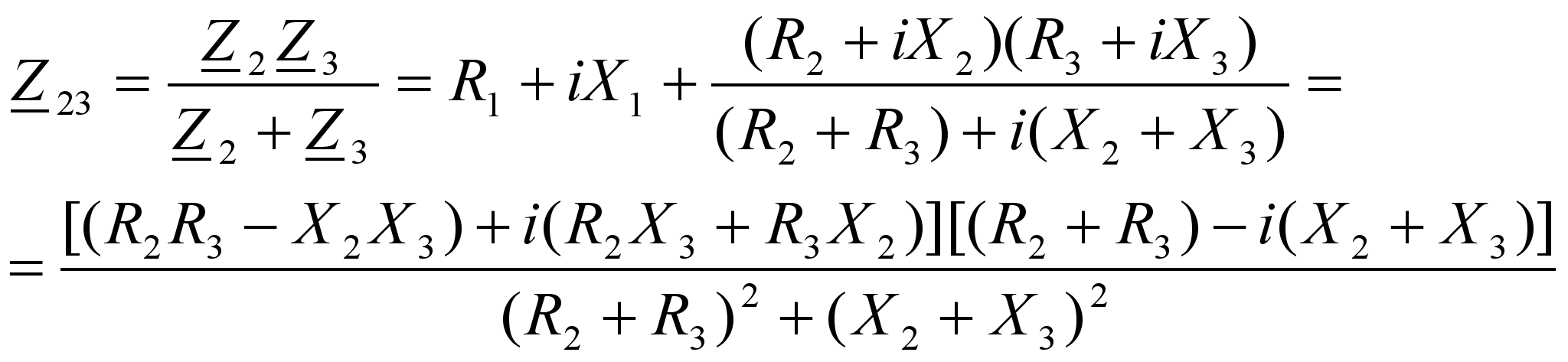Общее сопротивление цепи Z0, подключенное к источнику U :
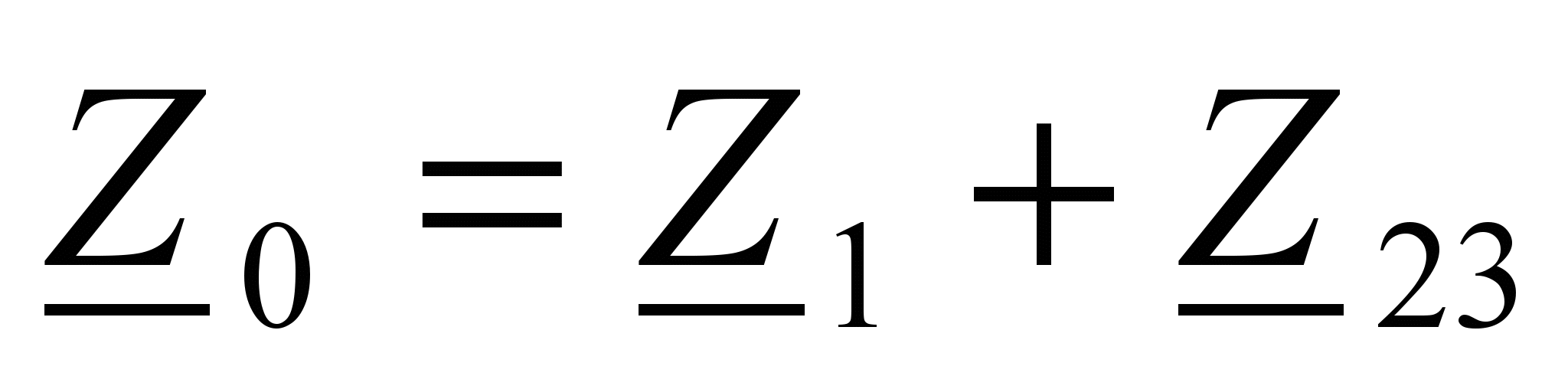(21)Тогда токи в цепи будут равны:
; 
; 
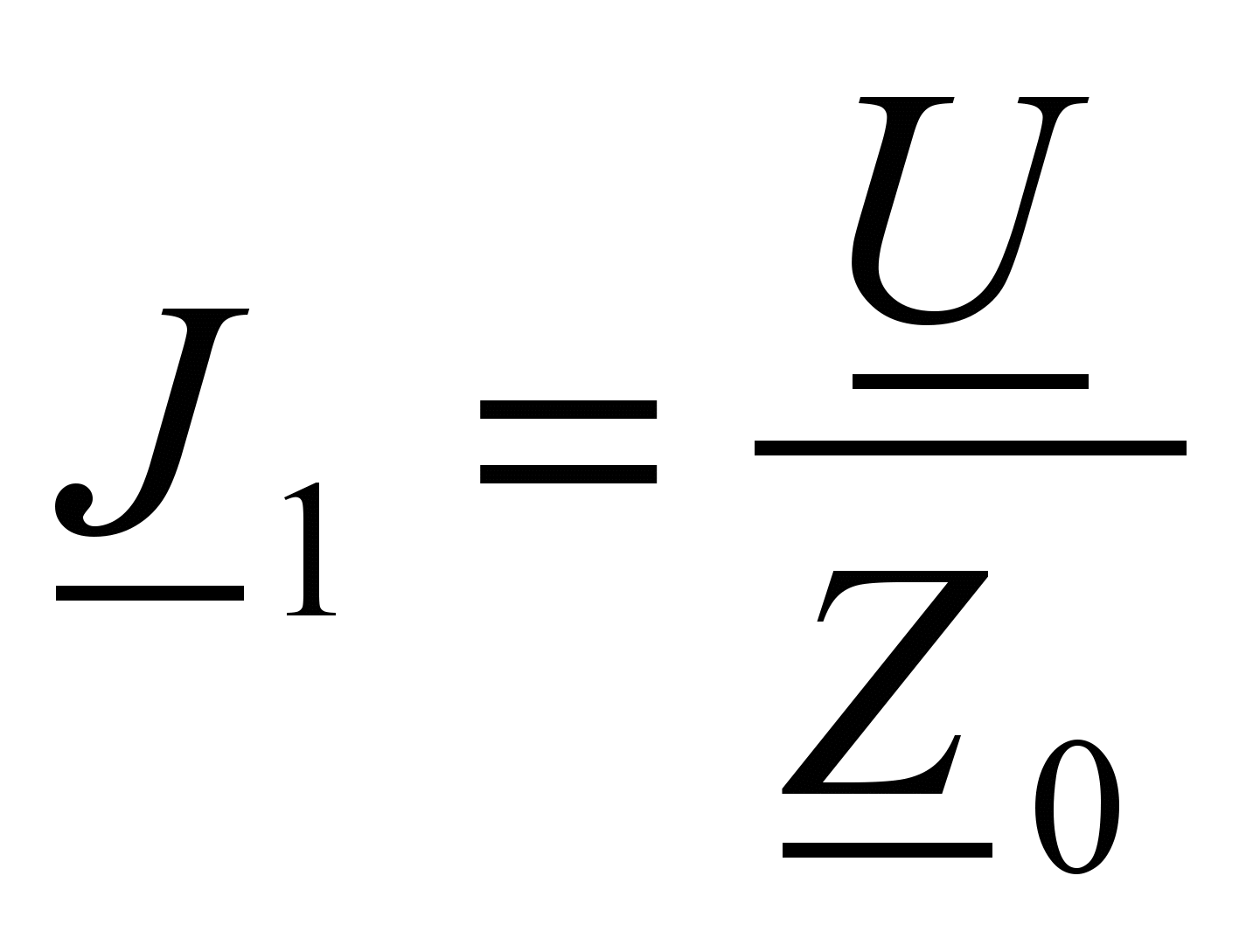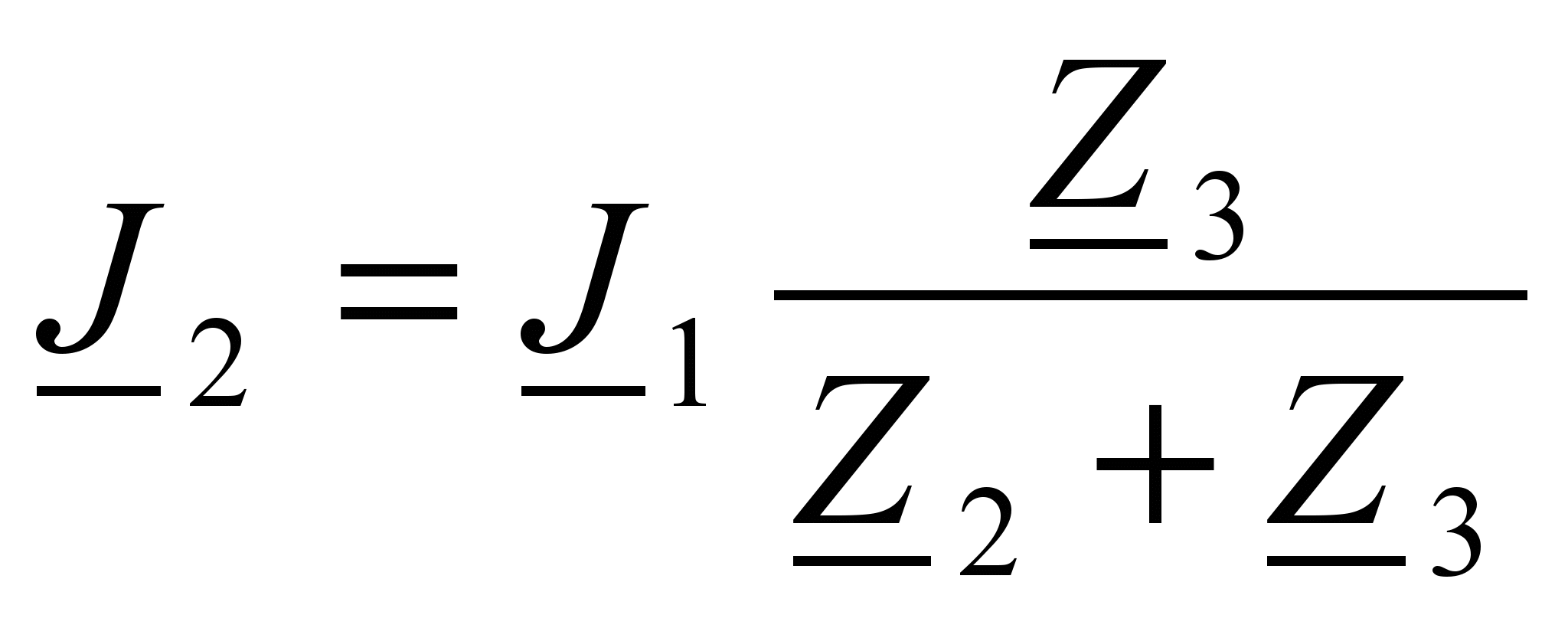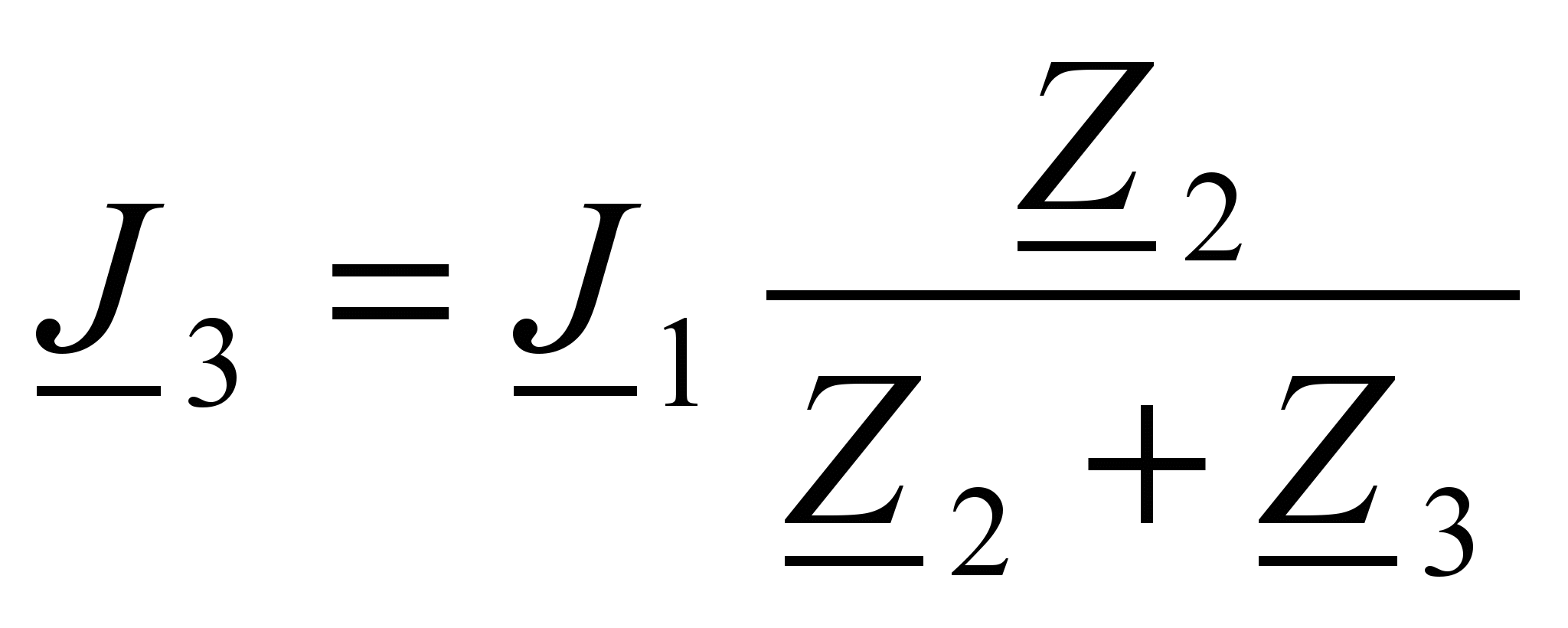(22)Отсюда можно найти падения напряжения на отдельных элементах схемы:
; 
; 
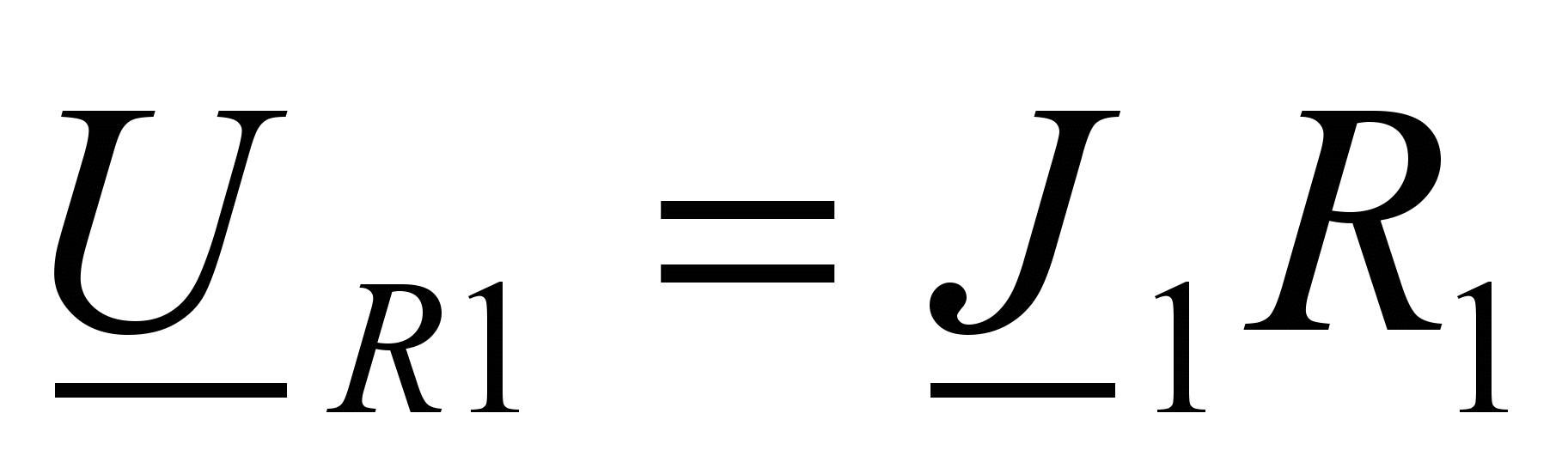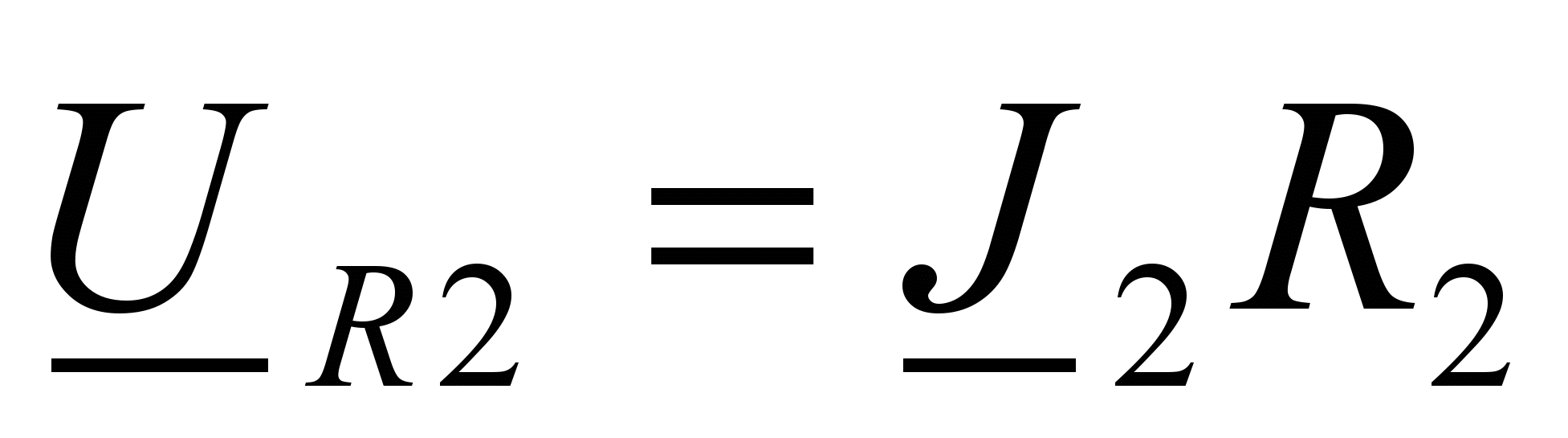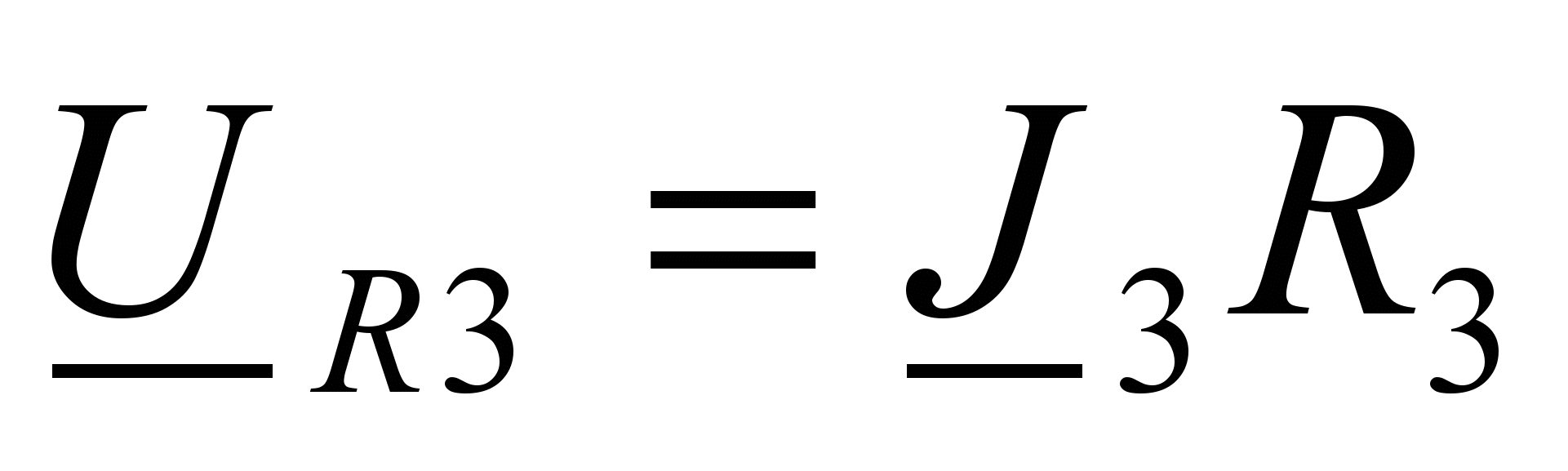(23)
; 
; 
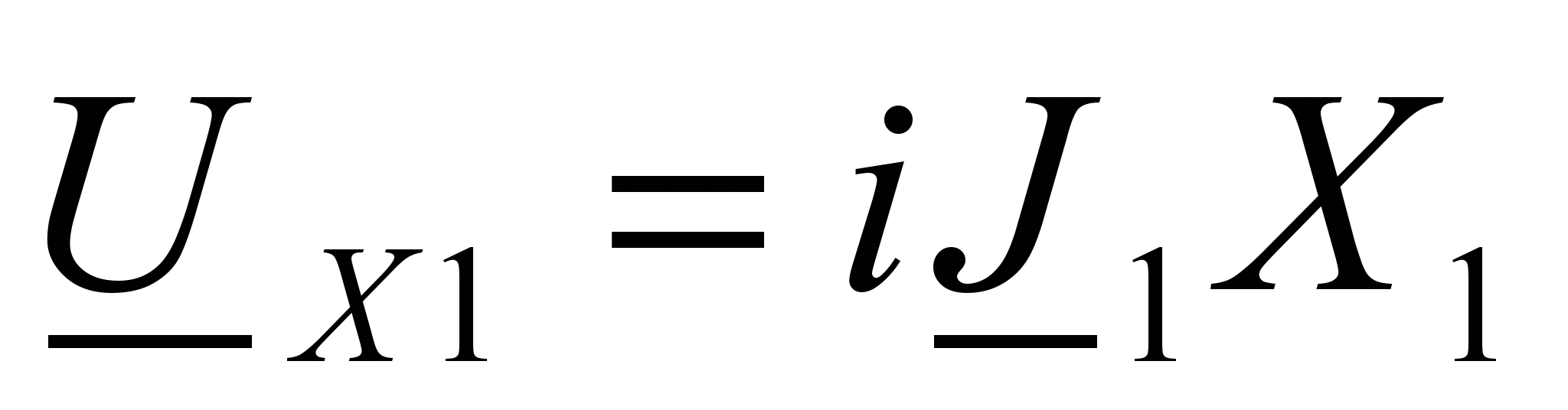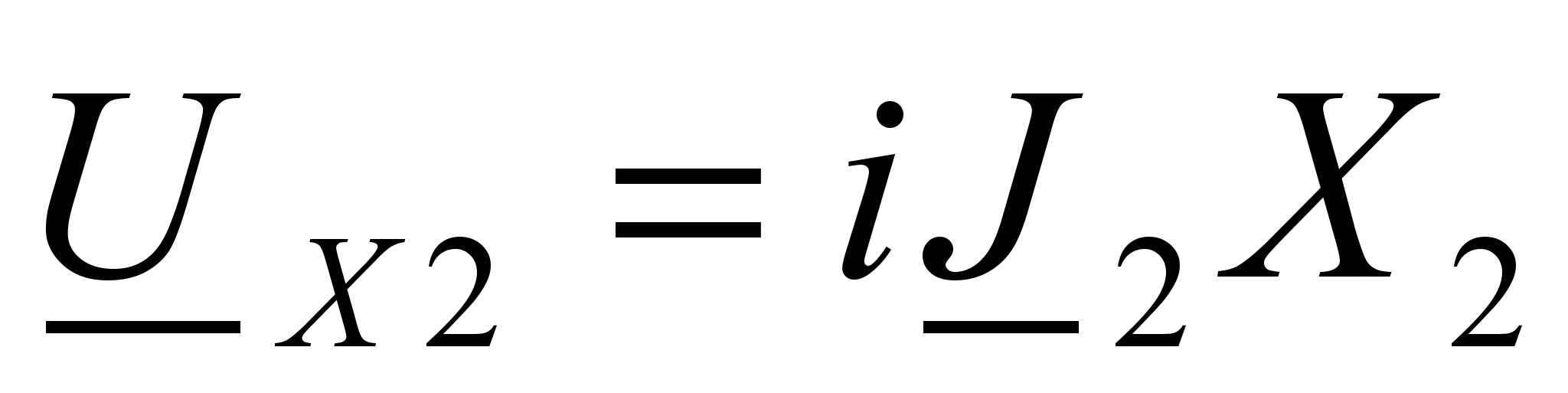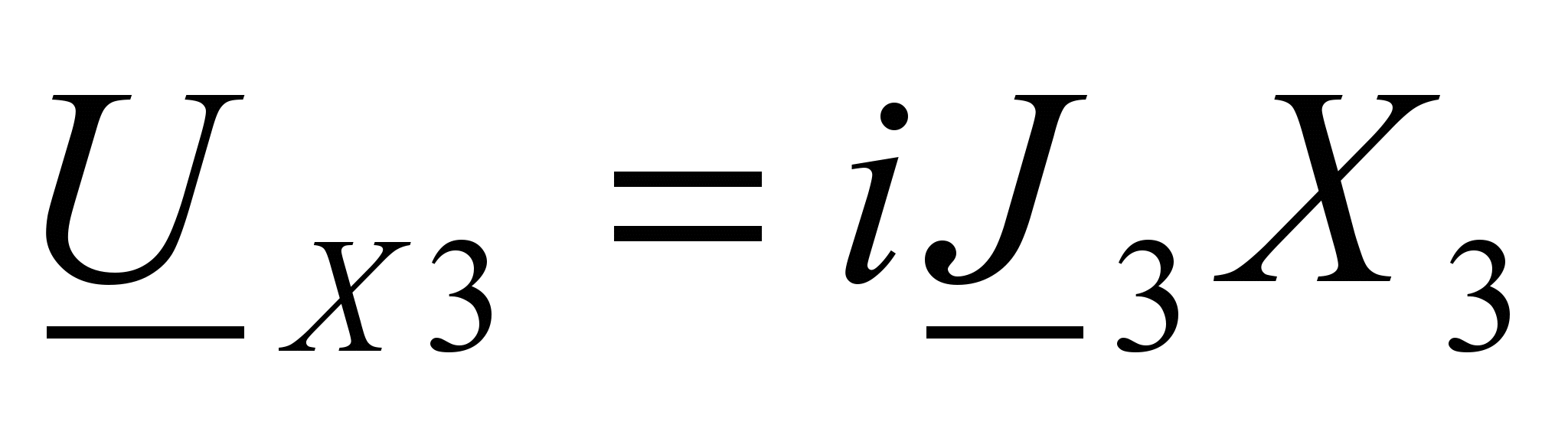(24)Результаты численных расчетов приведены в таблице:
| параметр | 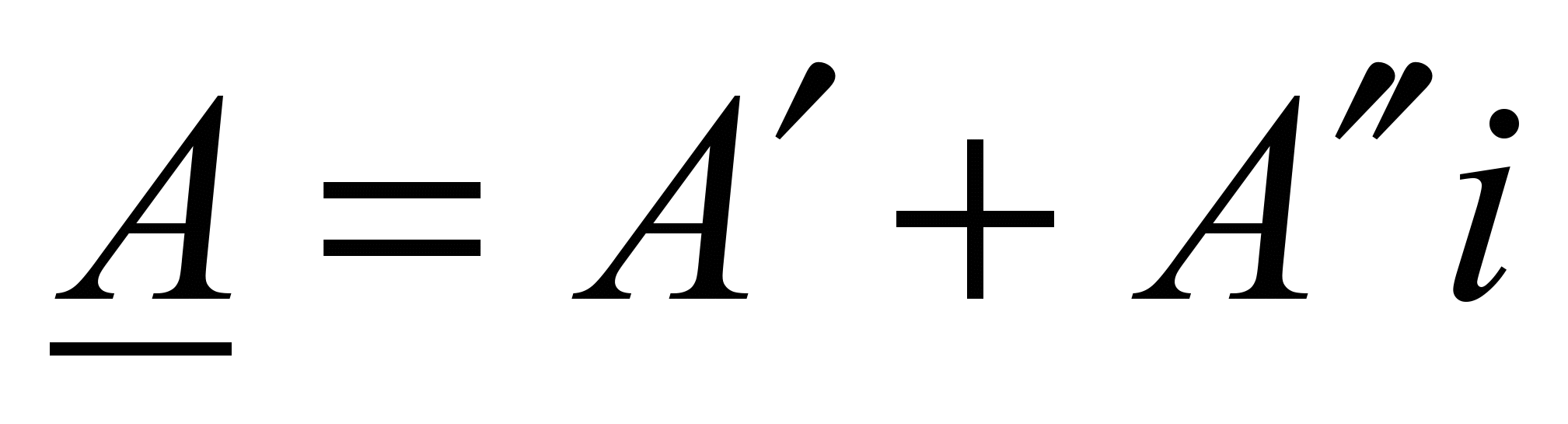 | модуль А | Ф, о |
| U, B | -60-104i | 120 | -120 |
| Z0, Ом | 70+15i | 71 | 12 |
| J1, A | -1,125-1,25i | 1,68 | -132 |
| J2, A | 0,138-0,94i | 0.95 | -81,6 |
| J3, A | -1,263-0,31i | 1,30 | -166 |
| UR1, B | -54-60i | 80,8 | -132 |
| UX1, B | 30-27i | 40,4 | -42 |
| UR2, B | 1.66-11,3i | 11,4 | -81,6 |
| UX2, B | -37,7-5,54i | 38,1 | -171 |
| UR3, B | -37,9-9,27i | 39,0 | -166 |
| UX3, B | 1,85-7,58i | 7,8 | -76 |