3. 1 Электромагнитные поля в эмус и их основные уравнения

Вид материала

Содержание

Рис. 4.7 Графическое пояснение определения местных координат
S 1 2 3 – площадь треугольного элемента – симплекса; S
3.12 Примеры расчёта электромагнитных полей численными методами
Рис. 4.9 Графическое пояснение получения остатков, не превышающих 5
Пример расчёта поля методом конечных элементов.
Рис. 4.11 Пояснение составления уравнения для  внутри одного элемента
N ] [ Ф ] методом Галеркина для одного элемента длиной l

Подобный материал:

1 2 3 4

При расчёте электромагнитных и тепловых полей в электромеханических преобразователях и системах, в частности входящих в состав электрооборудования летательных аппаратов (ЭЛА) наиболее часто применяют двумерные симплексы для решения двумерных или плоскопараллельных задач и трёхмерные симплексы для решения трёхмерных задач. Для решения многих двумерных задач целесообразно делить область на треугольные элементы (симплексы). В этом случае непрерывность искомой функции на границах двух смежных треугольников гарантируется лишь равенством значений функций в совпадающих вершинах треугольников. Кроме того, алгебраические выражения аппроксимирующих функций не зависят от расположения треугольников относительно общей системы координат. Целесообразно более подробно рассмотреть двумерный симплекс как более простой и, вместе с тем, достаточно часто применяемый при расчёте электромагнитных и тепловых полей в электромеханических преобразователях и системах, в частности входящих в состав ЭЛА.

1) Определение местных координат для треугольных элементов (симплексов), для чего внутри текущего элемента ставится точка Р ; её соединение с вершинами даёт три треугольника – подсимплекса (рис. 4.7).

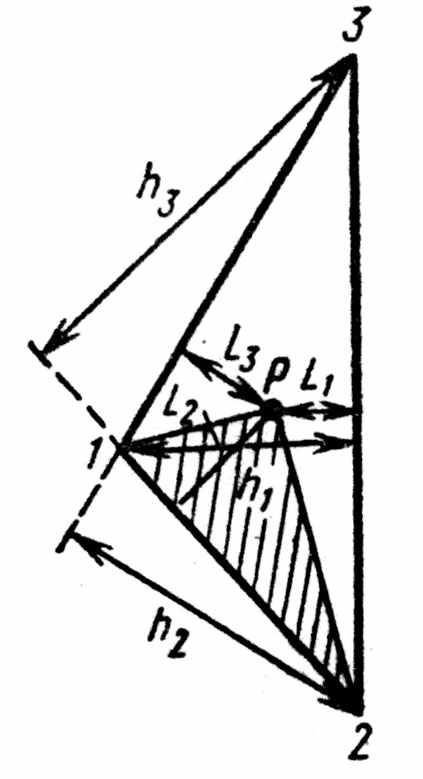Рис. 4.7 Графическое пояснение определения местных координат

2) Определение местных (симплексных) координат точки P. Местоположение точки Р определяется тремя координатами:

;

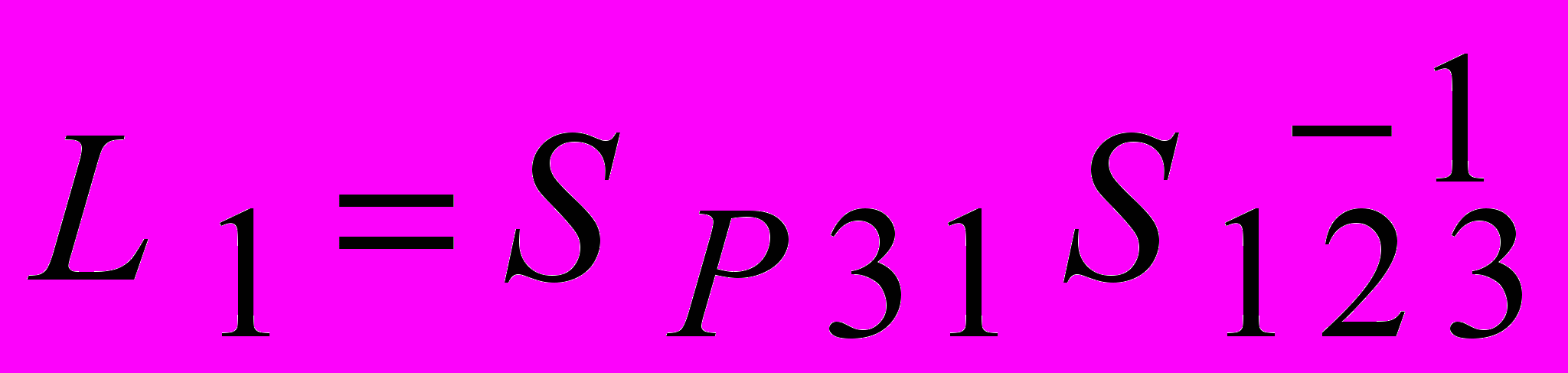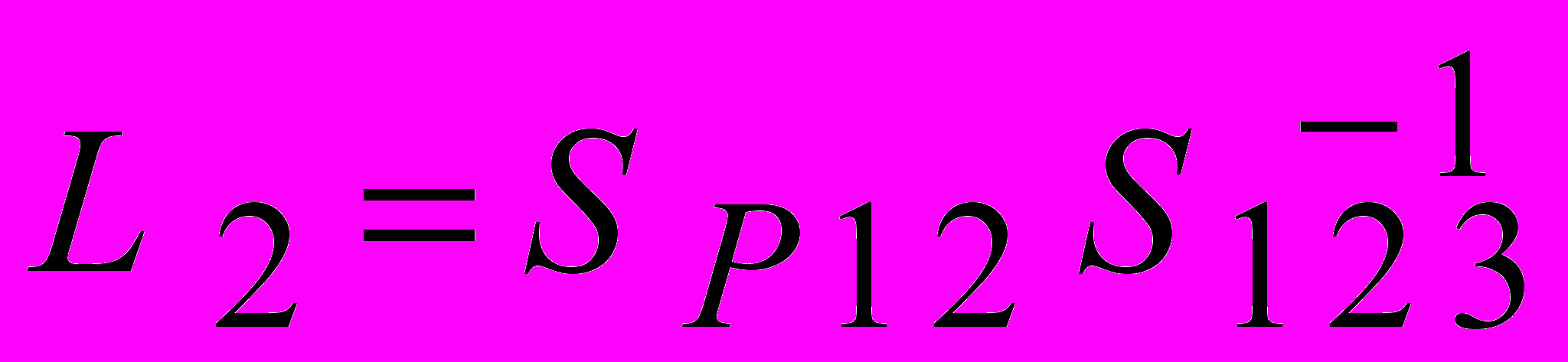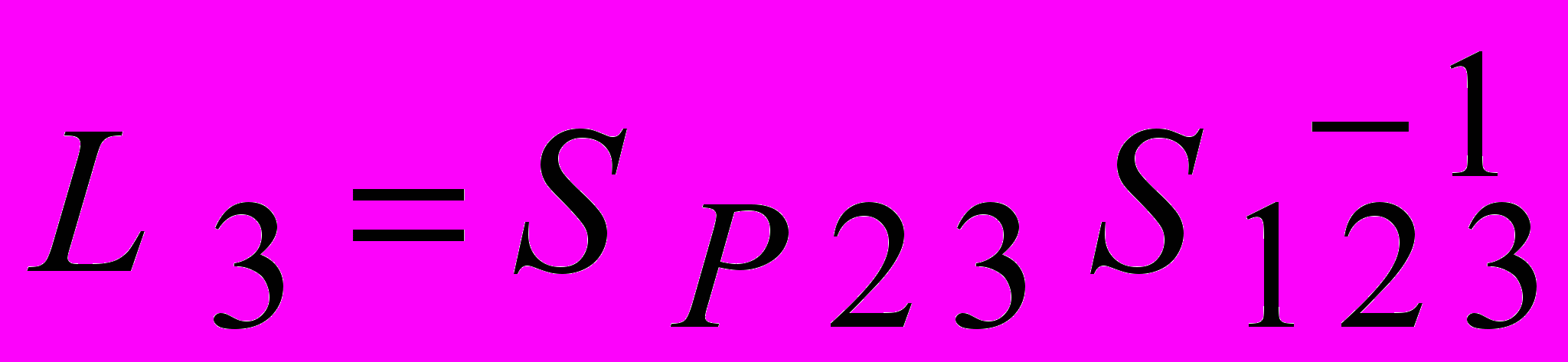где S _{1 2 3} – площадь треугольного элемента – симплекса; S _P_{3 1}, S _P_{1 2}, S _P_{2 3} – площади каждого подсимплекса.

3) Составление уравнения связи координат:

L ₁ + L ₂ + L ₃ = 1 ,

где L ₁, L ₂, L ₃ – координаты вершин x ₁ y ₁ , x ₂ y ₂ , x ₃ y ₃ треугольного элемента (симплекса), которые образуют единичный базисный вектор:

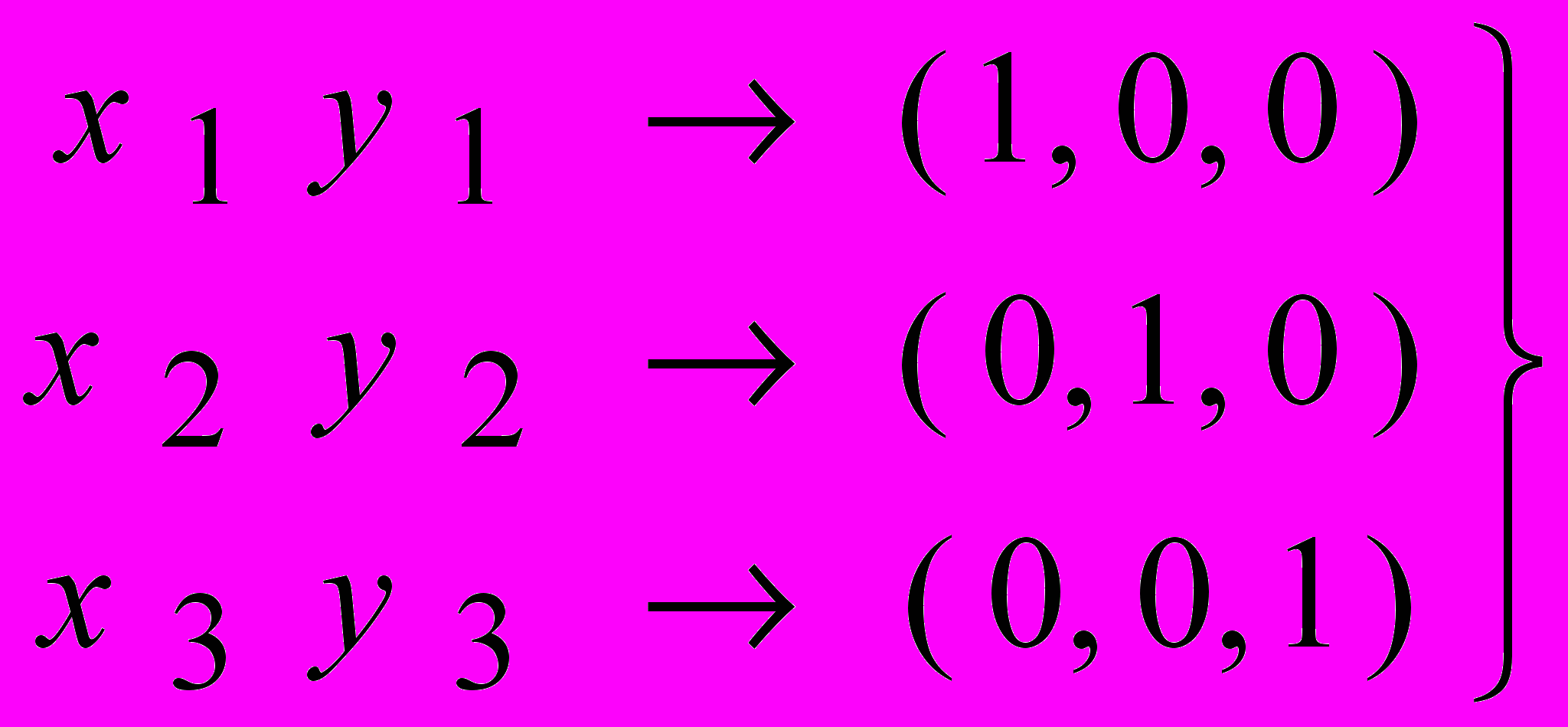4) Нахождение связи координат произвольной точки x y с L-координатам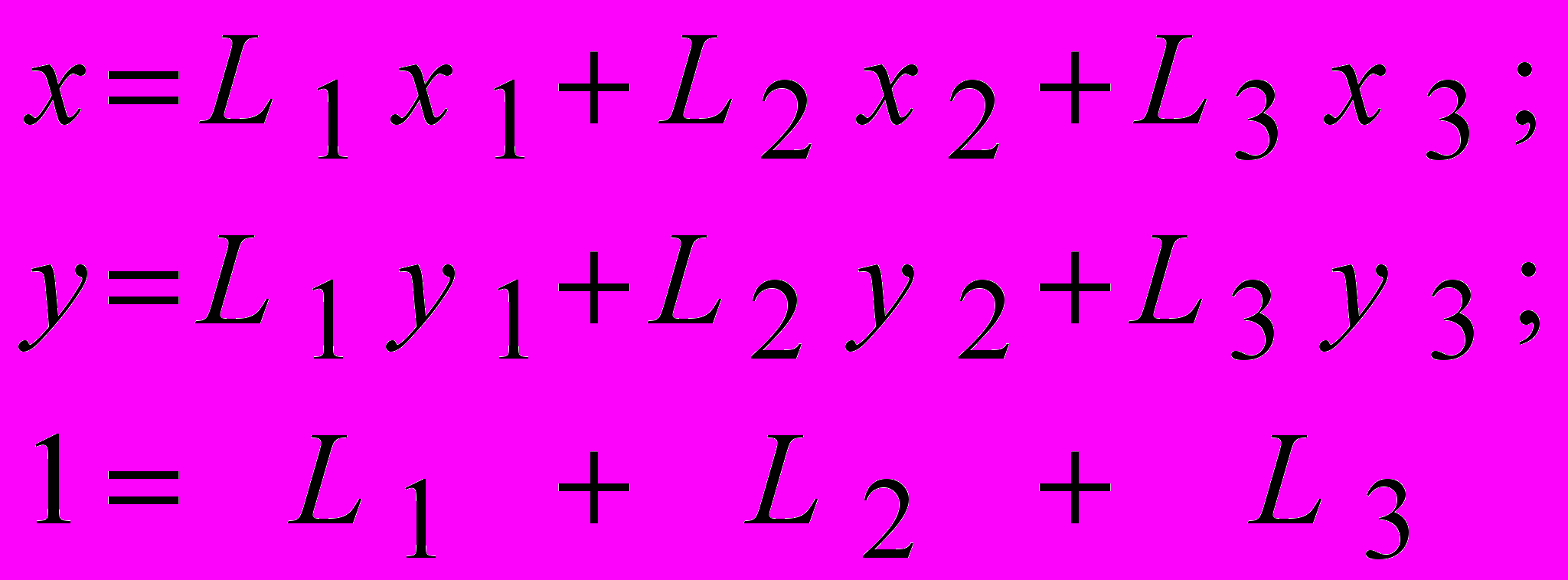и:

или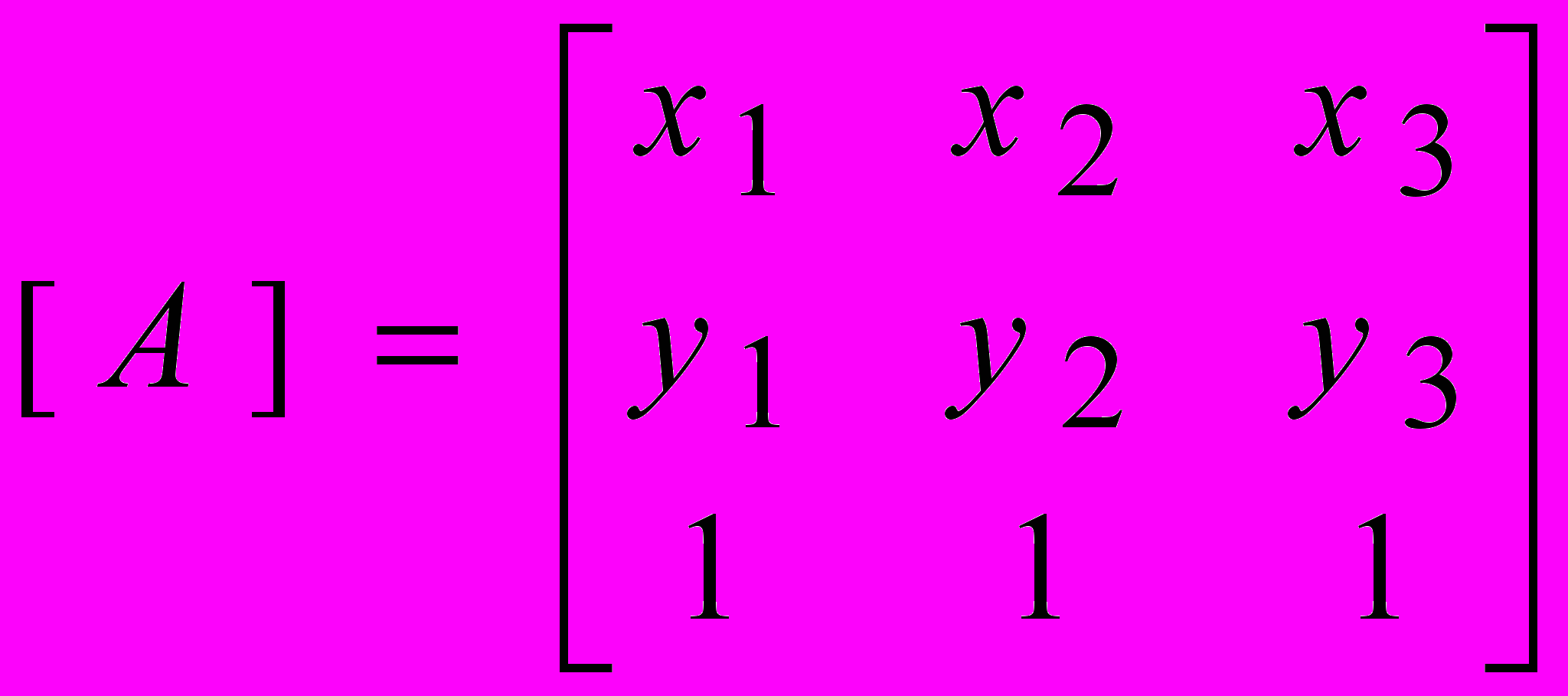

5) Составление формулы интегрирования по площади симплекса:

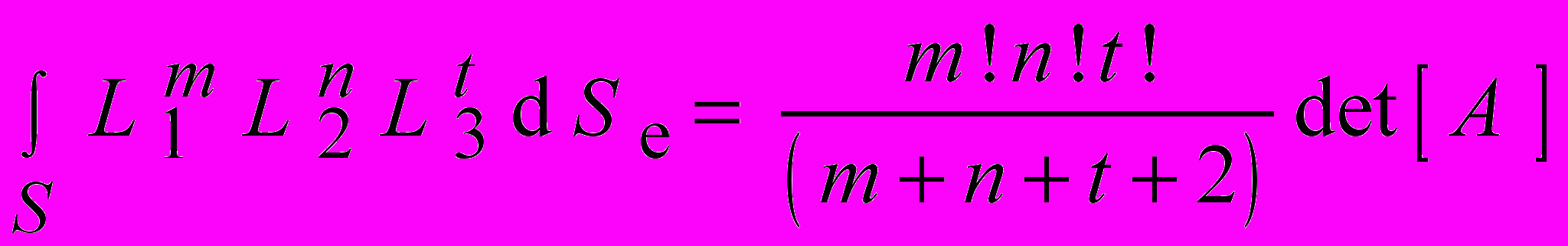6) Вычисление интегралов:

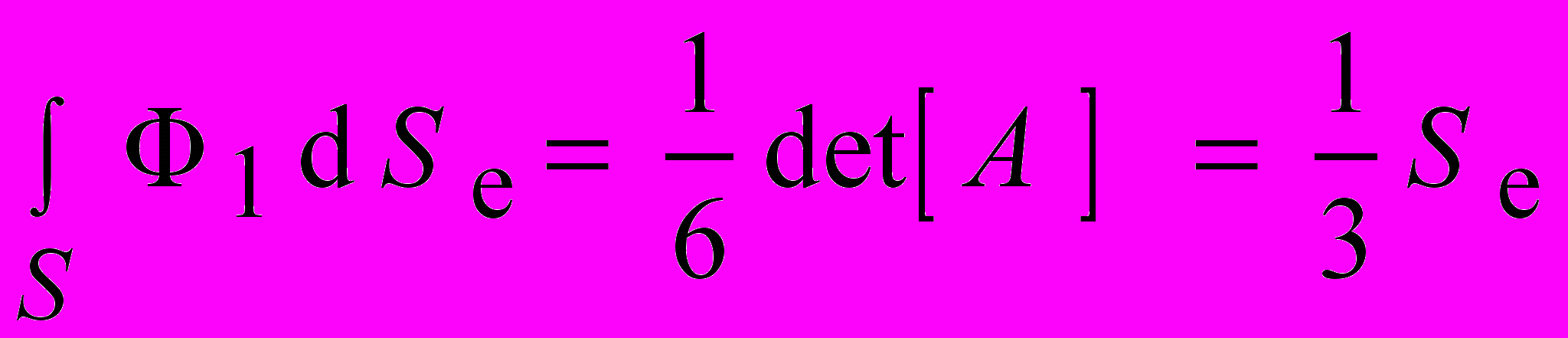где m = 1, n = 0, t = 0;

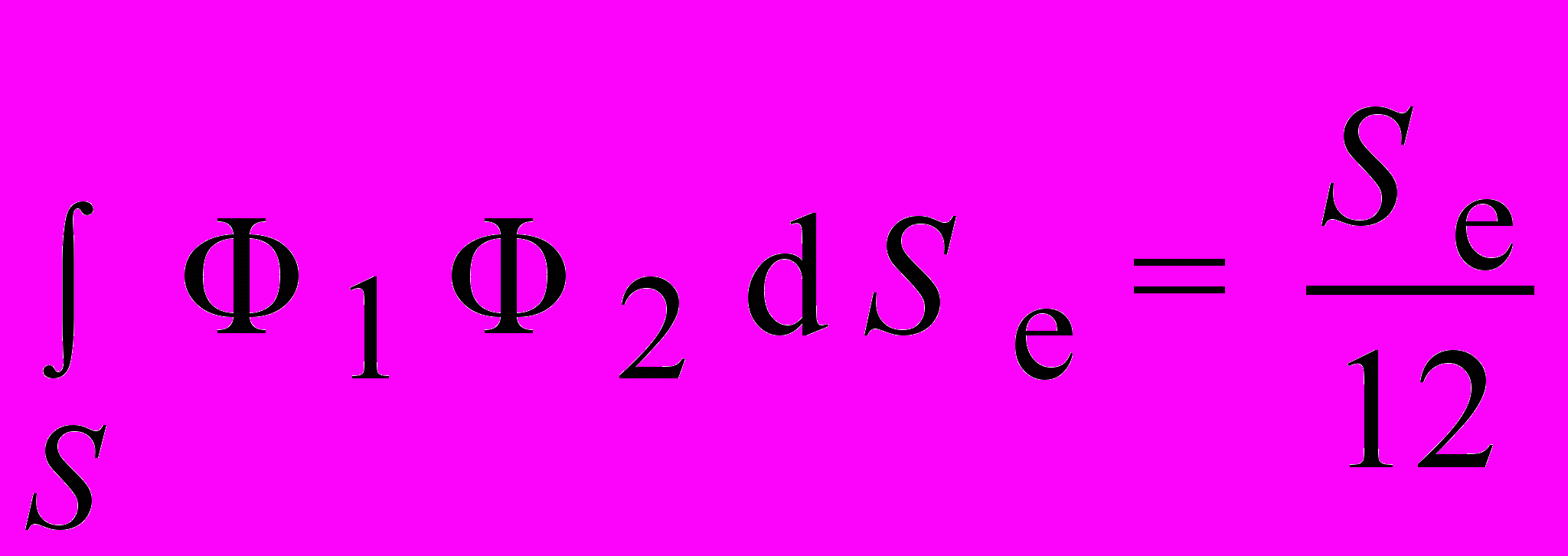При Ф ₁ = L ₁ ; Ф ₂ = L ₂ ; m = 1 , n = 1 , t = 0.

3.11 Подход к составлению схемы эквивалентной магнитной цепи

Подход к составлению схемы эквивалентной магнитной цепи.

Составление схемы эквивалентной магнитной цепи удобно пояснить на примере двухмерного магнитного поля в локальном объёме электрической машины (рис. 4.12) [7]. Это поле возбуждено периодической системой токов i чередующегося направления в пазах верхнего сердечника. Силовые линии магнитного поля (показаны сплошными) разбивают область поля на ряд трубок магнитного потока Т1 , Т2 , . . . , Т12 . Средние линии трубок поля в области паза, занятой током i , показаны пунктирными, эквипотенциальные линии Э1 , Э2 , . . . , Э16 – штрихпунктирными.

Для составления схемы эквивалентной магнитной цепи область магнитного поля разбивается на отдельные подобласти, состоящие из нескольких участков трубок магнитного потока, заключённых между двумя эквипотенциальными поверхностями. Каждой подобласти соответствует ветвь эквивалентной магнитной цепи, показанной на рис. 4.13. Например, подобласти, состоящей из участков трубок Т1–Т6 между эквипотенциалями Э1 и Э16, соответствует ветвь В1. Эта ветвь имеет магнитное сопротивление R _B₁ = i _B₁ / Ф _B₁ , где Ф _{В 1}= Ф _{Т 1}+ Ф _{Т 2} + Ф _{Т 3} + … + Ф _{Т 6} , i _B₁= = u _B₁=  _{Э 1}–  _{Э 16};  _{Э 1},  _{Э 16} – магнитные потенциалы на линиях Э1 и Э16 , соответствующих узлам цепи с теми же индексами.

Обычно в отдельную ветвь объединяются участки трубок магнитного потока, полностью или почти полностью размещающиеся в одной и той же среде. Например, ветви В7 и В15 лежат в ферромагнитной среде, ветви В4 , В9 почти целиком находятся в ферромагнитной среде, ветви В1 , В19 – в немагнитной среде. В контуры эквивалентной магнитной цепи введены МДС, равные токам, охваченным средними силовыми линиями магнитных потоков ветвей контура. Например, в контур, образованный ветвью В22 (трубкой Т12), введена МДС i ₁ , равная току, охваченному средней силовой линией магнитного потока ветви; в контур, образованный ветвями В22 , В21 и В7 , – МДС i ₂ , равная току, охваченному средними силовыми линиями магнитных потоков этих ветвей; в контур, образованный ветвями В21 , В8 , В20 , В6 , – МДС i ₃ , равная току, охваченному средними силовыми линиями магнитных потоков этих контуров, и т. д. Полная МДС в контурах, охватывающих весь ток паза i , равна сумме частичных МДС i = i ₁ + i ₂ + i ₃ + i ₄ + i ₅ + i ₆ .


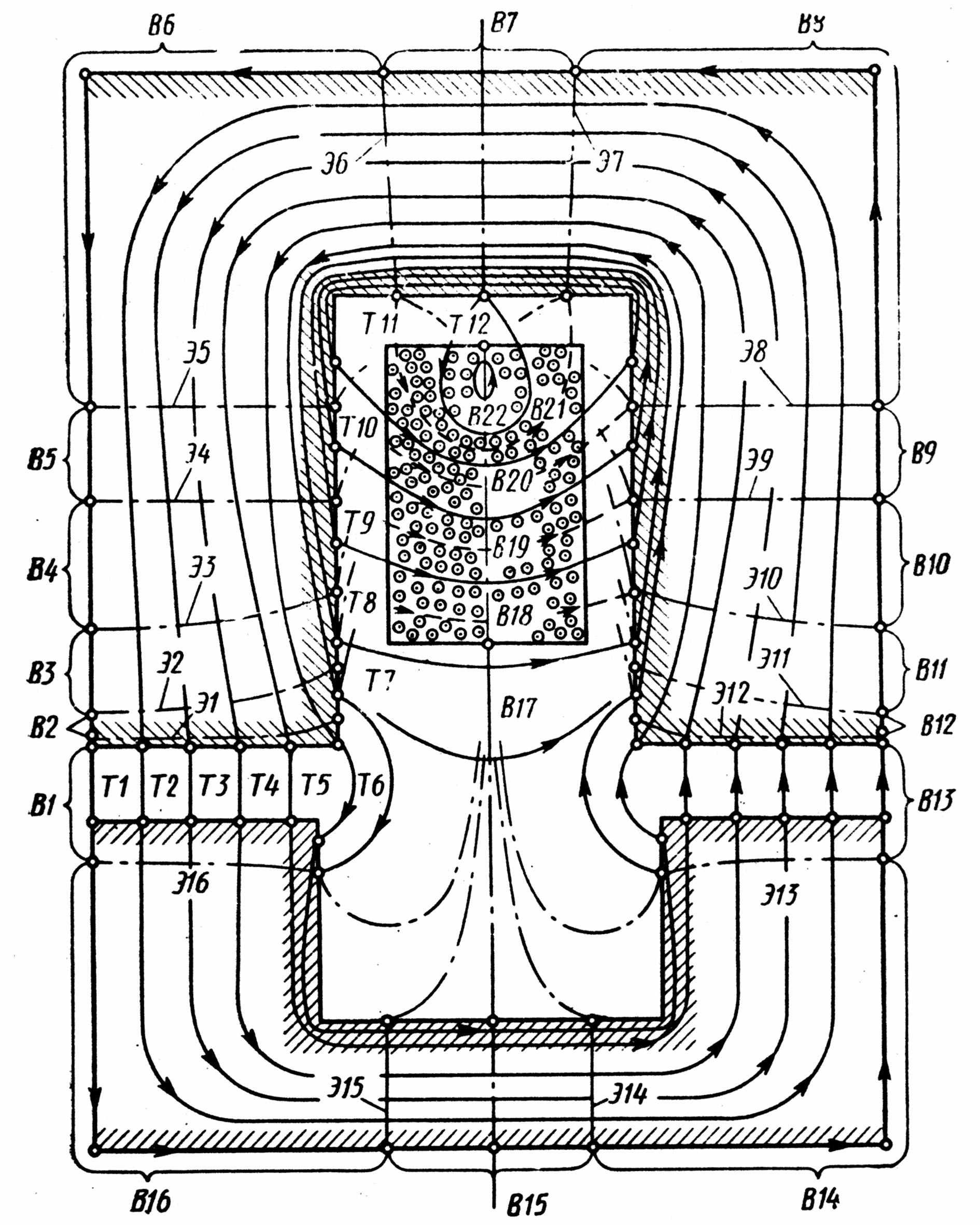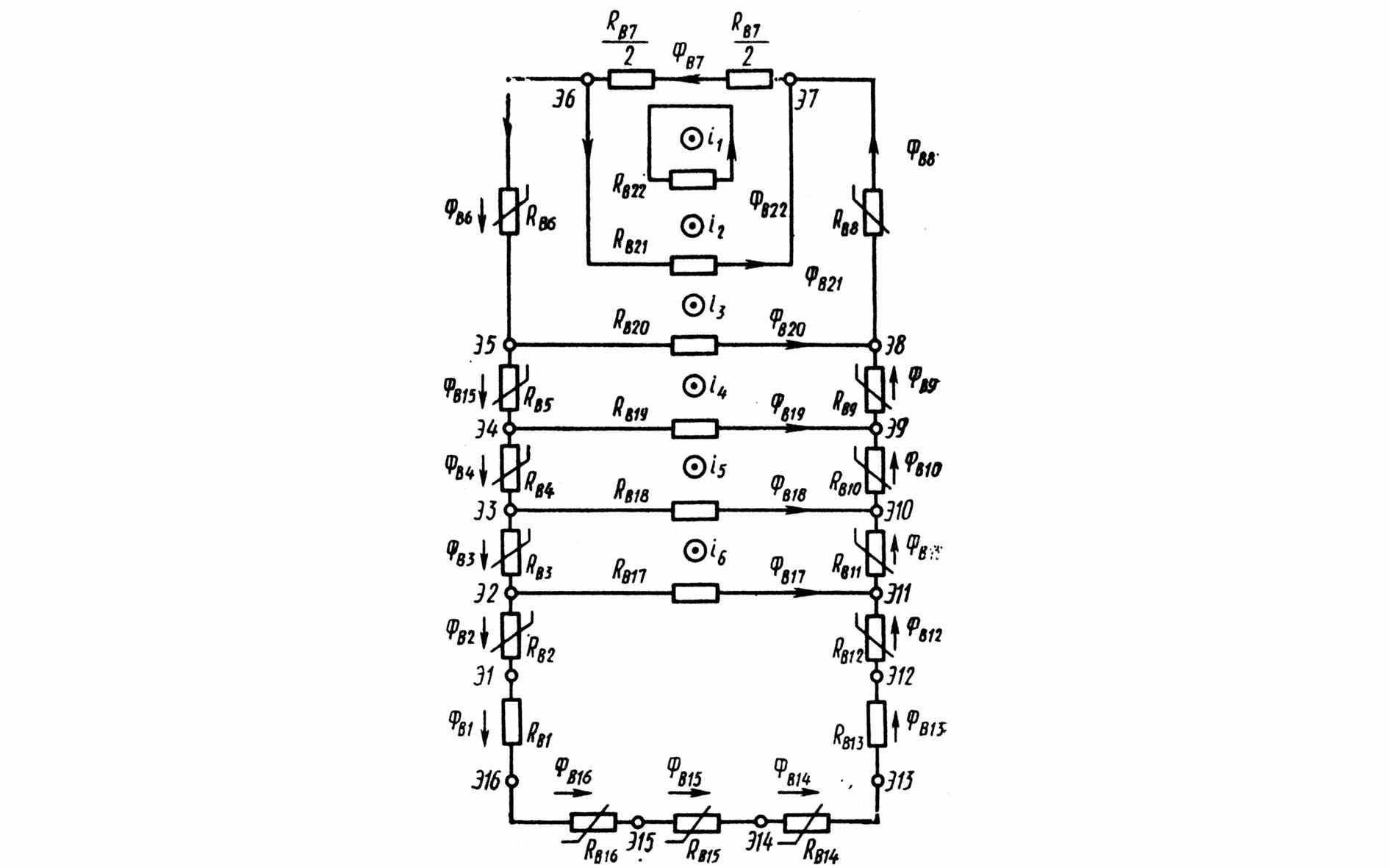Рис. 4.12 Разбиение области магнитного поля на ряд подобластей, соответствующих отдельным ветвям В1–В22 эквивалентной магнитной цепи		Рис. 4.13 Схема магнитной цепи, эквивалентной магнитному полю на рис. 4.12

Составленная схема магнитной цепи эквивалентна рассматриваемому магнитному полю в отношении магнитных потоков Ф _B_S , сопротивлений и напряжений или МДС u _B_S = i _B_S ветвей. Другими словами, в результате расчёта этой цепи при МДС в контурах, определённых указанным образом, потоки Ф _В_S и магнитные напряжения или МДС u _B_S = i _B_S ветвей не будут отличаться от тех же величин для подобластей поля, ограниченных соответствующими магнитными и эквипотенциальными поверхностями.

Эквивалентные магнитные цепи для любых двухмерных или трёхмерных магнитных полей в нелинейных системах независимо от их сложности составляются аналогичным образом. Точность расчёта с помощью схемы магнитной цепи непосредственно зависит от полноты воспроизведения интегральных величин магнитного поля, то есть от достоверности определения магнитных сопротивлений ветвей магнитной цепи, соответствующих элементам магнитного поля, и МДС (токов), охваченных контурами магнитной цепи.

3.12 Примеры расчёта электромагнитных полей численными методами

Пример использования метода сеток.

Найти распределение потенциала в поле плоского конденсатора, одна из обкладок которого деформирована. Остаток не должен превышать 5.

Р е ш е н и е.

1) Изображение прямоугольной сетки в области между обкладками конденсатора с обозначением её узлов буквами и эквипотенциалей при потенциалах обкладок  ₀ = 0 и  _n = 60 (рис. 4.8).

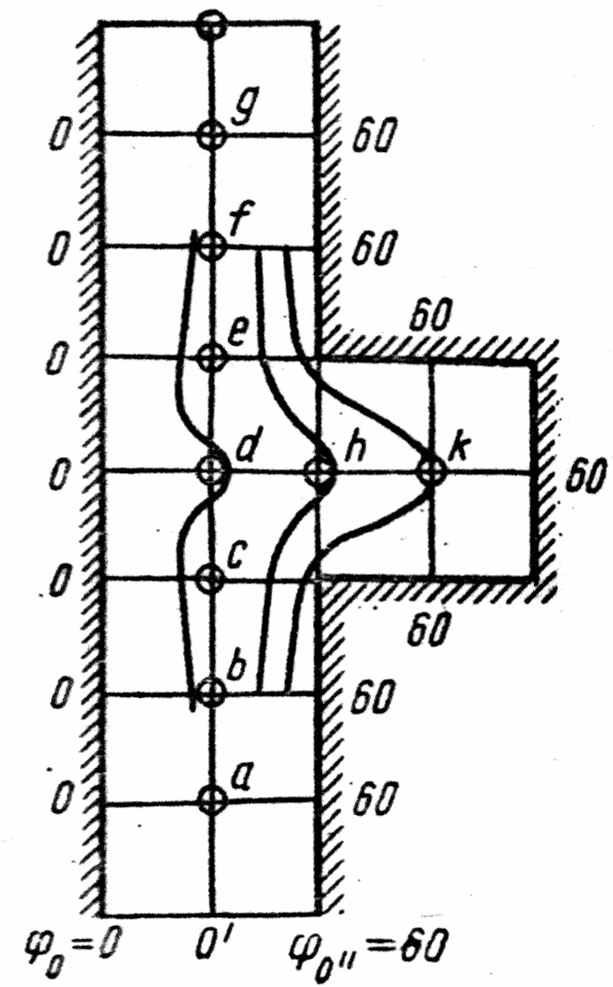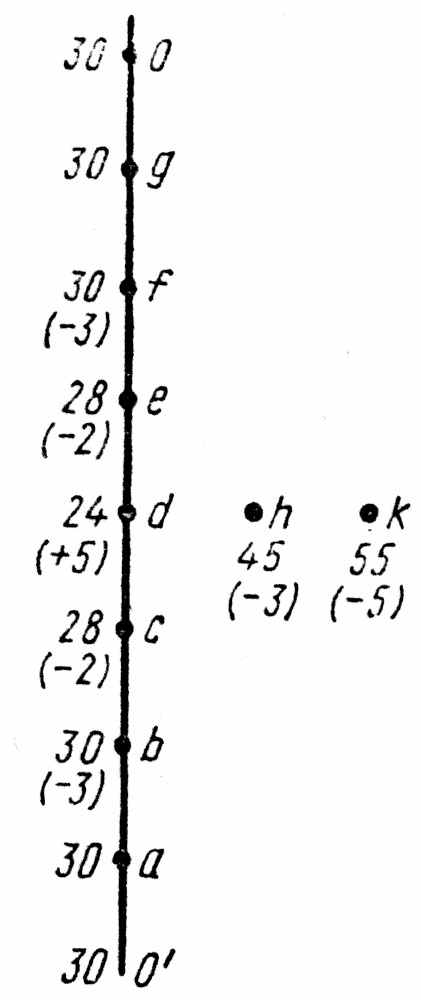Рис. 4.8 Прямоугольная сетка в области между обкладками конденсатора

Рис. 4.9 Графическое пояснение получения остатков, не превышающих 5

2) Нахождение остатков в уравнениях связи (3.24) для каждого узла, для чего произвольно устанавливаются начальные значения потенциалов в узлах с ориентацией на эквипотенциали. Например, для узла d :

;

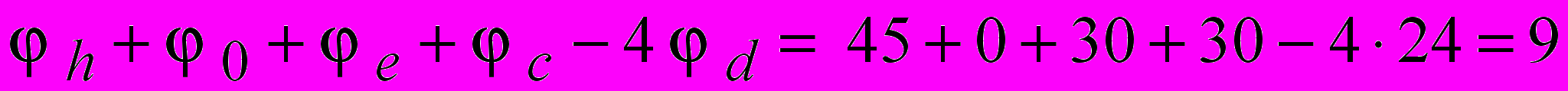3) Получение остатков, не превышающих 5, изменением значений потенциалов узлов с вычислением каждый раз остатков. Для узла d (рис. 4.9):

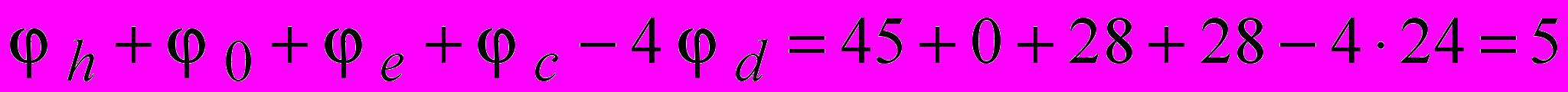Пример расчёта поля методом конечных элементов.

Решить методом конечных элементов, привлекая метод Галеркина, уравнение d ²  / d x ² = –  ( x ) / (  ₁  ₂ ) = M x электростатического поля между заряженными пластинами, расстояние между которыми d ,  = 0 при х = 0 и ( d  / d x ) _x_{= 0} = 0 при x = 0. Функция ρ ( х ) известна.

Р е ш е н и е.

1) Разбиение исследуемой области поля на элементы: область поля для простоты разбивается на три элемента (рис. 4.10).

2) Составление уравнений элементов.

 = α ₁+ α ₂ x ,

Аппроксимация  внутри каждого элемента полиномом с двумя коэффициентами (элементы имеют по два узла). Условия для узлов элемента:

 = Ф _i при x = X _i ;  = Ф _j при x = X _j ,

где i , j – индексы, указывающие номера узлов.

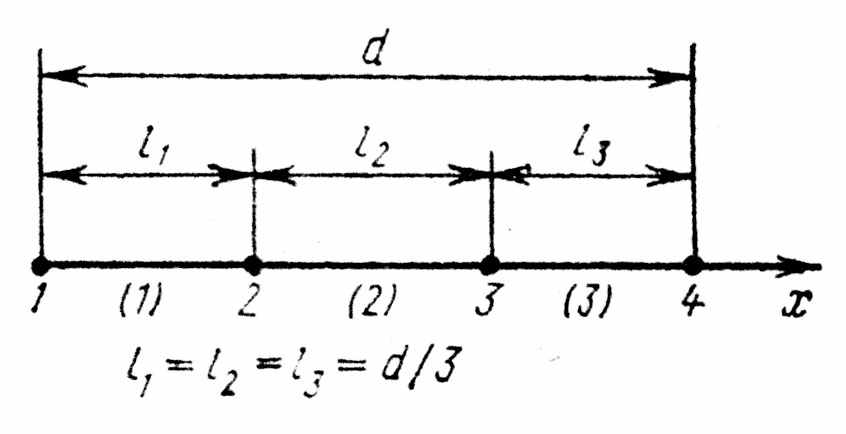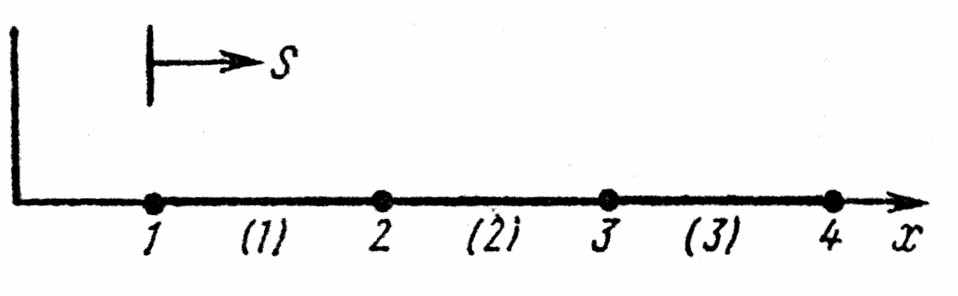Рис. 4.10 Разбиение области поля

на три элемента

Рис. 4.11 Пояснение составления уравнения для  внутри одного элемента

Составляется система уравнений для определения узловых значений Ф_i и Ф_j каждого узла на основании аппроксимирующего полинома:

Ф _i= α ₁+ α₂X _i ; Ф _j= α ₁+ α₂X _j ,

2) Составление уравнения для  внутри одного элемента при расположении начала координат вне элемента. После решения предыдущих уравнений относительно α₁ и α₂ и подстановки найденных значений в аппроксимирующий полином (рис. 4.11)

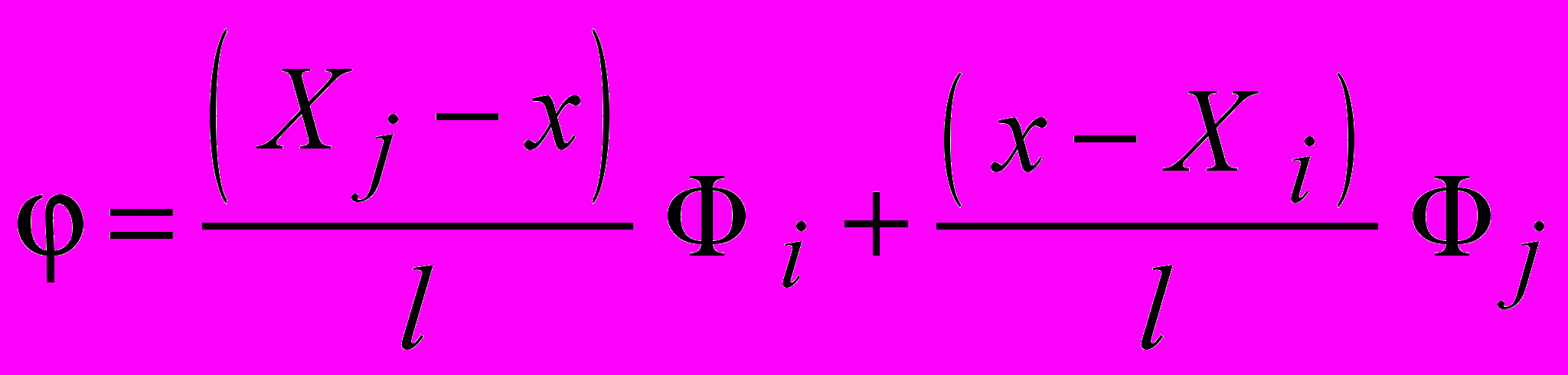3) Составление уравнения для  при расположении начала координат в i-м узле элемента (упрощает последующие вычисления):

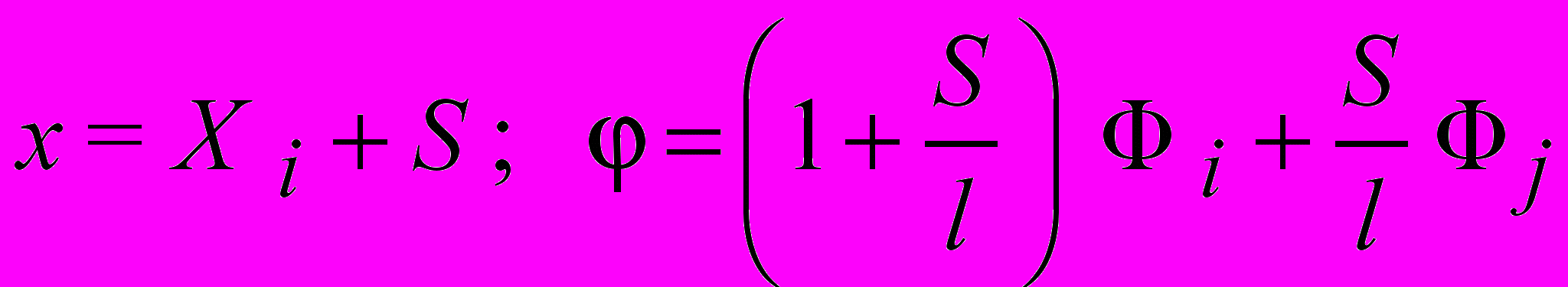Уравнения для  с интерполяционными функциями N для каждого узла

 = N _i Ф _i + N _j Ф _j,

где N _i = ( 1 + S / l ) ; N _j = S / l .

4) Составление уравнения для  в матричной форме для всей области

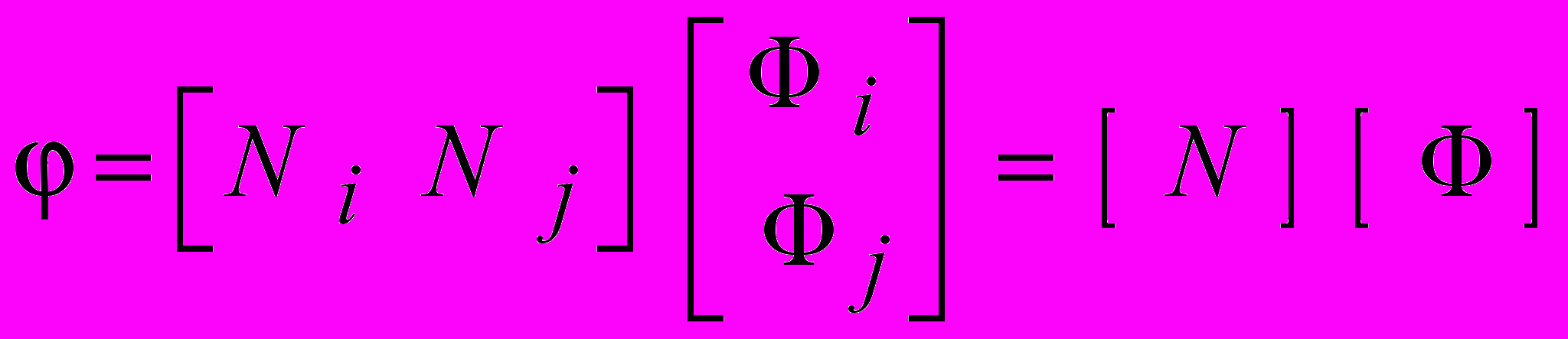4) Решение интерполяционного уравнения [  ] = [ N ] [ Ф ] методом Галеркина для одного элемента длиной l :

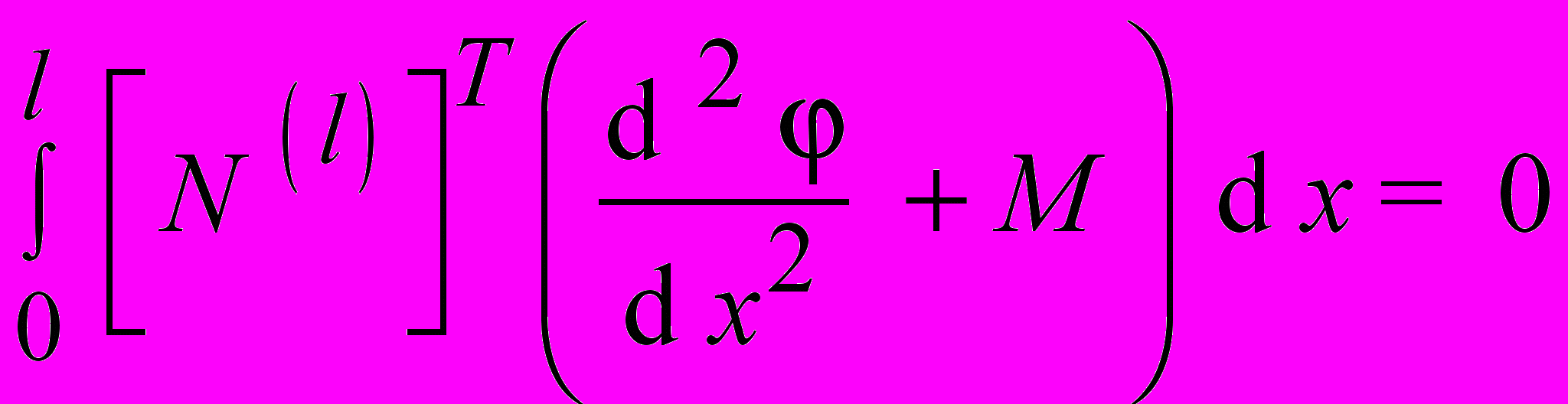где [ N ⁽^l⁾ ] ^T – транспонированная матрица элемента l .

При x = 0 d  / d x = 0 и  = 0 .

После преобразования интеграла, записанного по методу Галеркина, путём интегрирования его по частям (для снижения порядка производной):

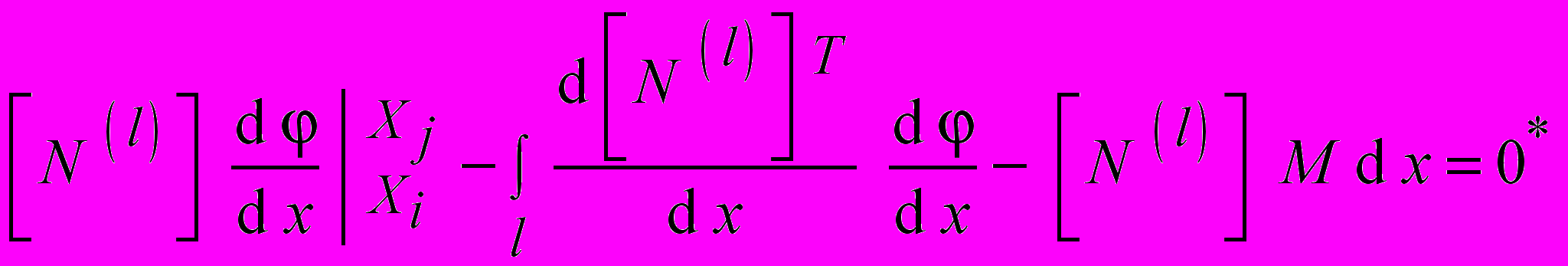где

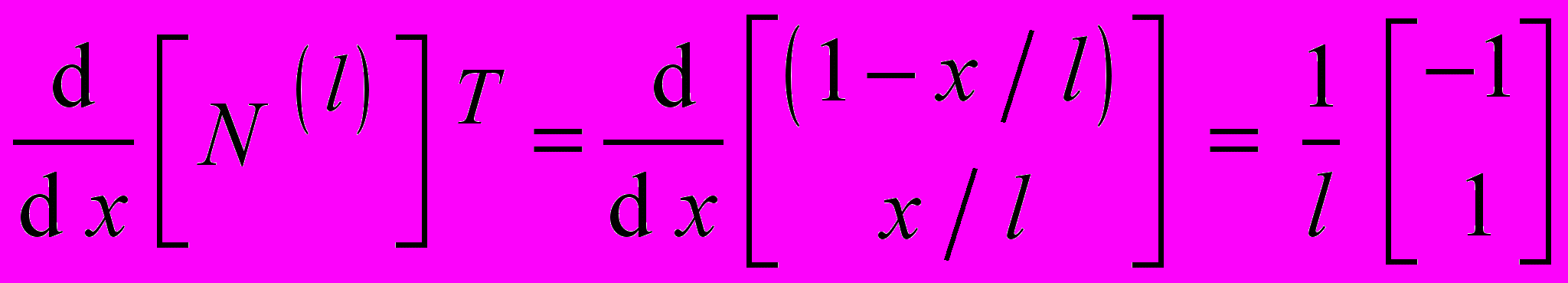; * – функция М = – ρ (x) / ε _rε ₀ аппроксимируется линейной моделью

.

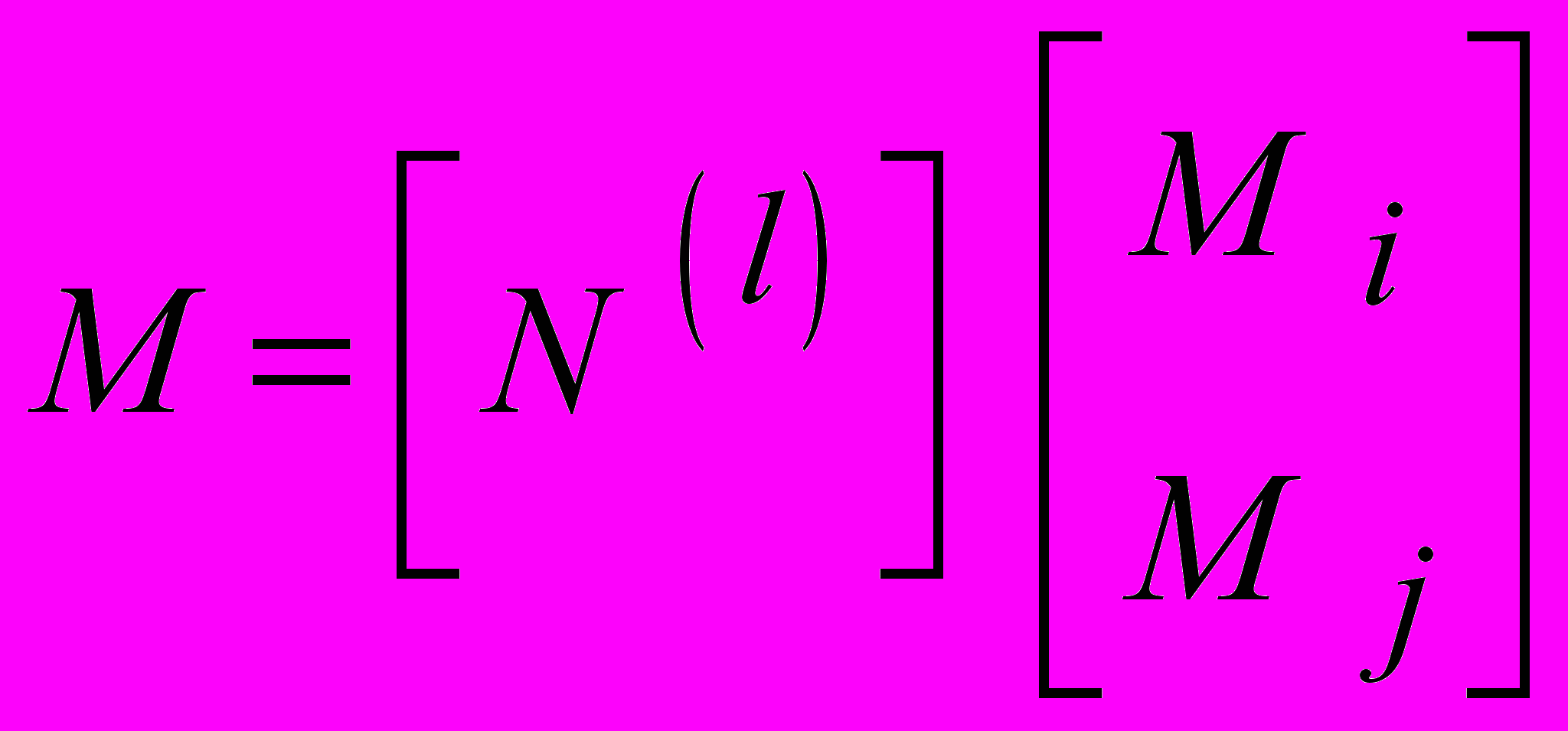5) Составление уравнения для элемента:

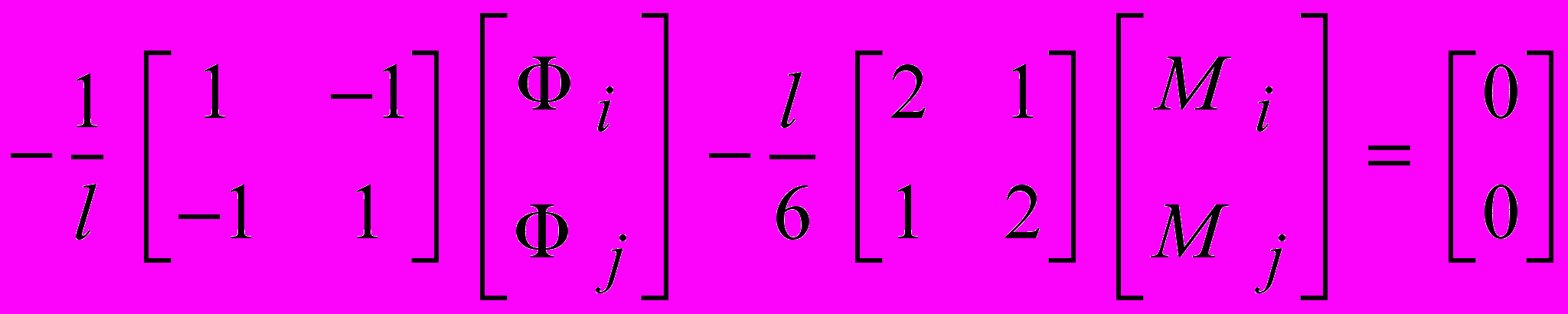6) Составление системы уравнений относительно узловых функций. После суммирования матриц в общих узлах элементов получается:

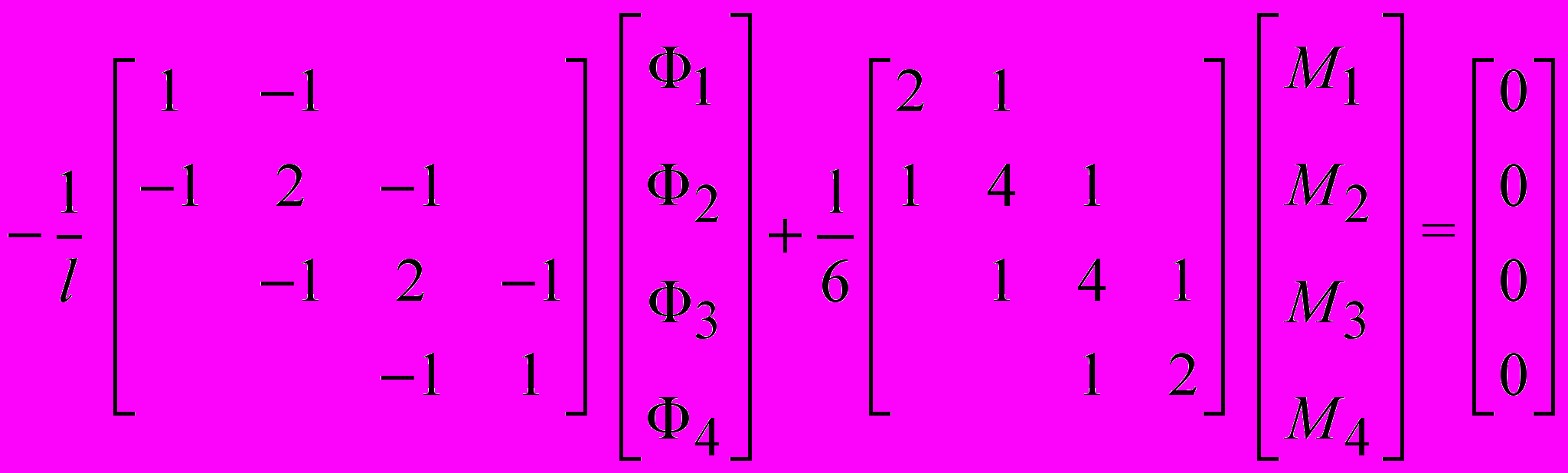7) Решение первого уравнения относительно Ф ₂ с учётом того, что Ф ₁ = 0 (по условию,  = 0 при x = 0):

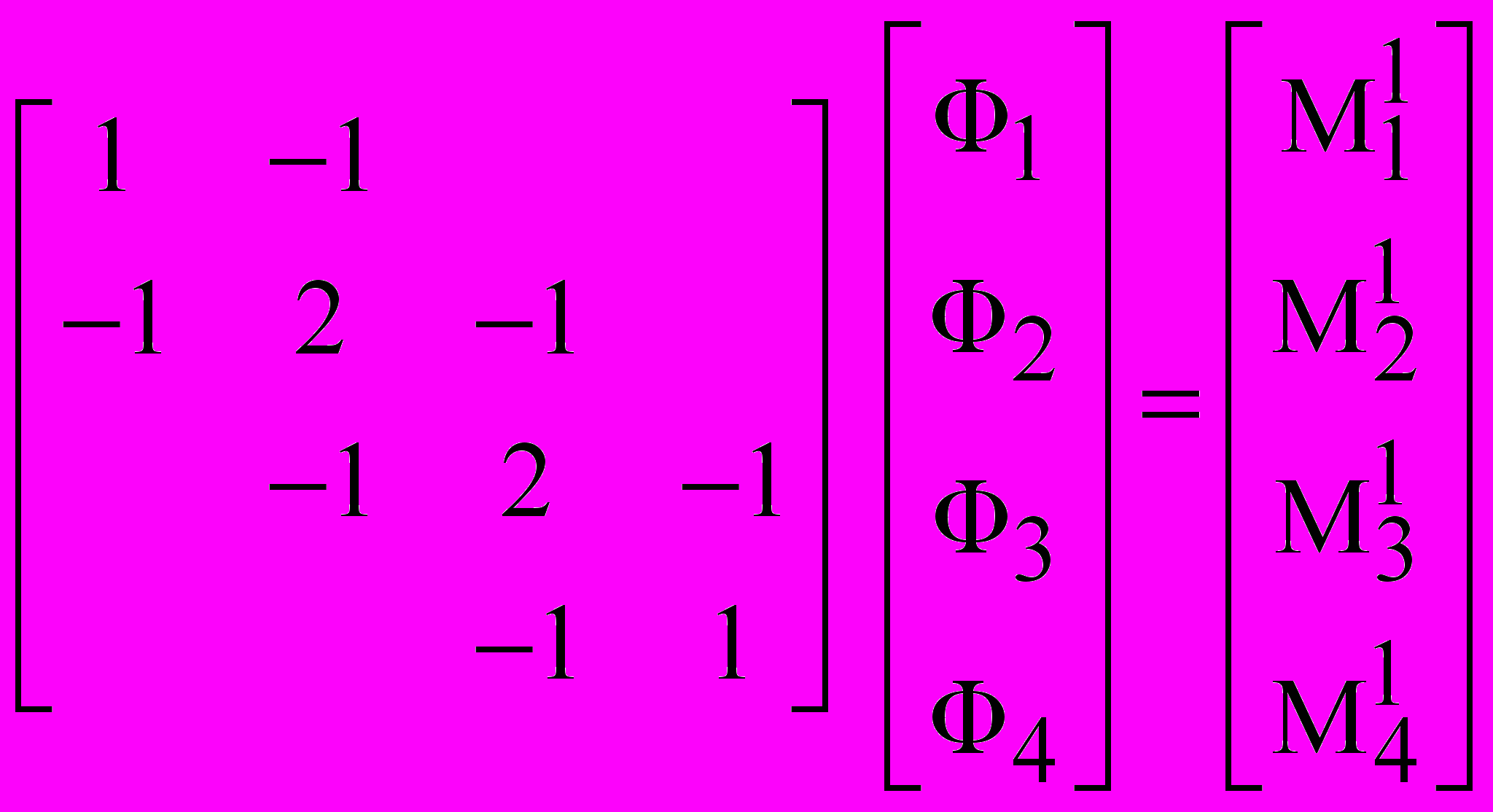откуда

;

.

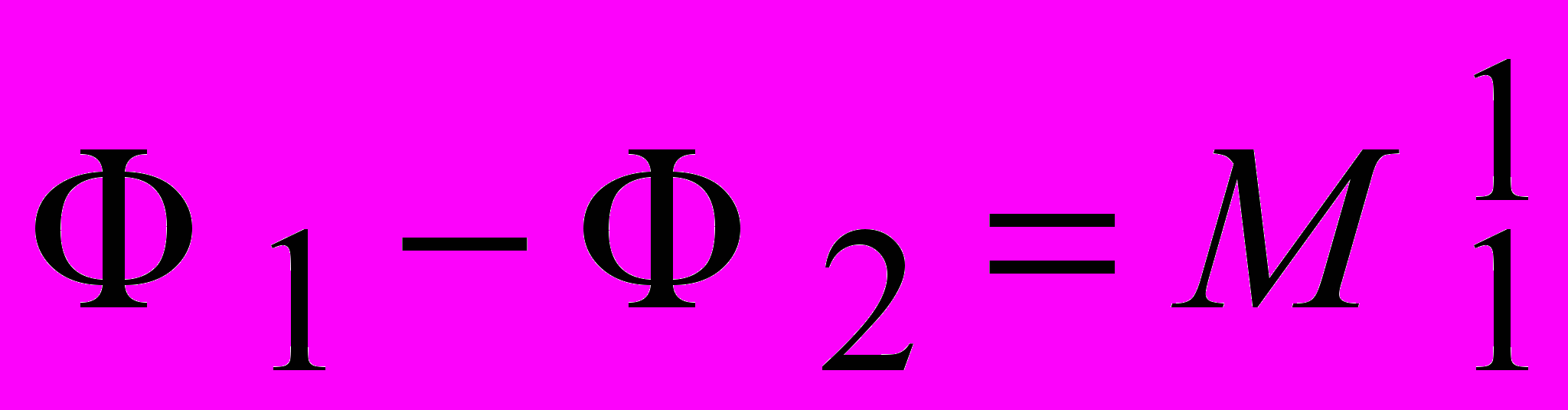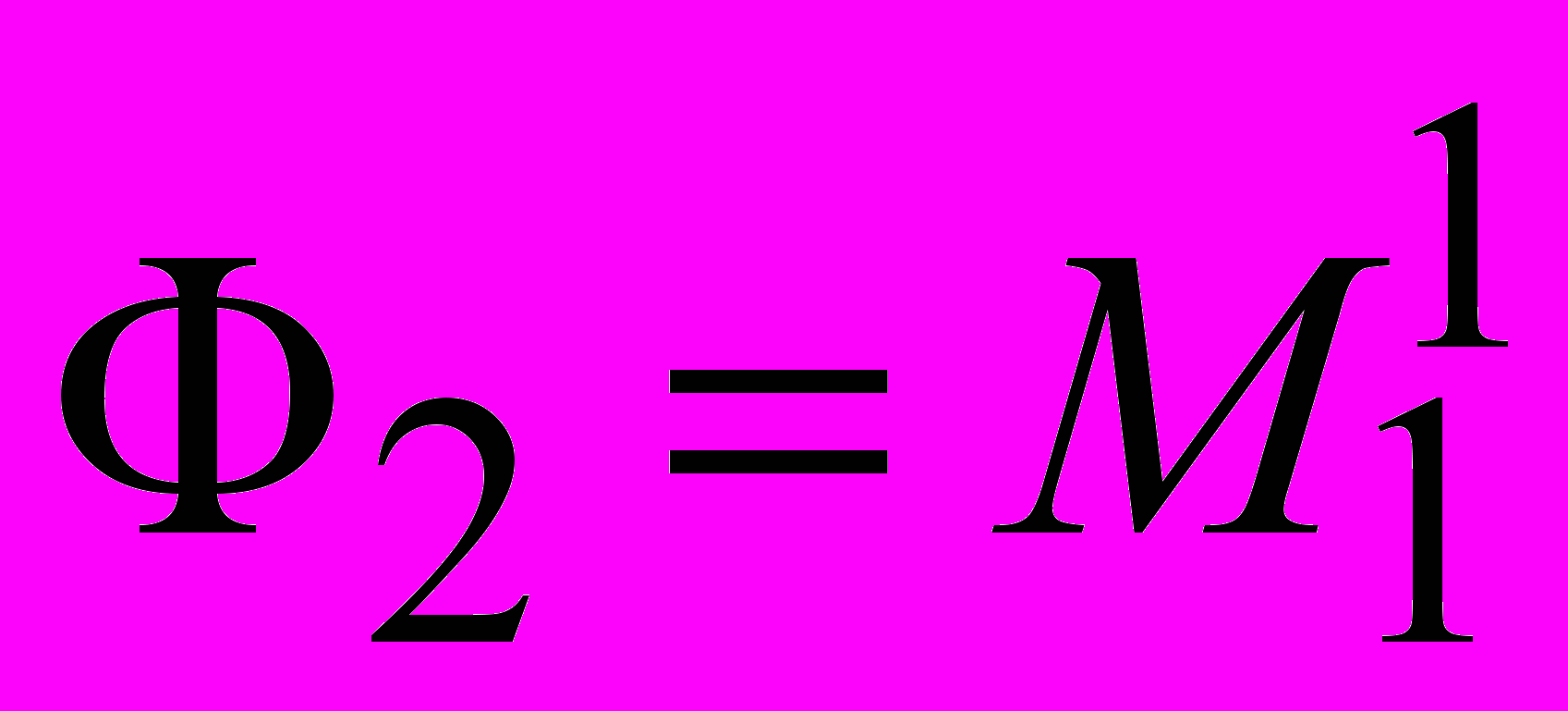8) Решение второго уравнения относительно Ф ₃, третьего – относительно Ф ₄ и n-го – относительно Ф_n₊₁:

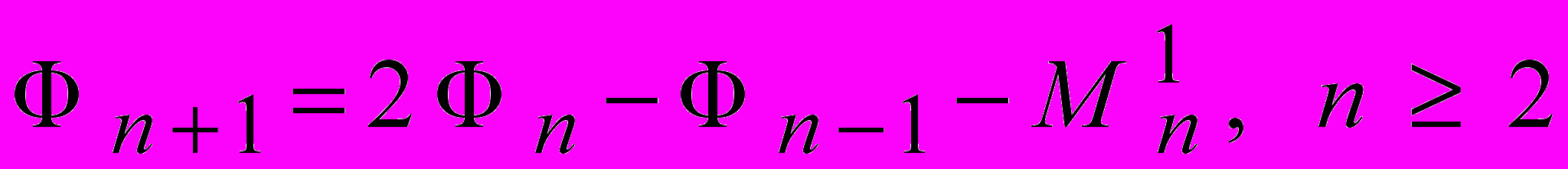ЛИТЕРАТУРА

Тозони О. В. Метод вторичных источников в электротехнике. М., 1975.
Татур Т. А. Основы теории электромагнитного поля: Справочн. пособие для электротехн. спец. вузов. – М.: Высш. шк., 1989. – 271 с.: ил.
Кулон Ж.-Л., Сабоннадьер Ж.-К. САПР в электротехнике: Пер. с франц. – М.: Мир, 1998. – 208 с., ил.
Корячко В. П., Курейчик В. М., Норенков И. П. Теоретические основы САПР. М.: Энергоатомиздат, 1987.
Гринберг Г. А. Избранные вопросы математической теории электрических и магнитных явлений. М., 1972.
Татур Т. А. Электромагнитное поле в реальных средах. Киев, 1976.
Универсальный метод расчёта электромагнитных процессов в электрических машинах. Иванов-Смоленский А. В, Абрамкин Ю. В., Власов А. И., Кузнецов В. А.: под ред. А. В. Иванова-Смоленского. М.: Энергоатомиздат, 1986.

Blog