3. 1 Электромагнитные поля в эмус и их основные уравнения

Вид материала

Содержание

3.9 Последовательность расчёта поля методом конечных элементов
Получение уравнений для элементов
Рис. 4.6 К получению полинома для треугольного элемента
Формирование уравнений для всей области
N изменят свои значения, поскольку в интерполяционные уравнения вместо i
Решение интерполяционных уравнений
3.10 Местная (симплексная) система координат

Подобный материал:

1 2 3 4

На рис. 4.3 при построении каждый элемент аффинно преобразуется с масштабом 0,9 и центром, совпадающим с его центром масс. Это позволяет выделить отверстия, например, пространство между элементами 13, 30, 31 и 32, и несовпадения, например, между элементами 34 и 42 с элементом 35.

3.9 Последовательность расчёта поля методом конечных элементов

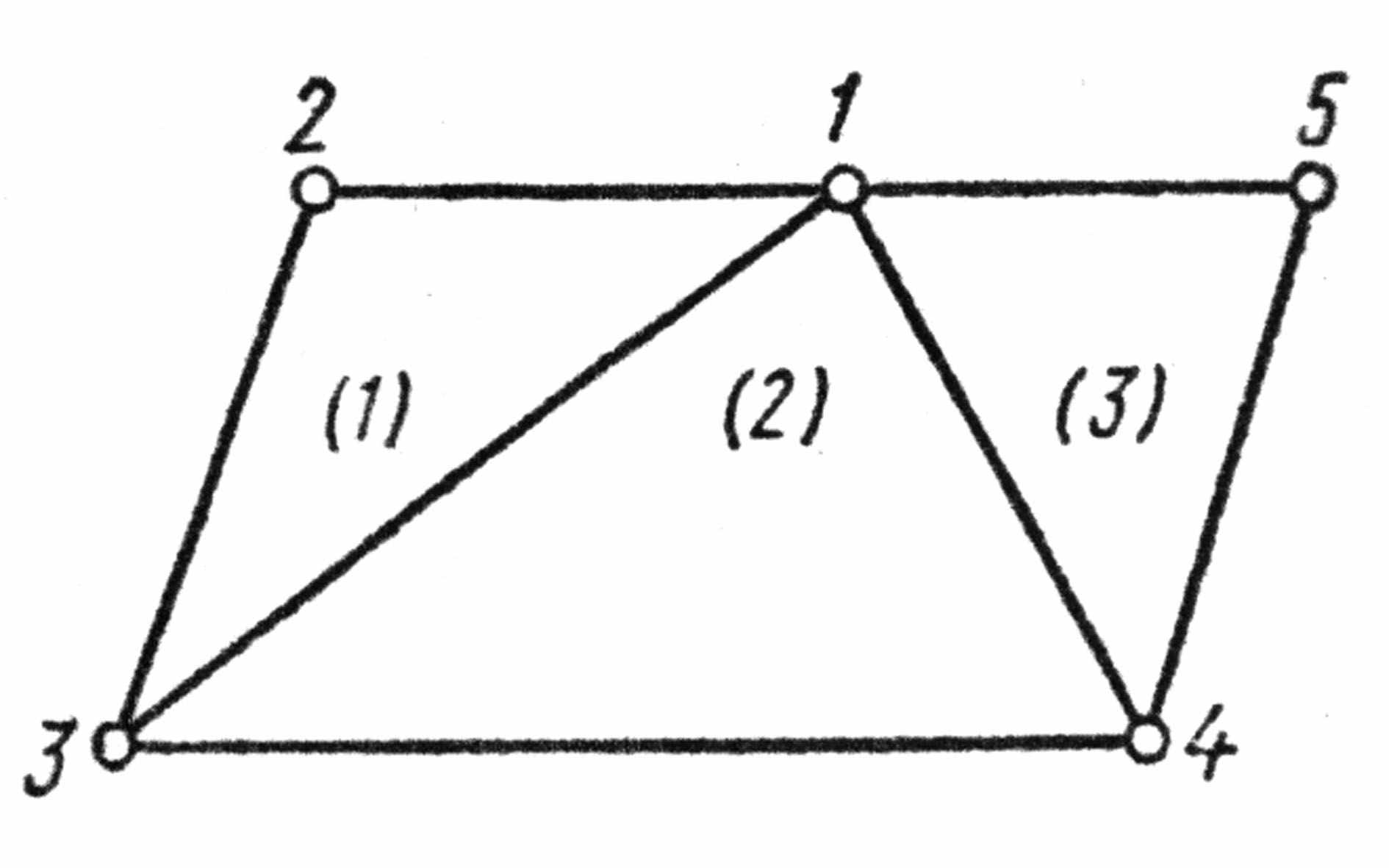
1) Разбиение области на конечные элементы. Область, занятая исследуемым полем, разбивается на ряд конечных элементов, которые имеют общие узлы. При этом используются элементы различных типов в зависимости от постановки задачи (рис. 4.1). Наиболее простыми являются одномерные, двумерные (треугольники и четырёхугольники) и трёхмерные (тетраэдры и параллелепипеды) элементы. Из двумерных элементов простейшим является треугольник, поскольку между двумя узлами искомая функция изменяется линейно вдоль каждой из его сторон. При моделировании криволинейных границ поля добавляются узлы в середину сторон элементов. Толщина элементов для трёхмерных полей может быть постоянной или зависеть от координат. Размеры элемента и его ориентация выбираются исходя из условия задачи. На рис. 4.5 приведён пример разбиения двумерной области на линейные треугольные конечные элементы.

2) Получение уравнений для элементов. Искомую функцию для каждого элемента аппроксимируют полиномом, например степенным. Аппроксимирующие функции должны удовлетворять условиям непрерывности на общих границах (сторонах) элементов и постоянства производных. Для треугольного элемента этот процесс поясняется рис. 4.6.

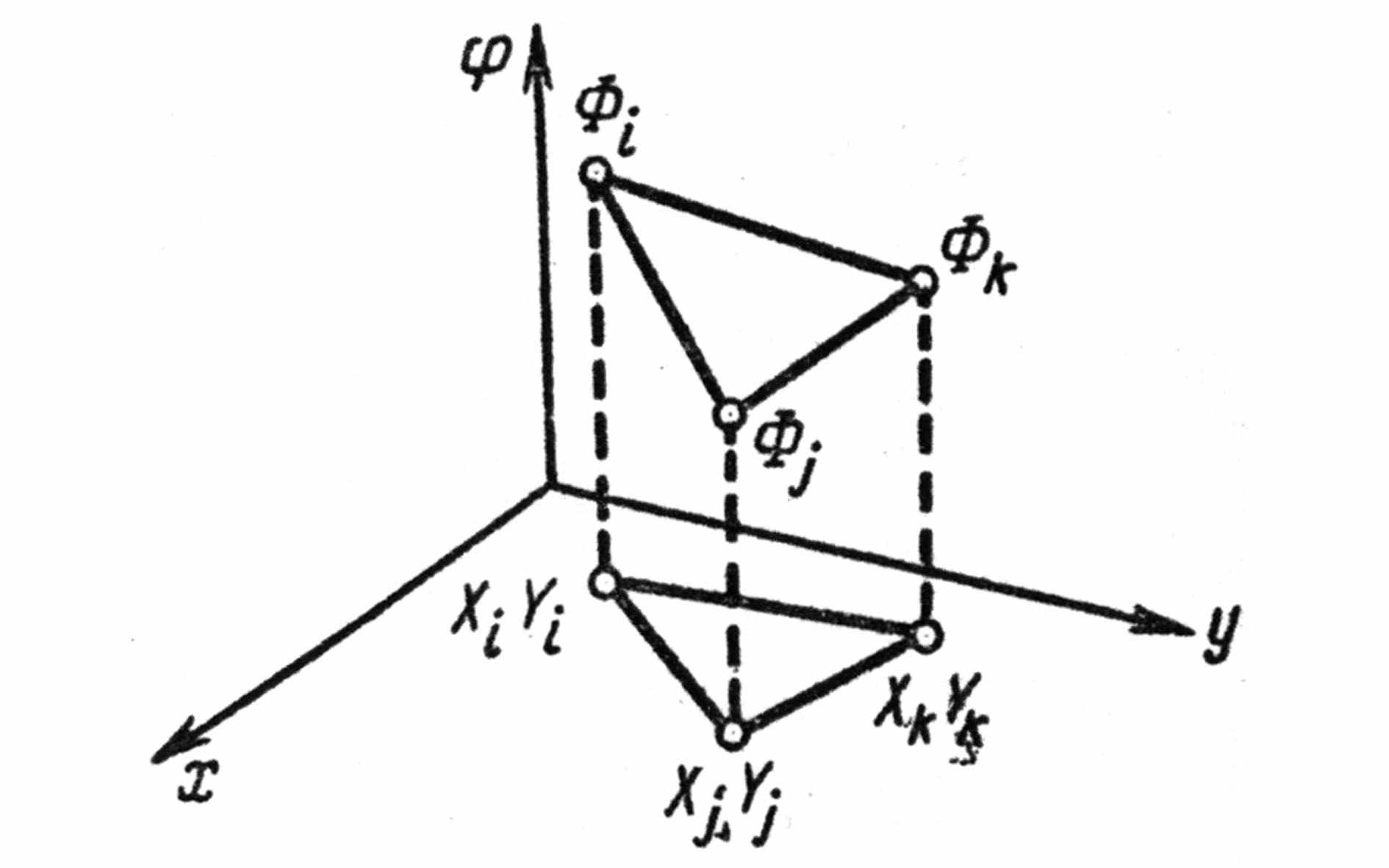Рис. 4.5 Разбиение двумерной области

на линейные треугольные элементы

Рис. 4.6 К получению полинома

для треугольного элемента

Затем аппроксимируется искомая функция  внутри треугольного элемента (имеющего три узла) полиномом с тремя коэффициентами:

(4.1)

Выражения для коэффициентов α записываются с использованием неизвестных значений Φ функции  в узлах:

 = Φ _i при x = X _i, y = Y _i;

 = Φ _j при x = X _j, y = Y _j;

 = Φ _k при x = X _k, y = Y _k.

(4.2)

При подстановке (4.2) в уравнение (4.1) получается система уравнений

Φ _i = α ₁ + α ₂ X _i + α ₃ Y _i ;

Φ _j = α ₁ + α ₂ X _j + α ₃ Y _j ;

Φ _k = α ₁ + α ₂ X _k + α ₃ Y _k .

Её решение даёт коэффициенты α₁, α₂,α₃ , подставляемые в полином (4.1):

 = N _i Φ _i + N _j Φ _j + N _k Φ _k,

где N _i, N _j, N _k – интерполяционные функции или функции формы, зависящие от координат X _i, Y _i и т. д.

Затем записывается система уравнений в матричной форме для некоторого элемента n :

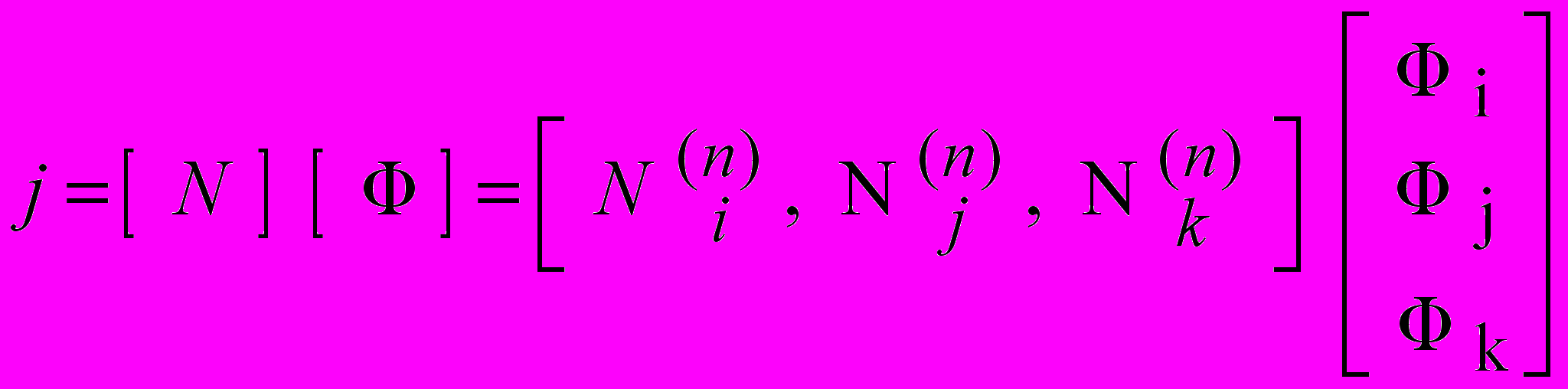3) Формирование уравнений для всей области. Аппроксимирующие полиномы каждого элемента и узловые значения выражаются в общей для всей области системе координат (при общей нумерации узлов и элементов). Сквозная нумерация узлов и элементов проводится в одном направлении: против или по часовой стрелке. На рис. 4.5 нумерация узлов против часовой стрелки. Произвольно выбирается и отмечается точкой первый узел каждого элемента. Номера узлов каждого элемента i , j , k заменяются номерами, полученные при общей нумерации всех элементов и обходе каждого элемента против часовой стрелки, начиная с первого узла (табл. 4.1).

Новые значения индексов подставляются в интерполяционные уравнения каждого элемента. Тогда

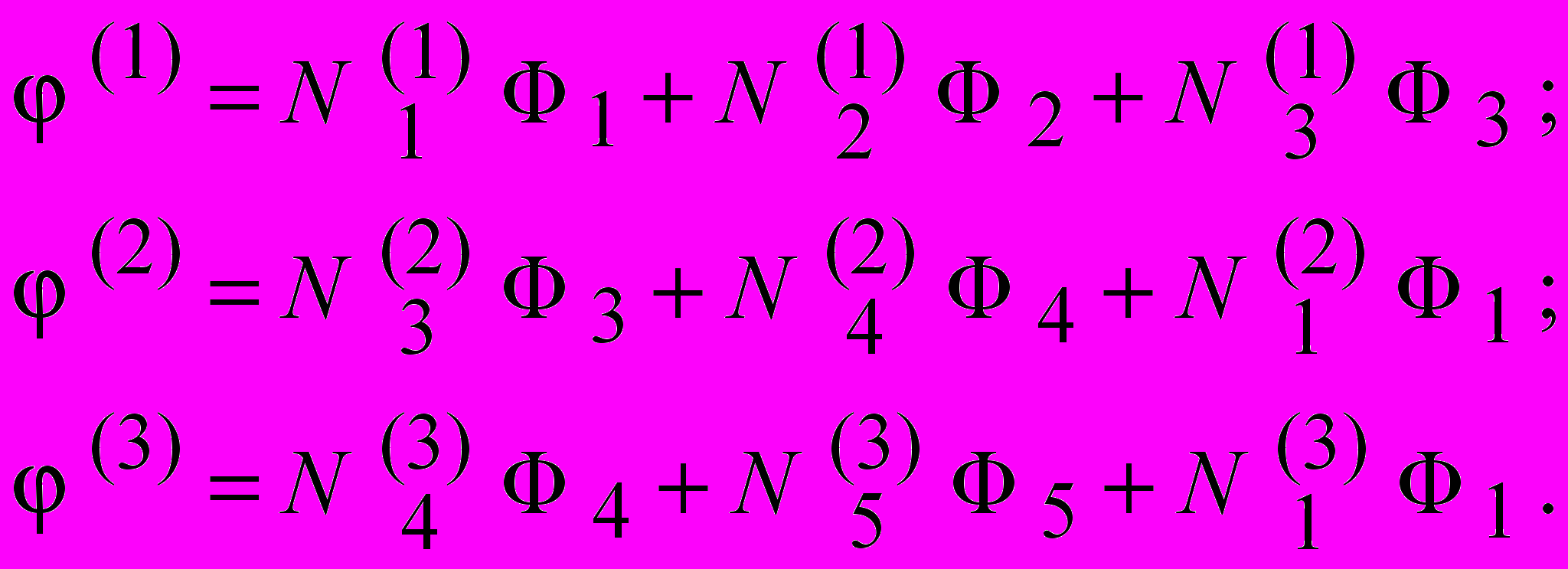Интерполяционные функции N изменят свои значения, поскольку в интерполяционные уравнения вместо i , j и k подставляются соответствующие числовые значения, полученные при общей нумерации.

Т а б л и ц а 4.1

Замена номеров узлов каждого элемента i, j, k

Номер элемента	i	j	k
1	1	2	3
2	3	4	1
3	4	5	1

4) Решение интерполяционных уравнений. Уравнения  = [ N ] [ Ф ] решаются относительно узловых значений искомой функции. Наиболее эффективным методом решения является метод Галеркина, с помощью которого получается приближённое решение исходного дифференциального уравнения. При этом должно выполняться условие ортогональности разности между приблизительным и точным решениями функций, используемых при аппроксимации. Применение метода Галеркина в сочетании с методом конечных элементов позволяет получить уравнение для одного l элемента:

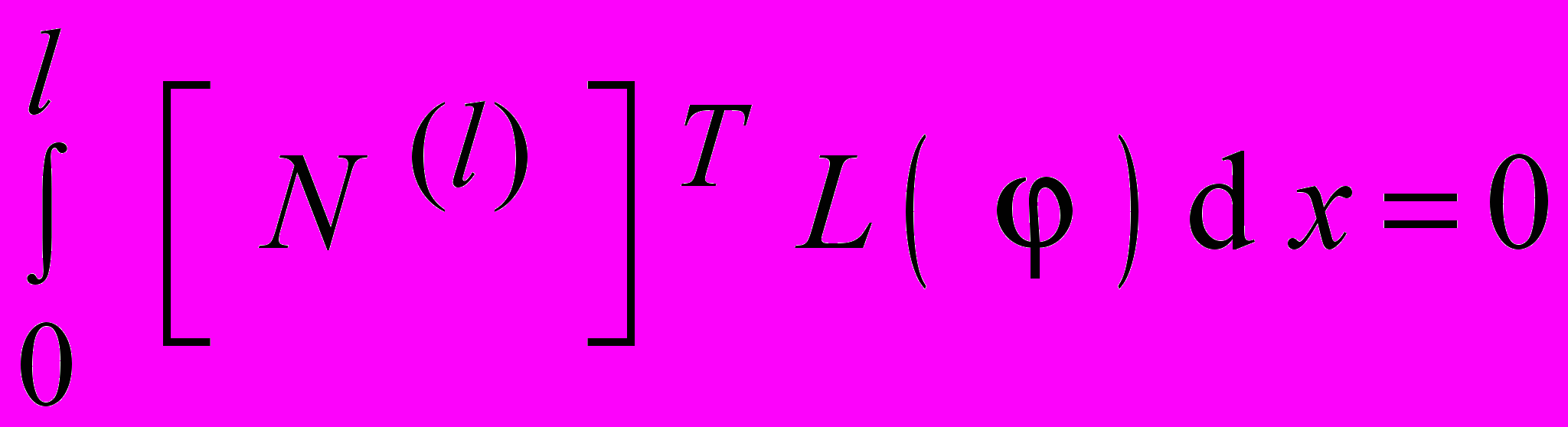где [ N ⁽^l⁾ ] ^T– транспонированная матрица;  – искомая величина, аппроксимируемая соотношением  = [ N _i, N _j, N _k, . . . ] [ Ф ]; L (  ) – дифференциальное уравнение, определяющее  ; l – длина одномерной области, в которой ищется решение. Для нескольких конечных элементов, на которые разбита область поля, имеет место соотношение

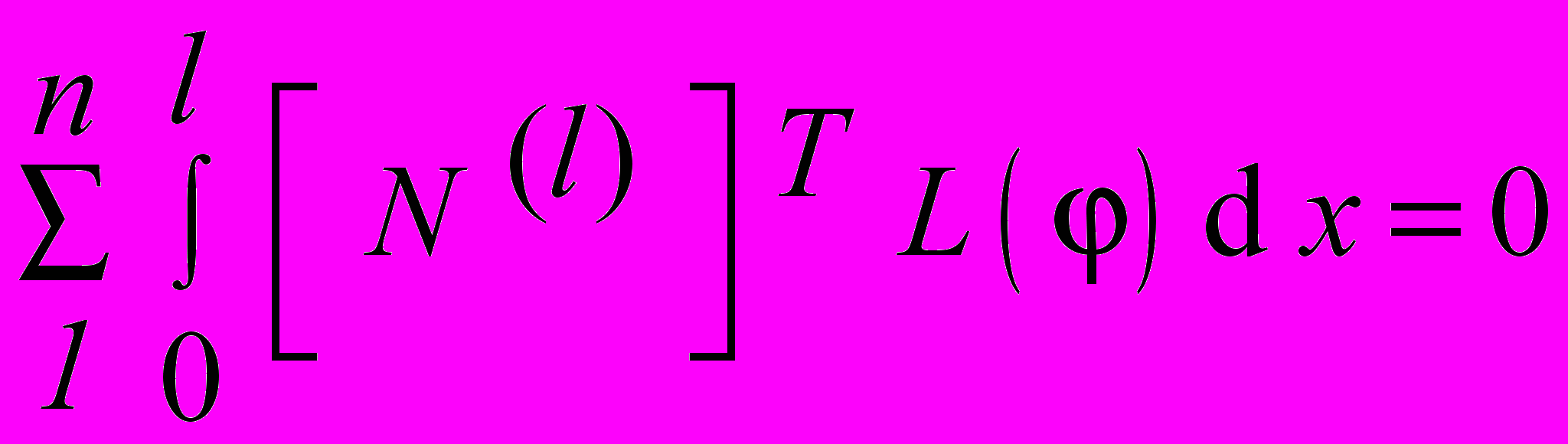3.10 Местная (симплексная) система координат

Местная (симплексная) система координат. Введение этой системы для каждого элемента упрощает вычисление интеграла, в частности методом конечных элементов. Конечный элемент при этом задаётся как симплекс – наиболее простая геометрическая фигура с n + 1 вершинами. Знание координат вершин этой фигуры достаточно для однозначного определения симплекса. В табл. 4.2 даны варианты симплексов в n-мерном пространстве.

Т а б л и ц а 4.2

Варианты симплексов в n-мерном пространстве

Симплекс в n-мерном пространстве	Наиболее простая геометрическая фигура с n+1 вершинами. Знание координат её вершин достаточно для однозначного определения симплекса.
Одномерный симплекс	В одномерном пространстве отрезок прямой линии заданной длины, размером которого является его длина.
Двумерный симплекс	В двумерном пространстве треугольник, размером которого считают его площадь.
Трёхмерный симплекс	В трёхмерном пространстве – тетраэдр, размером которого считают его объём.

Blog

3. 1 Электромагнитные поля в эмус и их основные уравнения

Содержание

Рис. 4.6 К получению полинома

для треугольного элемента