3. 1 Электромагнитные поля в эмус и их основные уравнения

Вид материала

Документы

Содержание Рис. 3.11 Графическое пояснение для случая полярной сетки Метод конечных разностей 3.7 Метод конечных элементов. Неавтоматизированная Рис. 4.1 Некоторые типы конечных элементов Дискретизация методом конечных элементов вручную Дискретизация методом конечных элементов с помощью ЭВМ 3.8 Автоматическая и адаптивная дискретизация Фронтальное распространение сети Глобальное распространение сети Адаптивная дискретизация методом конечных элементов. Рис. 4.4 Разбиение магнитной системы электродвигателя на конечные элементы

Подобный материал:

• Программа вступительных экзаменов в магистратуру 210300 "Радиотехника" Профилирующая, 50.13kb.
• Электромагнитные поля и волны, 43.24kb.
• Электромагнитные волны. Радиосвязь, 88.78kb.
• Название дисциплины, 7.63kb.
• Дифференциальные уравнения (вопросы к экзамену), 26.43kb.
• Название дисциплины, 13.7kb.
• Профессор Борис Александрович Луговцов программа курса, 97.88kb.
• 1. Основные понятия и законы электромагнитного поля и теории электрических и магнитных, 87.26kb.
• Электромагнитные волны, 61.37kb.
• Электромагнитные волны, электромагнитные колебания, распространяющиеся в пространстве, 134.85kb.

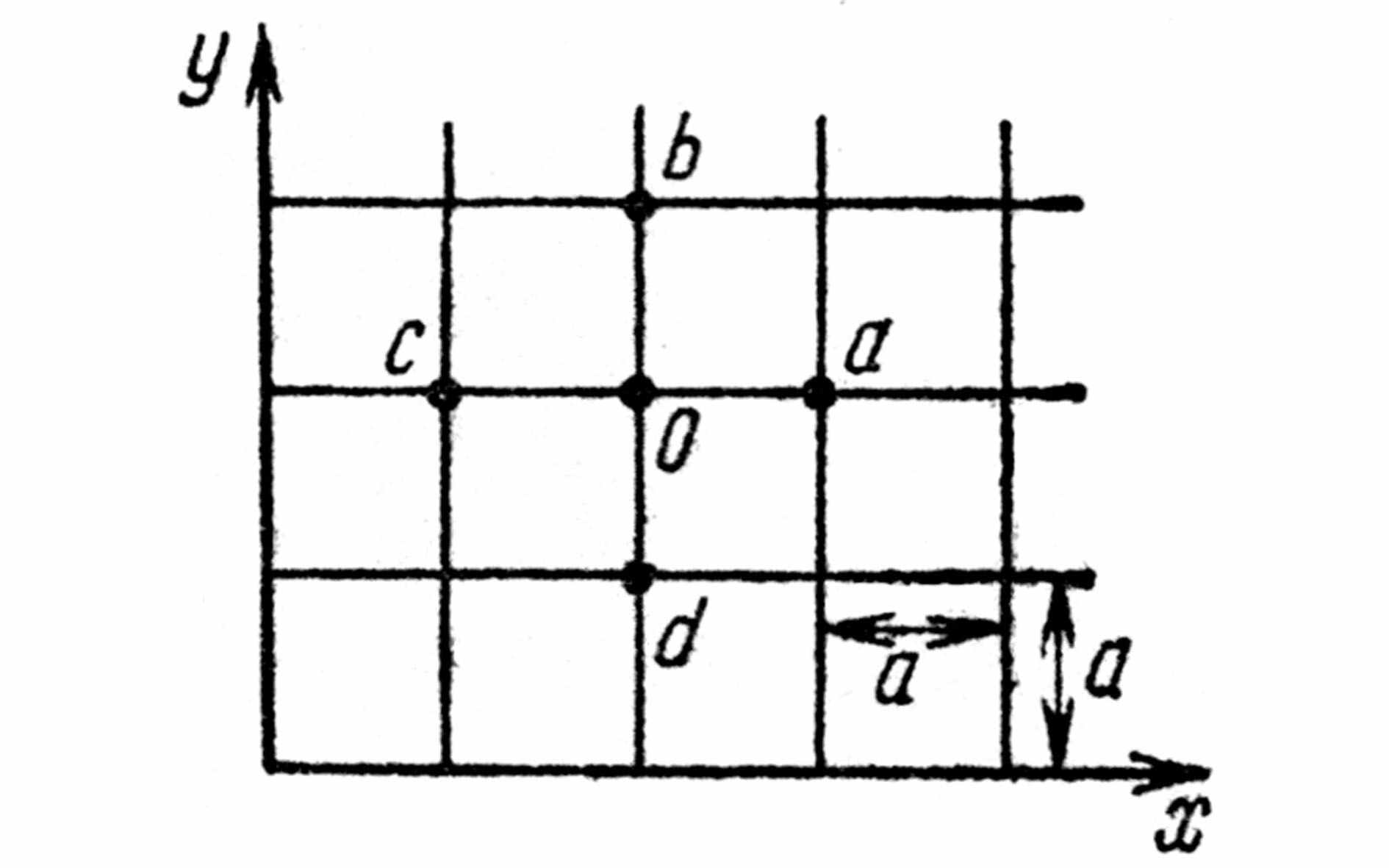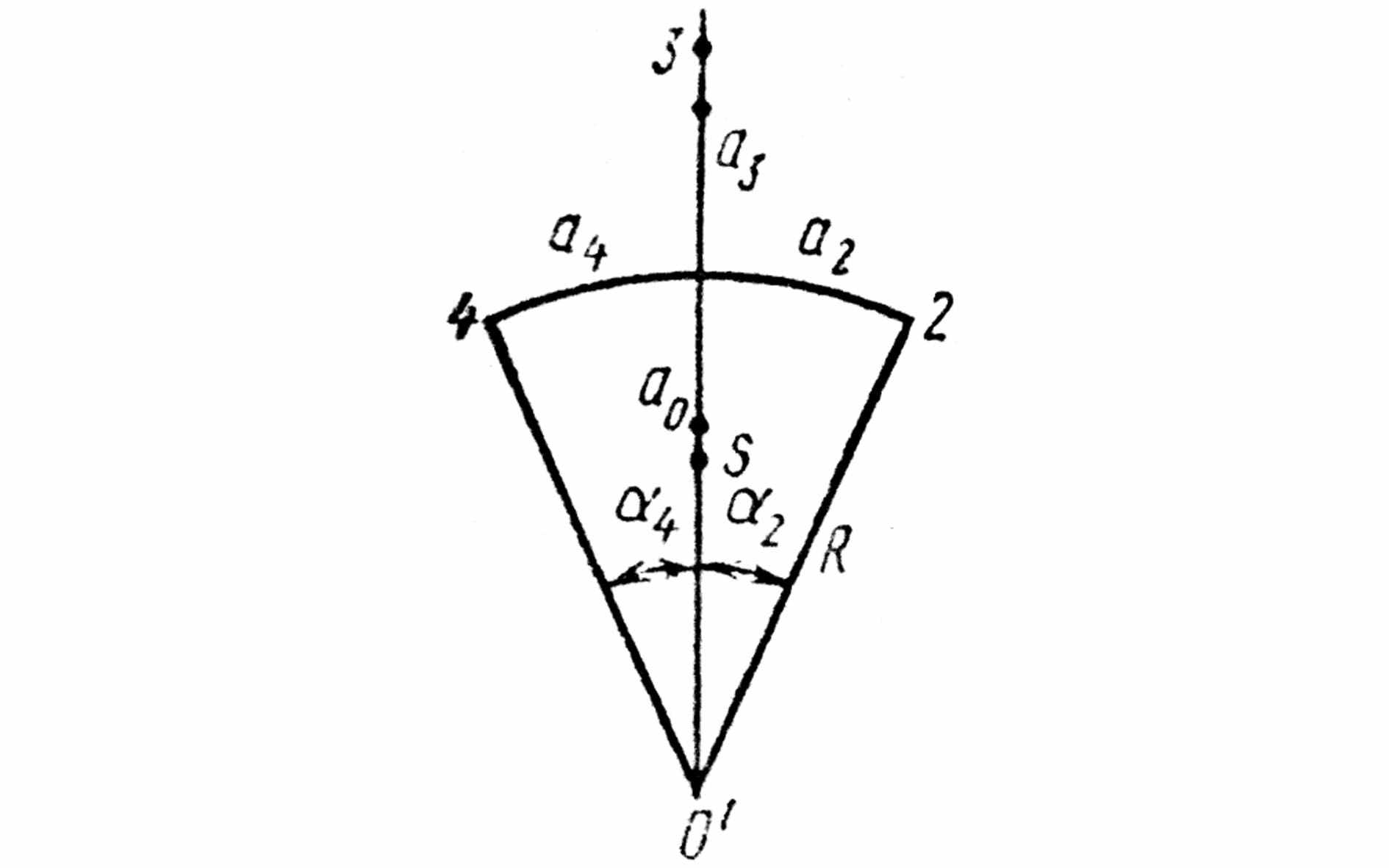Рис. 3.10 Графическое пояснение связи потенциалов рас­сматриваемой точки и соседних точек	Рис. 3.11 Графическое пояснение для случая полярной сетки

Уравнения связи решаются численным подбором (см. § 9.1 [2]). Для этого на область исследуемого поля между граничными поверхностями наносится квадратная или полярная координатная сетка, для узлов которой рассчитываются значения потенциалов с подстановкой для каждого узла  _k значений потен­циалов соседних узлов  _a ,  _b ,  _c и  _d . Уравнения (3.23), (3.24) справедливы и для прямоугольной сетки с квадратичными ячейками равного размера и для полярной сетки (рис. 3.11), если радиусы узлов ячеек выбраны в геометрической прогрессии со знаменателем β = 1 + + α ( 1 + α / 2 ). Погрешность при за­мене уравнений Пуассона и Лапласа уравнениями (3.23), (3.24) уменьшается с уменьшением шага сетки.

Для расчёта значений потенциалов для узлов сетки на сетку наносится предполагаемая картина поля с заданием значений потенциалов в узлах и по уравнению связи, полученному из уравнения Лапласа, находятся потенциалы узлов сетки. При первом подсчёте предполагаемые и рассчитанные значения потенциалов могут не совпадать, образуя остаток. Поэтому снова задаются потенциалы в узлах и опять вычисляются их значения. Расчёты проводятся до тех пор, пока значения потенциалов не совпадут или остаток во всех узлах не будет превышать некоторого, заранее за­данного значения, например .

Метод предполагает использова­ние ЭВМ. Он применим в случае граничных поверхностей произвольной формы для дву­мерных, трёхмерных с осевой симметрией и других, более сложных, полей. Метод позволяет найти распределение скалярного потенциала электрических и магнитных полей, а также распределение векторного потенциала магнитного поля. Распределение потенциала методом сеток находится следующим образом.

1) В области поля между граничными поверхностями наносится сетка в соответствующей системе координат и буквами обозначаются её узлы.

2) На сетке приближённо проводятся эквипотенциальные и силовые линии (см. § 13.1 [2]), а затем, с ориентацией на картину поля, задаются значения потенциалов каждого узла сетки.

3) При последовательном задании зна­чений потенциалов для каждого узла составляются уравнения связи (3.23) или, если ρ = 0, уравнения (3.24). При первоначально принятых значениях потенциалов узлов уравнение связи не равно нулю, а равно некоторому числу – остатку, который фиксируется, например, записывается около соответствующего узла.

4) Изменяются потенциалы узлов так, чтобы остаток в уравнениях связи для всех узлов не превышал некоторого, заранее за­данного значения . Для этого самый большой остаток можно уменьшить, например, на 1/4 и, снова задаваясь значениями по­тенциалов узлов, вычислить все остатки. Расчёт повторяется до тех пор, пока остатки не станут равными или меньшими .

Поскольку для расчётов применяется ЭВМ, то система уравнений для узлов записывается в матричной форме.

Метод конечных разностей позволяет получать удовлетворительные решения для многочисленных задач, в частности широко используется при рассмотрении тепловых явлений, но при его применении важное место отводится составлению алгоритма и проведению пробного эксперимента. Интегральные методы недостаточно освоены для задач электротехники, их практическое применение всегда очень сложное и относится к прерогативе специалистов по прикладной и вычислительной математике.

Поэтому для решения большинства задач в электротехнике, а также теплотехнике, механике деформируемого тела и других областях науки и техники, требующих решения задач в частных производных, используется метод конечных элементов. Это обусловлено тем, что, кроме того, что он исходит из соответствующей физической задачи, этот метод обладает большой гибкостью и подходит для описания устройств со сложной геометрией. В связи с этим, а также с ограниченностью объёма курса, в курсе детально рассматривается только метод конечных элементов.


3.7 Метод конечных элементов. Неавтоматизированная

и автоматизированная дискретизация магнитной системы


Метод конечных элементов основывается на исследовании глобальной функции, представляющей рассматриваемое явление, например, электромагнитное поле, тепловое поле, деформацию тела, во всех точках анализируемой области. Эта область должна быть предварительно разбита на конечное число смежных подобластей, называемых конечными элементами. Совокупность элементов, которые воспроизводят область, называется ансамблем или геометрической дискретизацией, или просто дискретизацией. Элементы имеют общие узловые точки, в совокупности они опи­сывают форму области. Внутри каждого элемента иско­мая функция аппроксимируется, чаще всего полиномом. Число коэффициентов аппроксимирующего полинома соответствует числу узлов рассматриваемого элемента. Полиномы должны быть такими, чтобы сохранилась непрерывность искомой величины вдоль границ элемента. Коэффициенты полинома выражаются через неиз­вестные значения искомой функции в узлах элемента и в аппроксимирующие полиномы элемента вместо коэф­фициентов вводятся (подставляются) полученные соотношения для коэффициентов (значения искомой функции в узлах элемента) и коэффициенты формы элемента. В результате этого составляется уравне­ние искомой функции в зависимости от узловых значений функции и функции формы элемента [3].

Искомая глобальная функция строится по частям для каждого из этих элементов. Полученная функция должна полностью удовлетворять соответствующим уравнениям в частных производных, дополненным граничными условиями и свойствами непрерывности, вытекающими из анализируемого явления, причём как в отдельном элементе, так и во всей области. В соответствии с рассматриваемыми уравнениями, как правило, можно доказать, что если размеры каждого элемента стремятся к нулю (число элементов стремится к бесконечности), то уравнения в частных производных будут выполняться во всех точках области.

Конечные элементы, используемые для дискретизации рассматриваемой области, обычно группируются по топологическим семействам: сегменты, треугольники, четырёхугольники, тетраэдры, параллелепипеды, призмы и т. п. Тип конечных элементов одновременно указывает их форму, например сегмент, и тип интерполяции, например, для треугольника – три узла с линейной интерполяцией и шесть узлов с параболической интерполяцией. На рис. 4.1 показаны несколько конечных элементов (линейных, поверхностных и объёмных) с номерами их кодов и локальной нумерацией узлов.

Линии	11				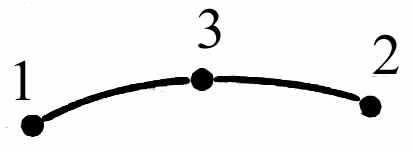сегмент
Поверхности	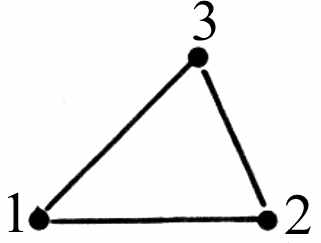12		32		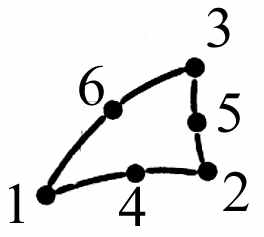треугольник
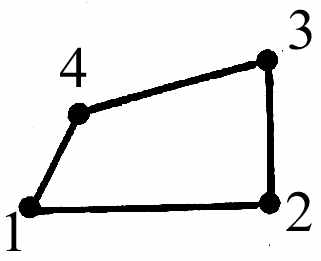22		42		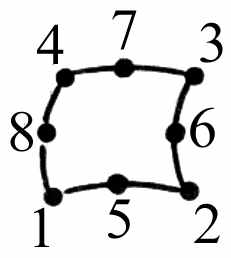четырёх-угольник
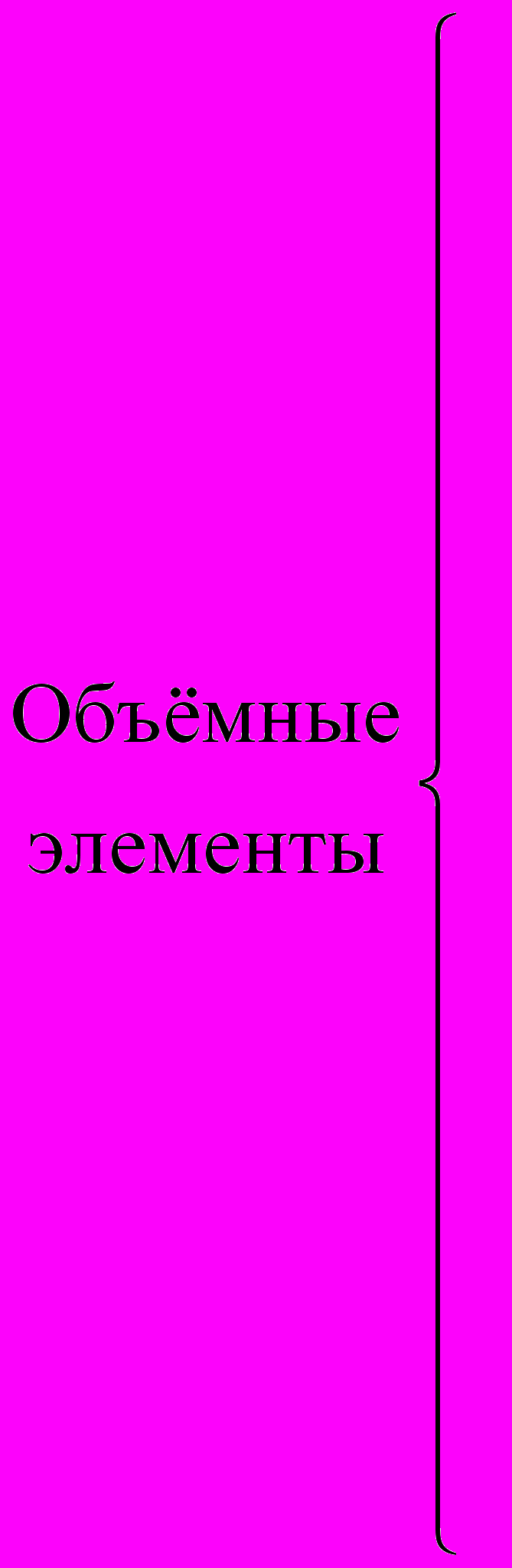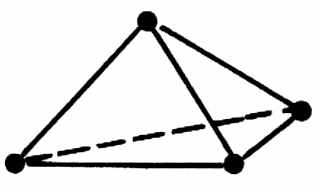	13		43		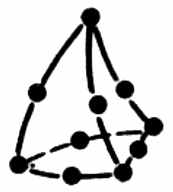Тетраэдр
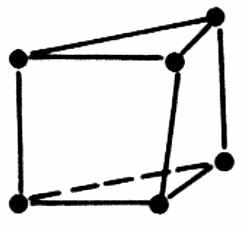23		53		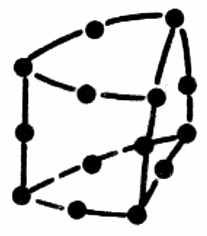Призма
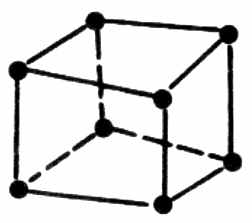33		63		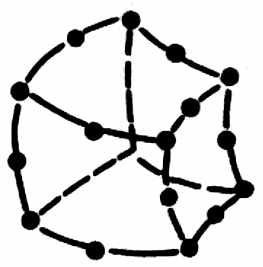Гексаэдр
Рис. 4.1 Некоторые типы конечных элементов

Коды и нумерация узлов появляются при разбиении на конечные элементы. Перечень узлов содержит метрическую информацию в одной из систем координат: плоскостных или пространственных прямоугольных, полярных, сферических и др. Перечень конечных элементов с использованием кодов содержит в себе топологическую информацию: о разбиении области конечными плоскостными или объёмными элементами и о разбиении границ конечными граничными элементами. Сведения об областях и границах служат для присвоения подобластям физических характеристик, относящихся к участкам и границам. Расположение узлов даёт картину, подобную случаю периодических граничных условий.

После проведения сквозной нумерации узлов и элементов и записи интерполяционного урав­нения для каждого элемента согласно сквозной нумерации всех элементов области получается си­стема уравнений для всей области. Каждое уравнение элемента содержит неизвестное значение искомой функции в узлах элемента и коэффициенты формы элемента. Затем находятся уравнения для узловых значений функции с помощью выбранного метода. Например, узловые значения функции определяются методом минимизации интегральной величины с помощью некоторого функционала методом взвешенных невя­зок, например методом Галеркина или наименьших квад­ратов и др. Функционал представляет собой определённый интеграл 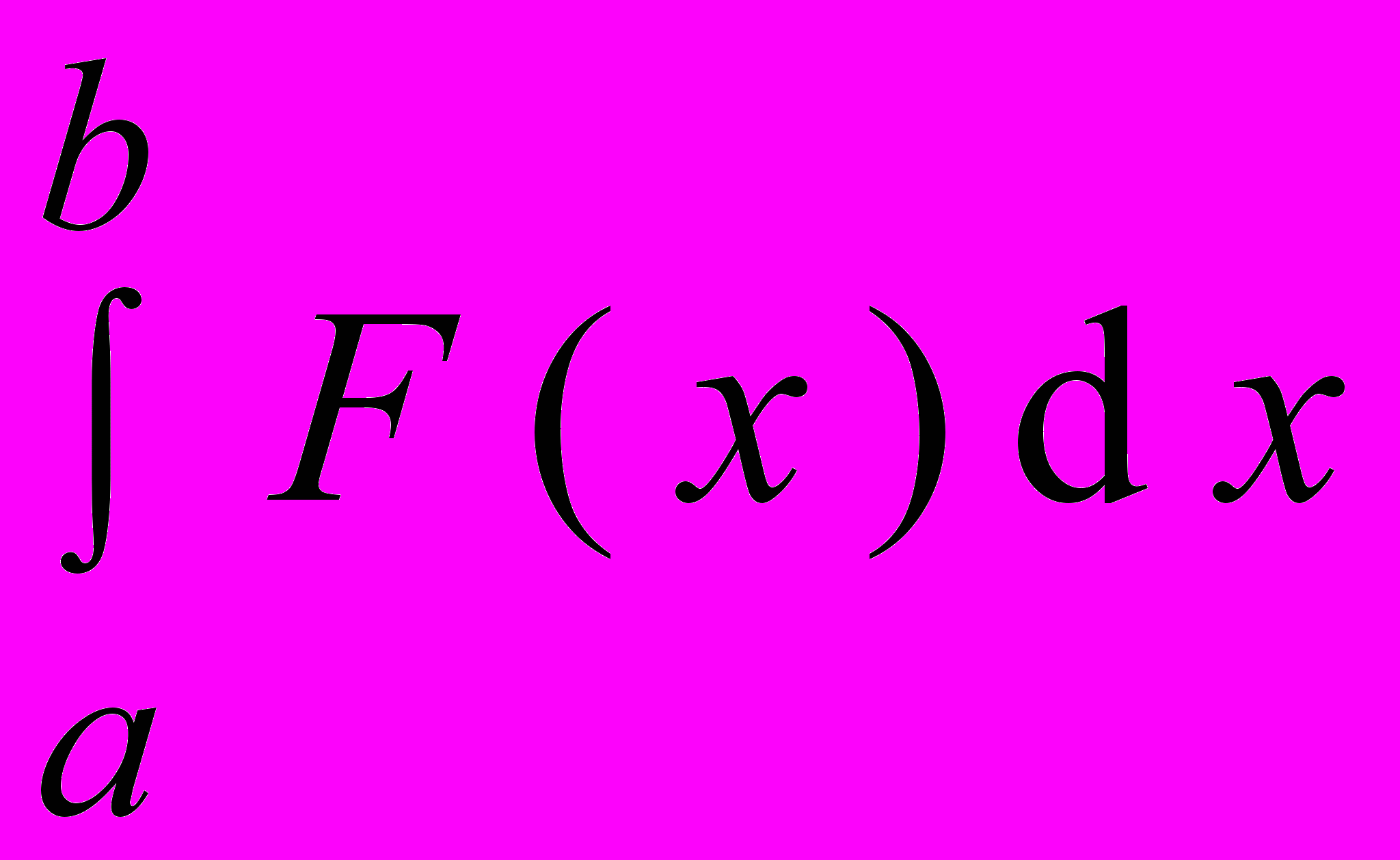, который принимает числовое значение при подстановке каждой конкретной функции F ( х ) в подынтеграль­ное выражение; при этом надо найти такую функцию F ( х ), чтобы при произвольном бесконечно малом её изменении интеграл имел постоянное значение. В методе Галеркина отправной точкой слу­жит само дифференциальное уравнение.

Внутри каждого элемента функция, моделирующая рассматриваемое явление, представляется интерполирующим полиномом, в зависимости от неизвестных физических величин в каждой вершине или узле этого элемента.

Основой метода является нахождение распределения узловых физических величин, удовлетворяющих уравнениям в частных производных для рассматриваемого явления, дополненных граничными условиями.

Некоторые применения метода конечных элементов требуют проведения расчётов методом краевых интегралов [3], зависящим от конечных элементов соседней области. Для конечного элемента границы, расположенного на перегородке, имеются два конечных элемента соседних областей: для линейного элемента в двумерной задаче – один справа, другой слева; для поверхностного элемента в трёхмерной задаче – один сверху, другой снизу. Для элемента границы, расположенного на краю области, имеется только один элемент соседней области.

Вся эта информация необходима для решения задачи методом конечных элементов и выражается в соответствующей форме при дискретизации, осуществляемой в зависимости от степени автоматизации одним из четырёх способов: вручную, с помощью ЭВМ, автоматически, адаптивно.

Дискретизация методом конечных элементов вручную непроизводительна и используется практически только при объяснении процесса дискретизации, например в учебном процессе.

Дискретизация методом конечных элементов с помощью ЭВМ благодаря возможностям ЭВМ в вычислительном, символьном, графическом и диалоговом плане существенно производительнее дискретизации вручную. Основные способы разбиения области поля с помощью ЭВМ следующие:

• непосредственное введение конечных элементов;
  
• введение блоков с их последующим автоматическим делением на конечные элементы;
  
• введение описания геометрии объекта, деление объекта на блоки с последующим автоматическим делением блоков на конечные элементы [3].
  

Непосредственное введение конечных элементов состоит в связанном введении координат всех узлов, объединение которых образует элементы, с помощью клавиатуры (точные координаты) или введении изображения (аппроксимированных координат и вершин элементов). Постоянный графический контроль процесса дискретизации позволяет избежать ошибки оператора. Этот метод очень прост в использовании и доступен при обучении. С точки зрения педагогики его важное преимущество состоит в том, что он не скрывает структуру данных конечных элементов. Его основной недостаток – необходимость манипулировать слишком большим объёмом информации, особенно в случае трёхмерного поля.

Введение данных блоками соответствует предварительному делению объекта на подобъекты, предназначенные для разбиения последних на конечные элементы. Описание геометрии этих блоков вводится посредством взаимодействия человека с ЭВМ, подобного взаимодействию при непосредственном введении конечных элементов. Однако при этом число блоков во много раз меньше числа конечных элементов, поэтому описание и введение существенно упрощаются. Как правило, эти блоки топологически очень просты, имеют такую же форму, как и конечные элементы: треугольники и четырёхугольники в двумерных задачах; тетраэдры, призмы и гексаэдры в трёхмерных, и могут быть прямолинейными или криволинейными. Необходимо также уточнить деление сторон блоков. Этой информации достаточно для проведения разбиения до конечных элементов с использованием процедуры, определённой заранее. Метод описания блоками с последующим разбиением на конечные элементы очень часто используется для двух- или трёхмерной дискретизации в соответствующих программах дискретизации. Один из часто используемых вариантов дискретизации блоками состоит в объединении фрагментов с заданными параметрами определённой сеткой и записью в памяти ЭВМ.

При дискретизации вручную и с помощью ЭВМ описание геометрии и локализация областей и границ ведётся на уровне элементов или суперэлементов. Дальнейшее развитие метода с ориентацией на более «естественное» разбиение основано на уже существующем геометрическом описании, определяющем взаимодействие суперэлементов, полученных методом разбиения блока. В этом случае метрическая и топологическая информация приводят к глобальной модели, которая сначала поблочно преобразуется в модель, а затем разбивается на элементы. Такая стратегия эффективна для реализации двух- или трёхмерной геометрической модели и составления сети методом блоков. На рис. 4.2 на примере электромагнита показана работа программы создания сетей конечных элементов для решения скалярных и векторных задач при расчёте эквипотенциальных сечений, магнитных потоков, электромагнитных сил [3].


3.8 Автоматическая и адаптивная дискретизация

при применении метода конечных элементов


Автоматическая дискретизация методом конечных элементов.

Создание сети конечных элементов достаточно трудоёмкая и однообразная задача, поэтому ведутся поиски максимальной разгрузки пользователя, в частности за счёт автоматического составления сети. Эффективная дискретизация должна удовлетворять следующим условиям:

• плотность расположения элементов должна быть больше в тех частях области, которые представляют наибольший интерес для исследования;
  
• элементы должны достаточно равномерно охватывать все направления, например, если элементы треугольной формы, то они должны быть максимально близки к равносторонним треугольникам.
  

Плотность расположения элементов определяется пользователем на основе его опыта или результатов предварительных исследований. При этом пользователь также проводит разбиение границ области: сторон двумерной области, граней – трёхмерной. Соответствующая программа автоматически генерирует сеть внутри области с соблюдением выбранной плотности.

Основными способами генерирования сети являются следующие.

Фронтальное распространение сети: начальный фронт граничной дискретизации задаётся пользователем; элементы строятся регулярно, послойно, опираясь на фронт; каждый новый слой элементов продвигает фронт внутрь области; разбиение заканчивается с исчерпанием области.

Глобальное распространение сети: с каждым начальным узлом, задаваемым пользователем, связывается заданная плотность расположения элементов с учётом требований для окрестности этого узла, например, средняя длина стороны, выходящей из узла. Таким образом, дискретизация,

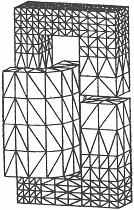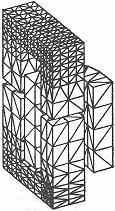Рис. 4.2 Пример разбиения электромагнита на конечные элементы

использующая простые элементы: треугольники в двумерном случае и тетраэдры в трёхмерном, опирающиеся на все начальные узлы, завершается. Эта первая дискретизация, разумеется, очень грубая, так как она не обладает внутренним узлом, и её надо уточнить последовательными итерациями таким образом, чтобы не было слишком больших элементов, то есть элементов, обладающих поверхностью в двумерном или объёмом в трёхмерном пространстве, значение которых превосходит произведение весов, приданных их вершинам. Когда такой элемент выявляется, в его центре масс создаётся новый узел с весом, равным средне весовому значению в вершинах элемента; этот узел позволяет уточнить сеть в процессе её создания.

В ходе итерационного процесса возникает проблема создания по имеющейся совокупности узлов эффективной дискретизации, опирающейся на эти узлы. Эту задачу можно решить разбиением объекта на треугольники – триангуляцией, или на тетраэдры – тетраэдризацией. При триангуляции и тетраэдризации устраняется наличие узлов треугольников или тетраэдров, находящихся внутри окружности, описанной около какого-либо другого треугольника, или внутри сферы, описанной около какого-либо другого тетраэдра. Такая дискретизация проводится методом итераций: строится первый элемент, затем проводится новая дискретизация с добавлением нового узла и т. д. Основное достоинство этого глобального приближения – оно одинаково хорошо действует и в двумерном и в трёхмерном случаях [3].

Применение этого подхода иллюстрируется рис. 4.2 (верхний рисунок), где показано разбиение на тетраэдры магнитной системы электромагнитного контактора методом глобального автоматического разбиения.


Адаптивная дискретизация методом конечных элементов.

Рассмотренные методы автоматического создания сети конечных элементов используют два вида информации: геометрическое описание области и требуемую плотность элементов.

На рис. 4.3, 4.4 показано разбиение магнитных систем электродвигателей на конечные элементы, иллюстрирующее последующее упрощение работы пользователя и определения плотности расположения элементов – автоматизацию и выполнение этих действий по программе, что связано с резким увеличением объёма работ по программному обеспечению.

Один из наиболее эффективных возможных алгоритмов следующий:

• программа, на основе исходного, грубого, расположения сети, определяет некоторое начальное решение;
  
• по полученному решению выделяются зоны, в которых ошибка, связанная с расположением сети, максимальна;
  
• в этих зонах уточняется расположение сети;
  
• находится решение, соответствующее новому расположению сети;
  
• такой итерационный процесс продолжается до тех пор, пока ошибка, связанная с расположением сети не станет приемлемой или не будет достигнуто максимальное число конечных элементов; при этом выбор сети и решение задачи тесно связаны между собой; оптимальный выбор сети зависит одновременно от геометрии объекта и физической задачи; одна и та же задача, в которой источник перемещается или изменяет своё значение, например ток в обмотке устройства, приводит к новому расположению сети.
  

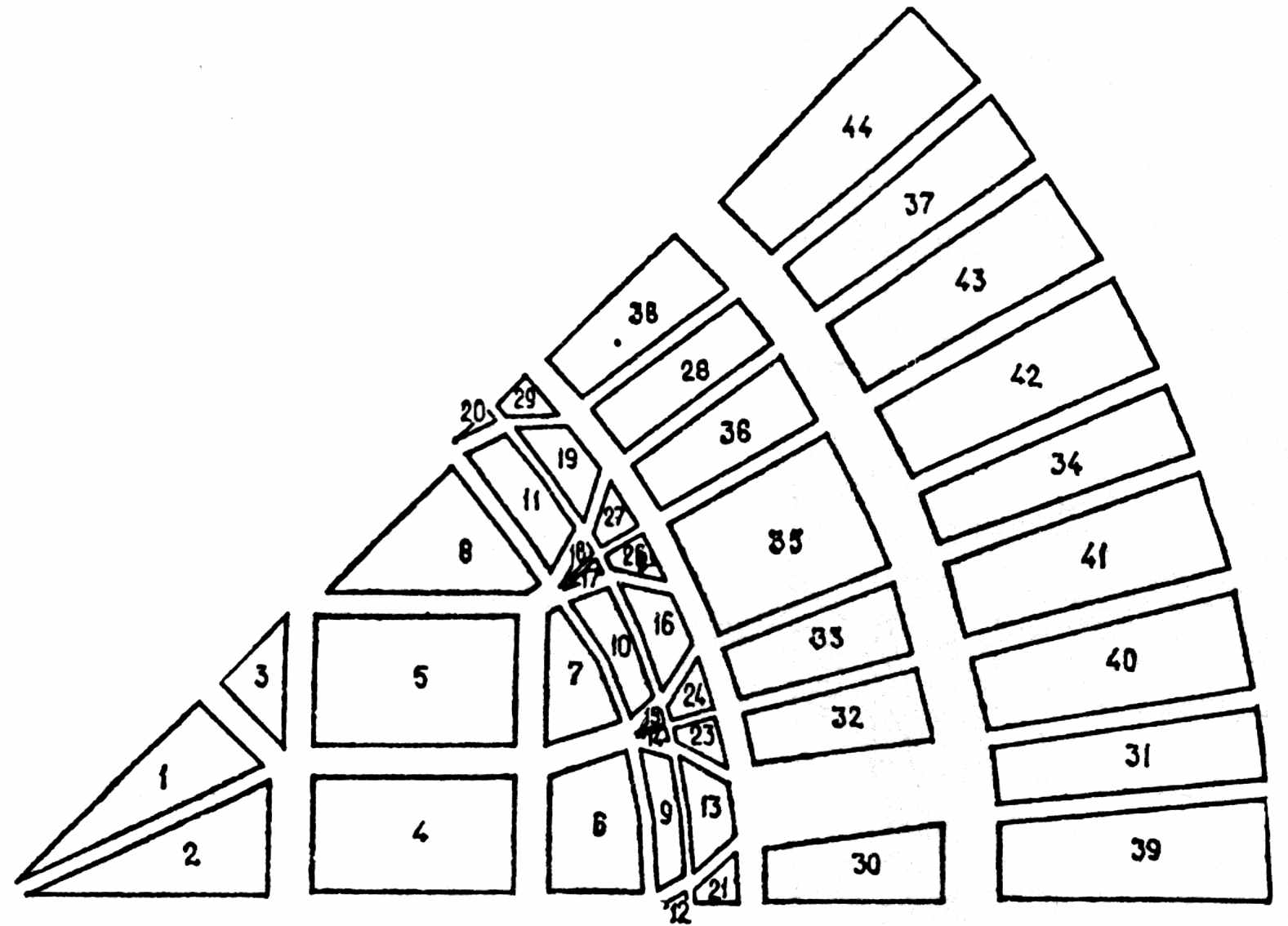Рис. 4.3 Разбиение магнитной системы электродвигателя на конечные элементы

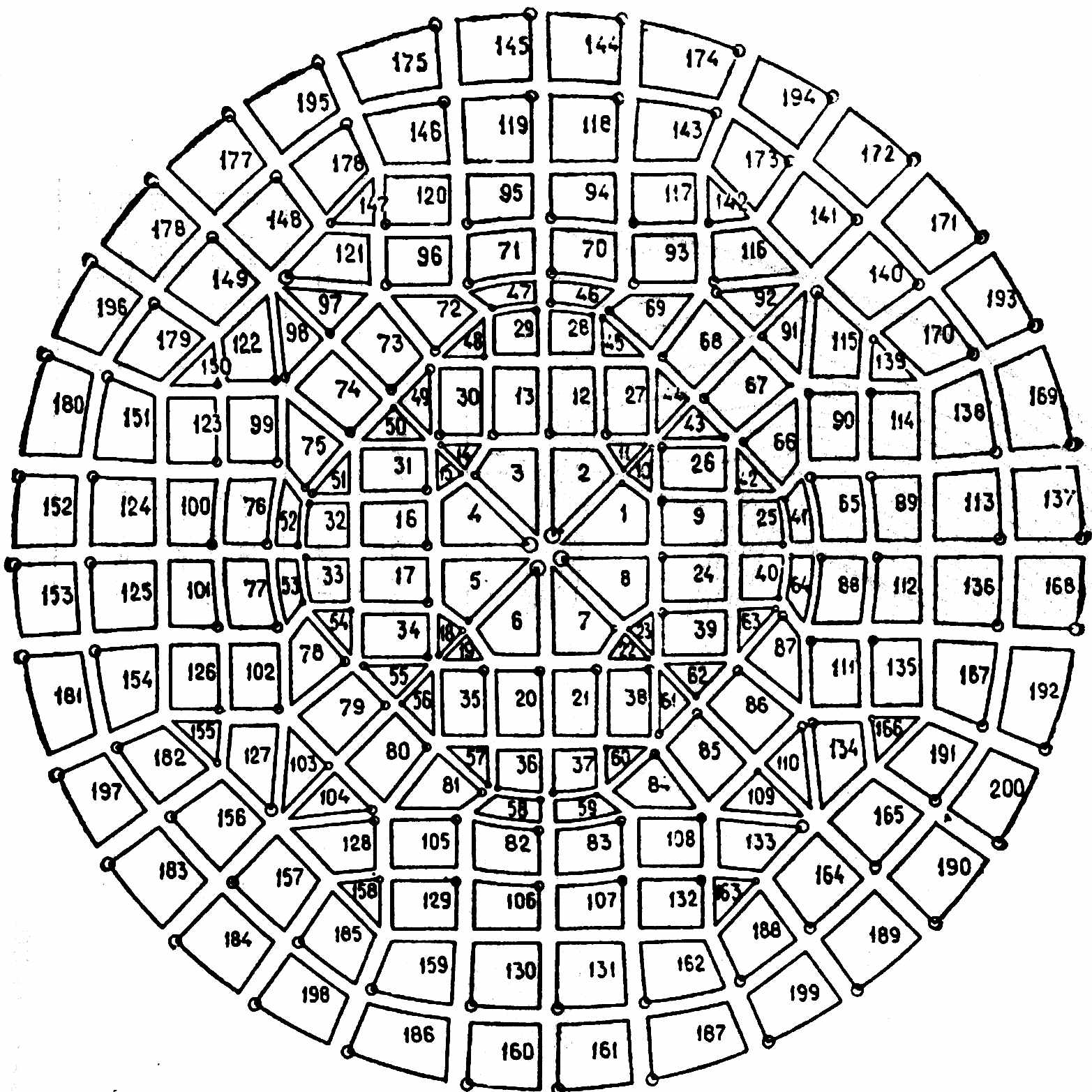Рис. 4.4 Разбиение магнитной системы электродвигателя на конечные элементы