Рабочая программа дисциплины Закреплена за кафедрой: Математического анализа
| Вид материала | Рабочая программа |
- Рабочая программа дисциплины Закреплена за кафедрой: Математического анализа, 241.07kb.
- Рабочая программа дисциплины Закреплена за кафедрой: Педагогика и методики преподавания, 435.93kb.
- Рабочая программа дисциплины Закреплена за кафедрой: Педагогики и методик преподавания, 450.57kb.
- Рабочая учебная программа дисциплины гсэ. Ф. 10 Экономика закреплена за кафедрой экономической, 144.71kb.
- Рабочая программа по дисциплине: «Моделирование случайных процессов с помощью математического, 72.45kb.
- Рабочая программа учебной дисциплины «Дискретная математика» Направление подготовки, 139.29kb.
- Рабочая программа «Практикум по алгебре» в 10 а классе, 70.39kb.
- Рабочая программа дисциплины Закреплена за кафедрой: Оборудование и технология сварочного, 637.32kb.
- Рабочая программа учебной дисциплины «Теория вероятностей и математическая статистика», 165.42kb.
- Рабочая учебная программа по дисциплине по выбору студентов «Математическое моделирование, 228.62kb.
1 2
| 4.2 Разделы дисциплины и виды занятий | ||||
| Код учебного занятия | Номер учебной недели | Вид и номер занятия (пары) | Объем в часах | Тема занятия |
| КУРС 1, 2 | ||||
| Раздел 1. Лекционные и практические занятия (36час.) | ||||
| 1.01.01.01 | 1 | Лекц. 1 | 4 | Погрешности вычислений. Определение количества верных значащих цифр. Погрешности алгебраических операций. Правила округления. |
| 1.01.01.02 | 1 | Практ. 1 | 4 | Погрешности вычислений. Определение количества верных значащих цифр. Погрешности алгебраических операций. Правила округления. |
| 1.01.01.03 | 2 | Лекц.2 | 4 | Методы решения нелинейных уравнений: графический, хорд, касательных, итераций. |
| 1.01.01.04 | 3 | Практ. .2 | 4 | Методы решения нелинейных уравнений: графический, хорд, касательных, итераций. |
| 1.01.01.05 | 3 | Лекц.3 | 4 | Оценка погрешностей. Требования к вычислительному алгоритму. Устойчивость и сложность алгоритма. |
| 1.01.01.06 | 4 | Практ. 3 | 4 | Линейная и сплайн-интерполяция. Интерполяция многочленами n-ой степени. Оценка погрешности интерполирования. |
| 1.01.01.07 | 4 | Лекц.4 | 4 | Численное интегрирование функций по формулам прямоугольников, трапеций и Симпсона. Погрешности численного интегрирования. |
| 1.01.01.08 | 5 | Практ. 4 | 4 | Численное интегрирование функций по формулам прямоугольников, трапеций и Симпсона. Погрешности численного интегрирования. |
| 1.01.01.09 | 5 | Практ. 5 | 4 | Интегрирование обыкновенных дифференциальных уравнений методами степенных рядов Эйлера, Эйлера с уравниванием и Рунге-Кутта. Оценка погрешностей. |
| 1.01.01.10 | 6 | Лекц.5 | 4 | Моделирование нормальной случайной величины. Метод наименьших квадратов. Подбор эмпирических формул. |
| 1.01.01.11 | 6 | Практ. 6 | 4 | Интегрирование обыкновенных дифференциальных уравнений методами степенных рядов Эйлера, Эйлера с уравниванием и Рунге-Кутта. Оценка погрешностей |
| 1.01.01.12 | 7 | Лекц.6 | 4 | Моделирование нормальной случайной величины. Метод наименьших квадратов. Подбор эмпирических формул. |
| 1.01.01.13 | 7 | Практ. 7 | 2 | Интегрирование обыкновенных дифференциальных уравнений методами степенных рядов Эйлера, Эйлера с уравниванием и Рунге-Кутта. Оценка погрешностей |
| Раздел 2. Темы для самостоятельного изучения (14 час.) | ||||
| 1.01.02.01 | 1 | Сам. работа | 8 | Понятие о вероятностной оценке погрешности. Комбинированный метод хорд и касательных. |
| 1.01.02.02 | 2 | Сам. работа | 10 | Методы численного решения систем линейных и нелинейных уравнений. |
| 1.01.02.03 | 3 | Сам. работа | 8 | Условия сходимости методов и оценка погрешностей. |
| 1.01.02.04 | 4 | Сам. работа | 10 | Интерполяционные формулы Лагранжа и Ньютона. Среднеквадратическое и равномерное приближение функций. |
| 1.01.02.05 | 5 | Сам. работа | 8 | Решение разностных уравнений первого и второго порядка с постоянными коэффициентами. Численное дифференцирование. Регуляризация дифференцирования. |
| 1.01.02.05 | 6 | Сам. работа | 10 | Понятие о методе Монте-Карло. Доверительный интервал. Сравнение величин. Нахождение стохастической зависимости. Преобразование Лапласа, Фурье и др. Функции математической статистики. |
| Раздел 2. Темы для выполнения лабораторных работ (14 час.) | ||||
| 1.01.03.01 | 1 | Лаб. раб 1 | | 1. Приближенные вычисления. Системы Mathcad 6.0+. Выполняется ряд примеров, иллюстрирующих работу систем Mathcad 6.0+ Затем в системе Mathcad 6.0+ решаются экономические задачи на определение абсолютной и относительной погрешностей вычислений и числа верных знаков результата. |
| 1.01.03.02 | 2 | Лаб. раб 2 | 2 | 2. Интерполирование функций. Используя корни приведенного многочлена Чебышева, строится интерполяционный многочлен пятой степени с оптимальным расположением узлов интерполяции для заданной функции 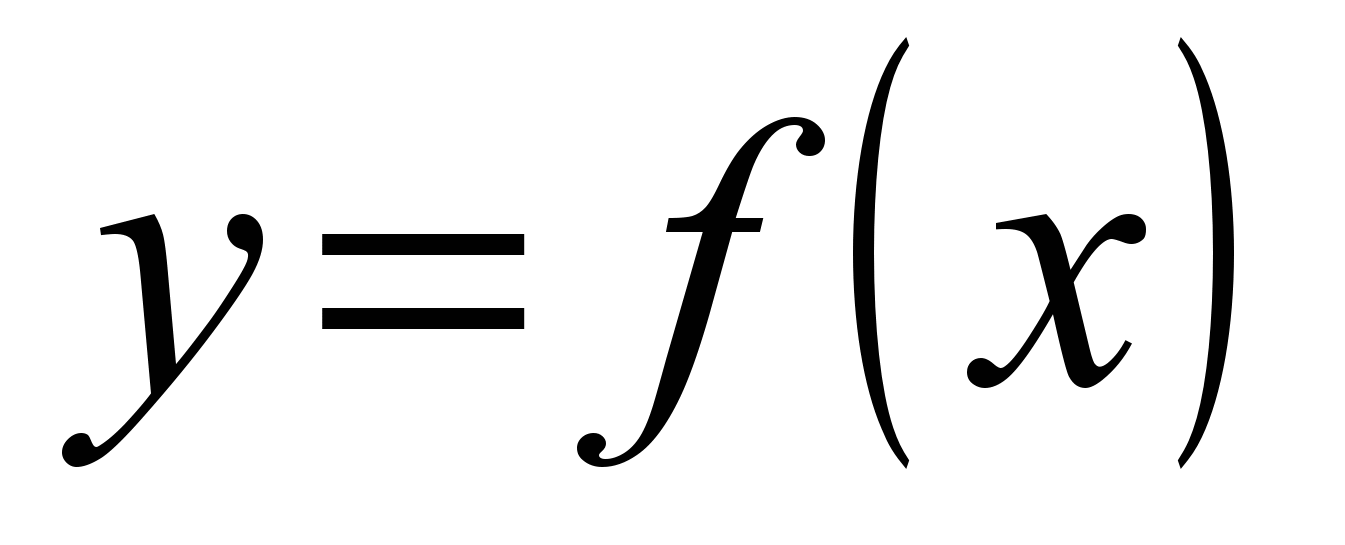 на отрезке на отрезке  . Находятся абсолютная и относительная погрешности в точках 0,4 и 1,0. Выполняется графическая иллюстрация заданной функции . Находятся абсолютная и относительная погрешности в точках 0,4 и 1,0. Выполняется графическая иллюстрация заданной функции  , полученного интерполяционного многочлена, а также соответствующей линейной и сплайн-интерполяции. , полученного интерполяционного многочлена, а также соответствующей линейной и сплайн-интерполяции. |
| 1.01.03.03 | 2 | Лаб. раб 3 | 2 | 3. Решение задач Коши для обыкновенных дифференциальных уравнений и систем методом Рунге-Кутта. Методом Рунге-Кутта четвертого порядка точность находятся в пяти точках отрезка 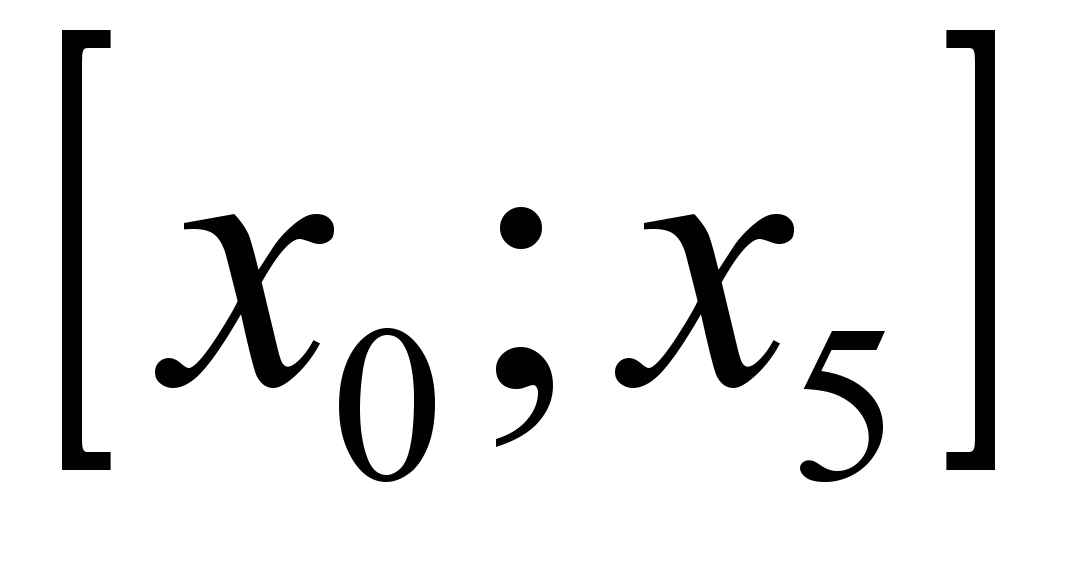 приближенное решение: а) дифференциального уравнения первого порядка приближенное решение: а) дифференциального уравнения первого порядка  с начальным условием с начальным условием 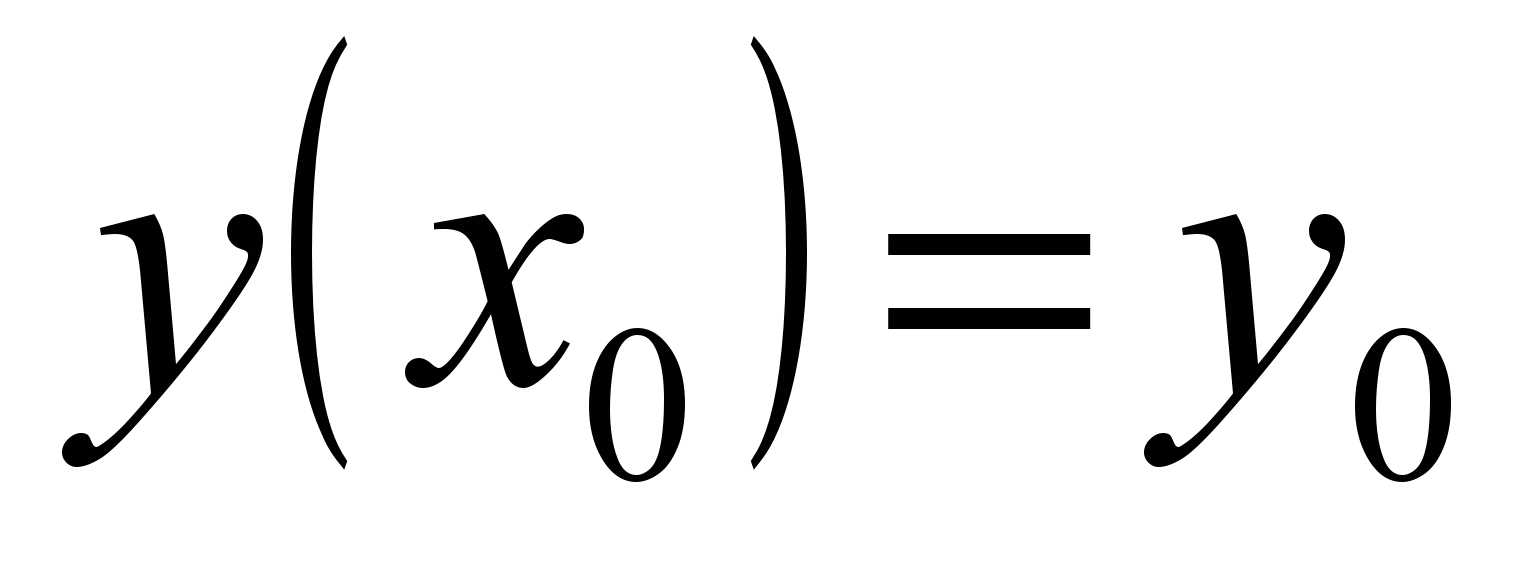 ; б) системы дифференциальных уравнений первого порядка ; б) системы дифференциальных уравнений первого порядка 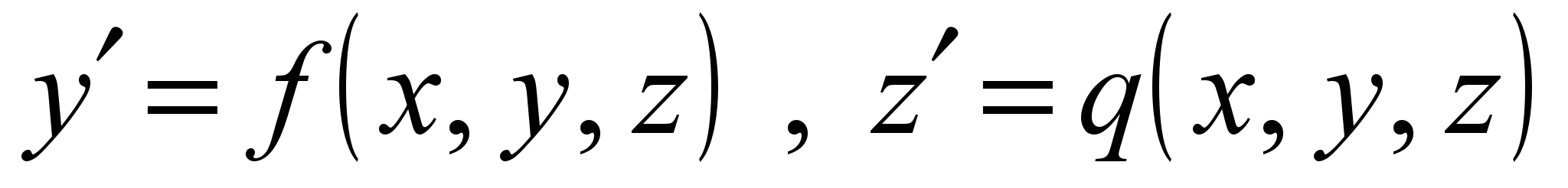 с начальными условиями с начальными условиями 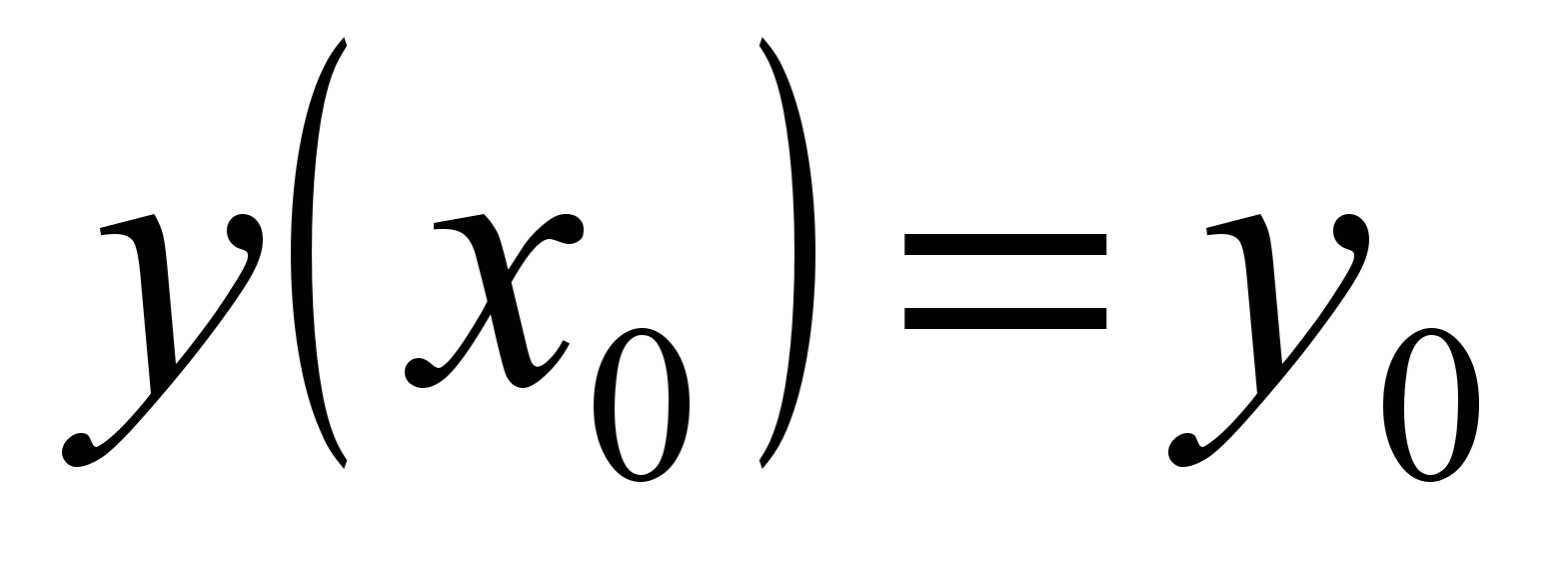 , ,  . Производится оценка погрешности полученных решений. . Производится оценка погрешности полученных решений. |
| 1.01.03.04 | 3 | Лаб. раб 4 | 5 | 4. Моделирование нормальной случайной величины. Подбор эмпирических формул. С помощью генератора случайных чисел создается массив из двенадцати реализаций равномерно распределенной на интервале 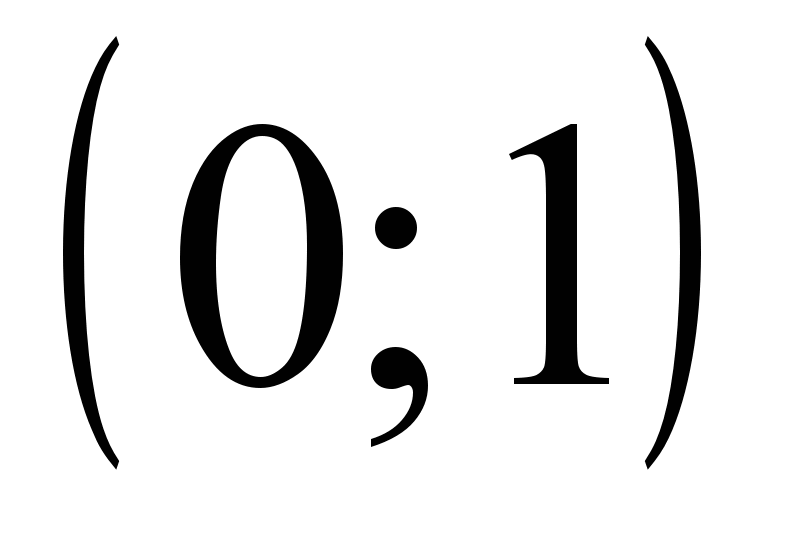 случайной величины и затем строится статистическая модель нормальной случайной величины, являющейся иллюстрацией предельной теоремы А.М. Ляпунова. случайной величины и затем строится статистическая модель нормальной случайной величины, являющейся иллюстрацией предельной теоремы А.М. Ляпунова. |
| 1.01.03.05 | 4 | Лаб. раб 5 | | 5. Решение системы обыкновенных дифференциальных уравнений операционным методом. Система дифференциальных уравнений первого порядка 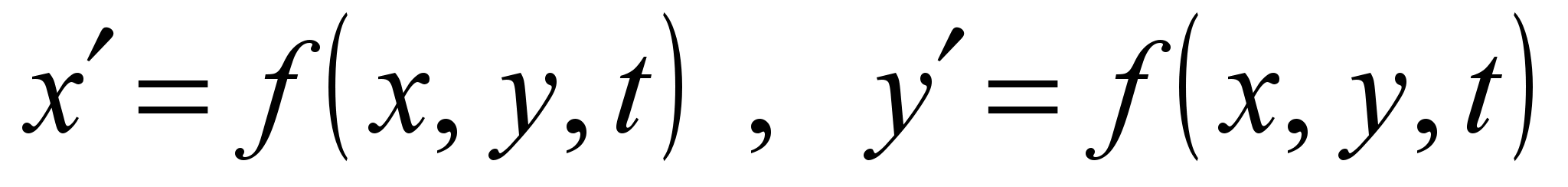 с начальными условиями с начальными условиями  решается определенным методом. Выполняется проверка найденного решения. решается определенным методом. Выполняется проверка найденного решения. |
| 1.01.03.06 | 5 | Лаб. раб 6 | | 6. Решение системы обыкновенных дифференциальных уравнений операционным методом. Система дифференциальных уравнений первого порядка 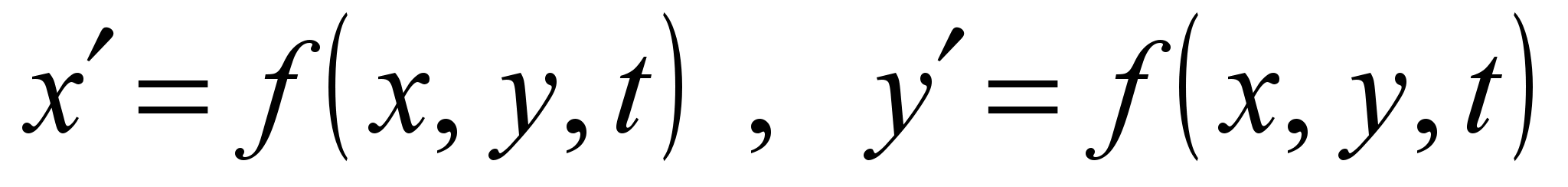 с начальными условиями с начальными условиями  решается каким-нибудь другим методом, чем в пред. лаб. методом. Выполняется проверка найденного решения решается каким-нибудь другим методом, чем в пред. лаб. методом. Выполняется проверка найденного решения |
| 5 Тематика лабораторных и письменных работ | |
| 5.1 | Лабораторные работы |
| № | |
| 5.2.1 | Приближенные вычисления. Системы Mathcad 6.0+. |
| 5.2.2 | Интерполирование функций. |
| 5.2.3 | Решение задач Коши для обыкновенных дифференциальных уравнений и систем методом Рунге-Кутта. |
| 5.2.4 | Моделирование нормальной случайной величины. Подбор эмпирических формул. |
| 5.2.5 | Решение системы обыкновенных дифференциальных уравнений операционным методом |
| 5.2.6 | Ре Решение системы обыкновенных дифференциальных уравнений операционным методом |
| 5.2 | Письменные работы |
| | Не не предусмотрены |
| | |
| | |
| 6 Учебно-методическое обеспечение дисциплины | |||||
| 6.1 Рекомендуемая литература | |||||
| Численные методы | |||||
| 6.1.1 Основная литература | |||||
| № | Автор(ы) | Наименование | Издательство, год издания | Назначение [учебник, учебное пособие, справочник и т.д.] | Количество в библиотеке |
| 1.001 | Волков Е.А. | Численные методы | М.: Наука, 1982. | Учебник | 12 |
| 1.002 | Самарский А.А., Гулин А.В. | Численные методы. | М.: Наука, 1989. | Учебник | 12 |
| 1.003 | Тихонов А.Н., Костомаров Д.П | Вводные лекции по прикладной математике. | М.: Наука, 1984. | Учебное пособие | 20 |
| 1.004 | Турчак Л.И. | Основы численных методов | М.: Наука, 1987. | Учебник | 12 |
| 1.005 | Н.С. Бахвалов, Н.П.Жидков, Г.М. Кобельков | Численные методы | Москва - Санкт-Петербург, | Учебное пособие | 25 |
| 1.006 | Выгодский М.Я. | Справочник по высшей математике | М.: Наука, 1973. | Справочник | 10 |
| 1.006 | MathCAD 6.0 PLUS. | Финансовые, инженерные и научные расчеты в среде WINDOWS 95 / Пер. с англ. | М.: Инф. - изд. Дом «Филинъ», 1996 | Учебное пособие | 10 |
| 6.1 Рекомендуемая литература | |||||
| Численные методы | |||||
| 6.1.2 Дополнительная литература | |||||
| № | Автор(ы) | Наименование | Издательство, год издания | Назначение [учебник, учебное пособие, справочник и т.д.] | Количество в библиотеке |
| 2.001 | Д.Кахамер, К.Моулер, С.Неш | Численные методы и программное обеспечение | Москва, Мир, 1998. | Учебное пособие | 10 |
| 2.002 | Дж. Бейкер, П.Грейвз-Моррис | Аппроксимации Паде | Москва, Мир, 1986 | Учебное пособие | 24 |
| 2.003 | . Г. Корн, Т. Корн | Справочник по математике | М., Наука, 1984 | Учебное пособие | 36 |
| 6.2 Средства обеспечения освоения дисциплины | ||||
| 6.2.1 Компьютерные программы. Инновационные методы (методы проблемного и проективного обучения, исследовательские методы, тренинговые формы и т.д.) | ||||
| № п/п | Код учебного занятия | Наименование программного продукта | Рег. № в ИТЦ | Назначение |
| КПр.001 | - | АСТ-тесты | - | Контроль знаний студентов |
| КПр.002 | - | MS Office, XP | - | Сервисная программа |
| 7 Материально-техническое обеспечение дисциплины | |||
| 7.1 Специализированные лаборатории и классы | |||
| № п/п | Номер, наименование, принадлежность помещения (аудитории, лаборатории, класса, мастерской) | Площадь, м2 | Количество посадочных мест |
| СпЛ.001 | Аудитория №13, | 50 | 50 |
| СпЛ.002 | Аудитория №8, | 25 | 20 |
| СпЛ.003 | Аудитория №2, | 25 | 25 |
| СпЛ.004 | Аудитория №20, компьютерный класс | 30 | 20 |
| СпЛ.005 | Аудитория №103, компьютерный класс | 50 | 20 |
| Обор.001 | Нет | | |
