Основы теории статистических решений

Вид материала

Лекция

Содержание В играх с природой вводят понятие риска Игровая модель является математической, упрощенной моделью реального конфликта, и при этом вводятся следующие основные ограничен В матричных играх предполагается, что игроку известны все стратегии противника, но неизвестно какой именно он воспользуется в пр Матрица рисков

Подобный материал:

• Рейтинг-план освоения дисциплины «Теория принятия решений» Недели, 83.54kb.
• Рабочая программа дисциплины основы теории принятия экономических решений цели и задачи, 92.73kb.
• Теоретические основы механизма принятия стратегических решений в организации Методологические, 627.49kb.
• Бакалаврская программа № 521200 Кафедра: Социологии Направление : Социология Дисциплина, 215.78kb.
• Рабочая программа по курсу «теория принятия решения», 87.49kb.
• Моделирование в управлении персоналом, 117.35kb.
• Методы обучения систем поддержки принятия решений, 64.31kb.
• Номинация исторические основы формирования и развития статистики как науки возникновение, 2000.33kb.
• Основы теории цепей, 32.22kb.
• Технология принятия управленческих решений, 1631.84kb.

Лекция №11

Основы теории статистических решений

(игры с природой)


В этих играх существует некая объективная реальность, которая может влиять на процесс принятия решения (т.е. под природой понимаются условия, которое влияют на принимаемые решения).


Рассмотрим игру в матричной форме G(mn).

	П1	…	Пj	…	Пn
A1	а11	…	а1j	…	а1n
…	…	…	…	…	…
Ai	аi1	…	аij	…	аin
…	…	…	…	…	…
Am	аm1	…	аmj	…	аmn

П_j , j=1, .. , n – ситуации, состояния природы (условия);

а_ij – выигрыш игрока А при выборе им стратегии А_i в состоянии природы П_j.


Использование методов теории антагонистических игр невозможно, т.к. нет сознательного противодействия противника (за исключением метода максимина).

В играх с природой вводят понятие риска:

То есть, риск – это разность между выигрышем, который игрок получил бы, зная, в каких условиях П_j он принимает решение, и выигрышем, который он получает, не зная условий, когда он выбирает стратегию A_i.

Методы решения игр с природой

Возможны различные ситуации:

1. Стохастическая неопределенность

Известны вероятности состояний «природы»:

 П_j  q_j, j=1,…,n


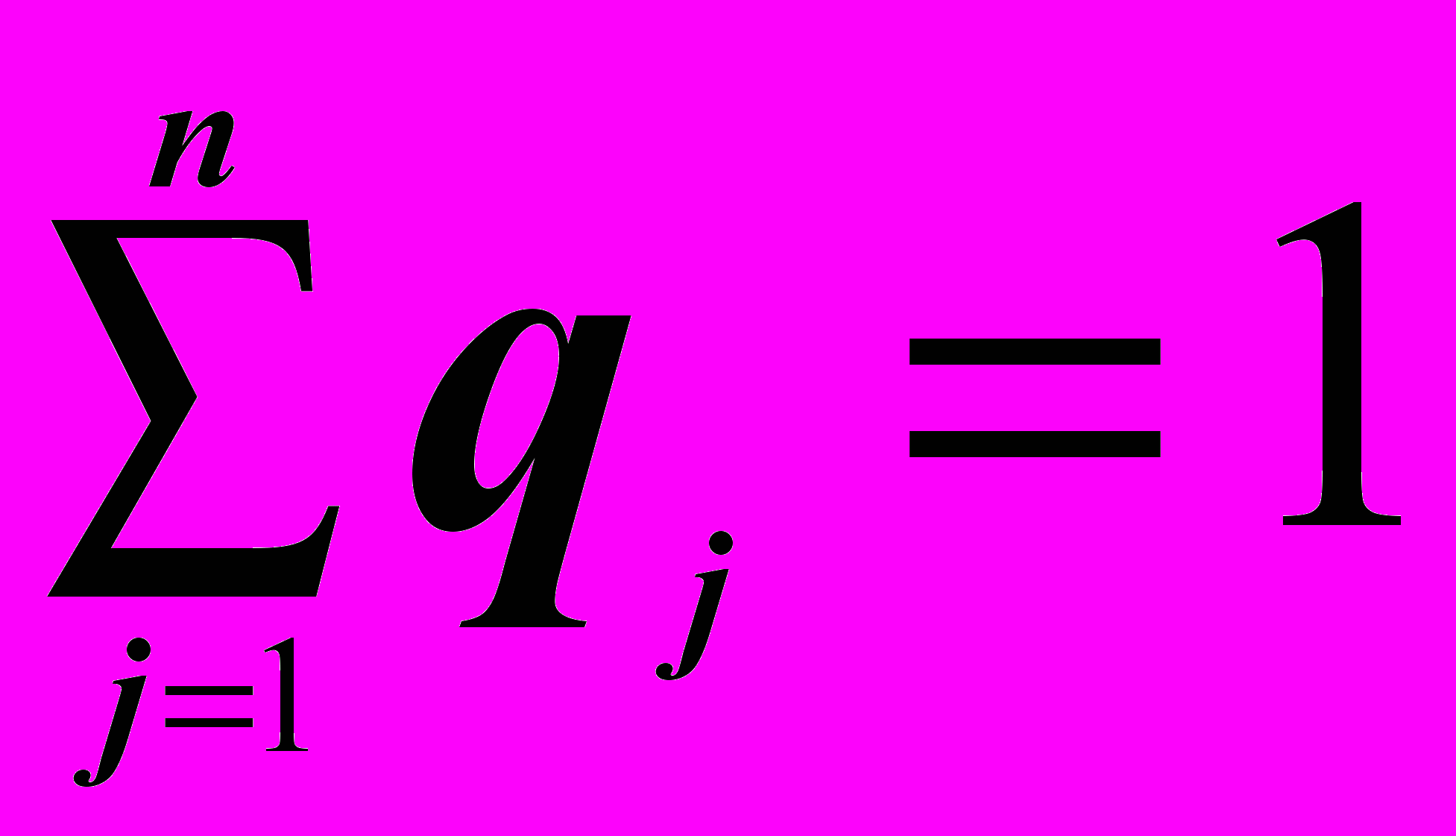
Тогда для поиска оптимального решения применяется критерий Лапласа.


Оптимальной является та стратегия, которая максимизирует средний выигрыш:



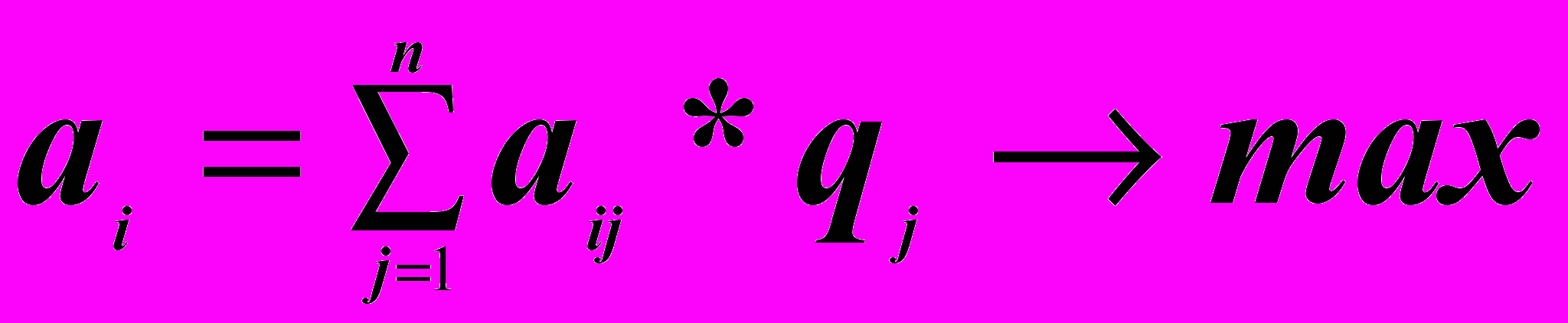
Эта же стратегия будет минимизировать средний риск:

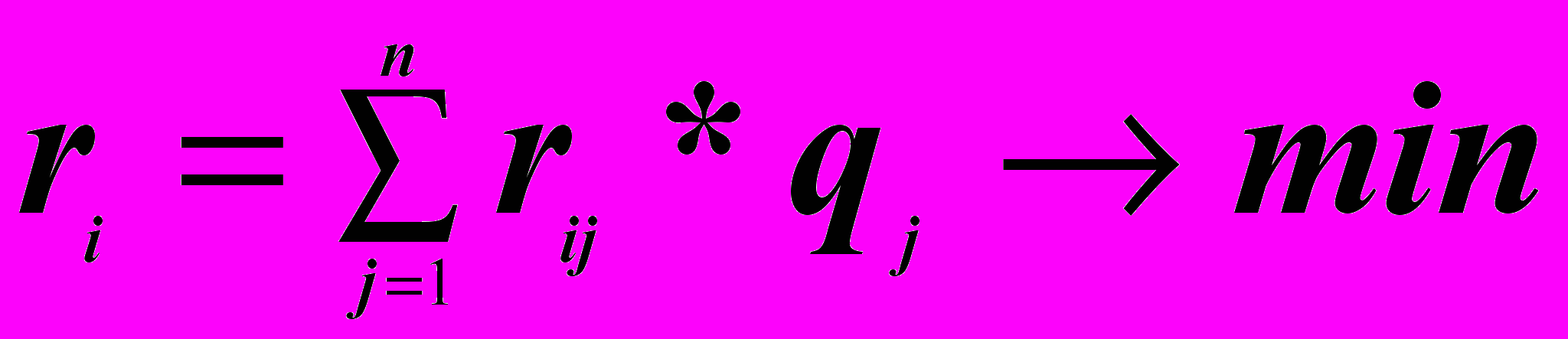
2. Вероятности q_j неизвестны или их не существует
   

В этом случае может использоваться ряд критериев поиска оптимального решения:

1. Максиминный критерий Вальда (крайнего пессимизма) – стратегия, максимизирующая минимальный выигрыш.
   

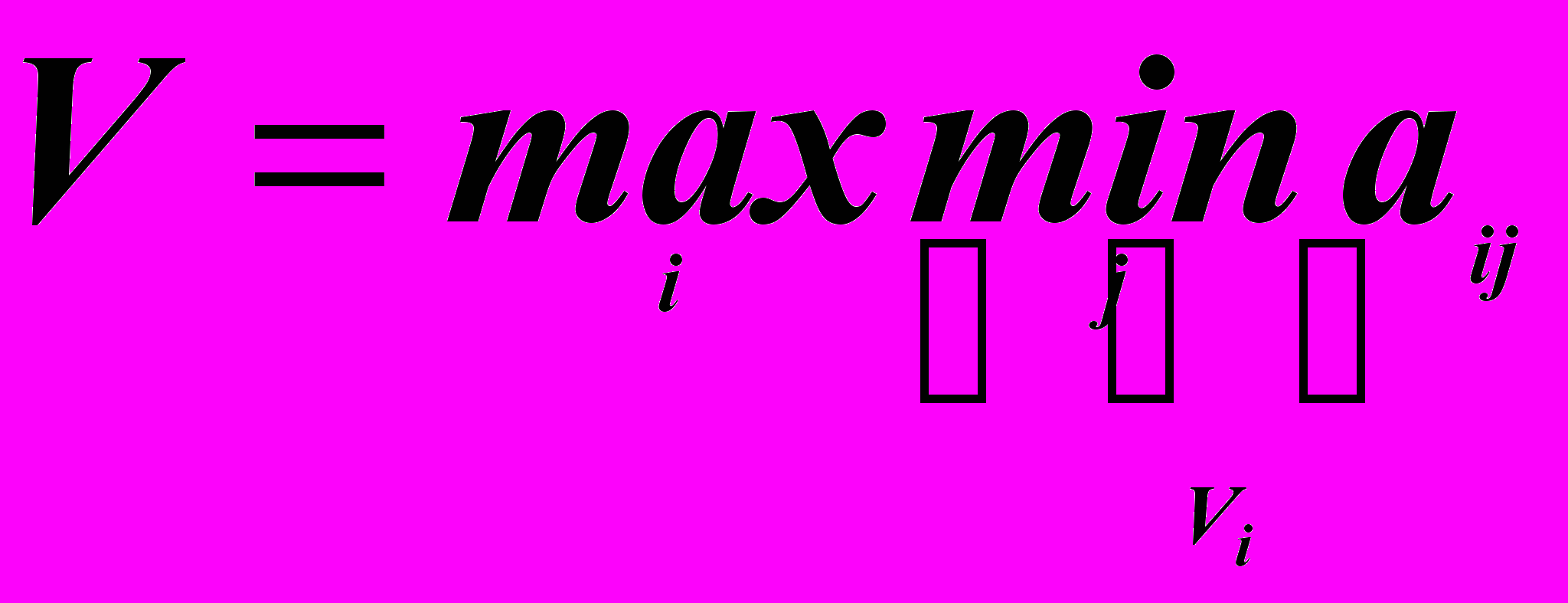
2. Критерий Сэвиджа – стратегия, минимизирующая максимальный риск
   

3. Компромиссный критерий Гурвица

В качестве оптимальной выбирается стратегия, зависящая от параметра пессимизма (оптимизма).



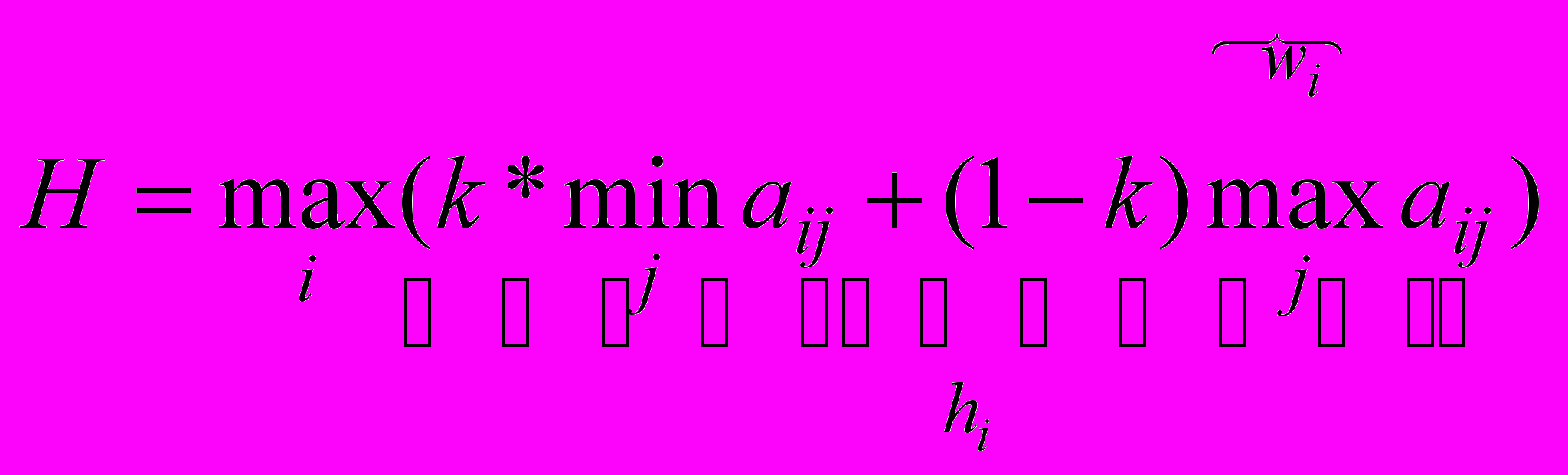
k – критерий осторожности или пессимизма 0k1

k=0 – максимизировать максимально возможный выигрыш

k=1 – критерий Вальда

Если нет дополнительной информации, то рекомендуется брать k  0.6.

При выборе оптимальной стратегии брать надо ту, которую советуют большинство критериев.


Замечание:


В играх с природой не используются смешанные стратегии по следующим причинам:

1. В антагонистических играх смешанные стратегии применяются часто для того, чтобы обмануть, запутать противника, что в играх с природой не имеет смысла.
   

2. Аппарат смешанных стратегий ориентирован на получение максимального среднего выигрыша в случае многократного повторения игры, но в играх с природой выявляется (накапливается) вероятность q_i, что позволяет перейти к методу Лапласа, который позволяет определить оптимальное решение в чистых стратегиях.
   

Общие выводы по теоретико-игровым моделям

Игровая модель является математической, упрощенной моделью реального конфликта, и при этом вводятся следующие основные ограничения:

1. Предполагается, что противник также разумен, как и сам игрок.
   

Выигрыш в реальном конфликте заключается в том, чтобы выявить слабые стороны противника и воспользоваться ими;

2. Теория игр ориентирует ЛПР на наиболее осторожное поведение, на исключение риска (определенный риск в играх с “природой”).
   

В реальных конфликтах есть возможность рисковать;

3. В матричных играх предполагается, что игроку известны все стратегии противника, но неизвестно какой именно он воспользуется в процессе игры.
   

Семинар №11


Поиск решения при известных вероятностях состояний природы


Матрица выигрышей

	П1	П2	П3	П4
A1	1	4	5	9
A2	3	8	4	3
A3	4	6	6	2

Матрица рисков

	П1	П2	П3	П4
A1	3	4	1	0
A2	1	0	2	6
A3	0	2	0	7

q₁=0.1

q₂=0.5

q₃=q₄=0.2


a₁=1*0.1+4*0.5+14*0.2=4.9

a₂=3*0.1+8*0.5+7*0.2=5.7 А₂ - оптимальная стратегия

a₃=4*0.1+6*0.5+8*0.2=5


r₁=3*0.1+4*0.5+1*0.2=2.5

r₂=1*0.1+0*0.5+8*0.2=1.7  А₂ - оптимальная стратегия

r₃=0*0.1+2*0.5+7*0.2=2.4

Поиск решения при отсутствии вероятностей состояний природы


Матрица выигрышей

	П1	П2	П3	П4	vi	wi	hi
A1	19	30	41	49	19	49	31
A2	51	38	10	20	10	51	26.4
A3	73	18	81	11	11	81	39

Матрица рисков

	П1	П2	П3	П4	Si
A1	54	8	40	0	54
A2	22	0	71	29	71
A3	0	20	0	38	38

1. Критерий Вальда – A₁
   
2. Критерий Сэвиджа – A₃
   
3. Критерий Гурвица – A₃ (k = 0.6)
   

Выбираем стратегию A₃.