Geum.ru

Это методическое пособие предназначено для желающих самостоятельно научиться решать задачи по основным разделам предмета на языках Бейсик и Паскаль. Предлагаемая методика включает

Вид материалаМетодическое пособие
Подобный материал:
1   ...   17   18   19   20   21   22   23   24   25

XI.3.Задачи  уровня

  1. Сколькими способами можно отобразить команду в составе 5 человек из 8 кандидатов; из 10 кандидатов? Подсчет количества способов отбора оформит в виде подпрограммы.

2. Футболист ударом ноги посылает мяч вертикально вверх с высоты 1 м с начальной скоростью 20 м/с. На какой высоте мяч будет через 1с., 3с., 4с?

3. Два спортсмена одновременно начинают движение из одной точки. Первый спортсмен начинает движение со скоростью 10 км/ч и равномерно за каждый следующий час увеличивает скорость на 1 км. Второй начинает движение со скоростью 9 км/ч и равномерно за каждый следующий час увеличивает скорость на 1.6 км/ч. Выяснить, какой спортсмен преодолеет больший путь через 1 час, через 4 часа. Вычисление путей оформить с помощью функций

4. В задаче 3 определить, когда второй спортсмен догонит первого. Решение квадратного уравнения оформить в виде подпрограммы.

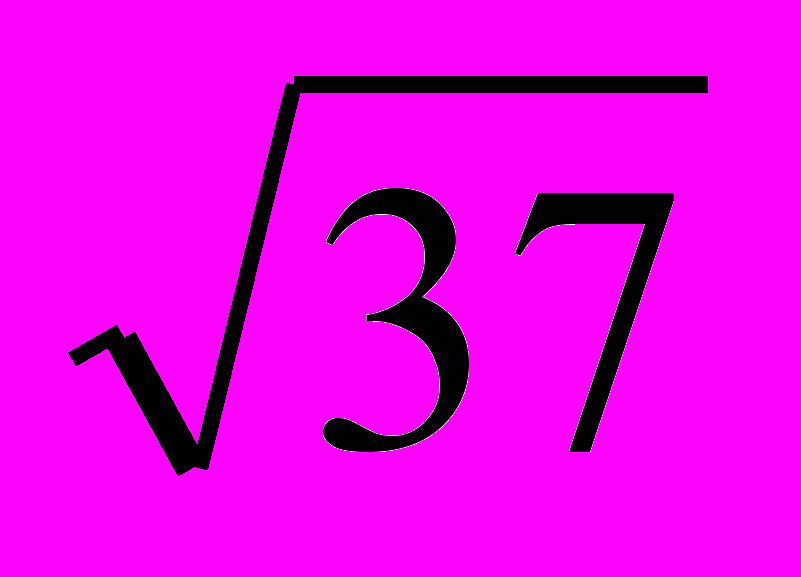
5. Два треугольника заданы своими сторонами a, b и c. Вычислить площади треугольника по формуле Герона и определить, какой треугольник имеет большую площадь. При решении задачи взять следующие данные: дя первого треугольника a=3, b=4, c=5; для второго треугольника a=2, b=

c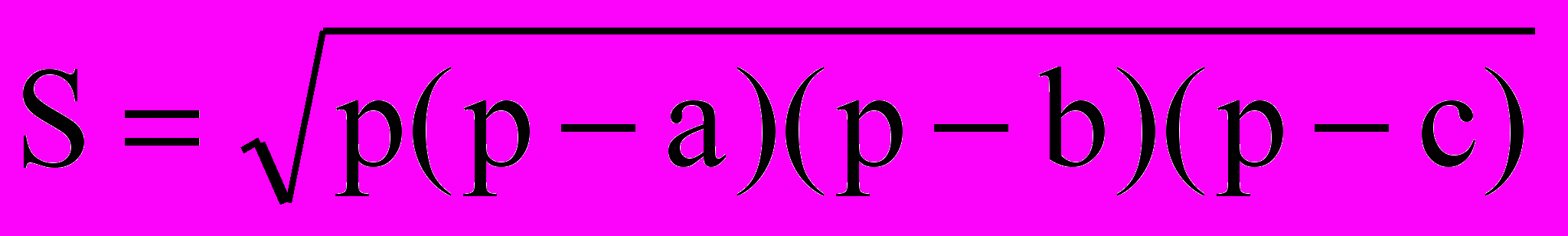= . Вычисление площади треугольника по формуле Герона оформить в виде функции. ( , где р-полупериметр).

XI.4.Задачи  уровня




  1. Вычислить приближенно площадь фигуры, ограниченной осью x, прямыми x=1 и x=3 и кривой y=y(x)=1/x+5; разбивая интервал изменения x на 10 частей и суммируя площади десяти прямоугольников с основанием 0.2 и высотой, равной значению функции в середине каждого интервала. Вычисление y(x) оформить с помощью функции. Вычисление площади оформить в виде подпрограммы.
  2. Даны А(7), В(7), С(7). найти длины этих трех одномерных массивов и определить наименьший из них. Вычисление длины оформить в виде подпрограммы.

XI.5.Задачи  уровня

  1. На плоскости заданы координаты пяти точек A, B, C, D, E. Выяснить, какие точки находятся на максимальном и минимальном расстояниях друг от друга, и вычислить сумму всех расстояний между точками. Задачу решить для A(1, 1), B(2, 3), C(4, 3), D(5, 6), E(6, 4), A(1, 2), B(2, 4), C(3, 3), D(5, 1), E(5, 5). Вычисление матрицы расстояний ммежду точками оформить в виде подпрограммы. Поиск максимального расстояния оформить в виде подпрограммы. Суммирование расстояний оформить в виде подпрограммы.

XI.6.Контрольные работы

XI.6.1.Контрольная работа №1

Диктант


1. Часть программы, к которой происходит неоднократное обращение?

2. Переменные, которым присваиваются значения исходных данных?

3. Переменные, в которых получаются результаты работы подпрограммы?

4. Остальные переменные основной программы

5. Переменные подпрограммы?

6. Оператор обращения к подпрограмме?

7. Как можно вывести на печать значения элементов матрицы?

XI.6.2.Контрольная работа №2

Вариант 1


1. Два треугольника заданы координатами своих вершин A, D, C. Вычислить площади треугольников с помощью формулы Герона и определить, какой треугольник имеет большую площадь. Пир решении задачи использовать следующие данные: для первого треугольника A(1, 1), B(4, 2), C(2, 3.5); для второго треугольника A(1, 2), B(4, 1), C(3, 3.5). Вычисление длин сторон треугольника и его площади по формуле Герона оформить в одной подпрограмме.

Вариант 2


1. Два треугольника заданы координатами своих вершин A, D, C. Вычислить площади треугольников с помощью формулы Герона и определить, какой треугольник имеет большую площадь. Пир решении задачи использовать следующие данные: для первого треугольника A(1, 1), B(5, 2), C(3, 3); для второго треугольника A(2, 5), B(4, 3), C(6, 4). Вычисление длин сторон треугольника и его площади по формуле Герона оформить в одной подпрограмме.

Вариант 3

  1. Два треугольника заданы координатами своих вершин A, D, C. Вычислить площади треугольников с помощью формулы Герона и определить, какой треугольник имеет большую площадь. Пир решении задачи использовать следующие данные: для первого треугольника A(1, 2), B(6, 3), C(4, 2); для второго треугольника A(2, 1), B(5, 1), C(4, 1). Вычисление длин сторон треугольника и его площади по формуле Герона оформить в одной подпрограмме.



XI.6.3.Вопросы для самопроверки


1. В каких случаях целесообразно использовать подпрограммы?

2. Оформление подпрограммы. Обращение к подпрограмме. Операторы описания.

3. Как осуществляется обмен информацией между основной программой и подпрограммой?

4. Взаимосвязь основной программы и подпрограммы.

5. Цель и содержание инструкции к подпрограммам.

XII. Создание программы в Turbo Паскале


Когда Вы в первый раз входите в Турбо-Паскаль, вы ока­зываетесь в основном меню. Нажмите клавишу Е для перехода в окно редактирования (или же вы можете использовать клавиши управления движением курсора для выбора команды Edit, а за­тем нажмите клавишу "Enter"). Теперь вы находитесь в редак­торе, и курсор расположен в верхнем левом углу. Можно начать набирать следующую программу, нажимая "Enter" в конце каждой строки:

program MyFirst;

var

A,В: integer;

Ratio: real;

begin

Write(' Введите два числа: ');

Readln(A,B);

Ratio:= A / В;

Writeln (' Отношение равно ', Ratio);

Writeln (' Нажмите клавишу ');

end.

Для передвижения в окне редактирования используйте кла­виши управления движением курсора. (Если Вы не знакомы с ко­мандами редактирования, где рассмотрены все имеющиеся в вашем распоряжении команды редактирова­ния). Отметим только необходимость точки с запятой в конце большинства строк и необходимость точки в конце последней строки. В случае, если вы допустите ошибку, можно использо­вать клавиши управления движением курсора для перемещения. Для удаления символов можно использовать клавишу "Backspace", а для вставки просто набирайте новый текст.