Муниципальное образовательное учреждение «Средняя образовательная школа №7» г. Ртищево

Вид материала

Творческая работа

Содержание Понятие симметрии Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относител Поиски обобщающих законов в природе Симметрия в живой природе. Симметрия в мире растений Симметрия в мире животных Плоскость симметрии. Типы симметрии у животных Типы симметрии. Вращательная симметрия. Поступательная симметрия. Вращательно-поступательная симметрия. Пришельцы из других миров Значение симметрии в познании природы

Подобный материал:

• Усовик Елена Рудольфовна, учитель биологии, высшей категории. Муниципальное образовательное, 141.02kb.
• Муниципальное образовательное учреждение «Средне образовательная школа №1 с. Карагач», 161.5kb.
• Публичный отчет муниципального общеобразовательного учреждения «ирбитская общеобразовательная, 549.17kb.
• Элективный курс по выбору «Как быть востребованным на рынке труда в эпоху информационных, 700.89kb.
• Муниципальное образовательное учреждение средняя общеобразовательная школа №20 города, 293.47kb.
• 1. Музыка Древнего мира и средневековья, 192kb.
• Программа развития муниципального образовательного учреждения Муниципальное образовательное, 340.53kb.
• Муниципальное образовательное учреждение, 508.51kb.
• Лазаренко Татьяна Александровна. Образовательное учреждение: Муниципальное общеобразовательное, 55.34kb.
• Алтайский край Родинский район Муниципальное образовательное учреждение «Покровская, 649.83kb.

Муниципальное образовательное учреждение

«Средняя образовательная школа №7» г. Ртищево




Творческая работа


Выполнила ученица 10 класса

Гаврюшина Людмила Андреевна


Руководитель:

Ефимова Галина Николаевна,

учитель математики


Ртищево - 2008

Оглавление

стр

1. Введение 3 - 4
   
2. Симметрия в природе
   

1. Понятие симметрии 4 - 5
   
2. Симметрия в пространстве 5 - 8
   
3. Поиски обобщающих законов в природе 8 - 10
   
4. Симметрия в живой природе 11 - 12
   
5. Симметрия в мире растений 12 - 13
   
6. Симметрия в мире животных 13 - 16
   
7. Пришельцы из других миров 16 - 17
   
8. Значение симметрии в познании природы 17 - 18
   

3. Заключение 18
   
4. Список литературы 19
   
5. Приложения 20 - 24
   

«...быть прекрасным значит быть симметричным и соразмерным»

Платон


ВВЕДЕНИЕ


Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В. И. Вернадский (1863—1945), «слагалось в течение десятков, сотен, тысяч поколений". «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но в известной мери и уверенностью человека в большей пригодности для практики правильных форм". Это слова другого нашего замечательного соотечественника, посвятившего изучению симметрии всю свою долгую жизнь, академика А. В. Шубникова (1887—1970). Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о «соразмерности», что и означает в переводе с греческого слово «симметрия», с течением времени приобрело универсальный характер, и было осознано как всеобщая идея инвариантности (т. е. неизменности) относительно некоторых преобразований. Таким образом, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что-то такое, после чего они останутся неизменными. Например, пятиконечная звезда, будучи повернута на 72° (360° · 5), займет первоначальное положение, а ваш будильник одинаково звенит в любом углу комнаты. Первый пример дает понятие об одном из видов геометрической симметрии — поворотной, а второй иллюстрирует важную физическую симметрию — однородность и изотропность (равнозначность всех направлений) пространства. Благодаря последней симметрии все физические приборы (в том числе и будильник) одинаково работают в разных точках пространства, если, конечно, не изменяются окружающие физические условия. Легко вообразить, какая бы царила на Земле неразбериха, если бы эта симметрия была нарушена!

Таким образом, не только симметричные формы окружают нас повсюду, но и сами многообразные физические и биологические законы гравитации, электричества и магнетизма, ядерных взаимодействий, наследственности пронизаны общим для всех них принципом симметрии. «Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности»,— писал Вернадский. Действительно, еще Платон мыслил атомы четырех стихий — земли, воды, огня и воздуха — геометрически симметричными в виде правильных многогранников. Я попыталась в своем реферате показать, что хотя сегодня «атомная физика» Платона кажется наивной, принцип симметрии и через два тысячелетия остается основополагающим. Важнейшим свойством симметрии является сохранение (инвариантность) тех или иных признаков (геометрических, физических, биологических и т. д.) по отношению к вполне определенным преобразованиям. Математическим аппаратом изучения симметрии сегодня является теория групп и теория инвариантов. В своей работе я затронула лишь самые общие черты, внешние формы, улавливаемые в большинстве случаев простым глазом. Я не рассматривала симметрию атомов. Тема, которую я раскрываю в реферате – внешние формы природных тел и характеризующие их общие геометрические законы.


Понятие симметрии


Слово «симметрия» в переводе с греческого означает «соразмерность». В этом смысле симметричное означает нечто пропорциональное, сбалансированное.

В «Современном словаре иностранных слов» под симметрией понимается «соразмерность, полное соответствие в расположении частей целого относительно средней линии, центра... такое расположение точек относительно точки (центра симметрии), прямой (оси симметрии) или плоскости (плоскости симметрии), при котором каждые две соответствующие точки, лежащие на одной прямой, проходящей через центр симметрии, на одном перпендикуляре к оси или плоскости симметрии, находятся от них на одинаковом расстоянии...». В Энциклопедическом словаре мы обнаружим шесть статей, начинающихся со слова «симметрия». Кроме того, это слово встречается во множестве других статей. В математике слово «симметрия» имеет не меньше семи значений (среди них симметричные полиномы, симметрические матрицы). В логике существуют симметричные отношения. Важную роль играет симметрия в кристаллографии. Интересно интерпретируется понятие симметрии в биологии. Там описывается шесть различных видов симметрии. Мы узнаем, например, что гребневики дисимметричны, а цветки львиного зева отличаются билатеральной симметрией, что соты – настоящий конструкторский шедевр¹. Мы обнаружим, что симметрия существует в музыке и хореографии (в танце). Она зависит здесь от чередования тактов. Оказывается, многие народные песни и танцы построены симметрично. Можно увидеть, что эта кажущаяся простота уведет нас далеко в мир науки и техники и позволит время от времени подвергать испытанию способности нашего мозга (так как именно он запрограммирован на симметрию).

Своим развитием чисто геометрическое учение о симметрии, как это ни странно, обязано в первую очередь не математикам, а естествоиспытателям, углубленно изучавшим кристаллические образования. Объясняется это тем, что формы кристаллов с древнейших времен Рис. 1

поражали глаз своей симметричностью (рис.1). В качестве иллюстрации приведем хотя бы очертания снежной кристаллической звездочки (рис.2,а). Вспомним также хорошо известные изумительно правильные восьмигранники (октаэдры) драгоценного алмаза (рис. 2,б). Изучение таких фигур представляло существенный практический интерес, так как многие природные кристаллы принадлежат к ценным полезным ископаемым. Почти все кристаллы, встречающиеся в природе, имеют центр, ось или плоскость симметрии.

История науки показывает, что учение о симметрии развивалось крайне медленно и трудно. Поражающе правильные очертания кристаллов вызывали в древности суеверные представления. «Такое могли сотворить только ангелы или подземные духи», - утверждали наши предки, не догадываясь о том, что кристаллы растут в природе сами собой из растворов, паров и в твердых каменных породах. Красота и гармония природной симметрии наталкивала даже испытанных мудрецов на Рис. 2, а Рис. 2,б самые фантастические мысли.

Симметрия в пространстве



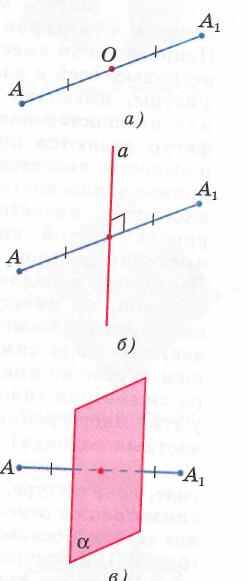
Точки и называются симметричными относительно точки О (центр симметрии), если О – середина отрезка 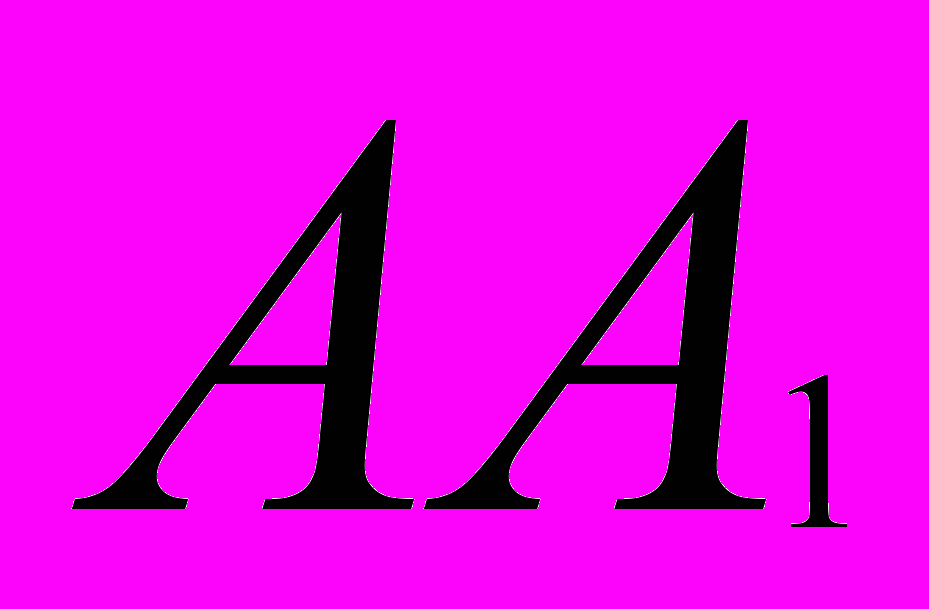(рис. 1,а). Точка О считается симметричной самой себе.

Точки и называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через середину отрезка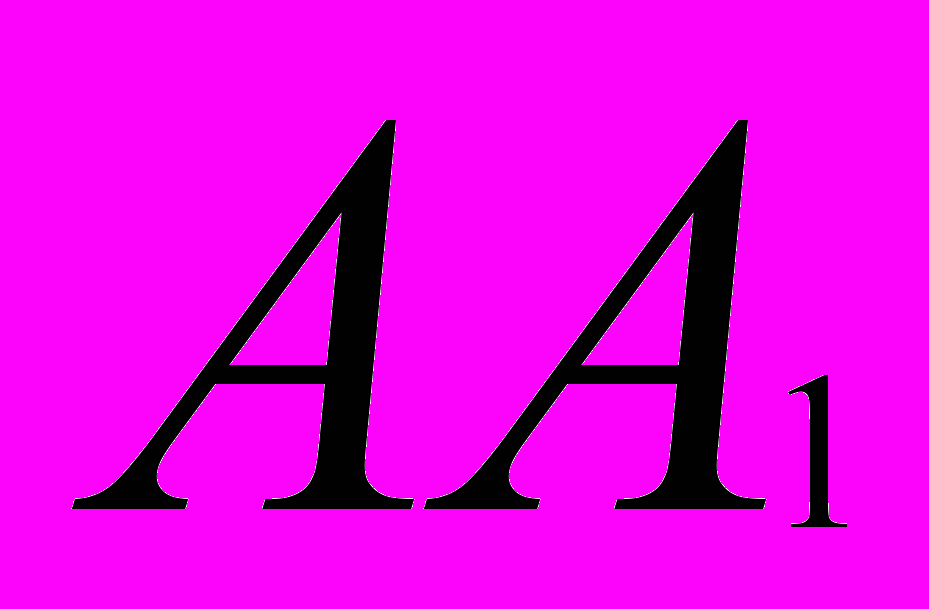 и перпендикулярна к этому отрезку (рис. 1, б). Каждая точка прямой а считается симметричной самой себе.

Точки и называются симметричными относительно плоскости (плоскость симметрии), если плоскость проходит через середину отрезка 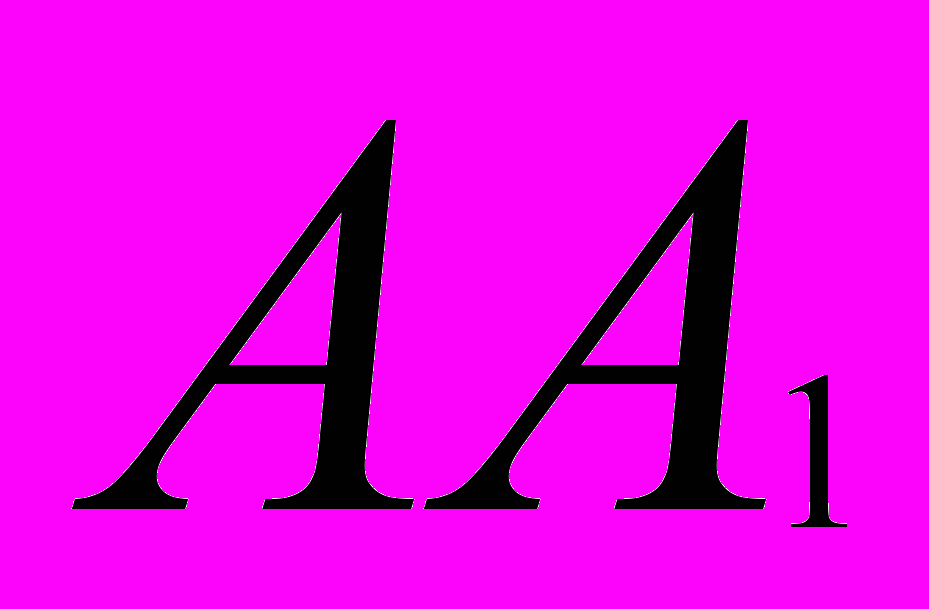и перпендикулярна к этому отрезку (рис.1,в). Каждая точка плоскости считается симметричной самой себе.

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно неё Рис. 3

некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость симметрии), то говорят, что она обладает центральной (осевой, зеркальной) симметрией.

Действие плоскости симметрии (обозначается буквой Р) можно уподобить отражению в двустороннем зеркале, играющем роль этой плоскости. Обратимся к рис. 4,а, изображающемуравнобедренный треугольник АВС. высота BD этого треугольника, разделяющая его на две зеркально равные половины ABD и BCD, представляет собой след плоскости симметрии Р, перпендикулярной к плоскости рисунка.




Рис. 4,а Рис. 4,б

Двустороннее отражение фигуры в плоскости симметрии называется «операцией симметрии». К операциям симметрии относятся повороты фигур вокруг определенных прямых (осей), отражения в особых точках, и т. д.

Квадрат имеет четыре плоскости симметрии, а в прямоугольнике можно провести только две. Прямоугольный параллелепипед (кирпичик, спичечный коробок) имеет три взаимноперпендикулярные плоскости симметрии (рис. 4,б), а куб обладает девятью плоскостями симметрии. Возьмем непосредственно из природы примеры: снежная звездочка имеет шесть плоскостей симметрии – 6Р, цветок – 5Р (рис. 3).



Рис. 5

Плоскость симметрии в природе проявляется очень часто. Выдающийся русский кристаллограф Г. В. Вульф (1863 - 1925) назвал плоскость симметрии «основным элементом симметрии».

Рассмотрим второй тип элементов симметрии: ось симметрии. Осью симметрии называется такая прямая линия, вокруг которой несколько раз повторяются равные части симметричной фигуры. Эти равные части расположены так, что после поворота вокруг оси на некоторый угол фигура занимает в пространстве то же положение, которое она занимала и до поворота, только на месте одних ее частей оказались другие равные им части. Число самосовмещений фигуры при ее повороте вокруг оси на 360º называется «порядком оси». Доказано, что порядок оси может быть только целым числом. Обозначим ось симметрии L_n, где n ее порядок.




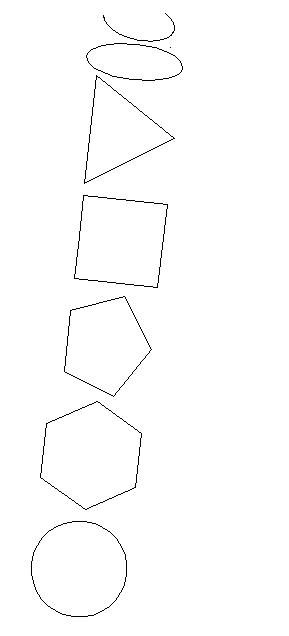
Рис.6

Изобразим ряд правильных многоугольников, расставив их в порядке увеличения числа сторон и вершин (рис. 6). Через центр равностороннего треугольника перпендикулярно к плоскости рисунка проходит ось L₃, через центр квадрата – L₄, через центр правильного пятиугольника – L₅ и т. д. В центре круга найдем ось симметрии бесконечного порядка 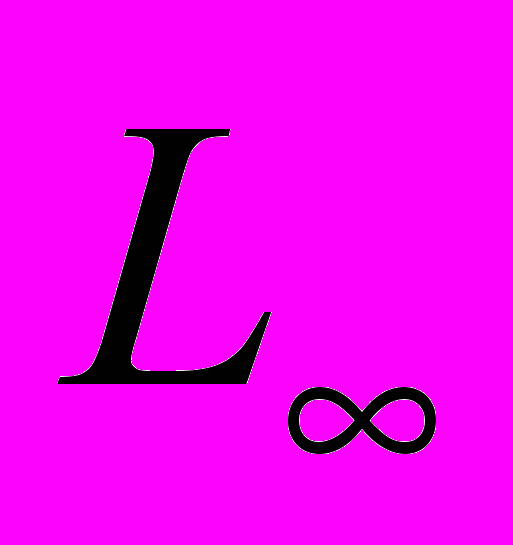. Слева от треугольника поместим овал, через его центр проходит ось L₂. Еще левее изобразим какую-нибудь неправильную фигуру – вроде запятой. Повернув «запятую» вокруг оси, перпендикулярной к плоскости бумаги, на 360º, вернем ее в исходное положение. Число самосовмещений «запятой» равно 1 и , следовательно, она обладает осью симметрии первого порядка. Вернемся к примерам из природы: снежная звездочка имеет одну ось шестого порядка L₆, цветок, изображенный на рис. 5, имеет одну ось пятого порядка L₅.

Перейдем к следующему элементу симметрии – к особой точке, называемой центром симметрии (обозначается буквой С). Центром симметрии является особая точка внутри фигуры, характеризующаяся тем, что любая проведенная через эту точку прямая по обе стороны от нее и на равных расстояниях встречает одинаковые точки фигуры. Из школьного курса математики мы знаем, что любой параллелограмм и любой параллелепипед обладает центром симметрии, тогда как пирамида не имеет его.

Итак, в нашем распоряжении имеется полный набор разных элементов симметрии для конечных фигур. Однако этого мало. Для полной характеристики таких фигур необходимо учитывать совокупности всех элементов симметрии, присутствующих на данном объекте. Так, например, полная совокупность элементов симметрии снежинки - L₆6Р; изображенный на рис. 5 цветок характеризуется симметрией L₅5Р. Для спичечной коробки (кирпичика) были найдены три плоскости, три двойные оси и центр симметрии - 3L₂3РС. Найденные совокупности элементов симметрии выводятся по определенным правилам сложения элементов. Существует ряд теорем, лежащих в основе этих правил. Пиведу в качестве примера одну из них: «При наличии оси симметрии L_n порядка n и плоскости симметрии Р, направленной вдоль этой оси, найдем всего n плоскостей симметрии, направленных вдоль оси L_n, т. е. L_n nР». Иллюстрацией к этой теореме могут служить симметрия узора снежной звездочки L₆6Р и симметрия цветка L₅5Р.


Поиски обобщающих законов в природе


Все окружающие нас природные тела находятся в поле земного тяготения и неминуемо несут на себе следы его влияния. И камни, и растения, и животные под влиянием силы земного тяготения приобретают внешне сходные черты.

Внешние формы природных тел – это то, что, прежде всего, бросается в глаза при знакомстве с окружающим миром. С самого раннего детства мы хорошо знаем очертания деревьев, животных, гор камней. Существует ряд научных дисциплин, детально изучающих формы тех или иных природных образований (морфология растений, Рис. 7 морфология беспозвоночных, морфология позвоночных и др.). Изучая природу, ученые обнаружили, что качественно разные предметы иногда имеют одинаковые геометрические формы и, наоборот, однородные по качеству предметы могут обладать весьма разными геометрически формами. Форма является вторичной по отношению к содержанию. Натуралисты, пытливо вглядываясь в разнообразные явления природы, вдруг к своему удивлению находят в них общие черты. Например, в старых учебниках географии обычно изображались зонтикообразные итальянские сосны пинии на фоне дымящегося вулкана Везувия (рис. 7) Султан из паров и газов над огнедышащей горой странным образом напоминает по форме растущую поблизости пинию. Случайно ли это? Прежде чем ответить на этот вопрос, подберем еще несколько примеров такого же неожиданного сходства. Зловещее облако после взрыва атомной бомбы неспроста называют «атомным грибом», оно и в самом деле похоже по форме на самый обыкновенный безобидный гриб. Кочан цветной капусты повторяет очертания белого кучевого облака; струя фонтана напоминает куст или плакучую иву и т.д. Зоркие поэты умеют особенно метко улавливать случаи такого, казалось бы, необъяснимого сходства.

В связи с этим возникает вопрос, а не существуют ли какие-то причины, придающие такое неожиданное сходство самым разнообразным телам? Ответ напрашивается сам собой. И растущее дерево, и пары Везувия, и атомный и простой гриб, и фонтан – все они с той или иной мощностью и быстротой устремляются вверх до тех пор, пока сила земного тяготения не остановит их движение и не заставит обратиться вспять к земле. Поэтому именно сила тяготения придает более или менее сходную форму всему растущему или направленному вверх. Такое сходство идет очень далеко, подчиняясь единой математической характеристике. Действие силы тяготения должно, конечно, сказываться на всех телах, формирующихся в поле ее влияния, как на безжизненных, так и на живых.

Если мы приглядимся к окружающей нас природе, мы можем найти сходство даже в самых незначительных ее деталях. Вот с дерева упал обыкновенный листок. Форма его не является случайной, она строго

Рис. 8 Рис. 9


закономерна. Листок как бы склеен из двух более или менее одинаковых половинок (рис. 8). Одна из этих половинок расположена зеркально относительно другой, совсем так, как располагаются друг относительно друга отражение какого-либо предмета в зеркале и сам предмет. Плоскость, разделяющая листок на две зеркально равные части называется «плоскостью симметрии». Ботаники и зоологи нередко называют симметрию листка «билатеральной» (в переводе с латинского – «дважды боковой»), а мы ее будем называть попросту «симметрией листка».

Только ли древесный листок обладает такой симметрией? Вот ползет жук (рис. 8). Мы и его можем мысленно разделить вдоль на две зеркально равные части. Пронеслась красавица бабочка с яркой расцветкой. Она тоже состоит их двух одинаковых половинок (рис. 8). Даже пятнистый узор на ее крыльях послушно подчиняется такой геометрии. Да и нас самих можно мысленно разделить на две зеркально равные половины. Итак, повсюду мы наталкиваемся на одно и то же. Везде упорно повторяется все та же «симметрия листка».

А вот возле самых наших ног выглядывает из травы обыкновенная ромашка. Сорвем и разглядим ее. Вокруг оранжевой середки, как лучи вокруг солнышка на детском рисунке, расположены белые лепестки (рис. 9) Имеет ли такое «цветочное солнышко» плоскость симметрии? Конечно! Без всякого труда можно его разрезать на две зеркально равные половинки по линии, проходящей через центр цветка и продолжающейся вдоль середины любого из лепестков или между ними. Это, однако, не все. Ведь лепестков-то много и вдоль каждого лепестка можно обнаружить плоскость симметрии. Значит, этот цветок обладает многими плоскостями симметрии, и все они пересекаются в его центре. Это уже не «симметрия листка» с одной только плоскостью симметрии, а целый веер или пучок пересекающихся плоскостей симметрии. Сходным образом можно охарактеризовать и геометрию ели, гриба (рис.9). У ботаников и зоологов такая «ромашково-грибная симметрия» обычно называется «лучевой» или «радиальной».

Итак, два вида симметрии с необычным упорством повторяются вокруг нас. Один отвечает зеркальной, или билатеральной, симметрии – «симметрии листка» (сам листок, жук, гусеница, бабочка, человек), другой соответствует радиально-лучевой симметрии (ромашка, подсолнечник, грибы, деревья, султан паров, фонтан).

Сформулируем в упрощенном виде общий закон, повсеместно проявляющийся в природе: «Все, что растет или движется по вертикали, т.е вверх или вниз относительно земной поверхности подчиняется радиально-лучевой («ромашково-грибной») симметрии в виде веера пересекающихся плоскостей симметрии. Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии – «симметрии листка» (одна плоскость симметрии)».

Этому всеобщему закону послушны не только цветы, животные, легкоподвижные жидкости и газы, но и твердые неподатливые камни (рис.10). Известный советский кристаллограф Г.Г.Леммлейн (1901-1961г.г.) установил, что кристаллы кварца, развивавшиеся в вертикальном направлении на дне хрусталеносной пещеры, имеют внешнюю радиальную симметрию. Вместе с тем внешняя симметрия кристаллов того же Рис. 10 кварца, образовавшихся на стенке пещеры и разраставшихся в косом или горизонтальном направлении, нередко отвечают «симметрии листка».

Учет закона симметрии помогает человеку возводить прочные постройки, конструировать подвижные машины. Невыполнение требований, вытекающих из этого закона, приводит к тому, что крупные, но неправильно запроектированные сооружения бывают неустойчивыми. Обратим внимание на то, что большинство предметов в комнате имеет «симметрию листка» (стул, кресло, диван) или же радиально-лучевую симметрию (круглый стол, круглый табурет, настольная и висячая лампы). Следовательно, все эти предметы хорошо согласуются с симметрией поля земного тяготения и вполне устойчивы. Итак, знание геометрических законов природы имеет огромное практическое значение. Мы должные не только научиться понимать эти законы, но и заставлять служить их нам на пользу.


СИММЕТРИЯ В ЖИВОЙ ПРИРОДЕ.


Симметрией обладают объекты и явления живой природы. Она не только радует глаз и вдохновляет поэтов всех времен и народов, а позволяет живым организмам лучше приспособиться к среде обитания и просто выжить. В живой природе огромное большинство живых организмов обнаруживает различные виды симметрий (формы, подобия, относительного расположения). Причем организмы разного анатомического строения могут иметь один и тот же тип внешней симметрии.

Внешняя симметрия может выступить в качестве основания классификации организмов (сферическая, радиальная, осевая и т.д.) Микроорганизмы, живущие в условиях слабого воздействия гравитации, имеют ярко выраженную симметрию формы.

Асимметрия присутствует уже на уровне элементарных частиц и проявляется в абсолютном преобладании в нашей Вселенной частиц над античастицами. Известный физик Ф. Дайсон писал: "Открытия последних десятилетий в области физики элементарных частиц заставляют нас обратить особое внимание на концепцию нарушения симметрии. Развитие Вселенной с момента ее зарождения выглядит как непрерывная последовательность нарушений симметрии. В момент своего возникновения при грандиозном взрыве Вселенная была симметрична и однородна. По мере остывания в ней нарушается одна симметрия за другой, что создает возможности для существования все большего и большего разнообразия структур. Феномен жизни естественно вписывается в эту картину. Жизнь - это тоже нарушение симметрии. Молекулярная асимметрия открыта Л. Пастером, который первым выделил "правые" и "левые" молекулы винной кислоты: правые молекулы похожи на правый винт, а левые - на левый. Такие молекулы химики называют стереоизомерами.

Молекулы стереоизомеры имеют одинаковый атомный состав, одинаковые размеры, одинаковую структуру - в то же время они различимы, поскольку являются зеркально асимметричными, т.е. объект оказывается нетождественным со своим зеркальным двойником. Поэтому здесь понятия "правый-левый" - условны. В настоящее время хорошо известно, что молекулы органических веществ, составляющие основу живой материи, имеют асимметричный характер, т.е. в состав живого вещества они входят только либо как правые, либо как левые молекулы. Таким образом, каждое вещество может входить в состав живой материи только в том случае, если оно обладает вполне определенным типом симметрии. Например, молекулы всех аминокислот в любом живом организме могут быть только левыми, сахара - только правыми. Это свойство живого вещества и его продуктов жизнедеятельности называют дисимметрией. Оно имеет совершенно фундаментальный характер. Хотя правые и левые молекулы неразличимы по химическим свойствам, живая материя их не только различает, но и делает выбор. Она отбраковывает и не использует молекулы, не обладающие нужной ей структурой. Как это происходит, пока не ясно. Молекулы противоположной симметрии для нее яд.

Если бы живое существо оказалось в условиях, когда вся пища была бы составлена из молекул противоположной симметрии, не отвечающей дисимметрии этого организма, то оно погибло бы от голода. В неживом веществе правых и левых молекул поровну. Дисимметрия - единственное свойство, благодаря которому мы можем отличить вещество биогенного происхождения от неживого вещества. Мы не можем ответить на вопрос, что такое жизнь, но имеем способ отличить живое от неживого. Таким образом, асимметрию можно рассматривать как разграничительную линию между живой и неживой природой. Для неживой материи характерно преобладание симметрии, при переходе от неживой к живой материи уже на микроуровне преобладает асимметрия. В живой природе асимметрию можно увидеть всюду. Очень удачно это подметил в романе "Жизнь и судьба" В. Гроссман: "В большом миллионе русских деревенских изб нет и не может быть двух неразличимо схожих. Все живое неповторимо.

Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте. На принципе симметрии основан метод аналогий, предполагающий отыскание общих свойств в различных объектах. На основе аналогий создаются физические модели различных объектов и явлений. Аналогии между процессами позволяют описывать их общими уравнениями.


СИММЕТРИЯ В МИРЕ РАСТЕНИЙ


Законы симметрии открывают пути к пониманию обобщающих геометрических законов морфологии растений.

Специфика строения растений и животных определяется особенностями среды обитания, к которой они приспосабливаются, особенностями их образа жизни. У любого дерева есть основание и вершина, "верх" и "низ", выполняющие разные функции. Значимость различия верхней и нижней частей, а также направление силы тяжести определяют вертикальную ориентацию поворотной оси "древесного конуса" и плоскостей симметрии. Для листьев характерна зеркальная симметрия. Эта же симметрия встречается и у цветов, однако у них зеркальная симметрия чаще выступает в сочетании с поворотной симметрией. Нередки случаи и переносной симметрии (веточки акации, рябины). Интересно, что в цветочном мире наиболее распространена поворотная симметрия 5-го порядка, которая принципиально невозможна в периодических структурах неживой природы. Этот факт академик Н. Белов объясняет тем, что ось 5-го порядка - своеобразный инструмент борьбы за существование, "страховка против окаменения, кристаллизации, первым шагом которой была бы их поимка решеткой". Действительно, живой организм не имеет кристаллического строения в том смысле, что даже отдельные его органы не обладают пространственной решеткой.

На рис. 11,а совокупность листьев при так называемом мутовчатом листорасположении не нарушает общей радиальной симметрии. Такие кольца из листьев совместно со стеблем подчиняются симметрии L_n nР. Совсем иная картина при очередном листорасположении. Здесь присутствуют винтовые оси². Угол поворота винтовой оси называется «углом расхождения листьев». Вертикальная прямая, Рис.11 соединяющая два листа, расположенные друг над другом на стебле, именуется «ортостихой».

В ботанике принято характеризовать винтовое листорасположение с помощью дроби, числителем которой является число оборотов в листовом цикле, а знаменателем – число листьев в этом цикле. На рис. 11, б показана пятерная винтовая ось 1/5. ботаники утверждают, что дроби, характеризующие винтовые оси, образуют ряд, называемый в математике рядом Фибоначчи:

1/2, 1/3, 2/5, 3/8, 5/13, 8/21,…

Дроби, входящие в ряд Фибоначчи, замечательны тем, что сумма числителей двух соседних дробей дает числитель следующей дроби, так же как и сумма знаменателей пары смежных дробей равна знаменателю дроби, стоящей вслед за ними. Дроби листорасположения некоторых растений: ½ свойственна злакам, березе, винограду; 1/3 – осоке, тюльпану, ольхе; 2/5 – груше, смородине, сливе; 3/8 – капусте, редьке, льну; 5/13 – ели, жасмину.

Винтовые оси на стеблях нагляднее всего демонстрируют существование правых и левых растений.

СИММЕТРИЯ В МИРЕ ЖИВОТНЫХ


Ось симметрии. Ось симметрии - это ось вращения. В этом случае у животных, как правило, отсутствует центр симметрии. Тогда вращение может происходить только вокруг оси. При этом ось чаще всего имеет разнокачественные полюса. Например, у кишечнополостных, гидры или актинии, на одном полюсе расположен рот, на другом - подошва, которой эти неподвижные животные прикреплены к субстрату (рис.12(1,2,3)). Ось симметрии может совпадать морфологически с переднезадней осью тела.

Плоскость симметрии. Плоскость симметрии - это плоскость, проходящая через ось симметрии, совпадающая с ней и рассекающая тело на две зеркальные половины. Эти половины, расположенные друг против друга, называют антимерами (anti – против; mer – часть). Например, у гидры плоскость симметрии должна пройти через ротовое отверстие и через подошву. Антимеры противоположных половин должны иметь равное число щупалец, расположенных вокруг рта гидры. У гидры можно провести несколько плоскостей симметрии, число которых будет кратно числу щупалец. У актиний с очень большим числом щупалец можно провести много плоскостей симметрии. У медузы с четырьмя щупальцами на колоколе число плоскостей симметрии будет ограничено числом, кратным четырём. У гребневиков только две плоскости симметрии - глоточная и щупальцевая (рис.12,5). Наконец, у двусторонне-симметричных организмов только одна плоскость и только две зеркальные антимеры – соответственно правая и левая стороны животного (рис.12(4,6,7)).


Типы симметрии у животных

1-центральная	2-осевая	3-радиальная	4-билатеральная
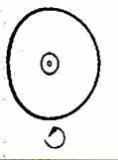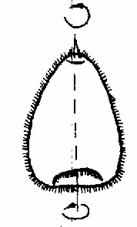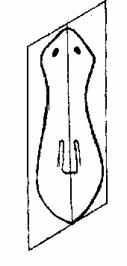5-двулучевая	6-поступательная (метамерия)		7-поступательно-вращательная

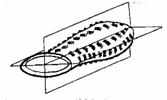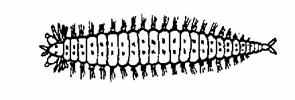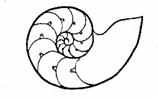Рис. 12

Типы симметрии. Известны всего два основных типа симметрии – вращательная и поступательная. Кроме того, встречается модификация из совмещения этих двух основных типов симметрии – вращательно-поступательная симметрия.

Вращательная симметрия. Любой организм обладает вращательной симметрией. Для вращательной симметрии существенным характерным элементом являются антимеры. Важно знать, при повороте на какой градус контуры тела совпадут с исходным положением. Минимальный градус совпадения контура имеет шар, вращающийся около центра симметрии. Максимальный градус поворота - 360º, когда при повороте на эту величину контуры тела совпадут. Если тело вращается вокруг центра симметрии, то через центр симметрии можно провести множество осей и плоскостей симметрии. Если тело вращается вокруг одной гетерополярной оси, то через эту ось можно провести столько плоскостей, сколько антимер имеет данное тело. В зависимости от этого условия говорят о вращательной симметрии определённого порядка. Например, у шестилучевых кораллов будет вращательная симметрия шестого порядка. У гребневиков две плоскости симметрии, и они имеют симметрию второго порядка. Симметрию гребневиков также называют двулучевой (рис.12,5). Наконец, если организм имеет только одну плоскость симметрии и соответственно две антимеры, то такую симметрию называют двусторонней или билатеральной (рис.12,4). Лучеобразно отходят тонкие иглы. Это помогает простейшим «парить» в толще воды. Шарообразны и другие представители простейших – лучевики (радиолярии) и солнечники с лучевидными отростками-псевдоподиями. «Глядя на них, так и кажется, что эти кружевные сплетения – не часть живых существ, а тончайшие ювелирные изделия, предназначенные украшать наряды морских.

Поступательная симметрия. Для поступательной симметрии характерным элементом являются метамеры (meta – один за другим; mer – часть). В этом случае части тела расположены не зеркально друг против друга, а последовательно друг за другом вдоль главной оси тела.

Метамерия – одна из форм поступательной симметрии. Она особенно ярко выражена у кольчатых червей, длинное тело которых состоит из большого числа почти одинаковых сегментов. Этот случай сегментации называют гомономной (рис.12, 6 ). У членистоногих животных число сегментов может быть относительно небольшим, но каждый сегмент несколько отличается от соседних или формой, или придатками ( грудные сегменты с ногами или крыльями, брюшные сегменты). Такую сегментацию называют гетерономной.

Вращательно-поступательная симметрия. Этот тип симметрии имеет ограниченное распространение в животном мире. Эта симметрия характерна тем, что при повороте на определённый угол часть тела немного проступает вперед и её размеры каждый следующий логарифмически увеличивает на определённую величину. Таким образом, происходит совмещение актов вращения и поступательного движения. Примером могут служить спиральные камерные раковины фораминифер, а также спиральные камерные раковины некоторых головоногих моллюсков (современный наутилус или ископаемые раковины аммонитов, рис. 12, 7). С некоторым условием к этой группе можно отнести также и некамерные спиральные раковины брюхоногих моллюсков.

Тип симметрии непременно входит в характеристику животных наряду с другими морфоэкологическими и физиологическими признаками, благодаря которым мы отличаем одни группы животных от других.

Всех животных делят на одноклеточных и многоклеточных. Наличие форм симметрии прослеживается уже у простейших – одноклеточных (инфузории, амёбы). Многоклеточные подразделяются на Лучистых и Двусторонне-симметричных или Билатеральных.

Значение формы симметрии для животного легко понять, если поставить её в связь с образом жизни, экологическими условиями³. Рассмотрим ещё один тип симметрии, который встречается в животном мире. Это винтовая или спиральная симметрия. Винтовая симметрия есть симметрия относительно комбинации двух преобразований - поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта. Встречаются левые и правые винты. Примерами природных винтов являются: бивень нарвала (небольшого китообразного, обитающего в северных морях) – левый винт; раковина улитки – правый винт; рога памирского барана – энантиоморфы (один рог закручен по левой, а другой по правой спирали). Спиральная симметрия не бывает идеальной, например, раковина у моллюсков сужается или расширяется на конце.

Хотя внешняя спиральная симметрия у многоклеточных животных встречается редко, зато спиральную структуру имеют многие важные молекулы, из которых построены живые организмы – белки, дезоксирибонуклеиновые кислоты – ДНК⁴.

Отметим, наконец, билатеральную симметрию человеческого тела (речь идёт о внешнем облике и строении скелета). Эта симметрия всегда являлась и является основным источником нашего эстетического восхищения хорошо сложенным человеческим телом. Наша собственная зеркальная симметрия очень удобна для нас, она позволяет нам двигаться прямолинейно и с одинаковой лёгкостью поворачиваться вправо и влево. Столь же удобна зеркальная симметрия для птиц, рыб и других активно движущихся существ.


ПРИШЕЛЬЦЫ ИЗ ДРУГИХ МИРОВ


Во многих фантастических произведениях обсуждается возможный облик пришельцев из других миров. Одни писатели считают, что пришельцы могут сильно отличаться по своему облику от людей; другие, напротив, полагают, что разумные существа во всей Вселенной должны походить друг на друга. Не останавливаясь подробно на обсуждении этого вопроса, приведу лишь некоторые соображения, связанные с симметрией. Каким бы не был пришелец, его внешний облик должен характеризоваться билатеральной симметрией: ведь на любой планете живое существо должно иметь выделенное направление движения и на любой планете действует сила тяжести. Пришелец может походить на сказочного дракона, но он не может походить на Тянитолкая. Он не может быть левоглазым или правоухим. Число конечностей слева и справа должно быть одинаковым. Требования симметрии позволяют существенным образом сократить число возможных вариантов облика пришельцев. И хотя мы не можем определенно указать, каким должен быть этот облик, мы в состоянии заключить, каким он не может быть.


ЗНАЧЕНИЕ СИММЕТРИИ В ПОЗНАНИИ ПРИРОДЫ


Идея симметрии часто являлась отправным пунктом в гипотезах и теориях ученых прошлого. Вносимая симметрией упорядоченность проявляется, прежде всего, в ограничении многообразия возможных структур, в сокращении числа возможных вариантов. В качестве важного физического примера можно привести факт существования определяемых симметрией ограничений разнообразия структур молекул и кристаллов. Поясним эту мысль на следующем примере. Допустим, что в некоторой отдаленной галактике обитают высокоразвитые существа, увлекающиеся среди прочих занятий также играми. Мы можем ничего не знать о вкусах этих существ, о строении их тела и особенностях психики. Однако достоверно, что их игральные кости имеют одну из пяти форм - тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Всякая иная форма игральной кости в принципе исключена, поскольку требование равновероятности выпадения при игре любой грани предопределяет использование формы правильного многогранника, а таких форм только пять.

Идея симметрии часто служила ученым путеводной нитью при рассмотрении проблем мироздания. Наблюдая хаотическую россыпь звезд на ночном небе, мы понимаем, что за внешним хаосом скрываются вполне симметричные спиральные структуры галактик, а в них – симметричные структуры планетных систем. Симметрия внешней формы кристалла является следствием ее внутренней симметрии – упорядоченного взаимного расположения в пространстве атомов (молекул). Иначе говоря, симметрия кристалла связана с существованием пространственной решетки из атомов, так называемой кристаллической решетки.

Согласно современной точке зрения, наиболее фундаментальные законы природы носят характер запретов. Они определяют, что может, а что не может происходить в природе. Так, законы сохранения в физике элементарных частиц запрещают любое явление, при котором изменялась бы "сохраняющаяся величина", являющаяся собственной «абсолютной» константой (собственным значением) соответствующего объекта и характеризующая его «вес» в системе других объектов. И эти значения являются абсолютными до тех пор, пока такой объект существует.

Всеобщность симметрии не только в том, что она обнаруживается в разнообразных объектах и явлениях. Всеобщим является сам принцип симметрии, без которого по сути дела нельзя рассмотреть ни одной фундаментальной проблемы, будь то проблема жизни или проблема контактов с внеземными цивилизациями.

Принципы симметрии лежат в основе теории относительности, квантовой механики, физики твердого тела, атомной и ядерной физики, физики элементарных частиц. Эти принципы наиболее ярко выражаются в свойствах инвариантности законов природы. Речь при этом идет не только о физических законах, но и других, например, биологических.

Примером биологического закона сохранения может служить закон наследования. В основе его лежат инвариантность биологических свойств по отношению к переходу от одного поколения к другому. Вполне очевидно, что без законов сохранения (физических, биологических и прочих) наш мир попросту не смог бы существовать.


ЗАКЛЮЧЕНИЕ


С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. В своем реферате я показала, что законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии как в растительном, так и в животном мире, но я считаю, что при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира. Еще одним интересным проявлением симметрии жизненных процессов являются биологические ритмы (биоритмы), циклические колебания биологических процессов и их характеристик (сокращения сердца, дыхание, колебания интенсивности деления клеток, обмена веществ, двигательной активности, численности растений и животных), зачастую связанные с приспособлением организмов к геофизическим циклам. Исследованием биоритмов занимается особая наука - хронобиология.

В моей работе отмечено так же, что помимо симметрии существует понятие асимметрии. Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте.

Работая над рефератом, я поняла слова видного ученого академика В. И. Вернадского, который писал в 1927 году: "Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности". Действительно, всеобщность симметрии поразительна. Симметрия устанавливает внутренние связи между объектами и явлениями, которые внешне никак не связаны.


ЛИТЕРАТУРА:

1. Гильде В. Зеркальный мир. — М.: Мир, 1982.

2. Современный словарь иностранных слов. — М.: Русский язык, 1993.

3. Советский энциклопедический словарь — М.: Советская энциклопедия, 1980.

4. Урманцев Ю.А. Симметрия природы и природа симметрии — М.: Мысль, 1974

5. Шафрановский И.И. Симметрия в природе. –Л.: Недра, 1985.


Приложение 1

	Соты- настоящий конструкторский шедевр. Они состоят из ряда симметричных шестигранных ячеек.
Это самая плотная упаковка, позволяющая наивыгоднейшим образом разместить в ячейке личинку и при максимально возможном объеме наиболее экономно использовать строительный материал-воск.

Приложение 2

Листья на стебле расположены не по прямой, а окружают ветку по спирали. Сумма всех предыдущих шагов спирали, начиная с вершины, равна величине последующего шага А+В=С, В+С=Д и т.д.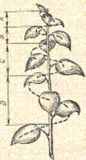
Расположение семянок в головке подсолнуха или листьев в побегах вьющихся растений соответствует логарифмической спирали

Приложение 3


Значение формы симметрии для животного легко понять, если поставить её в связь с образом жизни, экологическими условиями.

Если окружающая животное среда со всех сторон более или менее однородна и животное равномерно соприкасается с нею всеми частями своей поверхности, то форма тела обычно шарообразна , а повторяющиеся части располагаются по радиальным направлениям. Шарообразны многие радиолярии, входящие в состав так называемого планктона, т.е. совокупности организмов, взвешенных в толще воды и неспособных к активному плаванию; шарообразные камеры имеют немногочисленные планктонные представители фораминифер. Лучевики - исключительно морские животные, ведущие планктонный образ жизни. Они «парят» в толще морской воды и идеально к этому приспособлены. Именно для этого «парения» служат иглы их скелета, увеличивающие площадь тела. Лучевики обладают минеральным сложно устроенным внутренним скелетом, который, с одной стороны, защищает тело простейшего, а с другой, способствует «парению» в воде в результате увеличения поверхности путём образования многочисленных игл. От тела во все стороны отходят многочисленные нитевидные отростки-псевдоподии. Солнечники, в общем, походят на лучевиков, но встречаются преимущественно в пресных водах. Шаровидное тело солнечников посылает во все стороны многочисленные тонкие, нитевидные радиально расположенные псевдоподии, тело лишено минерального скелета. Такой тип симметрии называют равноосным, так как он характеризуется наличием многих одинаковых осей симметрии. Равноосная симметрия должна превратиться в одноосную вместе с переходом к сидячему или мало подвижному донному образу жизни; если, например, шарообразное тело приобретает стебелёк для прикрепления к субстрату, то ось симметрии должна будет проходить через стебелёк и сделается, таким образом, единственной. Примерами такой симметрии могут служить сидячие солнечники, жгутиковые, сосущие инфузории, бокалообразные губки. Тот же результат может получиться и при отсутствии стебелька, если животное постоянно обращено одним полюсом к субстрату а другим кверху. При активном плавании одной стороною тела вперёд эта сторона также может дифференцироваться в передний конец тела, и симметрия сложится одноосная (например, овальные или веретенообразные жгутиковые и инфузории). Во всех этих случаях соединяемые осью полюса тела находятся в неодинаковых экологических условиях и функционируют по-разному. Присутствие одной только оси симметрии не столь ещё характерно для данного типа (так как и в других типах симметрии, кроме равноосного, ось также одна), но весьма характерно, то что через эту ось можно провести много плоскостей симметрии, из которых каждая разделит тело на две одинаковые половины; поэтому данный тип симметрии называют полисимметрическим. Равноосный и полисимметрический типы встречаются преимущественно среди низкоорганизованных и малодифференцированных животных. Сидячие одноосные полисимметрические животные, усложняя свою организацию и приобретая различные органы, приобретают лучевую или радиальную симметрию тела, выражающуюся в том, что органы располагаются в радиальных (лучистых) направлениях вокруг одной главной продольной оси. От числа повторяющихся органов зависит порядок радиальной симметрии. Так, если вокруг продольной оси располагается 4 одинаковых органа, то радиальная симметрия в этом случае называется четырёхлучевой. Если таких органов шесть, то и порядок симметрии будет шестилучевым, и т.д. Так как количество таких органов ограничено (часто 2,4,8 или кратное от 6), то и плоскостей симметрии можно провести всегда несколько, соответствующее количеству этих органов. Плоскости делят тело животного на одинаковые участки с повторяющимися органами. В этом заключается отличие радиальной симметрии от полисимметрического типа. Радиальная симметрия характерна для малоподвижных и прикрепленных форм (двух-, четырёх-, восьми – и шести -лучевые кораллы, гидра, медузы, актинии). Экологическое значение лучевой симметрии легко понятно: сидячее животное окружено со всех боковых сторон одинаковой средою и должно вступать во взаимоотношения с этой средой при помощи одинаковых, повторяющихся в радиальных направлениях органов. Именно сидячий образ жизни способствует развитию лучистой симметрии.

Переход от лучевой или радиальной к двусторонней или билатеральной симметрии связан с переходом от сидячего образа жизни к активному передвижению в среде (от сидячести к ползанию по субстрату постоянно одним и тем же концом тела вперёд). Для сидячих форм отношения со средой равноценны во всех направлениях: радиальная симметрия точно соответствует такому образу жизни. У активно перемещающихся животных передний конец тела становится биологически не равноценным остальной части туловища, происходит формирование головы, становятся различимы правая и левая сторона тела. Благодаря этому теряется радиальная симметрия , и через тело животного можно провести лишь одну плоскость симметрии, делящую тело на правую и левую стороны. Двусторонняя симметрия означает, что одна сторона тела животного представляет собой зеркальное отражение другой стороны. Такой тип организации характерен для большинства беспозвоночных, в особенности для кольчатых червей и для членистоногих – ракообразных, паукообразных, насекомых, бабочек; для позвоночных – рыб, птиц, млекопитающих. Впервые двусторонняя симметрия появляется у плоских червей, у которых передний и задний концы тела различаются между собой. У кольчатых червей и членистоногих наблюдается ещё и метамерия – одна из форм поступательной симметрии, когда части тела располагаются последовательно друг за другом вдоль главной оси тела. Особенно ярко она выражена у кольчатых червей (дождевой червь). Кольчатые черви обязаны своим названием тому, что их тело состоит из ряда колец или сегментов (члеников). Сегментированы как внутренние органы, так и стенки тела. Так что животное состоит примерно из сотни более или менее сходных единиц – метамеров, каждая из которых содержит по одному или по паре органов каждой системы. Членики отделены друг от друга поперечными перегородками. У дождевого червя почти все членики сходны между собой. К кольчатым червям относятся полихеты – морские формы, которые свободно плавают в воде, роются в песке. На каждом сегменте их тела имеется пара боковых выступов, несущих по плотному пучку щетинок. Членистоногие получили своё название за характерные для них членистые парные придатки (как органы плавания, ходильные конечности, ротовые части). Для всех них характерно сегментированное тело. Каждое членистоногое имеет строго определённое число сегментов, которое остаётся неизменным в течение всей жизни. Зеркальная симметрия хорошо видна у бабочки; симметрия левого и правого проявляется здесь с почти математической строгостью. Можно сказать, что каждое животное, насекомое, рыба, птица состоит из двух энантиоморфов – правой и левой половин. Так, энантиоморфами являются правое и левое ухо, правый и левый глаз, правый и левый рог и т.д.

Упрощение условий жизни может привести к нарушению двусторонней симметрии, и животные из двусторонне-симметричных становятся радиально-симметричными. Это относится к иглокожим (морские звёзды, морские ежи, морские лилии, офиуры). Все морские животные имеют радиальную симметрию, при которой части тела отходят по радиусам от центральной оси, подобно спицам колеса. Степень активности животных коррелирует с их типом симметрии. Радиально-симметричные иглокожие обычно мало подвижны, перемещаются медленно или же прикреплены к морскому дну. Тело морской звезды состоит из центрального диска и 5-20 или большего числа радиально отходящих от него лучей. На математическом языке эту симметрию называют поворотной симметрией. У морской звезды и панциря морского ежа – поворотная симметрия 5-го порядка (рис.1). Это симметрия, при которой объект совмещается сам с собой при повороте вокруг поворотной оси 5 раз. Вся кожа морских звёзд как бы инкрустирована мелкими пластинками из углекислого кальция, от некоторых пластинок отходят иглы, часть которых подвижна. У офиур лучи длинные и тонкие. Морские ежи похожи на живые подушечки для булавок; шаровидное тело их несёт длинные и подвижные иголки. У этих животных известковые пластинки кожи Рис. 1 слились и образовали сферическую раковину панцирь. В центре нижней поверхности имеется рот. Амбулакральные ножки (воднососудистая система) собраны в 5 полос на поверхности раковины.


Приложение 4


Подлинным царством природных винтов является мир «живых молекул» - молекул, играющих принципиально важную роль в жизненных процессах. К таким молекулам относятся прежде всего молекулы белков. В человеческом теле насчитывают до 10 типов белков. Все части тела, включая кости, кровь, мышцы, сухожилия, волосы, содержат белки. Молекула белка представляет собой цепочку, составленную из отдельных блоков, и закрученную по правой спирали. Её называют альфа-спиралью. За открытие альфа-спирали американский учёный Лайнус Полинг получил Нобелевскую премию, самую высшую награду в научном мире. Молекулы волокон сухожилий представляют собой тройные альфа-спирали. Скрученные многократно друг с другом альфа-спирали образуют молекулярные винты, которые обнаруживаются в волосах, рогах, копытах.

Исключительно важную роль в мире живой природы играют молекулы дезоксирибонуклеиновой кислоты – ДНК, являющейся носителем наследственной информации в живом организме. Молекула ДНК имеет структуру двойной правой спирали, открытой американскими учёными Уотсоном и Криком. За её открытие они были удостоены Нобелевской премии. Двойная спираль молекулы ДНК есть главный природный винт.