Реферат по геометрии Работу
| Вид материала | Реферат |
- Реферат по геометрии «Стереометрия», 271.23kb.
- Урок общественная лекция по теме : «Развитие геометрии как науки экскурс в историю», 48.39kb.
- Программа курса повышения квалификации учителей математики, 15.17kb.
- Примерные билеты по геометрии для 9 класса, 112.5kb.
- Тема: Геометрия на службе архитектуры, 341.17kb.
- Формирование познавательного интереса учащихся на уроках геометрии в старших классах, 117.5kb.
- Изучение геометрии в начальной школе, 48.52kb.
- Урок «Путешествие в музей геометрии» Тип, 151.51kb.
- Учебного курса по геометрии для 9-го класса, 1015.27kb.
- Список рекомендованої літератури Александров А. Д. Основания геометрии. М: Наука,1987, 19.83kb.
Реферат по геометрии

Работу выполнила
ученица
7»А» класса
Рекк Юлия.
Проверила учитель
математики
Попова О. В.
Определение угла
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – вершиной угла.

∟ВОС – угол с вершиной в точке О и со сторонами ОВ и ОС.
Определение развёрнутого угла
Угол называется развёрнутым, если обе его стороны kежат на одной прямой. Можно сказать, что каждая сторона развёрнутого угла является продолжением другой стороны.
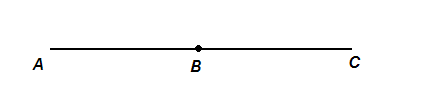
∟ АВС – развёрнутый угол с вершиной в точке В и со сторонами ВА и ВС.
Понятия внутренней и внешней областей угла
Л
 юбой угол разделяет плоскость на 2 части. Если угол неразвёрнутый, то одна из частей называется внутренней, а другая внешней областью этого угла.
юбой угол разделяет плоскость на 2 части. Если угол неразвёрнутый, то одна из частей называется внутренней, а другая внешней областью этого угла.Если угол развёрнутый, то любую из двух частей, на которые она разделяет плоскость можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области, так же называют углом.
Если луч исходит из вершины неразвёрнутого угла и проходит внутри угла, то он делит этот угол на два угла.

∟ СОВ разделен лучом ОА на два угла ∟СОА и ∟ВОА.

Сравнение углов
Чтобы установить, равны углы или нет, нужно наложить один из них на другой так, чтобы сторона одного угла совместилась со стороной другого, а две другие оказались по одну сторону от совместившихся сторон.
Если две другие стороны совместятся, то углы полностью совместятся и, значит, они равны. Если же эти стороны не совместятся, то меньшим считается тот угол, который составляет часть другого.
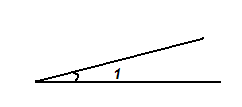


На рисунке угол 1 составляет часть угла 2, ∟1<∟2.
Неразвёрнутый угол составляет часть развёрнутого угла, поэтому развёрнутый угол больше неразвёрнутого угла. Любые два развёрнутых угла, очевидно, равны.

Неразвёрнутый угол АОВ составляет часть развёрнутого угла СОВ.
Определение биссектрисы угла
Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
∟
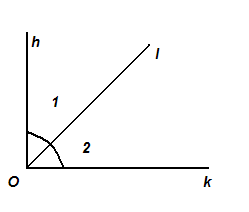 1=∟2
1=∟2Луч I – биссектриса угла hk.
∟
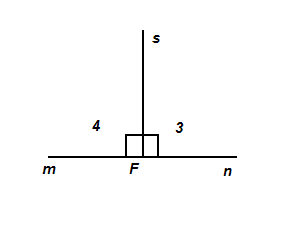 4=∟3.
4=∟3. Луч s является биссектрисой угла mn.
Измерение углов
Измерение углов аналогично измерению отрезков – оно основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус – угол, равный 1\180 части развёрнутого угла. Эта единица измерения углов была введена много веков назад, ещё до нашей эры. Определённые части градуса носят специальные названия: 1\60 часть градуса называется минутой, 1\60 часть минуты называется секундой. Минуты обозначаются знаком «’», а секунды – знаком «”». Например, угол в 60 градусов, 32 минуты и 17 секунд обозначается так: 60°32’17”.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла. Для измерения углов используется транспортир.
Если два угла равны, то градус и его части укладываются в этих углах одинаковое количество раз, т.е. равные углы имеют равные градусные меры.

Если же один угол меньше другого, то в нём градус (или его часть) укладывается меньшее число раз, чем в другом угле, т.е. меньший угол имеет меньшую градусную меру.
∟
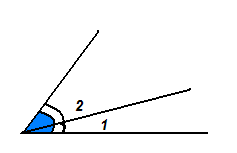 1<∟2.
1<∟2.Так как градус составляет 1\180 часть развёрнутого угла, то он укладывается в развёрнутом угле ровно 180 раз, т.е. развёрнутый угол равен 180°.
Неразвёрнутый угол меньше развернутого угла, поэтому неразвёрнутый угол меньше 180°.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
∟
 АВО+∟СВО=∟АВС
АВО+∟СВО=∟АВСВиды углов
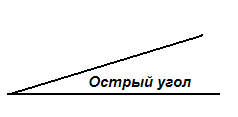
Угол называется прямым, если он равен 90°, острым, если он меньше прямого угла, т.е. меньше 90°, тупым, если он больше 90°, но меньше 180°, т.е. больше прямого, но меньше развёрнутого угла.


Измерение углов на местности
Измерение углов на местности производится с помощью специальных приборов. Простейшим из них является астролябия. Она состоит из двух частей: диска, разделённого на градус, и вращающийся вокруг центра диска линейки (алидады). На концах алидады находятся два узких окошечка, которые используются для установки её в определённом направлении. Для того чтобы измерить угол АОВ на местности, треножник с астролябией ставят так, чтобы отвес, подвешенный к центру диска, находился точно над точкой О. Затем устанавливают алидаду вдоль одной из сторон ОА или ОВ, и отмечают деление, против которого находится указатель алидады. Разность отсчёты и даёт градусную меру угла АОВ.
Измерения углов проводятся в различных исследованиях, например в астрономии при определении положения небесных тел. Очень важно с достаточной точностью измерять углы при определении положения искусственных спутников на орбитах. Для этой цели конструируют специальные приборы. Данные, полученные помощью этих приборов, обрабатываются на компьютерах.
Понятие смежных углов
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.

Угол FSV и угол DSV – смежные, так как лучи SF и SD образуют развёрнутый угол. ∟FSV+∟DSV=∟FSD=180°
Сумма смежных углов равна 180°.
Понятие вертикальных углов
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
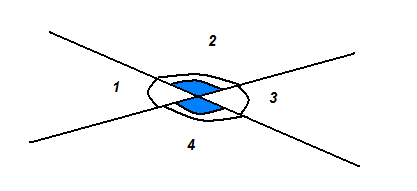
∟1 и ∟3 – вертикальные, а так же ∟2 и ∟4 тоже являются вертикальными. ∟2 является смежным с ∟1, а так же ∟2 является с ∟3. По свойству смежных углов : ∟1+∟2=180° и ∟2+∟3=180°.
∟1+∟2=180°
 ∟2=180° -∟1
∟2=180° -∟1  180° -∟1=180°-∟3
180° -∟1=180°-∟3  ∟1=∟3
∟1=∟3∟2+∟3=180°
 ∟2=180°-∟3
∟2=180°-∟3Вертикальные углы равны.
Работа выполнена по материалам учебника геометрии, 7-9 класс,
Л.С. Атанасян и др.
