Курс лекций 1999-2000 гг

Вид материала

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 20

Лекция 3

        Рассмотрим теперь элементарные взаимодействия атомов, не связанных ковалентно друг с другом.

       Но сначала вспомним, что основная причина образования химических связей — делокализация электронов, их "переход" с атома на атом и обратно — или, как говорят, пребывание электронов на совместной, "обобществленной" орбите, охватывающей два атома. При этом, согласно запрету Паули, в одном месте, на одной орбите может находиться не более двух электронов, — причем тогда их "спины" (т.е. моменты вращения электронов) должны быть противоположно направлены (или, как говорят, "спарены"). Спаривание двух электронов на одной совместной орбите (когда один электрон пришел от одного атома, а второй — от другого) ведет к прочной ковалентной связи.
       Если же у сближающихся атомов и так на каждой орбите — по два спаренных электрона, то эти атомы не могут образовать ковалентную связь. Иначе на каждой обобществленной орбите электронов было бы слишком много — четыре. А, согласно запрету Паули, одна орбита может вынести не более двух! Значит, уже насыщенные, заполненные электронной парой орбиты не могут далее обобществляться. И потому несущие такие "насыщенные" орбиты атомы отталкиваются на малых расстояниях, когда их электронные облака начинают перекрываться. Такие атомы непроницаемы друг для друга при обычных (не космических) температурах.
       То же происходит, если в сближающихся молекулах все их валентности уже насыщены: они отталкиваются, когда их атомы сближаются до 2-3

.

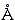Однако на больших расстояниях (когда нет перекрывания электронных облаков) все атомы и молекулы притягиваются — если только у них нет электрического заряда, о чем мы поговорим позже. Притяжение это имеет чисто квантовую основу. Оно связано с коррелированными, т.е. согласованными колебаниями электронов в обоих атомах. Дело в том, что энергия пары атомов, где электроны смещены (поляризованы) одинаковым образом, — чуть меньше, чем энергия пары неполяризованных атомов. Это ясно из следующей схемы (здесь два атома, "1" и "2", и у каждого — электрон "" и ядро "+")

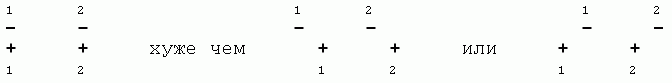
Глядя на схему, нужно помнить, что электрическая энергия растет с уменьшением расстояния r как 1/r. В результате смещения электронов взаимодействия электрон-электрон и ядро-ядро не меняются, но (рассмотрим самый правый рисунок) усиливается притяжение электрона 1 к ядру 2 — причем оно усиливается больше, чем ослабевает притяжение электрона 2 к ядру 1. Поэтому согласованное колебание электронов (а это и есть квантовый эффект) понижает энергию системы. При отдалении атомов их взаимодействие ослабляется. В результате энергия взаимодействия спадает с расстоянием r между ядрами атомов — можно показать, что она спадает пропорционально (1/r)⁶.

Общая энергия взаимодействия атомов — она еще называется энергией Вандерваальсова взаимодействия — охватывается рисунком 3-1 и приближенно описывается формой Леннард-Джонса:

U_LD(r) = E₀[(r₀/r)¹² - (r₀/r)⁶]

(3.1)

Здесь r₀ — как легко проверить, взяв производную U_LD по расстоянию r — есть то расстояние, на котором энергия U_LD проходит через минимум, а -E₀ — глубина этого минимума. Последний член формулы (3.1) — тот, что падает с расстоянием, как (const/расстояние)_в_шестой_степени — соответствует притяжению (знак "минус" перед ним указывет, что соответствующая энергия падает при сближении); а тот, где значится двенадцатая степень, соответствует отталкиванию (этот член положителен, т.е. соответствующая ему энергия растет при сближении).

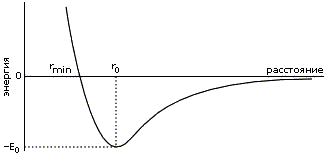
       Рис.3-1. Характерный вид потенциала Вандерваальсова взаимодействия.

       Формула 3.1 точно описывает только притяжение на больших (когда r << r₀) расстояниях. Отталкивание на малых расстояниях она описывает только качественно, как "очень сильное отталкивание, превосходящее любое притяжение, когда r стремится к нулю". То, что формула (3.1) — приближенная, видно хотя бы по тому, что она подразумевает округлость атомов (т.к. ею описываемое взаимодействие не зависит от направления), — а электронное облако у атома, вообще говоря, не круглое, — вспомните хотя бы о торчащих p-электронах. Вообще, правильно и совсем корректно взаимодействие атомов описывает только квантовая механика — но точно рассчитать она может только очень простые системы, вроде атома Не, иона Н₂⁺ или молекулы Н₂. Для всего остального приходится брать приближенные, "полуэмпирические" формулы — вроде (3.1) — где вид формулы берется из качественных физических соображений, а параметры (у нас — E₀ и r₀) — подбираются из опыта. Некоторые основные данные сведены в Таблицу 3/1.

       Таблица 3/1. Характерные параметры потенциалов Вандерваальсовых взаимодействий

Взаимодействие	E₀, ккал/моль	r₀,	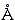r_min,	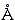Вандерваальсов радиус атома,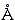
H . . . . H	0.12	2.4	2.0	H:	1.0
H . . . . C	0.11	2.9	2.4
C . . . . C	0.12	3.4	3.0	C:	1.5
O . . . . O	0.23	3.0	2.7	O:	1.35
N . . . . N	0.20	3.1	2.7	N:	1.35
CH₂ . . . CH₂	0.5	4.0	3.0	CH₂:	1.5

Примечания. Величины E₀, r₀ для межатомных взаимодействий взяты из R.A.Scott, H.A.Scheraga, J. Chem. Phys. (1965) 45:2091, а величины r_min — из G.N.Ramachandran, V.Sasisekharan, Adv. Prot. Chem. (1968) 23:283. Исходя из этих величин, оценены параметры взаимодействия CH₂...CH₂. Взаимодействие CH₂...CH₂ зависит от взаимной ориентации этих групп; поэтому приведенные в таблице числа — приблизительные; их, однако, часто приходится использовать, так как рентген "не видит" водородных атомов в белках.

       Обратите также внимание на то, что в таблице дано не только оптимальное расстояние r₀, но и r_min — минимальное расстояние, на котором соответствующие атомы встречаются в кристаллах. r_min примерно соответствует той точке Рис.3-1, где энергия при сильном сближении проходит через 0.
       Расстояния (r₀ , r_min) и энергии (E₀) в основном берутся из кристаллов — из их структур (расстояния) и теплот сублимации (энергии). Но кристаллы обычно состоят не из атомов, а из молекул. Например: СН₄, С₂Н₆,... Так что при расчете энергии всегда возникают вопросы типа: каков вклад С...С, каков — Н...Н, каков — С...Н взаимодействий? Разные авторы решают его по-разному — поэтому потенциалы у них порой заметно расходятся. Надо помнить, что нельзя самодеятельно брать одни параметры (например, энергию С...С взаимодействия) у одного автора, а другие — у другого: тут действует принцип "все или ничего", иначе будут ошибки.
       Приведенные в таблице величины помогают понять, почему trans-конформация С'

N связи допустима, а ее cis-конформация — нет (для всех аминокислотных остатков, кроме пролина, о чем мы уже говорили): в trans-конформации С'

N связи расстояние между С^атомами равно 3.8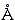

, а в cis- (когда эти атомы наиболее сближены) — всего 2.8

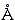, что меньше минимально допустимого расстояния r_MIN, равного 3.0

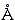для пары С...С.

Из-за жесткости trans-формы С'

N связи и из-за того, что в ней C^-атомы соседних по цепи аминокислот довольно далеко отстоят друг от друга, соседние по цепи остатки могут менять свою конформацию почти независимо друг от друга. Но внутри остатка вращения по углам  и  взаимосвязаны. Изображенные в координатах (, ) "разрешенные" и "запрещенные" конформации остатка называются картами Рамачандрана (или, более корректно, — картами Рамачандрана-Сасисекхарана).
Прежде чем рисовать их, — посмотрим, какие конформации разрешены (и какие — нет) при вращении по углу  (вокруг N-C^ связи) и по углу  (вокруг C^-С' связи) в отдельности.
Мы уже знаем, что вращение вокруг этих связей (соединяющих sp³-гибридизованный С^-атом с sp²-гибридизованными N или C') практически свободно. Однако в cis-конформациях (при =0^o или =0^o) вращающиеся вокруг таких связей атомы (C'_i-1 и C'_i при вращении по углу  вокруг N-C^ связи, и атомы N_i и N_i+1 при вращении по углу  вокруг C^-C' связи, см. Рис.3-2; i-1, i, i+1 - номера последовательных остатков в цепи) сближаются особенно сильно, и здесь возможен запрет конформации из-за отталкивания этих атомов — как говорят, стерический запрет.

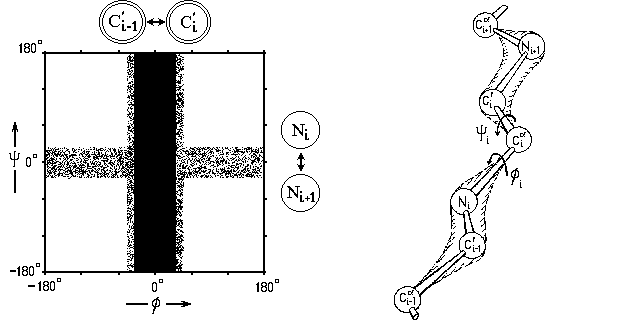
Рис.3-2. Так выглядела бы карта запрещенных

, напряженных

и полностью разрешенных

конформаций при вращении по углам  во фрагменте C^C'N - C^ - C'NC^ , если бы ко всем этим атомам не было бы прикреплено больше никаких других (см. справа).

Следующая схема показывает, что минимальное расстояние между атомами C'_i-1 и C'_i (при вращении по ) и между атомами N_i и N_i+1 (при вращении по ) — одно и то же, 2.9

: это чуть меньше, чем r_MIN=3.0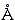

для C...C взаимодействия (так что здесь cis конформация запрещена), — и чуть больше, чем r_MIN=2.7

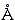(хоть и меньше, чем r₀=3.1

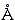) для N...N взаимодействия (так что здесь cis конформация не запрещена, но напряжена).

Если бы дело ограничивалось только этими С и N атомами, карта запрещенных

, напряженных

и разрешенных

конформаций выглядела бы так, как на Рис.3-2. При этом вращения по углам  и  не были бы взаимосвязаны.
Однако при атоме C' есть О и C^ атомы, а при N — есть H и C' атомы (причем в воде к Н-атому жестко приторочена водородной связью молекула Н₂О, см. ниже). Так что в результате карта Рамачандрана — карта запрещенных

и разрешенных

конформаций самого маленького аминокислотного остатка, глицина (боковой радикал -Н) — выглядит, на как Рис.3-3.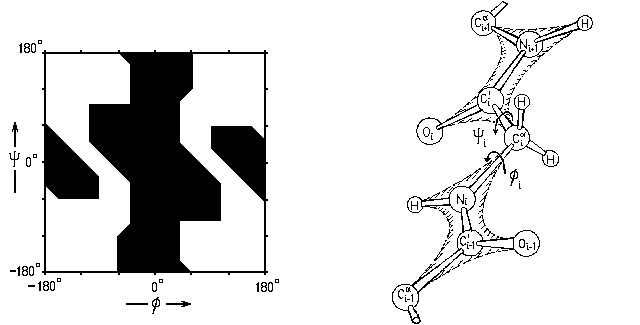

Рис.3-3. Карта запрещенных

и разрешенных

конформаций глицина (Gly) при вращении по углам  в белковой цепи.

У глицина нет массивного бокового радикала. У всех остальных аминокислотных остатков он есть, и столкновение этого радикала (точнее, его ближайшего к главной цепи С^-атома) с C'-атомом вырубает запрещенную область по углу , а с N-атомом — запрещенную область по углу  (Рис.3-4).

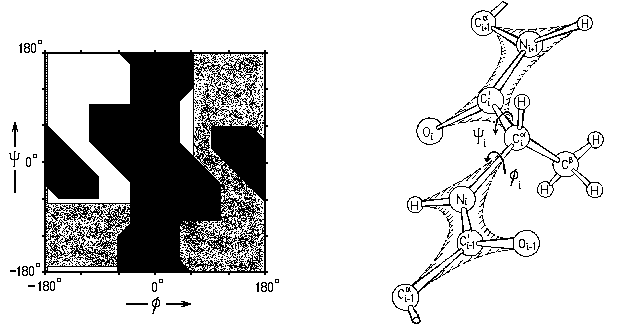
Рис.3-4. Карта разрешенных

конформаций аланина (Ala) при вращении по углам в белковой цепи;

— области, разрешенные лишь для глицина;

— области, запрещенные для всех остатков взаимодействиями в главной цепи.

Нарисованная на Рис.3-4 карта относится к аланину, боковой радикал которого мал: С^Н₃-группа. У всех остальных аминокислотных остатков радикал крупнее — с одним или двумя тяжелыми  атомами при С^-атоме. Однако от главной цепи эти "новые"  (и еще более далекие  и т.д. атомы) находятся далеко, и потому мало влияют на карту Рамачандрана. Точнее: в небольшой (оставленной белой на Рис.3-5) области столкновений этих -атомов с главной цепью нет вообще, а в других разрешенных для аланина конформациях они могут быть — при некоторых конформациях радикала и потому здесь разрешены не все конформации радикала; эти области я слегка заштриховал

на Рис.3-5.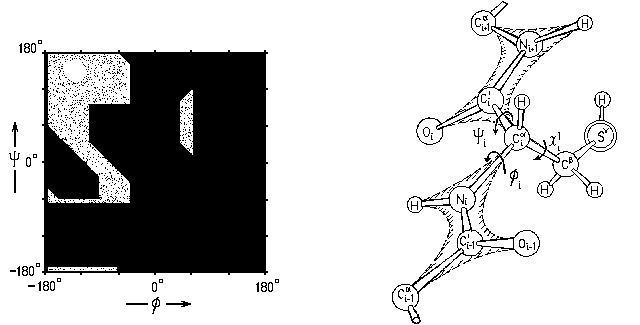

Рис.3-5. Карта запрещенных

и разрешенных

конформаций более крупных остатков при вращении по углам  в белковой цепи. В области

разрешены все конформации боковой группы по углу ₁, в области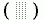

часть углов ₁ запрещена.

Столкновения  атомов с главной цепью особенно существенны для валина, изолейцина и треонина, имеющих по два крупных  атома.
В заключение рассмотрим карту Рамачандрана для иминокислоты пролина. У него угол  практически фиксирован при —70^о кольцом, образуемым боковой группой Pro при участии N-атома его главной цепи, а вращение по углу  — такое же, как у аланина. Так что его разрешенные конформации выглядят, как белая область на карте, Рис.3-6.

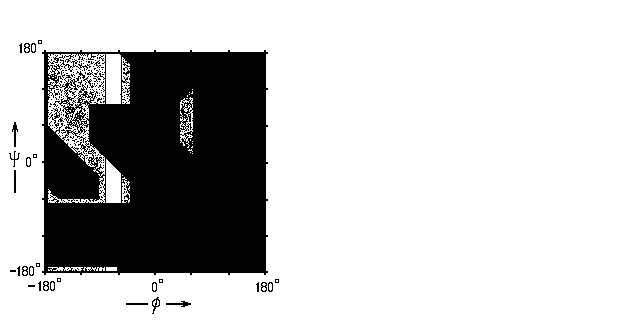
Рис.3-6. Карта разрешенных

для пролина конформаций на фоне конформаций, разрешенных для аланина

;

— конформации, запрещенные для них обоих.

Кольцо пролина сужает и область разрешенных конформаций остатка, лежащего перед ним в цепи (Рис.3-7).

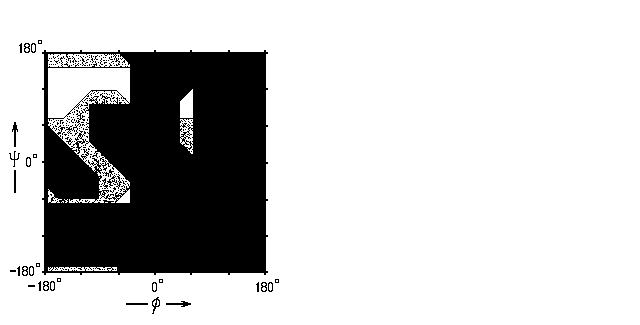
Рис.3-7. Область разрешенных

конформаций остатка аланина, лежащего перед пролином в белковой цепи. Область

была бы разрешена, если бы не пролин.

Наконец — посмотрим, как все эти теоретические выкладки (суммируемые Рис.3-3 для Gly и Рис.3-4 для прочих аминокислот) согласуются с наблюдаемыми (рентгеном) в белках конформациями аминокислотных остатков (на Рис.3-8 они отмечены точками, для Gly и для прочих аминокислотных остатков в отдельности). Как видим, согласие это весьма хорошее.

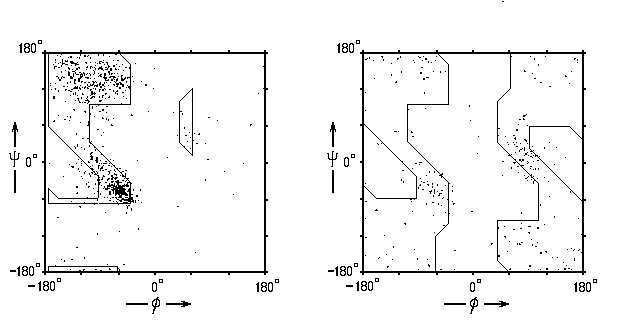
       Рис.3-8. Наблюдаемые в белках конформации аминокислотных остатков (точки) для глицина (справа) и для всех остальных остатков (слева). Контур очерчивает стерически разрешенные области. Картинка взята из [5] и адаптирована.

       Мы видим, что подавляющее большинство экспериментальных точек попадает в "стерически разрешенные" области. Однако некоторые точки лежат в "стерически запрещенных" областях. Последнее не удивительно, так как мы назвали "стерически запрещенными" те области, где энергия просто высока — не бесконечно велика, что, конечно, привело бы к полному запрету, — а скажем, на пару ккал/моль больше, чем в конформации с минимальной энергией. То есть белку надо затратить энергию, чтобы загнать аминокислотный остаток в такую область, но он вполне может это сделать. Может сделать, но делает редко.
       По ходу лекций мы убедимся, что это — общее правило: напряженные, высокоэнергетичные элеметы в белках встречаются редко — но все же встречаются. Что не удивительно: раз белок стабилен, он должен состоять, — в массе, но не обязательно целиком, — из стабильных деталей.

Blog

Курс лекций 1999-2000 гг

Лекция 3