А. Я. Хинчин писал: Перед учителем математики стоит нелегкая задача
| Вид материала | Задача |
СодержаниеЗаполняем таблицу |
- «Использование икт на уроках математики», 93.57kb.
- А. В. Буглак Опыт медиареконструкции Архангелогородской Новодвинской крепости: создание, 83.21kb.
- Внастоящее время в современной школе достаточно остро стоит задача повышения эффективности, 121.01kb.
- Перевод: Э. Кулиев, 11575.57kb.
- В муниципальных образованиях, 890.32kb.
- Штреккер Анна Эдуардовна, воспитатель мкдоу «Ручеек» г. Бородино Внастоящее время актуальными, 105.84kb.
- Программа факультативного курса «Народоведение», 213.44kb.
- Пять проблем современной молодёжи россии, 61.32kb.
- Пять проблем современной молодежи Казахстана, 603.65kb.
- Мы живём в эпоху взаимопроникновения культурных ценностей. Перед школой стоит задача, 18.86kb.
Межпредметные связи математики и литературы.
Известный советский математик и педагог А.Я.Хинчин писал: «Перед учителем математики стоит нелегкая задача - преодолеть в сознании учеников со стихийной неизбежностью возникающее представление о «сухости», формальном характере, оторванности от жизни и практики его науки».
Одним из способов решения этой проблемы является использование нестандартных и занимательных задач на уроках математики, поиск связей с другими предметами. Такие задачи должны быть связаны с изучаемым материалом. Их условия целесообразно формулировать коротко, просто и сопровождать красочными иллюстрациями, которые вызывают положительные эмоции у учащихся и экономят время на уяснение данных. Благодаря своей оригинальности, задачи способны активизировать учащихся, заставить их работать весь урок (учитывая данные психологов о том, что ученик в состоянии полноценно работать на уроке 35 минут).
Осуществление межпредметных связей является одним из основных принципов технологического подхода в обучении, при котором должны быть выявлены все условия, необходимые в достижении целей. При использовании технологического подхода в разработке отдельного курса, координируя изучение учебного материала с другими предметами, необходимо фиксировать межпредметные связи различного типа по отношению к той или иной цели курса. Задачами реализации межпредметных связей при конструировании содержания учебного предмета являются: выявление общих элементов содержания различных учебных предметов для определения «возможных» (сопутствующих) межпредметных связей; выявление элементов содержания, требующих предварительного изучения в другом предмете, для определения «необходимых» (предшествующих и перспективных) межпредметных связей.
Имея в качестве основного объекта изучения математику, предмет математика использует элементы знаний из других предметов для демонстрации собственных законов, теорий и т.п. Элементы содержания других учебных предметов, характеризующие какую-либо действительность с других позиций, могут стать основой для параллельного рассмотрения действительности, для создания интегрированных курсов. Это позволит существенно повысить уровень понимания, глубину изучения элементов содержания как математики, так и физики, биологии и других предметов.
Относительно какого-либо предмета «необходимые» межпредметные связи разделяют на межпредметные связи «как цель» (предшествующие) и межпредметные связи «как результат» (перспективные). Более важную роль при этом для конкретного предмета играют целевые межпредметные связи, так как без их реализации изучение рассматриваемого учебного материала считается невозможным. Реализация межпредметных связей «как результат» необходима для обеспечения другого предмета, но при этом и они способствуют более глубокому изучению рассматриваемого предмета.
Межпредметные связи «как цель» в курсе математики могут быть реализованы с информатикой, физикой, лингвистикой (русским языком), логикой, философией, историей, литературой, биологией, анатомией.
Еще с детства учащиеся знают о связи математики с литературой. Это сказки о 3 Поросятах, Белоснежка и 7 Гномов, 12 Месяцев, 3 Толстяка и др.
В своей практике межпредметную связь с литературой, я практикую при изучении темы «Минимальные и максимальные значения функции на отрезке».
Это заключается в следующем.
Ребятам задается вопрос: «Кто читал рассказ Толстого А.Н. «Много ли человеку земли надо?» Кто-то из ребят или преподаватель вкратце рассказывает краткое содержание произведения: «Жил трудолюбивый крестьянин Пахом, который отправился в чужие края, чтобы купить плодородные земли для возделывания и выращивания урожая. Он со старейшинами села договорился о покупке земли. Но было поставлено одно условие: «Надо с утра обойти столько земли, сколько сможешь, и вернуться до захода солнца». Пахом прошел 40 км.''
На доске изображается трапеция:
40км
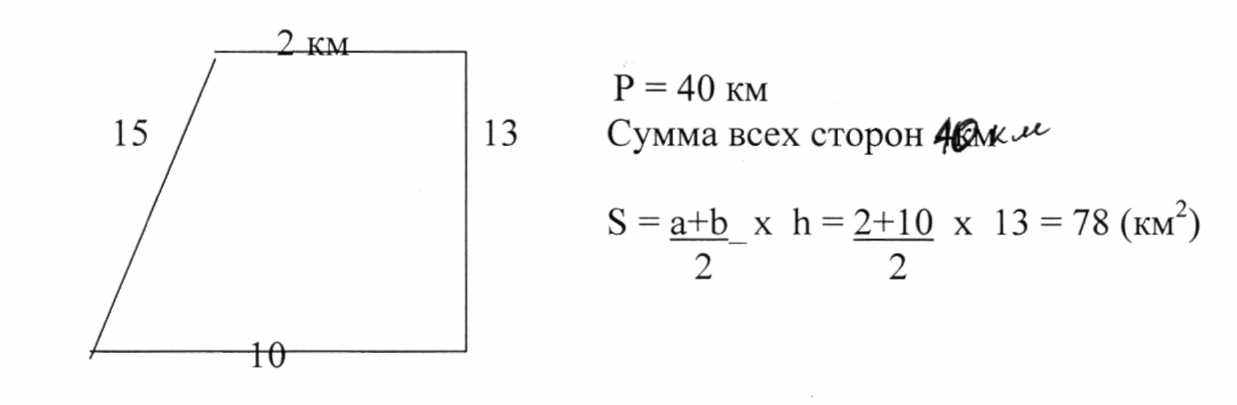
Наиболыпую ли площадь при заданном периметре прошел Пахом?
Заполняем таблицу:
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| В | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | |
| S | | | | | | | | | | | |
Выясняем, что наибольшая площадь 100 км со сторонами 10 х 10. Переводим ситуацию с Пахомом на математический язык: х - одна сторона у - вторая сторона
2х + 2у = 40 х + у = 20 у = 20-х
S = x(20-x)=20x-x2
Найдем производную: S'(x)
(20х - х2)' = 20 - 2х
Приравняем производную к нулю:
20 - 2х = 0
х= 10
у = 10.
Ответ: квадрат со сторонами 10 км.
Делаем вывод: Пахому можно было пройти участок, напоминающий форму квадрата, со сторонами 9 или 10 км. Далее записывается алгоритм нахождения min и max значения функции на отрезке, решаются примеры. Ребят интересует успел ли купить Пахом землю? Кроме примеров на дом задано прочитать это произведение и на следующий урок рассказать окончание рассказа.
Реализация межпредметных связей заключается в выявлении дидактических целей по другим предметам на этапе определения вспомогательных целей.
Многообразие межпредметных связей подчеркивает их знание в формировании у учащихся современной картины мира.
