Современные знания — в жизнь
| Вид материала | Документы |
СодержаниеСравнительный анализ прикладных пакетов геостатистических программ Научный руководитель Цеховая Т.В., кандидат физико-математических наук, доцент Теория одноресурсной фирмы |
- Регламент: Доклад на пленарном, 80.61kb.
- Формы организации урочной деятельности в профильных классах, 429.15kb.
- Надежда Николаевна Лыкова, 82.16kb.
- План урока литературы по теме: «Поговорим о Пушкине в шутку и всерьез», 217.65kb.
- Урок 6/33 Тема : Современные достижения и роль астрономии. Жизнь и разум во Вселенной, 278.29kb.
- Для избравшего путь воина борьба это жизнь, а жизнь это борьба и руководство для поиска, 3365.98kb.
- Образовательные программы Школы ориентированы на включение учеников в современные сферы, 63.17kb.
- Курс лекций «Гуманитарное знание: современные подходы», 64.92kb.
- Владимир вестник новые знания для благополучной жизни, 2638.68kb.
- Тема урока современные взгляды на возникновение земли и солнечной системы, 25.98kb.
СРАВНИТЕЛЬНЫЙ АНАЛИЗ ПРИКЛАДНЫХ ПАКЕТОВ ГЕОСТАТИСТИЧЕСКИХ ПРОГРАМММедведева А.М., студентка 4-го курса Белорусского государственного университетаНаучный руководитель Цеховая Т.В., кандидат физико-математических наук, доцент Любая человеческая деятельность нуждается в прогнозировании. Предвидение вероятного исхода событий дает возможность заблаговременно подготовиться к ним, учесть их положительные или отрицательные последствия и, если возможно, вмешаться в ход развития. Решения такого типа задач связаны с применением математического аппарата, базирующегося на исследовании зависимости стационарных случайных процессов во временной области. Современный период в развитии статистического анализа случайных процессов во временной области характеризуется появлением такого нового направления, как вариограмный анализ. У его истоков стоял инженер горного дела, математик Ж. Mатерон. В 1963 г. было введено понятие «геостатистика» как теория пространственно-распределенных переменных, сформулированная Ж. Maтероном для анализа данных о природных ископаемых в горнорудном деле [1]. В дальнейшем исследованиями в этой области занимались N. Cressie и D.M. Hawkins, Дж.С. Дэвис, Д.Е. Мейерс, М.Ф. Каневский, Е.А. Савельева, Л.С. Гандин, Т.В. Цеховая [2] и др. Сфера применения геостатистики, которая ранее была ограничена геологией, значительно расширилась в последние годы. Современная геостатистика – это область прикладной статистики с огромным набором методов для анализа, обработки и представления пространственной информации. В настоящее время геостатистические методы находят применение в экологии, метеорологии, медицине, эпидемиологии, лесном хозяйстве и т.д. Анализ данных предполагает оценку базовых статистических закономерностей, исследование и моделирование пространственной корреляции между составляющими изучаемого процесса. Мерой пространственной корреляции является вариограмма. На модели вариограммы исходных данных базируется кригинг – наилучший линейный несмещенный оцениватель, его оценка обладает минимальной дисперсией. Кригинг решает две основные задачи: построение оценки значения случайного процесса в точке, где наблюдение не проводилось, и определение точности этой оценки. Геостатистический анализ требует не только экспертных данных и опыта работы с ними, но и наличия современного и эффективного программного обеспечения. Географическая информационная система (ГИС) является специализированной. Она функционально направлена на решение задач в области географии. Основная задача ГИС – это работа с пространственно-распределенными данными. В настоящее время трудно назвать область деятельности, где бы не применялись географические информационные системы. Обычный набор функций ГИС включает [3]: управление базами данных; интерактивную трехмерную графику и картирование; статистическую обработку информации; ряд функций для решения задач прогнозирования, которые различны для каждой отдельной предметной области применения ГИС. В мире существует огромное количество разнообразных информационных систем. В наши дни лидерами в области глобальных ГИС являются продукты двух фирм: система ArcFM американской фирмы ESRI и MapInfo корпорации INTERGRAPH. Так, например, по результатам анализа структуры рынка ГИС в России, первое место занимает программное обеспечение ESRI Inc. – ArcInfo, ArcView, ArcCAD. Отмечается начало массового внедрения геоинформационных систем в Беларуси. Из отечественных разработок широкое распространение получила программа ГИС «Карта 2008» компании ЗАО КБ «Панорама», CREDO компании «Кредо-Диалог». В настоящее время существует ряд программных пакетов для реализации геостатистического подхода к анализу данных. Среди них можно выделить: – Geo-EAS, GS+ – содержат необходимые компоненты для проведения двумерного анализа случайных функций с применением методов геостатистики; – GSLIB – представляет наиболее мощные возможности для реализации трехмерного геостатистического оценивания и стохастического моделирования; – VARIOWIN – пакет включает в себя программы для поиска, выявления, анализа случайных корреляционных структур; – Surfer – в пакет включен метод кригинг, однако для корректного проведения анализа в системе отсутствуют средства вариографии; – ISATIS – содержит широкий спектр средств геостатистики, включая подготовку данных, структурный анализ, интерполяцию и моделирование; – ссылка скрыта – активно развивающийся статистический пакет, предоставляющий большие возможности в области моделирования и статистического анализа любых данных. ЛИТЕРАТУРА 1. Matheron G. Principles of Geostatistics // Economic Geology. – 1963. – Vol. 58. – P. 1246–1266. 2. Цеховая Т.В. Асимптотическое распределение оценки вариограммы // Вестник Брестского университета. – 2008. – № 2. – С. 32–37. 3. Проблемы окружающей среды и природный ресурсов. Обзорная информация / Арский Ю.М., Бочин Л.А., Виноградов В.Г. и др. // М. : Всероссийский ин-т научн. и техн. Информ. (ВИНИТ), 1999 – Вып. № 11. ТЕОРИЯ ОДНОРЕСУРСНОЙ ФИРМЫКостина Е.М., студентка 1-го курса Белорусского национального |

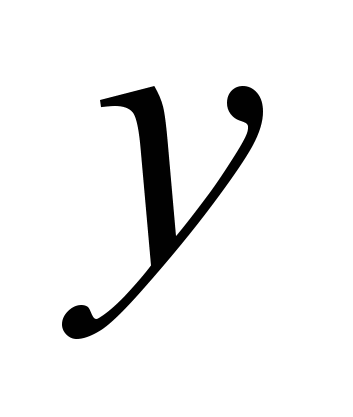 . Используется только один ресурс. Предприятие полностью характеризуется своей производственной функцией
. Используется только один ресурс. Предприятие полностью характеризуется своей производственной функцией 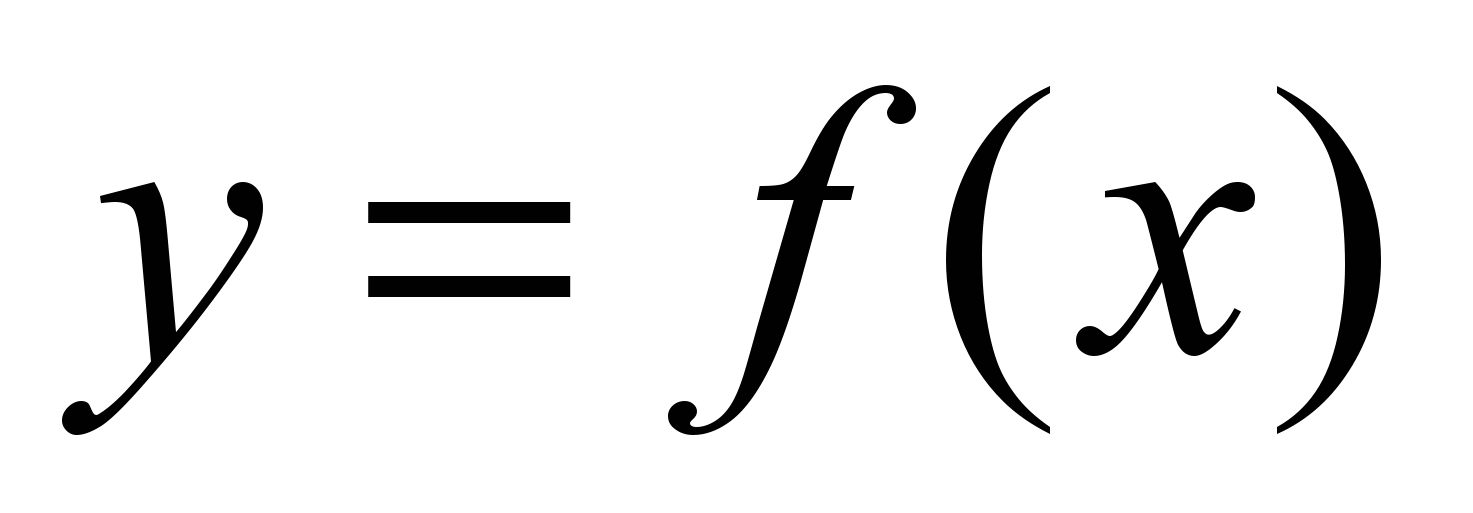 – зависимостью выпускаемого товара от объема затраченного ресурса
– зависимостью выпускаемого товара от объема затраченного ресурса 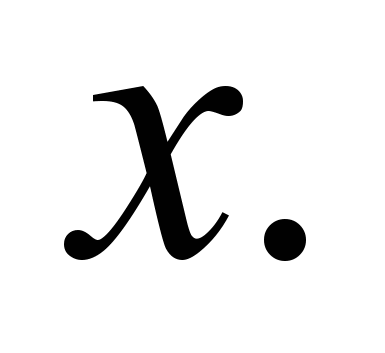
 , эта функция неубывающая, то есть увеличение объема перерабатываемого ресурса не приводит к уменьшению выпуска. Таким образом, если
, эта функция неубывающая, то есть увеличение объема перерабатываемого ресурса не приводит к уменьшению выпуска. Таким образом, если 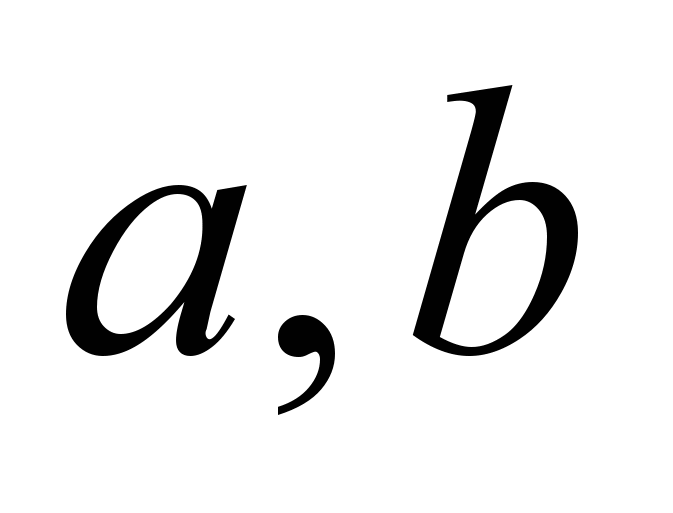 — две точки этой области, то
— две точки этой области, то 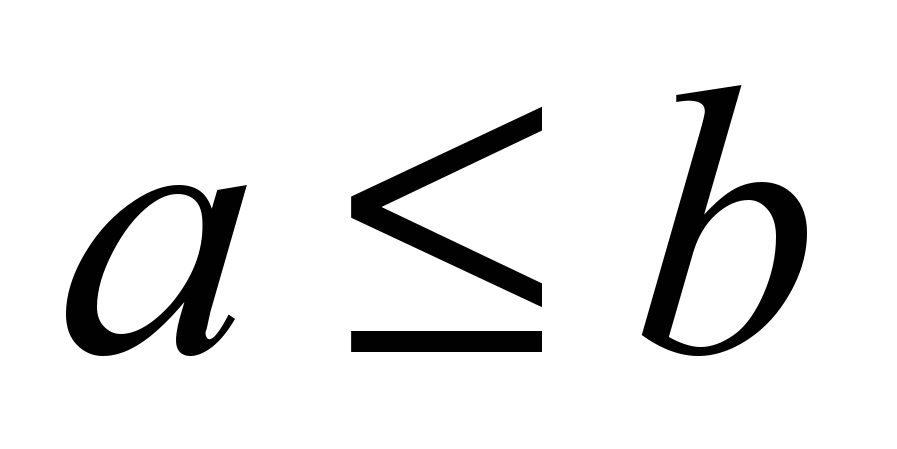 влечет за собой неравенство
влечет за собой неравенство 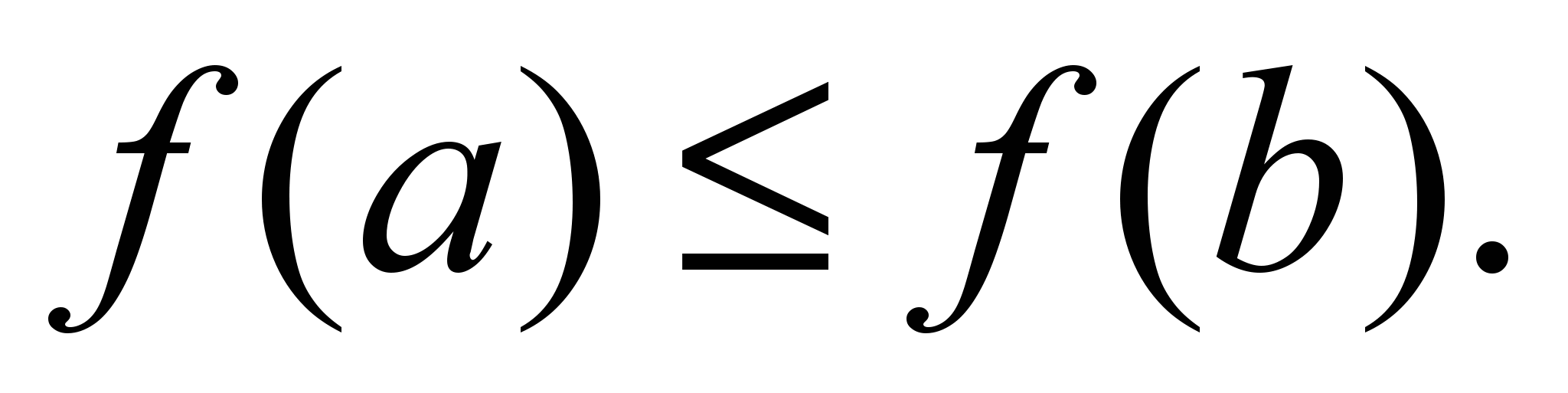 Следовательно, в этой области производная
Следовательно, в этой области производная 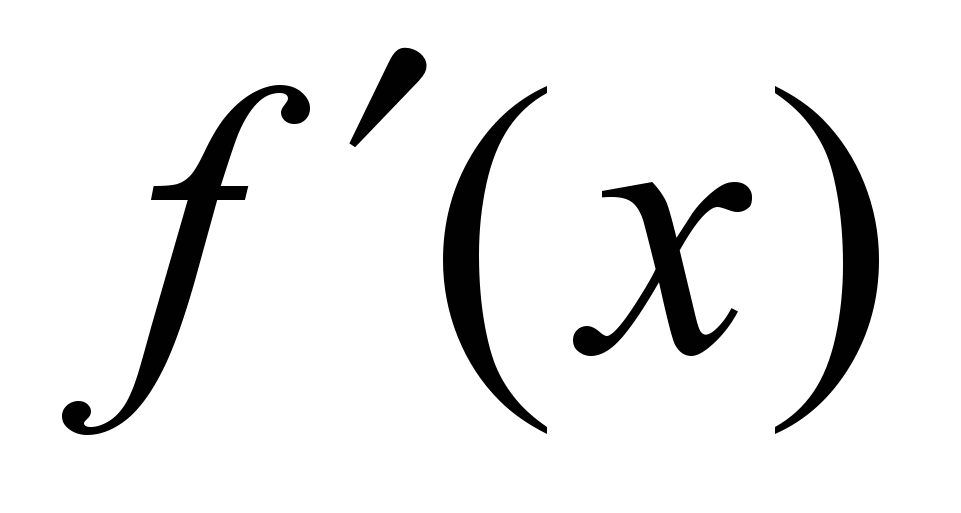 неотрицательна. Она называется предельным продуктом.
неотрицательна. Она называется предельным продуктом.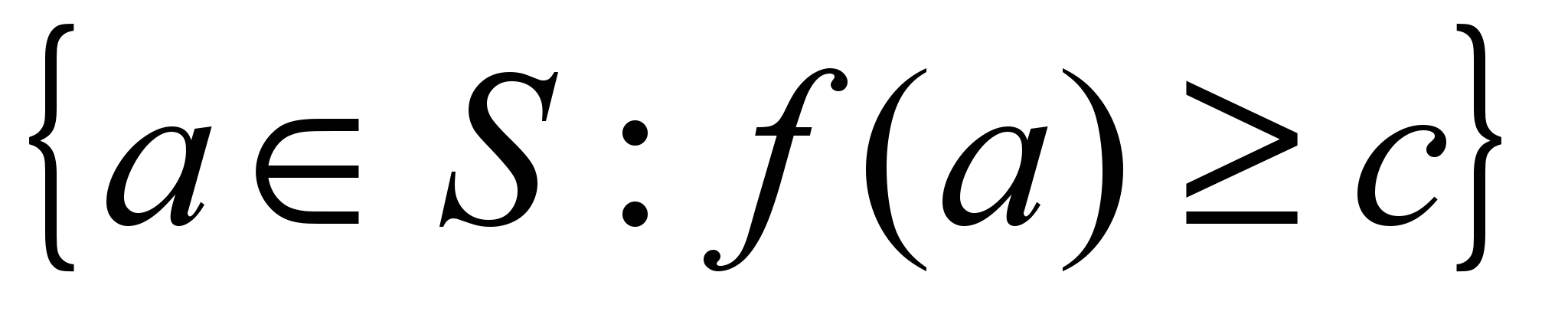 также выпукло для всех с. В этом подмножестве вторая производная неположительна.
также выпукло для всех с. В этом подмножестве вторая производная неположительна.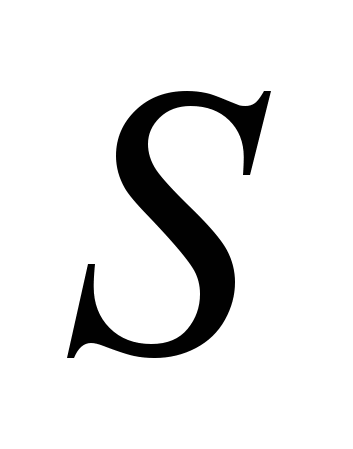 !) начинает уменьшаться предельный продукт. Классическим примером действия этого закона является добавление все большего и большего количества труда в производство зерна на фиксированном участке земли.
!) начинает уменьшаться предельный продукт. Классическим примером действия этого закона является добавление все большего и большего количества труда в производство зерна на фиксированном участке земли.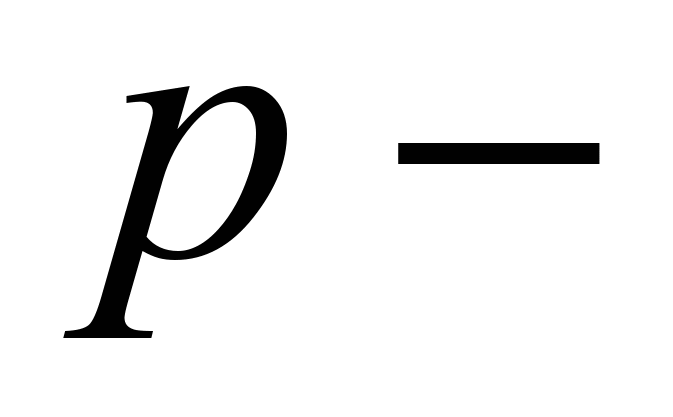 цена единицы ресурса и
цена единицы ресурса и 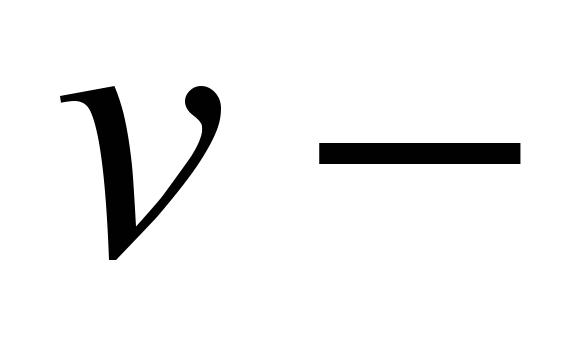 цена единицы выпускаемого товара. Следовательно, прибыль
цена единицы выпускаемого товара. Следовательно, прибыль 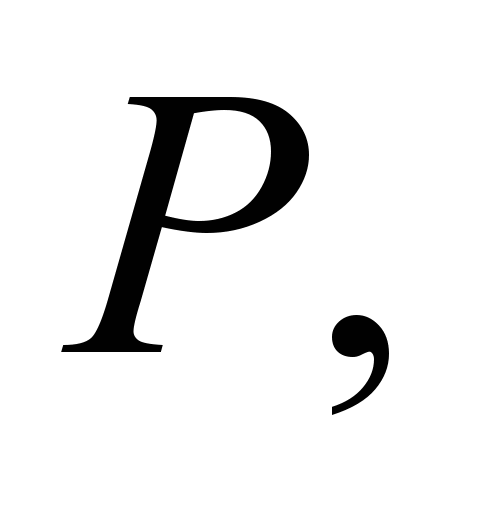 являющаяся в итоге функцией
являющаяся в итоге функцией 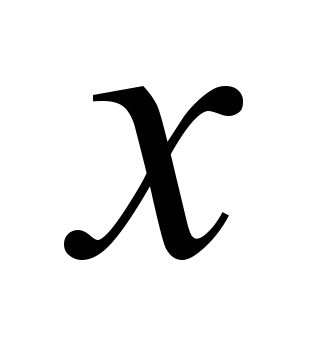 (и цен, но их будем считать постоянными), есть
(и цен, но их будем считать постоянными), есть 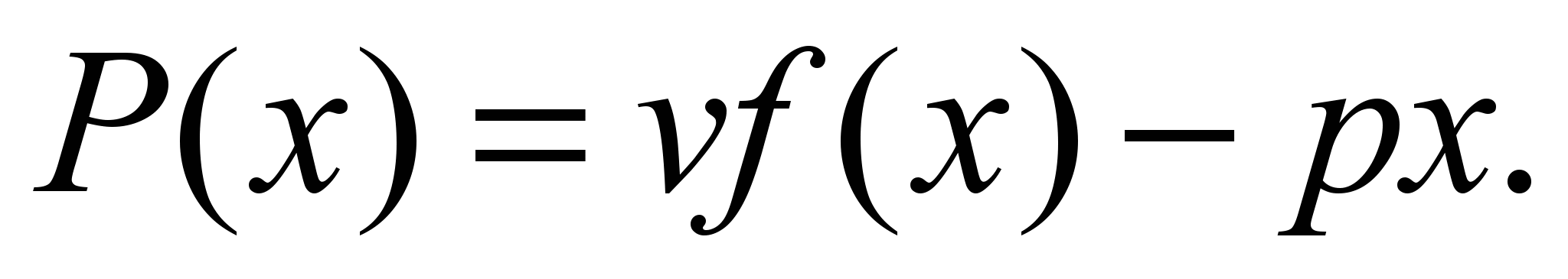 Следовательно, нашу задачу можно представить в виде:
Следовательно, нашу задачу можно представить в виде: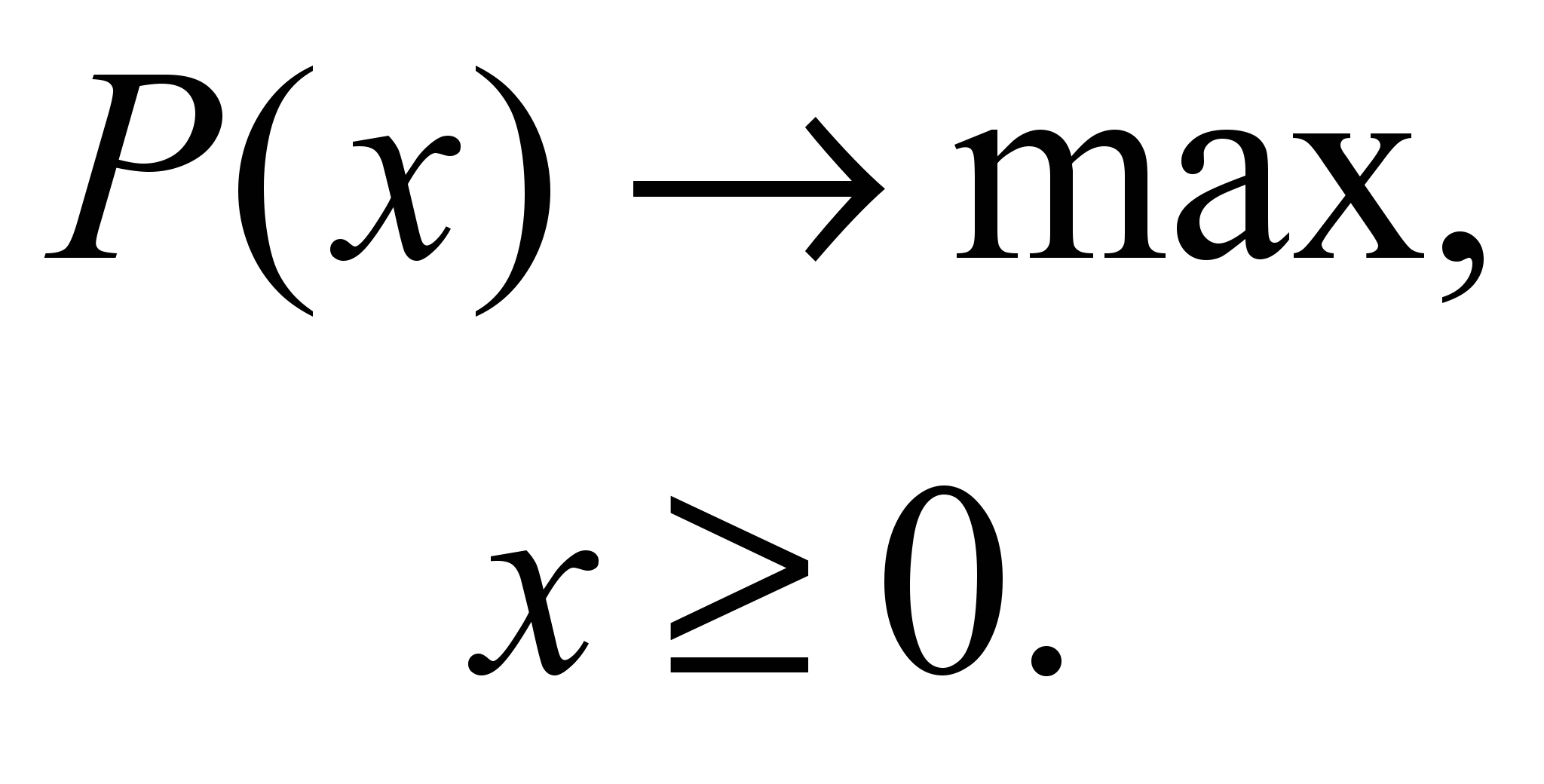
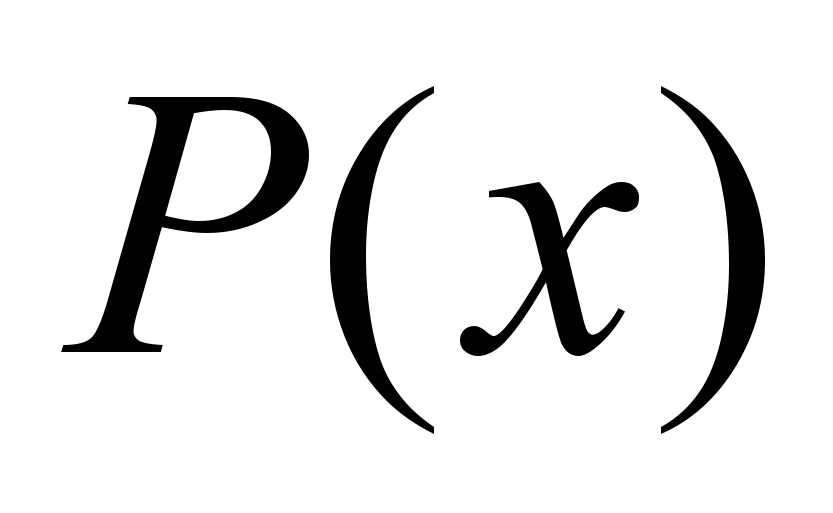 к нулю, получим:
к нулю, получим: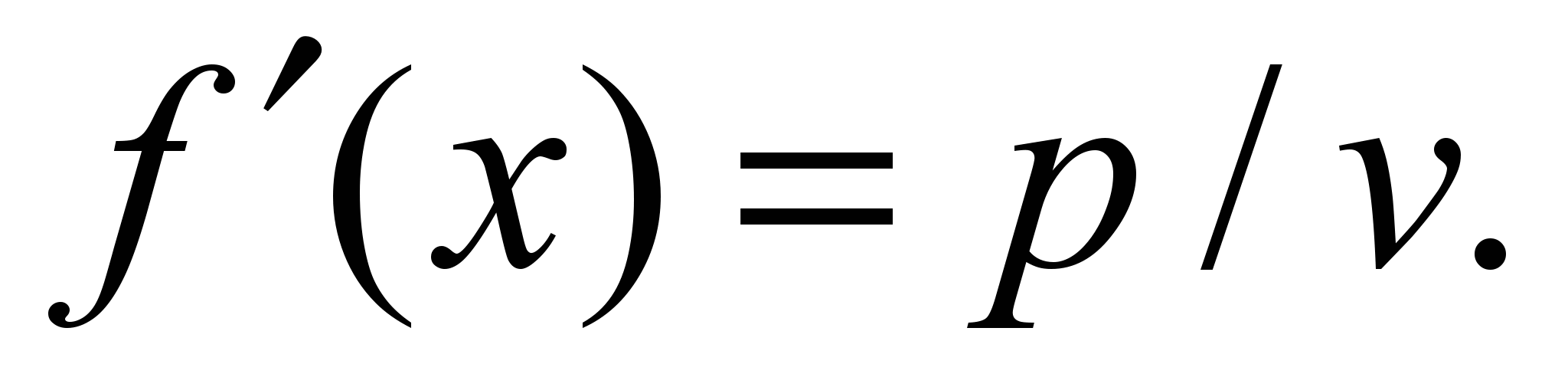
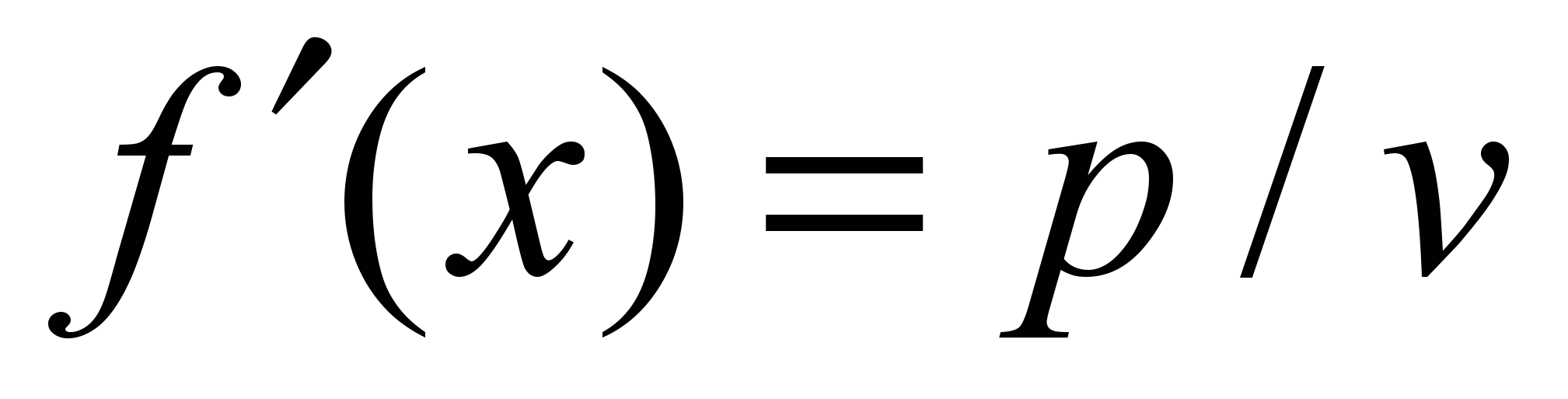 , оказывается внутренней, то есть точкой экстремума, и поскольку еще предполагается неположительность второй производной, то это точка максимума.
, оказывается внутренней, то есть точкой экстремума, и поскольку еще предполагается неположительность второй производной, то это точка максимума. , даваемую рассматриваемым соотношением, назовем оптимальным решением для нашего предприятия, то есть оптимальная точка
, даваемую рассматриваемым соотношением, назовем оптимальным решением для нашего предприятия, то есть оптимальная точка 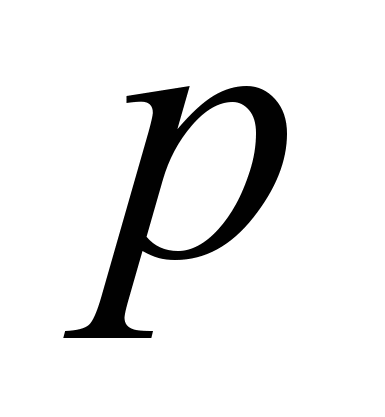 и
и 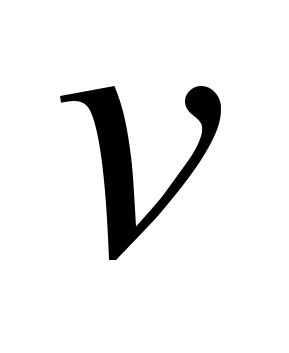 . Таким образом, получается функция
. Таким образом, получается функция 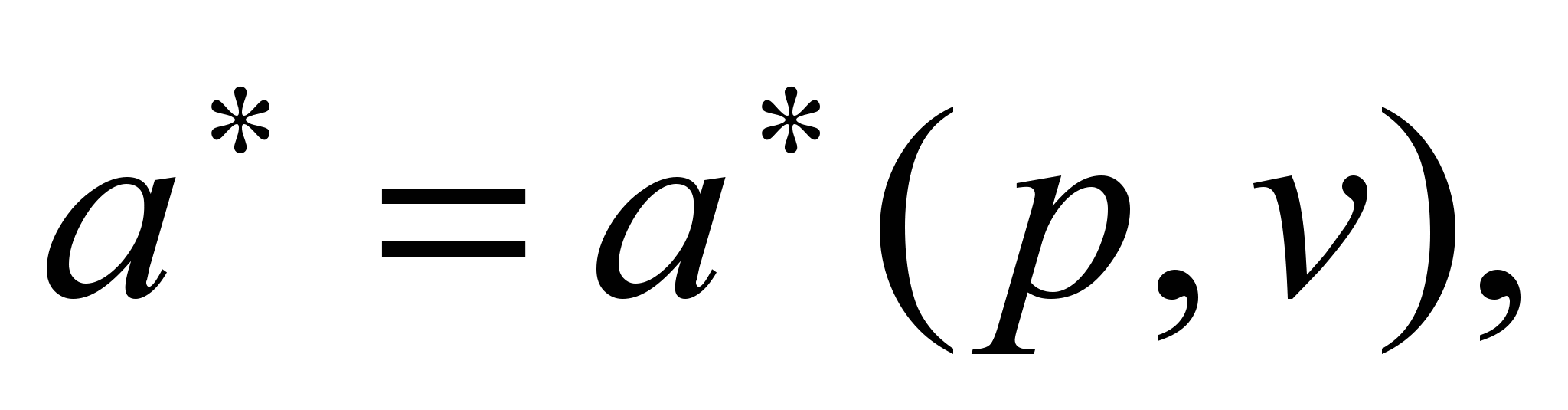 называемая спросом на ресурс. Смысл этой функции заключается в следующем.
называемая спросом на ресурс. Смысл этой функции заключается в следующем.