Линейное программирование

Вид материала

Документы

Содержание Основные условия, позволяющие строить модели ЛП Дополнительные переменные Теория линейного программирования Z=CX  min при ограничениях: A1x Угловыми точками Выпуклым многоугольником Опорной прямой Выпуклым многогранником Опорной плоскостью А является выпуклой линейной комбинацией А Х удовлетворяет системе (2). Т.к. X10, X20, 10, 20, то и Х X) принимает минимальное значение более чем в одной угловой точке, например в X Так как векторы Каждой угловой точке многогранника решений соответствует k

Подобный материал:

• Введение в линейное программирование линейное программирование (ЛП), 139.72kb.
• Программа дисциплины Линейное программирование Семестр, 17.93kb.
• Аттестационное тестирование в сфере профессионального образования, 72.49kb.
• 2. Линейное программирование (ЛП), 18.32kb.
• Контрольная работа по темам «Линейное программирование на Паскале» и«Условный оператор», 4.21kb.
• Федеральное агентство по образованию, 124.95kb.
• Курс является базовым как для изучения других математических дисциплин, так и для более, 39.9kb.
• Введение в линейное программирование Задача планирования производства, 90.61kb.
• В. В. Панферов, 64.65kb.
• Содержание, 1344.25kb.

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ


Линейное программирование (ЛП) - это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения


1930 г., А.Н. Толстой - составление оптимального плана перевозок, минимизирующего километраж


1931 г., Б. Эгервари - задача о назначениях ("венгерский метод")


1939 г., Л.В. Канторович - систематическое исследование задач ЛП, разработка общих методов (метод разрешающих множителей), применение к решению ряда практических задач


1941 г., Ф. Хичкок - постановка транспортной задачи ЛП, метод последовательного улучшения


1947 г., Дж. фон Нейман – теория двойственности


1947 г., Дж. Данциг – симплекс-метод решения общей задачи ЛП


1949 г., Л.В. Канторович, М.К. Гавурин - метод потенциалов для транспортной задачи ЛП

Основные условия, позволяющие строить модели ЛП

1. Пропорциональность

2. Аддитивность

3. Неотрицательность


Пропорциональность означает, что затраты ресурсов на некоторый вид деятельности, а также вклад этого вида деятельности в целевую функцию прямо пропорциональны его уровню (объему)


Аддитивность указывает на то, что общая величина ресурсов, потребляемых в системе всеми видами деятельности, равна сумме затрат ресурсов на отдельные виды деятельности. Аналогично интерпретируется и целевая функция.


Предположения о пропорциональности и аддитивности обеспечивают строгую линейность соответствующих функций (ограничений и целевой).


Неотрицательность означает, что ни одному из видов деятельности не может быть приписан отрицательный уровень.




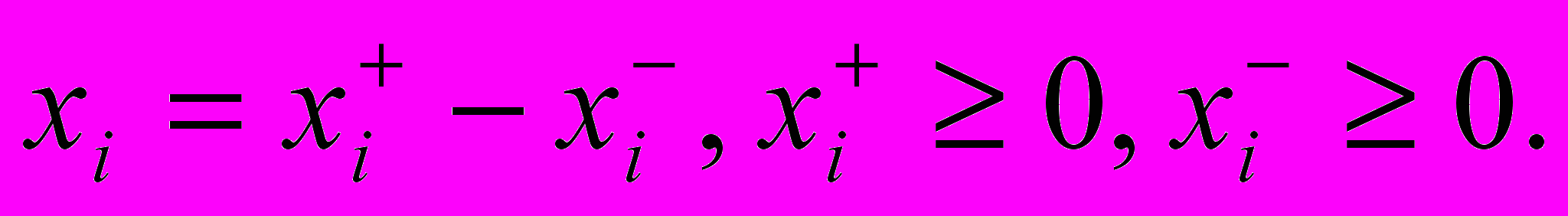
Каноническая и стандартная формы задач ЛП.

Переход от одной формы к другой


Каноническая форма задачи ЛП:


Z = c₁x₁ + c₂x₂ + . . . + c_nx_n  min (max)

при условиях:

x₁  0, x₂  0, . . ., x_n  0,

a₁₁x₁ + a₁₂x₂ + . . . + a_1nx_n = b₁,

a₂₁x₁ + a₂₂x₂ + . . . + a_2nx_n = b₂,

. . . . . . . . . .

a_m1x₁ + a_m2x₂ + . . . + a_mnx_n = b_m.


Стандартные формы задачи ЛП:


Z=C^TX  max, Z=C^TX  min,

AX  B, AX  B,

X  0. X  0.


Формы задачи ЛП эквивалентны, т.е. каждая из них может быть приведена к любой другой путем тождественных преобразований


min Z = - max (-Z).


Х=А: XA, XA

Дополнительные переменные

Графический метод решения задач ЛП


Графический метод основан на геометрической интерпретации задачи ЛП и применяется в основном при решении задач в двухмерном пространстве.


Рассмотрим задачу ЛП:


z = c₁x₁ + c₂x₂  min

при ограничениях




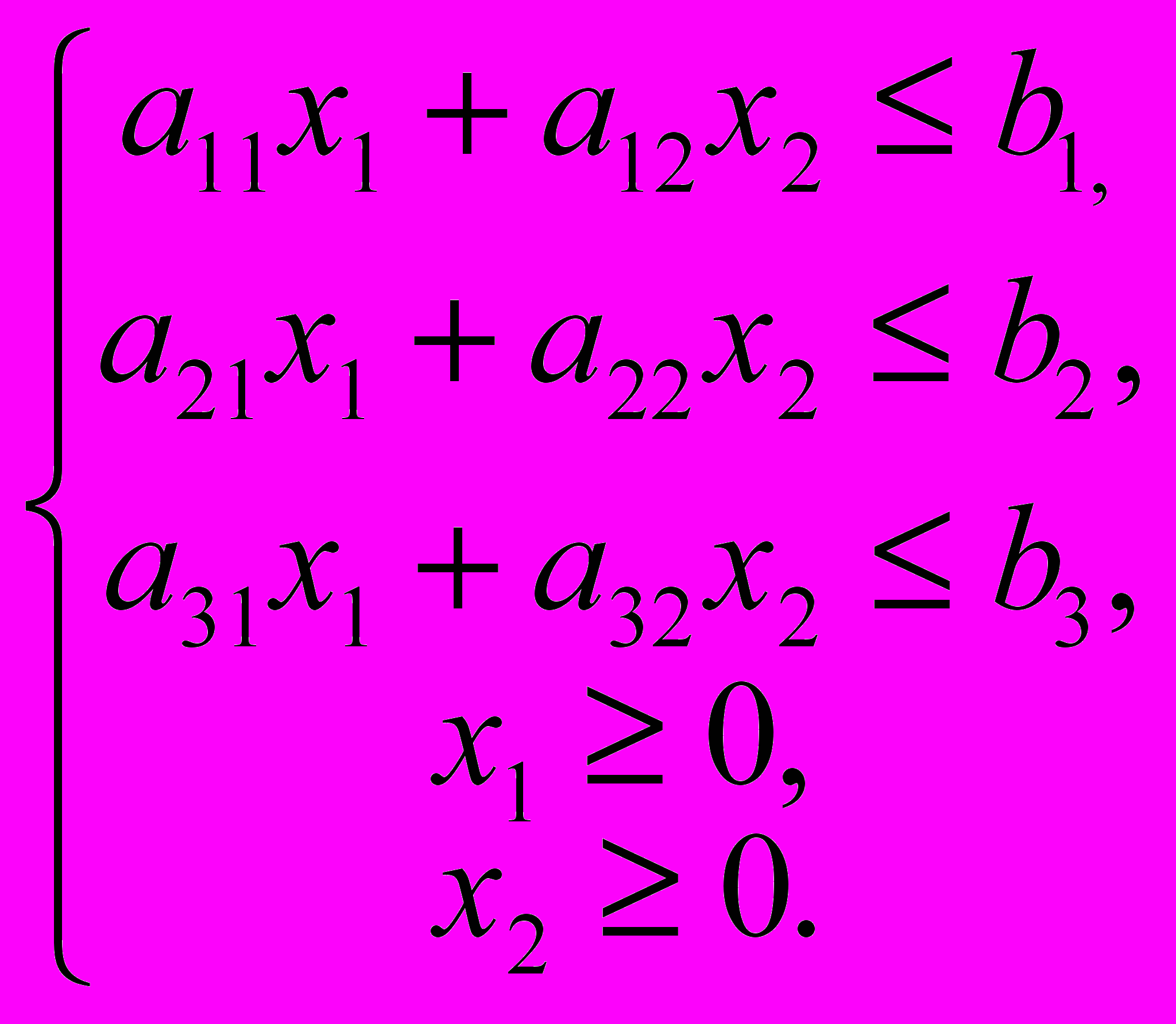
Каждое неравенство a_i2x₁ + a_i2x₂  b_i определяет в плоскости X₁ОX₂ полуплоскость с граничной прямой a_i2x₁ + a_i2x₂ = b_i. Точки, лежащие в полуплоскости, удовлетворяют данному неравенству.


Неравенства x₁0 и x₂0 определяют первый квадрант в системе координат.


Множество точек пересечения всех этих полуплоскостей образует многоугольник решений (область допустимых решений). Каждая точка этого многоугольника есть решение системы ограничений или допустимый план задачи ЛП.


Многоугольник решений может быть неограниченной областью или вырождаться в прямую (луч, отрезок) или в точку.

Если область допустимых решений пустая, то система ограничений несовместна.







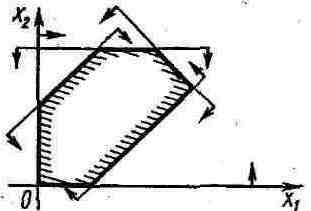
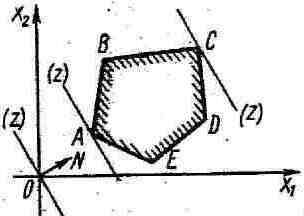
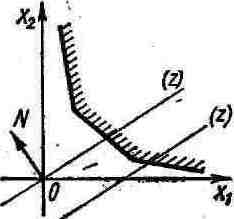
Характерные черты задач ЛП:

1. Допустимая область всегда является выпуклым многогранником даже в случае, когда она не ограничена

2. Оптимальное решение всегда достигается в вершинах допустимой области

3. Если оптимальное решение не одно, то значение функции совпадает во всех точках-решениях


Задача использования сырья


Z=50x₁+40x₂ max


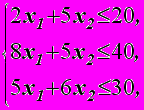x₁0, x₂0.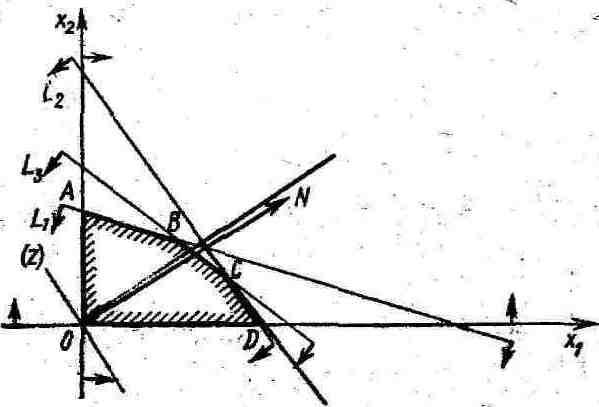







Теория линейного программирования

Даны линейная функция:

Z=C₁x₁+C₂x₂+…+C_nx_n (1)

и система линейных ограничений:

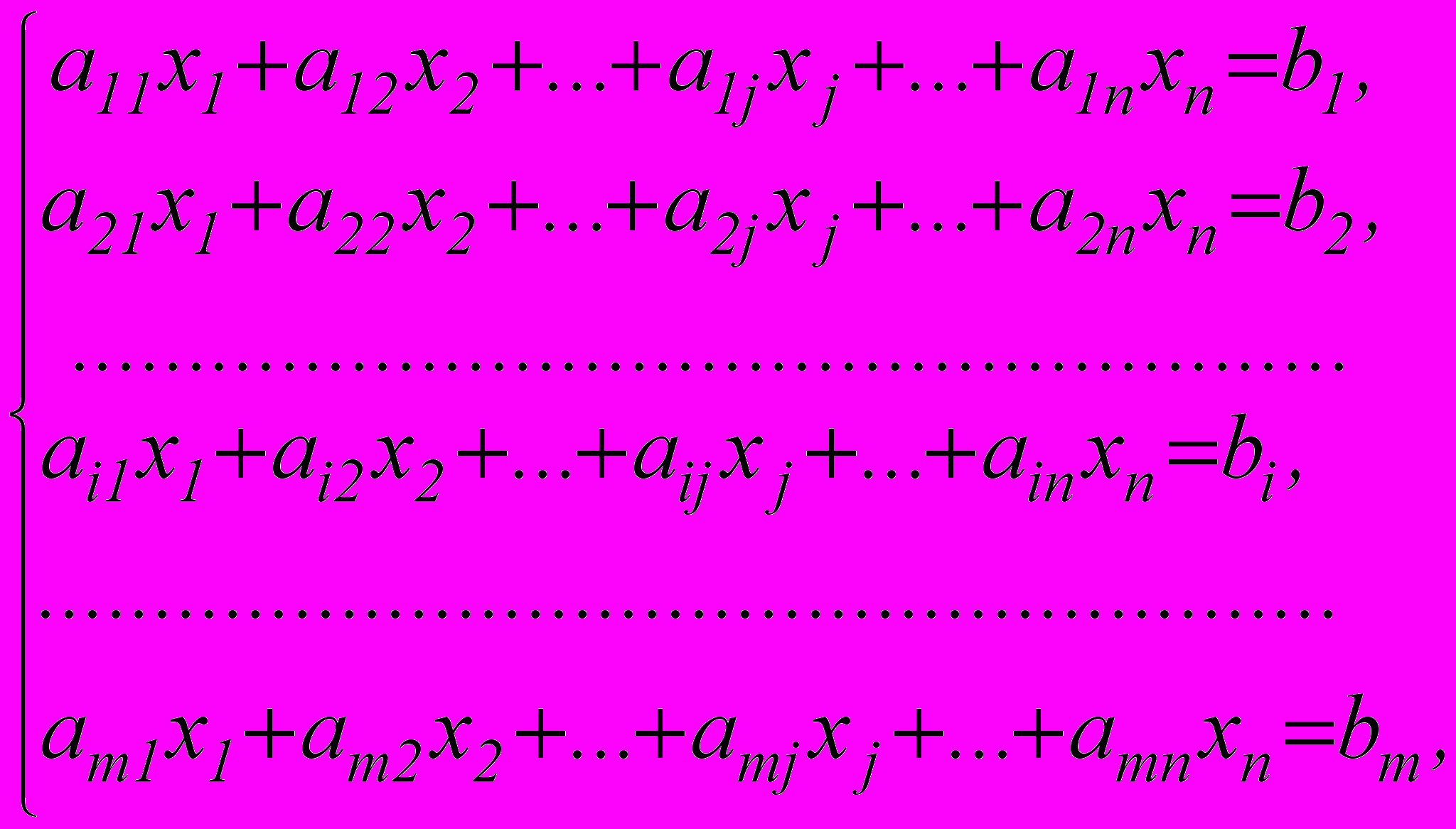
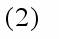
x_j0, (j=1, 2, …, n), (3)

где а_ij, b_i и C_j – заданные постоянные величины.

Найти такие неотрицательные значения x₁, x₂,…, x_n, которые удовлетворяют системе ограничений (2) и доставляют целевой функции (1) минимальное значение.

В системе ограничений (2) все b_i, i=1, 2, …, m, без потери общности можно считать неотрицательными.

В векторной форме:

Z=CX  min

при ограничениях:

A₁x₁+A₂x₂+…+A_nx_n=A₀, X0, (4)


A₁=, A₂=, …, A_n=, A₀= ,


Определение1. Планом или допустимым решением задачи линейного программирования называется вектор X=(x₁, x₂, …, x_n), удовлетворяющий условиям (2) и (3).

Определение2. План X=(x₁, x₂, …, x_n) называется опорным, если векторы A_i (i=1, 2, …, m), входящие в разложение (4) с положительными коэффициентами x_i, являются линейно независимыми.


Замечание. Так как векторы A_i являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не превышает m.


Определение 3. Опорный план называется невырожденным, если он содержит m положительных компонент, в противном случае опорный план называется вырожденным.

Определение 4. Оптимальным планом или оптимальным решением задачи линейного программирования называется план, доставляющий наименьшее (наибольшее) значение целевой функции.


Свойства решений задачи линейного программирования тесно связаны со свойствами выпуклых множеств.


Пусть на плоскости x₁Ox₂ заданы две точки: A₁ (x₁⁽¹⁾; x₂⁽¹⁾) и A₂ (x₁⁽²⁾; x₂⁽²⁾), определяющие прямолинейный направленный отрезок .

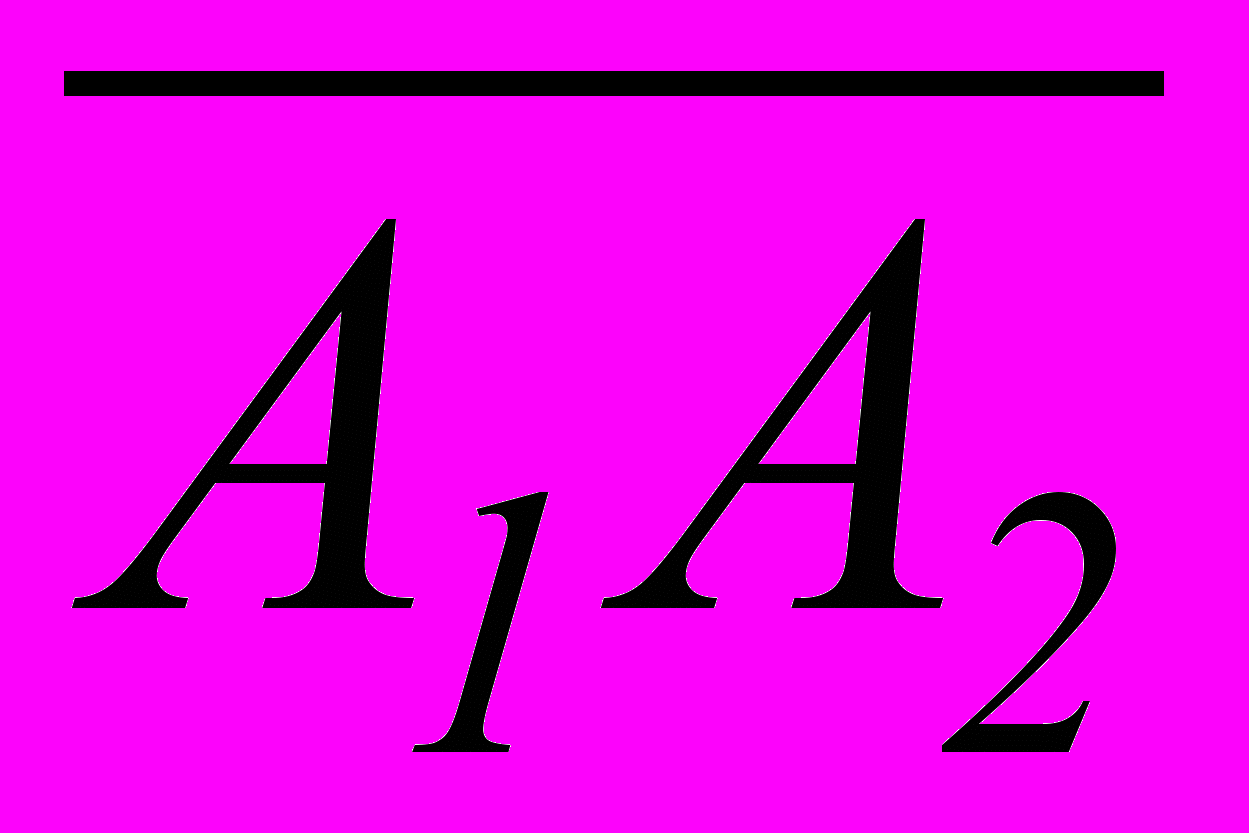Координаты произвольной внутренней точки A (x₁; x₂):

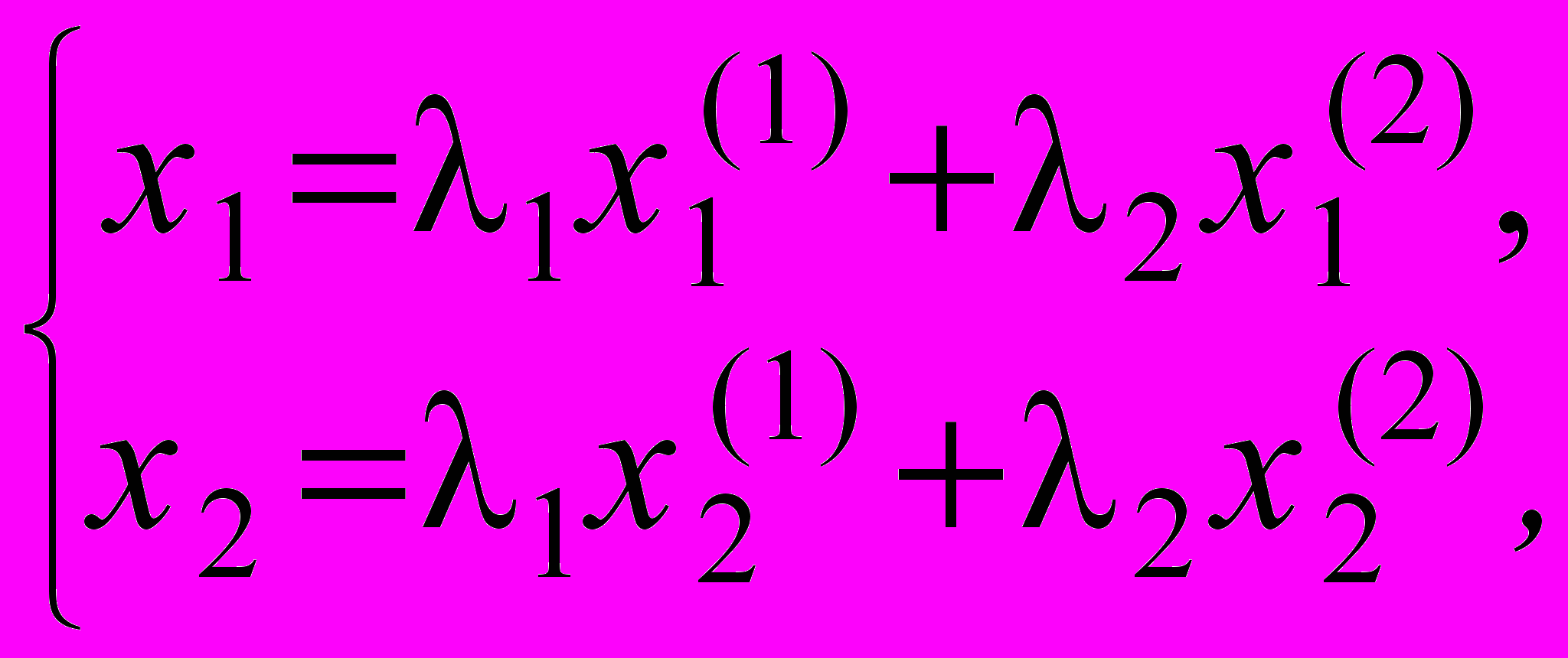, ₁0, ₂0, ₁+₂=1. (5)

или:

А=₁А₁+₂А₂, ₁0, ₂0, ₁+₂=1.


Точка А, для которой выполняются эти условия, называется выпуклой линейной комбинацией точек А₁ и А₂.

При ₁=1 и ₂=0 точка А совпадает с А₁, при ₁=0 и ₂=1 – с А₂.

Точки А₁ и А₂ называются угловыми или крайними точками отрезка .

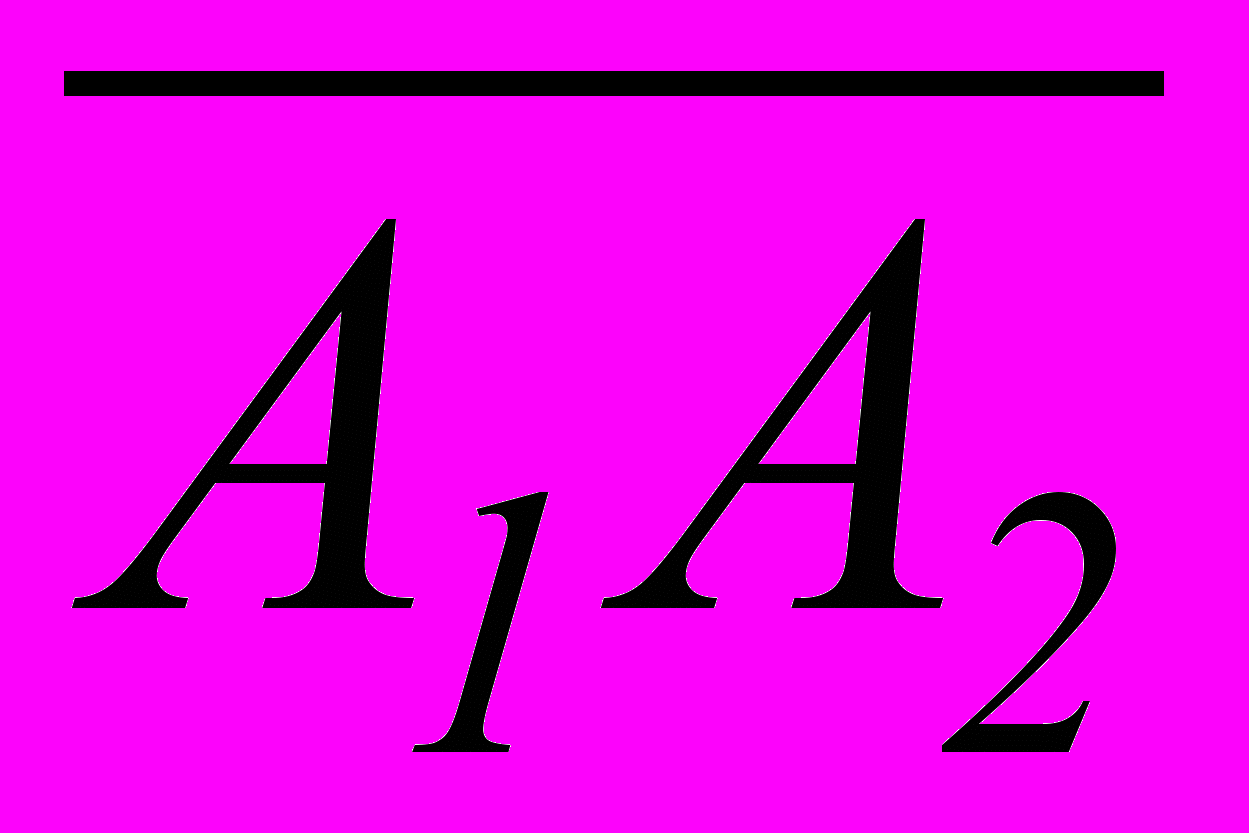Замечание. Из определения выпуклой линейной комбинации точек очевидно, что угловая точка не может быть представлена как выпуклая линейная комбинация двух других точек отрезка.


Определение5. Пусть имеется n точек А₁, А₂, …, А_n. Точка А является их выпуклой линейной комбинацией, если выполняются условия:

А=₁А₁+₂А₂+…+_nА_n, _j0 (j=1, 2, …, n), 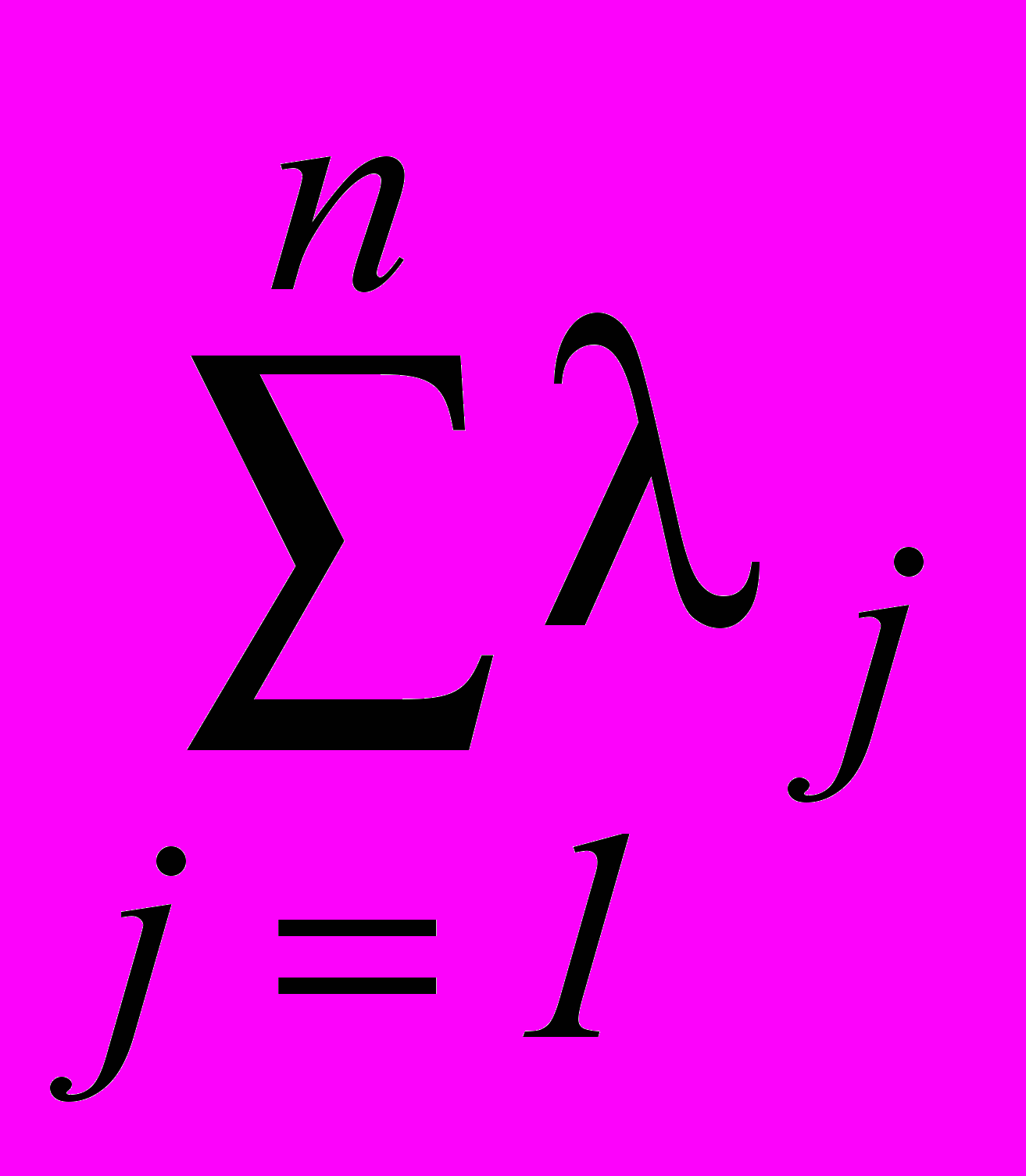=1.

Определение6. Множество точек называется выпуклым, если оно вместе с любыми двумя точками содержит и их произвольную выпуклую линейную комбинацию.

Геометрический смысл: множеству вместе с его двумя произвольными точками полностью принадлежит и прямолинейный отрезок, их соединяющий.

Определение7. Точка множества называется граничной, если любой шар с центром в этой точке содержит как точки, принадлежащие множеству, так и точки, не принадлежащие ему. Граничные точки множества образуют его границу.

Определение8. Замкнутым называется множество, содержащие все свои граничные точки.

Замечание. Замкнутое множество может быть ограниченным и неограниченным.

Определение9. Множество называется ограниченным, если существует шар радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество; в противном случае множество называется неограниченным.


Теорема 1. Пересечение выпуклых множеств является выпуклым множеством.

Доказательство. Пусть F = F₁F₂, F₁ и F₂ - выпуклые множества. А₁, А₂ - две произвольные точки в F. А₁,А₂  F₁ и F₂  отрезок 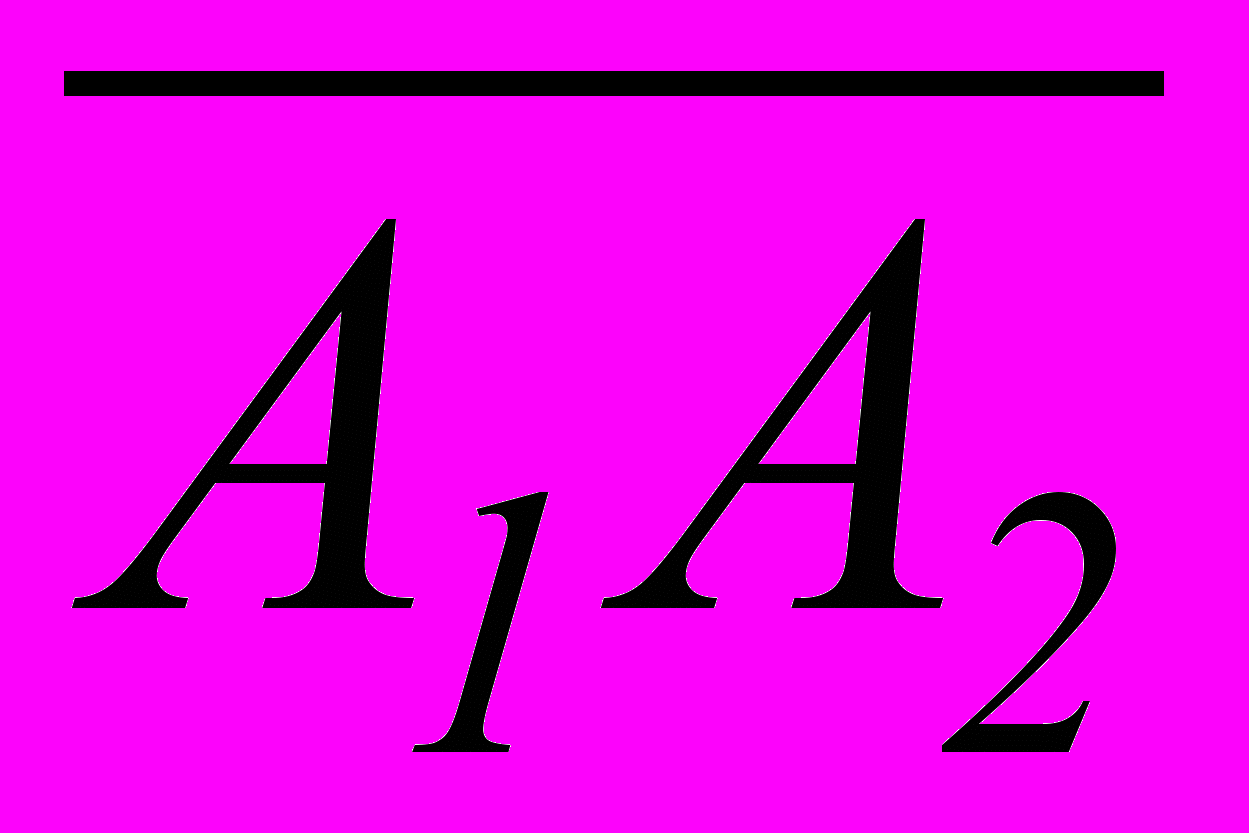 F₁ и F₂, т.к. они – выпуклые множества 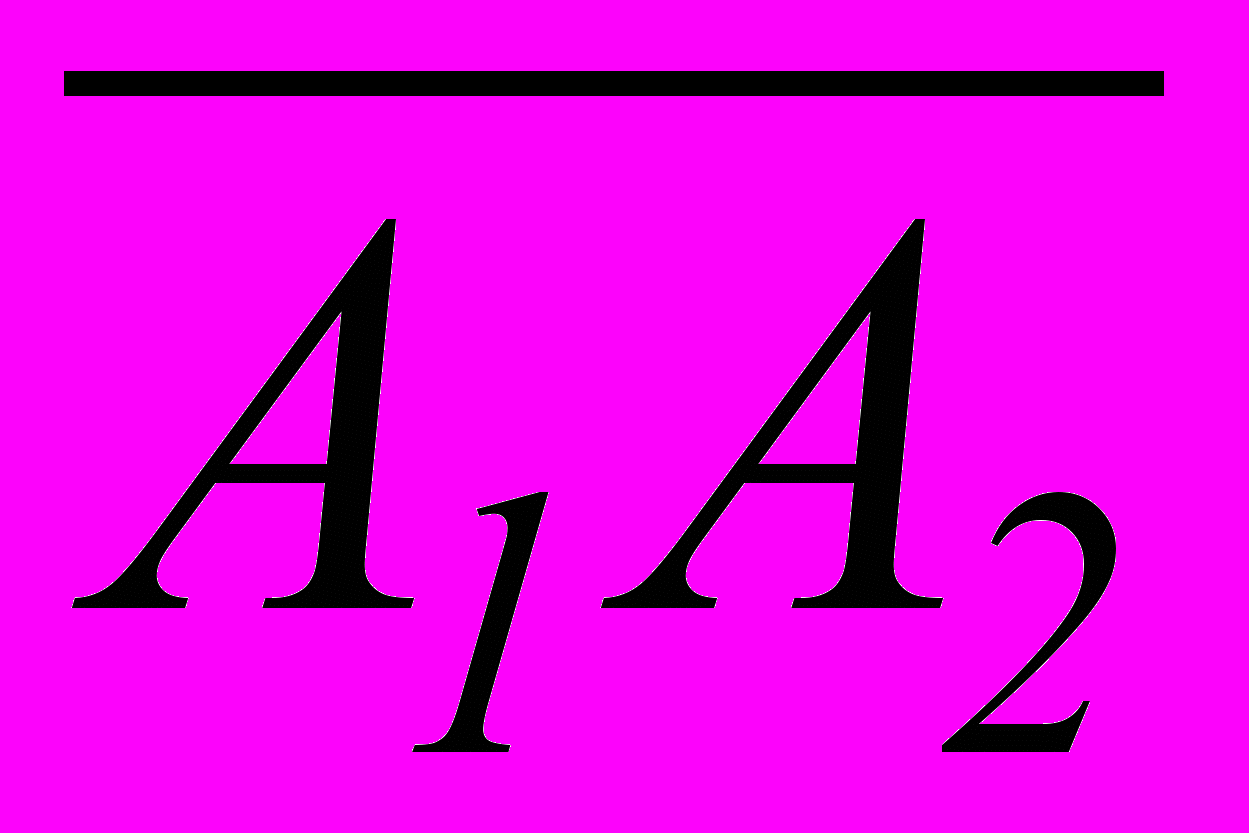  F₁F₂ 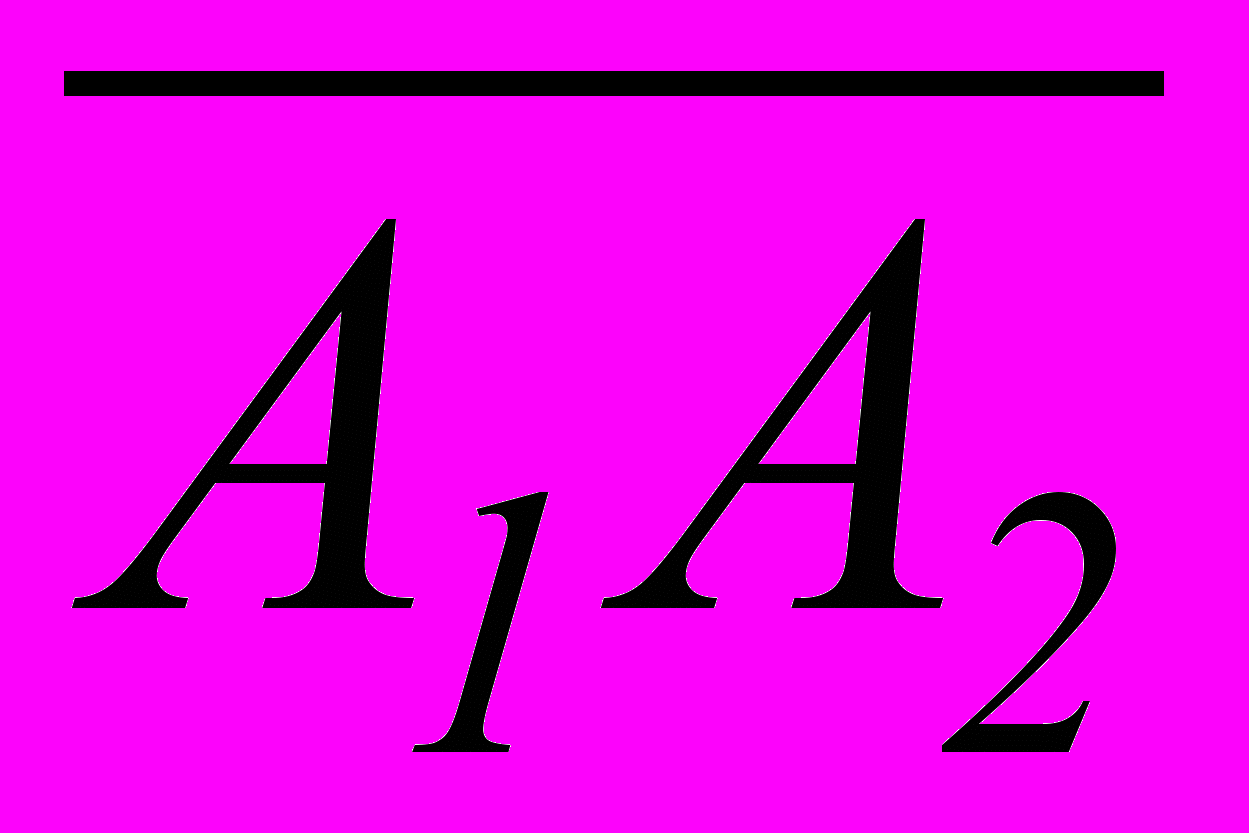  F  F – выпуклое множество. 


Определение10. Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой комбинацией двух произвольных точек множества.

Выпуклое множество может иметь конечное и бесконечное число угловых точек.

Определение11. Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек. Угловые точки многоугольника называются его вершинами, а отрезки, соединяющие две вершины и образующие его границу, - сторонами многоугольника.

Определение12. Опорной прямой выпуклого многоугольника называется прямая, имеющая с многоугольником, расположенным по одну сторону от нее, хотя бы одну общую точку.

Определение13. Выпуклым многогранником называется замкнутое ограниченное выпуклое множество трехмерного пространства, имеющее конечное число угловых точек. Угловые точки многогранника называются его вершинами; многоугольники, ограничивающие многогранник, - гранями, отрезки, по которым они пересекаются, - ребрами.

Определение14. Опорной плоскостью многогранника называется плоскость, имеющая с многогранником, расположенным по одну сторону от нее, хотя бы одну общую точку.


Теорема 2. Замкнутый, ограниченный, выпуклый многогранник является выпуклой линейной комбинацией своих угловых точек.

Доказательство. Докажем теорему для многоугольника, имеющего n вершин.

Сначала докажем, что любая точка треугольника удовлетворяет теореме. А - произвольная точка треугольника А₁А₂А₃.

А₁



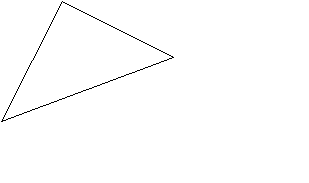
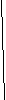
А А₂


А₄

А₃

А 

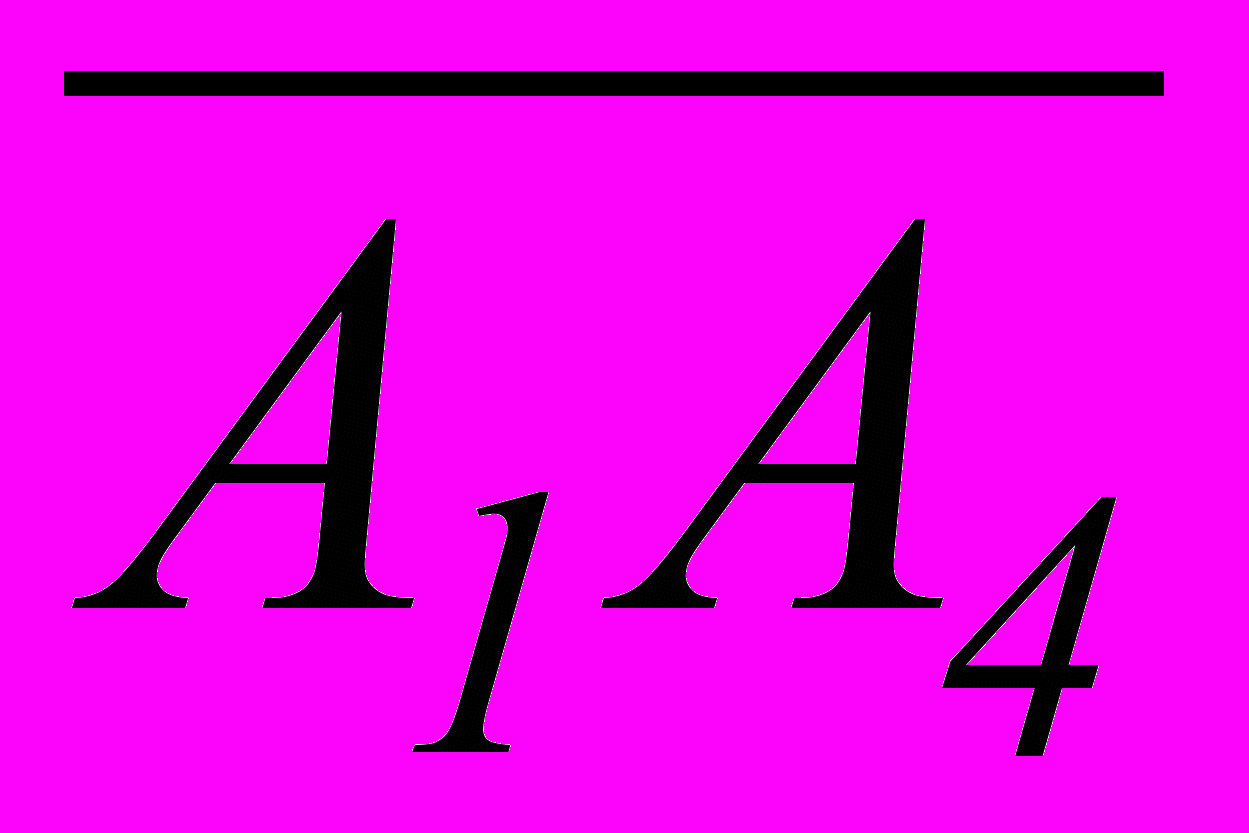
А=t₁А₁+t₄А₄, t₁0, t₄0, t₁+t₄=1 (*)


А₄ 

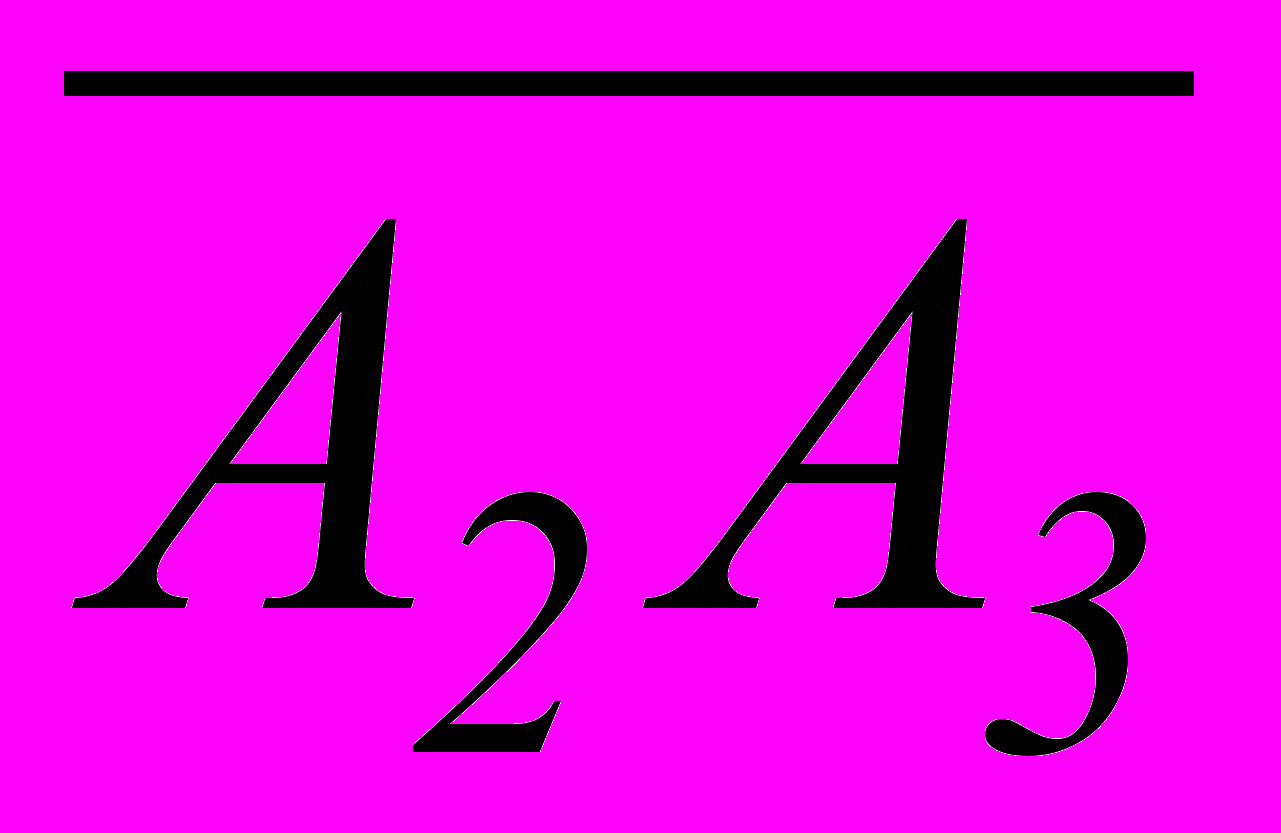
А₄=t₂А₂+t₃А₃, t₂0, t₃0, t₂+t₃=1. (**)


Подставляя (**) в (*):

A=t₁A₁+t₄(t₂A₂+t₃A₃)=t₁A₁+t₂t₄A₂+t₃t₄A₃.


Полагая t₁=₁, t₂t₄=₂, t₃t₄=₃:

А=₁А₁+₂А₂+₃А₃,

причем

₁0, ₂0, ₃0, ₁+₂+₃=1,

т. е. точка А является выпуклой линейной комбинацией А₁, А₂, А₃.

Выпуклый многоугольник, имеющий n вершин (n>3) разобьем на n–2 треугольника, произвольная точка А попадет в один из них. Без ограничения общности можно положить, что она попала в треугольник А₁А₂А₃. Тогда, как уже доказано, точка А является выпуклой линейной комбинацией трех вершин: А=₁А₁+₂А₂+₃А₃. Поэтому

А=₁А₁+₂А₂+₃А₃+0А₄+…+0А_n,

_j0 (j=1, 2, …, n), 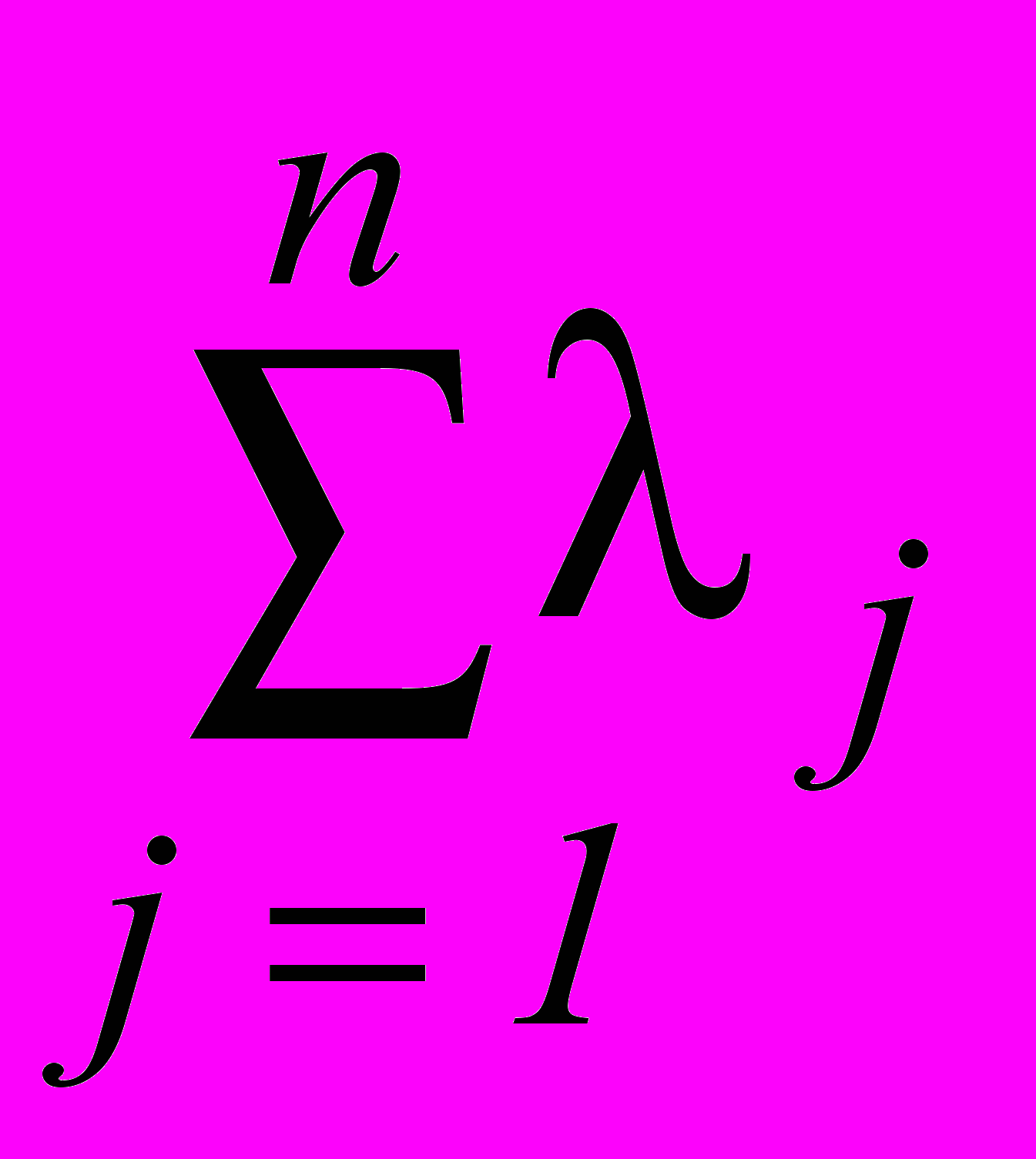=1,

т. е. точка А является выпуклой линейной комбинацией угловых точек многоугольника.

Доказательство для многогранника проводится аналогично. 


Теорема 3. Множество всех планов задачи линейного программирования выпукло.

Доказательство. Пусть Х₁ и Х₂ – планы задачи ЛП, т.е.

AX₁=A₀, X₁0; AX₂=A₀, X₂0,

Х=₁Х₁+₂Х₂, ₁0, ₂0, ₁+₂=1,

- их произвольная выпуклая линейная комбинация.

Тогда

АХ = А(₁Х₁+₂Х₂) = ₁АХ₁+₂АХ₂ = ₁А₀+₂А₀ =

= (₁+₂)А₀ = А₀,

т.е. Х удовлетворяет системе (2).

Т.к. X₁0, X₂0, ₁0, ₂0, то и Х0, т. е. удовлетворяет и условию (3)  Х тоже является планом задачи ЛП. 


Теорема 4. Целевая функция задачи линейного программирования достигает своего минимального значения в угловой точке многогранника решений.

Если целевая функция принимает минимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Доказательство. Предположим, что многогранник решений К является ограниченным, имеющим конечное число угловых точек.

Пусть X₁, Х₂, ..., Х_р,- угловые точки К, Х₀ - оптимальный план задачи ЛП.

Тогда Z(Х₀)  Z(X) ХК. Если Х₀ – угловая точка, то первая часть теоремы доказана.

Предположим, что Х₀ не является угловой точкой; тогда по теореме 2

Х₀=₁Х₁+₂Х₂+...+_pХ_p, _i0 (i=1, 2, …, p), 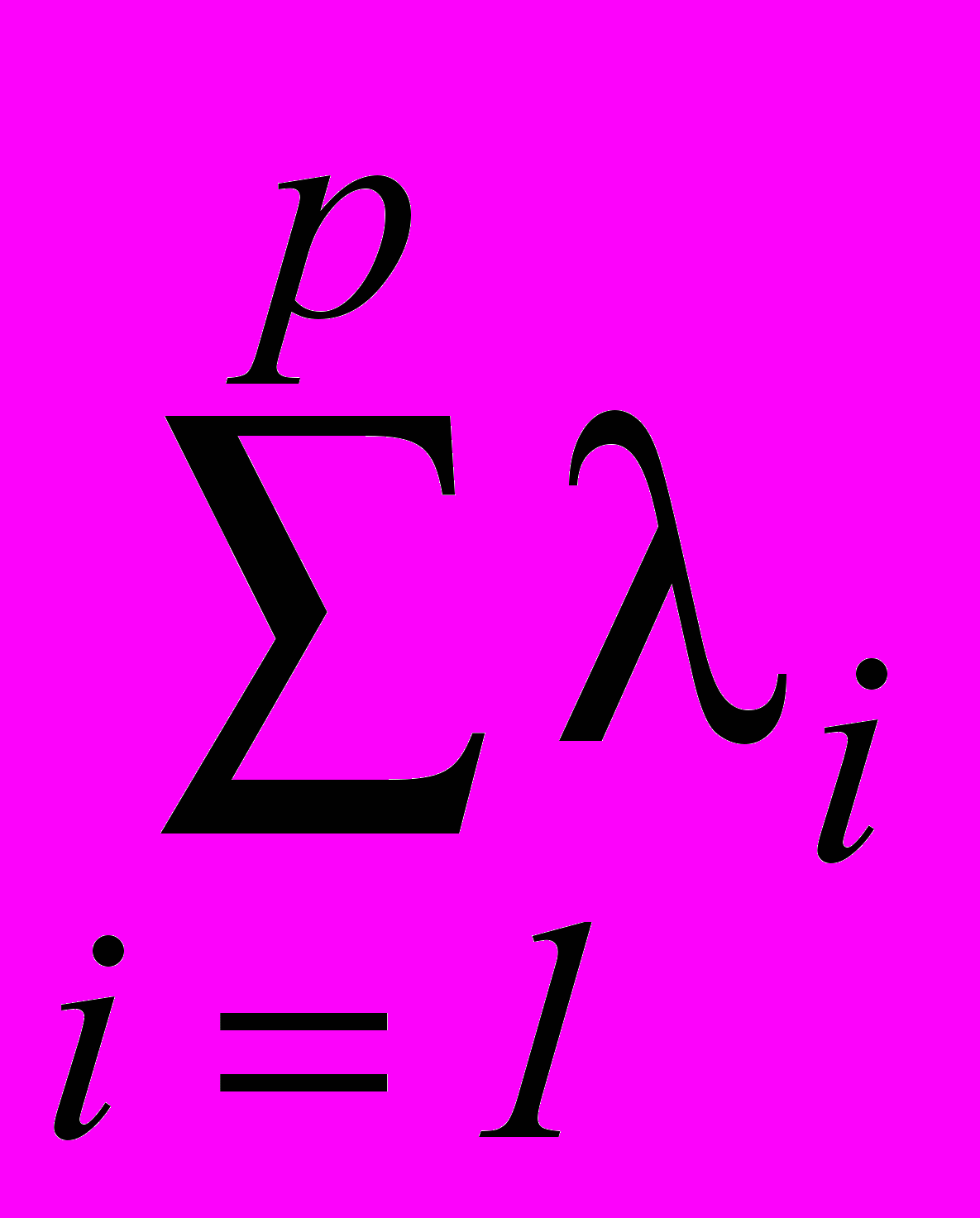=1.

Так как Z(X) – линейная функция

Z(Х₀) = Z(₁Х₁+₂Х₂+...+_pХ_p) =

= ₁Z(X₁)+₂Z(X₂)+...+_pZ(X_p) (*)


Пусть т = Z(Х_k) – наименьшее из Z(Х_i) (i=1,2, ..., р) в разложении (*), X_k – одна из угловых точек.

Заменим в (*) каждое Z(Х_i) на m.

Тогда Z(X₀)  ₁m + ₂m +...+ _pm = т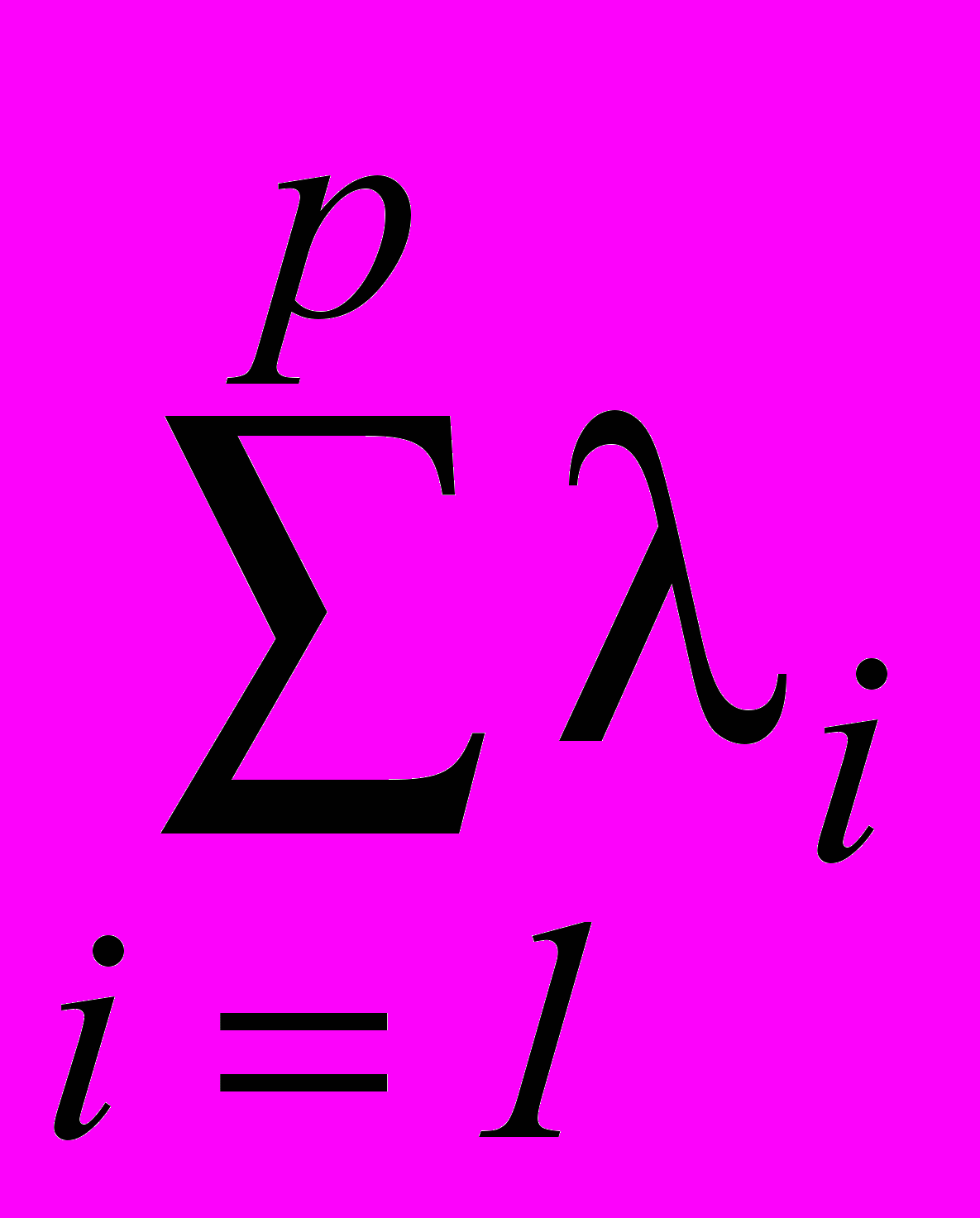= m,

так как _i0, 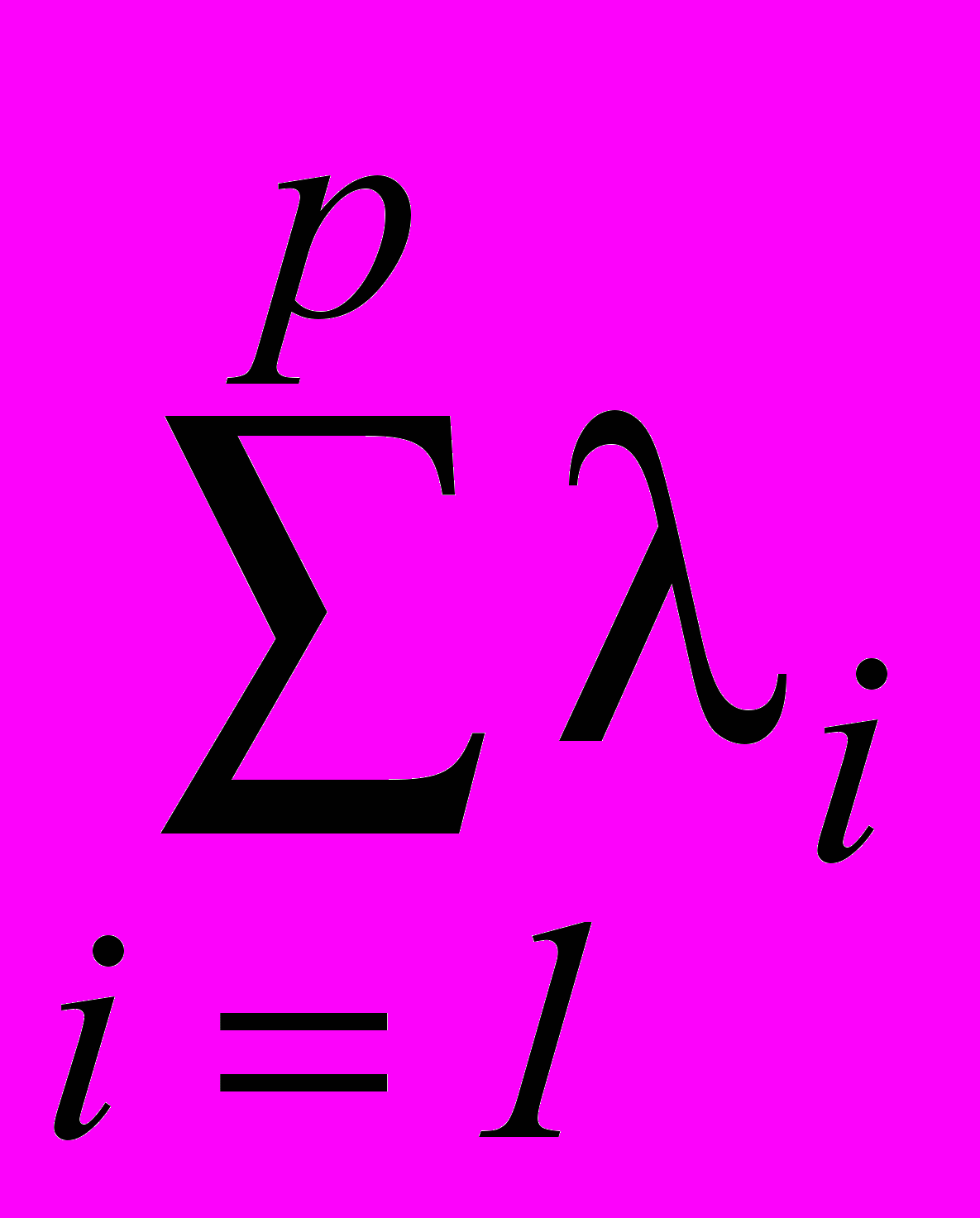=1.


Т.е. Z(X₀)  т, но по предположению Х₀ – оптимальный план, т.е. Z(X₀)  т, следовательно Z(X₀) = т = Z(X_k), где X_k – угловая точка.

Для доказательства второй части теоремы допустим, что Z( X) принимает минимальное значение более чем в одной угловой точке, например в X₁, Х₂, ..., Х_q, 1<qр; тогда Z(X₁)=Z(Х₂)=...=Z(X_q)=т.

Пусть

Х = ₁Х₁+₂Х₂+...+_qХ_q, _i0 (i=1,2,…,q), 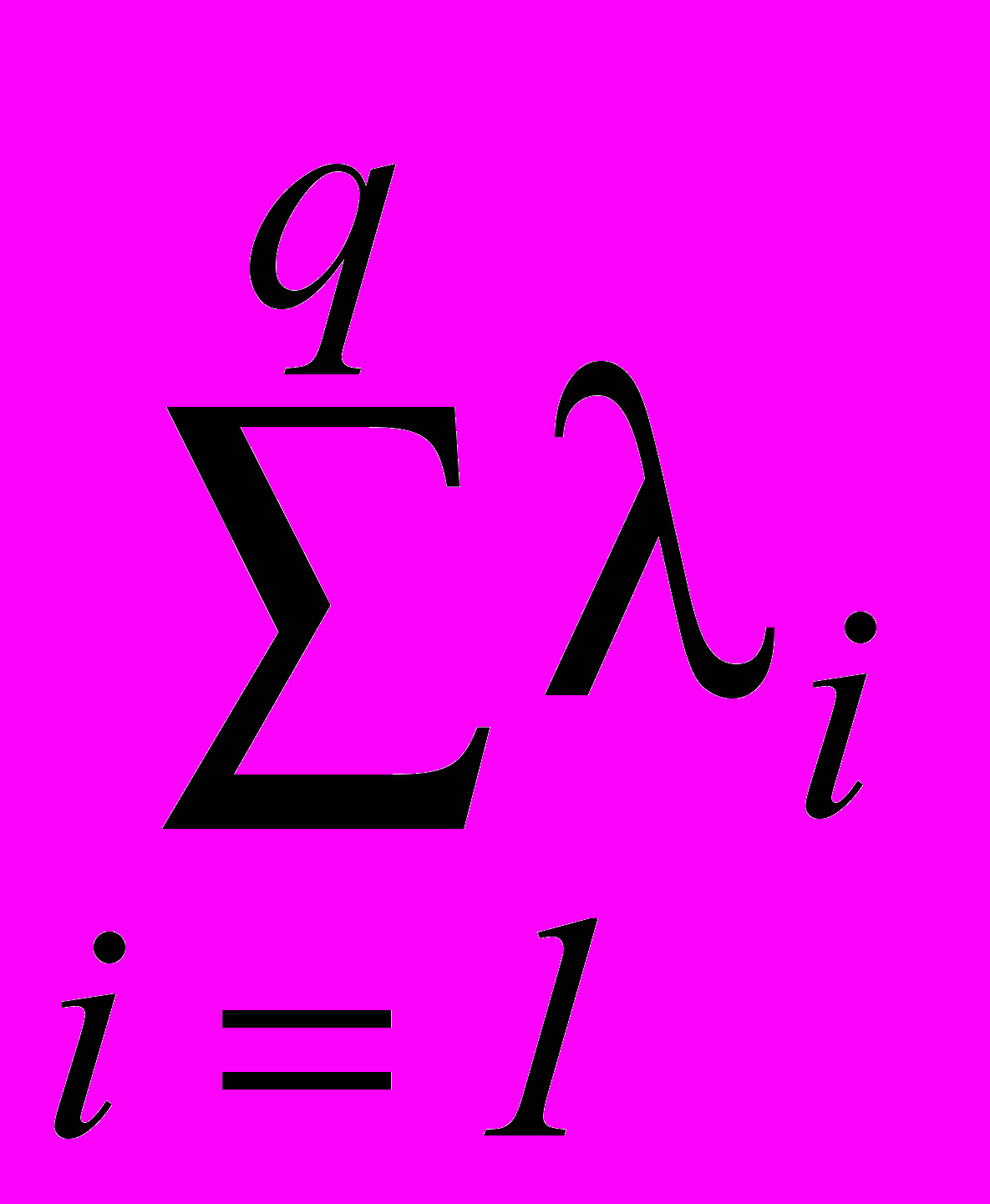=1,

тогда

Z(Х₀) = Z(₁Х₁+₂Х₂+...+_qХ_q) =

= ₁Z(X₁) + ₂Z(X₂) +...+ _qZ(X_q) =

= ₁m + ₂m +...+ _qm = т 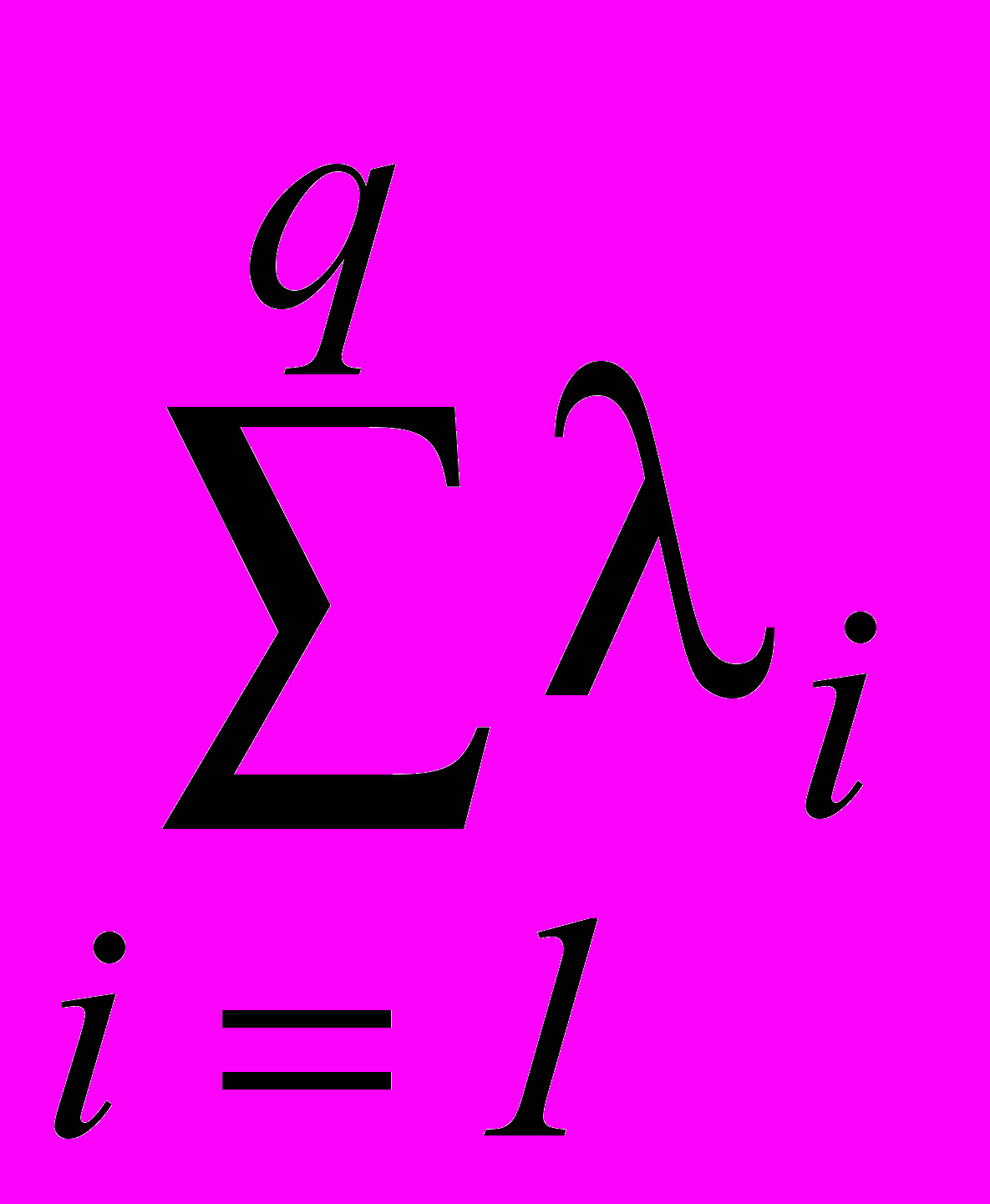= m,

т. е. целевая функция Z принимает минимальное значение в произвольной точке X, являющейся выпуклой линейной комбинацией угловых точек X₁, Х₂, ..., Х_q. 

Замечание. Если многогранник решений является неограниченной областью, то не каждую точку области можно представить выпуклой линейной комбинацией угловых точек области. Задачу ЛП с многогранником решений, представляющим собой неограниченную область, можно привести к задаче с ограниченной областью, вводя дополнительное ограничение x₁+x₂+...+x_пQ, где Q – достаточно большое число.


Теорема 5. Если известно, что система векторов A₁,А₂,..., A_k (kп) в разложении (4) линейно неза­висима и такова, что

A₁x₁ + А₂x₂ + ... + A_kx_k = А₀,

где все x_j0, то точка Х=(x₁, x₂, ..., x_k, 0, …, 0) яв­ляется угловой точкой многогранника решений.

Здесь Х – n-мерный вектор, последние п-k компо­нент которого равны нулю.

Доказательство. Предположим, что точка Х не является угловой. Тогда

Х=₁Х₁+₂Х₂, ₁0, ₂0, ₁+₂=1,

где X₁ и Х₂ – некоторые точки многогранника решений.

Очевидно, что

Х₁=(x₁⁽¹⁾, x₂⁽¹⁾, …, x_k⁽¹⁾, 0, …, 0),

Х₂=(x₁⁽²⁾, x₂⁽²⁾, …, x_k⁽²⁾, 0, …, 0).

Поскольку X₁ и Х₂ – планы, то

A₁x₁⁽¹⁾ + A₂x₂⁽¹⁾ +…+ A_kx_k⁽¹⁾=A₀,

A₁x₁⁽²⁾ + A₂x₂⁽²⁾ +…+ A_kx_k⁽²⁾ =A₀

Вычитая из первого соотношения второе:

(x₁⁽¹⁾-x₁⁽²⁾)A₁ + (x₂⁽¹⁾-x₂⁽²⁾)A₂ + … + (x_k⁽¹⁾–x_k⁽²⁾)A_k = 0.


По предположению, векторы A₁, А₂, ..., A_k линейно неза­висимы, поэтому последнее соотношение выполняется, если

x₁⁽¹⁾-x₁⁽²⁾ = 0; x₂⁽¹⁾–x₂⁽²⁾ = 0; … ; x_k⁽¹⁾–x_k⁽²⁾ = 0.

Отсюда x₁⁽¹⁾=x₁⁽²⁾; x₂⁽¹⁾=x₂⁽²⁾; …; x_k⁽¹⁾=x_k⁽²⁾.

Итак, Х невозможно представить как выпуклую линей­ную комбинацию других двух точек многогранника реше­ний. Следовательно, Х – угловая точка. 


Теорема 6. Если Х=(x₁, x₂, ..., x_n) - угловая точка многогранника решений, то векторы в разложении (4), соответствующие положительным x_i являются линейно независимыми.

Доказательство. Без ограничения общности можно положить не равными нулю первые k компонент вектора X, так что

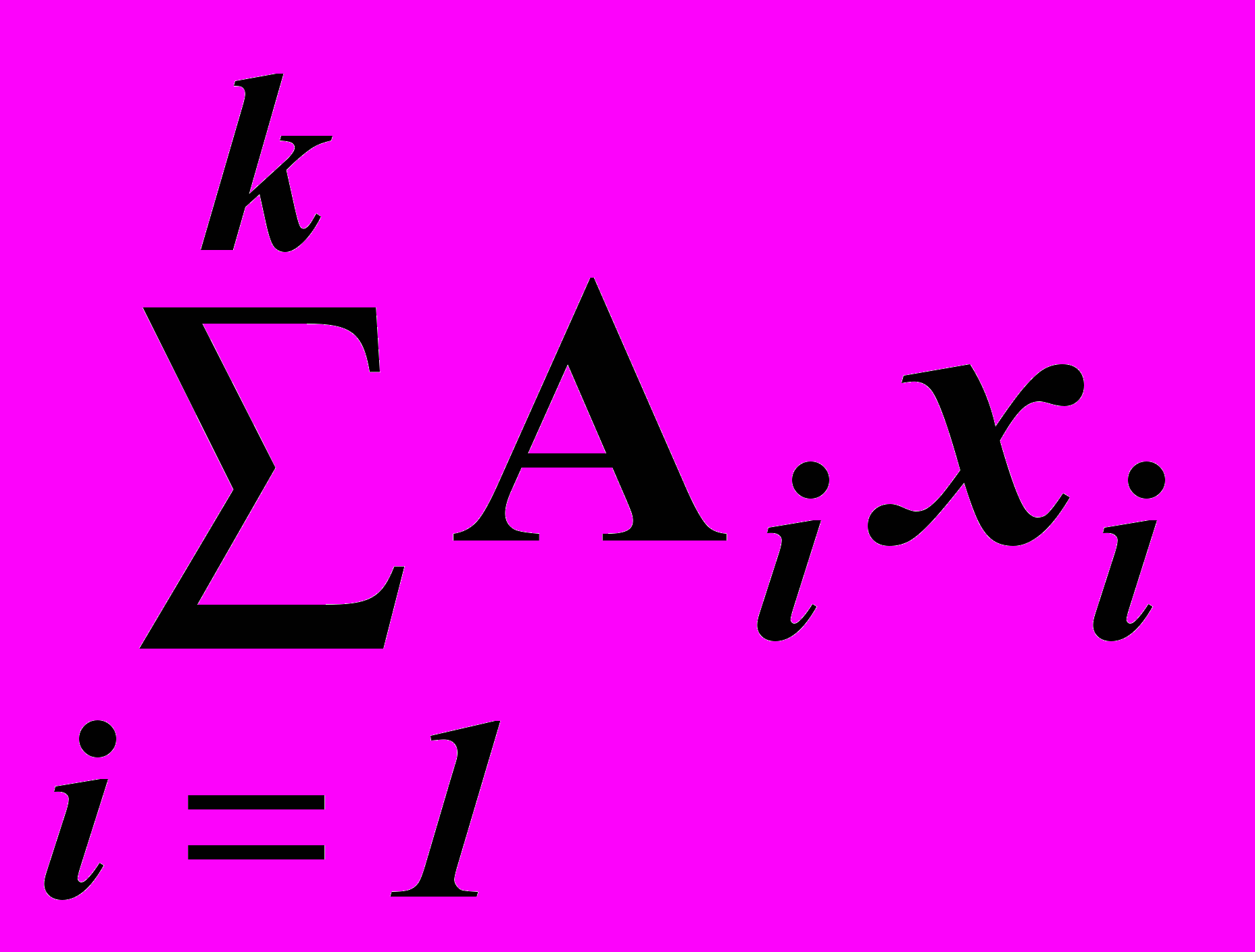= A₀.

Допустим, что система векторов A₁, А₂, ..., A_k линейно зависима. Тогда существуют такие числа l₁, l₂, ..., l_k, не все равные нулю, при которых выполняется соотношение

l₁A₁ + l₂А₂ + ... + l_kA_k = 0. (*)

По условию,

x₁A₁ + x₂А₂ + ... + x_kA_k = A₀. (**)

Зададим некоторое число >0, умножим на него равенство (*); прибавляя и вычитая результат из (**), получим:

(x₁+l₁)A₁ + (x₂+l₂)A₂ + … + (x_k+l_k)A_k = A₀,

(x₁ - l₁)A₁ + (x₂ - l₂)A₂ + … + (x_k - l_k)A_k = A₀.


Т.е. система уравнений (4) имеет два решения, которые могут и не быть планами:

Х₁=(x₁+l₁; x₂+l₂; …; x_k+l_k; 0; …; 0),

Х₂=(x₁ - l₁; x₂ - l₂; …; x_k - l_k; 0; …; 0).

Так как все x_i>0, то число  можно выбрать настолько малым, что все первые k компонент Х₁ и Х₂ примут положительные значения, тогда Х₁ и Х₂ - планы.


При этом 0.5Х₁ + 0.5Х₂ = X,

т. е. Х - выпуклая линейная комбинация точек Х₁ и Х₂, что противоречит условию теоремы о том, что Х - угловая точка.

Итак, допущение, что система векторов A₁, А₂, ..., A_k линейно зависима, привело к противоречию. Следовательно, сделанное допущение неверно и система векторов линейно независимая. 


Следствие1. Так как векторы A₁, А₂, ..., A_n имеют размерность т, то угловая точка многогранника решений имеет не более чем т положительных компонент.


Следствие2. Каждой угловой точке многогранника решений соответствует kт линейно независимых векторов системы A₁, А₂, ..., A_n.


Не теряя общности, можно предположить, что система векторов A₁, А₂, ..., A_n задачи линейного программирования (1) - (3) всегда содержит т линейно независимых векторов. Если при решении частной задачи это свойство не очевидно, то первоначальную систему векторов дополняют т линейно независимыми векторами, затем находят решение расширенной задачи.


Итак, если целевая функция задачи линейного программирования ограничена на многограннике решений, то:


1) существует такая угловая точка многогранника решений, в которой целевая функция задачи линейного программирования достигает своего оптимума;


2) каждый опорный план соответствует угловой точке многогранника решений.


Поэтому для решения задачи линейного программирования необходимо исследовать только угловые точки многогранника решений, т. е. только опорные планы.