Введение в линейное программирование Задача планирования производства
| Вид материала | Задача |
- Введение в линейное программирование линейное программирование (ЛП), 139.72kb.
- Линейное программирование, 346.17kb.
- Программа дисциплины Линейное программирование Семестр, 17.93kb.
- Аттестационное тестирование в сфере профессионального образования, 72.49kb.
- Курс является базовым как для изучения других математических дисциплин, так и для более, 39.9kb.
- Под названием "транспортная задача" объединяется широкий круг задач с единой математической, 142.19kb.
- 2. Линейное программирование (ЛП), 18.32kb.
- Контрольная работа по темам «Линейное программирование на Паскале» и«Условный оператор», 4.21kb.
- Федеральное агентство по образованию, 124.95kb.
- Вопросы к зачету по дисциплине «Корпоративное планирование», 48.25kb.
Введение в линейное программирование
Задача планирования производства
Задача планирования производства содержательно ставится следующим образом.
Пусть имеется некоторый экономический объект (предприятие, цех, артель и т. п.). Необходимо спланировать производство n видов продукции, если известно:
- на производство всех видов продукции используется m видов ресурсов, причем запасы каждого из них ограничены, и пусть bi (i=1,2,…,m) – это количество ресурса i-го вида, которое имеется в наличии;
- известна величина aij – количество i-го ресурса (i=1,2,…,m), которое затрачивается на производство одной единицы j-го продукта (j=1,2,…,n);
- известна стоимость cj (j=1,2,…,n) реализации одной единицы j-го продукта.
Требуется составить оптимальный план производства продукции, то есть такой план, который максимизирует суммарную прибыль от реализации всей произведенной продукции и при этом не происходит перерасхода ресурсов.
^ Строим экономико-математическую модель задачи.
- Выбираем управляемые переменные, то есть такие переменные, на которые вы можете воздействовать и значения которых собираетесь искать в вашей задаче. Имеющиеся данные, на значения которых вы не можете влиять, называются константами или параметрами.
Введем переменную xj (j=1,2,…n) – количество выпускаемой продукции j-го вида.
- Построим функцию цели, отражающую эффективность решения задачи. Ее значения зависят от значений управляющих переменных, и она дает возможность сравнивать варианты решений по эффективности.
В нашем случае такой функцией является суммарная прибыль
 .
.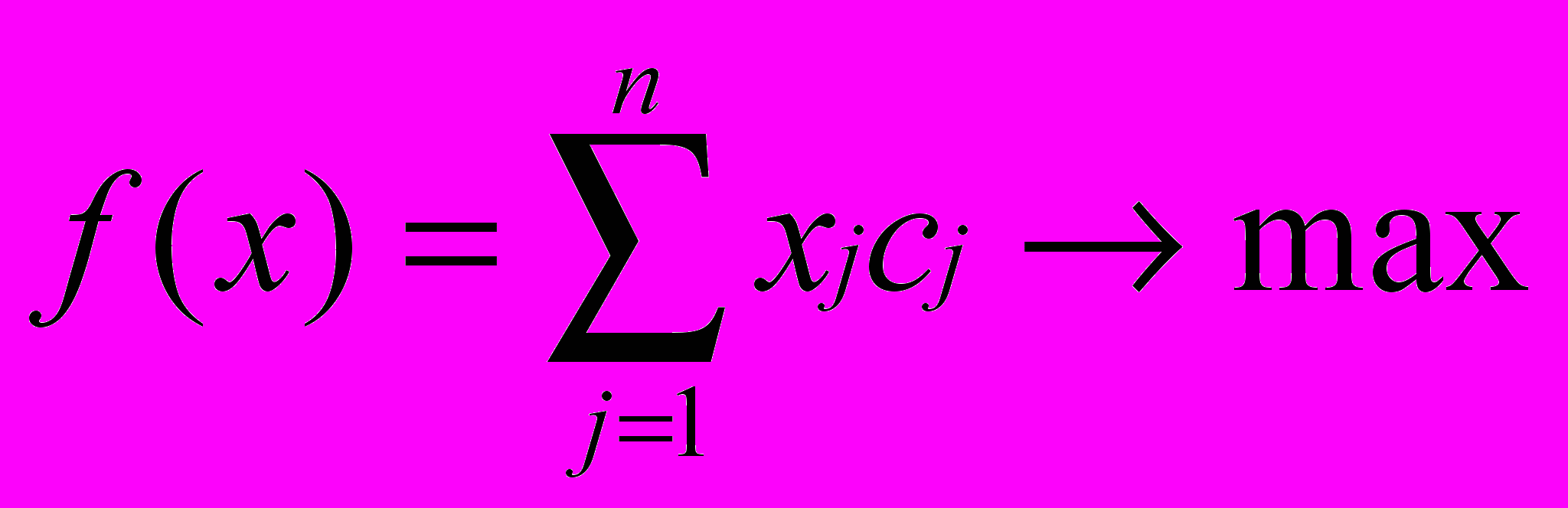 (1)
(1)Мы будем максимизировать функцию цели.
- Введем ограничения на управляемые переменные – количество ресурсов каждого вида ограничено величиной bi (i=1,2,…,m).
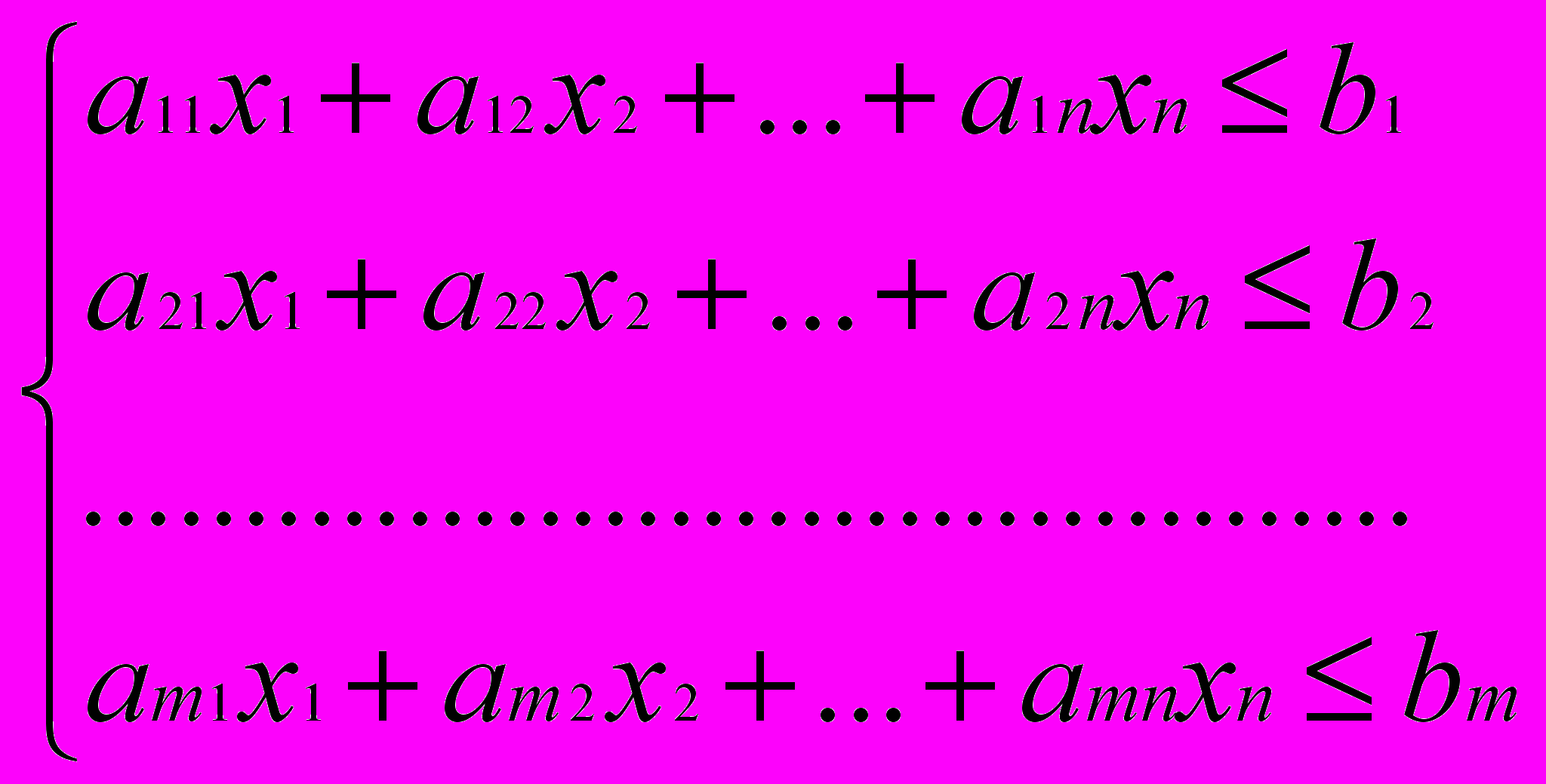 (2)
(2)К системе (2) также должны быть добавлены естественные ограничения на неотрицательность компонентов плана производства:
xj 0, j=1,2,…,n (3)
^ Решить задачу – значит найти такой вектор
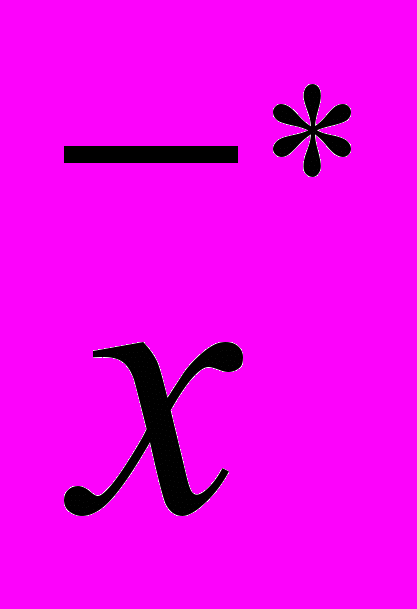 ,который будет удовлетворять всем ограничениям (2), (3) и максимизировать функцию цели.
,который будет удовлетворять всем ограничениям (2), (3) и максимизировать функцию цели.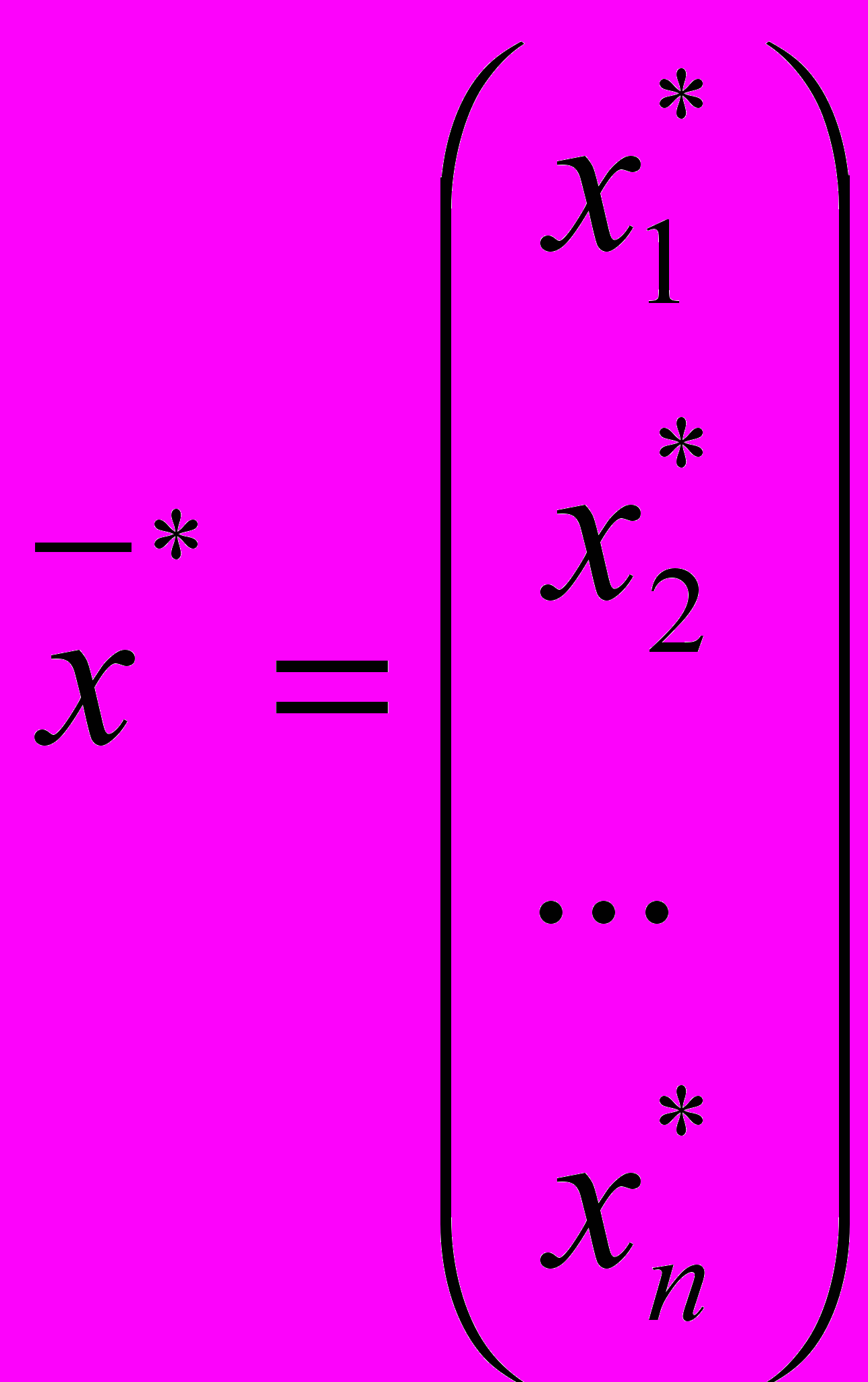
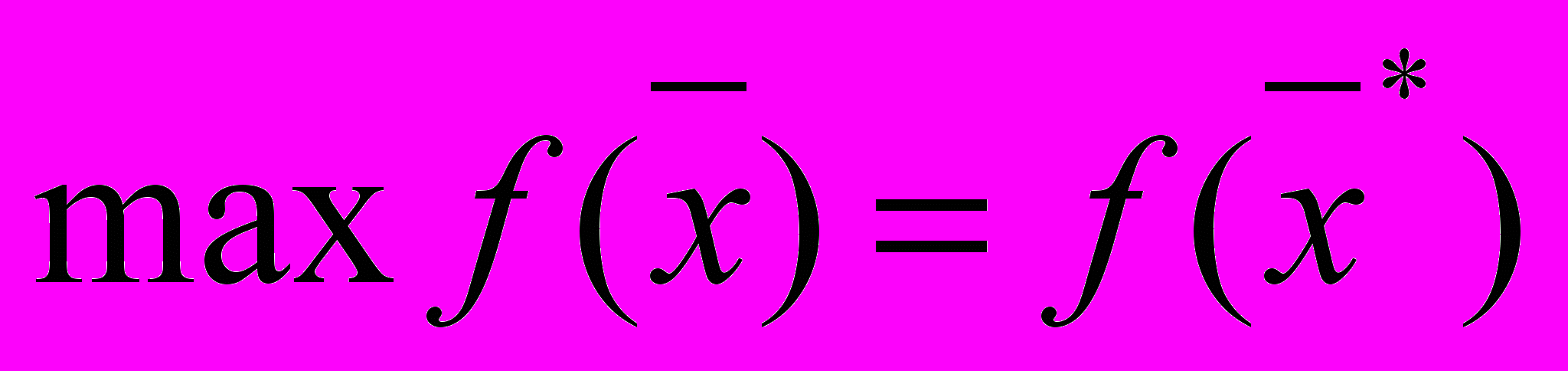
Легко заметить, что функция
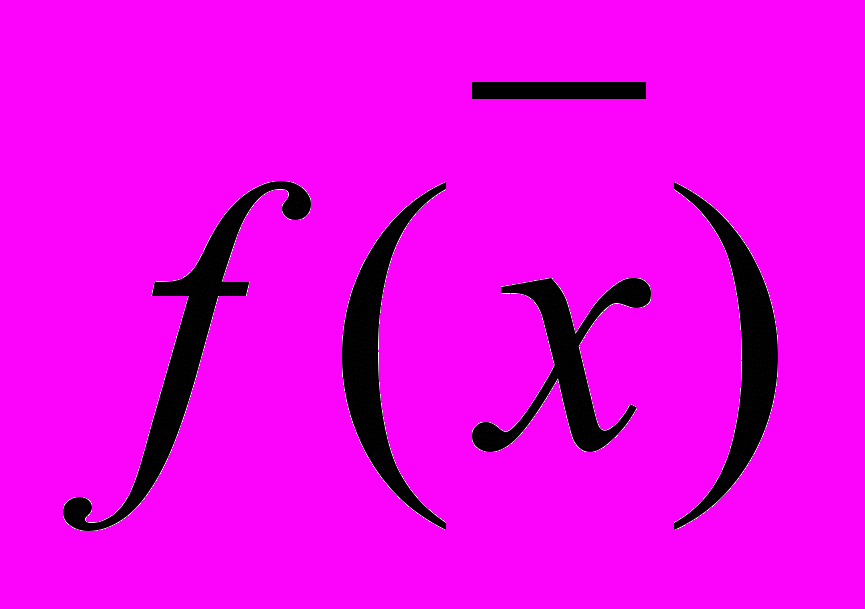 - линейная, так как все переменные используются в ней только в первой степени. Ограничения (2) представляют собой систему линейных неравенств, (3) – также линейное неравенство. Такую задачу называют задачей линейного программирования (ЗЛП).
- линейная, так как все переменные используются в ней только в первой степени. Ограничения (2) представляют собой систему линейных неравенств, (3) – также линейное неравенство. Такую задачу называют задачей линейного программирования (ЗЛП).Несмотря на явную условность рассматриваемой ситуации и кажущуюся простоту задачи (1)-(3), ее решение является далеко не тривиальным и во многом стало практически возможным только после разработки специального математического аппарата. Существенным достоинством используемых здесь методов решения является их универсальность, поскольку к модели (1)-(3) могут быть сведены очень многие как экономические, так и неэкономические проблемы.
^ Задача о составлении рациона (о диете, о смесях)
Имеется n видов продуктов питания и m химических элементов, необходимых для суточного потребления.
aij – содержание i-го (i=1,2,…,m) химического элемента в одной единице j-го (j=1,2,…,n) продукта питания.
bi – минимальное суточное потребление i-го химического элемента.
cj – стоимость одной единицы j-го продукта питания.
Требуется составить суточный рацион питания – сколько продуктов каждого вида нужно приобрести, чтобы рацион имел минимальную стоимость, и питание было разнообразным.
В задаче о диете стоимость можно заменить на калорийность продуктов питания, и сформулировать задачу в следующем виде: питание должно быть низкокалорийным, но содержать все необходимые для суточного потребления химические элементы.
^ Строим экономико-математическую модель.
Управляемая переменная xj – количество продукта j-го вида, которое будем приобретать (j=1,2,…,n).
Функция цели – суммарная стоимость продуктов питания
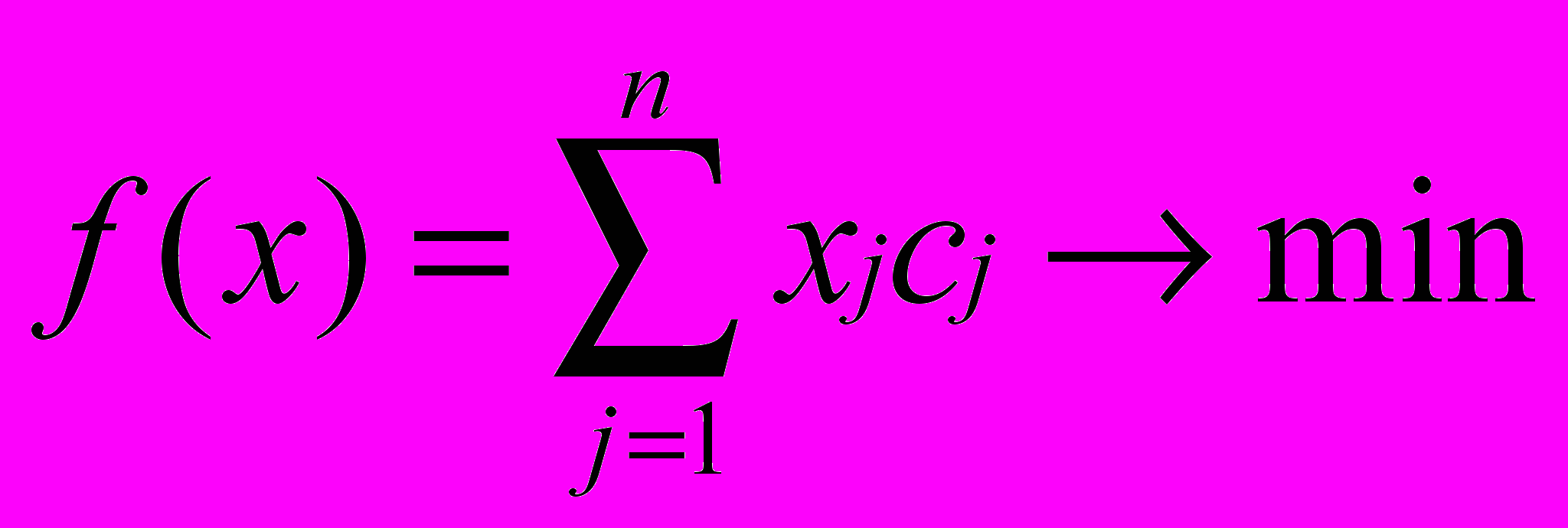 (1)
(1)Ограничения
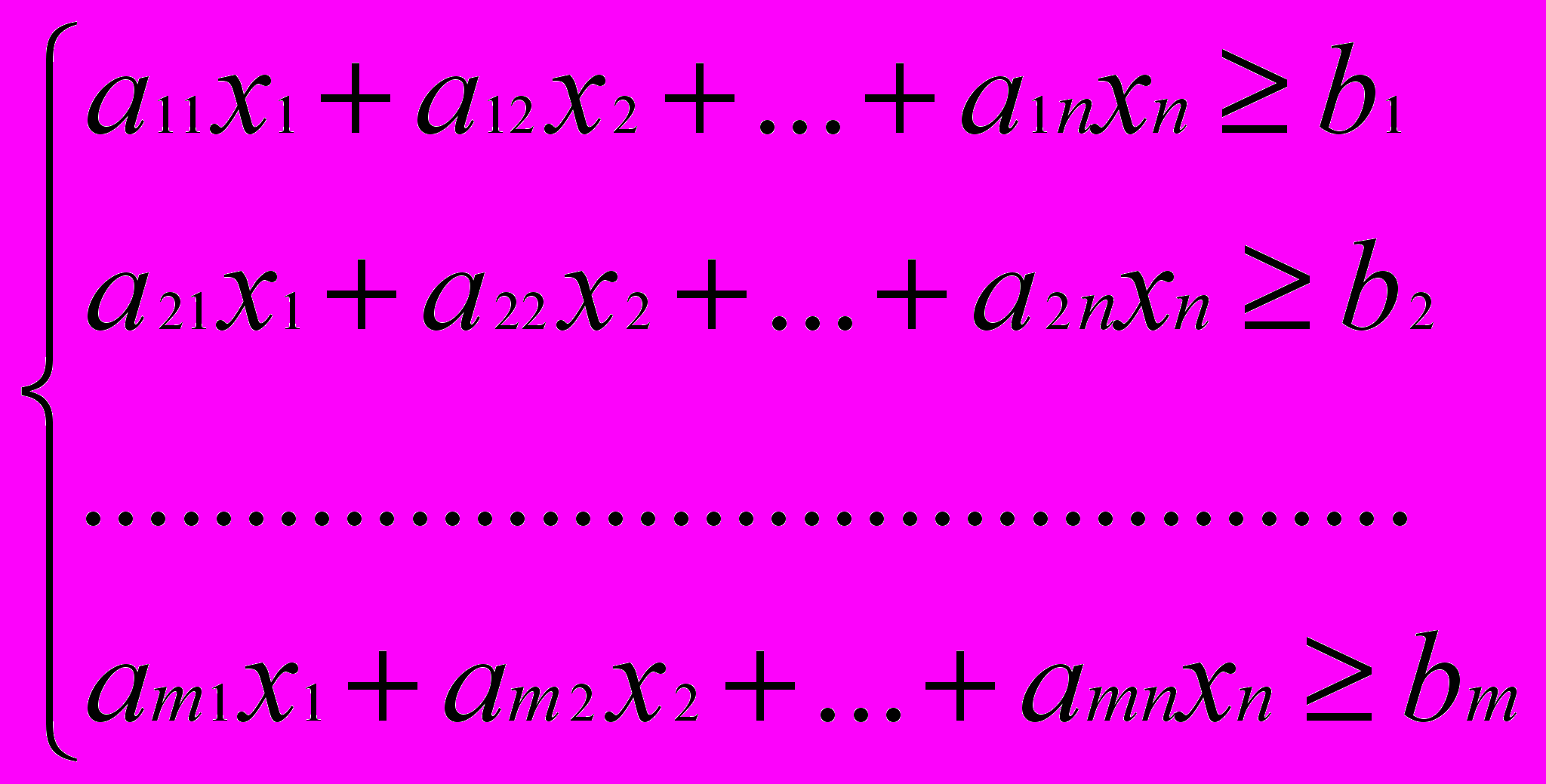 (2)
(2)xj 0, j=1,2,…,n (3)
Решить задачу – значит найти вектор
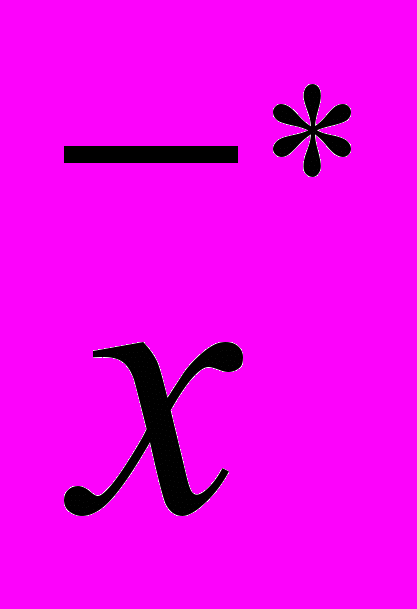 , такой, что
, такой, что  при условиях (2) и (3).
при условиях (2) и (3).Эта задача также является задачей линейного программирования. Можно формально свести эту задачу к предыдущей, если вместо минимизации функции
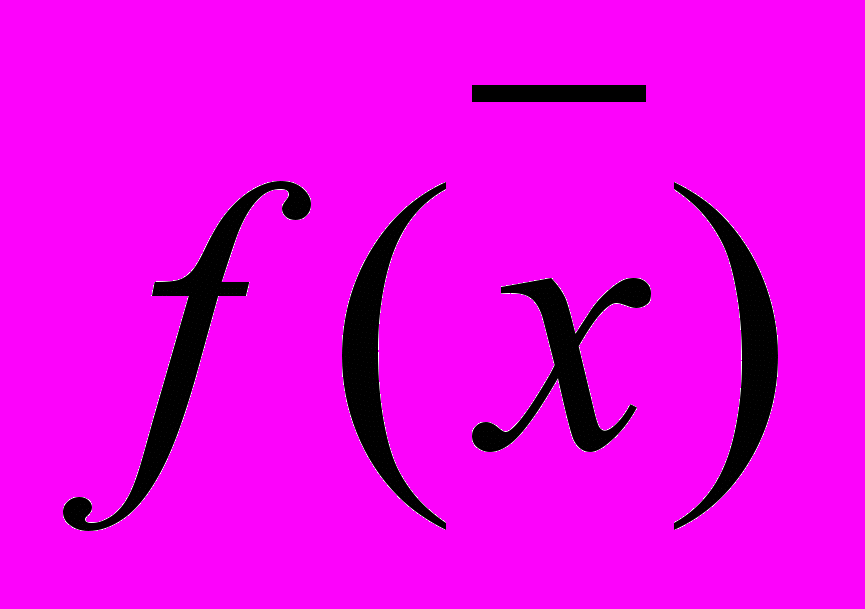 рассматривать максимизацию функции
рассматривать максимизацию функции 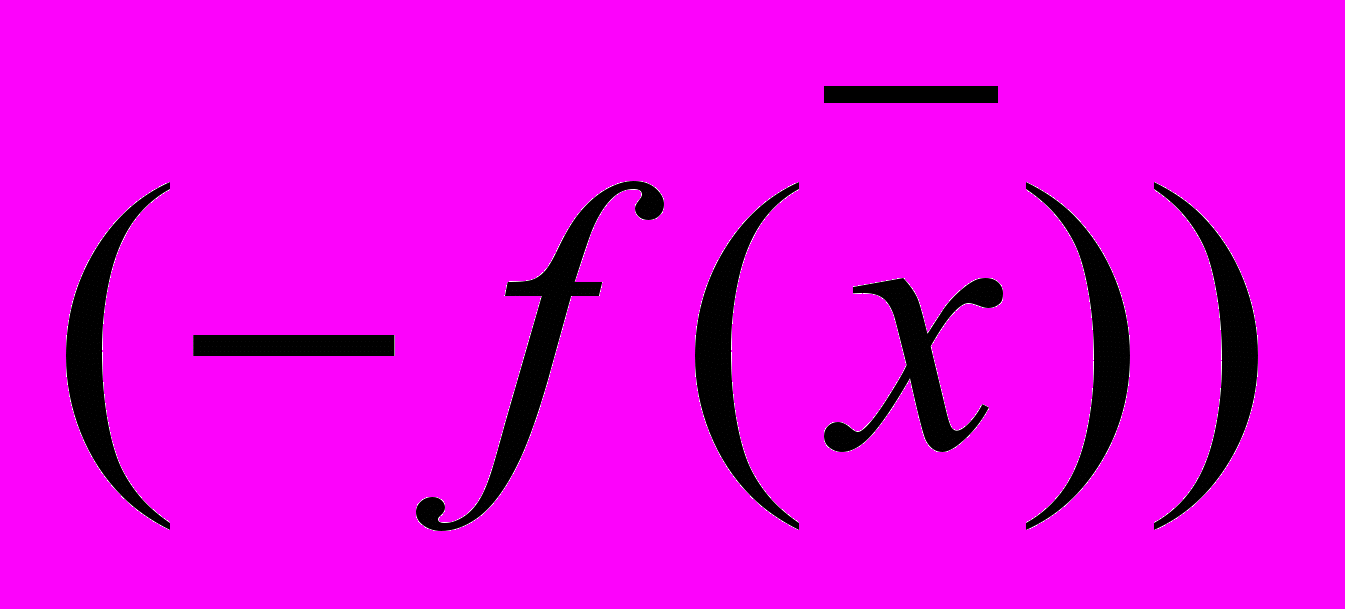 , а ограничение вида
, а ограничение вида 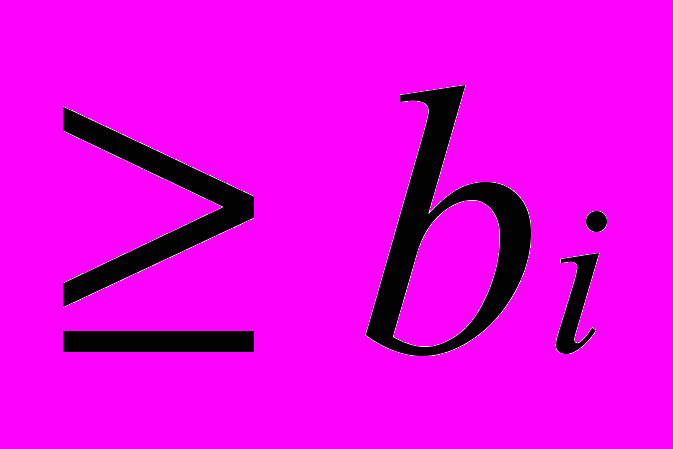 свести к ограничению вида
свести к ограничению вида 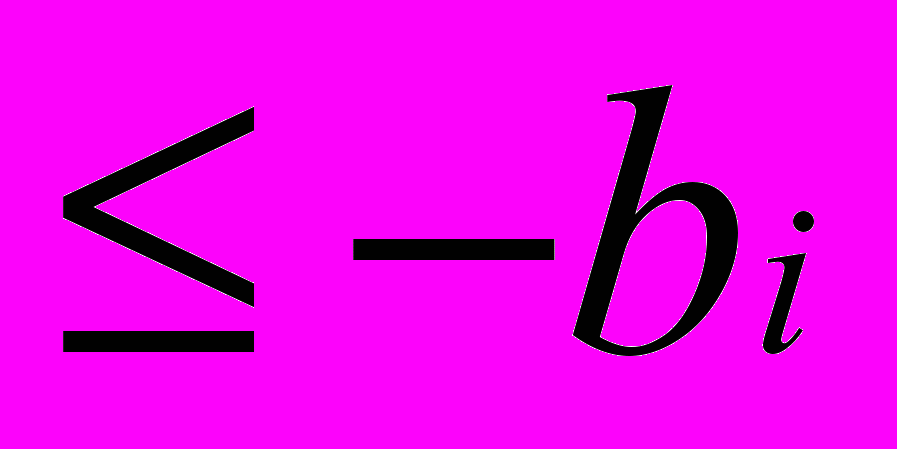 .
.^ Задача об использовании мощностей (задача о загрузке оборудования).
Предприятию задан план производства продукции по времени и номенклатуре: требуется за время T выпустить n1, n2, …, nk единиц продукции P1, P2, …, Pk. Продукция производится на станках S1, S2, …, Sm. Для каждого станка известны производительность aij (т.е. число единиц продукции, которое можно произвести на станке Si) и затраты bij на изготовление продукции Pj на станке Si в единицу времени.
Необходимо составить такой план работы станков (т.е. так распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.
^ Составим экономико-математическую модель задачи.
Обозначим хij- время, в течение которого станок Si будет занят изготовлением продукции Pj (i-1,…,m; j=1,…,n).
Время работы каждого станка ограничено и не превышает Т. Следовательно:
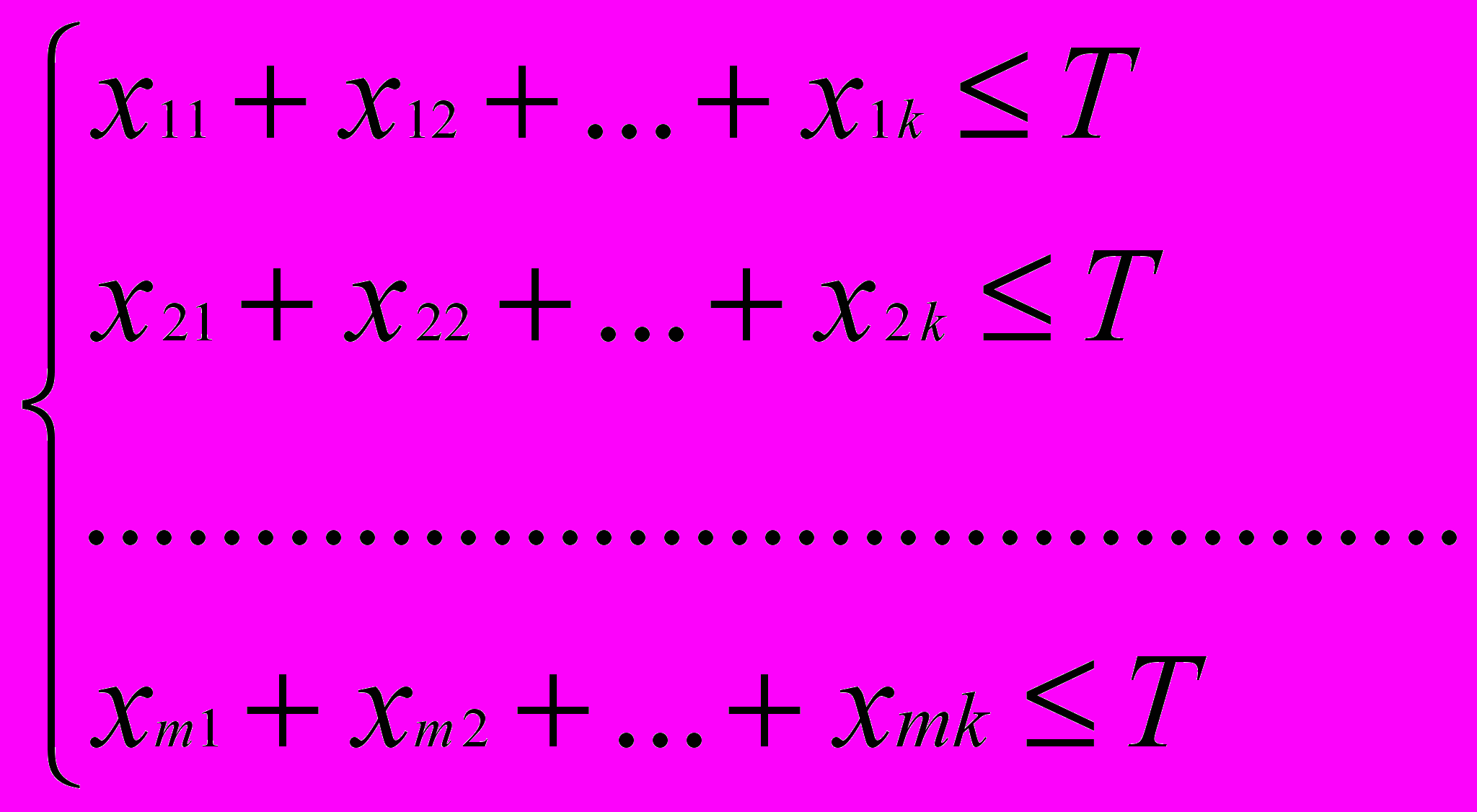 (1)
(1)Для выполнения плана по номенклатуре необходимо, чтобы выполнялись следующие равенства:
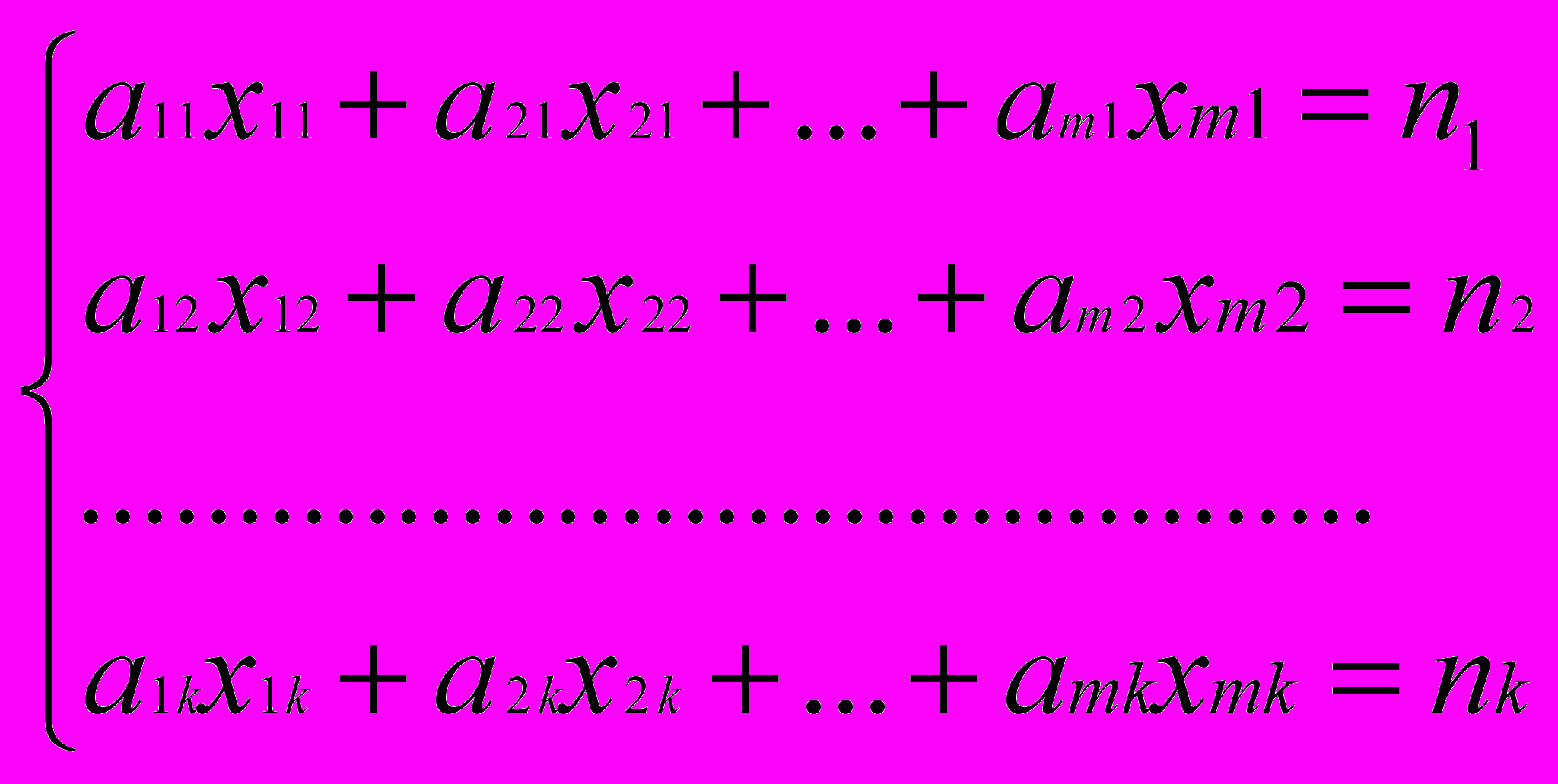 (2)
(2)Кроме того xij≥0 (i-1,…,m; j=1,…,k) (3)
Затраты на производство всей продукции выразятся функцией
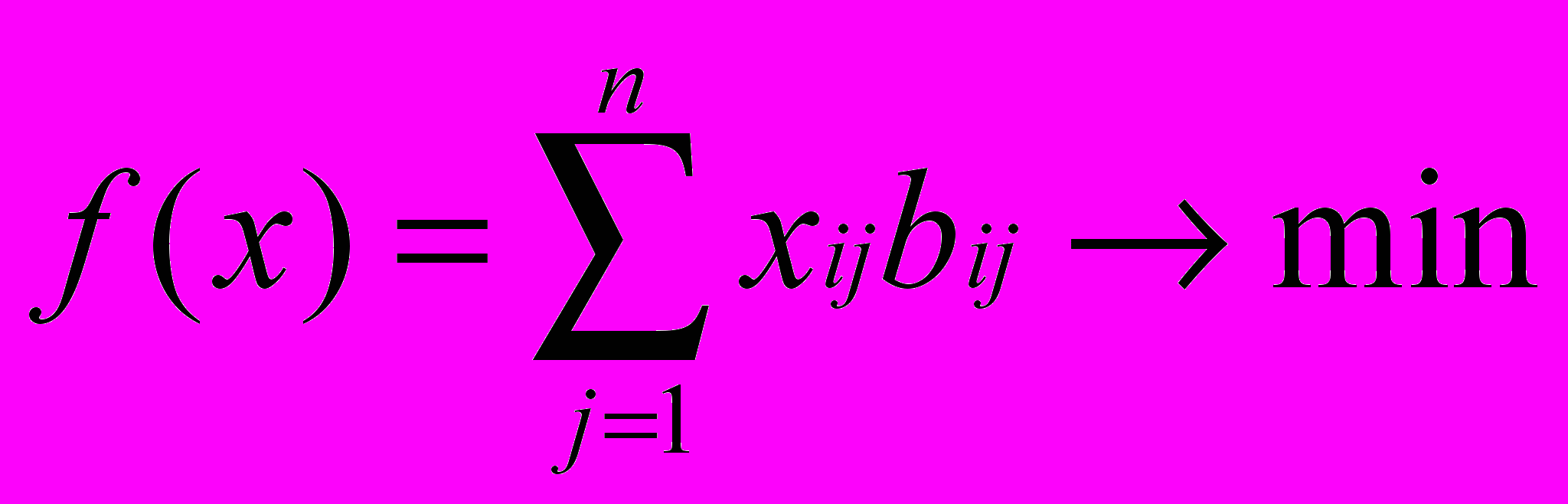
Задача состоит в том, чтобы найти Х-(хij), удовлетворяющее всем условиям (1)-(3) ограничений, при котором функция f(x) принимает минимальное значение.
Общим для рассмотренных выше задач является то, что в них стоит проблема поиска наибольшего или наименьшего (оптимального) значения некоторой функции, отражающей цель управления системой, или, как еще говорят, функции цели. Поиск оптимального значения осуществляется на некотором подмножестве допустимых значений переменных, описывающих состояние этой системы, именуемом множеством допустимых планов.
^ Общая постановка задачи линейного программирования (ЗЛП)
Найти вектор
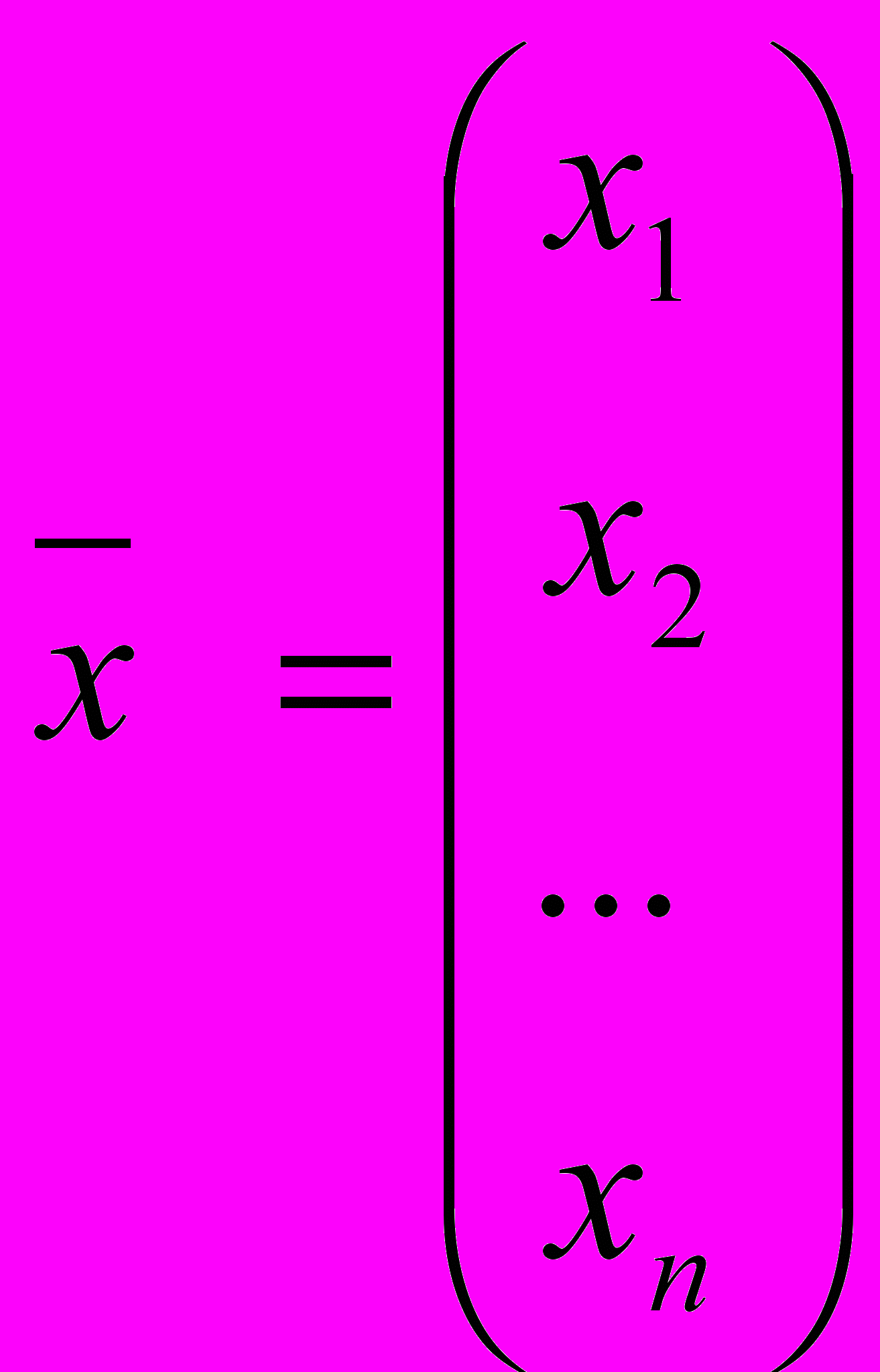 пространства En который максимизирует (минимизирует) функцию цели
пространства En который максимизирует (минимизирует) функцию цели 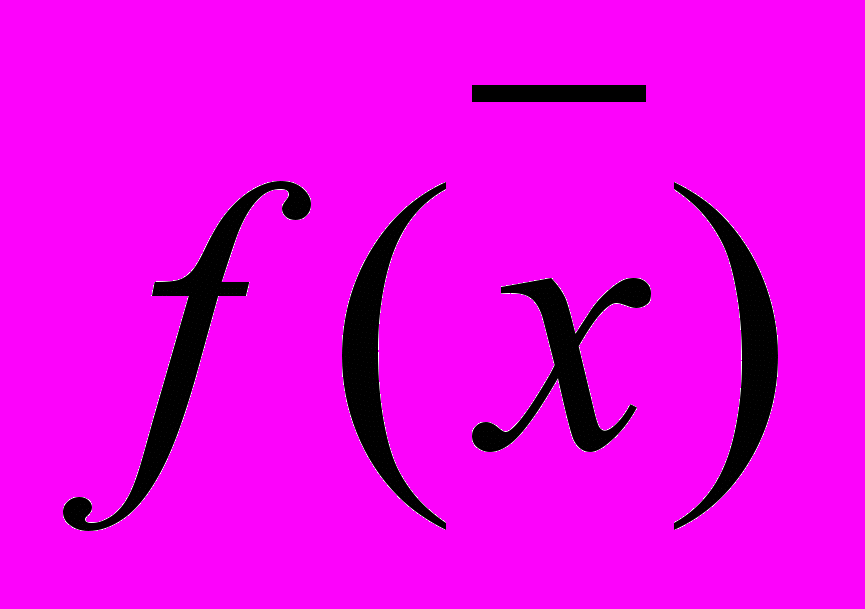
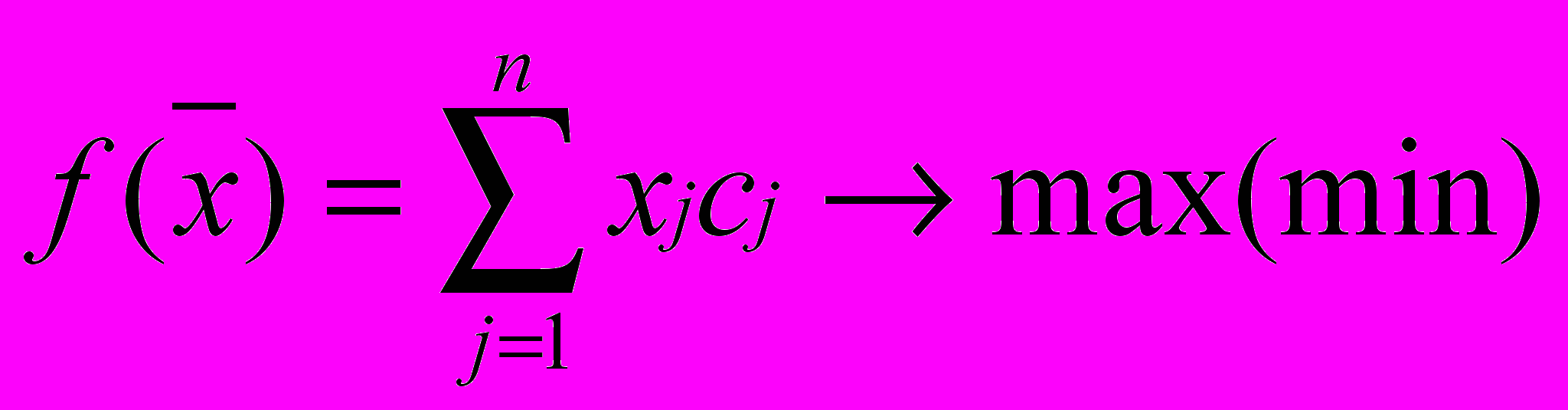 (1)
(1)при следующих условиях
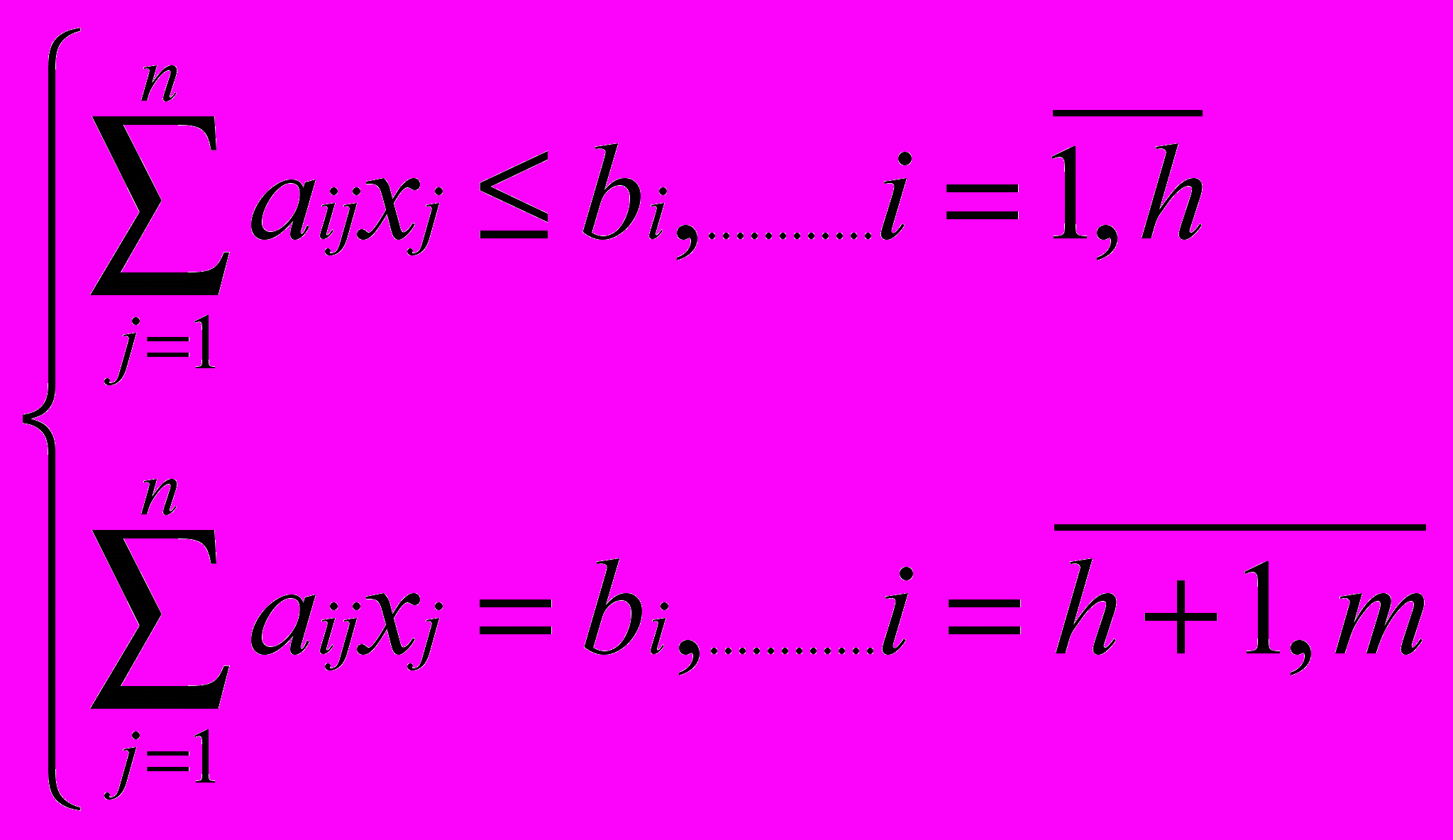 (2)
(2)x1,x2,…,xp≤0, (p≤n) (3)
- - функция цели
- - функциональные ограничения задачи (система линейных неравенств и уравнений)
- - прямые ограничения задачи
Условимся относительно терминологии, которую будем использовать в дальнейшем.
Вектор
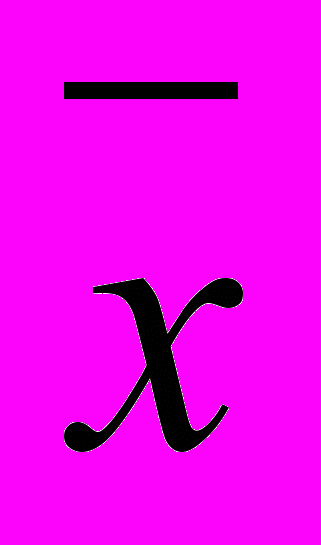 пространства En, координаты которого удовлетворяют всем ограничниям (2) и (3) общей задачи линейного программирования называется планом (допустимым планом) ЗЛП.
пространства En, координаты которого удовлетворяют всем ограничниям (2) и (3) общей задачи линейного программирования называется планом (допустимым планом) ЗЛП.Множество всех планов ЗЛП называется областью допустимых планов ЗЛП и обозначается ОДП. Решение ЗЛП находится на границе области ОДП.
^ Оптимальным планом ЗЛП (решением ЗЛП) называется такой план
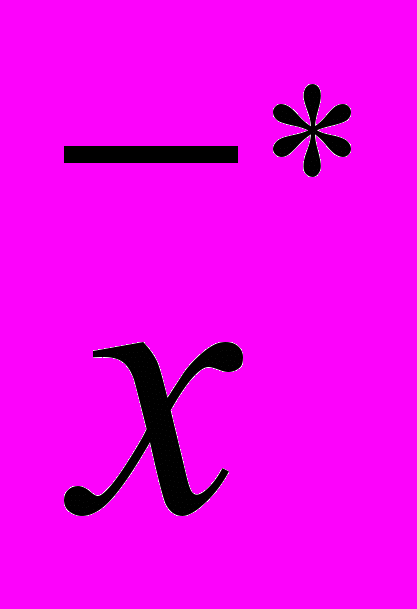 , при котором целевая функция достигает оптимального (в нашем случае максимального) значения -
, при котором целевая функция достигает оптимального (в нашем случае максимального) значения - 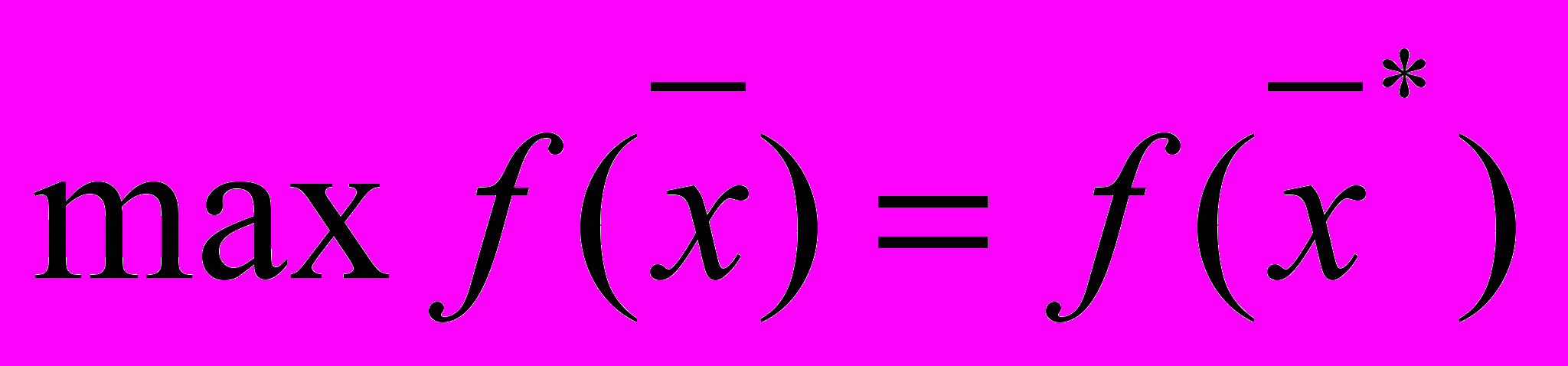 .
.^ Каноническая задача линейного программирования (КЗЛП)
Эффективного программного решения общей задачи линейного программирования не существует, так как в ней присутствуют линейные неравенства. Поэтому задачи линейного программирования решают косвенно посредством другой задачи – канонической задачи линейного программирования (КЗЛП). Вся теория линейного программирования разработана для канонической задачи.
Кроме того, легко показать, что:
- Для каждой ЗЛП существует соответствующая ей КЗЛП
- Соответствующие задачи эквивалентны:
- Если ЗЛП имеет конечное решение, то и соответствующая ей КЗЛП имеет конечное решение. Причем решая КЗЛП, мы находим одновременно решение ЗЛП.
- Если ЗЛП не имеет конечного решения (т.е. функция
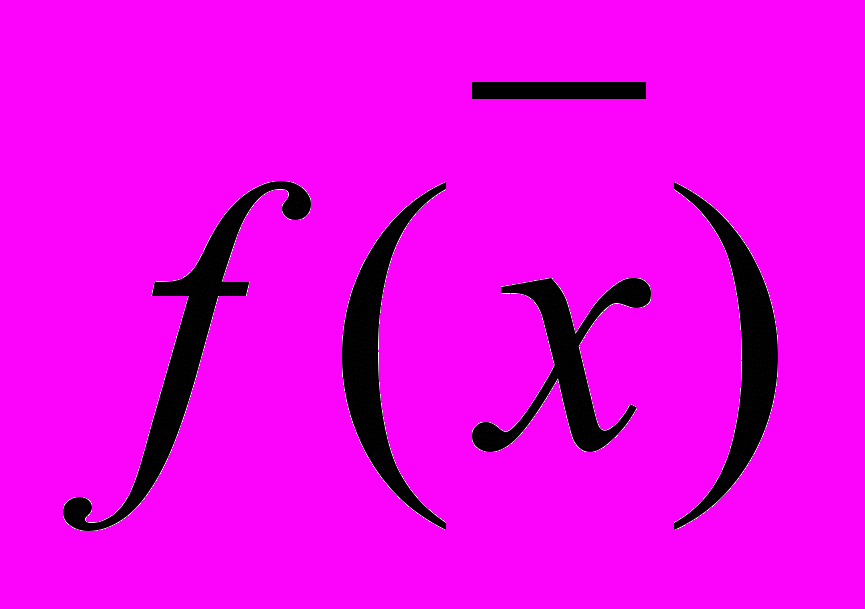 неограниченно растет на множестве планов), то и КЗЛП не имеет конечного решения.
неограниченно растет на множестве планов), то и КЗЛП не имеет конечного решения.
- Если множество планов ЗЛП пусто (Р=Ø), то есть система ограничений несовместна (не имеет решений), то и множество планов КЗЛП пусто.
- Если ЗЛП имеет конечное решение, то и соответствующая ей КЗЛП имеет конечное решение. Причем решая КЗЛП, мы находим одновременно решение ЗЛП.
^ Канонической задачей линейного программирования называют следующую задачу:
Найти вектор
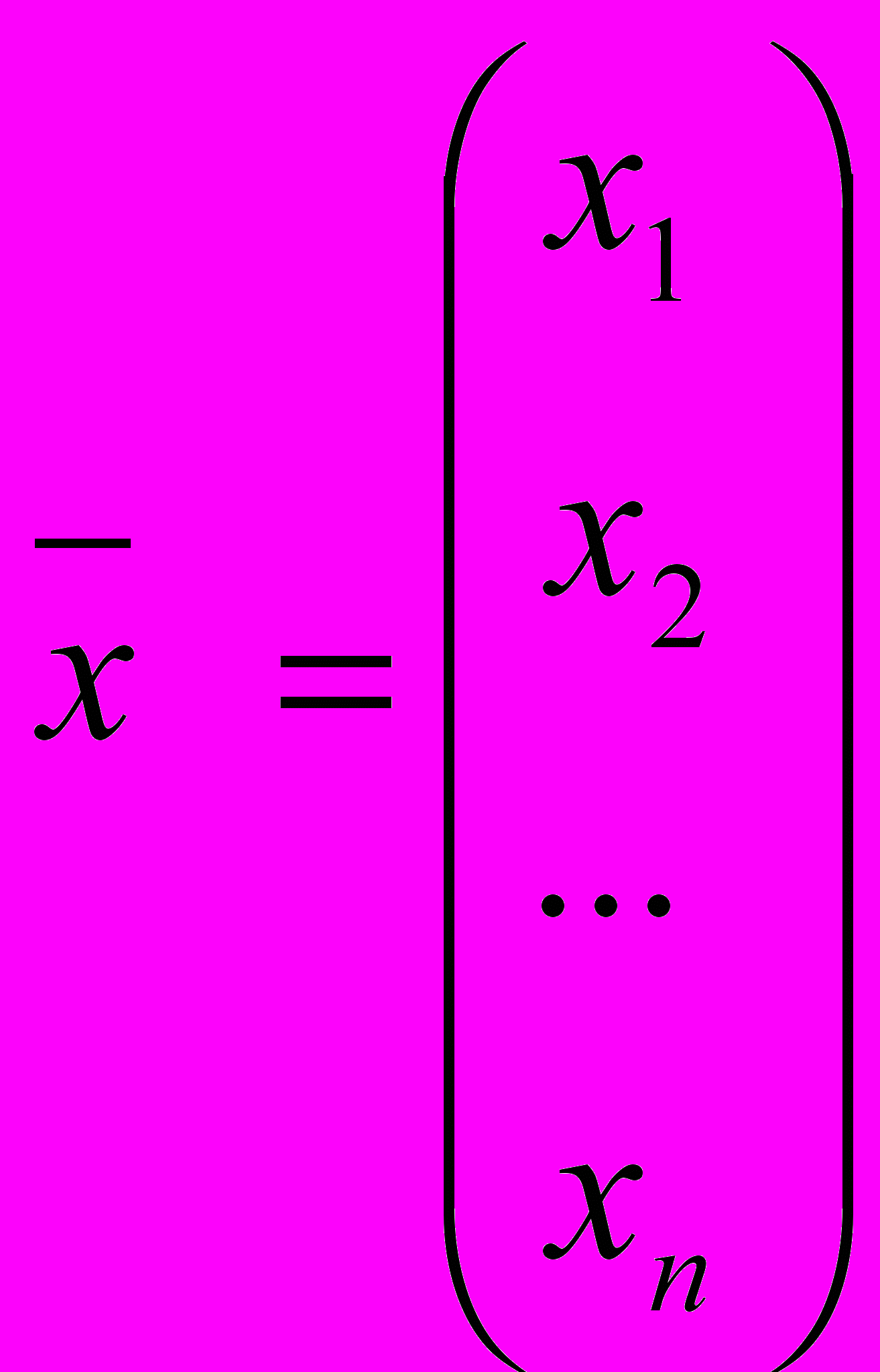 пространства En который максимизирует функцию цели
пространства En который максимизирует функцию цели 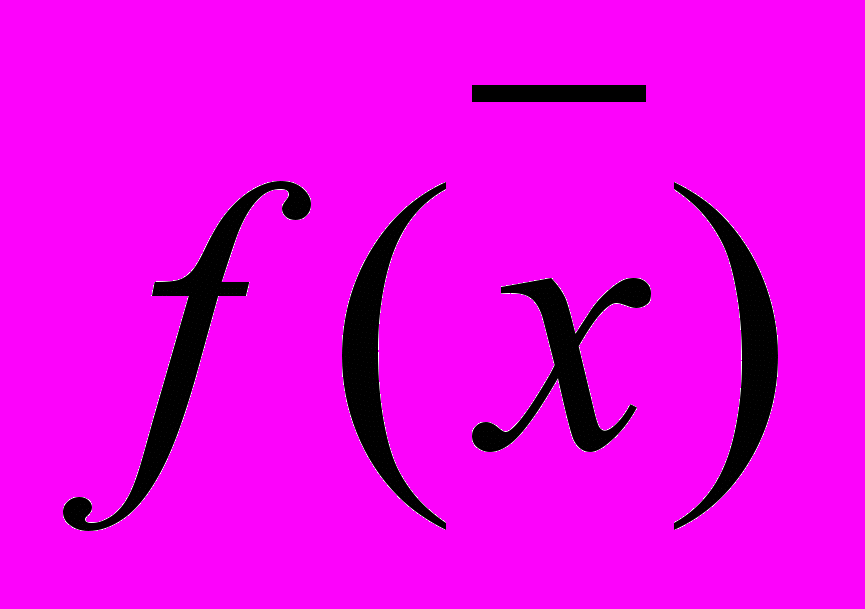
 (1)
(1)при следующих условиях
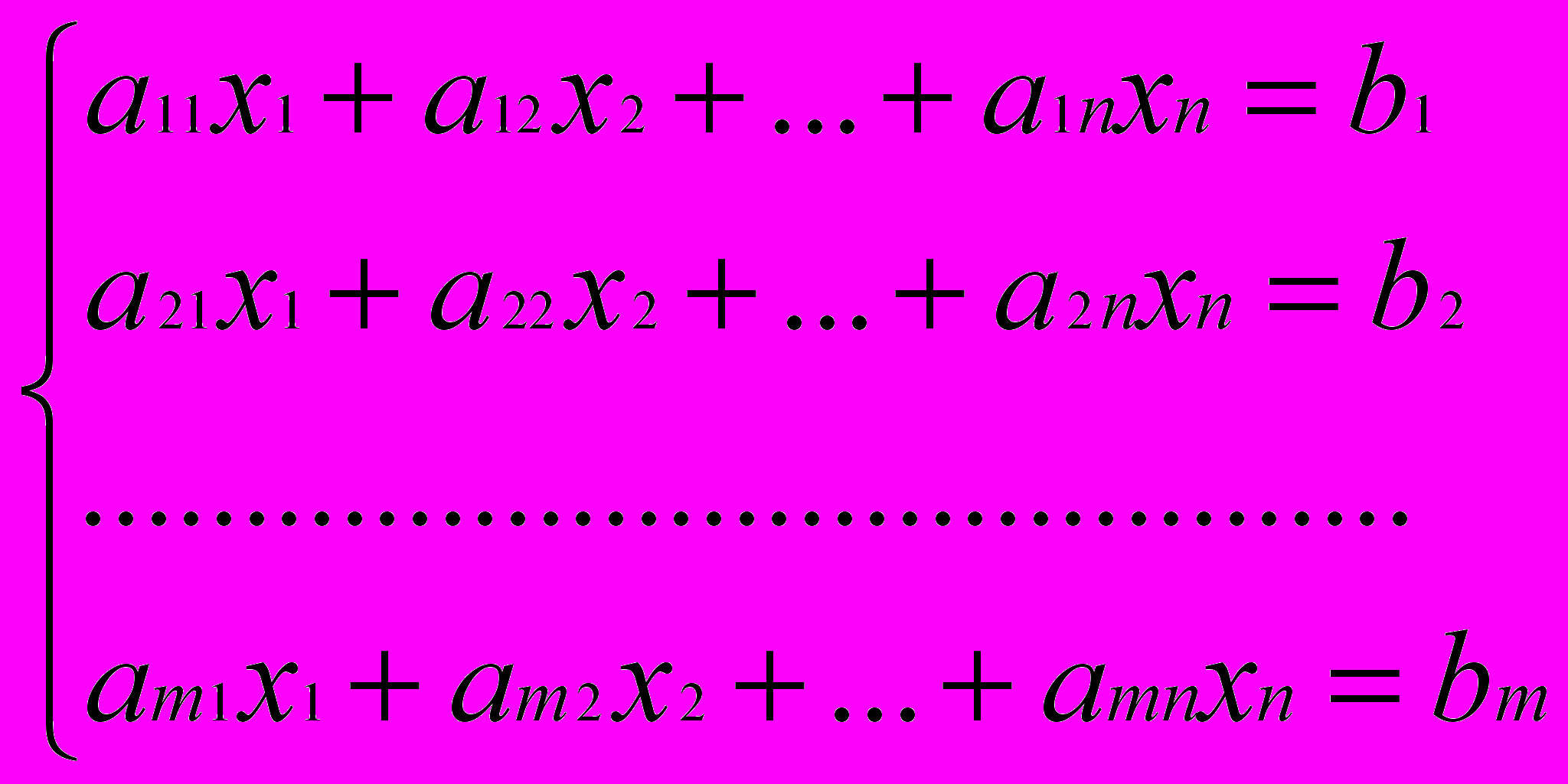 (2)
(2)x1,x2,…,xn≥0 (3)
Характерные особенности канонической задачи:
- Максимизация функции цели
- Функциональные ограничения представляют собой систему линейных уравнений (СЛУ)
- Все без исключения переменные должны быть неотрицательными
Общая идея перехода от ЗЛП к КЗЛП достаточно проста:
- ограничения в виде неравенств преобразуются в уравнения за счет добавления фиктивных неотрицательных переменных
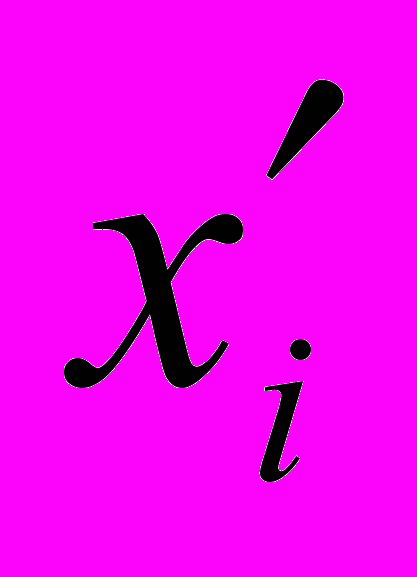 (i=1,2,…,m), которые одновременно входят в целевую функцию с коэффициентом 0, то есть не оказывают влияния на ее значение;
(i=1,2,…,m), которые одновременно входят в целевую функцию с коэффициентом 0, то есть не оказывают влияния на ее значение;
- переменные, на которые не наложено условие неотрицательности, представляются в виде разности двух новых неотрицательных переменных:
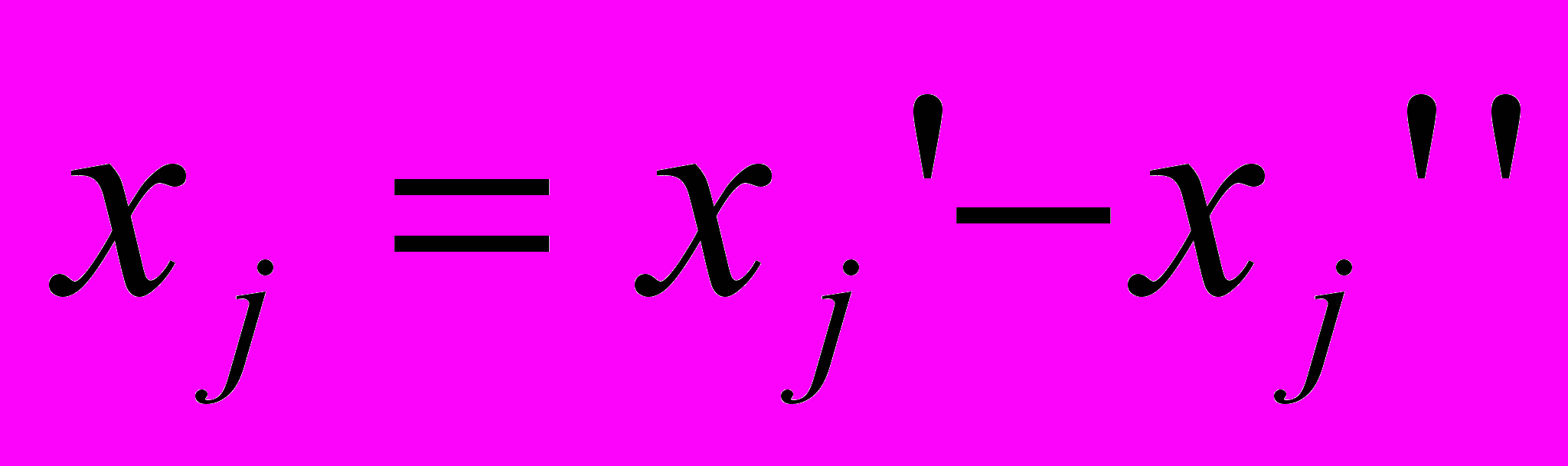 ,
, 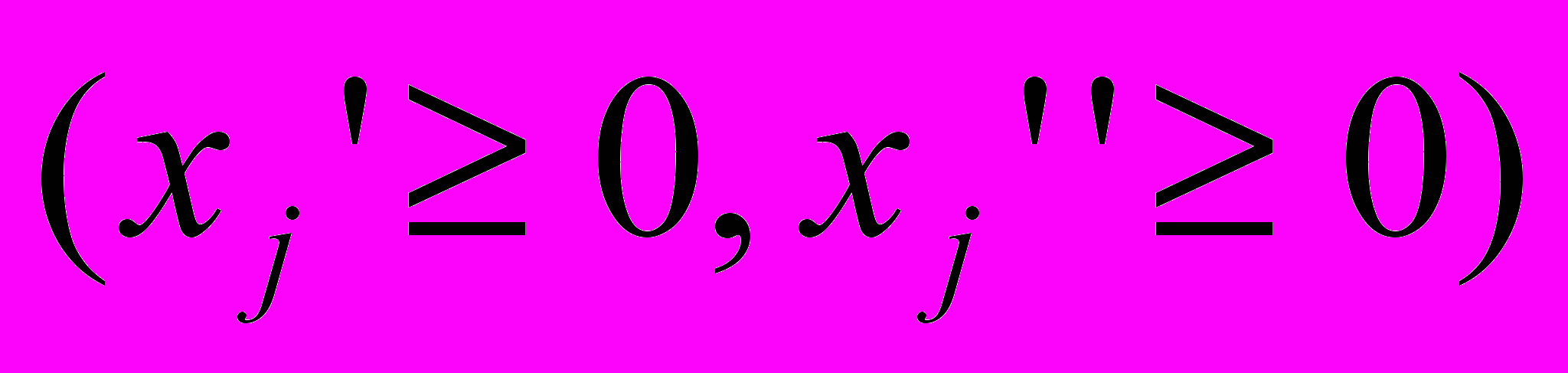
Рассмотрим на примере как приводить ЗЛП к КЗЛП.
Пример 1.
Пусть дана ЗЛП
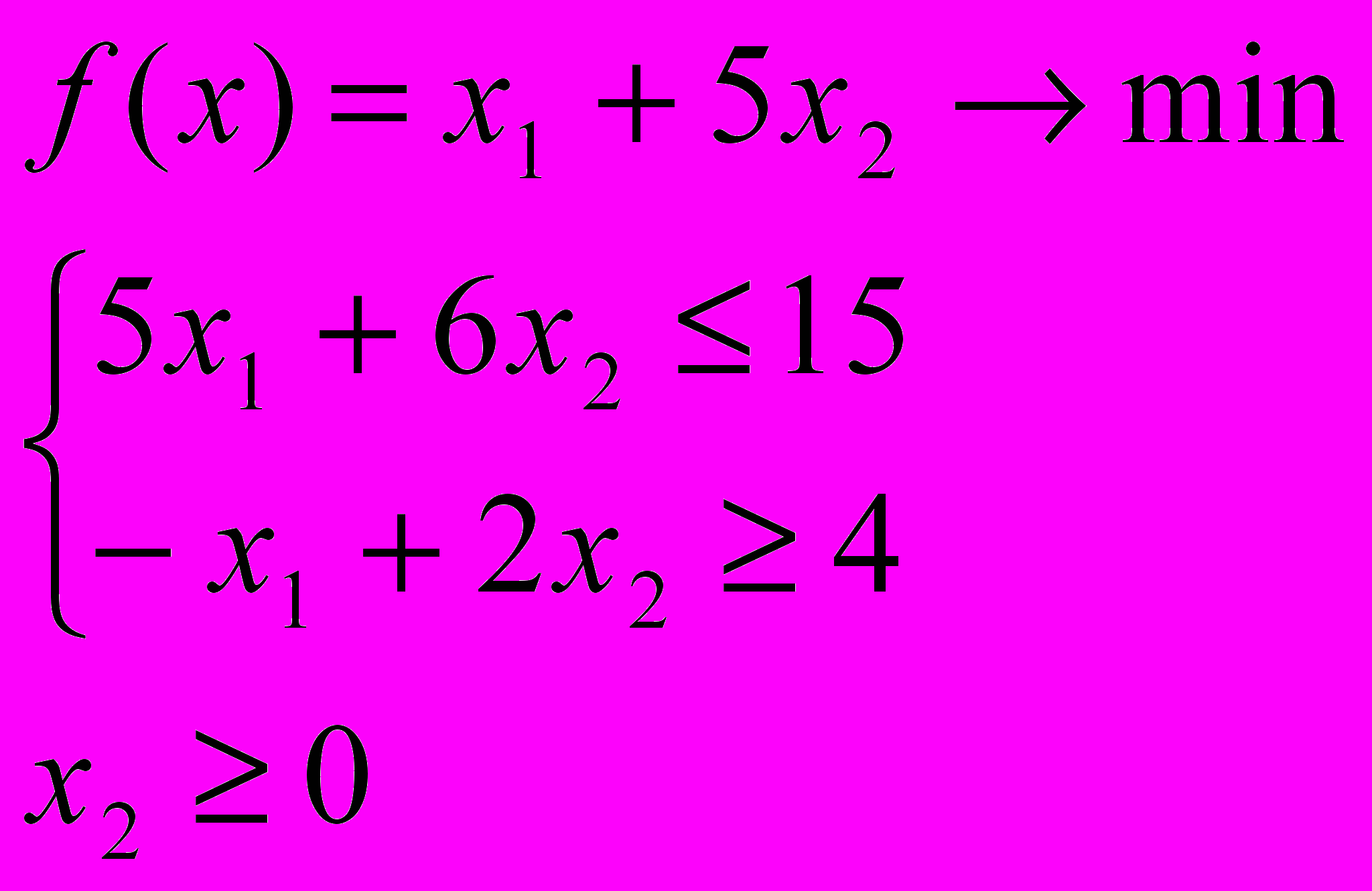
Приводим к КЗЛП
Функция цели для КЗЛП будет выглядеть следующим образом:
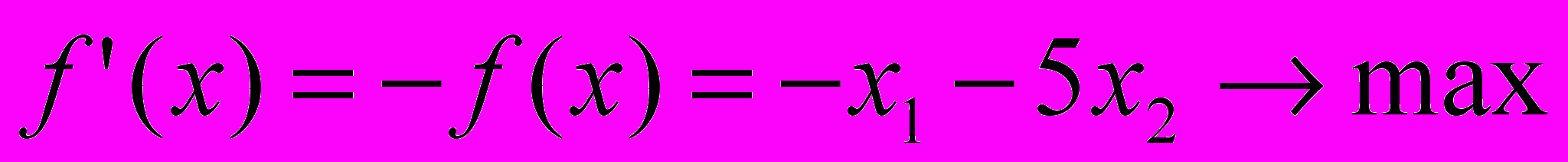
Далее приведем к нужному нам виду прямые ограничения задачи. Любое число можно представить как разницу двух неотрицательных чисел (например 1-6=5). Так мы поступим со всеми переменными, на которые нет прямых ограничений в ЗЛП.
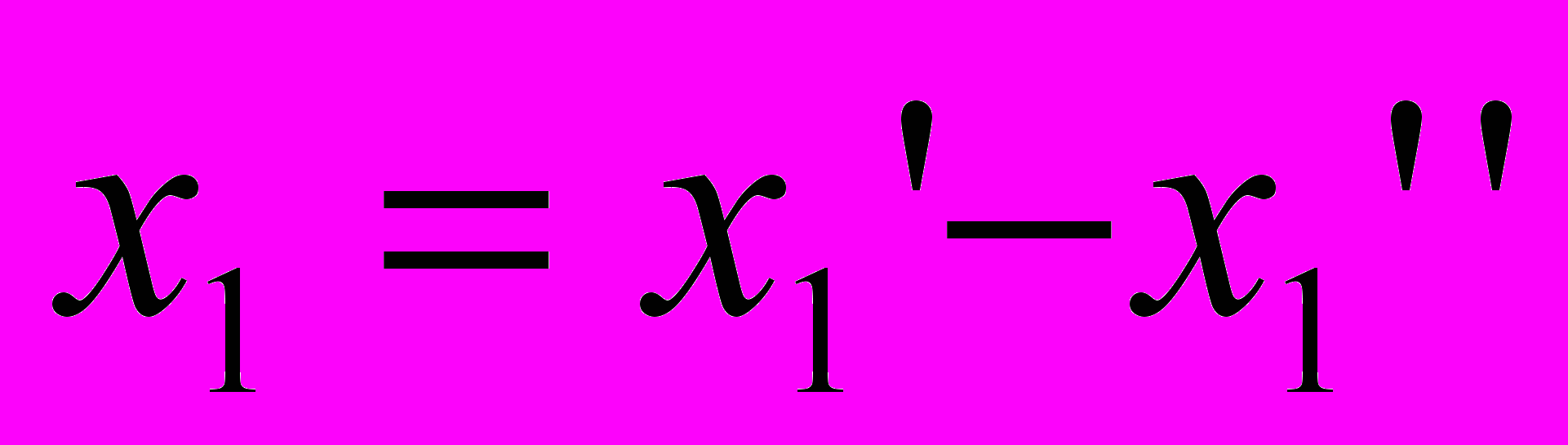 ,
, 
Теперь рассмотрим функциональные ограничения. Чтобы из неравенства получить равенство достаточно к правой части неравенства добавить или вычесть какое-то число (например, 5-6<0 – 5-6+1=0). Тогда получим:
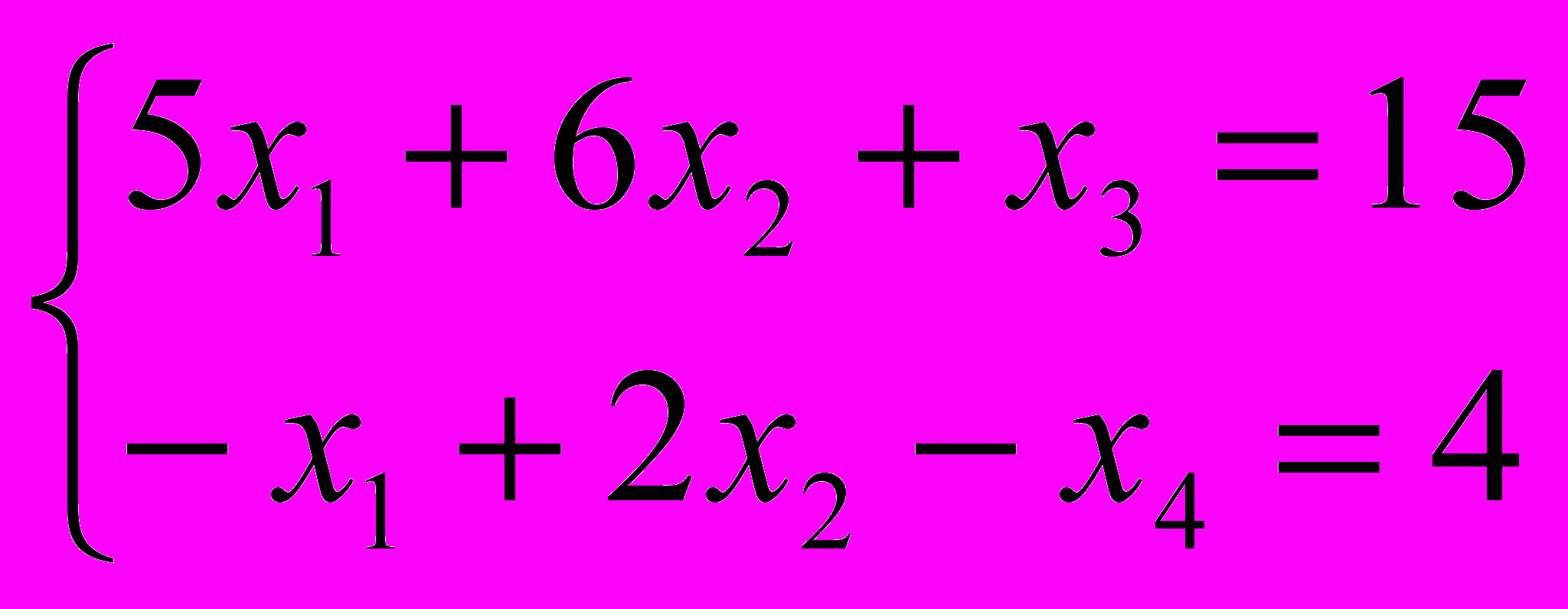
В результате получаем КЗЛП:
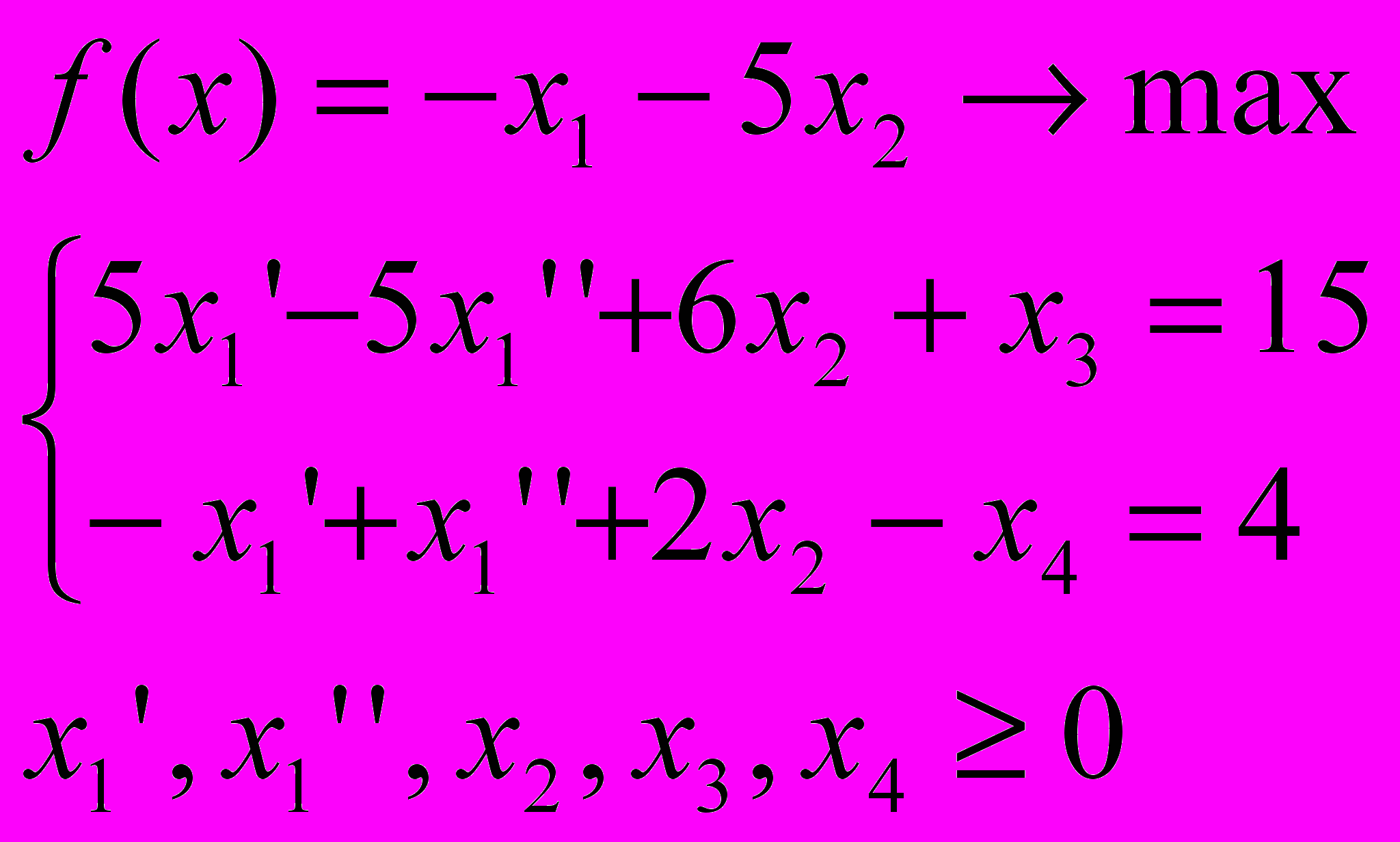
Нетрудно заметить, что «платой» за переход от общей формы задачи линейного программирования к канонической является рост ее размерности, что, при прочих равных условиях, является фактором, усложняющим процесс решения.
Пример 2.
Пусть дана ЗЛП
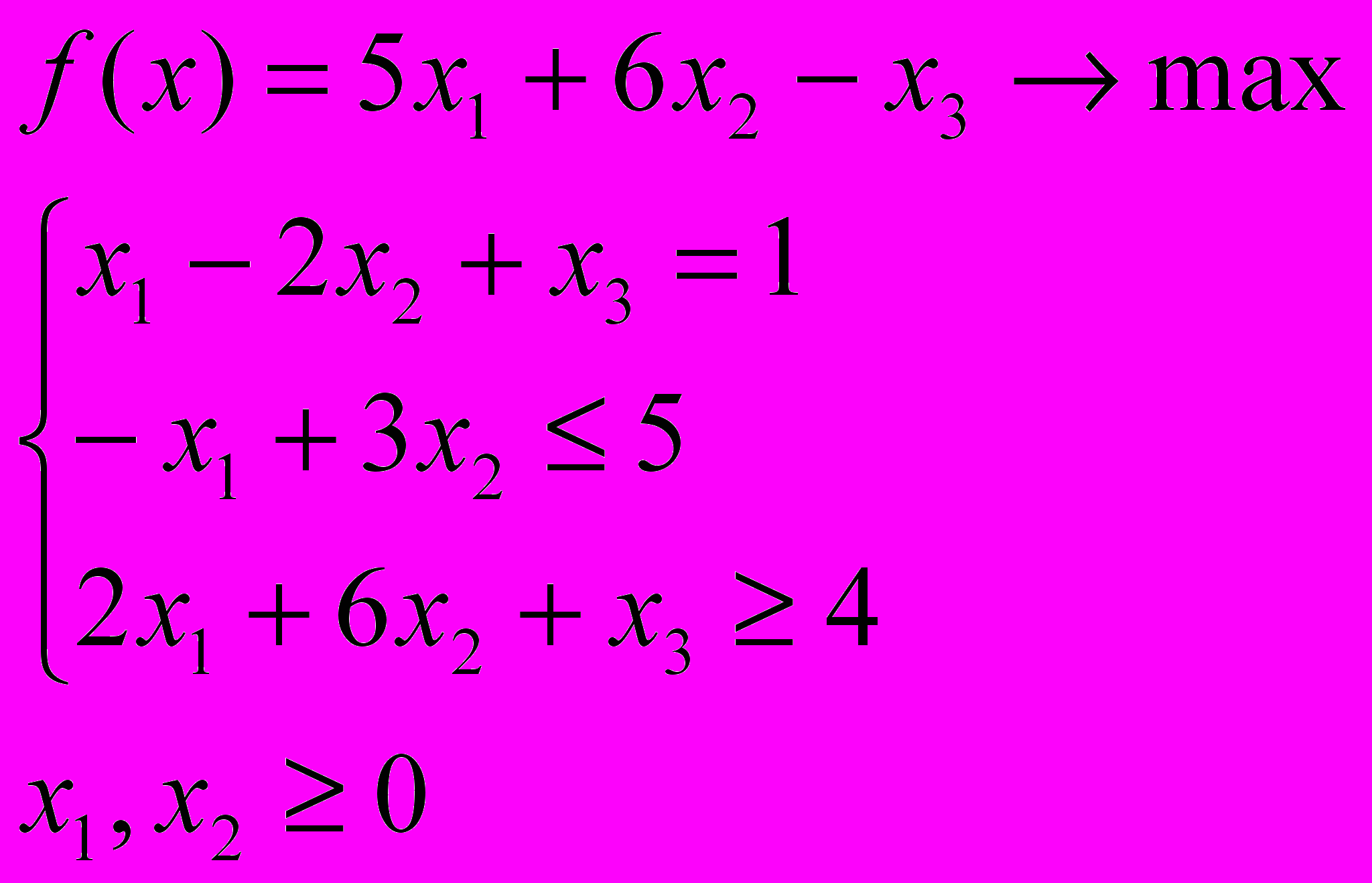
Решение.
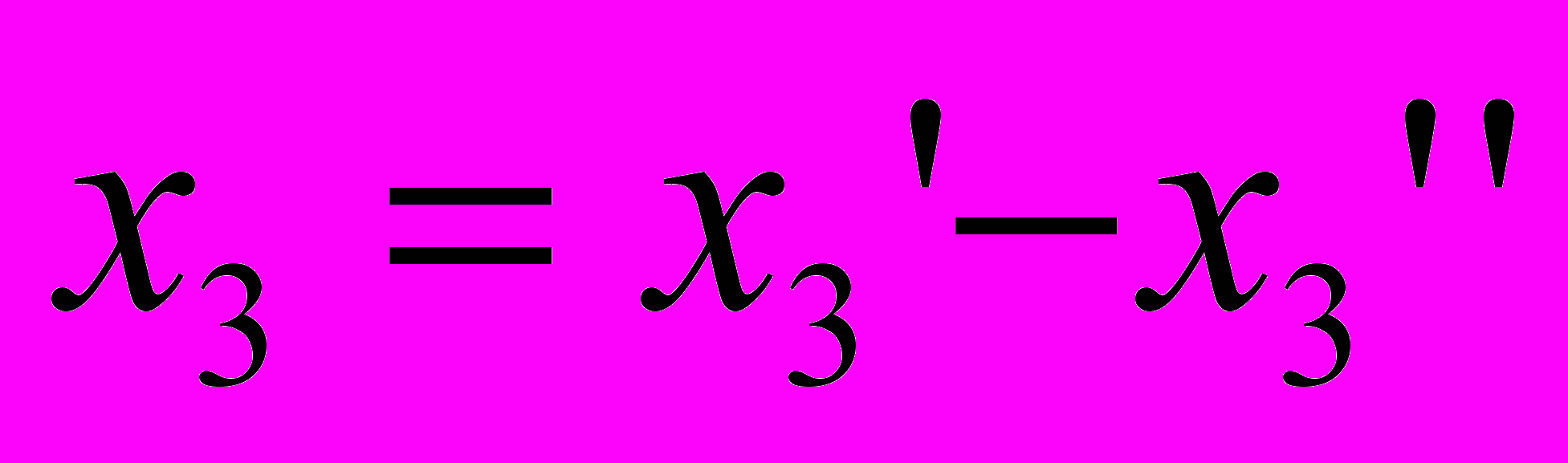 ,
, 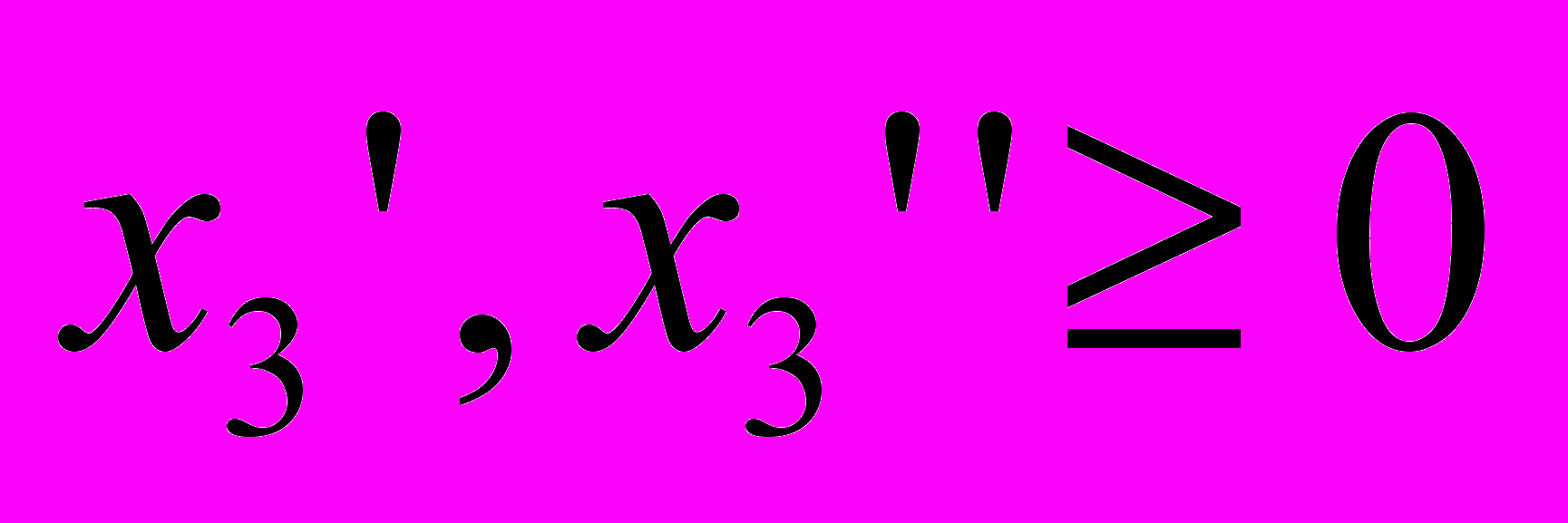
КЗЛП
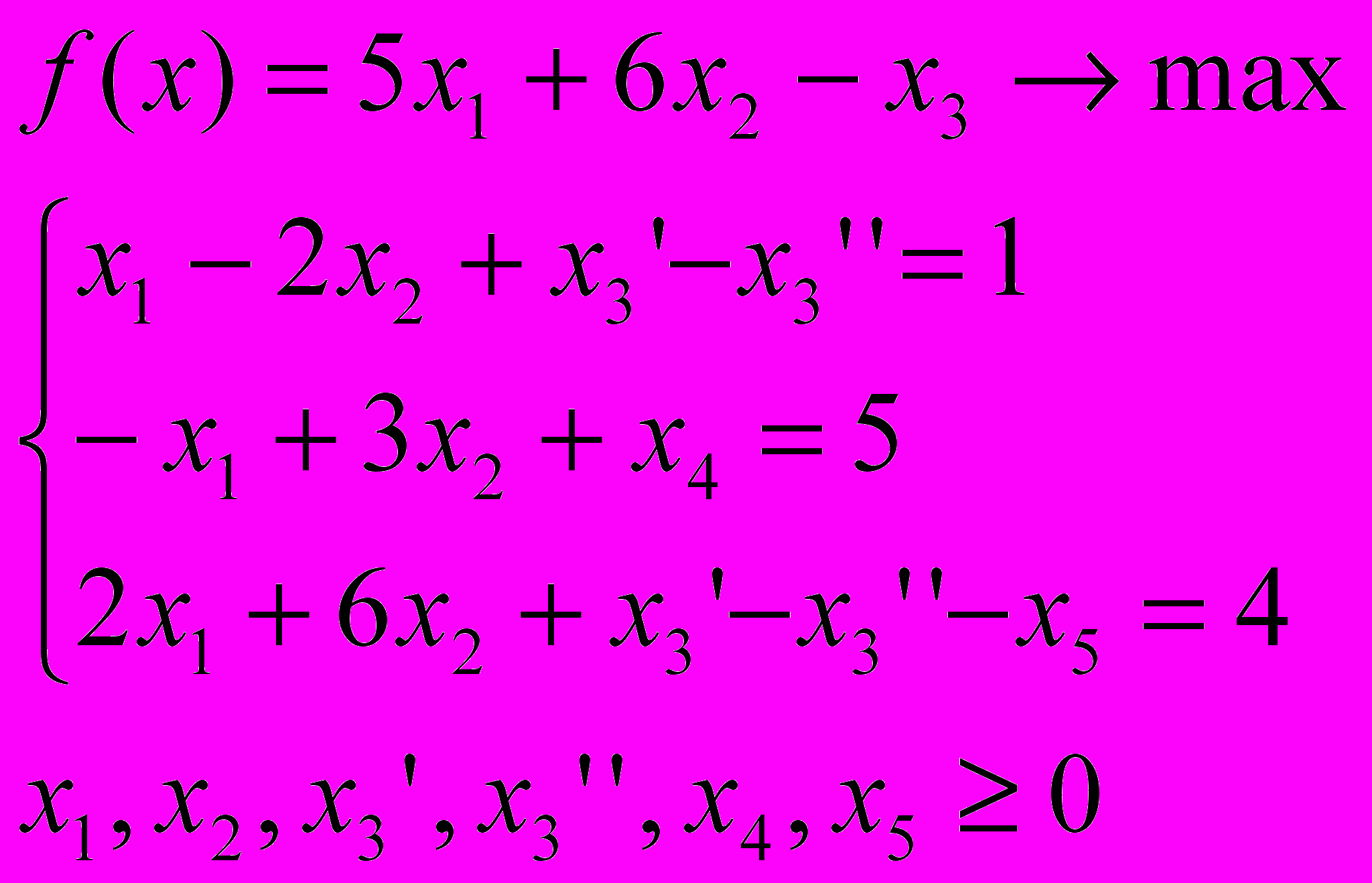
Исследование операций – лекция 2
