Теория графов и их применение
| Вид материала | Курсовая |
СодержаниеАлгебраические операции |
- 1. Элементы теории графов Введение в теорию графов: основные понятия и определения., 32.17kb.
- «Теория графов», 114.81kb.
- Задача является np-полной для кубических планарных графов, реберных графов, ориентированных, 39.45kb.
- «Применение информационный технологий в теории графов», 272.84kb.
- Билеты по Дискретной математике «Теория Графов», 12.79kb.
- Программа вступительного экзамена в аспирантуру по специальностям 05. 13. 05 - "Элементы, 88.59kb.
- Спецкурс «Теория графов» пм 4 курс История возникновения и развития теории графов., 13.97kb.
- Задание графов соответствием 9 > Матричное представление графов 10 Вопросы применения, 230.14kb.
- Знать содержание программы курса; иметь навыки структурного моделирования типовых объектов;, 56.2kb.
- Теория конечных графов и её приложения прак зан, 29.91kb.
Алгебраические операции
Поскольку граф состоит из двух множеств (вершины и ребра), то различные операции над множествами естественным образом порождают соответствующие операции над графами. Например, объединение двух графов
 и
и 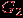 определяется как граф
определяется как граф  , у которого
, у которого 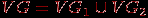 ,
,  , а пересечение - как граф
, а пересечение - как граф  , у которого
, у которого 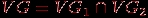 ,
,  . Обе операции иллюстрирует рис. 1.12.
. Обе операции иллюстрирует рис. 1.12.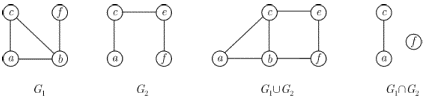
Рис. 1.12.
Дополнением (дополнительным графом) к графу
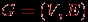 называется граф
называется граф  , у которого множество вершин то же, что у
, у которого множество вершин то же, что у  , а множество ребер является дополнением множества
, а множество ребер является дополнением множества  до множества всех неупорядоченных пар вершин. Иначе говоря, две различные вершины смежны в графе
до множества всех неупорядоченных пар вершин. Иначе говоря, две различные вершины смежны в графе  тогда и только тогда, когда они несмежны в графе
тогда и только тогда, когда они несмежны в графе  . Например,
. Например,  . Другой пример показан на рис. 1.13. Очевидно, что всегда
. Другой пример показан на рис. 1.13. Очевидно, что всегда  .
.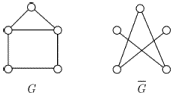
Рис. 1.13.
Под суммой
 двух абстрактных графов понимают объединение графов с непересекающимися множествами вершин. Точнее говоря, имеется в виду следующее. Сначала вершинам графов-слагаемых присваиваются имена (пометки, номера) так, чтобы множества вершин не пересекались, затем полученные графы объединяются. Операция сложения ассоциативна, то есть
двух абстрактных графов понимают объединение графов с непересекающимися множествами вершин. Точнее говоря, имеется в виду следующее. Сначала вершинам графов-слагаемых присваиваются имена (пометки, номера) так, чтобы множества вершин не пересекались, затем полученные графы объединяются. Операция сложения ассоциативна, то есть 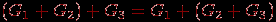 для любых трех графов. Поэтому можно образовывать сумму любого числа графов, не указывая порядка действий с помощью скобок. Если складываются
для любых трех графов. Поэтому можно образовывать сумму любого числа графов, не указывая порядка действий с помощью скобок. Если складываются 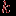 экземпляров одного и того же графа
экземпляров одного и того же графа  , то полученный граф обозначается через
, то полученный граф обозначается через  . Например,
. Например,  . На рис. 1.14 изображен граф
. На рис. 1.14 изображен граф 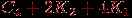 .
.
Рис. 1.14.
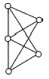
Рис. 1.15.
Соединением двух графов
 и
и 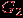 называется граф, получаемый из их суммы добавлением всех ребер, соединяющих вершины первого слагаемого с вершинами второго. Будем записывать эту операцию как
называется граф, получаемый из их суммы добавлением всех ребер, соединяющих вершины первого слагаемого с вершинами второго. Будем записывать эту операцию как  . На рис. 1.15 представлен граф
. На рис. 1.15 представлен граф  . Легко видеть, что операции сложения и соединения графов связаны друг с другом следующими простыми соотношениями:
. Легко видеть, что операции сложения и соединения графов связаны друг с другом следующими простыми соотношениями:
Введем еще два типа специальных графов, которые легко описываются с помощью операции соединения. Первый - полный двудольный граф
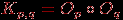 . В этом графе множество вершин разбито на два подмножества (доли), в одном из которых
. В этом графе множество вершин разбито на два подмножества (доли), в одном из которых 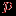 вершин, в другом
вершин, в другом 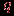 , и две вершины в нем смежны тогда и только тогда, если они принадлежат разным подмножествам. Второй - колесо
, и две вершины в нем смежны тогда и только тогда, если они принадлежат разным подмножествам. Второй - колесо  . На рис. 1.16 показаны графы
. На рис. 1.16 показаны графы 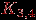 и
и  .
.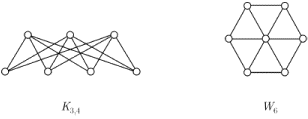
Рис. 1.16.
Произведение
 графов
графов  и
и  определяется следующим образом. Множеством вершин графа
определяется следующим образом. Множеством вершин графа  является декартово произведение множеств
является декартово произведение множеств  и
и  , то есть вершины этого графа - упорядоченные пары
, то есть вершины этого графа - упорядоченные пары 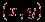 , где
, где 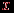 - вершина первого сомножителя,
- вершина первого сомножителя, 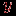 - вершина второго. Вершины
- вершина второго. Вершины 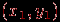 и
и 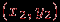 в
в  смежны тогда и только тогда, если
смежны тогда и только тогда, если  и
и 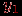 смежна с
смежна с 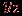 в графе
в графе 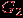 , или
, или  и
и  смежна с
смежна с 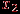 в графе
в графе  . С помощью операции произведения можно выразить некоторые важные графы через простейшие. Например, произведение двух цепей дает прямоугольную решетку (см. рис. 1.17). Если один из сомножителей превратить в цикл, добавив одно ребро, то прямоугольная решетка превратится в цилиндрическую, а если и второй сомножитель превратить в цикл, то получится тороидальная решетка.
. С помощью операции произведения можно выразить некоторые важные графы через простейшие. Например, произведение двух цепей дает прямоугольную решетку (см. рис. 1.17). Если один из сомножителей превратить в цикл, добавив одно ребро, то прямоугольная решетка превратится в цилиндрическую, а если и второй сомножитель превратить в цикл, то получится тороидальная решетка.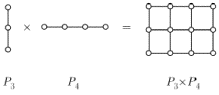
Рис. 1.17.
Другой пример -
 - мерный куб
- мерный куб  , определяемый следующим образом. Вершинами его являются всевозможные упорядоченные двоичные наборы длины
, определяемый следующим образом. Вершинами его являются всевозможные упорядоченные двоичные наборы длины 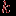 . Всего, таким образом, в этом графе
. Всего, таким образом, в этом графе 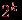 вершин. Вершины
вершин. Вершины  и
и  смежны в нем тогда и только тогда, когда наборы
смежны в нем тогда и только тогда, когда наборы 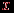 и
и 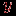 различаются точно в одной координате. С помощью операции произведения граф
различаются точно в одной координате. С помощью операции произведения граф 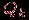 можно определить рекурсивно:
можно определить рекурсивно: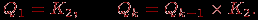
На рис. 1.18 показано, как получается
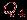 из
из 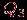 .
.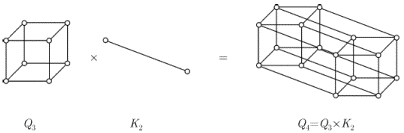
Рис. 1.18.
