Теория графов и их применение

Вид материала

Курсовая

Содержание Операции над графами Локальные операции

Подобный материал:

• 1. Элементы теории графов Введение в теорию графов: основные понятия и определения., 32.17kb.
• «Теория графов», 114.81kb.
• Задача является np-полной для кубических планарных графов, реберных графов, ориентированных, 39.45kb.
• «Применение информационный технологий в теории графов», 272.84kb.
• Билеты по Дискретной математике «Теория Графов», 12.79kb.
• Программа вступительного экзамена в аспирантуру по специальностям 05. 13. 05 - "Элементы, 88.59kb.
• Спецкурс «Теория графов» пм 4 курс История возникновения и развития теории графов., 13.97kb.
• Задание графов соответствием 9 > Матричное представление графов 10 Вопросы применения, 230.14kb.
• Знать содержание программы курса; иметь навыки структурного моделирования типовых объектов;, 56.2kb.
• Теория конечных графов и её приложения прак зан, 29.91kb.

Операции над графами

Для получения новых графов можно использовать разнообразные операции над графами. Здесь мы рассмотрим два вида операций - локальные, при которых заменяются, удаляются или добавляются отдельные элементы графа, и алгебраические, когда новый граф строится по определенным правилам из нескольких имеющихся.

Локальные операции

Простейшая операция - удаление ребра. При удалении ребра сохраняются все вершины графа и все его ребра, кроме удаляемого. Обратная операция - добавление ребра.

При удалении вершины вместе с вершиной удаляются и все инцидентные ей ребра. Граф, получаемый из графа удалением вершины , обозначают . При добавлении вершины к графу добавляется новая изолированная вершина. С помощью операций добавления вершин и ребер можно "из ничего", то есть из графа 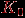, построить любой граф.

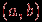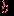Операция стягивания ребра определяется следующим образом. Вершины и удаляются из графа, к нему добавляется новая вершина и она соединяется ребром с каждой вершиной, с которой была смежна хотя бы одна из вершин .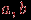

Операция подразбиения ребра 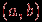действует следующим образом. Из графа удаляется это ребро, к нему добавляется новая вершина и два новых ребра и 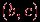. На рис. 1.10 изображены исходный граф , граф , полученный из него стягиванием ребра 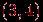и 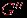, полученный подразбиением того же ребра. В обоих случаях вновь добавленная вершина обозначена цифрой .


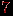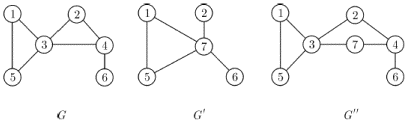
Рис. 1.10. 

Подграфы

Граф называется подграфом графа , если , . Всякий подграф может быть получен из графа удалением некоторых вершин и ребер. На рис. 1.11 изображены граф и его подграфы , , , .


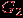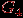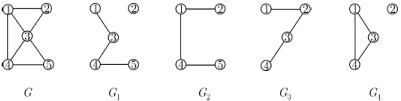
Рис. 1.11. 

Подграф графа называется остовным, если . Остовный подграф может быть получен из графа удалением некоторых ребер, вершины же остаются в неприкосновенности. На рис. 1.11 - остовный подграф графа , а , и не являются остовными подграфами.

Другая важная разновидность подграфов - порожденные подграфы. Пусть задан граф и в нем выбрано множество вершин . Рассмотрим подграф , где состоит из всех тех ребер графа , у которых оба конца принадлежат 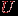. Говорят, что этот подграф порожден множеством вершин 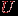. Он обозначается через . Порожденный подграф может быть получен из графа удалением "лишних" вершин, т.е. вершин, не принадлежащих .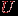

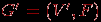Можно определить также подграф, порожденный множеством ребер . Это подграф , где 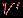состоит из всех вершин, инцидентных ребрам из .

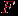На рис. 1.11 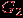- подграф графа , порожденный множеством вершин 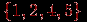, т.е. 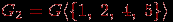, он же порождается множеством ребер ; подграф не порождается множеством вершин, но порождается множеством ребер 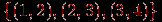; подграф 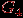не является ни остовным, ни порожденным в каком-либо смысле.