Задание графов соответствием 9 > Матричное представление графов 10 Вопросы применения графов в программировании 12 > Вопросы визуализации и визуальной обработки графов 14

Вид материала

Литература

Подобный материал:

• Задача является np-полной для кубических планарных графов, реберных графов, ориентированных, 39.45kb.
• 1. Элементы теории графов Введение в теорию графов: основные понятия и определения., 32.17kb.
• Вопросы к экзамену, 14.82kb.
• «Применение информационный технологий в теории графов», 272.84kb.
• Программа дисциплины Комбинаторные алгоритмы Семестры, 18.74kb.
• Лекция 12: Алгоритмы на графах и деревьях, 395.7kb.
• Программа вступительного экзамена в аспирантуру по специальностям 05. 13. 05 - "Элементы, 88.59kb.
• Билеты по Дискретной математике «Теория Графов», 12.79kb.
• «Теория графов», 114.81kb.
• Спецкурс «Теория графов» пм 4 курс История возникновения и развития теории графов., 13.97kb.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ФГОУ ВПО

«ЧУВАШСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ И.Н.УЛЬЯНОВА»

АЛАТЫРСКИЙ ФИЛИАЛ

 

ФАКУЛЬТЕТ УПРАВЛЕНИЯ И ЭКОНОМИКИ

Кафедра высшей математики и информационных технологий

 

 


КУРСОВАЯ РАБОТА

По дисциплине «Дискретная математика»

на тему:

«Представление графов в ЭВМ»

 

 


Студент: Яшин А.В.

Группа: АФТ-0508

Руководитель: асс. Немкова М.П.


 

«Допустить к защите»

«______» __________ 2009 г.

Дата представления работы: «______» __________ 2009 г.

Дата защиты:                         «______» __________ 2009 г.

Оценка: _________________

 

 

Алатырь,

2009 год

Содержание

Введение 3

1. Графы и способы их представления. Основные определения 6

2. Способы описания графов 8

3. Задание графов соответствием 9

4. Матричное представление графов 10

5. Вопросы применения графов в программировании 12

6. Вопросы визуализации и визуальной обработки графов 14

7. Визуализация графовой модели и интерфейс в системе HIGRES 16

8. Визуальная обработка графов в системе HIGRES 19

9. Реализация графов на языке Turbo Pascal 20

Заключение 23

Литература 24


Введение

В последние годы особую важность приобрели те разделы математики, которые имеют отношение к развитию цифровых устройств, цифровой связи и цифровых вычислительных машин. Базой для преподавания этих дисциплин наряду с классическими методами анализа непрерывных физических моделей стали алгебраические, логические и комбинаторные методы исследования различных моделей дискретной математики.

Значительно возросла популярность теории графов – ветви дискретной математики. Графы встречаются во многих областях под разными названиями: "структуры" в гражданском строительстве, "сети" – в электронике, "социограммы" – в социологии и экономике, "молекулярные структуры" – в химии, "дорожные карты", электрические или газовые распределительные сети и т. д.

Родившись при решении головоломок и игр, таких, например, как задача о кенигсбергских мостах и игра Гамильтона, теория графов стала мощным средством исследования и решения многих задач, возникающих при изучении больших и сложных систем. Для специалистов по вычислительной технике, информационным системам и системам цифровой связи теория графов – это удобный язык выражения понятий из этой области; многие результаты теории графов имеют непосредственную связь с задачами, с которыми им приходится сталкиваться.



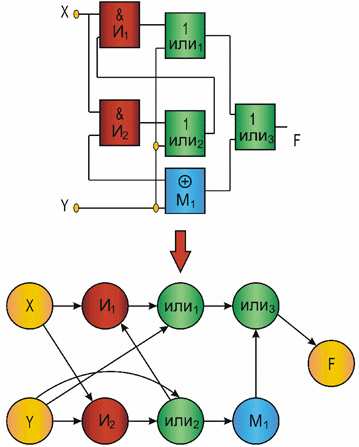
Рис. 1

Так в виде ориентированных графов можно представить любую логическую или функционально - логическую схему (рис. 1). На таких графовых моделях можно, например, оценить быстродействие схемы. Блок-схема алгоритма может быть представлена вероятностным графом (рис. 2), который позволяет оценить временные характеристики алгоритма, затраты процессорного времени, трудоемкость и другие.



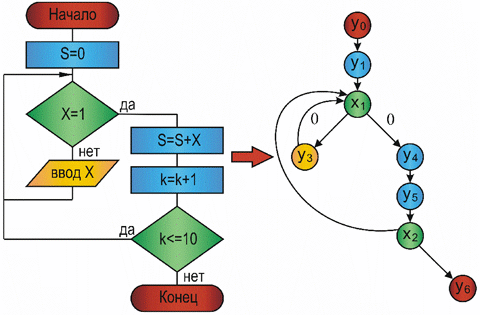
Рис. 2

Графом типа "дерево" можно отобразить практически любую структуру организации или предприятия (рис. 3).



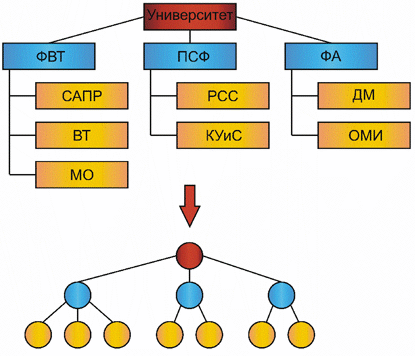
Рис. 3

Широкое применение теория графов получила при исследовании так называемой проблемы оптимизации, возникающей при конструировании больших систем как технических, так и программных, например, таких, как компиляторы.

В рамках этих исследований были разработаны многие, неизвестные ранее теоретико-графовые понятия. Теория графов имеет большую привлекательность для специалистов в области проектирования для построения эффективных алгоритмов и анализа их сложности. Использование аппарата теории графов оказало существенное влияние на разработку алгоритмов конструкторского проектирования схем. Непосредственное и детальное представление практических систем, таких, как распределительные сети, системы связи, приводит к графам большого размера, успешный анализ которых зависит в равной степени, как от эффективных алгоритмов, так и от возможностей компьютерной техники. Поэтому в настоящее время основное внимание сосредоточено на разработке и описании компьютерных алгоритмов анализа графов. В связи с этим основной упор в данном учебном пособии делается на машинные способы представления графов и алгоритмы решения задач на графах, легко реализуемых на ЭВМ.


Графы и способы их представления. Основные определения

Граф задается множеством точек или вершин х₁, х₂, ..., х_n и множеством линий или ребер a₁, a₂, ... , a_m, соединяющих между собой все или часть точек. Формальное определение графа может быть дано следующим образом.

Графом называется двойка вида

G = (X, A),

где X = {x_i}, i = 1, 2, ..., n – множество вершин графа, A = {a_i}, i = 1, 2,... , m – множество ребер графа.

Графы могут быть ориентированными, неориентированными и смешанными (рис. 4). Если ребра у множества A ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным графом или орграфом (рис. 4,а).




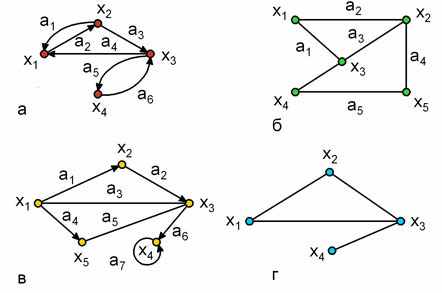
Рис. 4

Если ребра не имеют ориентации, то граф называется неориентированным (рис. 4,б). Граф, в котором присутствуют и ребра, и дуги называется смешанным (рис. 4,в). В случае, когда G = (X, A) является орграфом, и мы хотим пренебречь направленностью дуг из множества A, то неориентированный граф, соответствующий G, будет обозначаться и называться неориентированным дубликатом или неориентированным двойником (рис. 4,г).

Дуга a_i может быть представлена упорядоченной парой вершин (х_n, х_k), состоящей из начальной х_n и конечной х_k вершин. Например, для графа G₁ (рис. 4,а) дуга a₁ задается парой вершин (x₂, x₁), а дуга а₃ парой (x₂, x₃). Если х_n, х_k – концевые вершины дуги a_i, то говорят, что вершины х_n и х_k инцидентны дуге a_i или дуга a_i инцидентна вершинам х_n и х_k.

Дуга, у которой начальная и конечная вершины совпадают, называется петлей. В графе G₃ (рис. 4,в) дуга a₇ является петлей.

Каждая вершина орграфа х_i может характеризоваться полустепенью исхода d₀(х_i) и полустепенью захода d_t(х_i).

Полустепенью исхода вершины х_i — d₀(х_i) называется количество дуг, исходящих из этой вершины. Например, для орграфа G₁ (рис. 4,а) характеристики полустепеней исхода следующие: d₀(х₁)=1, d₀(х₂)=2, d₀(х₃)=2, d₀(х₄ )=1.

Полустепенью захода вершины х_i — d_t(х_i) называется количество дуг, входящих в эту вершину. Например, для орграфа G₁: d_t(х₁)=2, d_t(х₂)=1, d_t(х₃)=2, d_t(х₄ )=1.

Очевидно, что сумма полустепеней исхода всех вершин графа, а также сумма полустепеней захода всех вершин графа равна общему числу дуг графа, т. е.

ⁿ_i=1d₀(x_i)=ⁿ_i=1d_t(x_i)=m

где n – число вершин графа, m – число дуг.

Каждая вершина неориентированного графа х_i может характеризоваться степенью вершины d(х_i).

Степенью вершины х_i – d(х_i) называется количество ребер, инцидентных этой вершине. Например, для орграфа G₁ (рис. 4,б) характеристики степеней следующие: d(х₁)=2, d(х₂)=3, d(х₃)=2, d(х₄ )=2.


Способы описания графов

Теоретико-множественное представление графов

Граф описывается перечислением множества вершин и дуг. Примеры описания приведены для орграфов на рис. 5 и рис. 6.

G₄ = (Х, А),

где Х = {х_i}, i = 1, 2, 3, 4 – множество вершин; А = {a_i }, i = 1, 2, ..., 6 – множество дуг, причем А = {(х₁, х₂), (х₄, х₂), (х₂, х₄ ), (х₂, х₃), (х₃, х₃), (х₄ , х₁)}.




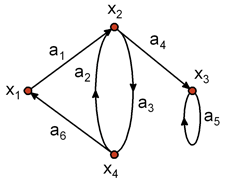
Рис. 5 

G₅ = (X, A),

где X = {B, C, D, E, F} – множество вершин графа, A = {a_i}, i = 1, 2, ..., 5 – множество дуг графа, причем a₁ = (F, B), a₂ = (B, E), a₃ = (F, D), a₄ = (E, C), a₅ = (C, D).




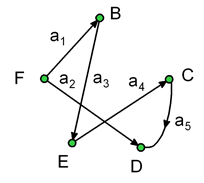
Рис. 6 


Задание графов соответствием

Описание графов состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины.

Соответствием Г называется отображение множества Х в Х, а граф в этом случае обозначается парой G = (X, Г).

Отображением вершины х_i — Г(х_i) является множество вершин, в которые существуют дуги из вершины х_i, т. е. Г(х_i) = { х_j: дуга (х_i, х_j)A}.

Так для орграфа на рис. 5 описание заданием множества вершин и соответствия выглядит следующим образом:

G₄=(X, Г),

где X = {х_i}, I = 1, 2, ..., 4 – множество вершин, Г(х₁) = { х₂ }, Г(х₂) = { х₃, х₄ }, Г(х₃) = { х₃ }, Г(х₄) = { х₁, х₂ } – отображения.

Для неориентированного или смешанного графов предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, для графа на рис. 4,б Г(х₂) = { х₁, х₃, х₅ }, Г(х₄) ={ х₃, х₅} и т. д.


Матричное представление графов

Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций.

Матрица смежности – это квадратная матрица размерностью n x n, (где n – число вершин графа), однозначно представляющая его структуру.

A = {a_ij}, i, j = 1, 2, ..., n, а каждый элемент матрицы определяется следующим образом:

a_ij = 1, если дуга (х_i, х_j),

a_ij = 0, если нет дуги (х_i, х_j).

Матрица инциденций представляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m – количество дуг графа. Обозначается матрица инциденций B = {b_ij}, i = 1, 2, ..., n, j = 1, 2, ..., m.

Каждый элемент матрицы определяется следующим образом:

b_ij = 1, если х_i является начальной вершиной дуги a_j,

b_ij = –1, если х_i является конечной вершиной дуги a_j,

b_ij = 0, если х_i не является концевой вершиной дуги a_j или если a_j является петлей.

На рис. 7, а,б приведен граф и его матрица смежности, по которой можно найти характеристики вершин. Так сумма элементов i-ой строки матрицы дает полустепень исхода вершины х_i, а сумма элементов i-го столбца дает полустепень захода вершины х_i. По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i-ю строку матрицы. Если элемент a_ij=1, то элемент графа х_j входит в отображение Г(х_i). Например, во 2-й строке матрицы А (рис. 7,б) единицы стоят в 2-м и 5-м столбцах, следовательно, Г(х₂) = { х₂, х₅}.




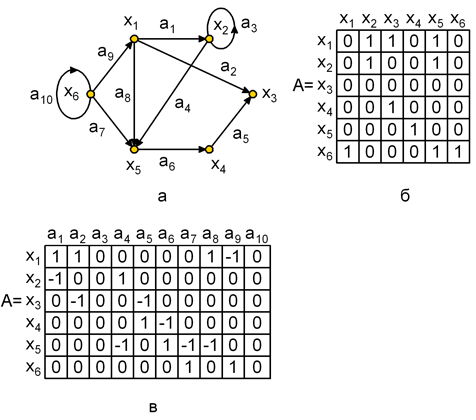
Рис. 7.  Орграф и его матричное представление: а – орграф; б – матрица смежности; в – матрица инциденций

Для графа на рис. 7, а матрица инциденций приведена на рис. 7,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.

Для неориентированного графа, матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.


Вопросы применения графов в программировании

Современное состояние программирования нельзя представить себе без теоретико-графовых алгоритмов. Хорошо известно, что многие за­дачи повышения качества трансляции, как в смысле улучшения рабочих характеристик транслятора, так и в смысле повышения качества полу­чаемых машинных программ формулируются и решаются как задачи на графах. Сюда относятся в первую очередь задачи, связанные с пред­ставлением программ в виде теоретико-графовых моделей, важнейшей из которых является управляющий граф. Кроме того, необходимо ука­зать на такие области применения граф-моделей, как эффективное использование ресурсов вычислительной системы (оптимизация исполь­зования памяти, регистров, уменьшение обменов между оперативной и внешней памятью и т.д.). организация больших массивов информации (деревья и, вообще, графы данных для повышения эффективности ин­формационного поиска), увеличение степени параллелизма программы, повышение эффективности работы многопроцессорных и многомашин­ных систем (распределение загрузки процессоров, обмен сообщениями между процессами, синхронизация, конфигурация сетей связи между процессорами и т.д. 1. Решение этих и подобных задач привело к появ­лению множества граф-моделей, связанных как с программами и струк­турами данных, так и с вычислительными системами, в том числе па­раллельными.

Как уже отмечалось выше, теория графов из академической дисци­плины все более превращается в средство, владение которым становится решающим для успешного применения ЭВМ во многих прикладных об­ластях. Причем совершенно ясно, что, несмотря на наличие обширной специальной литературы по решению задач на графах, широкое приме­нение в практике программирования полученных математических ре­зультатов затруднено в силу отсутствия их систематического описа­ния, ориентированного на программистов. Поэтому значительный класс практических задач, по существу сводящихся к простому выбору под­ходящего способа решения и к построению конкретных формулировок абстрактных алгоритмов, для многих программистов все еще остается полем для интеллектуальной деятельности по переоткрытию методов.

В данный момент математики ориентируются на вы­сокоуровневое описание алгоритмов в терминах специального псевдо­языка (лексикона) программирования с использован нем традиционных конструкций математики и языков программирования высокого уров­ня. Такой подход позволяет формулировать алгоритмы в естественной форме, допускающей прямой анализ их корректности и сложности, а также простой перенос алгоритмов на традиционные языки программи­рования и ЭВМ с сохранением полученных оценок сложности. Кроме того, подобный стиль описания алгоритмов является базой для дока­зательного стиля программирования: он позволяет понять алгоритм на содержательном уровне, оценить пригодность его для решения конкрет­ной задачи и осуществить модификацию алгоритма, не снижая степень математической достоверности окончательного варианта программы.

Среди теоретико-графовых алгоритмов и методов, применяемых в программировании, естественно выделяются классы алгоритмов, общим для которых является тот или иной тип графов, используемых в каче­стве модели. Здесь в первую очередь следует назвать класс алгоритмов обработки деревьев, класс алгоритмов обработки бесконтурных графов (ациклические графы, ВАС), моделирующих частично упорядоченные множества, решетки и полурешетки, а также класс алгоритмов обработ­ки регуляризуемых графов (сводимые графы), моделирующих програм­му при потоковом анализе, оптимизирующей трансляции и распарал­леливании и являющихся основой современных технологий программи­рования, таких как структурное программирование, трансформацион­ное программирование и др. Поэтому нам показалось естественным при изложении теоретико-графовых методов и алгоритмов для программи­стов использовать указанное их разделение на классы.


Вопросы визуализации и визуальной обработки графов

Существующие системы визуализации графов можно условно раз­делить на два класса.

К первому (более широкому) классу относятся узкоспециальные си­стемы, которые ориентированы на графовые модели с определенной се­мантикой и топологией. Каждая такая система является, как правило, частью некоторого большого проекта, включающего ее в качестве визуализатора каких-либо специфических для данного проекта данных. Более широкое использование таких систем либо очень затруднено, ли­бо просто невозможно.

Второй класс — это универсальные системы визуальной обработки графовых моделей, такие как, например, системы daVinci, GraphEd, Graphlet, GraVis, VCG, а также библиотеки LEDA, AGD, ffGraph, Graph Layout Toolkit, Graph Editor Toolkit и др. Несмотря на значительный прогресс в создании универсаль­ных систем, следует отметить ряд недостатков подавляющего большин­ства из них. Прежде всего для российского пользователя общим недо­статком этих систем является их ориентация на работу в ОС UNIX на больших рабочих станциях, которыми в достаточной степени оснащены иностранные университеты, их разрабатывающие. Как правило, уни­версальность существующих систем весьма ограничена, в частности, ни одна из них не позволяет графовым моделям быть иерархическими и не поддерживает визуализацию алгоритмов их обработки

Требования к универсальным системам визуализации и визуальной обработки информационных моделей сложны для формализации и нуж­даются в отдельном исследован ни. Отметим лишь, что такие системы должны обладать базовыми возможностями поддержки визуальной об­работки, связанной с решением широкого крута задач анализа и синте­за иерархических графовых моделей в irx конструкторском, исследова­тельском и учебном применении.

Система должна поддерживать визуализацию и редактирование по­меченных иерархических графов. В частности, при изображении гра­фовой модели тип ее элементов может быть связан с определенной гео­метрической формой соответствующих представлении и/или их цвето­вой гаммой, а также местом и способом представления пометок, от­носящихся к элементам соответствующего типа. Система должна об­ладать современным графическим интерфейсом, ориентированным на иерархичность графовых моделей и поддерживающим их многооконное редактирование и визуализацию с возможностями регулирования мас­штаба, использования разных геометрических и цветовых образов для формирования изображения графа, работы с прямоугольной сеткой для выравнивания объектов и т.п.

Система должна обладать рядом возможностей, облегчающих и ав­томатизирующих отдельные операции конструирования, визуализации и изучения различных объектов и явлений в рамках их иерархических графовых моделей, включая возможности отката, ге­нерации случайных графов, автоматического расположения графов на плоскости, анимации процессов обработки графовых моделей и специ­ализации системы.

При использовании правил преобразований для задания семантиче­ской части графовой модели возникают вопросы поддержки визуальной обработки системы преобразований, связанные с их визуальным кон­струированием, применением и анализом. В частности, весьма важной является возможность поддержки управляемого визуального примене­ния системы преобразований, позволяющего в каждый момент зада­вать, какое преобразование и каким образом нужно применять к теку­щему виду модели, а также возвращаться к виду модели, имеющемуся у нее до преобразования. Нужно подчеркнуть важную роль вопросов визуальной обработки систем преобразований и для случая явного опи­сания семантической части графовой модели. Многие из порождающих процессов удобно не рассматривать как неделимое глобальное преоб­разование, а задавать с помощью системы локальных преобразований. Именно такая ситуация, например, имеет место для сетей Петри, функ­ционирование которых описывается в терминах локальных преобразо­ваний, представляющих срабатывания переходов.


Визуализация графовой модели и интерфейс в системе HIGRES

Визуализация графа в системе HIGRES организована таким обра­зом, чтобы максимально наглядно изобразить как иерархическую струк­туру графа, так и его семантику.

Каждому фрагменту графа соответствует некоторый прямоуголь­ник плоскости, внутри которого располагаются все его вершины (см. рис. 2). Кроме того, для каждого фрагмента можно открыть отдель­ное окно, в котором видны только вершины данного фрагмента и его подфрагменты. При этом каждый подфрагмент можно объявить за­крытым — тогда изображаются только его контуры, либо открытым — тогда изображаются все его вершины и инцидентные им дуги. Для изоб­ражения контуров фрагментов в системе используется прием создания эффекта тени. Закрытые фрагменты выглядят слегка выступающими вверх, как будто они закрыты крышками, открытые же слегка утопле­ны вниз.




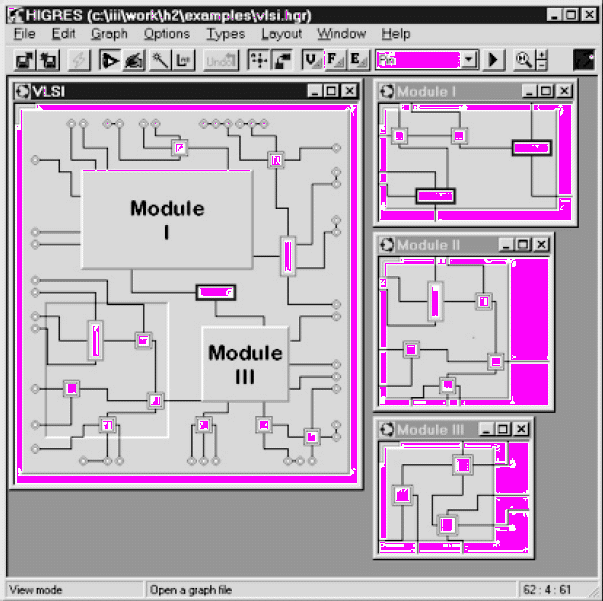
Рис. 8. Модель СБИС, представленная иерархическим графом


Для изображения вершин используется несколько вариантов геомет­рических фигур. Кроме того, можно выбирать стиль и цвет контура и заливки вершины. Эти параметры задаются отдельно для каждого ти­па вершин. Таким образом, вершины, принадлежащие к одному типу, визуально похожи друг на друга, хотя могут отличаться текстом меток. Ребра (дуги) графа изображаются либо ломаными линиями, задаваемы­ми точками сгиба, либо гладкими кривыми, для задания которых также используется некоторый набор точек на плоскости, вдоль которых про­ходит дуга (эти точки по аналогии также называются точками сгиба). Вариант изображения дуги, стиль ее линии и стиль стрелки на конце (если граф ориентированный) задается отдельно для каждого типа дут. Для визуализации атрибутов объектов (вершин, ребер, фрагментов) ис­пользуется гибкая система, позволяющая изображать их не просто как список значений меток, а более наглядным и естественным образом.

Для каждого типа объектов задается "строка визуализации", пред­ставляющая собой шаблон текста, изображающего атрибуты каждого объекта данного типа. В этой строке определяются места, в которые при визуализации подставляются значения меток конкретного объекта. Кроме того, строка может содержать специальные символы, отмечаю­щие места начала новой строки В конечном итоге для каждого объек­та определяется некоторый текст, который называется текстом меток. Более точно, для типов вершин задаются две строки визуализации и соответственно два текста меток: внутренний и внешний. При визуа­лизации вершины внутренний текст меток располагается внутри нее, а внешний — рядом с ней. Точно так же для типов фрагментов задают­ся две строки визуализации, порождающих "закрытый" и "открытый'' текст меток. Первый изображается внутри фрагмента, когда он закрыт, а второй — когда открыт. Е1динственная строка визуализации, задава­емая для каждого типа дуг, порождает текст меток для каждой дуги данного типа, который располагается рядом с одной из точек сгиба дуги либо рядом с одной из конечных точек данной дуги.

Интерфейс системы придерживается основных общепринятых стан­дартов для приложений Windows 95. Система имеет главное окно, внут­ри которого расположены окна фрагментов, которые пользователь мо­жет открывать п закрывать по мере надобности, переходя вверх и вниз по иерархии Главное окно системы содержит меню и toolbar, обеспечи­вающий быстрый доступ к часто используемым операциям. Пользова­тель может переключаться с режима просмотра на режим редактиро­вания графа.

В режиме просмотра можно только открывать и закрывать фраг­менты графа и их окна, просматривая содержимое, скроллировать изоб­ражение в окнах и изменять его масштаб.

В режиме редактирования левая кнопка мыши служит для выде­ления объектов, а правая — для высвечивания всплывающего меню, с помощью которого можно выбрать операцию, производимую с выде­ленным объектом. Кроме того, выбрав соответствующий пункт в этом меню, можно добавить в граф новую вершину, фрагмент или дугу. С по­мощью левой кнопки мыши пользователь может перемещать вершины, фрагменты и сгибы дуг, а также изменять размеры вершин и границы фрагментов. При этом никакие две вершины не должны накладывать­ся друг на друга и каждый фрагмент должен целиком включать в себя все свои вершины и подфрагменты. По выбору пользователя система может поддерживать выполнение данного условия одним из двух спосо­бов. Она может либо автоматически слегка корректировать расположе­ние графа после каждого его изменения пользователем, нарушающего данное условие, либо просто запретить любые такие изменения.

Существуют также два дополнительных режима редактирования, использование которых может ускорить выполнение некоторых часто производимых операций, — режим создания объектов и режим редак­тирования меток.


Визуальная обработка графов в системе HIGRES

С интерфейсной точки зрения процесс визуальной обработки иерар­хического графа в системе HIGRES выглядит следующим образом. Поль­зователь с помощью системы выбирает нужный ему внешний модуль и запускает его. Система передает текущий граф обрабатывающему мо­дулю и открывает специальное окно, предоставляющее пользователю интерфейс для управления работой модуля. Пользователь может регу­лировать параметры обработки, прерывать ее на любом шаге, просмат­ривать промежуточные результаты в любую сторону в форме анимации либо в покадровом режиме. Для каждого модуля определяется набор числовых и текстовых параметров, которые пользователь может изме­нять в процессе работы. Кроме того, модуль может сам инициировать запрос необходимых ему данных, а также генерировать сообщения, ко­торые вместе с другой рабочей информацией записываются в протокол. выдаваемый на экран.

От программиста, создающего свой собственный внешний модуль, не требуются знания деталей внутреннего представления иерархических графов в системе, поскольку все взаимодействие внешнего модуля с си­стемой обеспечивается функциями библиотеки HGL. Создавая модуль, программист должен позаботиться, кроме программирования непосред­ственно самого процесса обработки, лишь о разбиении этого процесса на шаги, число которых не фиксируется. Внешний модуль представляет собой отдельное Windows-приложение и может быть получен с исполь­зованием любого компилятора C++ для Windows, понимающего шаб­лоны классов. В настоящий момент для иллюстрации возможностей ви­зуальной обработки создано несколько примеров графовых моделей и внешних модулей к ним. К этим моделям относятся конечные автоматы (рис. 9), сети Петри и простейшие схемы программ.



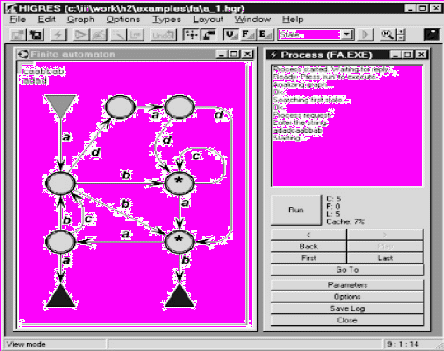
Рис. 9. Моделирование работы конечного автомата

Реализация графов на языке Turbo Pascal

Как было сказано выше для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций.

Матрица смежности – это квадратная матрица размерностью n x n, (где n – число вершин графа), однозначно представляющая его структуру.

Рассмотрим матрицу на рис. 10.

A = {a_ij}, i, j = 1, 2, ..., n, а каждый элемент матрицы определяется следующим образом:

a_ij = 1, если дуга (х_i, х_j),

a_ij = 0, если нет дуги (х_i, х_j).

Матрица инциденций представляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m – количество дуг графа. Обозначается матрица инциденций B = {b_ij}, i = 1, 2, ..., n, j = 1, 2, ..., m.

Каждый элемент матрицы определяется следующим образом:

b_ij = 1, если х_i является начальной вершиной дуги a_j,

b_ij = –1, если х_i является конечной вершиной дуги a_j,

b_ij = 0, если х_i не является концевой вершиной дуги a_j или если a_j является петлей.



Рис. 10

Из всего перечисленного следует что любой граф имеет матрицу инцидентности, которая характеризует данных граф. На языке Turbo Pascal матрица представляется в виде набора логических констант и определяется в разделе const. Вот так выглядит матрица инцидентности для графа на рис. 10.

const n=6;

m: array[1..n, 1..n] of boolean=

(

(False, True, True, False, True, False),

(False, True, False, False, True, False),

(False, False, False, False, False, False),

(False, False, True, False, False, False),

(False, False, False, True, False, False),

(True, False, False, False, True, True),

);


Мною была разработана программа умножения двух матриц:

Program proizvedenie_matric;

uses crt;

type

mat_a = array [1..15,1..15] of real;

mat_b = array [1..15,1..15] of real;

mat_c = array [1..15,1..15] of real;

var

n, m, r : integer;

i, j, k : integer;

a : mat_a;

b : mat_b;

c : mat_c;

begin clrscr;

writeln('kolichestvo strok matrici a');

readln (m);

writeln('kolichestvo stolbcov matrici b');

readln (r);

writeln ('kolichestvo stolbcov matrici a i kolichestvo strok matrici b');

readln (n);

for i:= 1 to m do

for j:= 1 to n do

begin

write('a[',i:2,',',j:2,']=');

readln (a[i,j]); end;

writeln ('vivod matrici a');

for i:= 1 to m do begin

for j:= 1 to n do

write(a[i,j]:4:0,'':3); writeln; end;

for j:= 1 to n do

for k:= 1 to r do

begin write('b[',j:2,',',k:2,']=');

readln (b[j,k]); end;

writeln ('vivod matrici b');

for j:= 1 to n do begin

for k:= 1 to r do

write(b[j,k]:4:0,'':3); writeln; end;

for i:= 1 to m do

for k:= 1 to r do

c[i,k]:= 0;

for i:= 1 to m do

for k:= 1 to r do

begin

for j:= 1 to n do

c[i,k]:= c[i,k] + a[i,j]*b[j,k];

end;

writeln ('proizvedenie matric a i b (matrica c)');

for i:= 1 to m do begin

for k:= 1 to r do

write(c[i,k]:5:0,'':3); writeln; end;

readkey;

end.


Заключение

Теория графов стала активно применяться в программировании од­новременно с использованием ЭВМ в силу удобного выражения задач обработки информации на теоретико-графовом языке. Среди первых работ, существенно использующих теоретико-графовые методы в реше­нии задач программирования, можно отметить широко известные рабо­ты А.П. Ершова по организации вычисления арифметических выраже­нии (1958 г.) и оптимальному использованию оперативной памяти (1962 г.), а также заметку Р. Карпа (1960 г., на русском языке — 1962 г.), в которой была введена теоретико-графовая модель программы в виде управляющего графа. Эта модель стала к настоящему времени клас­сической для решения задач трансляции и конструирования программ.

Модель программы в виде управляющего графа, модель арифме­тического выражения в виде ориентированного дерева, синтаксические деревья, деревья сортировки, сети Петри и другие теоретико-графовые конструкции внесли свой существенный вклад в развитие программи­рования и его автоматизации. Появление суперкомпьютеров и сетей и возникшая при этом проблема эффективной организации параллель­ных и распределенных вычислений над информационными массивами большого объема подтвердили тенденцию использования графов как наиболее эффективного средства автоматизации программирования.

Расширение круга задач, решаемых на ЭВМ, потребовало выхода на модели дискретной математики, что привело к подлинному расцве­ту теории графов и комбинаторики, которые за сорок лет трансформи­ровались из разделов ''досуговой" математики в основной инструмент решения огромного числа задач.

Современное состояние информатики и программирования нельзя представить себе без теоретико-графовых методов и алгоритмов. Ши­рокая применимость графов связана с тем, что они являются очень естественным средством объяснения сложных ситуаций на интуитивном уровне. Эти преимущества представления сложных структур и процессов графами становятся еще более ощутимыми при наличии хороших средств их визуализации. Поэтому неслучайно в настоящее время в мире растет интерес к методам и системам визуальной обработки графов и графовых моделей.


Список использованной литературы

1. Касьянов В.Н. Оптимизирующие преобразования программ. — М.: Наука, 1988.

2. Касьянов В.Н., Поттосин И.В. Методы построения трансляторов. — Новосибирск: Наука, 1986.

3. Di Battista G., Eades P., Tamassia R., Tollis I.G. Algorithms for drawing graphs: an annotated bibliography // Comput. Geom. Theory Appl. — 1994. —Vol. 4. — P. 235—282.

4. Кнут Д. Искусство программирования для ЭВМ. — М.: Мир; Том 1: Основные алгоритмы, 1976; Том 2: Получисленные алгоритмы, 1977; Том 3: Сортировка и поиск, 1978.

5. Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки деревьев. — Новосибирск: Наука, 1994.

6. Евстигнеев В.А., Касьянов В.Н. Теория графов: алгоритмы обработки бесконтурных графов. — Новосибирск: Наука, 1998.

7. Евстигнеев В.А., Касьянов В.Н. Сводимые графы и граф-модели в программировании. — Новосибирск: Изд-во ИДМИ, 1999.