Задача является np-полной для кубических планарных графов, реберных графов, ориентированных графов, тотальных графов, двудольных графов и для графов, не содержащих треугольников [1]

Вид материала

Задача

Содержание 1 Постановка задачи 2 Алгоритм решения задачи 3 Разработка программы

Подобный материал:

• 1. Элементы теории графов Введение в теорию графов: основные понятия и определения., 32.17kb.
• Задание графов соответствием 9 > Матричное представление графов 10 Вопросы применения, 230.14kb.
• Спецкурс «Теория графов» пм 4 курс История возникновения и развития теории графов., 13.97kb.
• «Применение информационный технологий в теории графов», 272.84kb.
• Программа вступительного экзамена в аспирантуру по специальностям 05. 13. 05 - "Элементы, 88.59kb.
• Билеты по Дискретной математике «Теория Графов», 12.79kb.
• Вопросы к экзамену, 14.82kb.
• «Теория графов», 114.81kb.
• Программа дисциплины Комбинаторные алгоритмы Семестры, 18.74kb.
• Лекция 12: Алгоритмы на графах и деревьях, 395.7kb.

Федеральное агентство по образованию

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ОмГТУ)

Кафедра «Автоматизированные системы обработки информации и управления»


ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К ПРАКТИЧЕСКОМУ ЗАДАНИЮ

по дисциплине «Современные проблемы информатики и вычислительной техники»

поиск наибольшего независимого множества вершин графа


Принял:

к.т.н, доц. каф АСОИУ Задорожный В.Н.

подпись, дата

Выполнил:

студент гр. РАС-518 Сосняков С.И.

подпись, дата


Омск 2008

1 Постановка задачи

Дан граф G = (V,E). Необходимо определить наибольшее независимое множество вершин графа, то есть такое подмножество вершин V’, в котором никакие две вершины не соединены ребром из множества E.

Задача является NP-полной для кубических планарных графов, реберных графов, ориентированных графов, тотальных графов, двудольных графов и для графов, не содержащих треугольников [1].

2 Алгоритм решения задачи

Для данной задачи заведомо не существует эффективного алгоритма [2]. Задача отыскания наибольшего независимого множества вершин принадлежит к числу трудоемких.

Примем следующие обозначения для описания алгоритма:

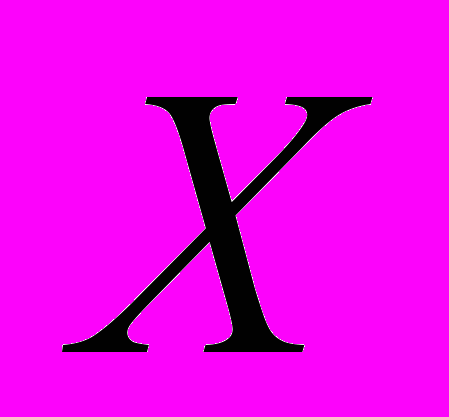• – множество всех вершин графа;
  
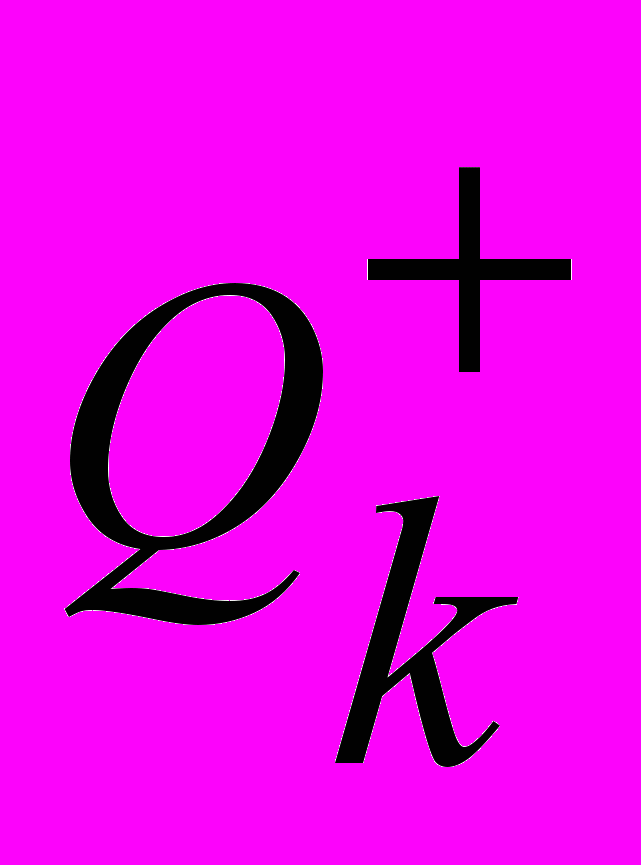• – множество вершин, которые можно включать в максимальное независимое подмножество;
  
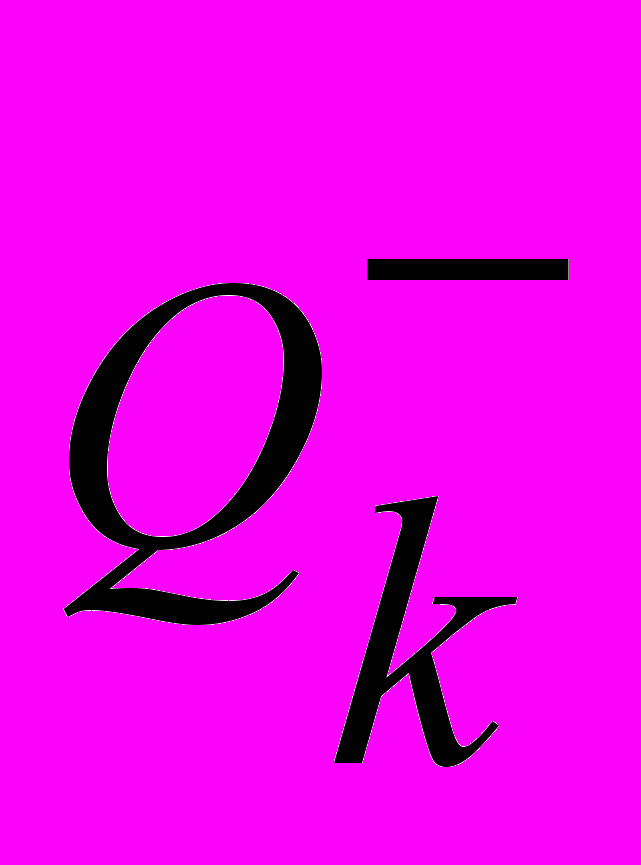• – множество вершин, которые включались, а потом были удалены;
  
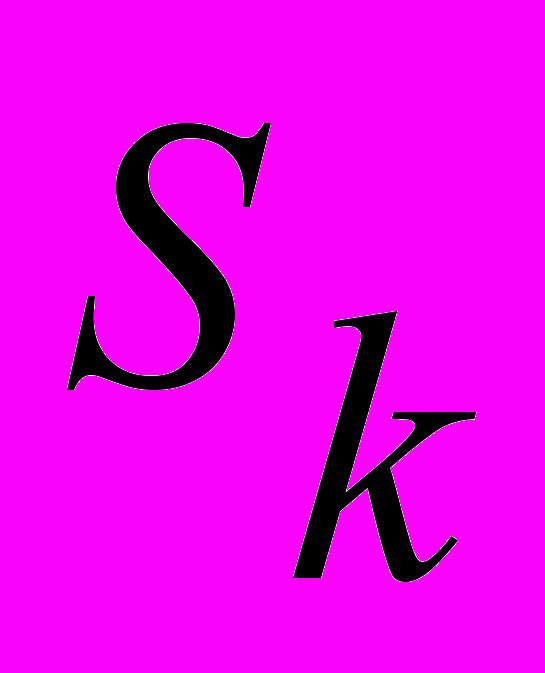• – множество, в которое будут записываться вершины максимального независимого подмножества.
  

Алгоритм состоит из шагов добавления вершин к множеству 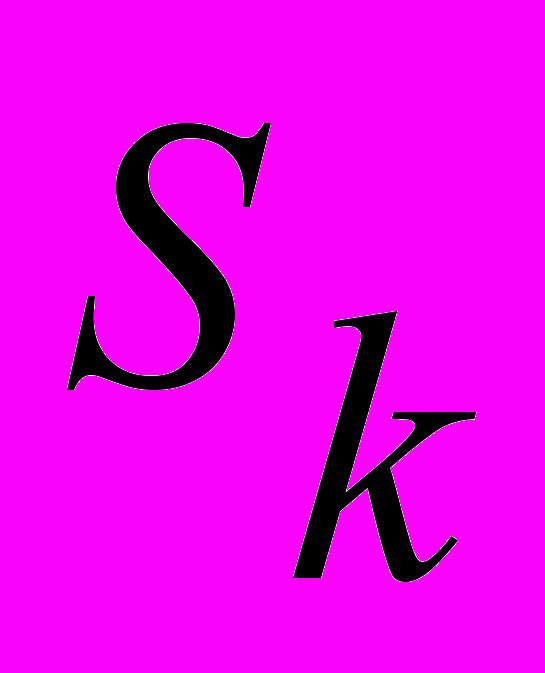и из шагов возвращения.

Критерии алгоритма:

1) 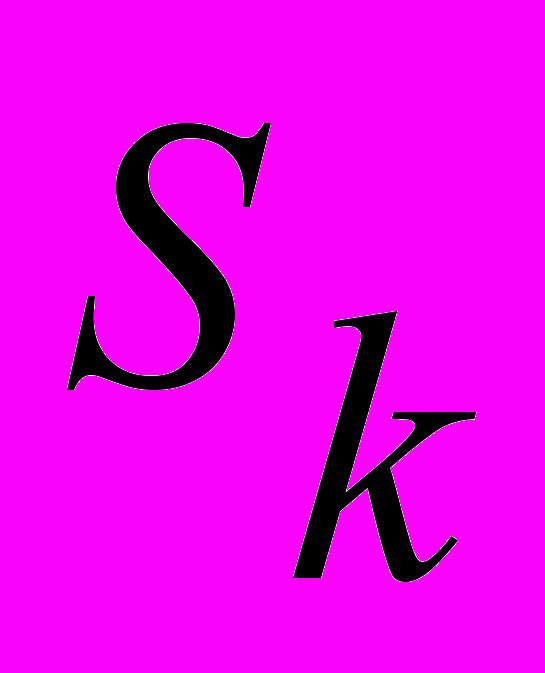- максимальное независимое подмножество, есл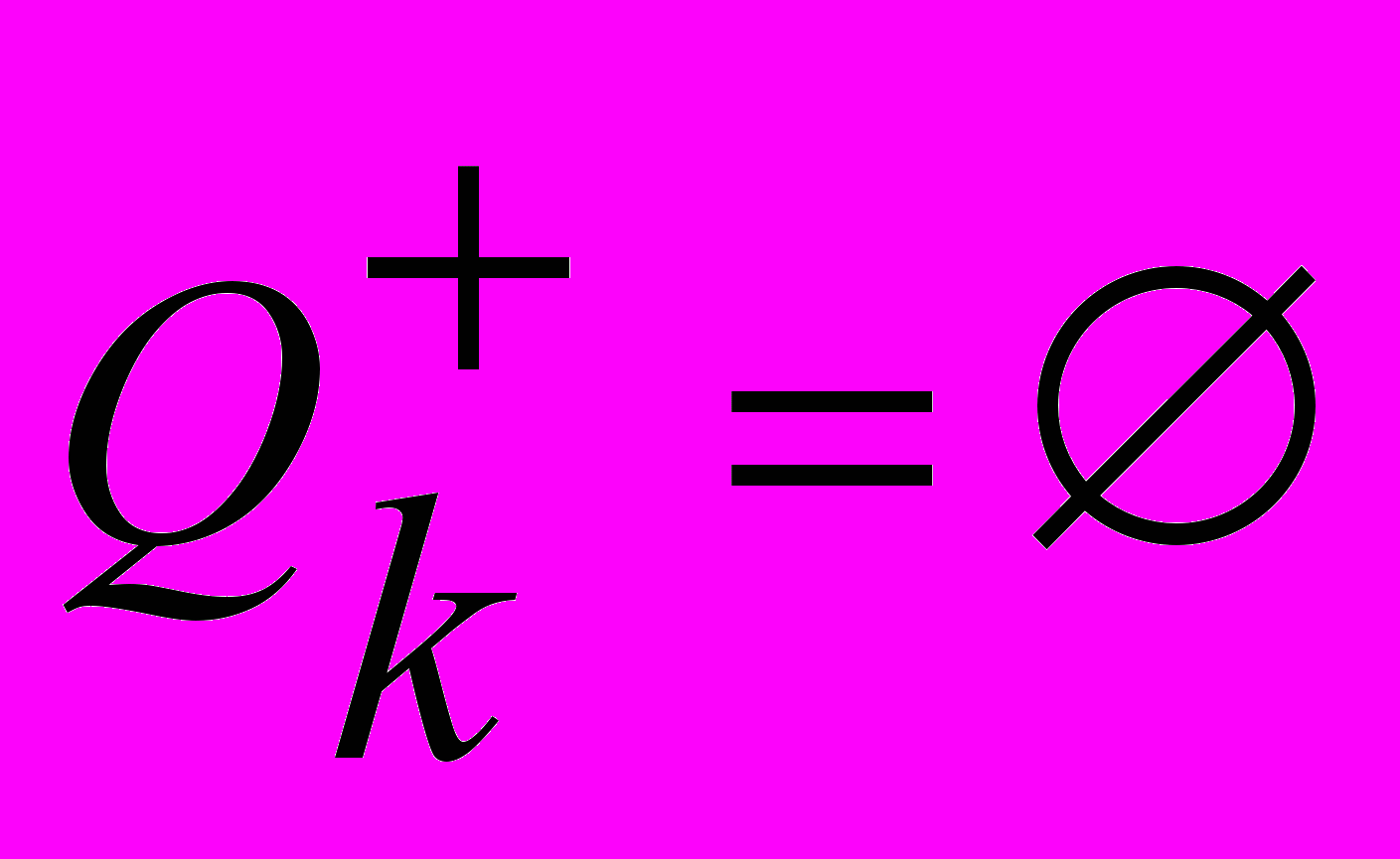и и .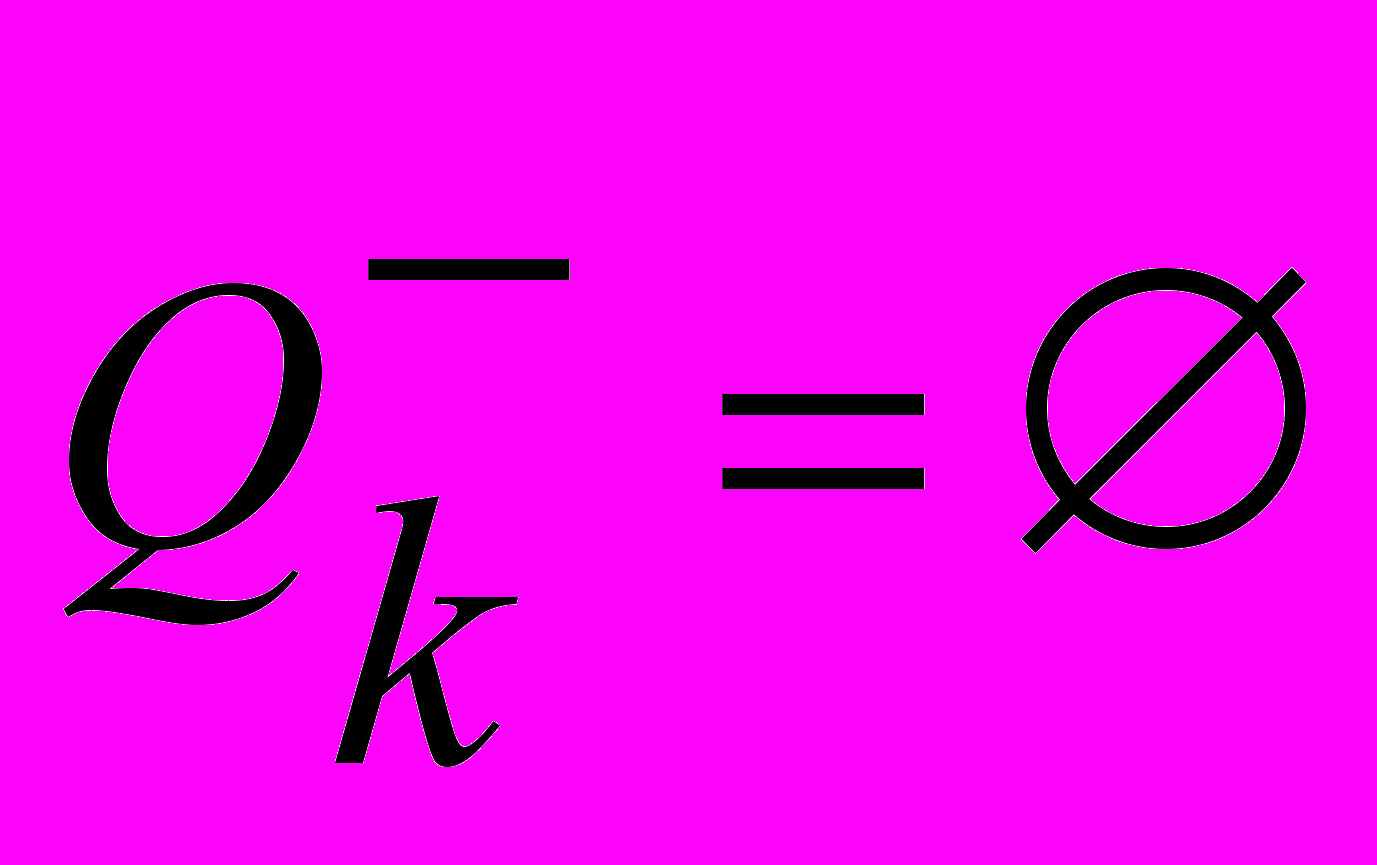

2) шаг добавления состоит в добавлении к множеству 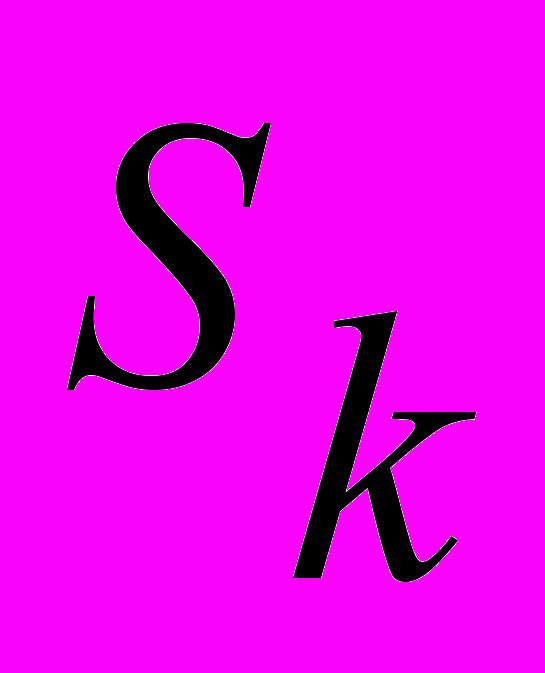очередной вершины:

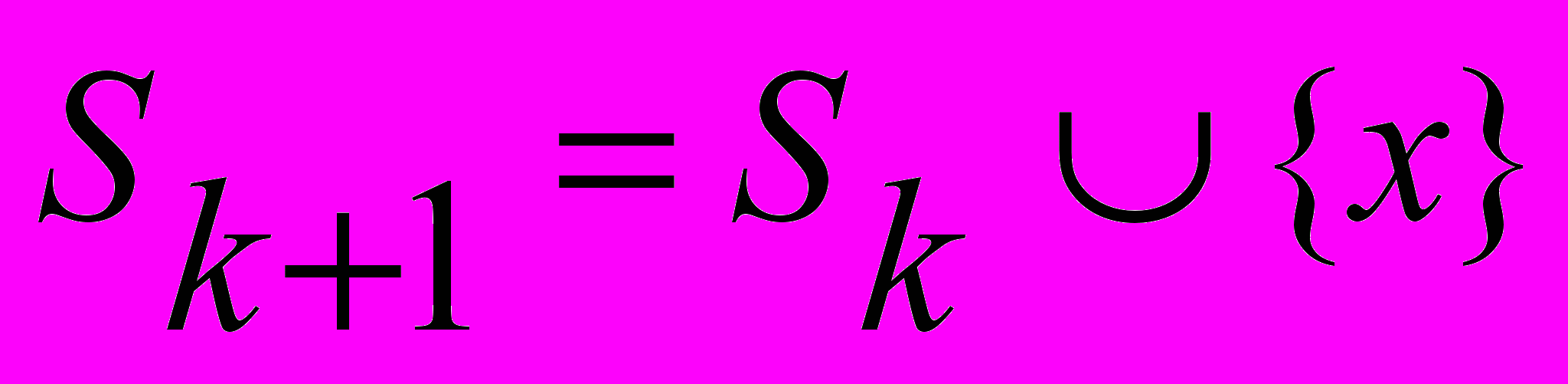, (1)

где:

• ;
  
• ;
  
• ;
  
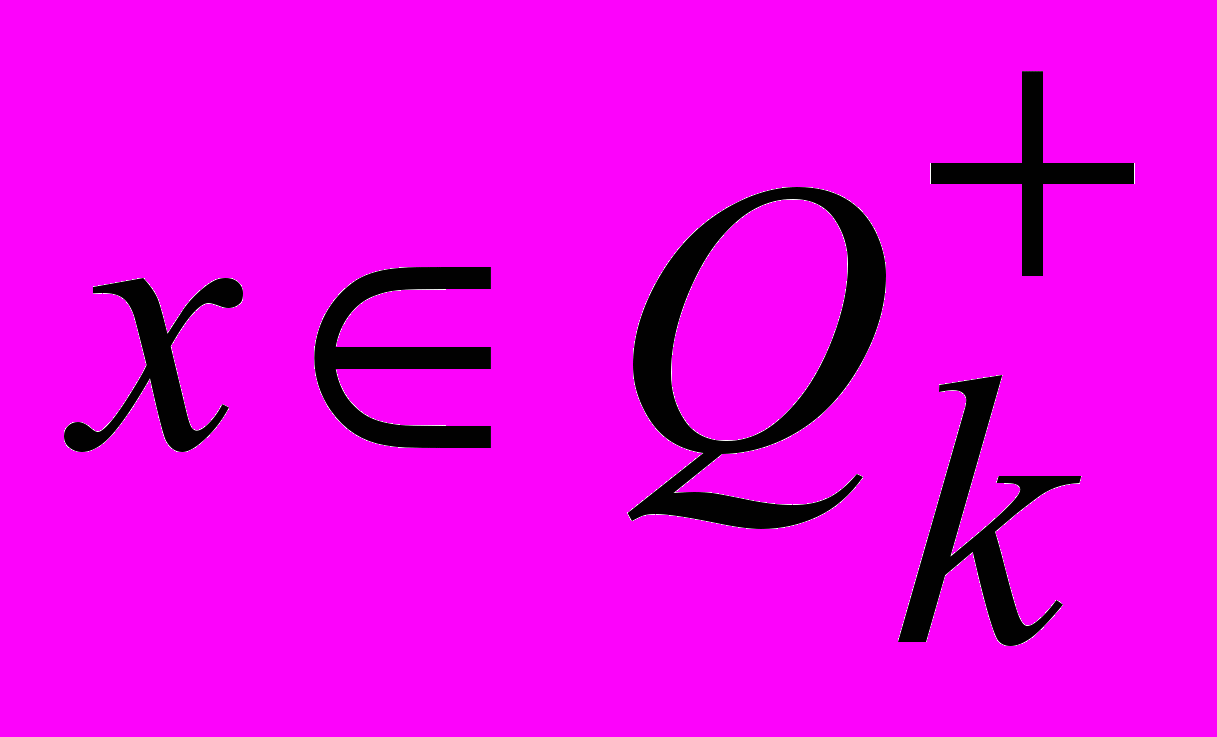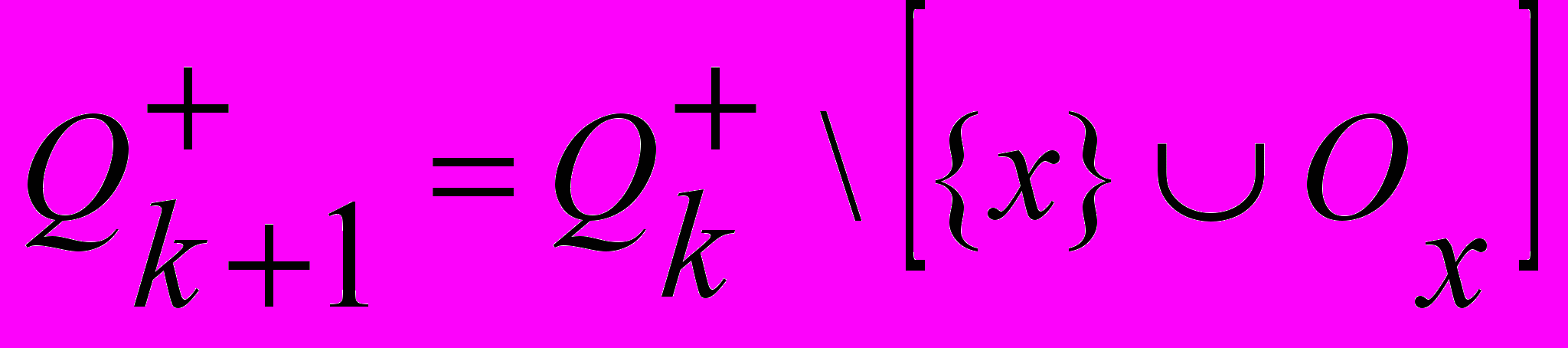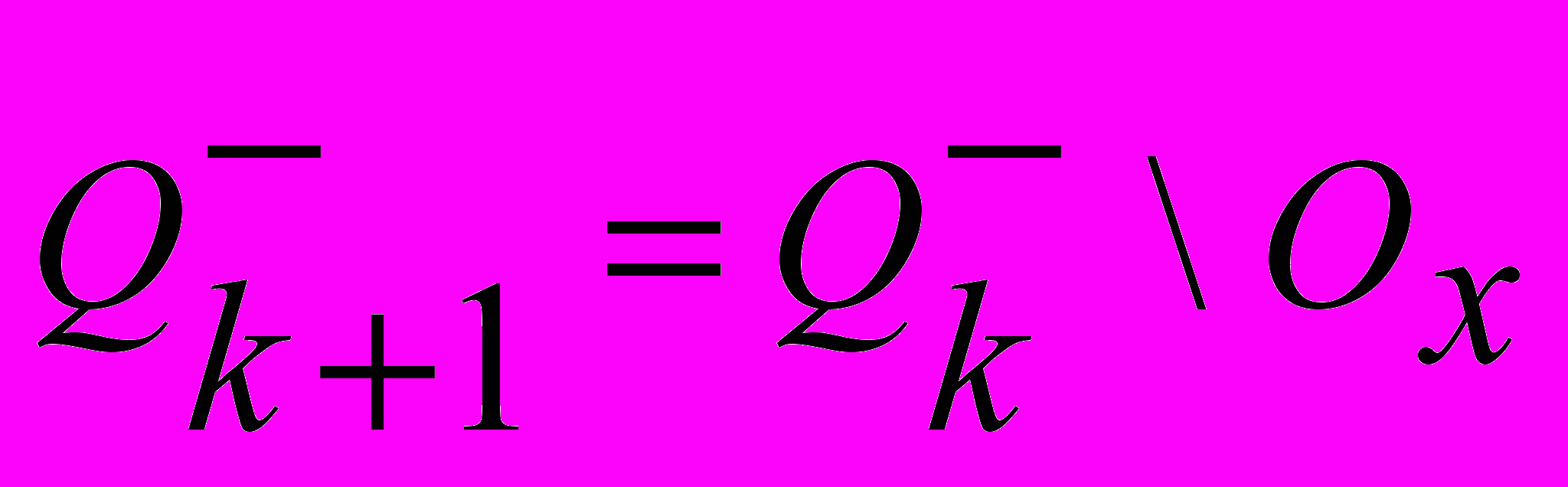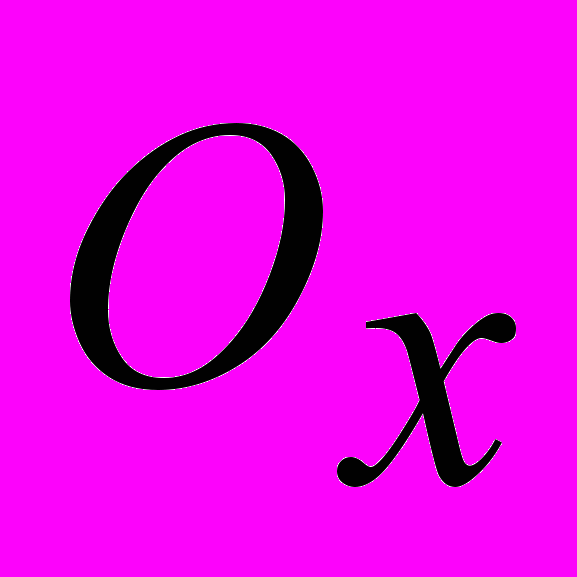• – окрестность вершины 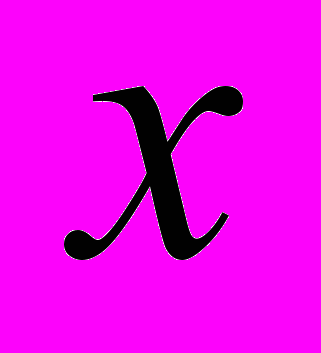(множество смежных с 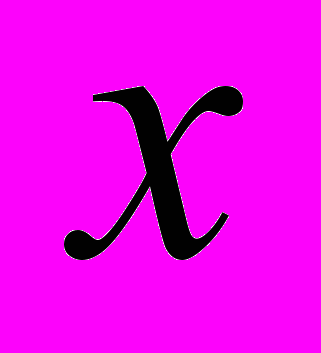вершин в данном графе).
  

3) шаг возвращения реализуется, когда

а) построено очередное подмножество, то есть 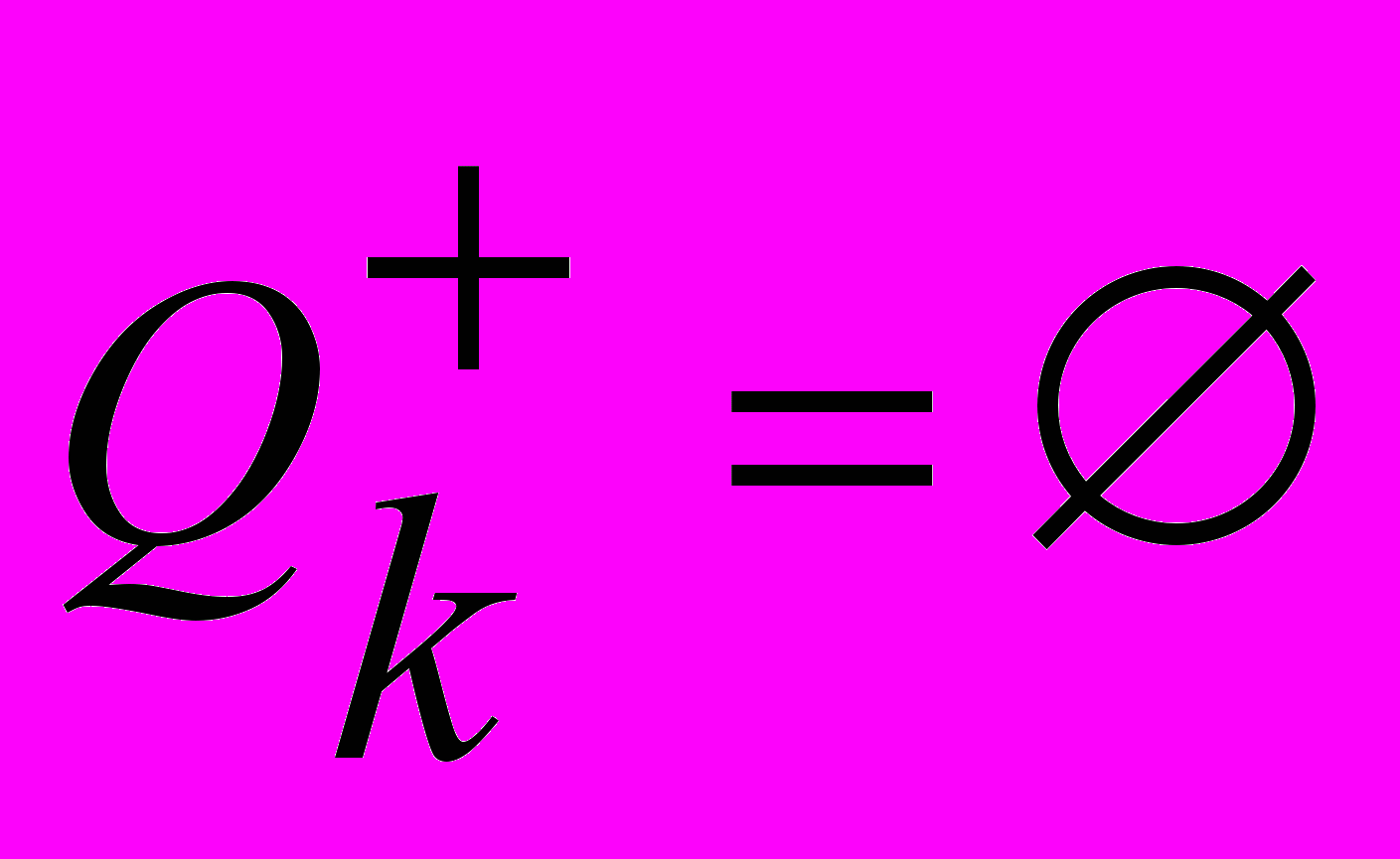и ;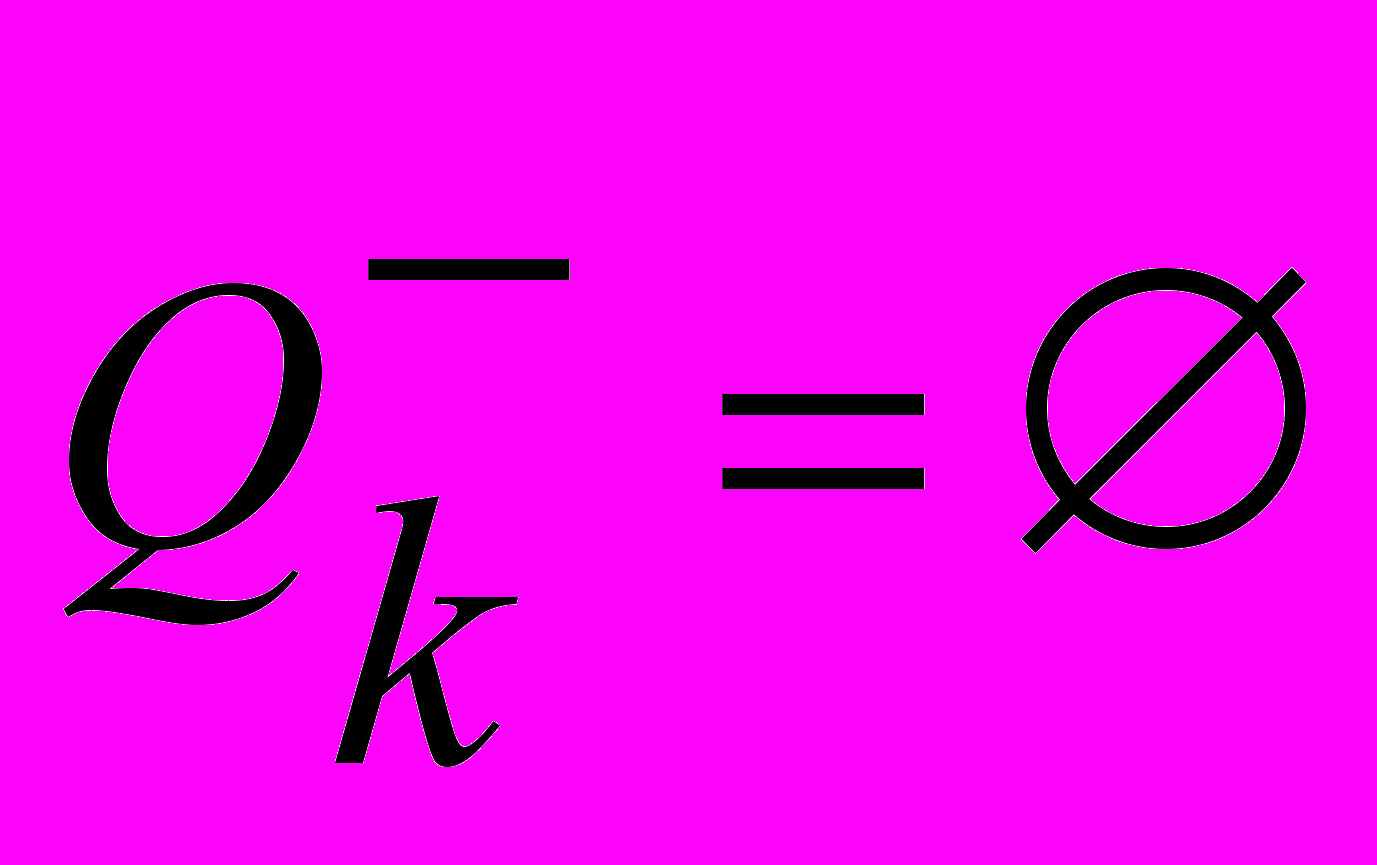

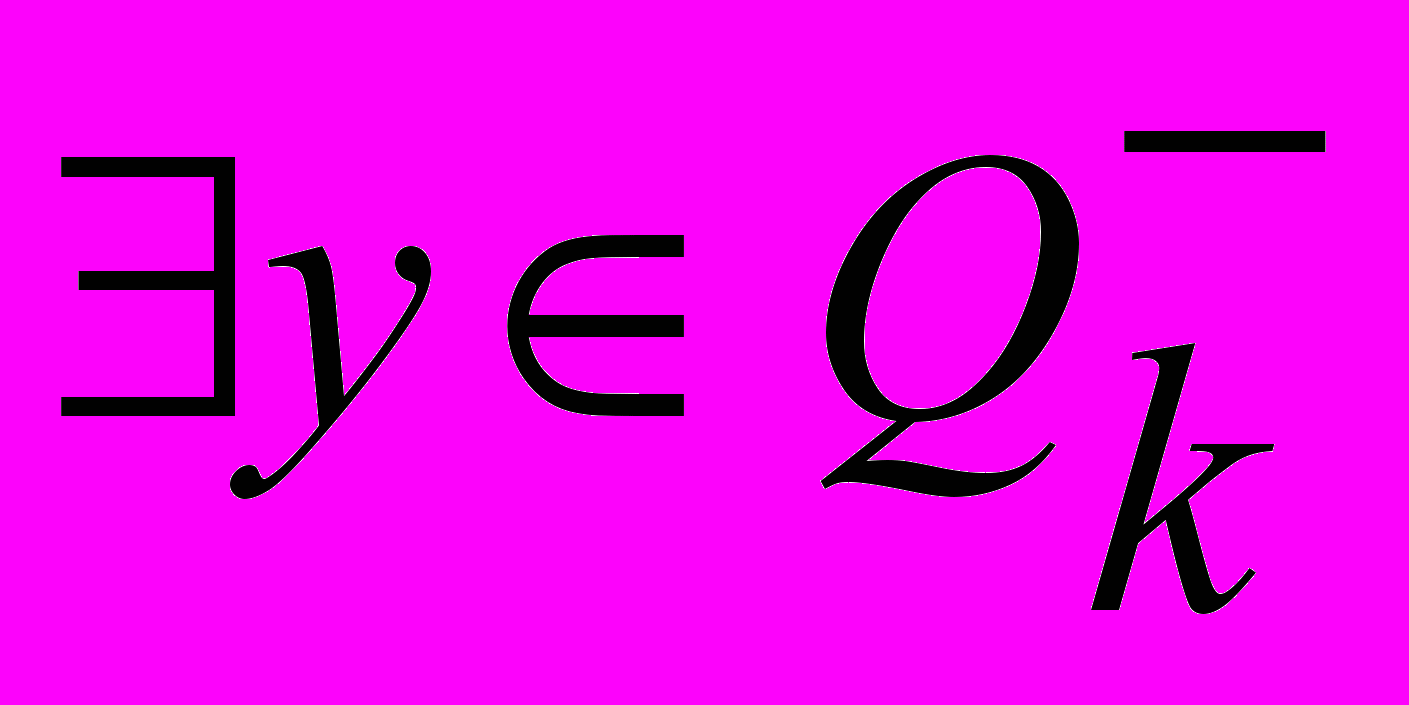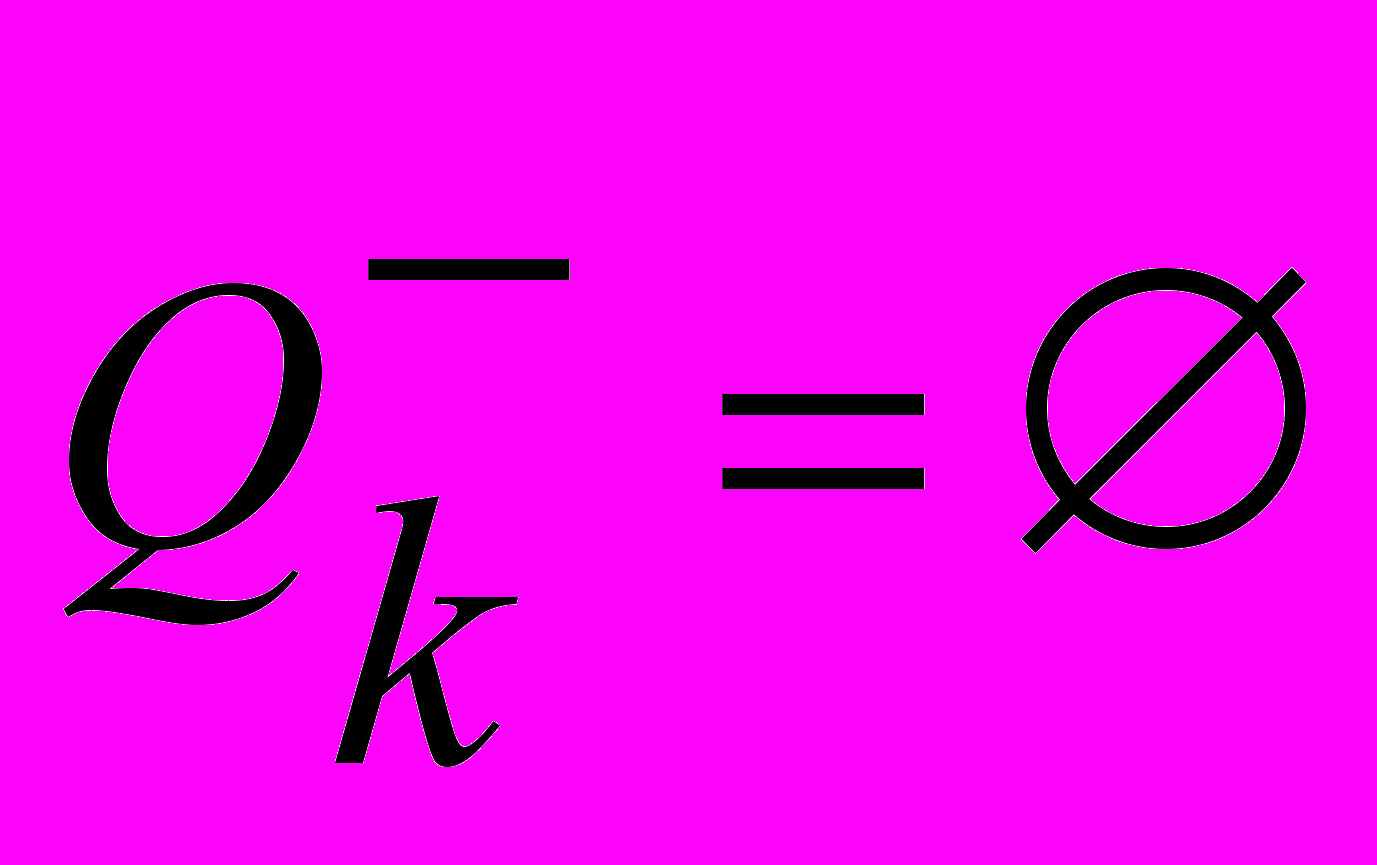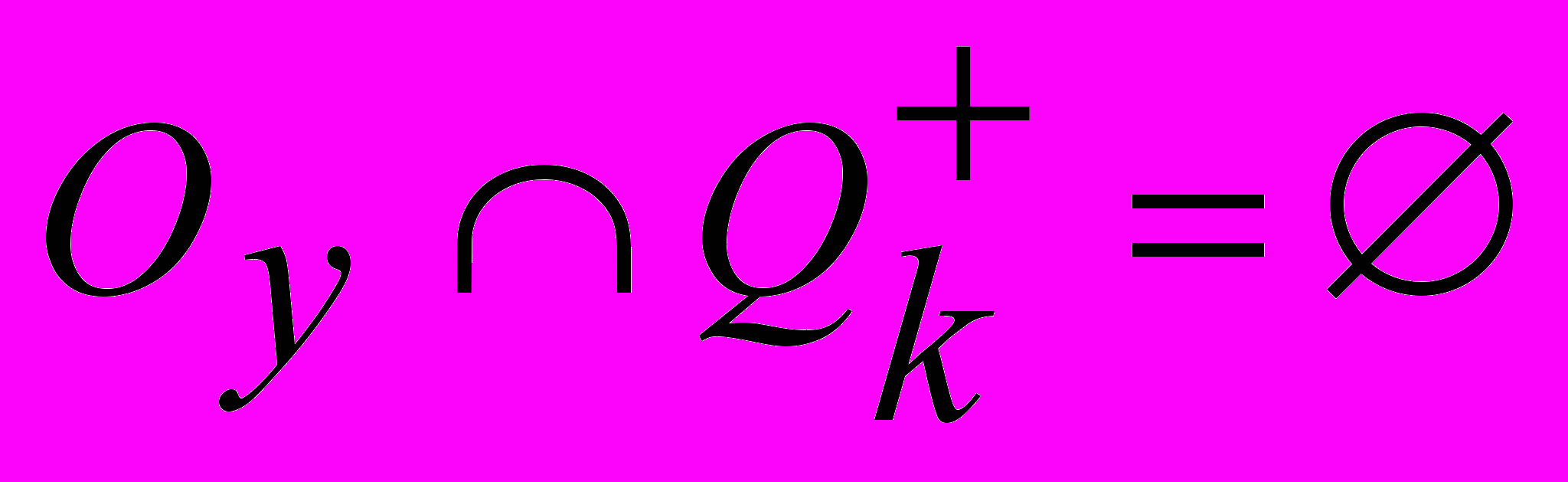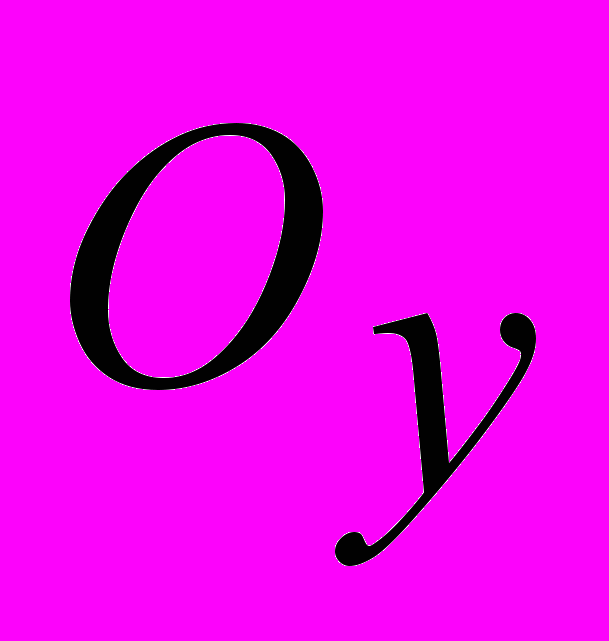б) , такое, что , где – окрестность вершины 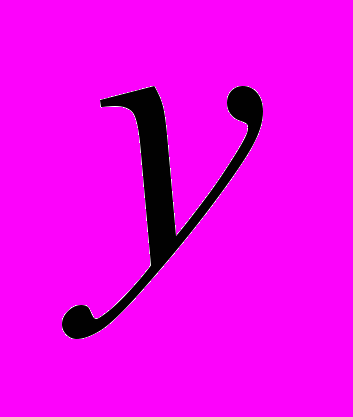(множество смежных с 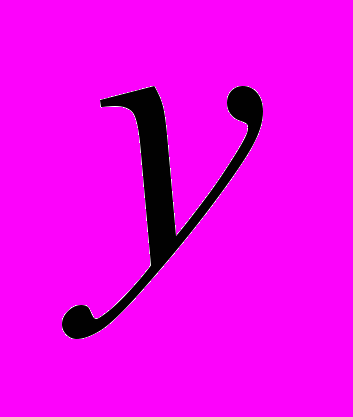вершин в данном графе). При шаге возвращения возвращаемся к старому множеству 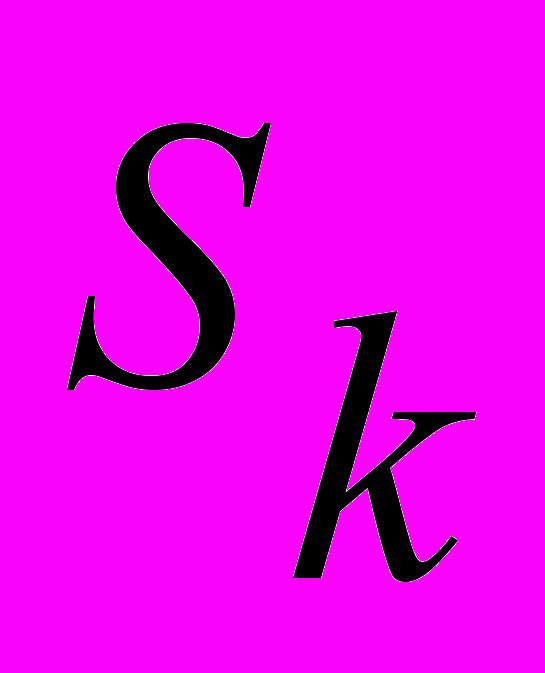и старым 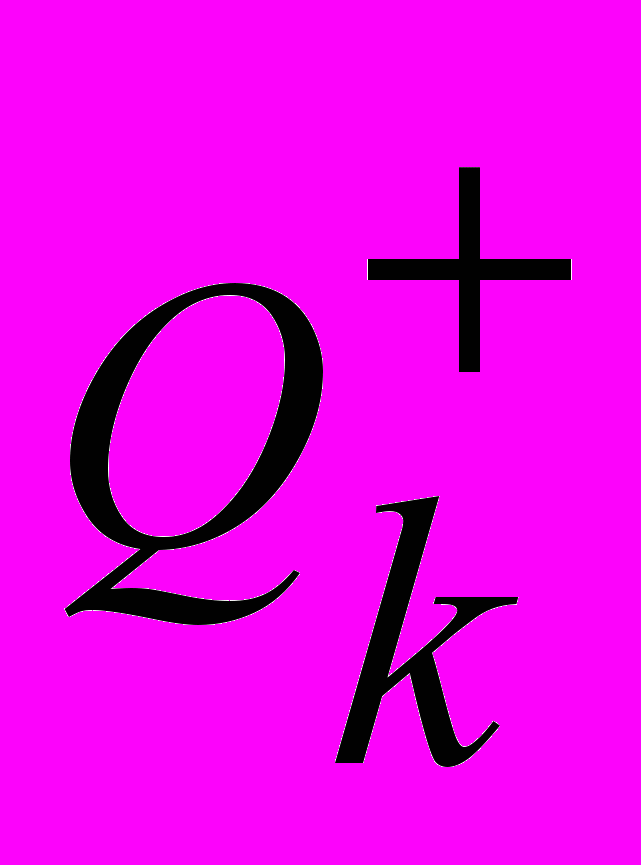и 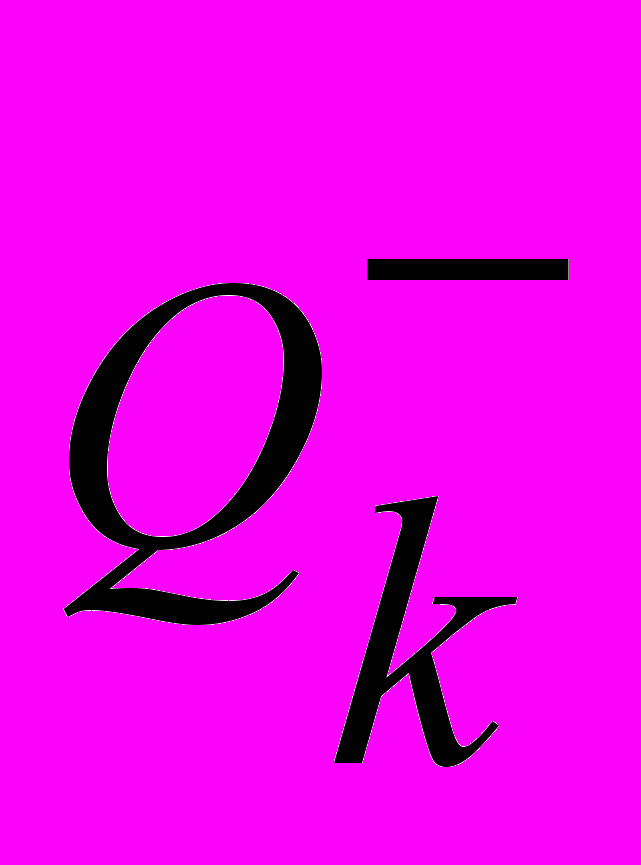. При этом , ,

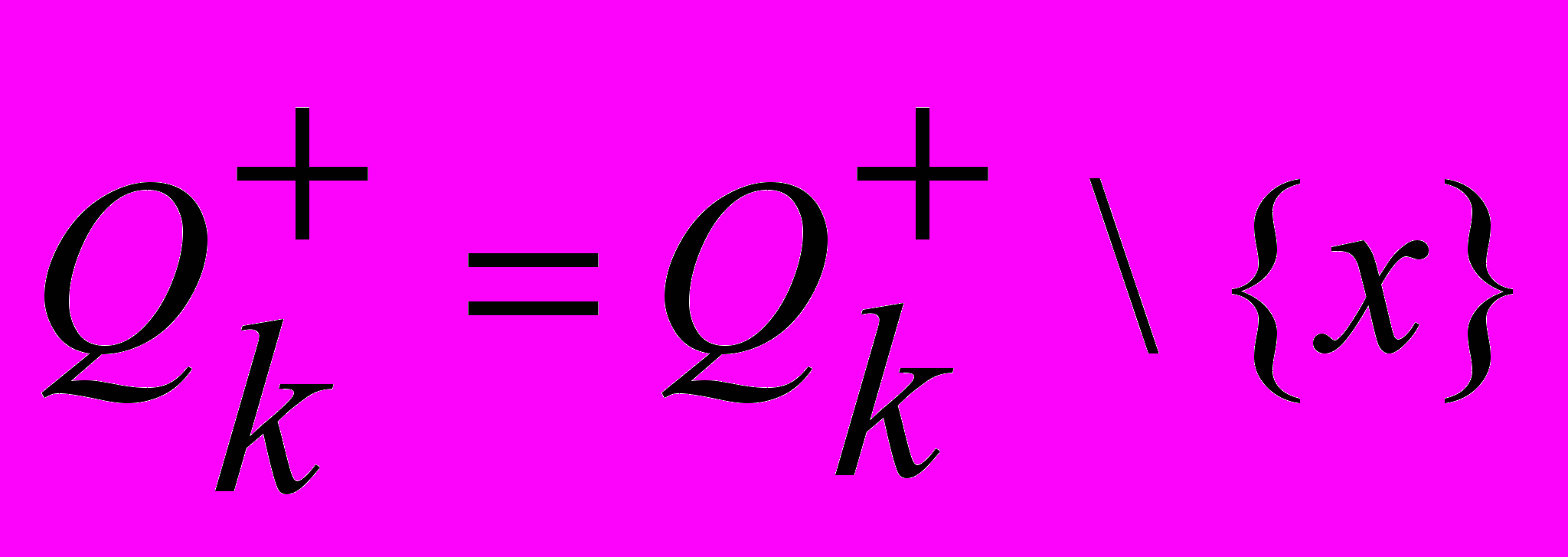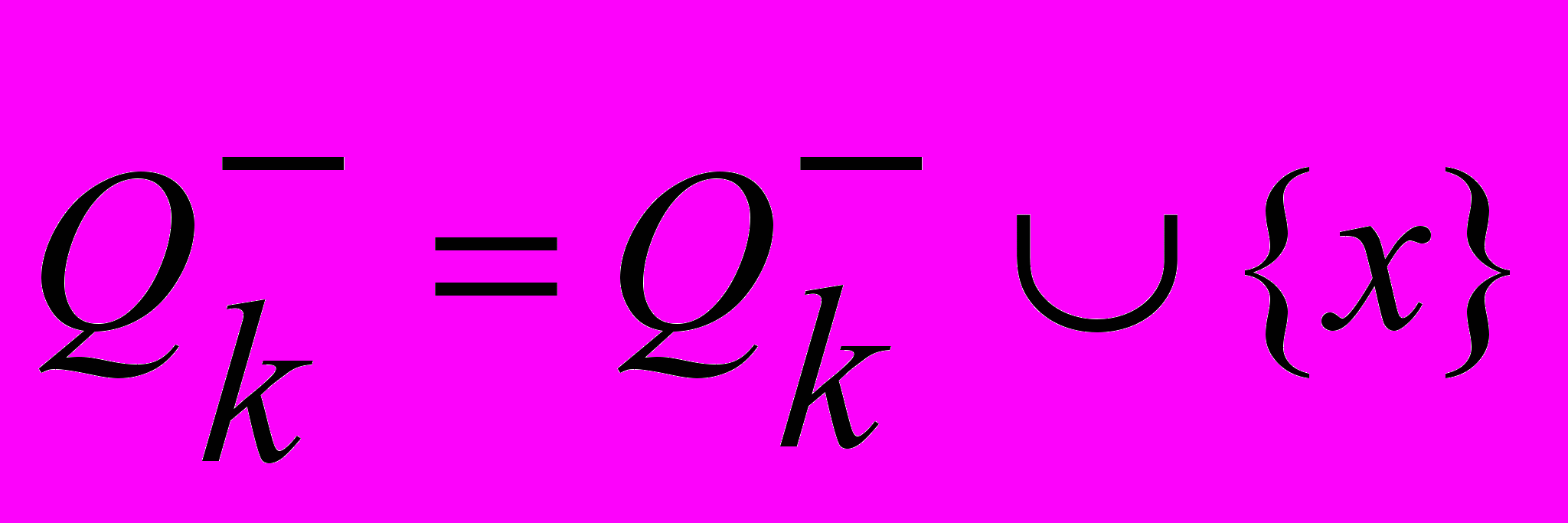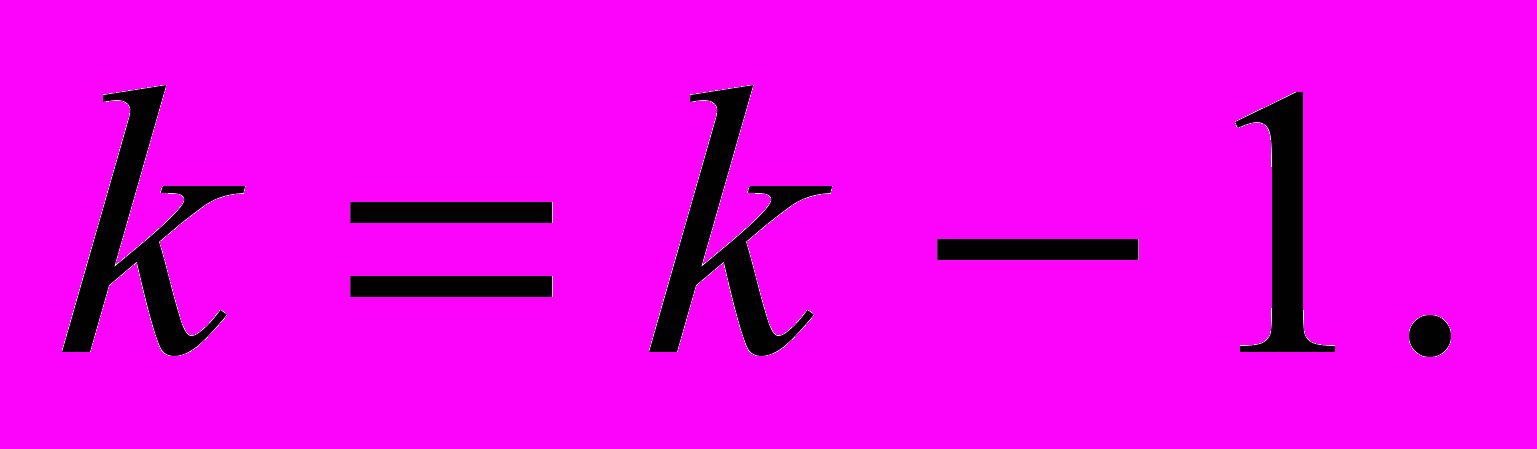
Вначале алгоритма , , , .

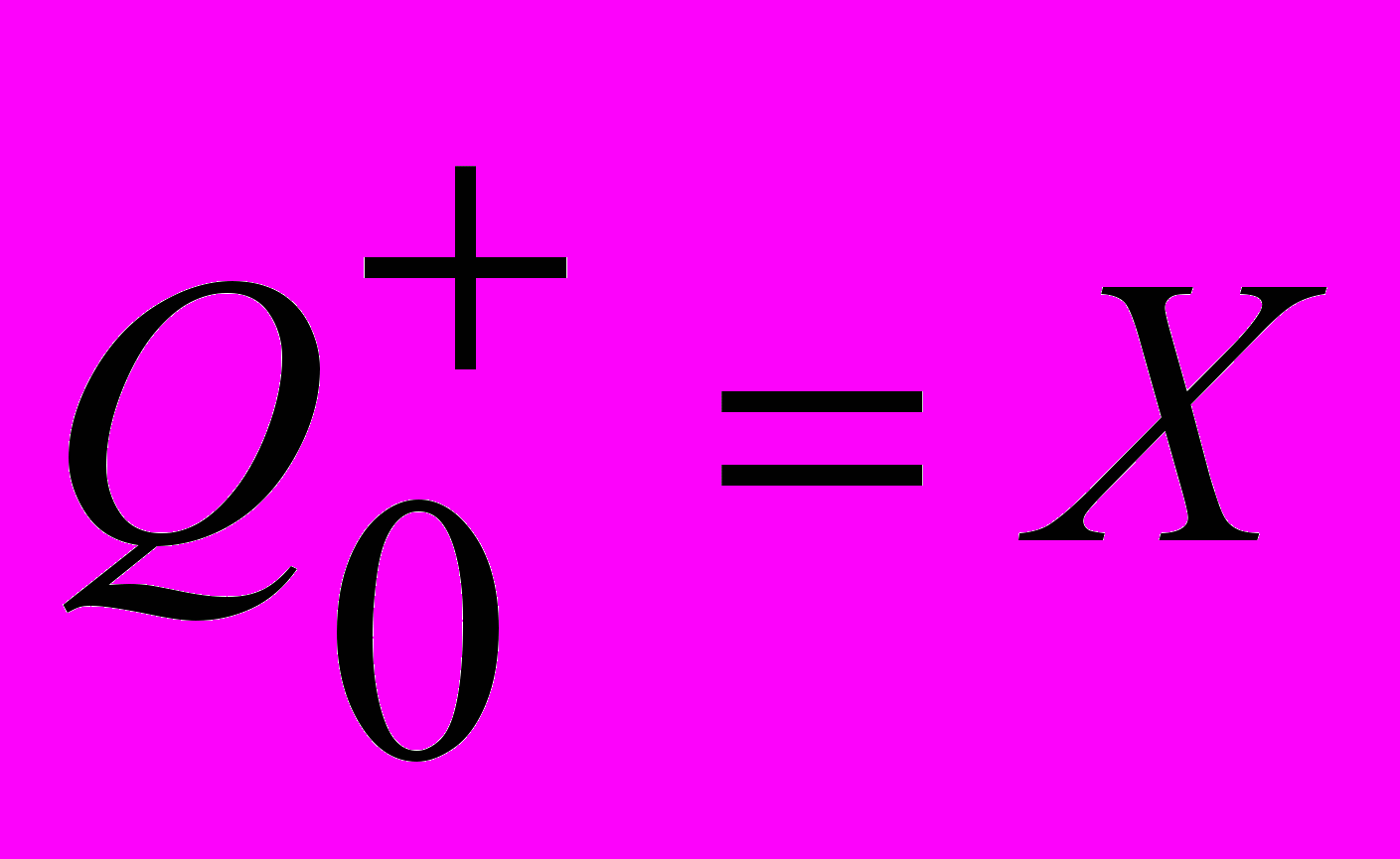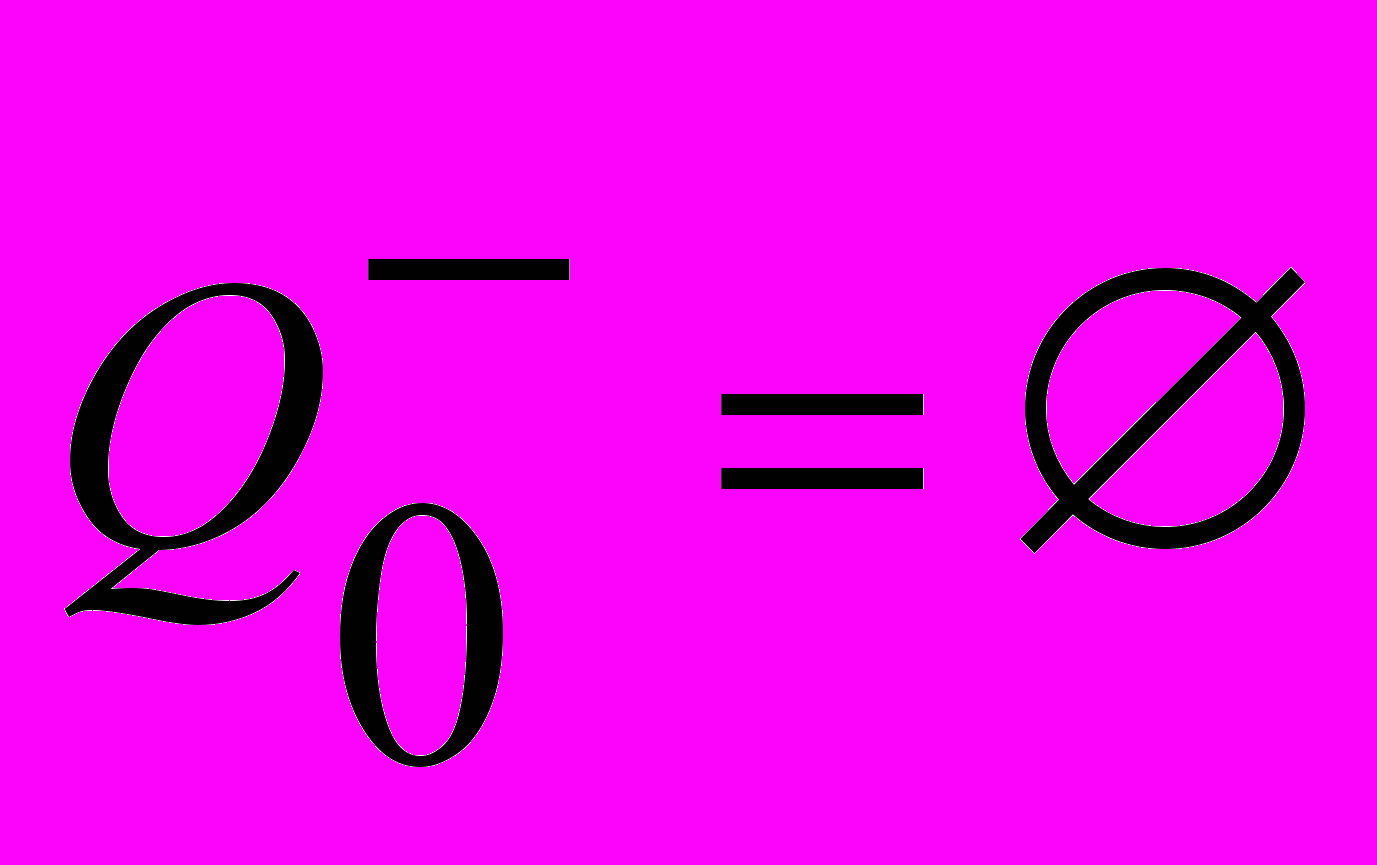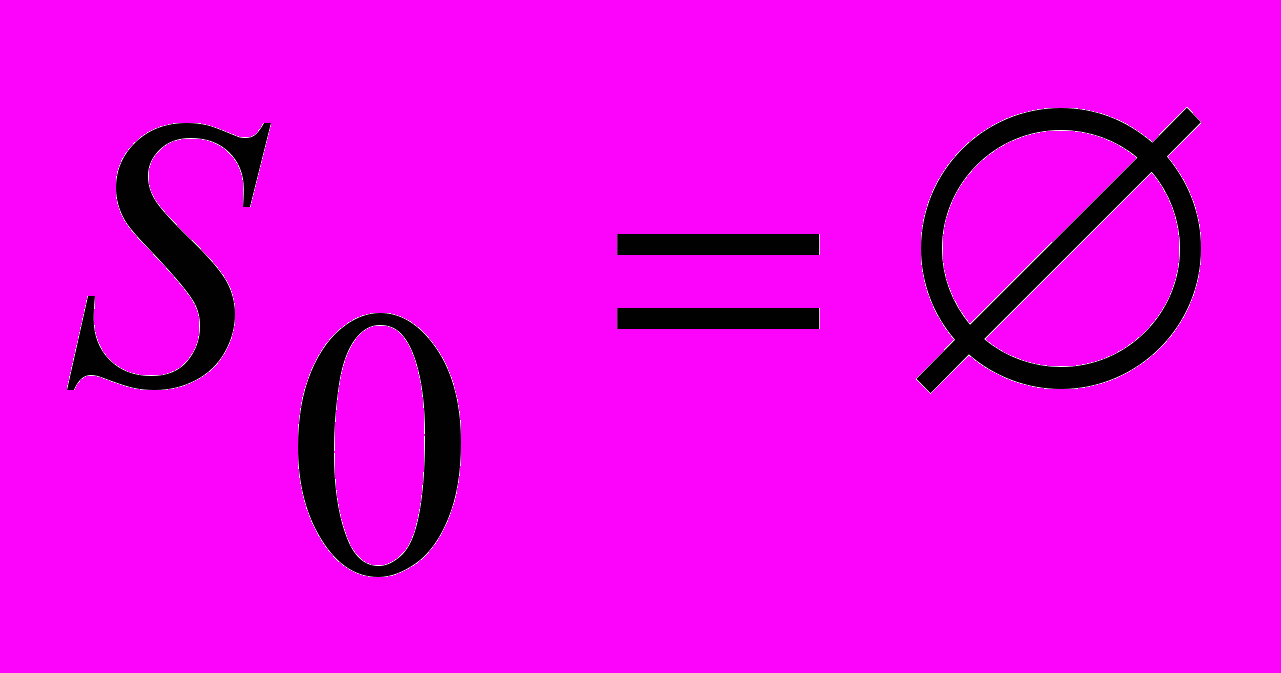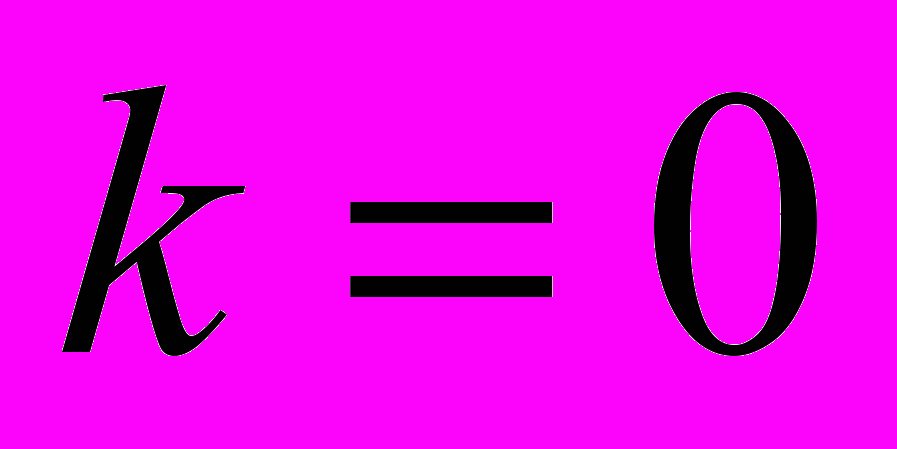Если необходимо построить все возможные максимальные независимые подмножества, то алгоритм продолжает работать до тех пор, пока не будут выполнены следующие условия: 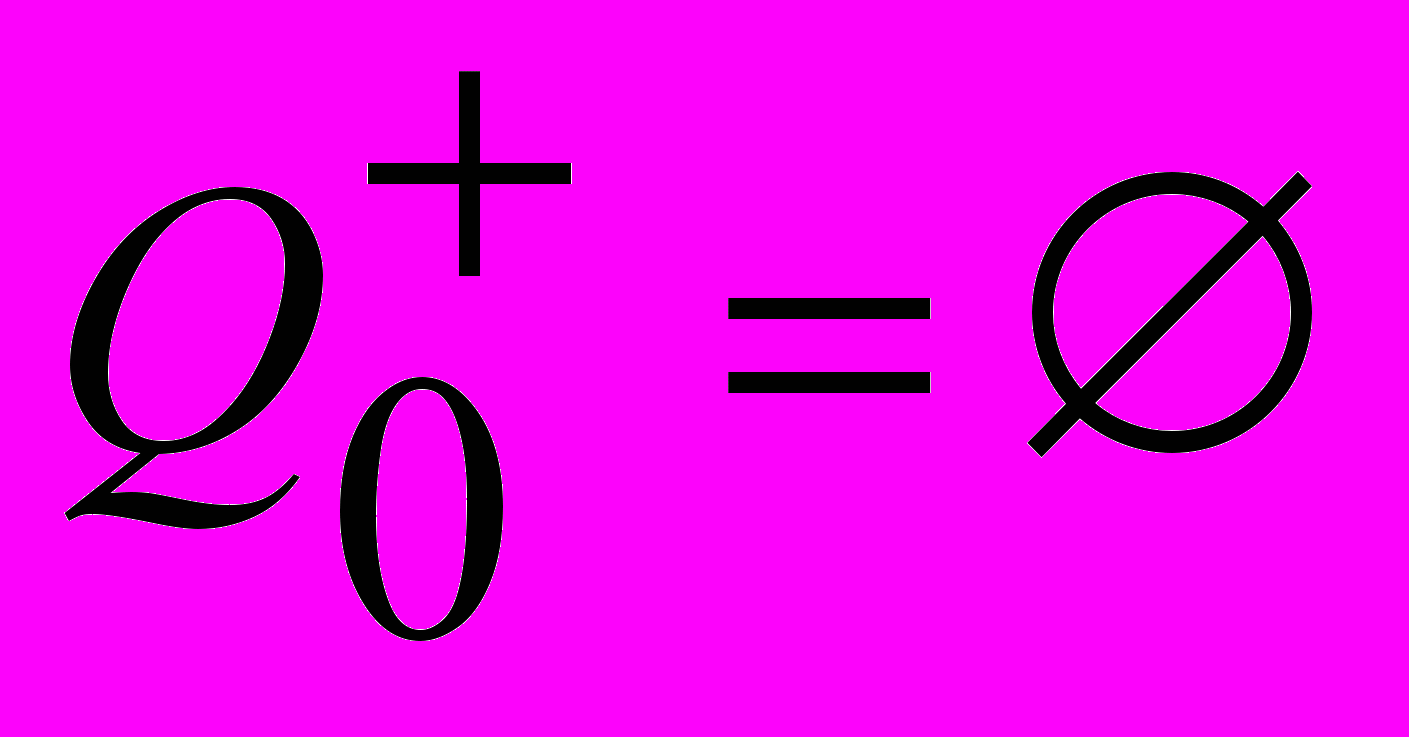и .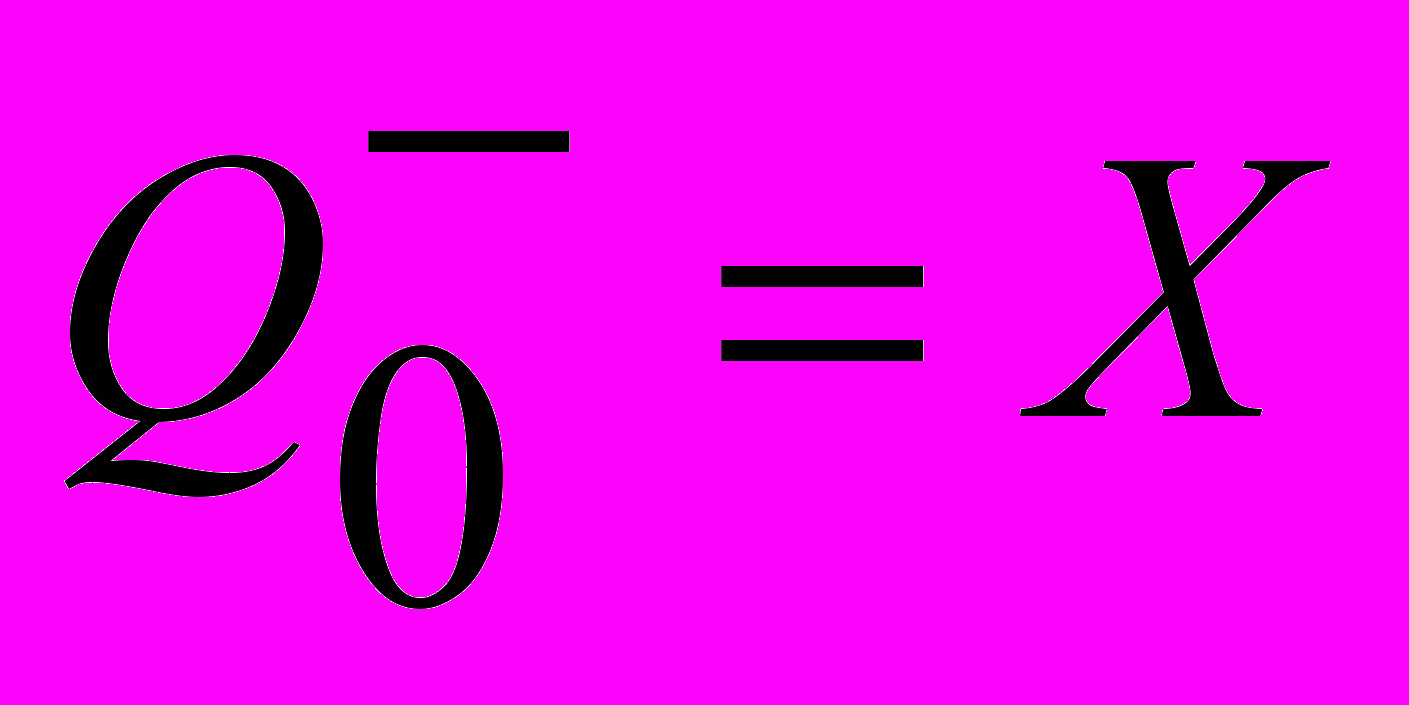

В разрабатываемой программе задача решается методом полного перебора. То есть алгоритм завершается, когда рассмотрены все независимые множества. Для повышения быстродействия из расчета исключаются вершины, не связанные с остальными вершинами графа. Также не рассматриваются потенциальные множества, вес которых меньше веса текущего максимального независимого множества.

3 Разработка программы

На основе описанного выше алгоритма была написана программа на языке С++. Интерфейс программы представлен на рисунке 1.



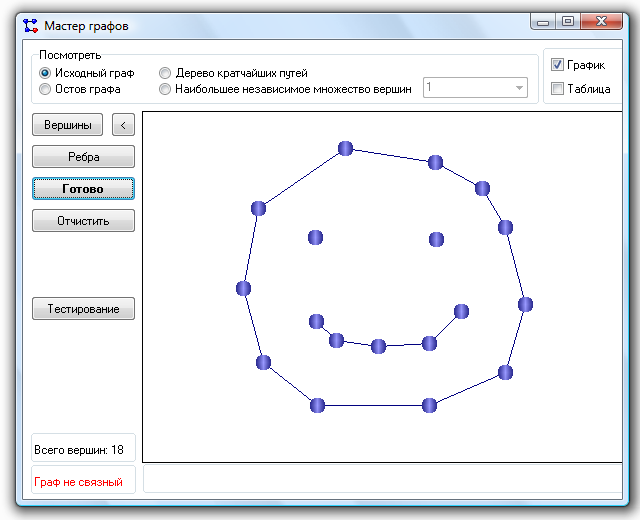
Рисунок 1 – Интерфейс программы

Новая вершина графа создается каждый раз при нажатии левой кнопкой мыши на панель редактирования графа. Ребра задаются отдельно в специальной таблице, которая появляется при нажатии на кнопку «Ребра».

После того как задано множество вершин и ребер графа, можно найти максимальное независимое множество вершин графа. Пример отображения наибольшего независимого множества графа представлен на рисунке 2.



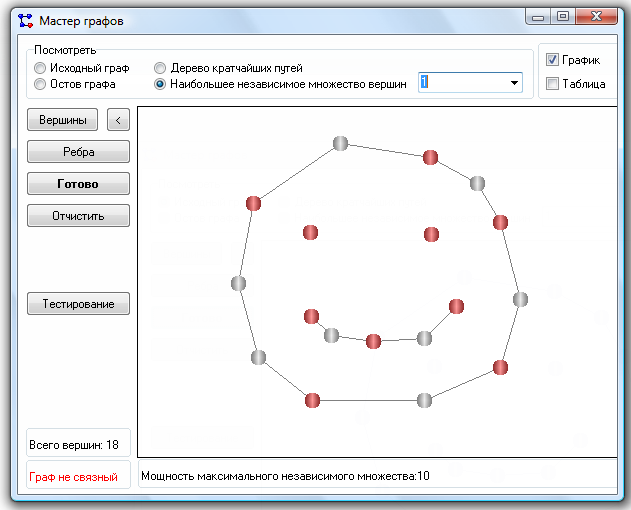
Рисунок 2 – Результат поиска наибольшего независимого множества вершин графа

Для оценки зависимости времени поиска наибольшего независимого множества графа от количества вершин добавлена специальная форма поиска максимального независимого множества вершин на множестве разных графов с одинаковым количеством вершин. Форма для тестирования работы алгоритма представлена на рисунке 3.



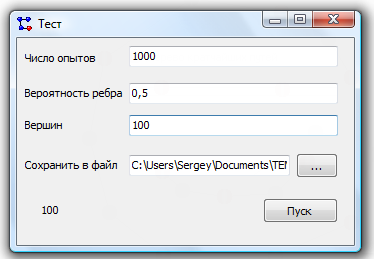
Рисунок 3 – Форма для тестирования работы алгоритма

Форма, показанная на рисунке 3, позволяет посмотреть зависимость между временем работы алгоритма и количеством вершин графа, которое изменяется от единицы до некоторого максимального значения. При этом алгоритм применятся к различным наборам графов с одинаковым количеством вершин. Количество графов и среднее количество ребер графов задается на форме.

На рисунке 4 показан пример зависимости времени работы алгоритма от количества вершин графа, у которого вероятность того, что две вершины соединены ребром, равна 0,5.



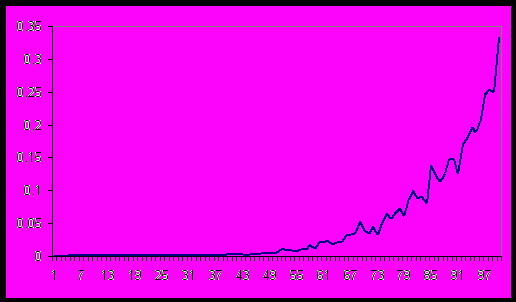
Рисунок 4 – Зависимость времени работы алгоритма от количества вершин графа

Из рисунка 4 видно, что с увеличением количества вершин графа среднее время работы алгоритма увеличивается экспоненциально.

Список использованных источников

1. Гэри М., Джонсон Д. Дискретная математика для программистов. Изд. 2 [Текст]. – М: Мир, 1982. – 416 с.
   
2. Новиков Ф. Дискретная математика для программистов. Изд. 2 [Текст]. – СПб: Питер, 2005. – 364 с.