Математическое моделирование русловых деформаций как важнейший компонент мероприятий по предотвращению вредного воздействия вод (на примере реки томи у томска)
| Вид материала | Документы |
СодержаниеМетодика математического моделирования Г – гидромеханический параметр наносов, вычисляемый для i Результаты исследований. |
- С. Б. Томашевский влияние упругопластических деформаций на результаты решения контактных, 118.32kb.
- Т. А. Дуюн моделирование тепловых деформаций с целью обеспечения точности механической, 116.36kb.
- Методика оценки экономической, бюджетной и социальной эффективности оценка экономической, 140.87kb.
- Математическое моделирование управляемого движения космических аппаратов, 213.72kb.
- Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
- Математическое моделирование многомерных квазистационарных электромагнитных полей, 380.28kb.
- Математическое моделирование деформаций дна в покрытых льдом нестационарных потоках, 269.74kb.
- Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
- И математическое моделирование, 1392.77kb.
- Математическое моделирование термомеханических процессов в системах армированных стержней, 259.01kb.
УДК 556.537
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РУСЛОВЫХ ДЕФОРМАЦИЙ КАК
ВАЖНЕЙШИЙ КОМПОНЕНТ МЕРОПРИЯТИЙ ПО ПРЕДОТВРАЩЕНИЮ
ВРЕДНОГО ВОЗДЕЙСТВИЯ ВОД (НА ПРИМЕРЕ РЕКИ ТОМИ У ТОМСКА)
В.А. Льготин, Ю.В. Макушин, О.Г. Савичев
ОГУП Территориальный центр Томскгеомониторинг», г. Томск, Россия
Томь – крупнейший после Иртыша приток р. Оби. На водосборной территории этой реки расположены города Томск, Кемерово, Новокузнецк, Северск, Междуреченск, Прокопьевск, Киселевск, Осинники, Юрга и сосредоточены крупнейшие в России предприятия угольной, металлургической и химической отраслей. Примерно до 1960-х годов в нижнем течении р. Томи достаточно часто отмечались заторные и зажорные явления, а также связанные с ними затопления и подтопления территории г. Томска и окрестных сел [5]. С 1950-х до середины 1980-х годов непосредственно в речном русле проводилась интенсивная добыча песчано-гравийного материала (ПГМ), ставшая, по мнению ряда авторов, причиной уменьшения на 2,5 м отметок дна, а вслед за ними и уровней воды [1-3, 7]. Кроме того, произошло изменение очертаний береговой линии и русловых образований, в результате которого некоторые осередки и острова либо исчезли, либо изменились в плане и уменьшились по площади. Примерно в это же время весенние половодья перестают представлять угрозу для г. Томска в части его затопления. В 1985 г. работы по русловой добыче ПГМ у г. Томска были свернуты, а в конце 1990-х здесь стали отмечаться случаи заметного повышения уровней воды весной вследствие заторов, не наблюдавшиеся около 40 лет. В связи с необходимостью объяснения этого явления в Областном государственном унитарном предприятии «Территориальный центр Томскгеомониторинг» (ТЦ Томскгеомониторинг) были начаты исследования, целью которых является прогноз русловых процессов р. Томь у г. Томска и выработка рекомендаций по предупреждению опасных ледовых явлений и русловых деформаций. Один из важнейших этапов этого исследования – разработка и апробация математической модели, результаты которых и изложены в данной работе. Исходной информацией для моделирования послужили данные режимных наблюдений Росгидромета за расходами и уровнями воды р. Томи, содержанием в воде взвешенных веществ в створах, расположенных в 74,8 и 68,1 км от устья, а также материалы русловой съемки, проведенной в 1993, 2002, 2003, 2004 гг. Томским филиалом Обского государственного бассейнового управления водных путей и судоходства, Томским государственным университетом и ТЦ «Томскгеомониторинг».
Методика математического моделирования. Моделирование русловых деформаций проводилось по методу, предложенному А.В. Караушевым [4] и основывающемуся на допущении однонаправленности руслового процесса в пределах расчетных элементов русла реки. Базовое уравнение имеет вид
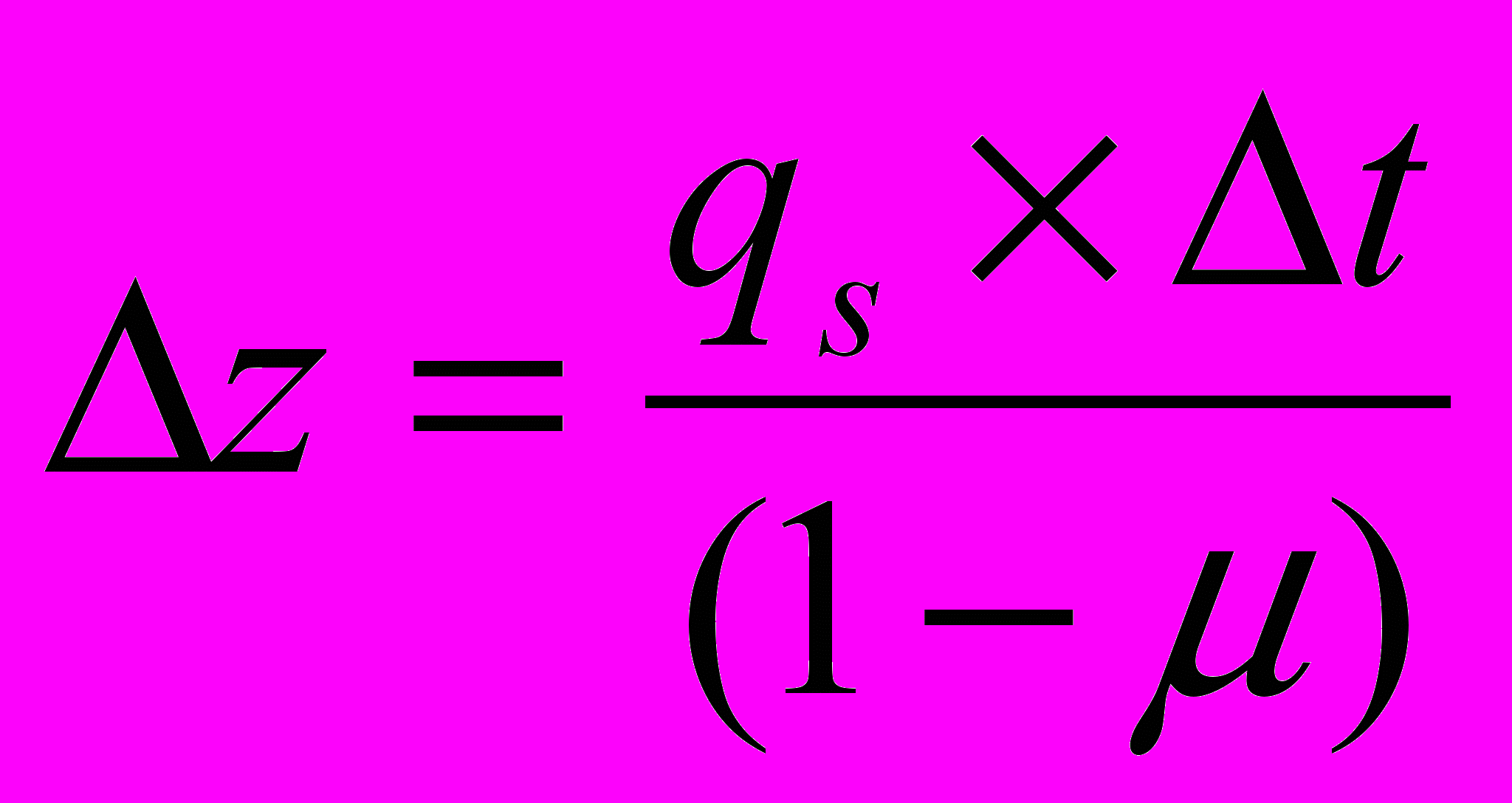 , (1)
, (1)где z – деформация дна (м) в конце расчетного интервала времени t (z – высотная отметка дна реки, м БС); qs – результирующий вертикальный секундный расход наносов через единицу поверхности дна в конце расчетного элемента x, м/с; – пористость грунта (согласно А.В. Караушеву, = 0,3…0,5; в данной работе принято = 0,4). Величина qs определяется по формуле
qs=(uср.+ku)Sкон.–kuSвзм., (2)
где uср.– гидравлическая крупность наносов, м/с; ku – коэффициент, определяемый по формуле (3) из условия равновесия русла; Sвзм – мутность взмыва, вычисленная для элемента транзитной струи, г/м3; Sкон – средняя мутность воды в конце элемента x, г/м3;
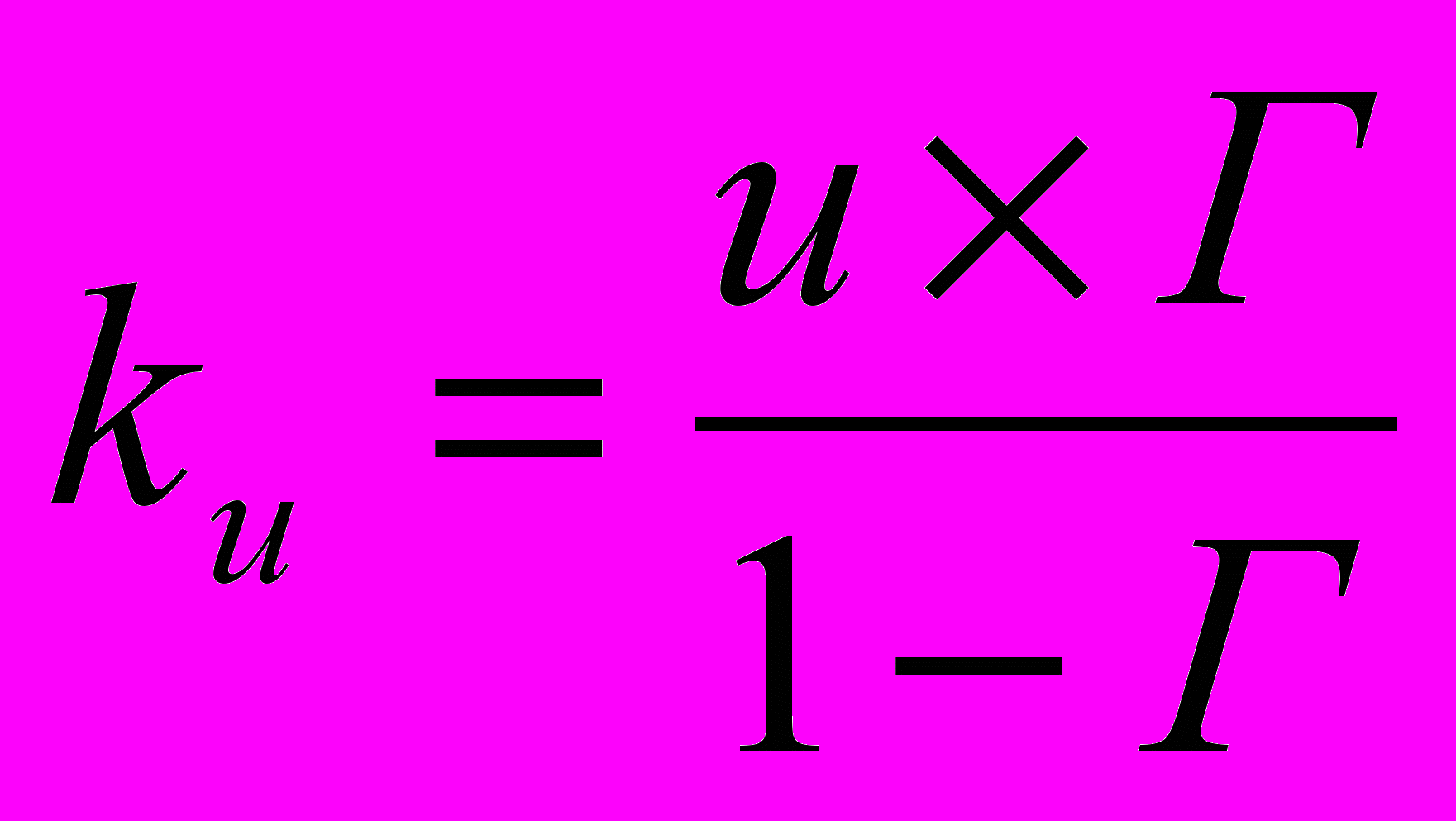 , (3)
, (3)где Г – гидромеханический параметр наносов, вычисляемый для i-й фракции наносов в зависимости от функций Бi(ui/vср.; Сш) и Фi(ui/vz) по формуле
Гi=БiФi. (4)
Функции Бi и Фi определяются интерполяцией по соответствующим графикам из работы [4] в зависимости от гидравлической крупности наносов u, вертикальных пульсаций vz, средней скорости течения vср. и значений коэффициента Шези Сш, определяемых по формулам (5-8):
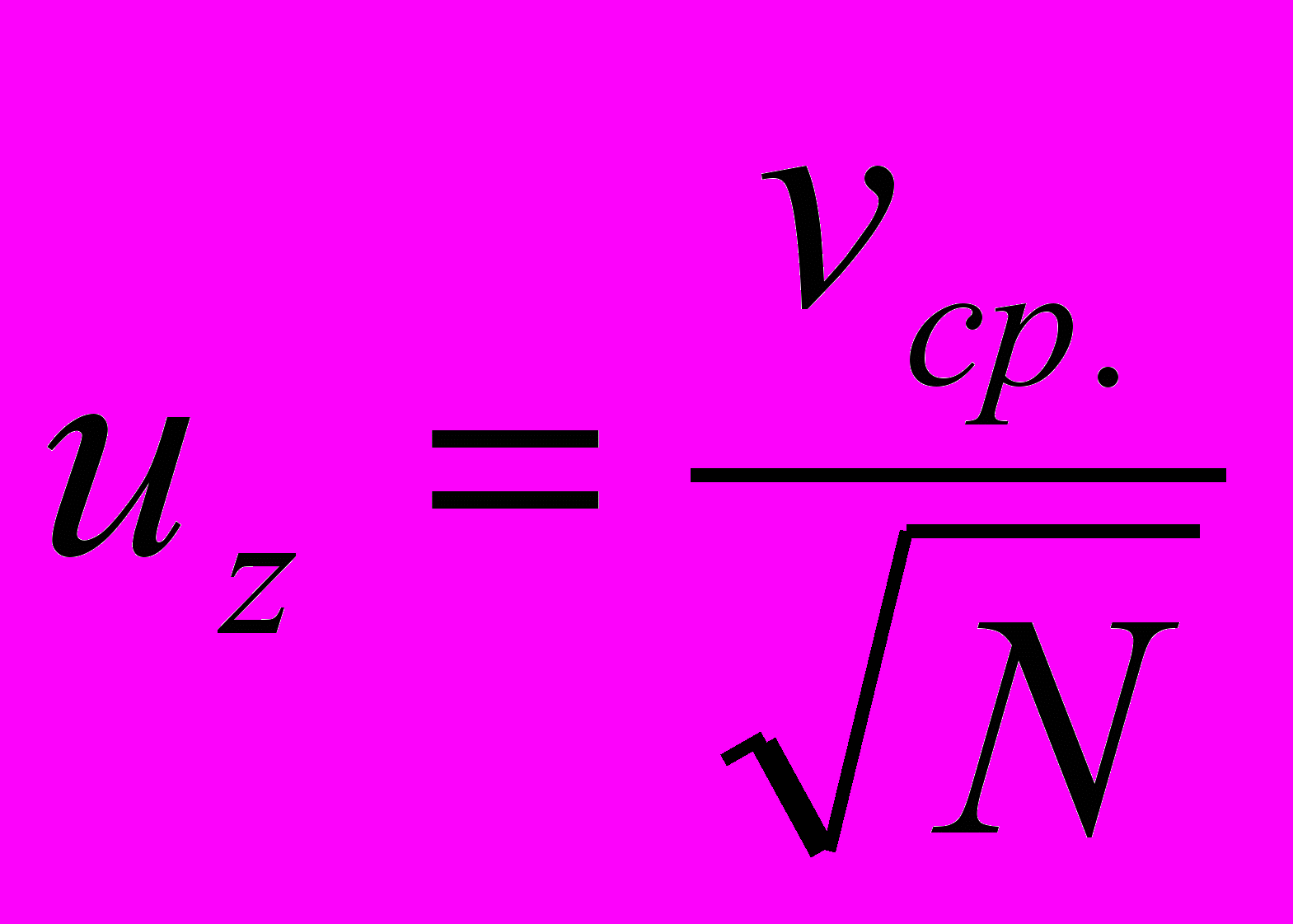 , (5)
, (5)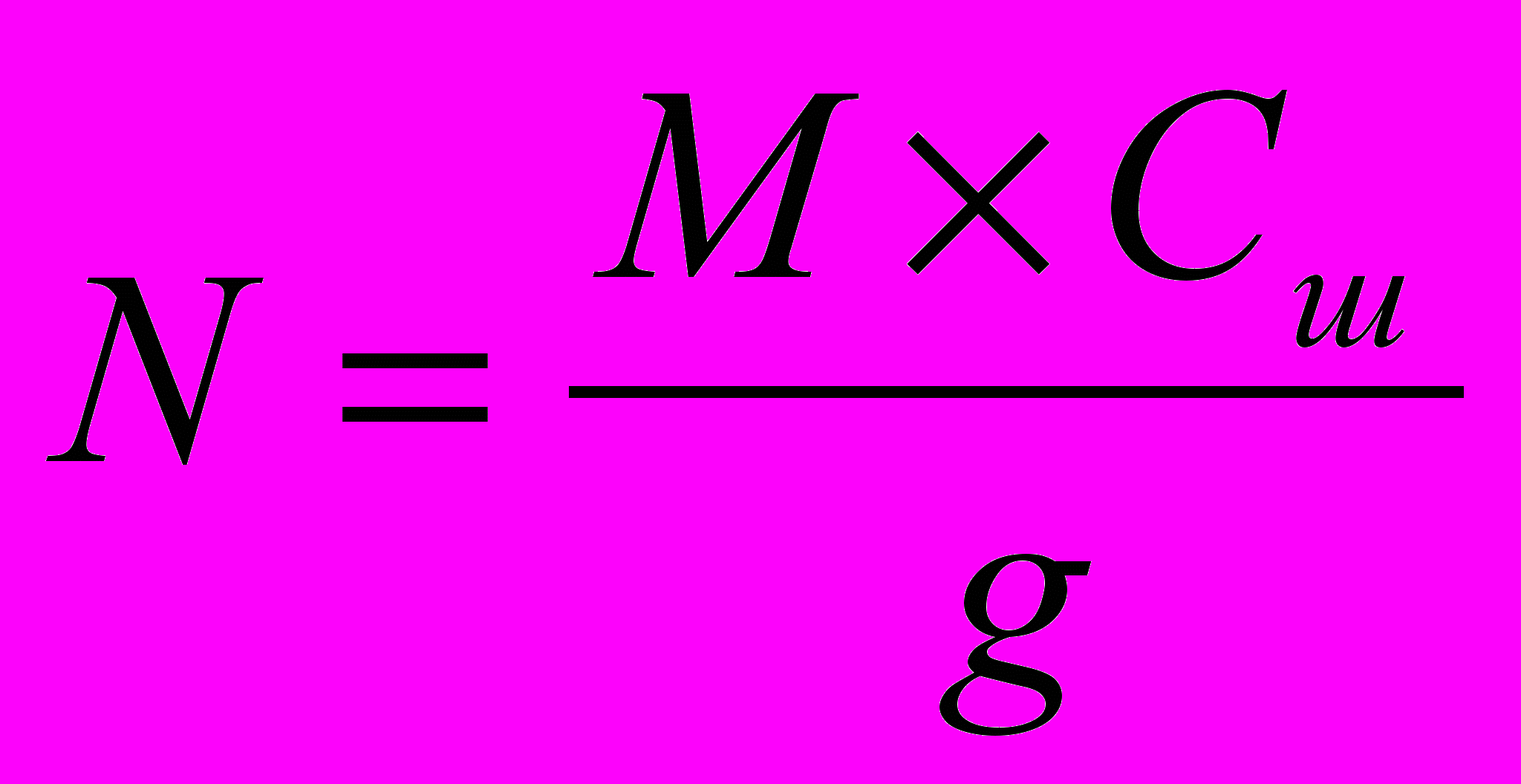 , (6)
, (6)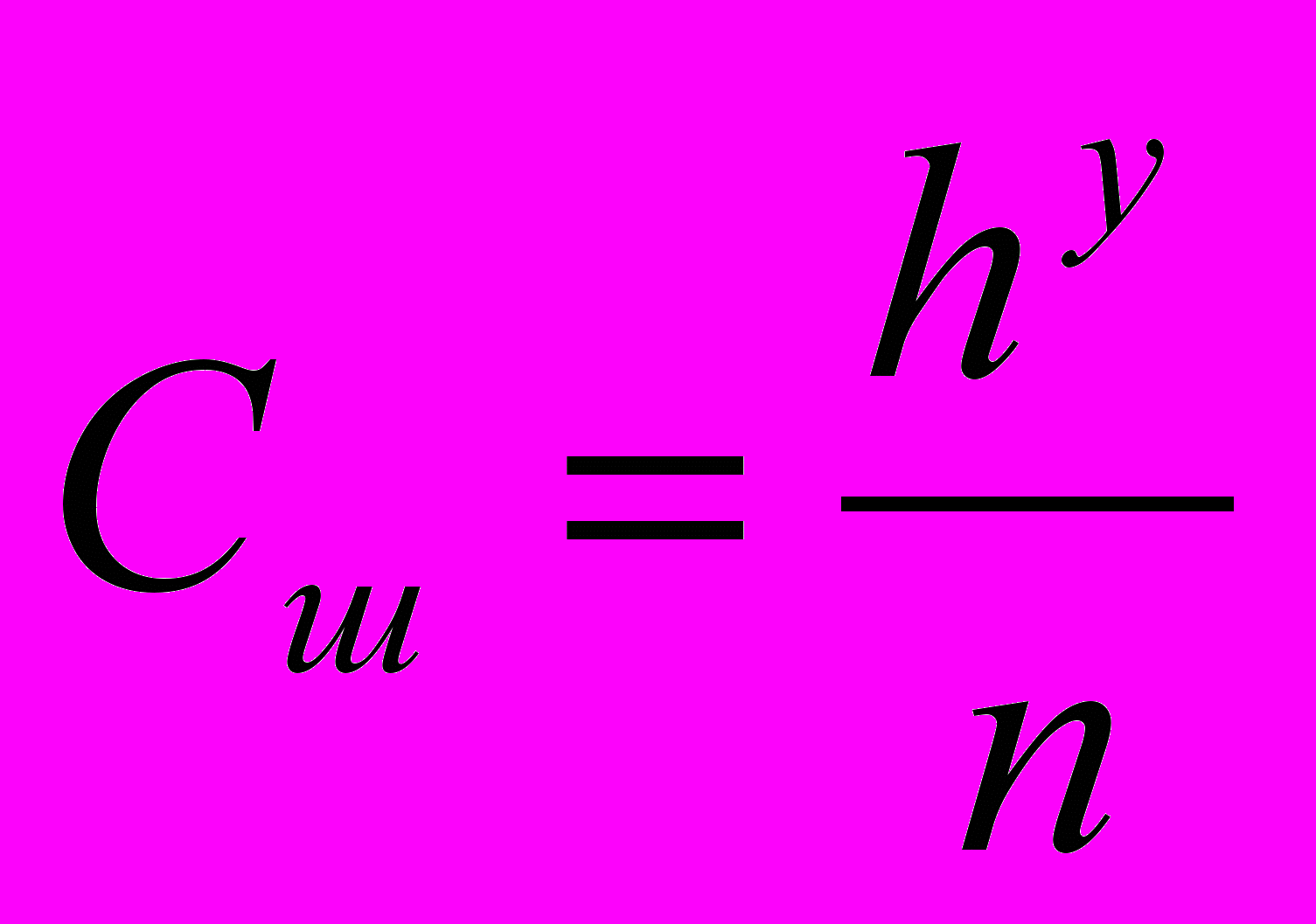 , (7)
, (7) , (8)
, (8)где h – средняя глубина потока, м; y – коэффициент, определяемый по формуле Н.Н. Павловского или принимаемый равным 1/6 (формула Маннинга); n – коэффициент шероховатости, определяемый по специальным таблицам и связанный со средним диаметром частиц донных отложений d (мм) формулой Штриклера:
 , (9)
, (9)n = 0.03 d1/6. (10)
Средняя скорость течения в условиях установившегося равномерного движения водных масс определяется по формуле Шези
 . (11)
. (11)Мутность взмыва Sвзм (в г/м3) находится по формуле
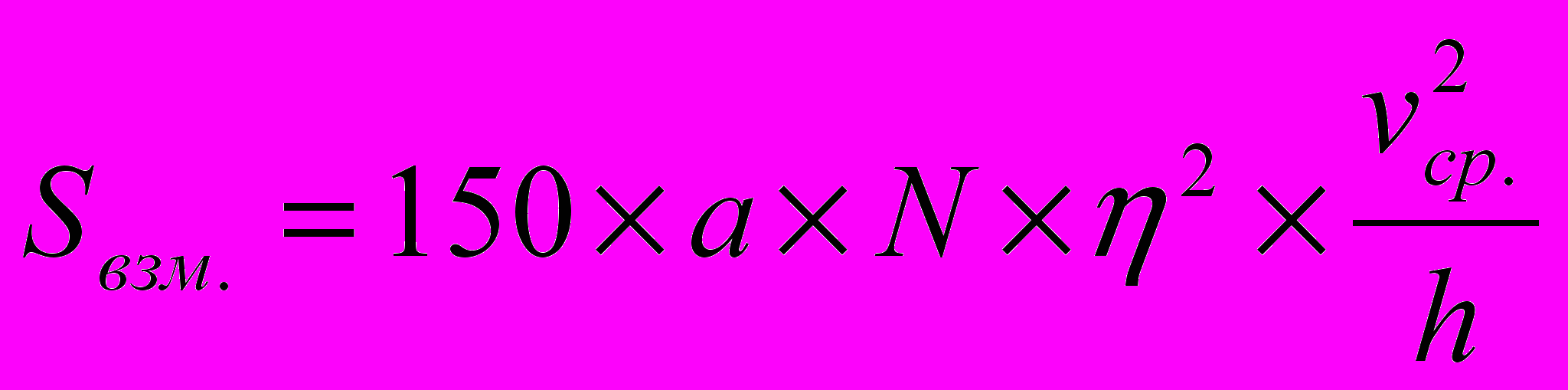 , (12)
, (12)где а – поправочный коэффициент, определяемый из соотношения средней измеренной мутности Sср.изм. и расчетной транспортирующей способности потока Sтр. (а=Sср.изм./Sтр.); – коэффициент перехода от средней скорости потока к донной скорости, вычисляемый по формуле
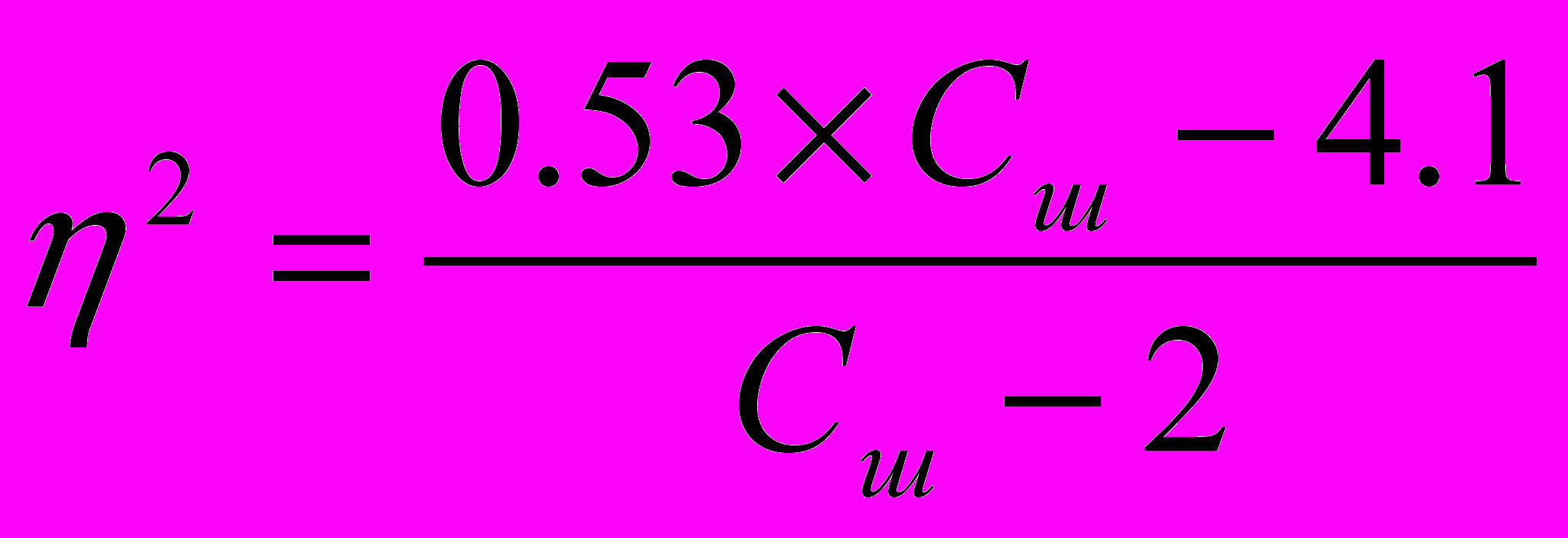 . (13)
. (13)Транспортирующая способность потока Sтр. (г/м3) вычисляется по формуле:
Sтр.=ГSвзм, (14)
Средняя мутность воды Sкон в конце элемента x определяется выражением
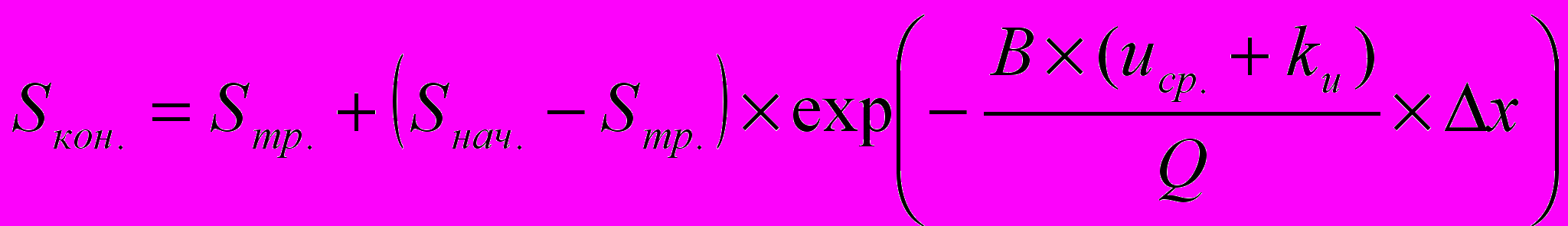 , (15)
, (15)где Sнач .– средняя мутность воды в начале элемента x, г/м3; B – ширина реки, м;
Q – расход воды, м3/с.
В рассматриваемой работе моделирование проводилось в створе, расположенном в 72,5 км от устья реки. Значения z и все необходимые для их вычисления величины определялись в фиксированных точках, расположенных через 50 м от оси ограждающей дамбы на правом берегу р. Томи. Учитывая, что модель апробировалась по данным за период 1993-2003 гг., для упрощения расчетов мутность воды в расчетных створах определялась не по выражению (15), а по эмпирическим зависимостям от скорости течения
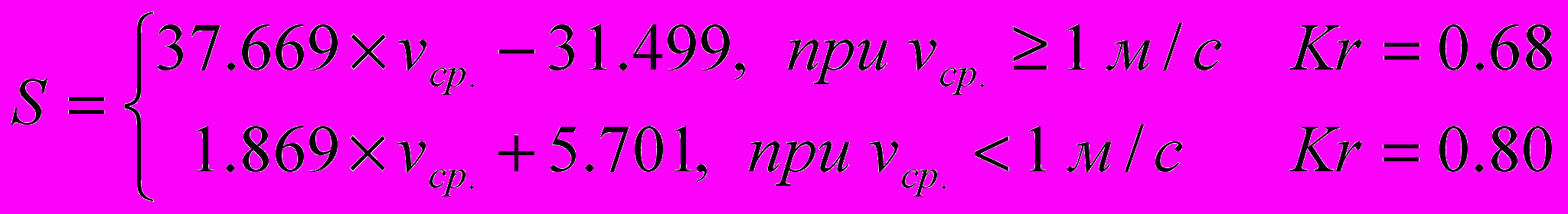 ; (16)
; (16)Kr – принятый в России в гидрологической практике критерий применимости методики [6]; при большом объеме выборки (более 25 элементов) методика прогноза считается применимой, если Kr ≤ 0.8.
Указанные зависимости и величина коэффициента а определялись по данным Росгидромета, полученным в гидростворе в 74,8 км от устья. Кроме того, при расчете деформации дна вводился эмпирический коэффициент а*, учитывающий поправку на взаимную компенсацию разнонаправленных деформаций в течение расчетного шага по времени t=60602430,4=2626560 с (1 месяц) и вычисленный обратным путем по формуле (1) для гидроствора (а = 0,0095; а* = 3,95910-9). Уклоны водной поверхности приняты приближенно по разнице среднемесячных уровней воды (в м БС) в гидростворе в 74,8 км от устья и на водпосту в 68,1 км от устья. В свою очередь, среднемесячные значения уровней воды (в гидростворе и на водпосту) и расходов воды (в гидростворе) приняты по данным Росгидромета. Последовательность моделирования заключалась в следующем: 1) по данным об уровнях воды р. Томи в гидростворе (74,8 км от устья и на водпосту) (68,1 км от устья) приближенно линейной интерполяцией вычисляется уровень воды в расчетном створе в м БС; 2) по заданным высотным отметкам дна реки (в м БС; с поправкой на уклон рельефа между гидроствором и водпостом) и уровню водной поверхности в расчетном створе определяются расстояния уреза воды на левом и правом берегу реки от нулевой точки отсчета (на правом берегу по оси дамбы), ширина реки, глубины потока в j-точках через каждые 50 м, площади между этими точками; выбирается максимальная глубина потока и определяется расстояние до вертикали с максимальной глубиной от нулевой точки отсчета; в каждой j-й точке рассчитывается радиус кривизны rj (в м); 3) рассчитывается суммарная площадь сечения реки
 , где j – площадь сечения между соседними вертикалями через 50 м или между вертикалью и точкой уреза воды, м2; далее рассчитывается средняя скорость течения
, где j – площадь сечения между соседними вертикалями через 50 м или между вертикалью и точкой уреза воды, м2; далее рассчитывается средняя скорость течения  , м/с; 4) приближенно определяется максимальная скорость (средняя по вертикали) в расчетном створе в предположении пропорциональности отношений максимальной и средней скоростей и максимальной и средней глубин потока
, м/с; 4) приближенно определяется максимальная скорость (средняя по вертикали) в расчетном створе в предположении пропорциональности отношений максимальной и средней скоростей и максимальной и средней глубин потока  ; затем определяются средние скорости течения в каждой j-й вертикали через 50 м (там, где есть вода) по формуле
; затем определяются средние скорости течения в каждой j-й вертикали через 50 м (там, где есть вода) по формуле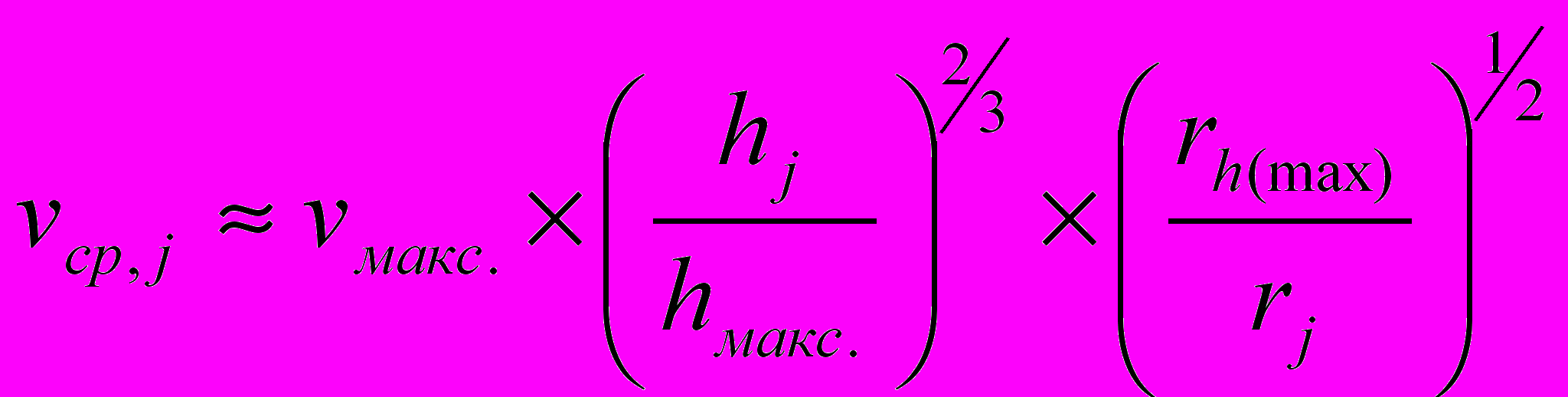 , (17)
, (17)где rh(max) – радиус кривизны в точке с максимальной глубиной потока, м; 5) в каждой j-й точке рассчитывается мутность воды Sj, расход наносов qs,j и деформация дна zj; 6) пересчитывается высотная отметка дна в j-й точке на следующий интервал времени =t по формуле zj,+1=zj, +zj, ; расчет повторяется до заданной временной точки.
Методика прогноза русловых деформаций аналогична методике их моделирования, за исключением того, что вместо измеренных используются среднемноголетние месячные значения расходов воды в гидростворе с поправкой на изменение водности при потеплении климата. В зависимости от них определяются среднемесячные уровни воды Zw в гидростворе и на водпосту по формулам вида Zw=aQ+b, где a и b – эмпирические коэффициенты. Кроме того, при прогнозе последствий возможной санитарной выемки песчано-гравийного материала из русла реки вводятся соответствующие поправки в значения высотных отметок дна в начале расчетного периода времени – в мае 2003 г.
Результаты исследований. Выполненные моделирование русловых деформаций за одиннадцатилетний период на основе данных о высотных отметках дна реки в 1993 г. и анализ картографического материала русловых съемок показали, что используемая модель, несмотря на ряд достаточно грубых допущений, соответствует реальным русловым процессам и может использоваться в прогнозных целях (см. рисунок).
Критерий применимости модели Kr для створа 72,5 км от устья составляет 0,25 при объеме выборки 18 точек (начиная с 50 м до 900 м от оси дамбы). В целом, полученные результаты позволили сделать следующие выводы: 1) выход слабо размываемых кристаллических пород (мыс «Бойец») у Лагерного Сада обусловливает сжатие руслового потока и заметное увеличение скоростей течения воды, а поэтому и транспортирующей способности реки; 2) при удалении на 400…700 м и далее от мыса «Боец» происходит увеличение площади живого сечения, уменьшение уклонов водной поверхности и, следовательно, уменьшение скоростей течения, приводящее к снижению транспортирующей способности русла; 3) образование осередков и береговых отмелей ниже по течению от мыса «Боец» привело к изменению оси руслового потока после прохождения пика весеннего половодья и его отклонению к правому берегу; 4) изменение высотных отметок дна происходит неравномерно по ширине русла и во времени – наиболее заметная аккумуляция песчано-гравийного материала в створе 72,5 км от устья происходила в начале 1990-х гг. в 150…500 м от оси дамбы на правом берегу р. Томи; 5) в отсутствие дноуглубительных работ в створе 72,5 км маловероятны существенные изменения средней высоты дна (см. рисунок), что объясняется «сползанием» вниз по течению осередка у левого берега реки; 6) в ближайшие 3…4 года после возможных дноуглубительных работ со сработкой дна до отметки 68 и 69 м над уровнем моря восстановление высотных отметок дна на отработанном участке маловероятно (рисунок).

Прогнозные значения высотных отметок дна р. Томи на май 2007 г. в створе 72,5 км от устья в случае отсутствия дноуглубительных работ и при сработке дна до 69 и 68 м БС
Заключение. Анализ картографического материала и результатов математического моделирования позволил сделать предварительный вывод о том, что в 2005-2007 гг. вероятно дальнейшее ухудшение зажороопасной ситуации на участке р. Томи у г. Томска вследствие формирования русловых образований (трансформация существующего в настоящее время осередка в остров и образования комплекса осередков ниже по течению) и понижения пропускной способности русла. Для предотвращения возможных ледовых зажоров и связанных с ними затоплений и подтоплений части территории г. Томска целесообразно провести изъятие части ПГМ, накопившегося на участке в 72,75…72,2 км от устья у левого берега. Максимальный объем аккумуляции ПГМ на этом участке за период 1993-2004 гг. составил не менее 100 тыс.м3. Однако разовое изъятие всего этого материала может привести к нежелательным непрогнозируемым изменениям руслового процесса в створах скального выступа и у моста. По этой причине целесообразно первоначально произвести выемку ПГМ в несколько меньшем объеме и обязательно следует выполнить комплекс мониторинговых работ, начиная с момента, предшествующего дноуглубительным работам, в течение 1…2 лет. По результатам мониторинга будет уточнена математическая модель и прогноз русловых деформаций и сделан вывод о целесообразности дальнейшего проведения дноуглубления. Следует также отметить, что проведение дноуглубительных работ у г. Томска в 72,75…72,2 км от устья у левого берега должно сочетаться с берегоукрепительными работами на участке, расположенном выше по течению, и с реконструкцией дамбы г. Томска, поскольку в настоящее время остается открытым вопрос об источнике речных наносов вследствие отсутствия достоверных разновременных данных о рельефе дна реки выше по течению от коммунального моста. Для формулирования более точных выводов требуются проведение русловой съемки дна реки на участке р. Томи не только у г. Томска, но выше и ниже по течению от него, организация мониторинга береговых деформаций и разработка более точной плановой математической модели всего этого участка.
Библиографический список
- Дубровская Л. И., Земцов В. А. Изменение уровней реки Томи и грунтовых вод поймы в районе города Томска. //Вопросы географии Сибири. 1997. Вып.22. С. 100-105.
- Земцов В.А., Вершинин Д.А., Инишев Н.Г., Лещенко П.Н., Нарожный Ю.К. Добыча гравия в русле Томи: уроки и возможности //Томское отделение СНИИГИМС – 30 лет на службе геологии: /Сб. науч. тр. под ред. Пешкова В.Е. Новосибирск, 2002. С. 222-225.
- Каменсков Ю.И. Русловые и пойменные процессы. – Томск: Изд-во Томск. гос. ун-та, 1987. 171 с.
- Караушев А.В. Речная гидравлика. Л.: Гидрометеоиздат, 1969. 416 с.
- Марусенко Я.И., Земцов А.А., Семлянская Л.П. и др. Гидрография Западной Сибири. Томск: Изд-во Томск. гос. ун-та, 1961. Т. 1. 169 с.
- Наставление по службе прогнозов. Раздел 3. Служба гидрологических прогнозов, Прогнозы режима вод суши. Л.: Гидрометеоиздат, 1962. Ч. 1. 194 с.
- Чалов Р.С. Естественные и антропогенные изменения рек России за историческое время. //Соровский образовательный журнал. 2000. Т. 6. № 1. С. 71-78.
