Математическое моделирование управляемого движения космических аппаратов

Вид материала

Автореферат диссертации

Содержание Математическое моделирование управляемого движения космических аппаратов Научный руководитель доктор физико-математических наук, доцент кандидат технических наук, старший научный сотрудник Степанов Геннадий Николаевич. Институт проблем механики имени А.Ю. Ишлинского РАН. Общая характеристика работы Цель диссертационной работы. Предмет исследования. Методы исследования. Научная новизна. Положения, выносимые на защиту. Апробация результатов исследований. Структура и объем работы. Краткое содержание работы В первой главе Во второй главе В третьей главе В четвертой главе Выводы по результатам диссертации Список публикаций по теме диссертации ... Полное содержание

Подобный материал:

• Реферат спуск и посадка космических аппаратов (КА), 175.67kb.
• Математическое и компьютерное моделирование динамического состояния систем передачи, 388.39kb.
• Математическое моделирование системы управления для управляемого выпрямителя на igbt-транзисторах, 26.76kb.
• П. П. Порешин московский инженерно-физический институт (государственный университет), 23.75kb.
• Курсивом выделены основные моменты, которые желательно отразить в докладе, 172.09kb.
• Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
• Математическое моделирование многомерных квазистационарных электромагнитных полей, 380.28kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• Математическое моделирование термомеханических процессов в системах армированных стержней, 259.01kb.
• И математическое моделирование, 1392.77kb.

Ф.И.О.	Ручинская Елена Валерьевна
Название диссертации:	"Математическое моделирование управляемого движения космических аппаратов"
Специальность:	05.13.18. – математическое моделирование, численные методы и комплексы программ
Отрасль науки:	Технические науки
Шифр совета:	Д212.110.08
Тел. ученого секретаря диссертационного совета:	8-499-141-94-55
E-mail:	electron_inform@mail.ru
Предполагаемая дата защиты диссертации	25 июня 2010г.
Место защиты диссертации	Оршанская, 3, ауд. 612А

На правах рукописи


РУЧИНСКАЯ Елена Валерьевна


МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ УПРАВЛЯЕМОГО ДВИЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ


Специальность 05.13.18 – Математическое моделирование, численные методы и комплексы программ


Автореферат

диссертации на соискание ученой степени

кандидата технических наук


Москва–2010

Работа выполнена в ГОУ ВПО «МАТИ» - Российском государственном технологическом университете имени К.Э. Циолковского

Научный руководитель:		доктор технических наук, профессор Иванов Виталий Александрович.
Официальные оппоненты:		доктор физико-математических наук, доцент Лемак Степан Степанович;
		кандидат технических наук, старший научный сотрудник Степанов Геннадий Николаевич.
Ведущая организация:		Институт проблем механики имени А.Ю. Ишлинского РАН.

Защита состоится «___» __________ 2010г. в ____ ч. ___ мин. на заседании диссертационного совета Д 212.110.08 при «МАТИ» - Российском государственном технологическом университете имени К.Э. Циолковского по адресу: 121552, Москва, ул. Оршанская, д.3, ауд. 612 А.


С диссертацией можно ознакомиться в библиотеке «МАТИ» - Российского государственного технологического университета имени К.Э. Циолковского


Автореферат разослан «____»_______________2010 г.


Ученый секретарь диссертационного совета Д 212.110.08

кандидат физико-математических наук

Спыну М.В.

Общая характеристика работы


Актуальность темы исследования. Процесс управляемого движения маневрирующего космического аппарата (КА) в общем случае описывается системой нелинейных дифференциальных уравнений. Получить решение системы нелинейных дифференциальных уравнений в квадратурах удается лишь в очень частных случаях. Поэтому основным подходом для изучения управляемого движения КА является применение методов математического моделирования, использование которого позволило получить целый ряд практически важных результатов. Вместе с тем классическое математическое моделирование не позволяет составить общее представление обо всех возможных режимах движения КА при том или ином методе управления и очень часто не дает ответа на многие вопросы, выдвигаемые практикой.

Применение методов качественной теории динамических систем и теории бифуркации позволяет установить качественную структуру фазовых траекторий изучаемых динамических систем и общий подход к определению бифуркационных значений параметров, и установить количество качественных структур полностью определяющих поведение системы. Синтез методов математического моделирования в сочетании с математическим аппаратом качественной теории динамических систем и теории бифуркаций, численными методами и комплексами прикладных программ, позволяет провести исследования всех возможных режимов управляемого движения КА и разработать практические рекомендации по определению требуемых значений параметров управления и начальных условий движения, необходимых для реализации того или иного типа маневров КА.

В данной диссертации решены конкретные задачи исследования динамических систем управляемого движения КА при выполнении межорбитальных маневров с малой тягой и маневров относительного движения.

Цель диссертационной работы. Целями исследования являются:

• разработка комплекса прикладных программ, с помощью совместно применяемых методов математического моделирования, численных методов и методов исследования качественных структур и бифуркаций динамических систем, определяющих абсолютное движение КА с малой радиальной тягой и относительное движение КА при управляющих воздействиях по осям визирной системы координат;
  
• разработка практических рекомендаций по использованию полученных при исследовании результатов для выполнения межорбитальных и локальных маневров КА.
  

Предмет исследования. Предметом исследования в диссертационной работе является движение КА с малой радиальной тягой, и относительное движение КА при управляющих воздействиях по осям визирной системы координат.

Методы исследования. При проведении исследований в диссертации были использованы методы математического моделирования абсолютного и относительного движения КА, методы теории обыкновенных дифференциальных уравнений, методы качественной теории динамических систем и теории бифуркаций, численные методы, комплексы программ, а также теоретические основы механики космического полета и механики полета системы гибко связанных космических объектов.

Научная новизна. Научная новизна полученных результатов в диссертационной работе заключается:

• в разработке комплексного подхода к исследованию управляемого движения КА на основе сочетания математического моделирования и исследования качественных структур и бифуркаций динамических систем абсолютного и относительного движение КА с помощью численных методов и комплексов программ;
  
• в разработке методики определения и исследования качественных структур и бифуркаций динамических систем абсолютного движения КА при малой радиальной тяге;
  
• в разработке методик определения и исследования качественных структур и бифуркаций динамических систем относительного движения КА при управляющих воздействиях по осям визирной системы координат.
  

Практическая ценность работы. Практическая ценность работы заключается:

• в создании программ математического моделирования управляемого абсолютного и относительного движения КА;
  
• в определении возможных режимов абсолютного и относительного движения КА при малой радиальной тяге и создании управляющего воздействия по осям визирной системы координат;
  
• в разработке рекомендаций по использованию рассматриваемых режимов движения для выполнения межорбитальных и локальных маневров КА, а также управления движением орбитальной тросовой системой для осуществления орбитальных переходов и сближения в космосе.
  

Положения, выносимые на защиту. На защиту выносятся следующие положения:

• общая методология исследования управляемого движения КА на основе сочетания методов математического моделирования, численных методов и методов качественной теории динамических систем и теории бифуркаций;
  
• комплекс математических моделей в виде автономных динамических систем второго порядка, определяющих управляемое абсолютное и относительное движение КА;
  
• результаты математического моделирования и исследования качественных структур и бифуркаций динамических систем управляемого абсолютного движения КА с малой радиальной тягой;
  
• совокупность реализуемых режимов абсолютного движения КА с малой радиальной тягой и рекомендации по их практическому применению для осуществления орбитальных маневров;
  
• результаты математического моделирования и исследование качественных структур и бифуркаций динамической системы управляемого относительного движения КА при постоянной угловой скорости линии визирования;
  
• совокупность режимов управляемого относительного движения КА при постоянной угловой скорости линии визирования и рекомендации по их практическому применению для решения задач сближения в космосе и обслуживания орбитальных станций;
  
• результаты математического моделирования и исследования качественных структур и бифуркаций динамической системы относительного движения КА при ориентации управляющего воздействия по линии визирования;
  
• совокупность режимов управляемого относительного движения КА при ориентации управляющего воздействия по линии визирования и рекомендации по их практическому применению для реализации локальных маневров КА в окрестности орбитальной станции и для управления движением орбитальной тросовой системы;
  
• результаты решения задачи маневрирования в космосе с малой радиальной тягой и наведения КА по методу параллельного сближения;
  
• результаты решения задач орбитальных переходов и сближения в космосе с использованием орбитальных тросовых систем.
  

Апробация результатов исследований. Основные результаты, полученные в ходе выполнения диссертации, докладывались на семи международных молодежных научных конференциях «Гагаринские чтения» (Москва, 2000-2010 гг.), на трех Всероссийских научно-технических конференциях «Новые материалы и технологии» (Москва, 2004, 2006, 2008 гг.), на Четвертом, Пятом и Шестом Международном Аэрокосмическом Конгрессе (Москва 2003, 2006, 2009 гг.), на Всероссийском совещании заведующих кафедр ВУЗов РФ в г. Пермь, на 9-ом Всероссийском съезде по теоретической и прикладной механике в г. Нижний Новгород. Работа обсуждалась на научных семинарах на механико-математическом факультете МГУ им. М.В.Ломоносова и в «МАТИ» - РГТУ им. К.Э.Циолковского.

Публикации. По теме диссертации опубликовано 35 работ (научные статьи, учебные пособия и тезисы докладов), в том числе одна статья из списка журналов, рекомендованных ВАК [30].

Структура и объем работы. Работа состоит из введения и пяти глав на 149 страницах, списка литературы (205 наименований) и приложения. В работе имеется 52 рисунка и 7 таблиц.


Краткое содержание работы


Во введении обосновывается актуальность темы диссертационной работы с учетом современного развития космической техники и определяется научная новизна и практическая значимость выполненного исследования. Формулируются цели исследования и основные положения, выносимые на защиту.

В первой главе представлены математические модели управляемого абсолютного и относительного движения КА. Уравнения абсолютного движения записаны в сферической системе координат, а также в виде уравнений в оскулирующих элементах, когда ускорение от малой тяги фигурирует в качестве возмущающего воздействия.

В случае компланарного абсолютного управляемого движения КА уравнения в сферической системе координат при переходе к безразмерным величинам могут быть представлены в виде математической модели 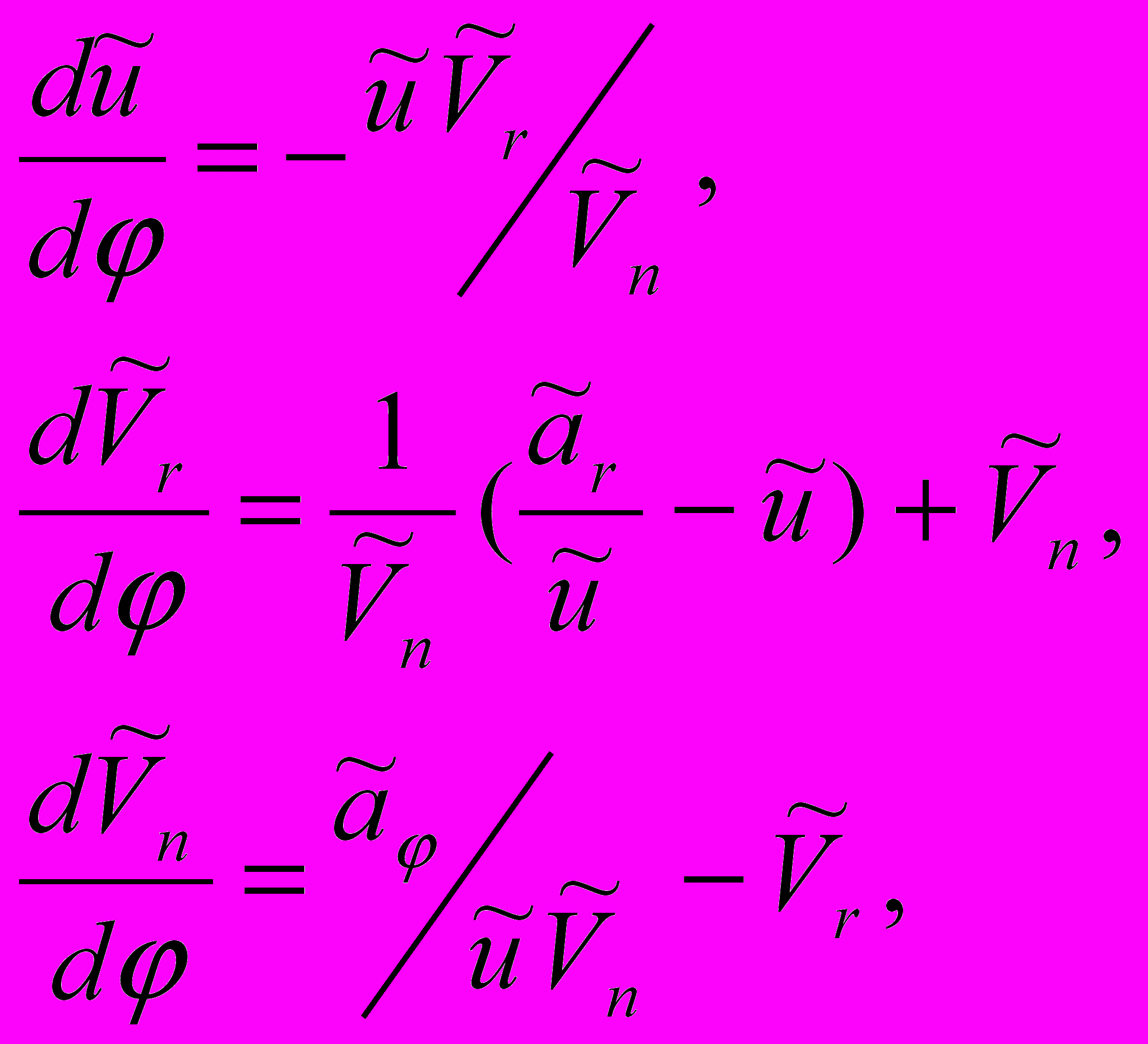(1).

(1)

где - текущее значение угла, определяющего положение радиуса вектора 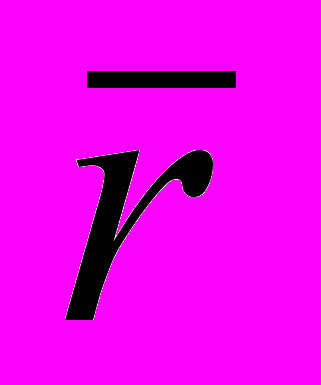аппарата относительно оси абсолютной геоцентрической системы координат;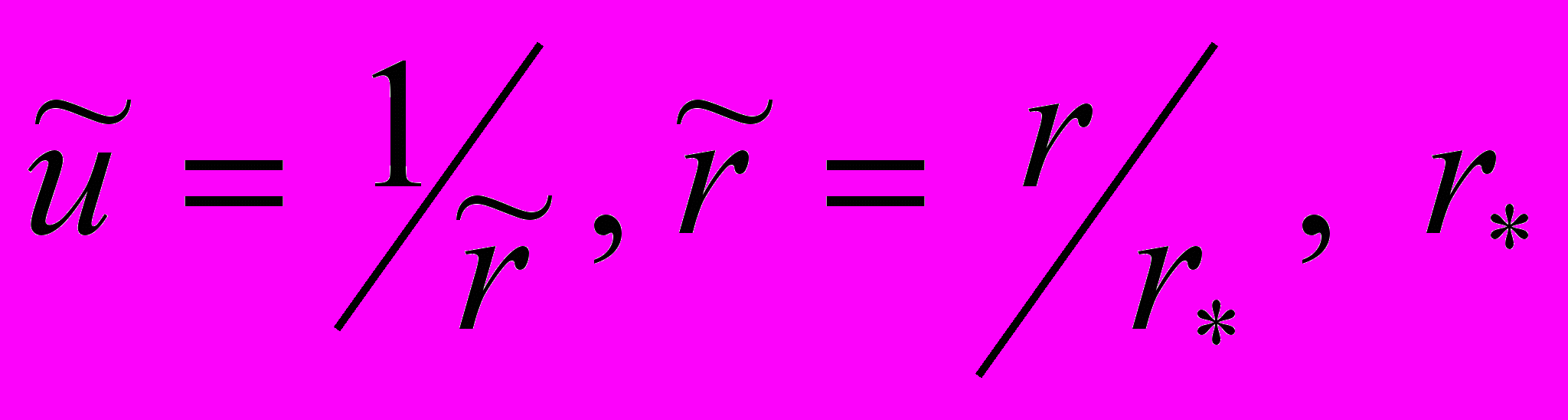

- масштабное значение радиуса ;

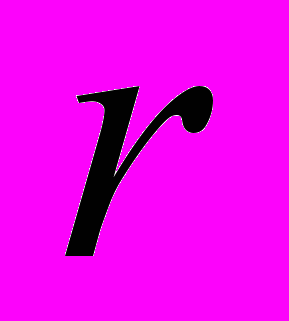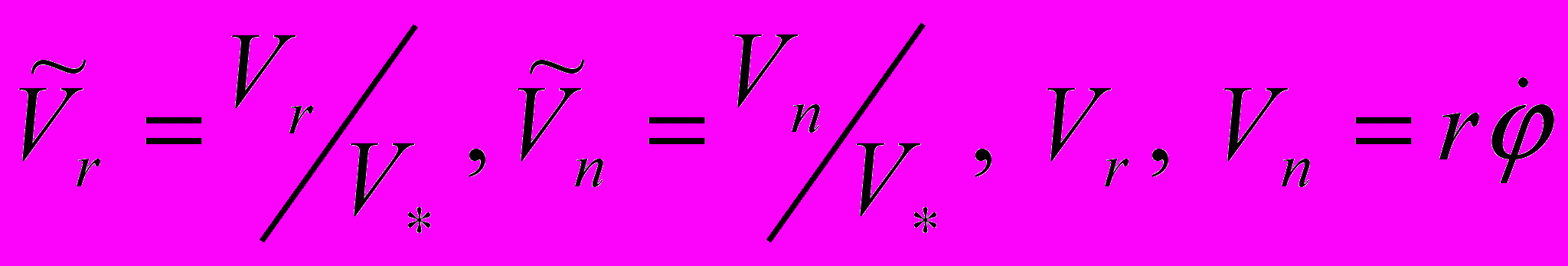- радиальная и нормальная составляющие абсолютной скорости КА, 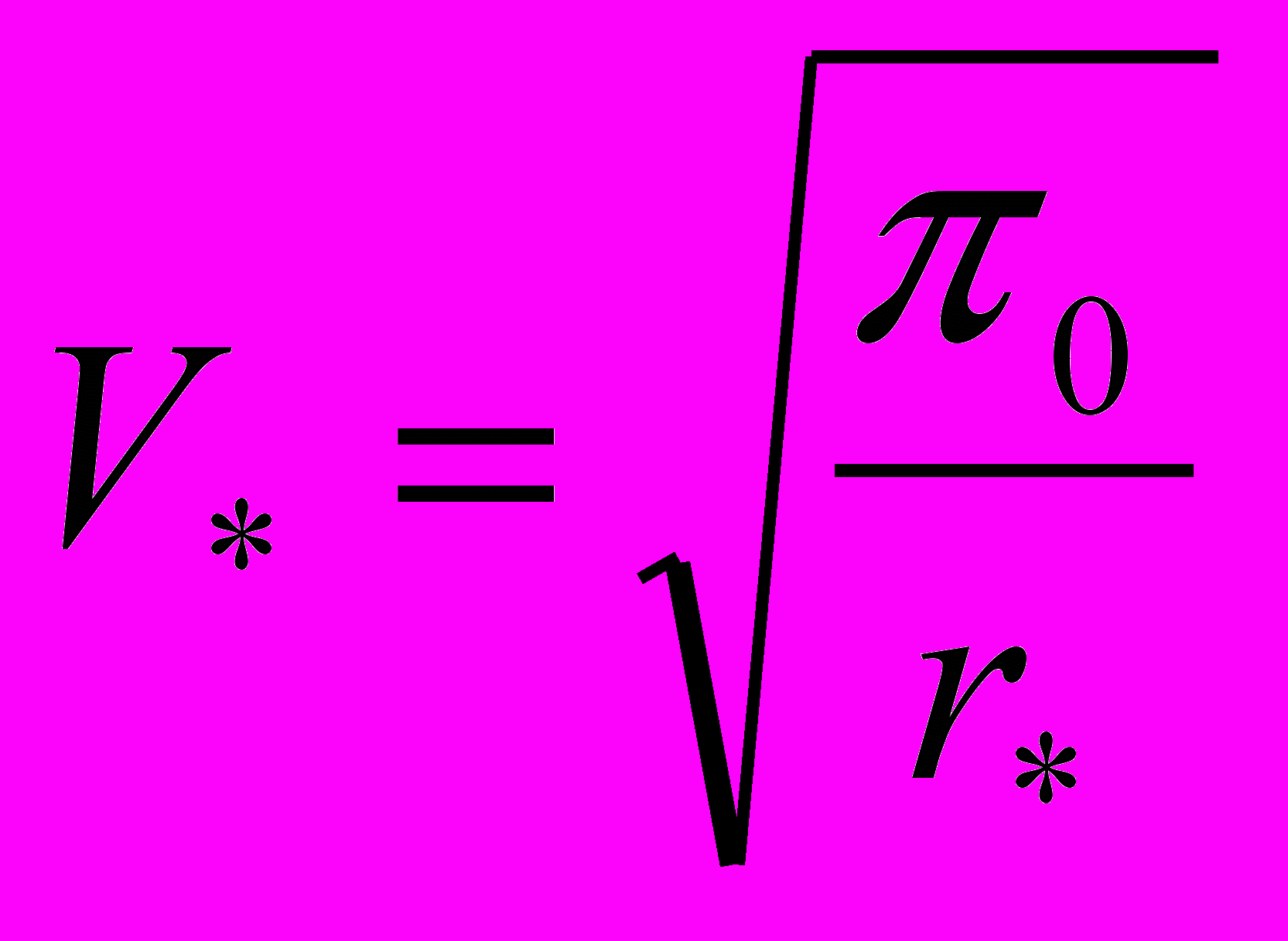, 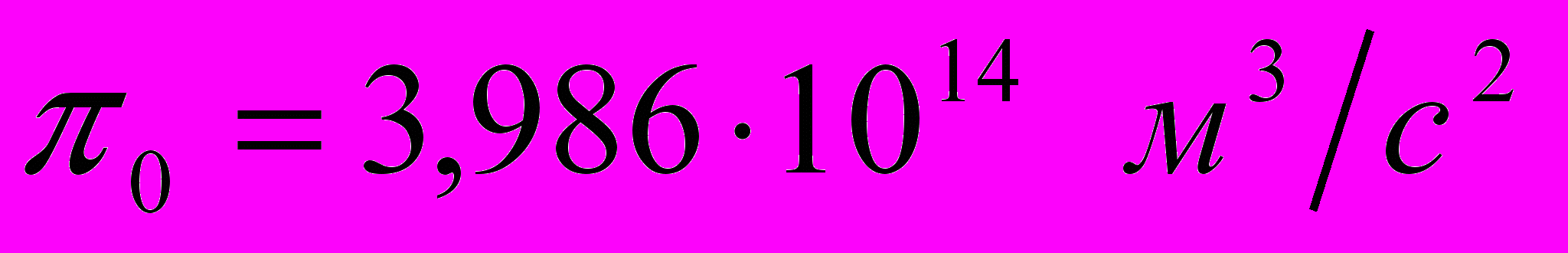- гравитационная постоянная Земли;

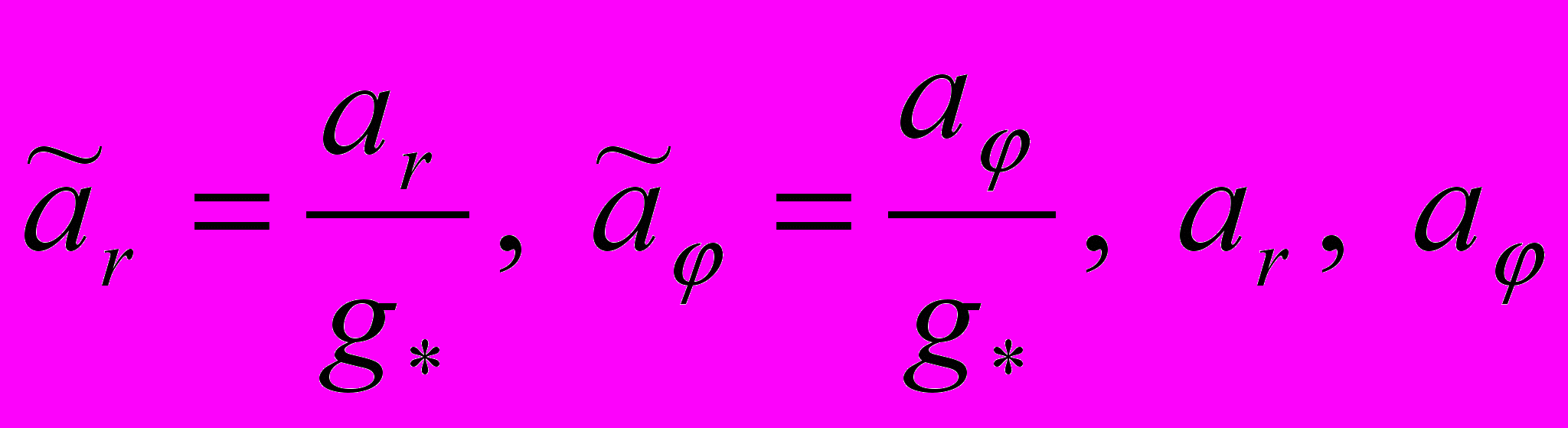- ускорения КА соответственно от малой радиальной и нормальной тяги, .

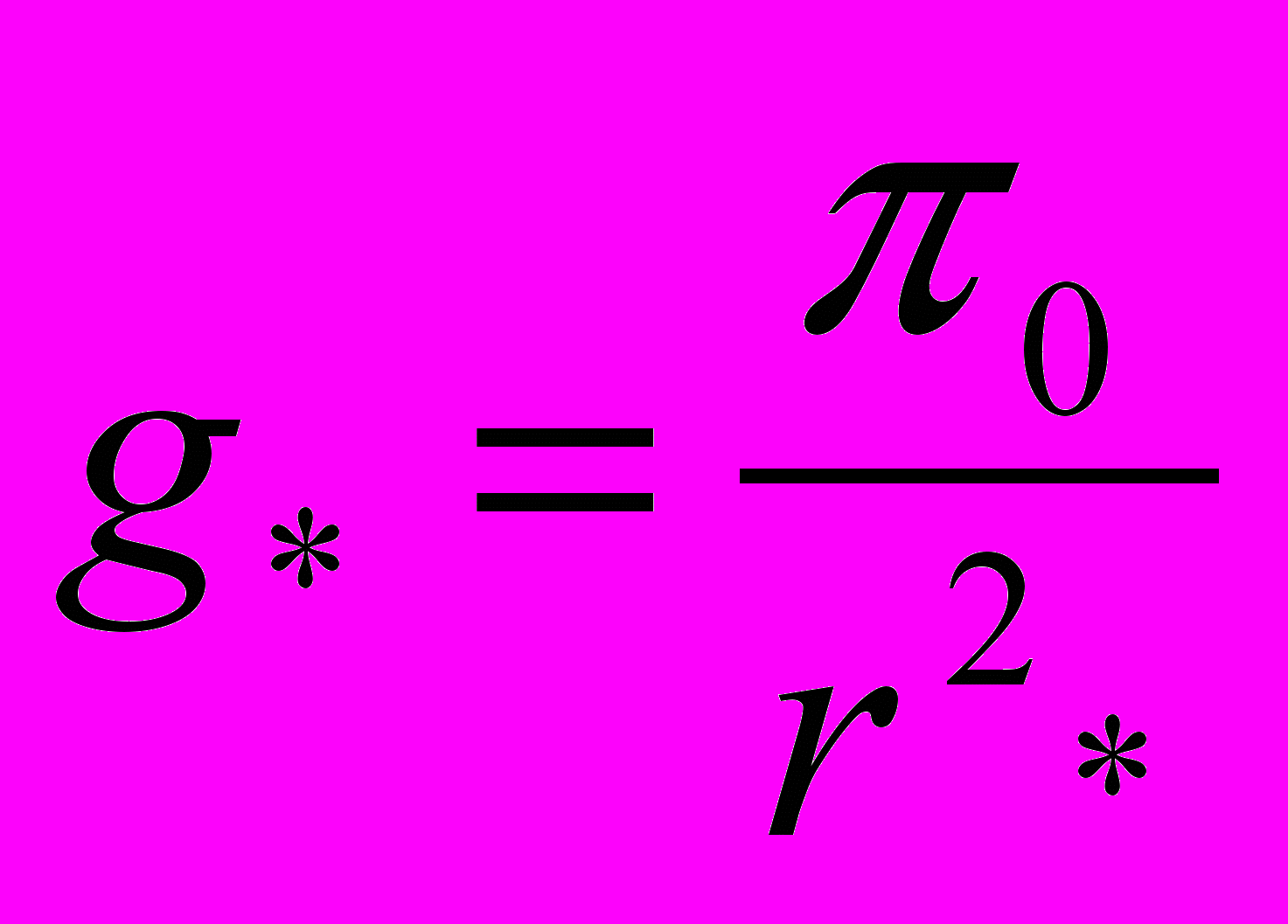Используя математическую модель (1), управляемое движение КА под действием малой радиальной тяги может быть представлено в виде двух динамических систем, одна из которых определяет общий случай криволинейного движения, а вторая – вертикальное движение КА.

Математическая модель относительного движения КА при управляющих воздействиях по осям визирной системы координат может быть представлена:



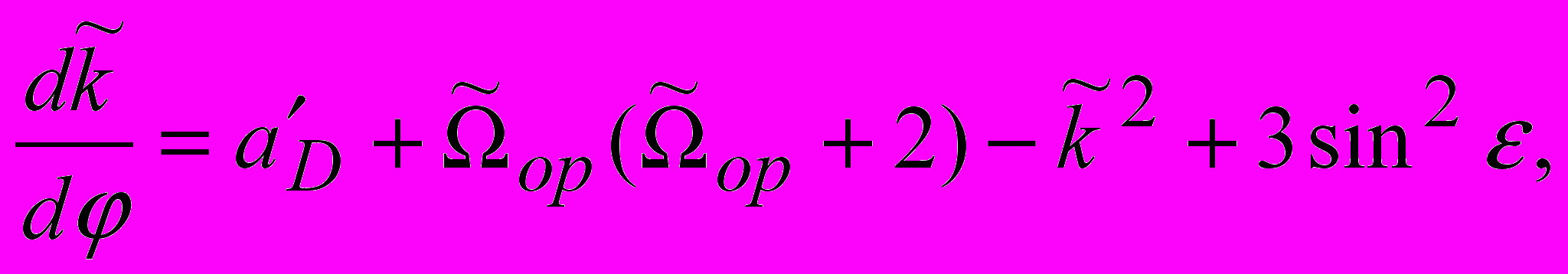
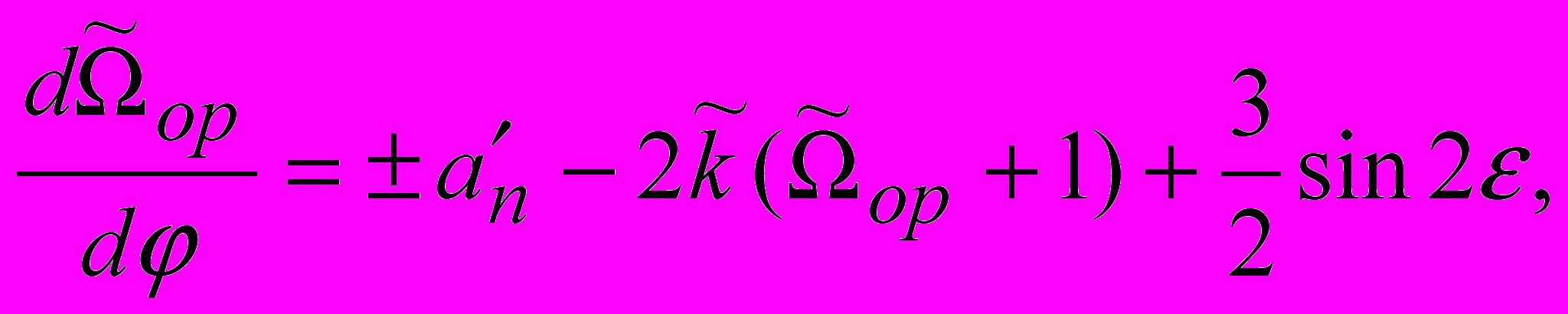(2)

,

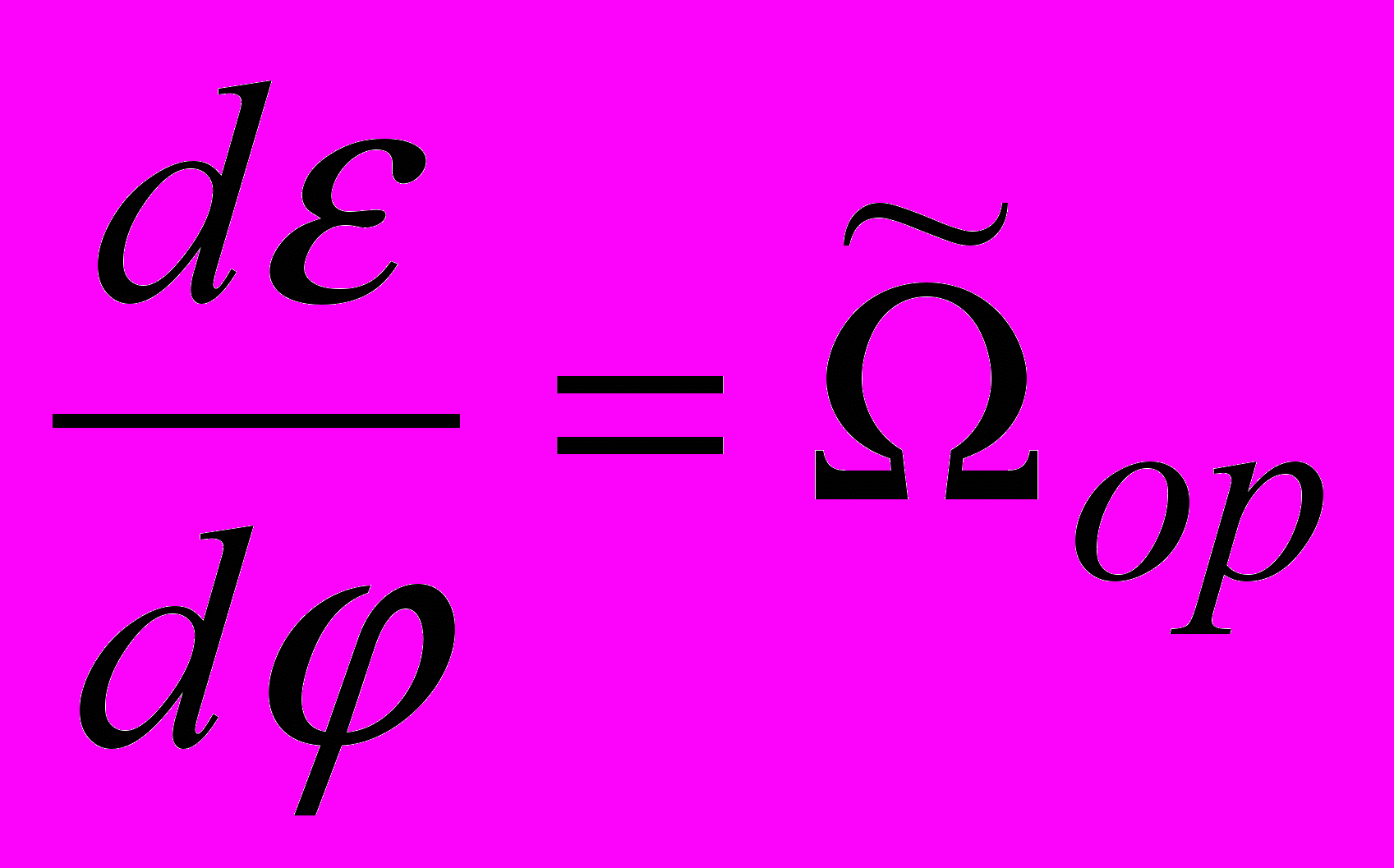где 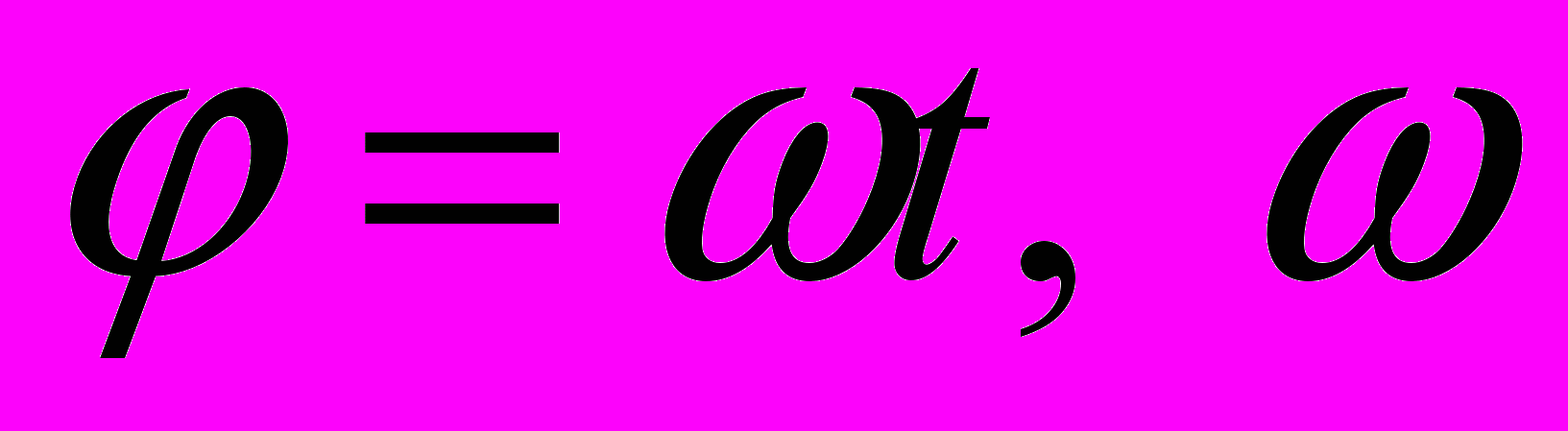- орбитальная угловая скорость движения пассивного КА;

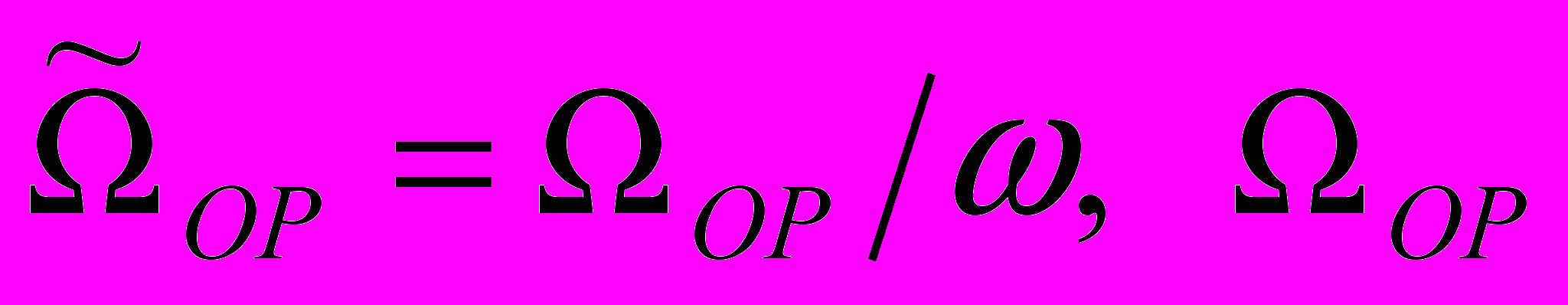- угловая скорость вращения линии визирования относительно орбитальной системы координат;

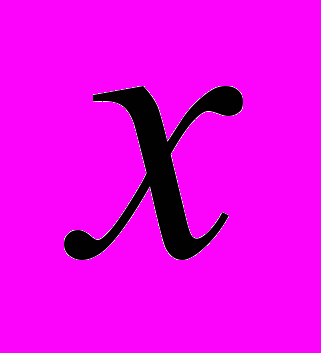- угол между осью орбитальной системы координат и вектором ;

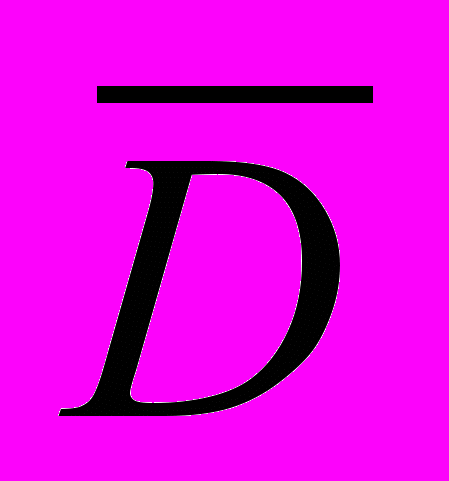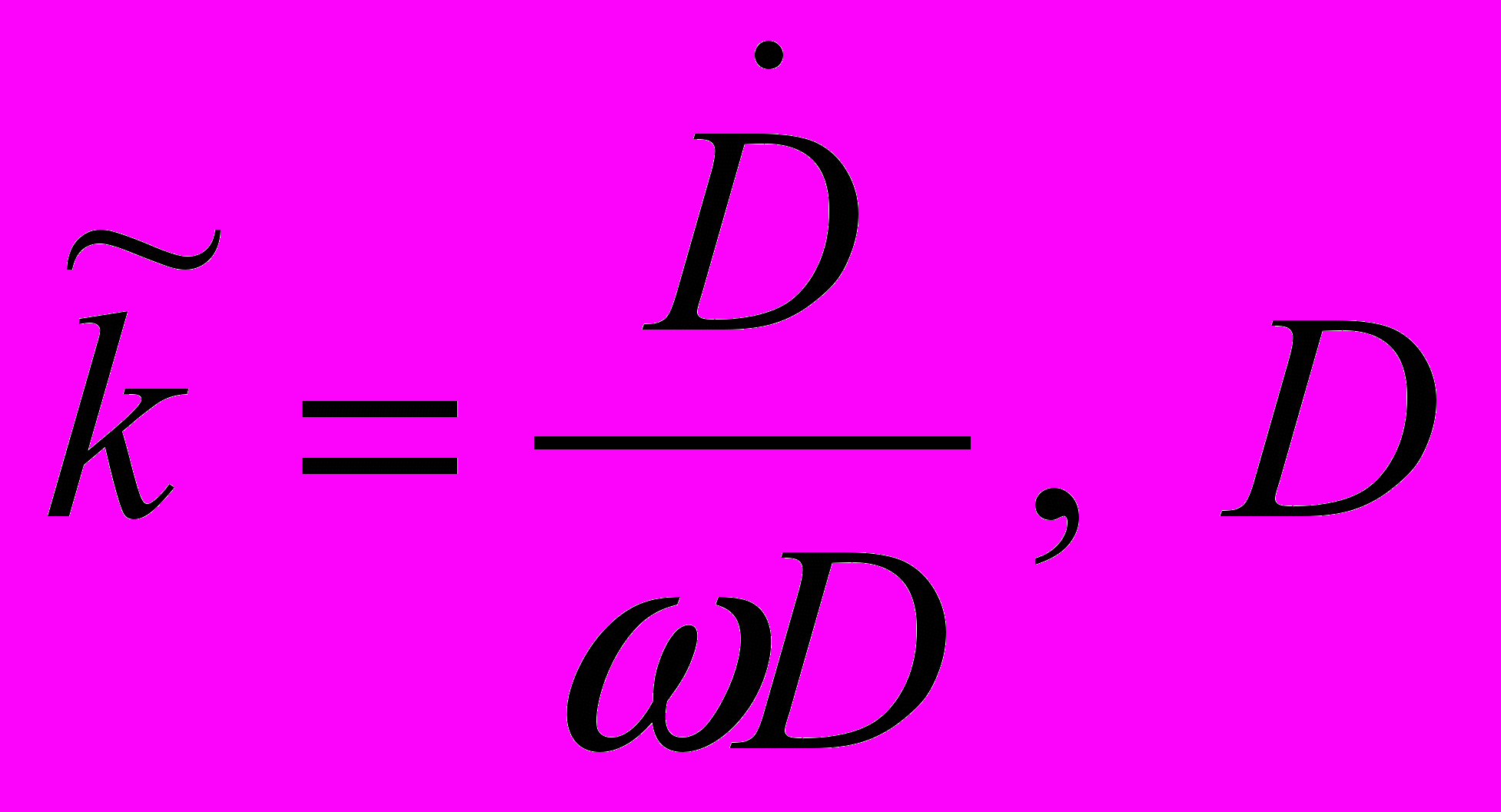- расстояние между двумя КА, 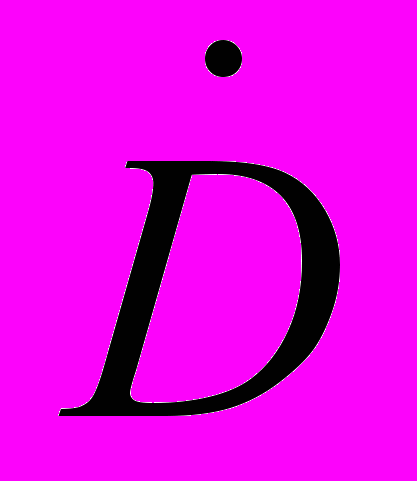- скорость изменения относительной дальности;

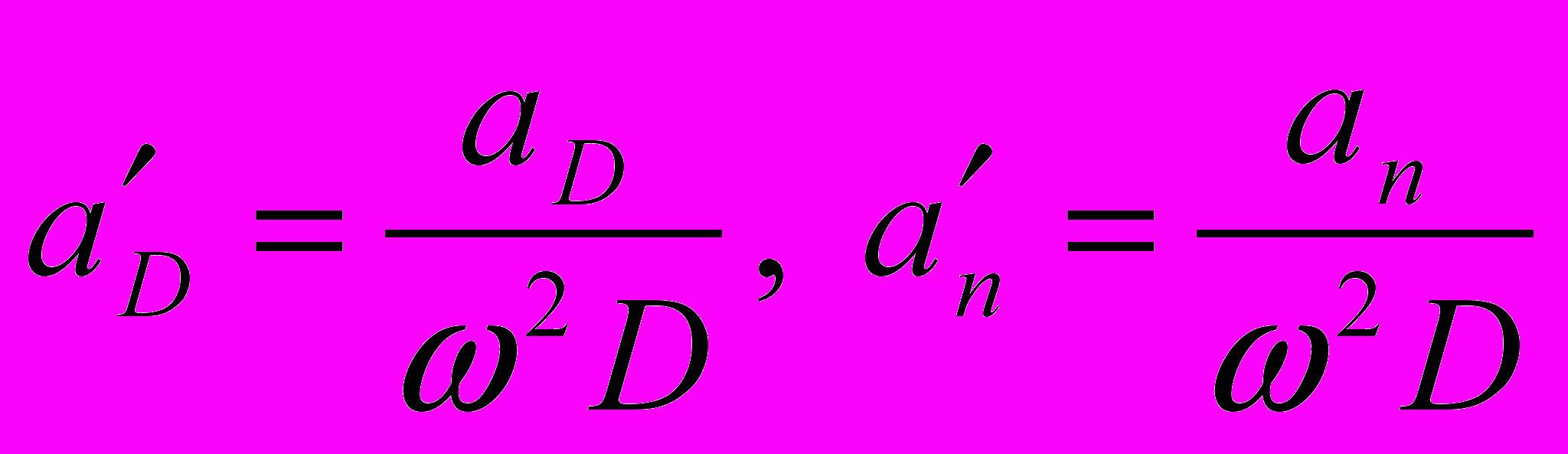- безразмерные управляющие воздействия по осям визирной системы координат, 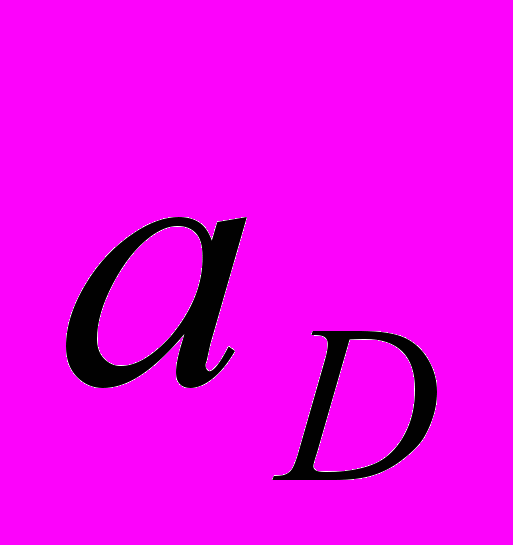- управляющее ускорение по линии визирования, 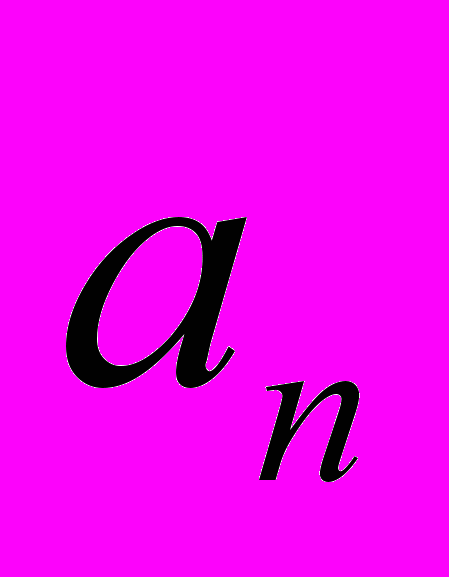- управляющее ускорение по нормали к линии визирования.

Во второй главе проводится математическое моделирование и исследование динамической системы абсолютного движения КА при постоянном радиальном управляющем ускорении.

В данном случае динамические системы являются консервативными. Пространством параметров системы, определяющий общий случай криволинейного движения, является плоскость безразмерных параметров ,

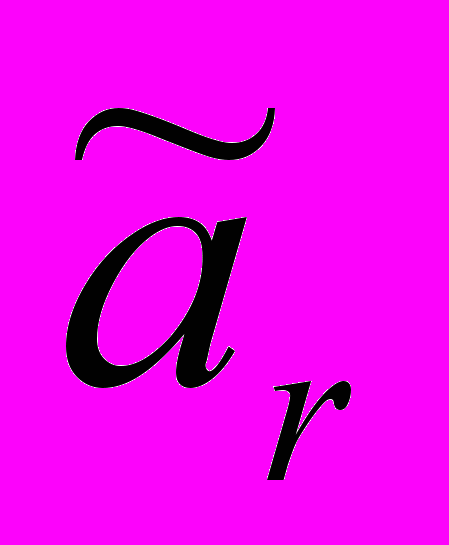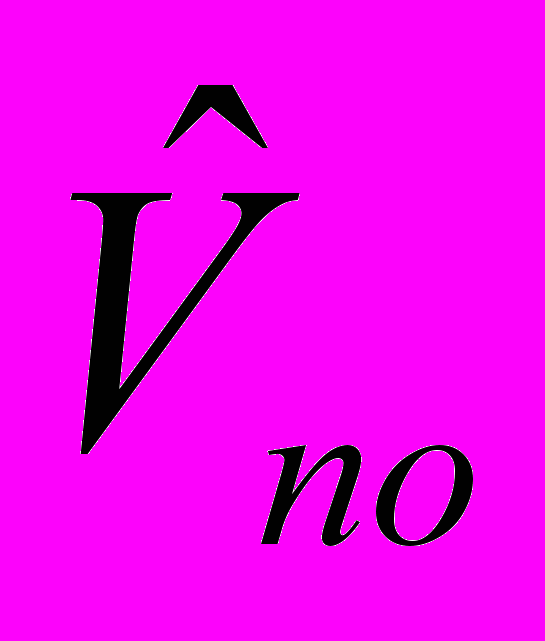, где 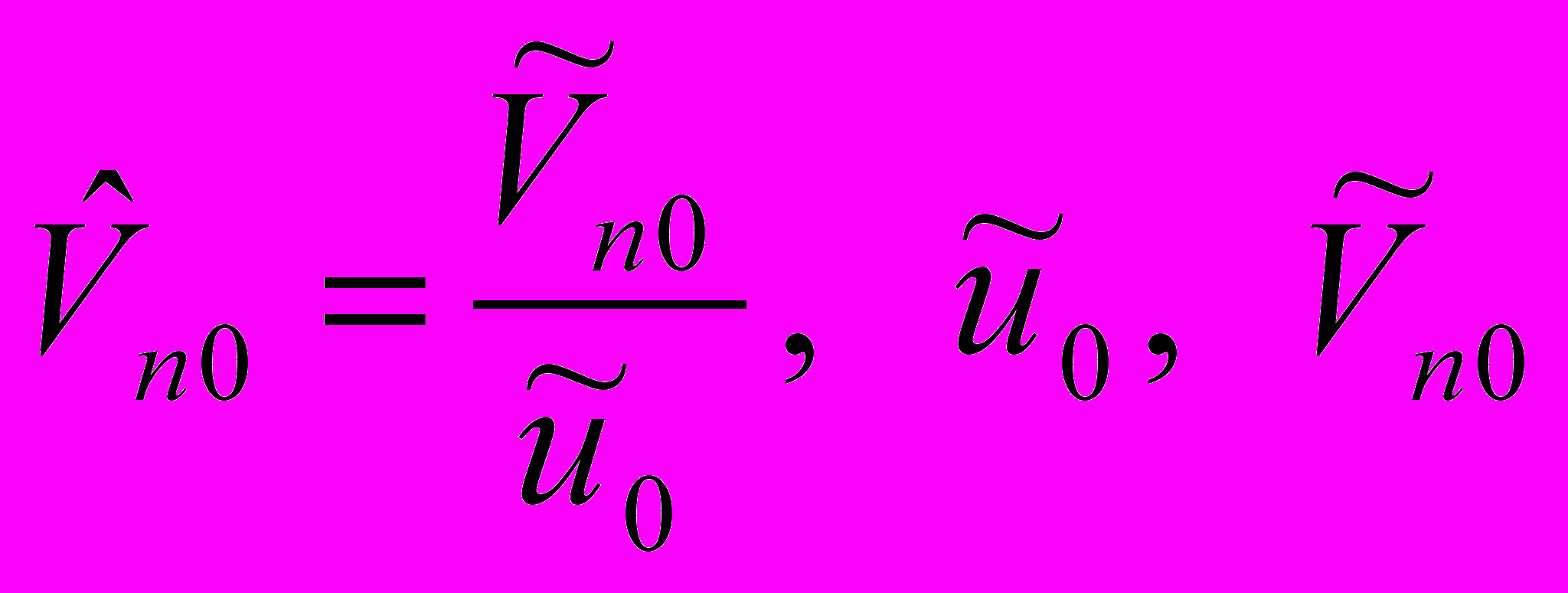- начальные значения переменных 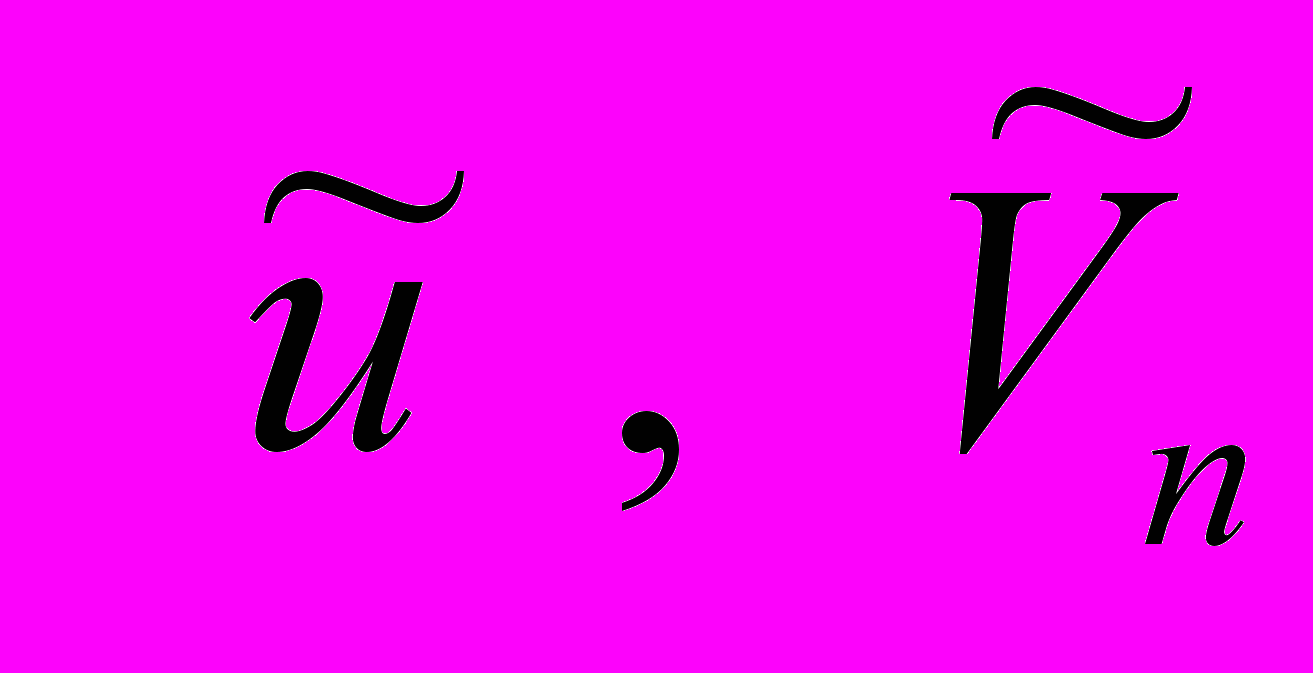. Две бифуркационные кривые 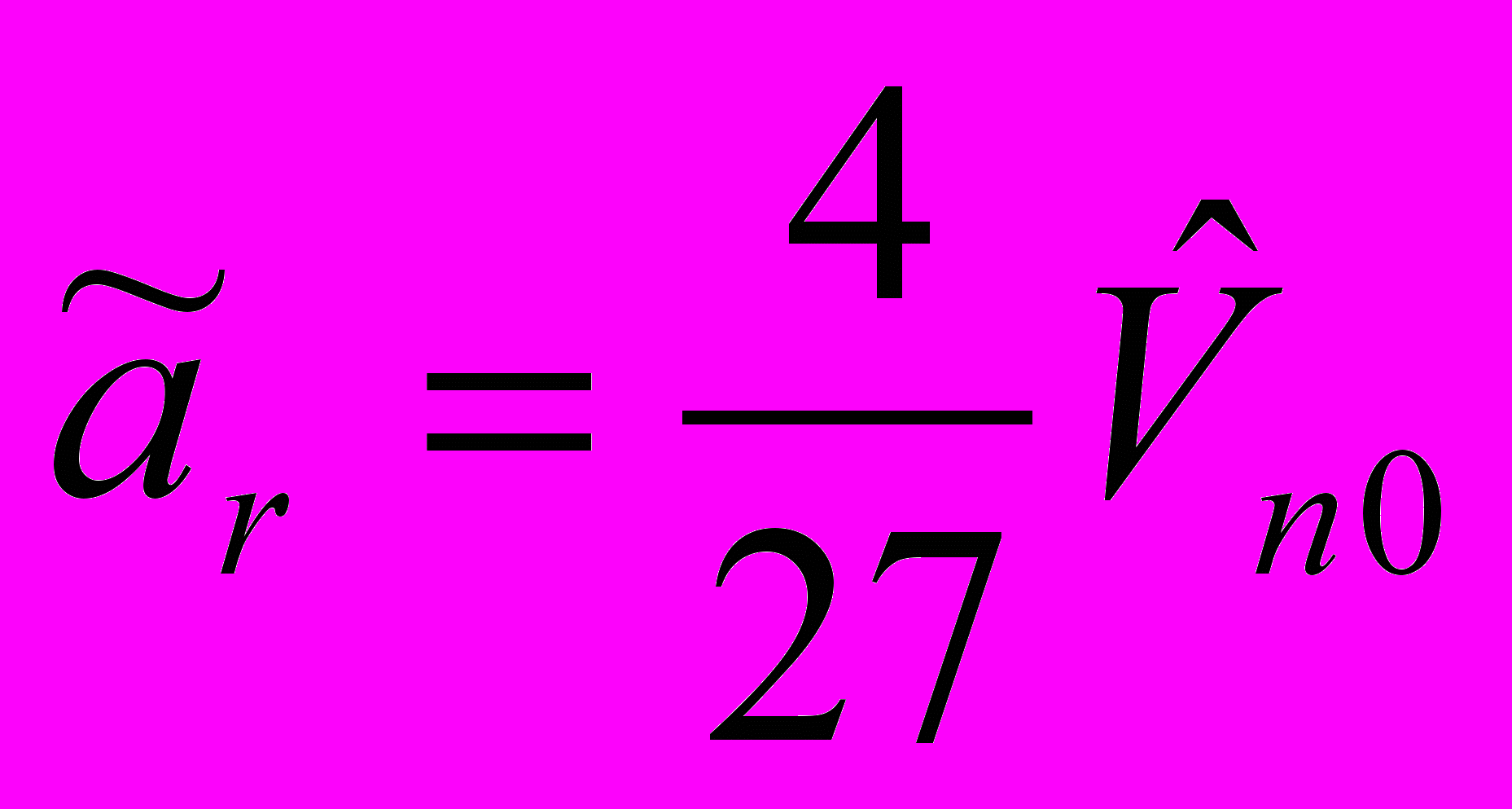и 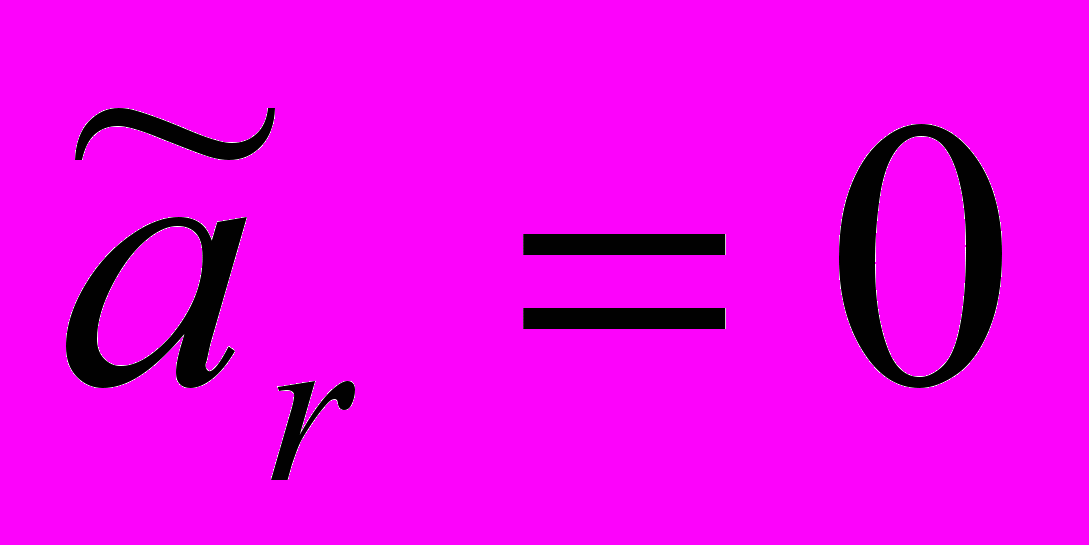разделяют плоскость параметров на три области с различной качественной структурой фазовых траекторий (рис. 1).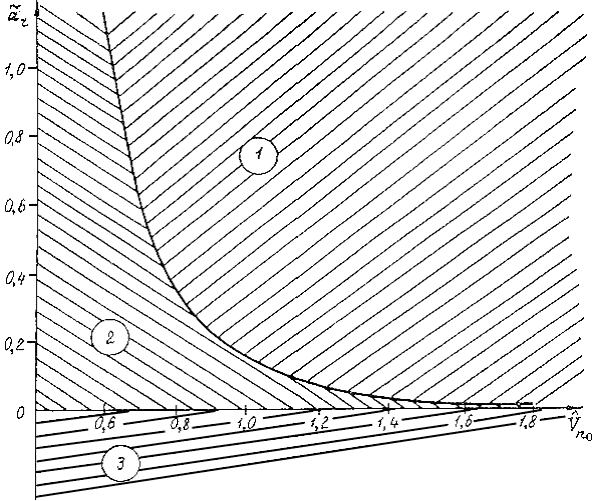




Рис. 1

В первой области система имеет одно состояние равновесия типа седло, оно расположено в области отрицательных значений переменной и поэтому не имеет практического значения.

В области 2 система имеет три состояния равновесия (центр и два седла, одно из которых лежит в отрицательной части переменной и поэтому также не имеет практического значения). Особенностью качественной структуры для этой области является наличие сепаратрисы, образующую петлю и идущую из седла в то же самое седло. Качественная структура представлена на рис. 2.

Состояния равновесия, отвечающие третьей области, являются устойчивыми состояниями равновесия типа центр, которые лежат на положительной части оси 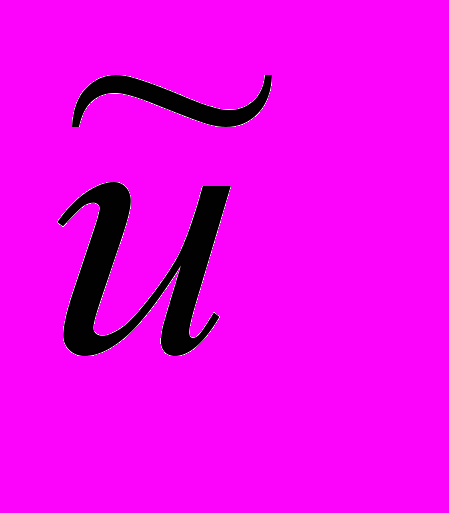(рис. 3).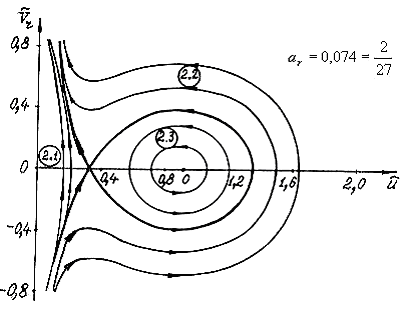



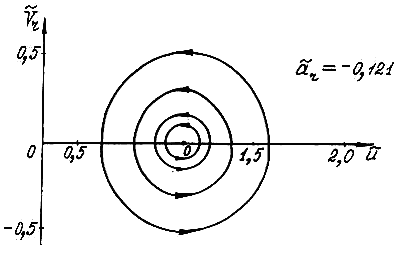
Рис. 2 Рис. 3

Полученные результаты позволили установить все возможные режимы движения КА при малой радиальной тяге.

В третьей главе проводится математическое моделирование и исследование динамической системы управляемого относительного движения КА при постоянной угловой скорости линии визирования ().

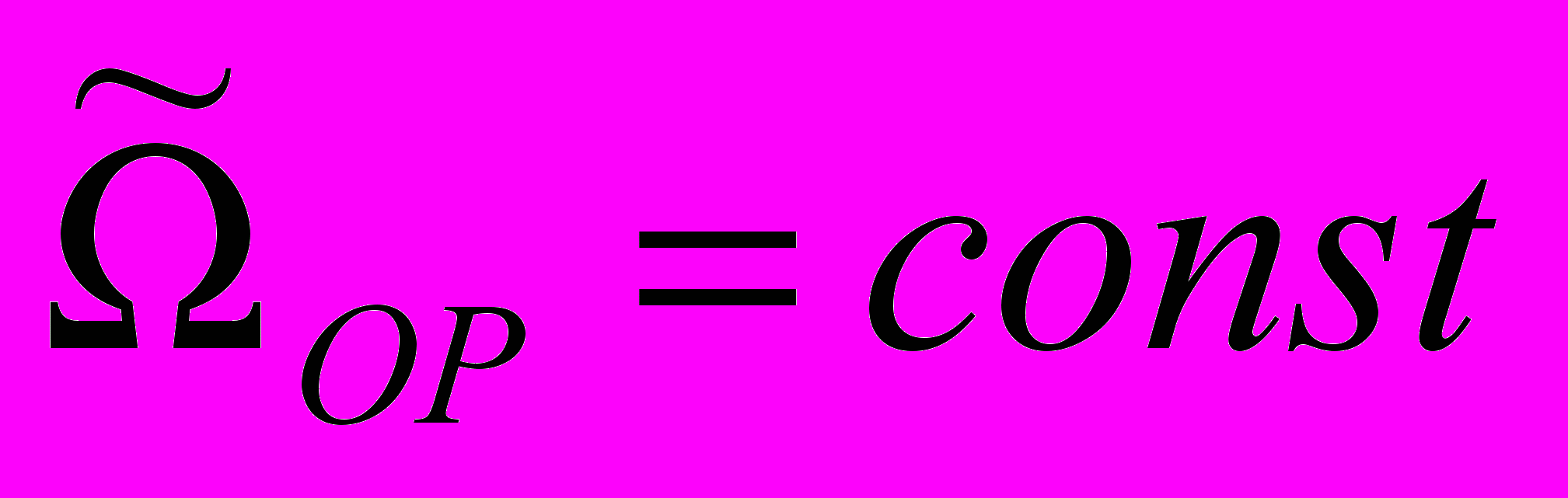В качестве частных случаев этого метода управления можно рассматривать различные модификации широко известного метода параллельного сближения.

Пространством параметров динамической системы является числовая ось безразмерной угловой скорости линии визирования 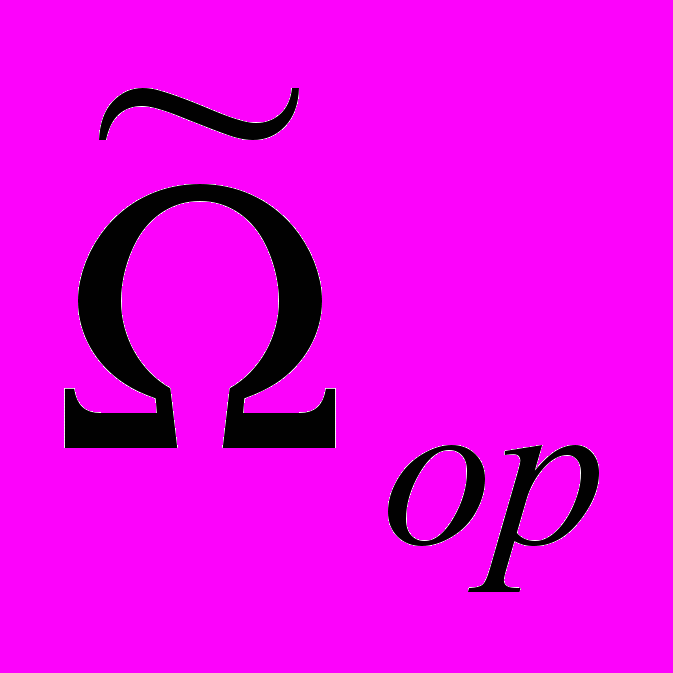. Система имеет два бифуркационных значения параметра: 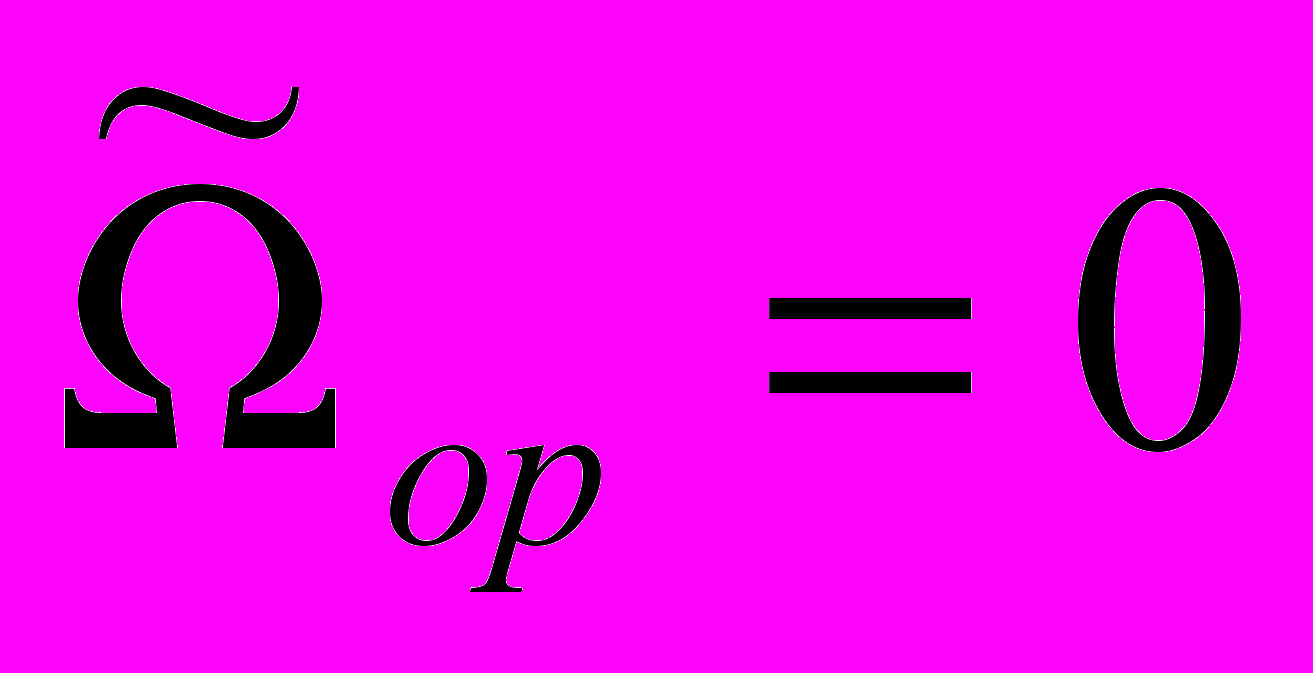и 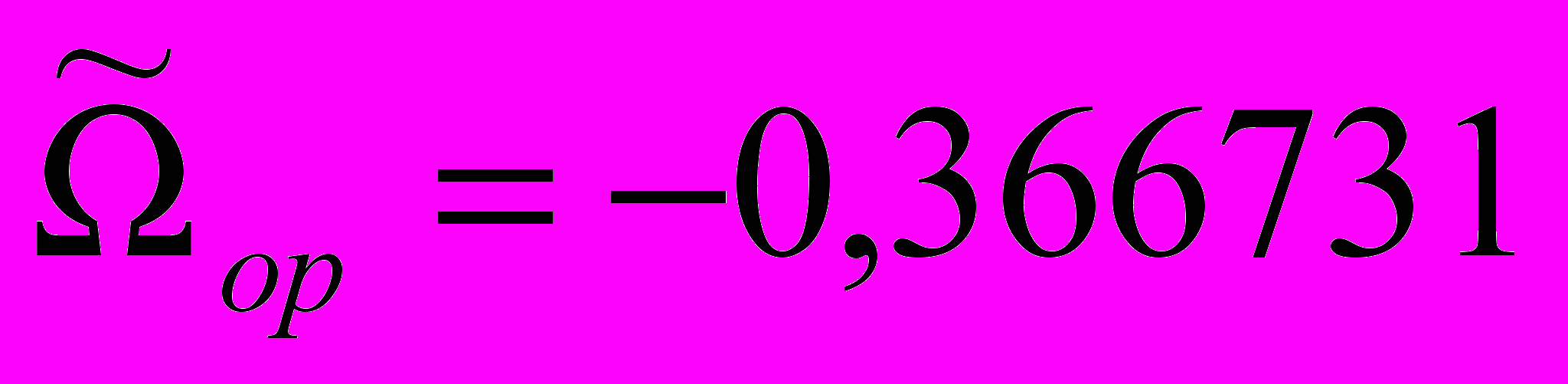. Следовательно, она имеет пять различных типов качественных структур, каждой из которых соответствует свой набор возможных режимов относительного движения КА.

Рассмотрение изменений качественной структуры системы показывает, что ее бифуркации связаны с появлением состояний равновесия, которые имеют место при 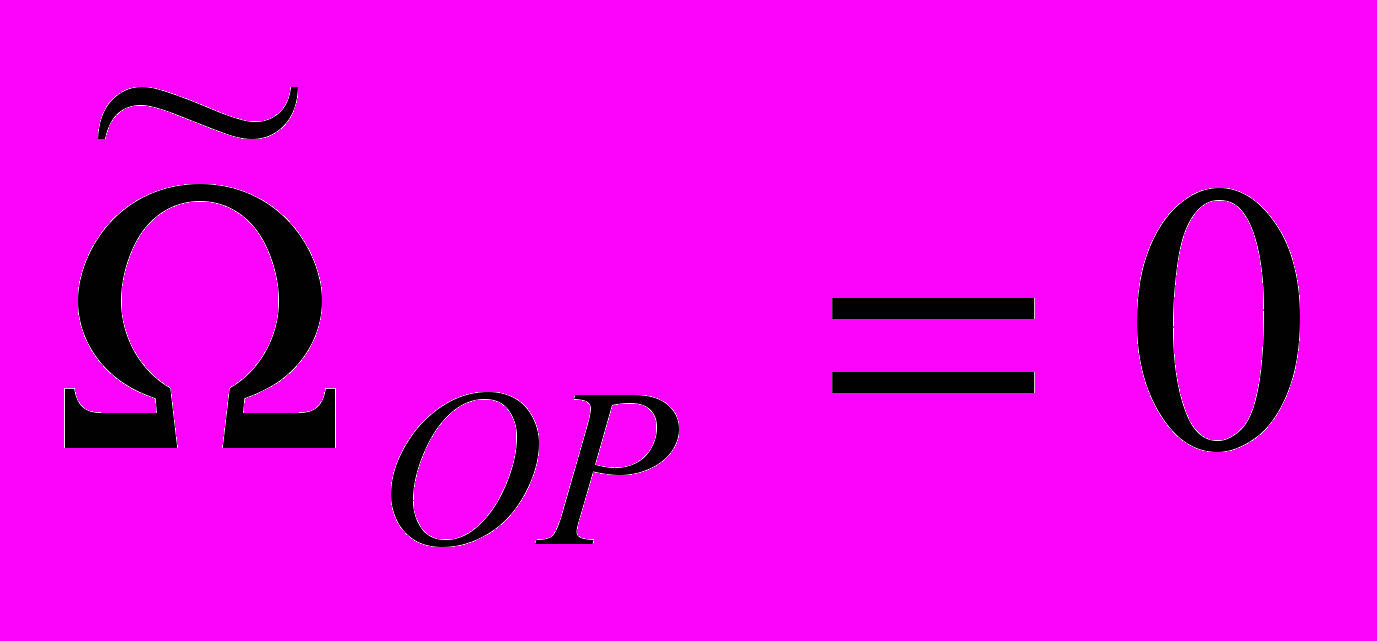и изображены в виде кривых на рис. 4, и предельных циклов, охватывающих фазовый цилиндр.

В работе доказана теорема о существовании предельных циклов, охватывающих фазовый цилиндр. В соответствии с этой теоремой, пр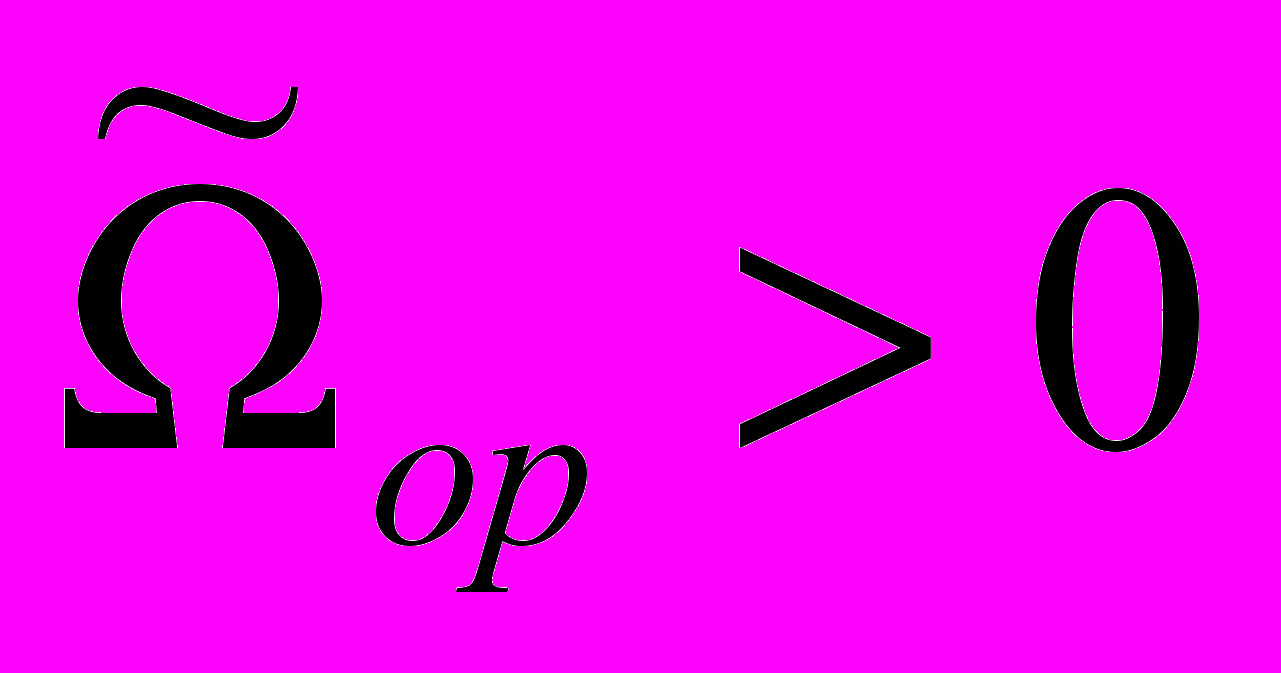и и 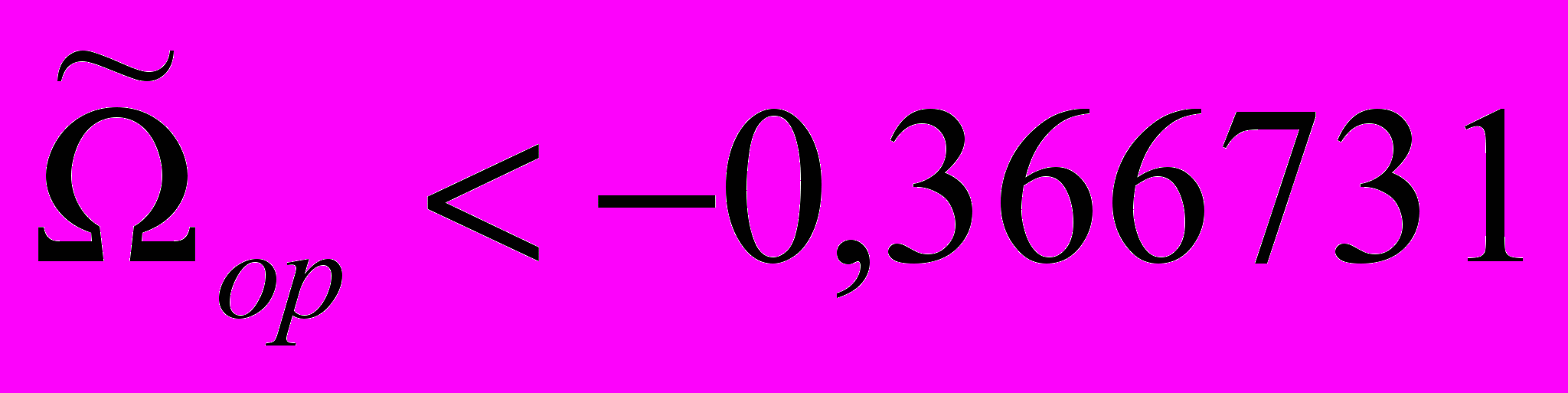, имеют место два предельных цикла, охватывающие фазовый цилиндр (один устойчивый, другой неустойчивый, рис. 5 и рис. 6). При 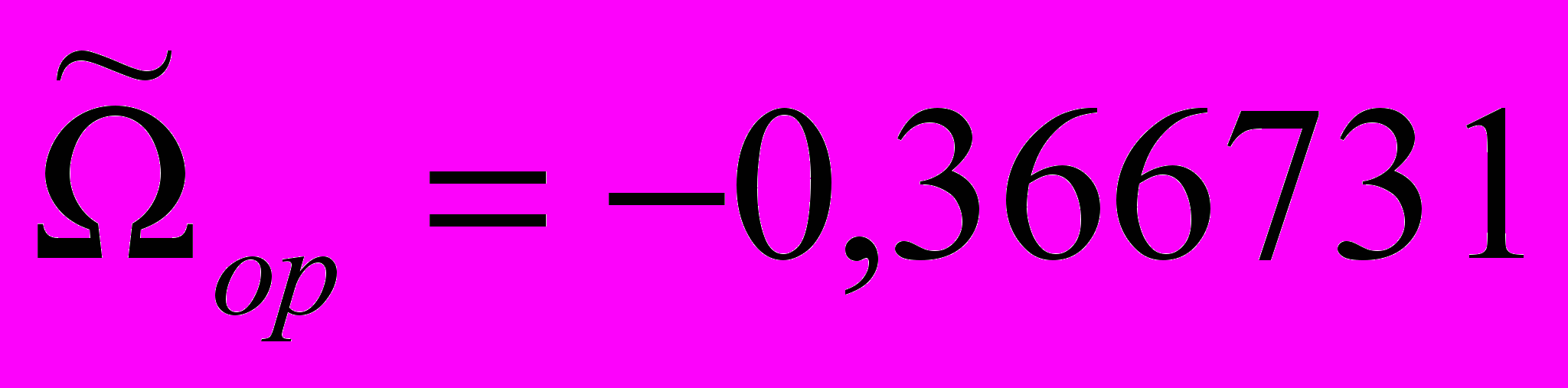имеет место полуустойчивый предельный цикл (рис. 7).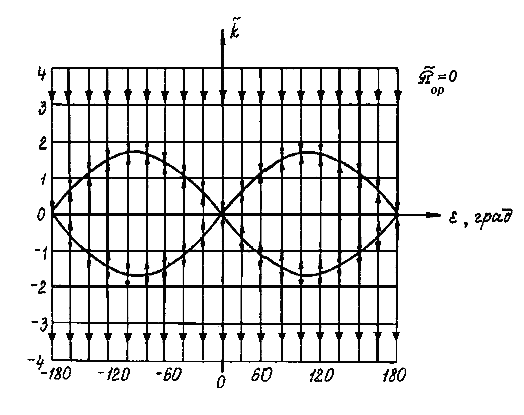



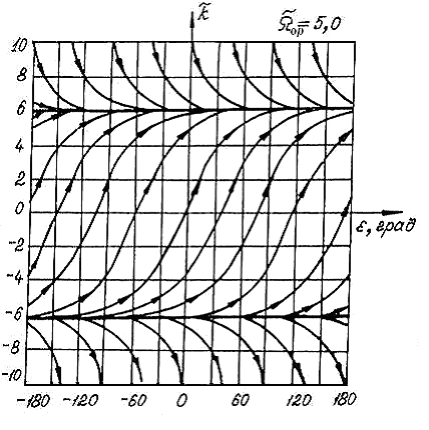
Рис. 4 Рис. 5

Показано, что применение метода управления при постоянной угловой скорости линии визирования позволяет реализовать как прямолинейные траектории сближения и удаления КА, так и траектории сближения и удаления с одновременным облетом пассивного КА. Неустойчивым предельным циклам и состояниям равновесия соответствуют траектории сближения КА, заканчивающиеся встречей при нулевой относительной скорости.



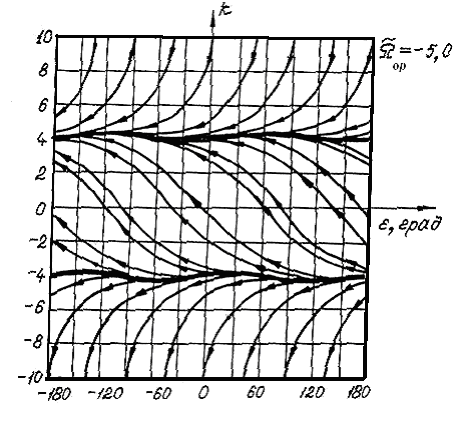
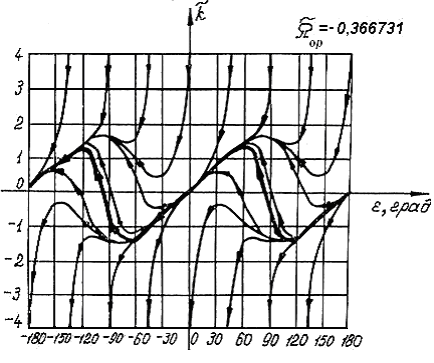
Рис. 6 Рис. 7

В четвертой главе проводится математическое моделирование и исследование динамической системы, определяющей относительное движения КА при ориентации управляющего воздействия по линии визирования, когда скорость изменения дальности между объектами пропорциональна самой дальности 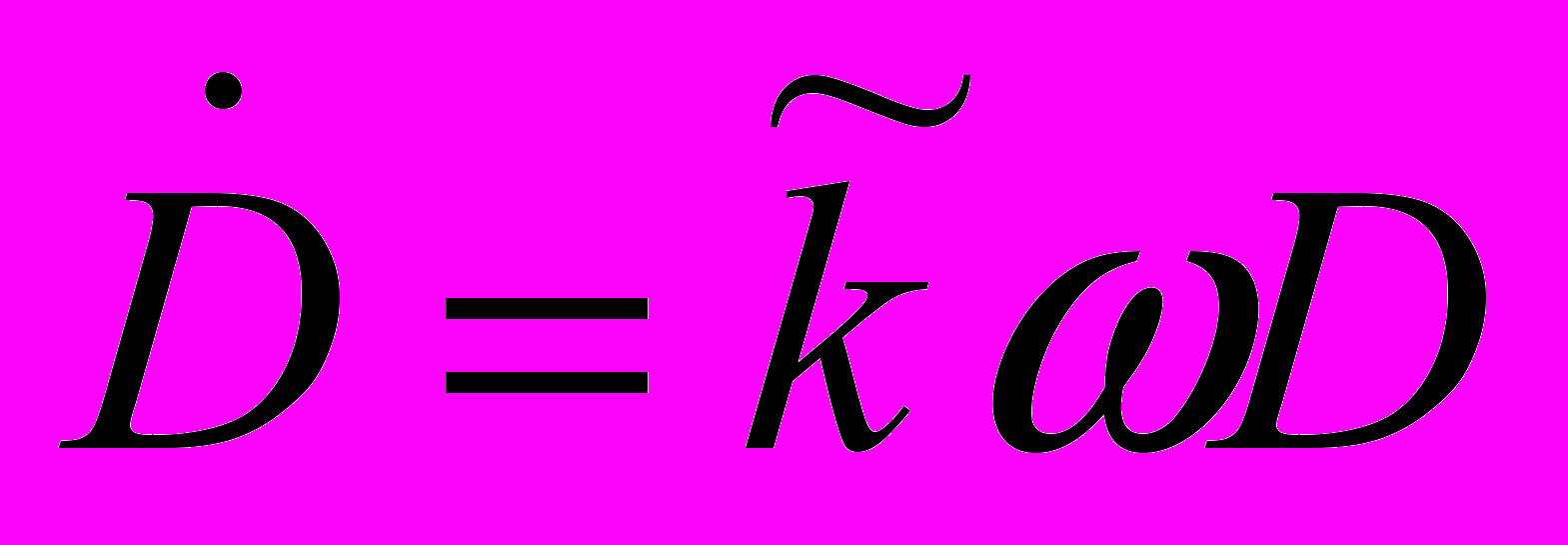(экспоненциальный метод наведения).

Этот метод представляет особый интерес для решения задач облета и совместного полета КА, а также для управления движением орбитальных тросовых систем.

Установлено, что динамическая система относительного движения КА имеет пять бифуркационных значений параметра 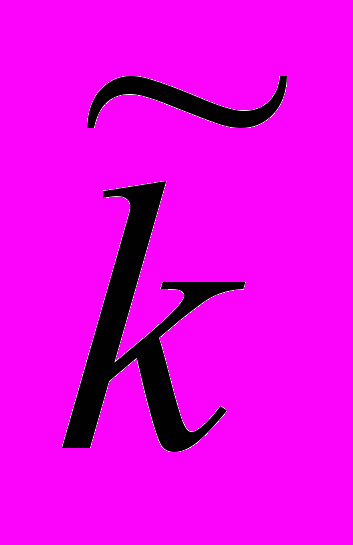: 0; 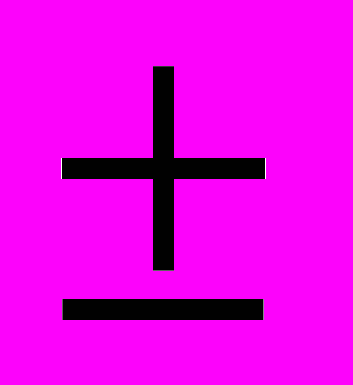0,532815; 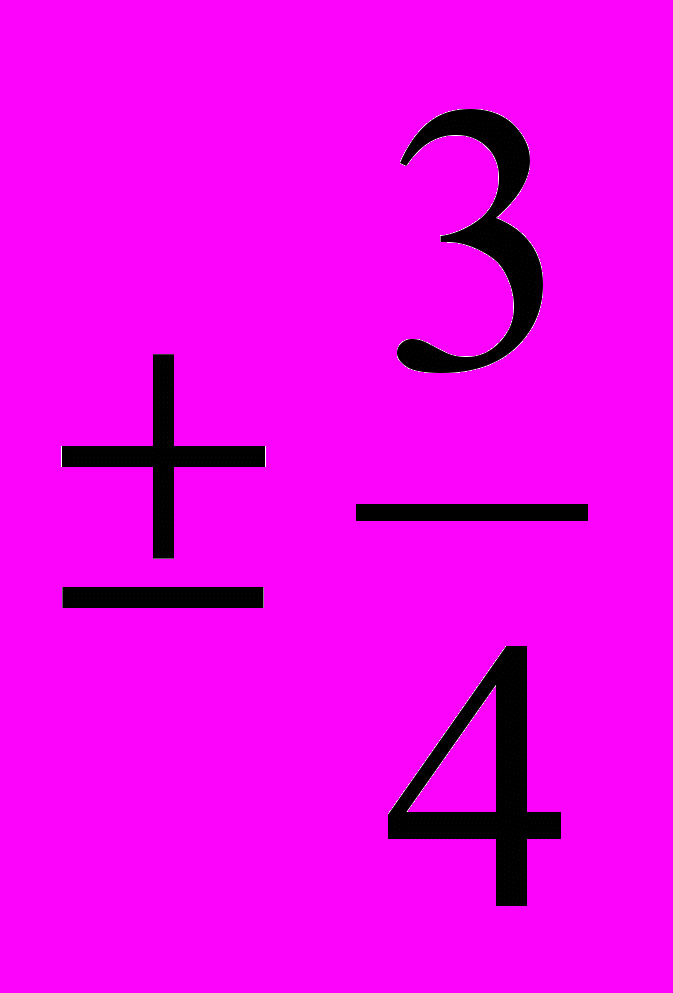. Поэтому, чтобы составить представление о пространстве состояний системы и возможных режимах относительного движения КА, необходимо определить качественную структуру системы для одиннадцати диапазонов значений параметра управления .

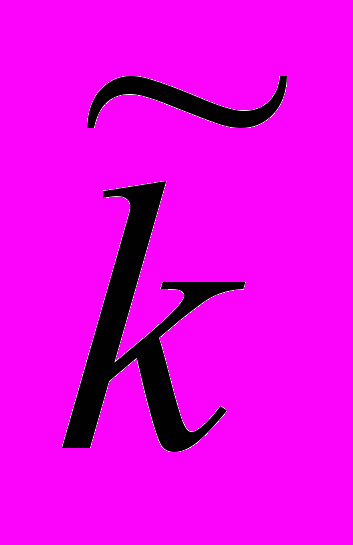Доказаны две теоремы, определяющие условия существования предельных циклов системы, охватывающих фазовый цилиндр. Установлено, что при значени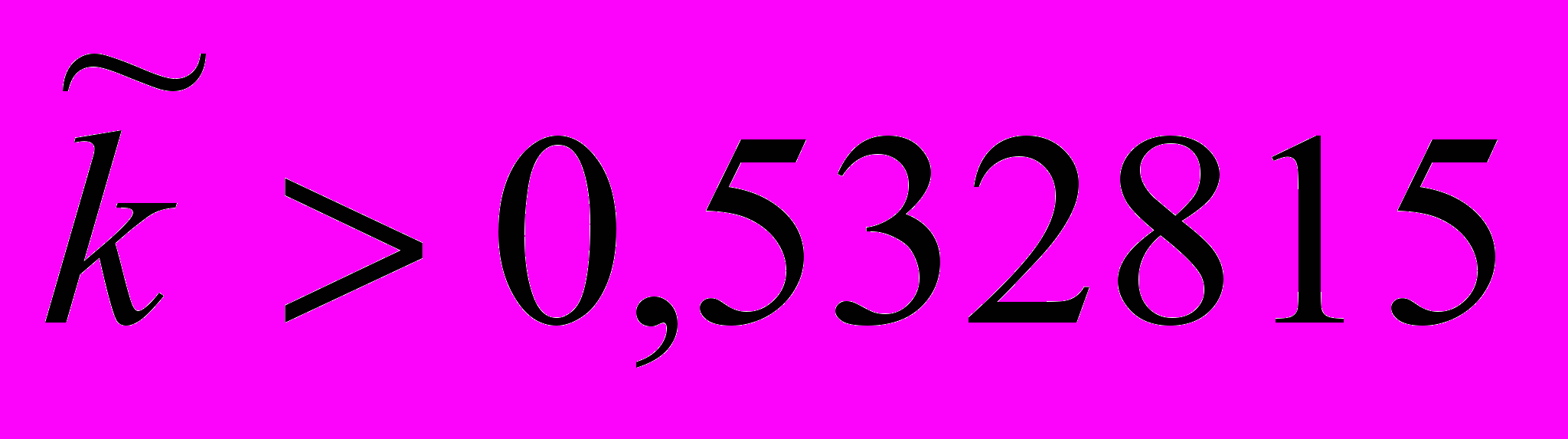и и 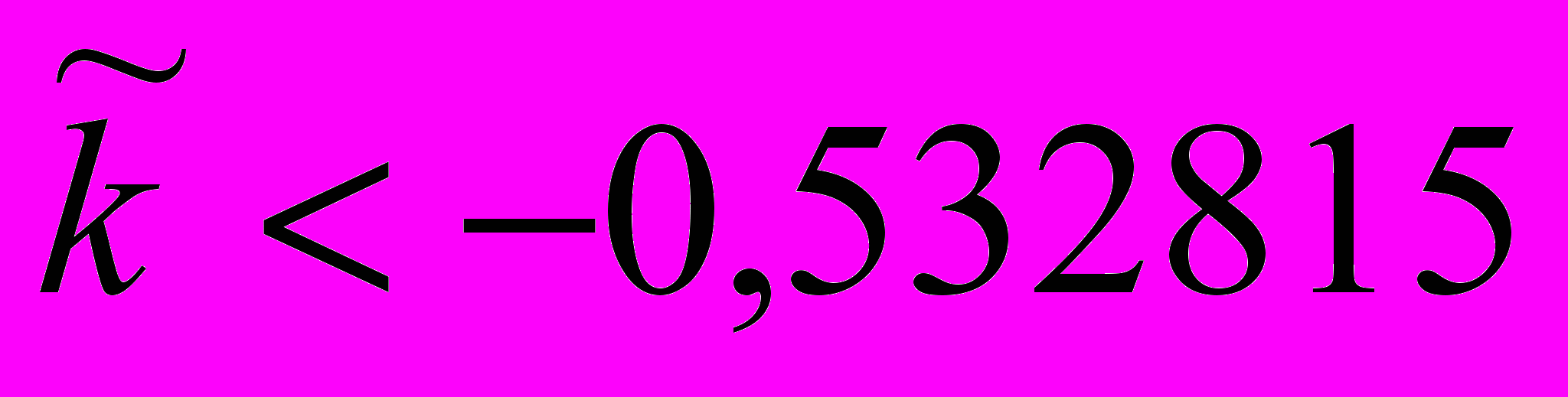появляется предельный цикл, охватывающий цилиндр (устойчивый при 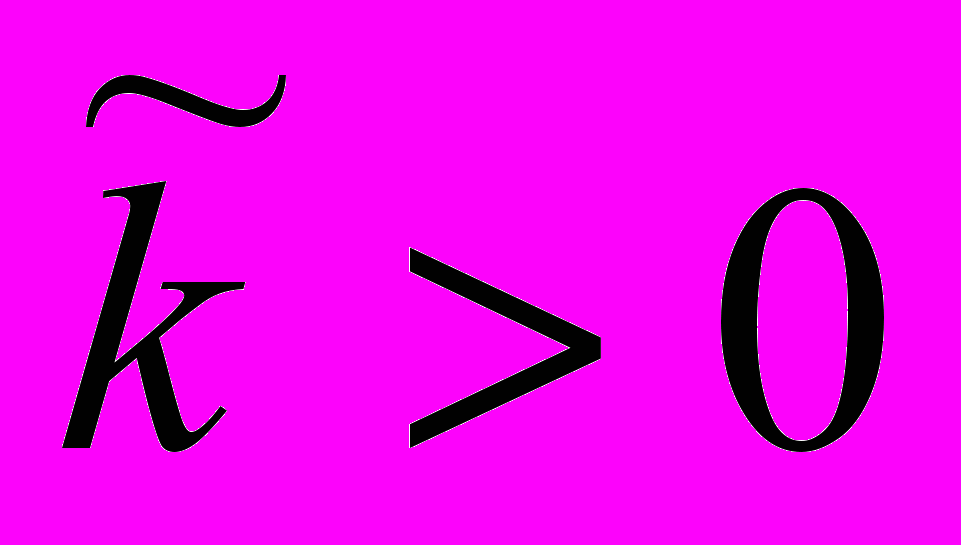и неустойчивый при ).

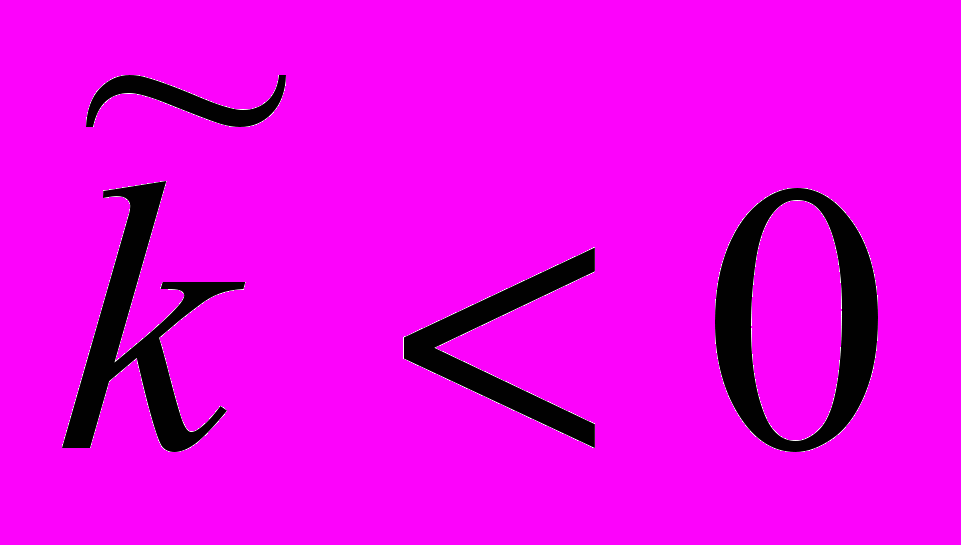Изучение всех одиннадцати типов качественных структур системы показывает, что применение рассматриваемого метода управления позволяет реализовать режимы совместного полета и облета КА, а также режимы сближения и удаления КА. При этом характер маневра КА определяется выбранным значением параметра управления 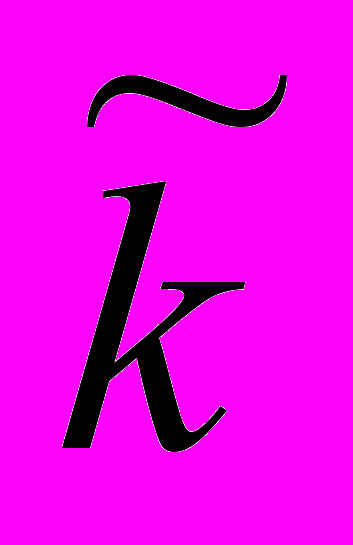и начальными значениями фазовых координат , .

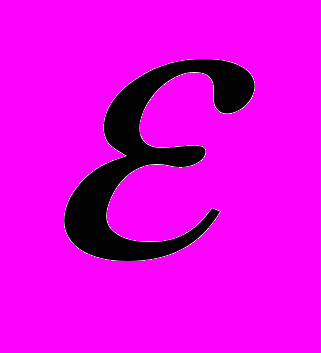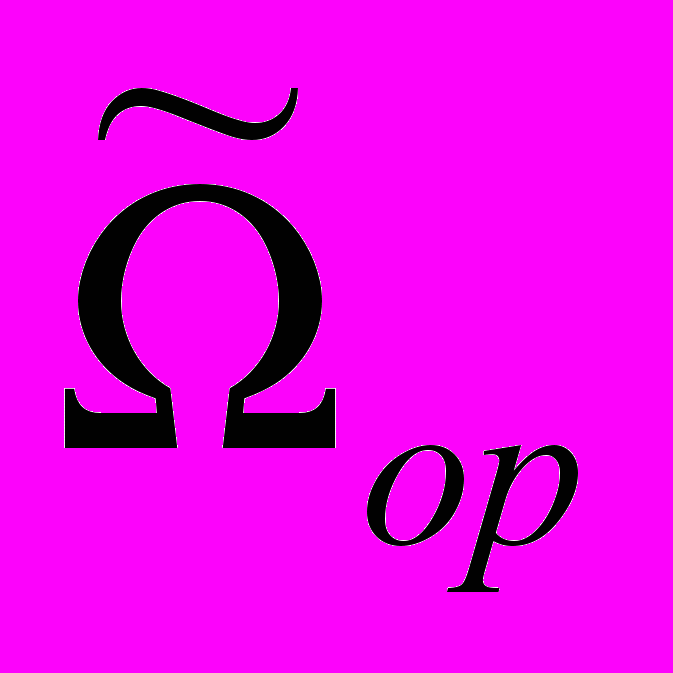В пятой главе рассматривается применение результатов математического моделирования управляемого движения КА для решения практических задач. Первый из рассматриваемых маневров с малой радиальной тягой представляет собой движение КА по круговой траектории со скоростью отличной от орбитальной. Этот тип маневра соответствует состояниям равновесия динамической системы с малым радиальным управляющим ускорением.

Такого рода маневры могут быть использованы для формирования требуемой структуры расположения системы КА на круговых орбитах.

Вторая из представленных задач – это маневры, связанные с изменением эксцентриситета и аргумента перигея орбиты КА.

Получены зависимости, определяющие изменения эксцентриситета 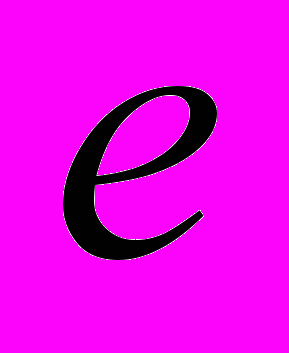и аргумента перигея орбиты КА за счет действия малой радиальной тяги.

Установлено, что при старте КА с круговой орбиты при

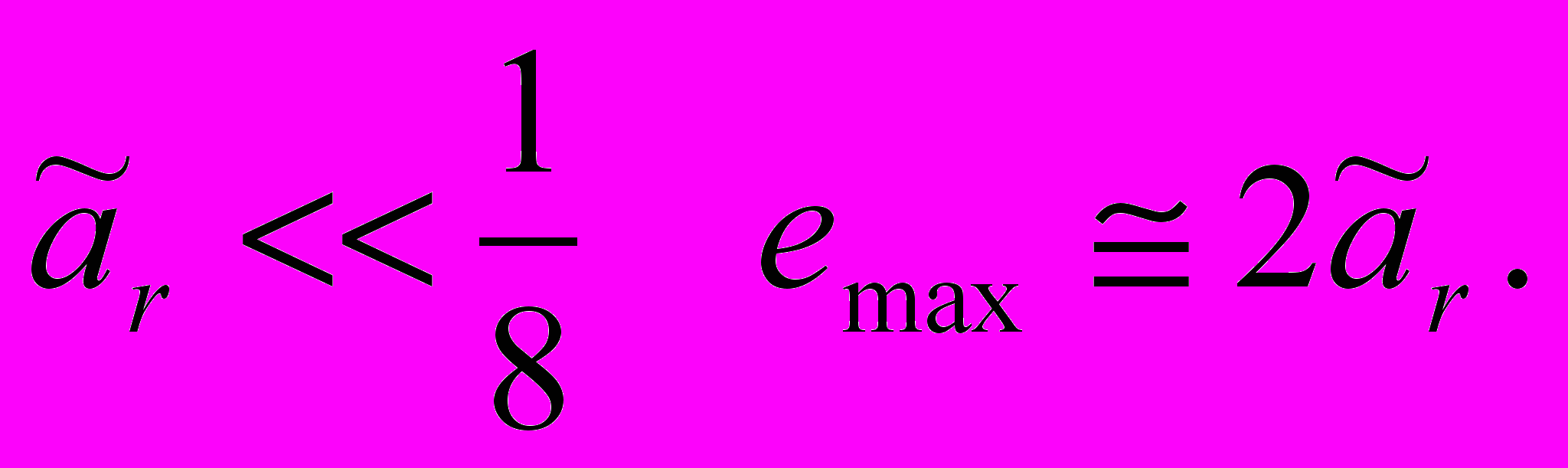
Третий тип из представленных маневров с малой радиальной тягой - это маневры перехода КА между компланарными орбитами.

В качестве частого случая рассмотренного в работе метода постоянной угловой скорости линии визирования анализируются возможности применения метода параллельного сближения для встречи КА.

Анализ всех особых и не особых фазовых траекторий позволяет определить основные виды траекторий сближения КА:

1. сближение КА с отличной от нуля относительной скоростью в момент встречи (область ячейки ниже неустойчивого предельного цикла);
   
2. сближение и встреча КА с нулевой относительной скоростью (нижний предельный цикл);
   
3. удаление объектов друг от друга соответствует области выше устойчивого предельного цикла.
   

Одно из направлений практического применения результатов исследования движения КА при управляющих воздействиях по линии визирования связано с управлением движения орбитальной тросовой системы (ОТС).

ОТС рассматриваются в качестве перспективного направления развития космической техники, так как они позволяют более эффективно и экономично решать в космосе целый ряд задач: проведение геофизических исследований и зондирование верхних слоев атмосферы, выполнение орбитальных переходов и сближение в космосе, транспортное и техническое обслуживание объектов на орбите, вывод КА на орбиту и спуск с орбиты и др. При этом полагают, что ОТС состоит из орбитальной станции (ОС) и привязного объекта (ПО).

Можно выделить следующие основные режимы движения ОТС при использовании экспоненциального закона управления:

• равновесный стационарный режим, когда тросовая система в процессе движения все время располагается вертикально;
  
• режим колебаний относительно вертикального положения равновесия;
  
• режим вращения вокруг центра масс;
  
• режим прямолинейного развертывания и свертывания ОТС.
  

Рассмотрено применение ОТС для решения задачи сближения космических объектов.

Разработана аналитическая методика определения необходимой длины троса 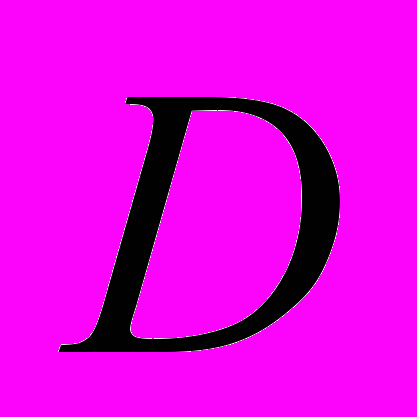и основных характеристик процесса сближения: относительной скорости в момент встречи 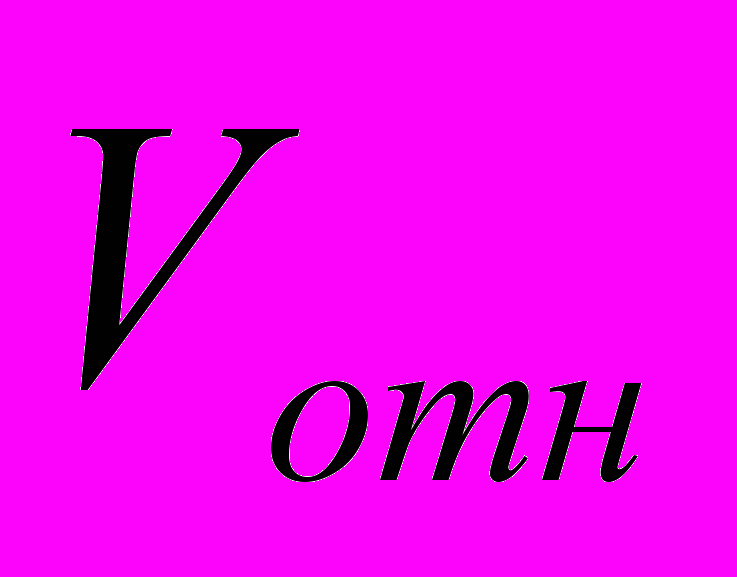, времени полета 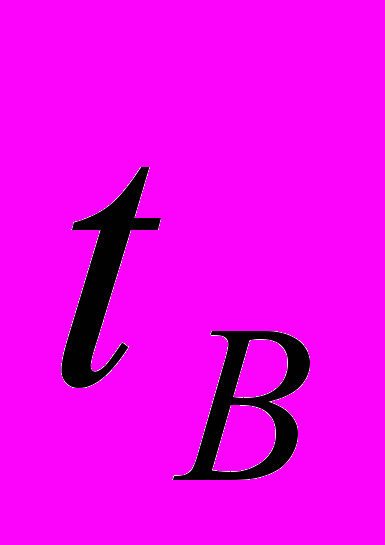от момента расцепления связки до момента встречи, выигрыша в энергетике за счет применения ОТС для сближения с КА.

Полученные результаты свидетельствуют о достаточно высокой эффективности применения ОТС для решения задачи сближения в космосе.


Выводы по результатам диссертации

1. Разработаны комплексы программ на основе синтеза методов математического моделирования, методов качественной теории динамических систем (в виде автономных динамических систем второго порядка, определяющих управляемое абсолютное и относительное движение КА), теории бифуркаций и численных методов.
   
2. На основании разработанных комплексов математических моделей и программ проведено исследование, которое позволило сократить (в 5-6 раз) машинного времени решения задач на ЭВМ:
   

• качественных структур и бифуркаций динамических систем управляемого абсолютного движения КА с малой радиальной тягой, и установлены реализуемые при этом режимы движения;
  
• качественных структур и бифуркаций динамической системы управляемого относительного движения КА при постоянной угловой скорости линии визирования с определением реализуемых режимов относительного движения;
  
• качественных структур и бифуркаций динамической системы относительного движения КА при ориентации управляющих воздействий по линии визирования с определением реализуемых режимов относительного движения.
  

3. Решены конкретные задачи маневрирования и наведения КА по методу параллельного сближения, задачи орбитальных переходов КА и сближения в космосе с использованием орбитальных тросовых систем.
   
4. Основные результаты использованы при разработке математических моделей и программного обеспечения для компьютерного моделирования относительного движения перспективных КА и этапов проведения космического эксперимента с орбитальной тросовой системой на Международной космической станции (ОКР «Трос-МКС»):
   

• разработанная программа определения необходимой длины троса и основных характеристик процесса сближения КА применена для быстрой оценки параметров новых орбит концевых КА и отцепленного троса после разделения тросовой системы, что сокращает вычислительные затраты на 20%;
  
• разработанный алгоритм расчета времени полета КА от момента расцепления связки позволяет прогнозировать планируемое время выполнения маневра спуска транспортных грузовых кораблей после предварительного понижения их орбиты с помощью длинного троса, что сокращает время планирования на 35%;
  
• разработанный алгоритм расчета выигрыша в энергетике за счет применения тросовой системы позволяет определить существенную экономию топлива при тросовом спуске транспортных грузовых кораблей после выполнения ими задач по обслуживанию пилотируемой космической станции.
  

5. Точность построенных решений, а также возможность значительного сокращения машинного времени решения задач на ЭВМ позволяет сделать вывод о перспективности использования разработанного в диссертации метода на этапе проектирования и создания новых типов КА.
   

Список публикаций по теме диссертации

1. Ручинская Е.В. Развертывание орбитальной тросовой системы // Тезисы докладов Международной молодежной научной конференции «XXVI Гагаринские Чтения». - М.: МАТИ, 2001. С. 156.
   
2. Ручинская Е.В. Исследование движения связанных космических объектов при выполнении орбитальных переходов в случае фиксированной длины соединительного троса // Тезисы докладов Международной молодежной научной конференции «XXVIII Гагаринские Чтения». - М.: МАТИ, 2002. С. 112-113.
   
3. Ручинская Е.В. Математическая модель движения связанных космических объектов с фиксированной длиной троса и ее исследование // Тезисы докладов Международной молодежной научной конференции «XXVII Гагаринские Чтения». - М.: МАТИ, 2002. С. 104.
   
4. Ручинская Е.В. Активные и пассивные методы управления движением орбитальной тросовой системы // Тезисы докладов Международной молодежной научной конференции «XXIX Гагаринские Чтения». - М.: МАТИ, 2003. С. 101.
   
5. Иванов В.А, Ручинская Е.В. Качественные методы исследования динамики связанных космических аппаратов при комбинированном управлении // Труды Четвертого Международного Аэрокосмического Конгресса. IAC’03. - М., 2003. С. 341-344.
   
6. Иванов В.А., Ручинская Е.В. Методы качественной теории динамических систем при исследовании управляемого движения гибко связанных космических аппаратов // Сборник тезисов Четвертого Международного Аэрокосмического Конгресса. IAC’03. - М.: СИП РИА, 2003. С. 238-240.
   
7. Иванов В.А., Ручинская Е.В. Некомпланарные и компланарные орбитальные переходы гибко связанных космических аппаратов из режима колебаний связки // Сборник тезисов Четвертого Международного Аэрокосмического Конгресса. IAC’03. - М.: СИП РИА, 2003. С. 241-242.
   
8. Ручинская Е.В. Математическая модель динамики движения системы гибко связанных космических объектов с учетом вязко-упругих свойств соединительного троса // Тезисы докладов Международной молодежной научной конференции «XXX Гагаринские Чтения». - М.: МАТИ, 2004. Т.6. С. 126.
   
9. Ручинская Е.В. Методика демпфирующего воздействия на связку // Тезисы докладов Международной молодежной научной конференции «XXX Гагаринские Чтения». - М.: МАТИ, 2004. Т.6. С. 127-128.
   
10. Ручинская Е.В. Применение равновесного стационарного режима движения орбитальной тросовой системы для сближения в космосе // Новые материалы и технологии. НМТ-2004. Материалы Всероссийской научно-технической конференции. - М.: ИЦ МАТИ, 2004. С. 56-57.
    
11. Ручинская Е.В. Сближение космических аппаратов с использованием орбитальных тросовых систем // Новые материалы и технологии. НМТ-2004. Материалы Всероссийской научно-технической конференции. - М.: ИЦ МАТИ, 2004. С. 55-56.
    
12. Иванов В.А., Ручинский В.С., Ручинская Е.В. Механика полета системы гибко связанных космических объектов // III Всероссийское совещание-семинар заведующих кафедрами теоретической механики ВУЗов Российской Федерации. Тезисы докладов. - Пермь: - изд-во Пермского университета, 2004. С. 44-45.
    
13. Ручинская Е.В. Качественное исследование динамики управляемого движения космических аппаратов с малой радиальной тягой // Тезисы докладов Международной молодежной научной конференции «XXXI Гагаринские Чтения». - М.: МАТИ, 2005. Т.5. С. 72-73.
    
14. Иванов В.А., Купреев С.А., Ручинский В.С., Ручинская Е.В. Математические модели и методы исследования динамики связанных космических объектов при решении практических задач // Учебное пособие. - М.: МАТИ, 2005. - 185 с.
    
15. Ручинская Е.В. Задача орбитального перехода на заданную эллиптическую орбиту // Тезисы докладов Пятого Международного Аэрокосмического конгресса. IAC’06. - М., 2006. С. 329.
    
16. Ручинская Е.В. Метод параллельного сближения // Тезисы докладов Пятого Международного Аэрокосмического конгресса. IAC’06. - М., 2006. С. 330.
    
17. Ручинская Е.В. Управление движением орбитальной тросовой системы // Труды Пятого Международного Аэрокосмического конгресса. IAC’06. - М., 2006. С. 718-721.
    
18. Иванов В.А, Ручинская E.B. Основные направления практического использования космических тросовых систем // Новые материалы и технологии. НМТ-2006. Материалы Всероссийской научно-технической конференции. - М.: ИЦ МАТИ, 2006. Т. 2. С. 60-61.
    
19. Иванов В.А, Ручинская Е.В. Развертывание орбитальной тросовой системы на эллиптической орбите // Научные Труды «МАТИ» - Российского государственного технологического университета им. К.Э. Циолковского. Вып. 10(82). - М.: ИЦ МАТИ, 2006. С. 184-188.
    
20. Иванов В.А, Ручинская Е.В. Уравнения управляемого движения гибко связанных объектов на эллиптических орбитах // Научные Труды «МАТИ» - Российского государственного технологического университета им. К.Э. Циолковского. Вып. 11(83). - М.: ИЦ МАТИ, 2006. С. 193-196.
    
21. Иванов В.А., Ручинский В.С, Ручинская Е.В. Особенности функционирования космических тросовых систем на эллиптических орбитах. // Новые материалы и технологии. НМТ-2006. Материалы Всероссийской научно-технической конференции. - М.: ИЦ МАТИ, 2006. Т 2. С. 61-62
    
22. Иванов В.А., Ручинский В.С, Ручинская Е.В. Уравнение управляемого движения гибко связанных космических объектов на эллиптических орбитах // Тезисы докладов 9-го Всероссийского съезда по теоретической и прикладной механике. - Нижний Новгород, 2006. Т.1. С. 59.
    
23. Иванов В.А, Ручинская Е.В. Математическое моделирование управляемого движения гибко связанных космических объектов на эллиптических орбитах // Научные Труды «МАТИ» - Российского государственного технологического университета им. К.Э. Циолковского. Вып. 12(84). - М.: ИЦ МАТИ, 2007. С. 186-191.
    
24. Ручинская Е.В. Инерциальное параллельное наведение // Тезисы докладов Международной молодежной научной конференции «XXXIV Гагаринские Чтения». - М.: МАТИ , 2008. Т. 5. С. 138-139.
    
25. Ручинская Е.В. Маневры изменения эксцентриситета и аргумента перигея орбиты // Научные труды Международной молодежной научной конференции «XXXIV Гагаринские Чтения». - М.: МАТИ, 2008. Т. 5. С. 137-138.
    
26. Иванов В.А, Ручинская E.B. Динамика орбитального функционирования тросовой системы на эллиптической орбите при фиксированной длине соединительного троса // Новые материалы и технологии. НМТ-2008. Материалы Всероссийской научно-технической конференции. - М.: ИЦ МАТИ, 2008. Т. 2. С. 75-76.
    
27. Иванов В.А, Ручинская E.B. Орбитальное функционирование тросовой системы на эллиптической орбите в режиме прямолинейного развертывания связки // Новые материалы и технологии. НМТ-2008. Материалы Всероссийской научно-технической конференции. - М.: ИЦ МАТИ, 2008. Т. 2. С. 76-77.
    
28. Иванов В.А, Ручинская E.B. Перспективы увеличения дальности полета ЛА за счет применения тросовой системы в режиме вращения вокруг центра масс // Новые материалы и технологии. НМТ-2008. Материалы Всероссийской научно-технической конференции. - М.: ИЦ МАТИ, 2008. С. 77-78.
    
29. Ручинская E.B. Математическое моделирование орбитального функционирования тросовой системы на эллиптической орбите при фиксированной длине соединительного троса // Тезисы докладов Шестого Международного аэрокосмического конгресса. IAC’09. – М., 2009. С. 271-272.
    
30. Иванов В.А., Ручинская E.B. Методика определения эффективности различных режимов движения орбитальных тросовых систем для сближения в космосе // Вестник МГТУ им. Н.Э. Баумана. Сер. «Машиностроение», 2009. № 4 (77). С. 37-44.
    
31. Иванов В.А., Купреев С.А., Ручинская Е.В. Равновесный стационарный режим движения тросовой системы и его применение для решения задачи вывода объекта на орбиту // Известия Российской Академии Ракетных и Артиллерийских наук. Вып. 3 (61). - М., 2009. С. 25-29.
    
32. Иванов В.А., Купреев С.А., Ручинский В.С., Ручинская Е.В. Математическое моделирование вывода космического аппарата на стационарную орбиту с использованием тросовой системы // Научные труды «МАТИ» - Российского государственного технологического университета им. К.Э. Циолковского. Вып. 15(87). М.: ИЦ МАТИ, 2009. С. 176-180.
    
33. Иванов В.А., Купреев С.А., Ручинский В.С., Ручинская Е.В. Решение задачи вывода космического аппарата на стационарную орбиту с использованием тросовой системы // Научные труды «МАТИ» - Российского государственного технологического университета им. К.Э. Циолковского. Вып. 16(88). - М.: ИЦ МАТИ, 2009. С. 170-174.
    
34. Ручинская E.B. Математическое моделирование прямолинейного развертывания связки орбитальной тросовой системы // Научные труды Международной молодежной научной конференции «XXXVI Гагаринские Чтения». - М.: МАТИ, 2010. Т. 5. С. 179-180.
    
35. Ручинская E.B. Математическое моделирование выведения привязного объекта связки в расчетную точку встречи с космическим аппаратом // Научные труды Международной молодежной научной конференции «XXXVI Гагаринские Чтения». - М.: МАТИ, 2010. Т. 5. С. 180-181.