С. Б. Томашевский влияние упругопластических деформаций на результаты решения контактных задач железнодорожного транспорта
| Вид материала | Документы |
СодержаниеУпругопластический контакт колеса вагона и рельса. Упругопластический контакт упрочняющего ролика и оси грузового вагона. Список литературы |
- Влияние процессов реструктуризации железнодорожного транспорта на структуру профсоюзов, 511.29kb.
- Министерство транспорта российской федерации федеральное агентство железнодорожного, 557.64kb.
- Инструкция по безопасному поведению детей на объектах железнодорожного транспорта Чтобы, 17.73kb.
- Г. П. Петракова на Совете Федерального агентства железнодорожного транспорта Об итогах, 306.19kb.
- В, кабельных линий напряжением до 220 кВ, релейной защиты, силового электрооборудования,, 1087.95kb.
- Л. С. Вздорнова Пермский институт железнодорожного транспорта, 73.52kb.
- Инструкция по безопасному поведению детей на объектах железнодорожного транспорта, 20.28kb.
- Программа проведения педагогической конференции по теме : «Пути интеграции профессиональных, 24.69kb.
- Ринадцатый год отсчет ведется с момента принятия Постановления Правительства, 307.19kb.
- «Итоги работы Федерального агентства железнодорожного транспорта за 2008 год», 179.82kb.
Вестник Брянского государственного технического университета. 2011. № 3(31)
УДК 621.787.4: 620.186.4
С.Б. Томашевский
ВЛИЯНИЕ УПРУГОПЛАСТИЧЕСКИХ ДЕФОРМАЦИЙ НА РЕЗУЛЬТАТЫ РЕШЕНИЯ КОНТАКТНЫХ ЗАДАЧ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Рассмотрен алгоритм решения контактной задачи с учётом физической нелинейности материалов взаимодействующих тел. Проведено математическое моделирование физических процессов при взаимодействии: 1) колеса и рельса; 2) упрочняющего ролика и оси колёсной пары. Получены данные о размерах и форме областей контакта, распределении напряжений и деформаций в контактирующих деталях.
Ключевые слова: упругопластические деформации, контактная задача, физическая нелинейность, метод конечных элементов, ось, колесо, рельс, упрочнение.
Контактное взаимодействие возникает в процессе совместной работы сопряжённых элементов машин и конструкций, при столкновении движущихся объектов с преградой, упрочнении деталей машин поверхностным пластическим деформированием (ППД), выполнении соответствующих технологических операций формоизменения заготовок и во многих других случаях. Учёт контактного нагружения деталей необходим при проектировании и производстве надёжных и экономичных машин и конструкций. На железнодорожном транспорте контактное взаимодействие учитывается при расчёте таких объектов, как колесо, рельс, подшипники качения и скольжения, буксовый узел, тормоза, а также при расчёте технологических режимов упрочнения деталей (например, осей колёсных пар и др.) ППД. Поэтому особую актуальность приобретают исследования, направленные на получение решений указанных контактных задач с необходимой степенью достоверности.
Экспериментальные исследования образцов, вырезанных из осей колёсных пар, подвергнутых упрочнению обкаткой роликами, фиксируют увеличение микротвёрдости подповерхностного слоя металла по сравнению с микротвёрдостью исходного материала. Это свидетельствует о пластическом деформировании подповерхностного слоя, наличии остаточных напряжений, изменении механических свойств материала оси.
Материалы железнодорожных колёс и рельсов в области контактирования также деформируются упругопластически. Экспериментально установлено, что пластические деформации в рельсе проникают на глубину до 20 мм. Что касается первых циклов перекатывания колеса по рельсу или упрочняющего ролика по детали, когда их материалы ещё не были пластически деформированы, то необходимо решать задачу качения при упругопластическом деформировании материалов.
Таким образом, упругопластическое поведение материала существенно влияет на физические процессы в области контакта. Следовательно, одним из направлений уточнения решения контактной задачи является учёт физической нелинейности материалов контактирующих тел.
Исследованиями упругопластического деформирования занимается раздел механики деформируемых тел – теория пластичности. В настоящее время разработаны различные теории пластичности, в том числе так называемые технические (простейшие): теория малых упругопластических деформаций и теория течения. Технические теории пластичности базируются на принципах предельных поверхностей и максимального рассеяния механической энергии при пластическом деформировании. В деформационной теории [1] устанавливается связь между напряжениями и деформациями, поэтому физические уравнения записываются в конечных величинах:
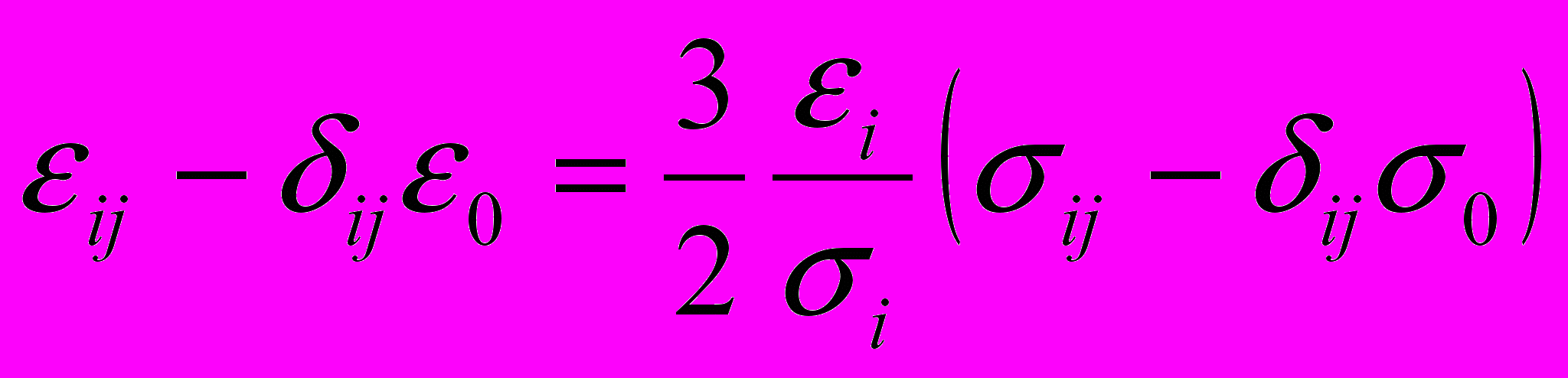,где
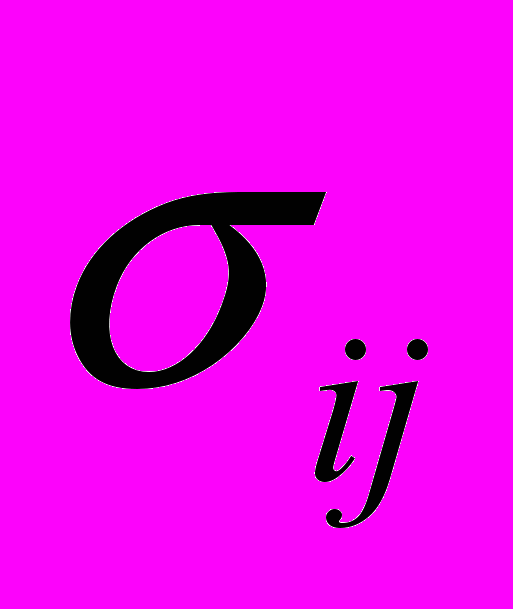- тензор напряжений; 
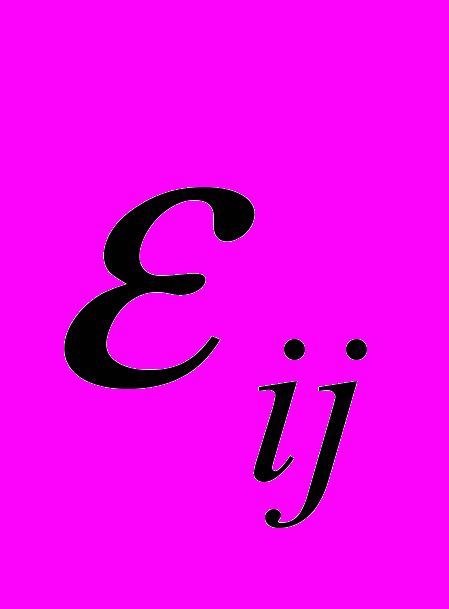- тензор деформаций; 
- символ Кронекера; 
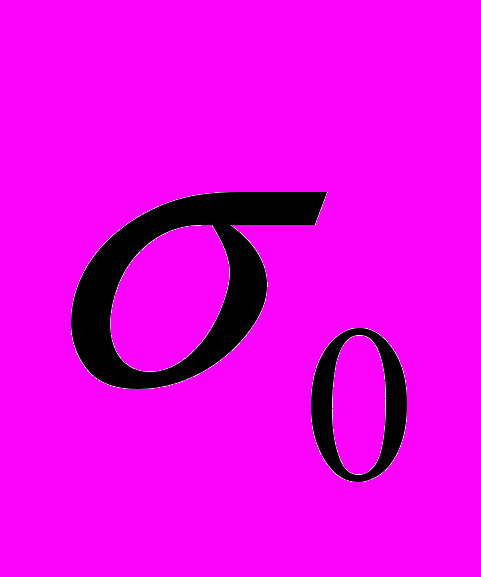- среднее давление в точке; 
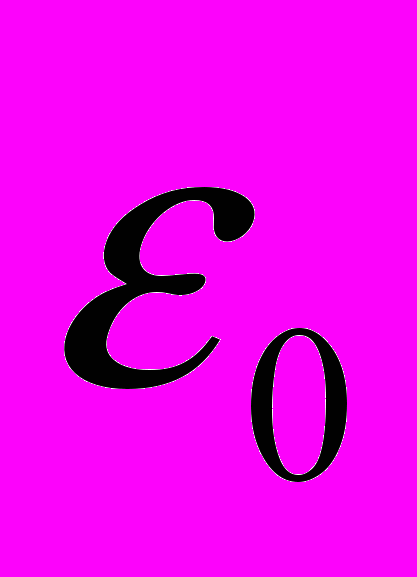- средняя деформация в точке; 
- интенсивность напряжений;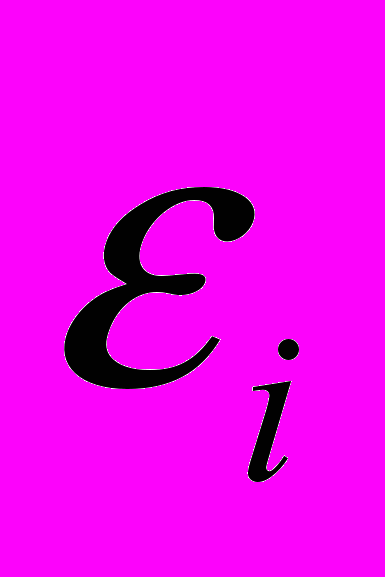 
- интенсивность деформаций; 
, 
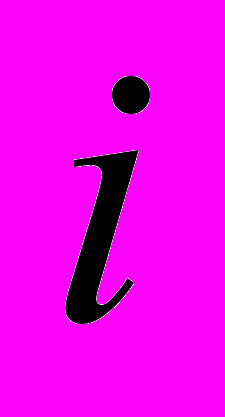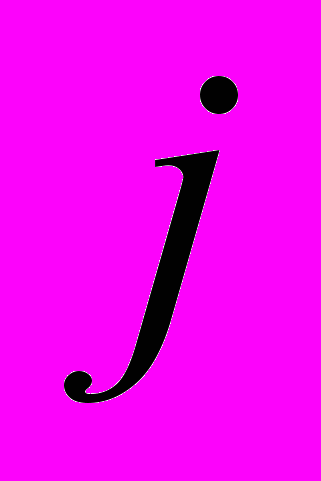= 1, 2, 3.Следовательно, при использовании этой теории задачу можно решать как в шаговой, так и в итерационной постановке. Между тем в теории течения [1] связываются бесконечно малые приращения пластических деформаций и напряжений, поэтому решать задачу с применением данной теории можно только при шаговом приращении нагрузки:
,
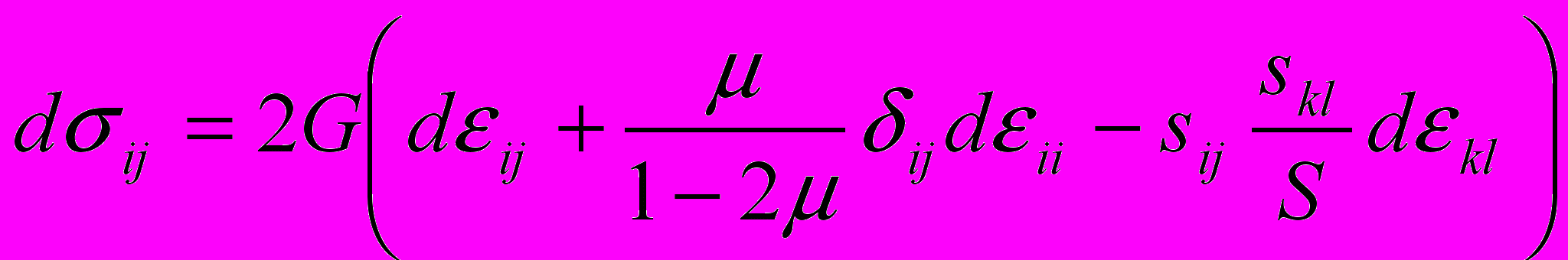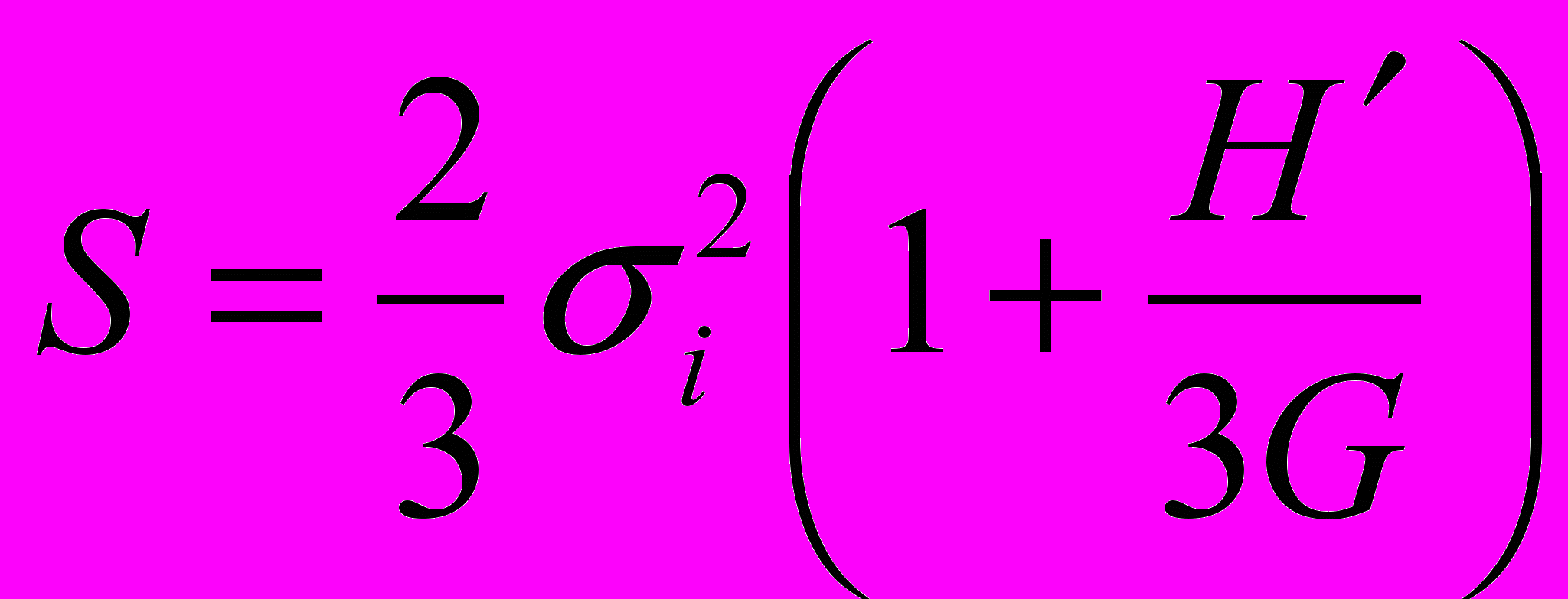,где
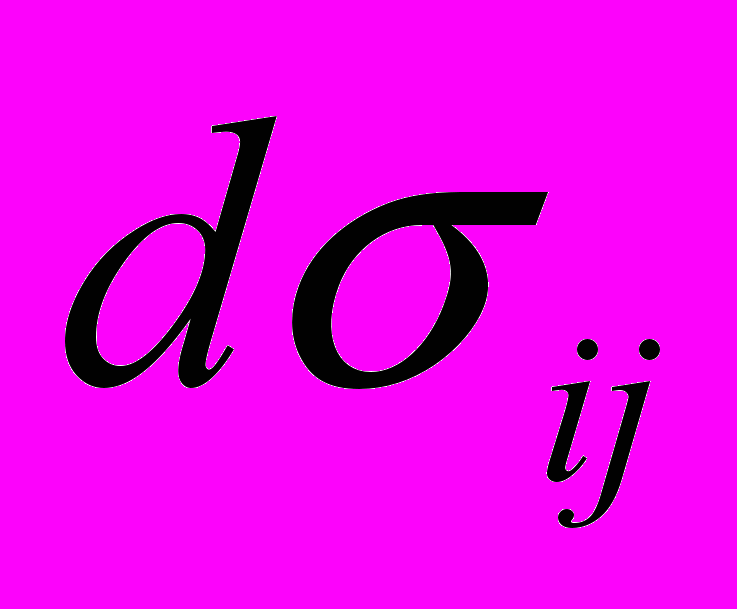- приращение тензора напряжений; 
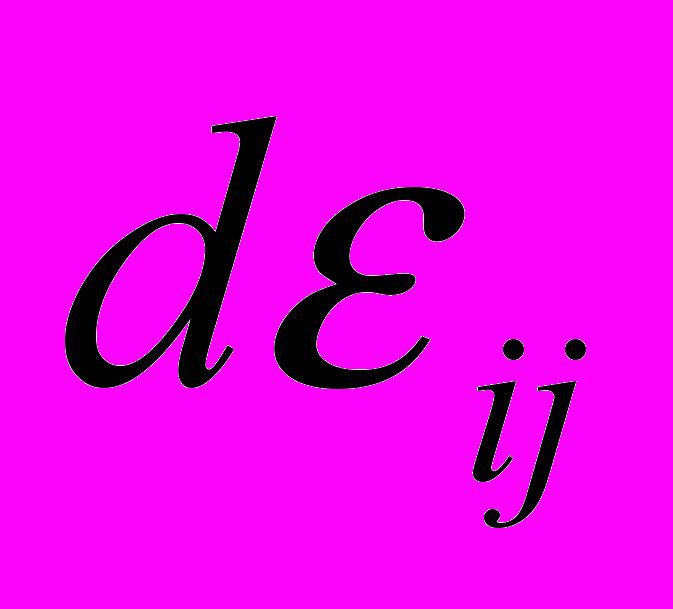- приращение тензора деформаций; 
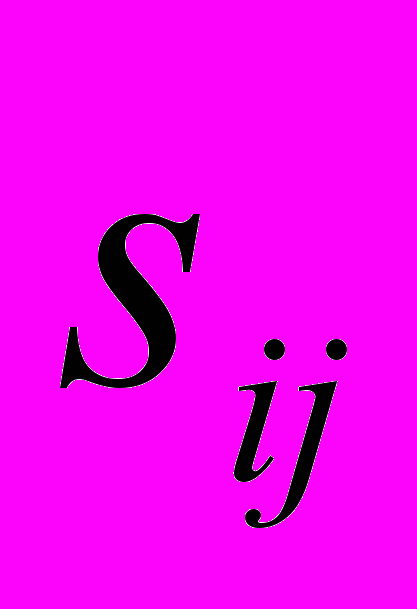- приращение девиатора напряжений; 
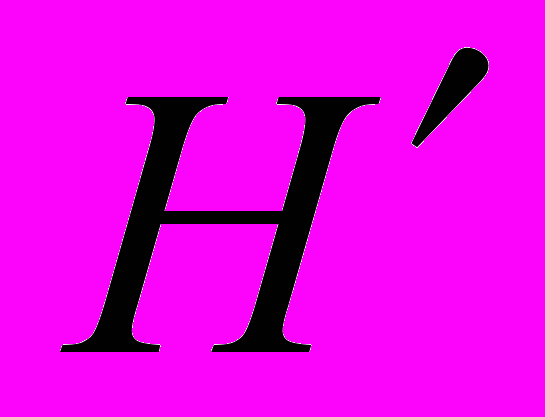- тангенс угла наклона деформационной кривой в точке, соответствующей 
; 
- коэффициент Пуассона;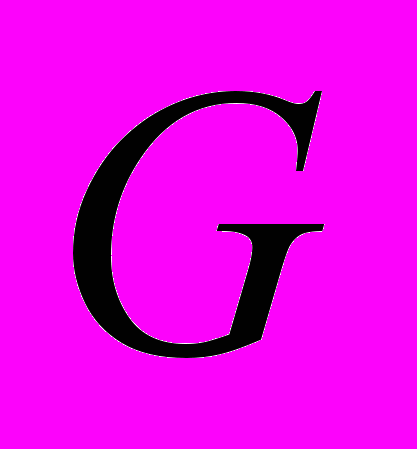 
- модуль упругости второго рода; , , 
, 
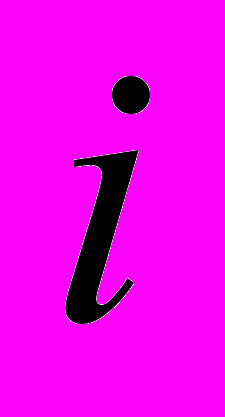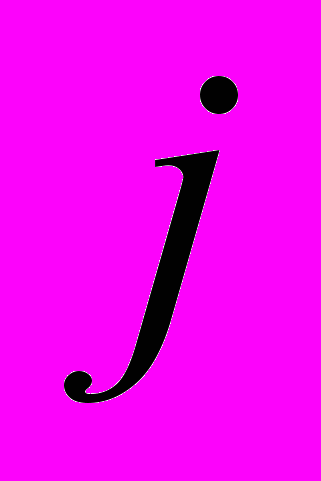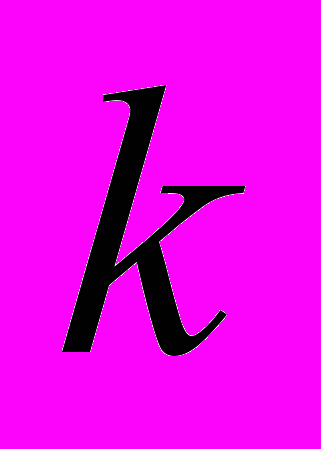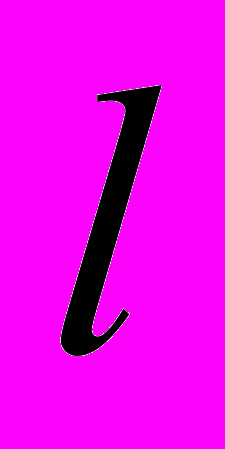= 1, 2, 3.Для описания процесса сложного нагружения, а именно такое нагружение происходит при контактном взаимодействии, лучше использовать теорию течения. Но, как свидетельствуют исследования ряда авторов, например И.А. Биргера и Р.Р. Мавлютова [2], если реализовать процесс решения с использованием деформационной теории в шаговой постановке, то и она вполне пригодна для расчёта сложного нагружения. К тому же процесс решения задачи с использованием деформационной теории происходит значительно быстрее, чем при использовании теории течения, что особенно заметно при решении контактных задач качения. Поэтому в данной научно-практической работе для моделирования упругопластического поведения материалов применялась теория малых упругопластических деформаций.
Для решения упругопластических задач могут быть использованы различные методы: метод начальных напряжений, метод начальных деформаций, метод Ньютона-Рафсона, метод переменных параметров упругости и др. Как теория течения, так и теория малых упругопластических деформаций могут быть реализованы любым из перечисленных методов. При этом среди известных алгоритмов универсального метода не существует – эффективность того или иного метода зависит главным образом от типа и параметров проявляющейся нелинейности. При выполнении расчётов в данной работе применялся метод переменных параметров упругости совместно с релаксационным методом решения контактной задачи [3].
Описанная схема решения была реализована с использованием метода конечных элементов [4] в виде специализированного программного комплекса ITFEMCP, ориентированного на решение нелинейных задач механики деформируемых тел. С помощью этого программного комплекса выполнены решения ряда тестовых [5] и прикладных задач. В рамках данной работы проведены исследования по определению напряжённо-деформированного состояния в контакте: 1) железнодорожного колеса и рельса; 2) упрочняющего ролика и оси колёсной пары грузового вагона. Результаты решения обеих задач, полученные в упругопластической постановке, сопоставлены с соответствующими величинами, рассчитанными в упругой постановке.
Упругопластический контакт колеса вагона и рельса. С помощью довольно совершенной конечноэлементной модели, содержащей 68952 узла и 62500 восьмиузловых объёмных конечных элементов (рис. 1), смоделирован контакт нового вагонного колеса и нового рельса R 65.
Р
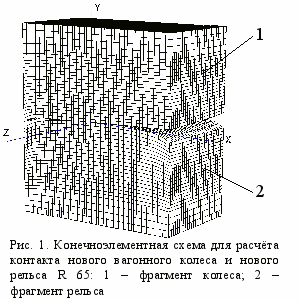азмер конечноэлементной схемы в направлении оси X - 60 мм, в направлении оси Y - 65 мм, в направлении оси Z - 30 мм. Расчётная схема построена с учётом симметрии относительно плоскости XY, перпендикулярной направлению движения колеса по рельсу и проходящей через точку первоначального контакта профилей. Модуль упругости и коэффициент Пуассона для колеса и рельса приняты одинаковыми: 
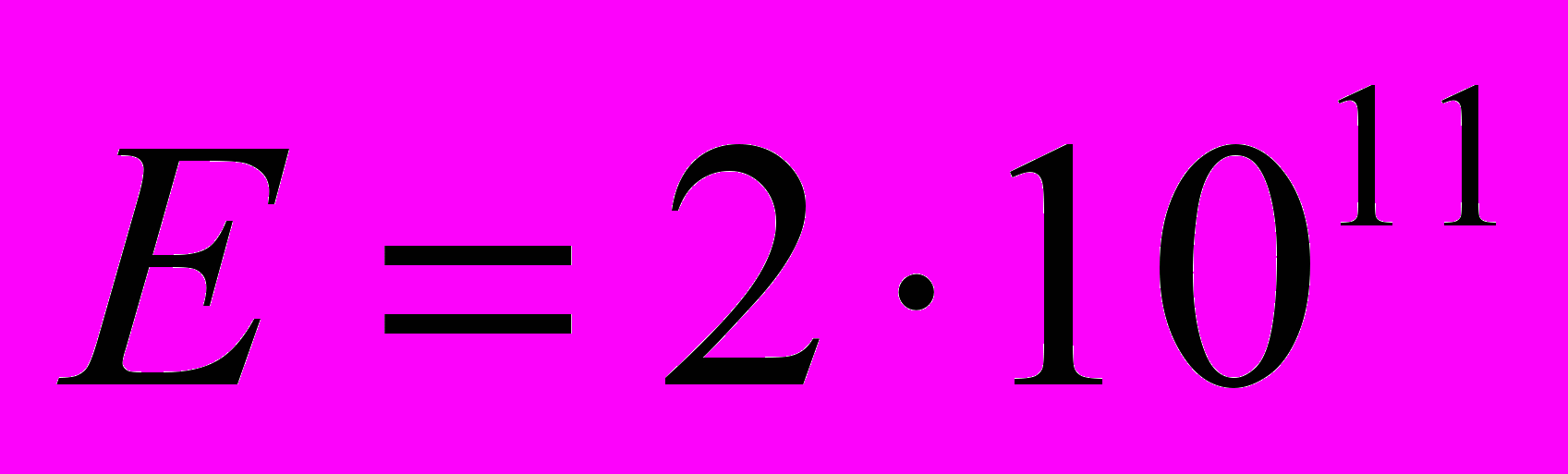Па,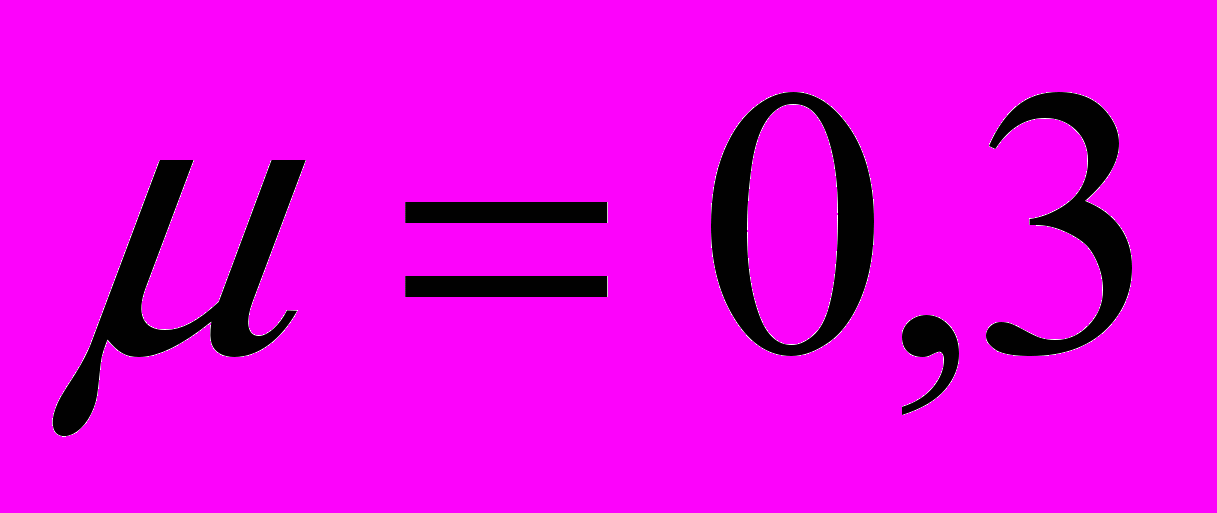 
. Коэффициент трения между колесом и рельсом fmp=0,17. К верхней горизонтальной грани фрагмента колеса в расчётной схеме прикладывалась равномерно распределенная вертикальная нагрузка. Расчёты выполнены для трёх вариантов нагрузок, которые могут возникнуть при эксплуатации вагона (125, 220 и 300 кН).Для решения задачи в упругопластической постановке использовались полигональные аппроксимации диаграмм деформирования образцов из бандажной и рельсовой стали, полученные автором. Для рельсовой стали полигональная аппроксимация действительной диаграммы растяжения в относительных координатах имеет вид (1а), а для бандажной стали - (1б).
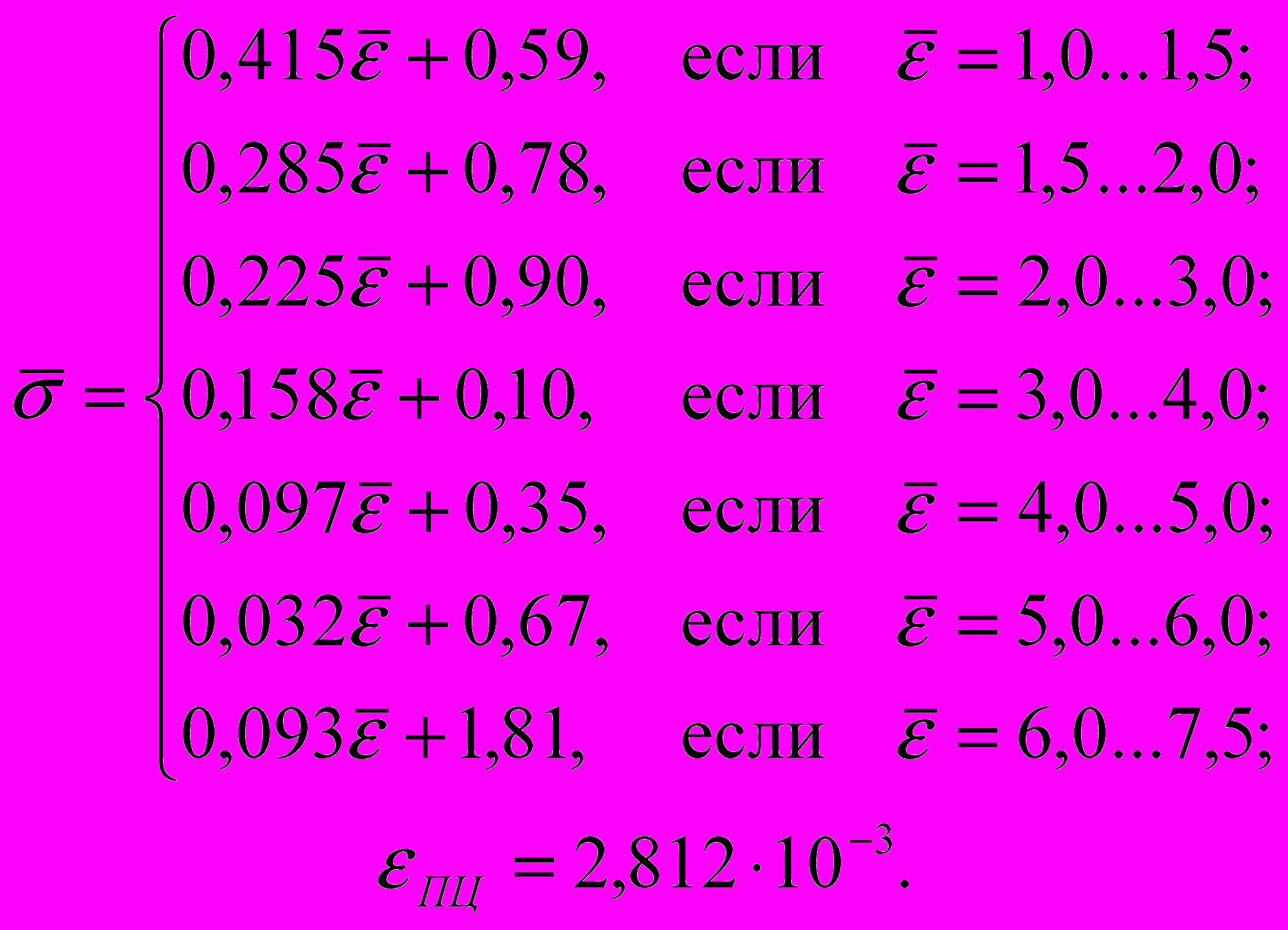(1а)
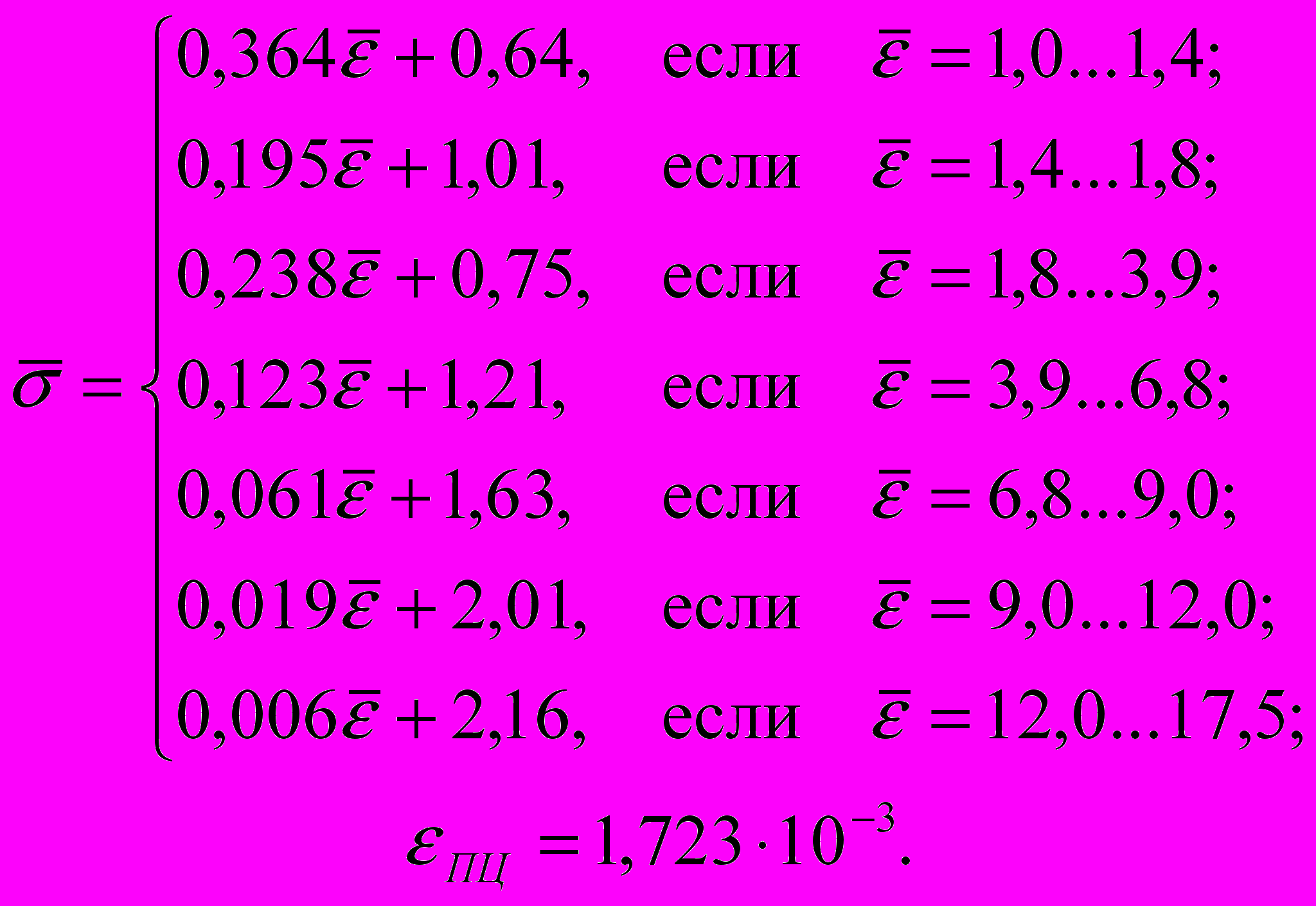(1б)Здесь
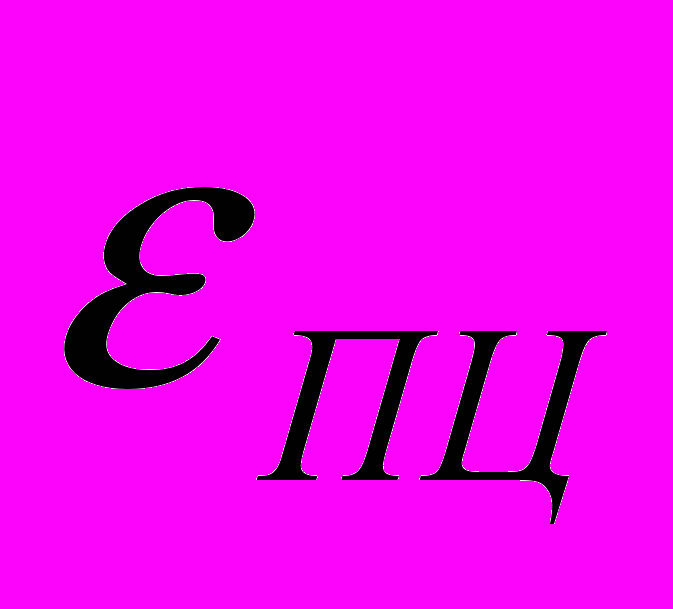- деформация, при которой нарушается прямая пропорциональность между напряжениями (
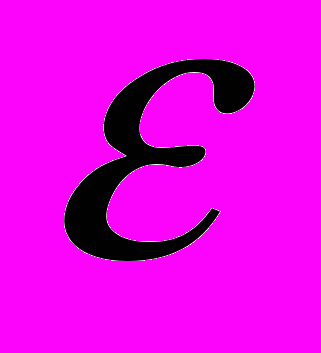) и деформациями (
); 
и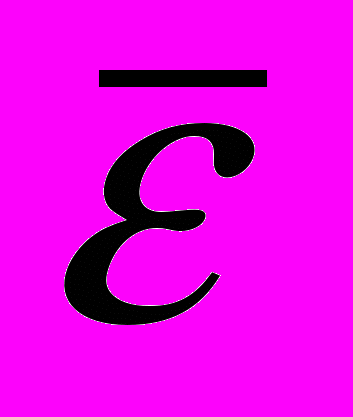 
вычисляются по следующим зависимостям: 
, 
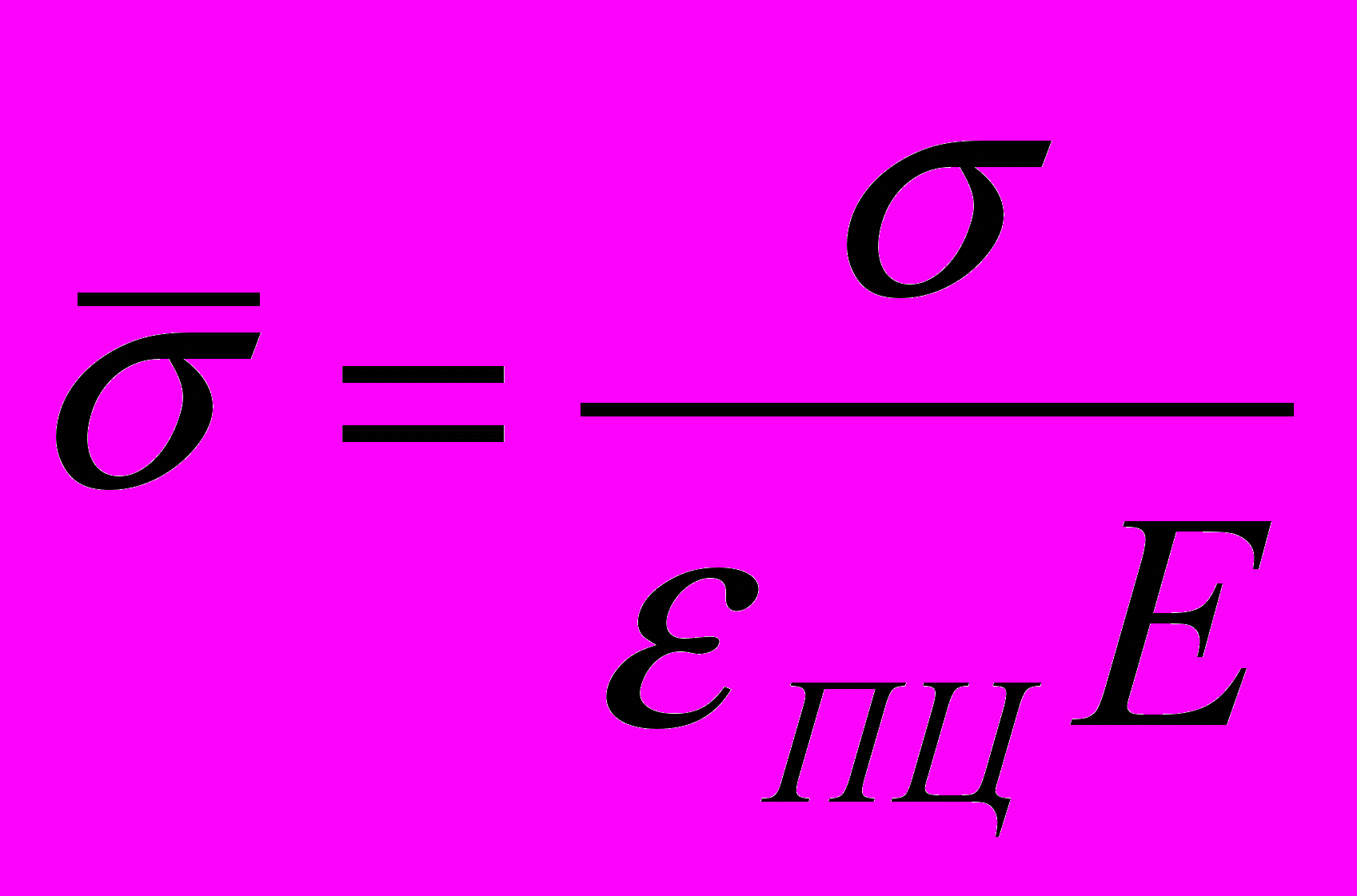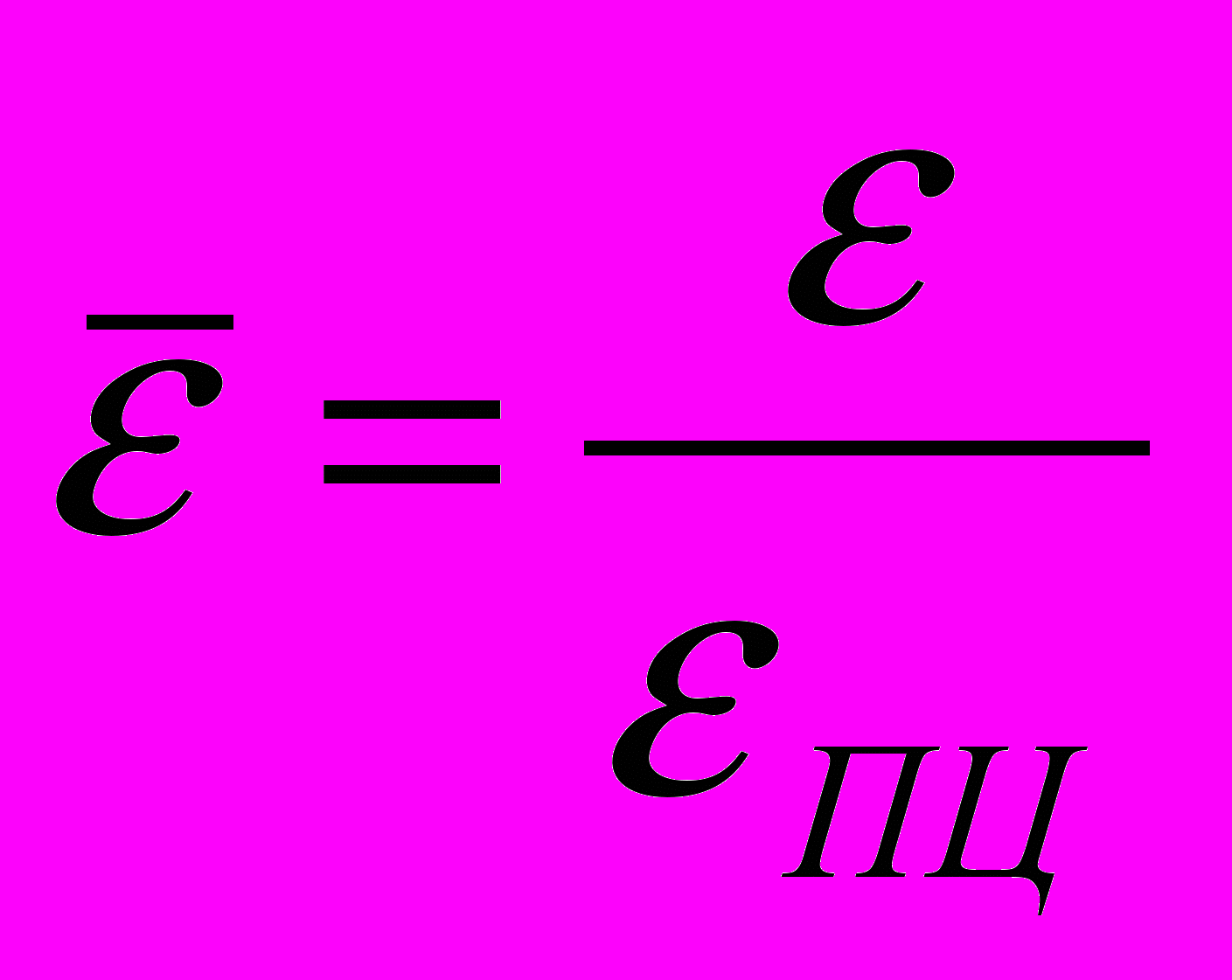.На рис. 2а показана форма эпюры распределения контактных давлений при нагрузке 220 кН (решение выполнено в упругой постановке). Максимальное контактное давление составило 1287,21 МПа. Максимальная интенсивность напряжений в рельсе равна 796,12 МПа, а в колесе - 863,2 МПа. При этом отношение максимальной интенсивности деформаций
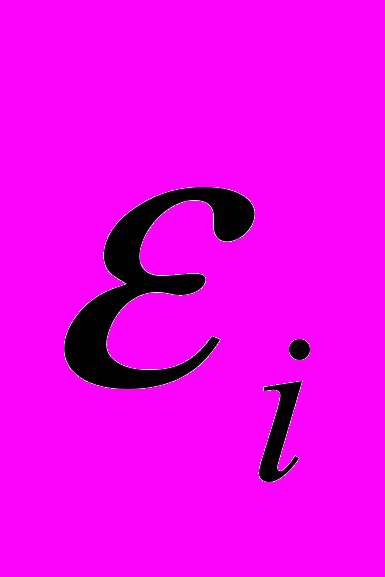к деформации начала текучести 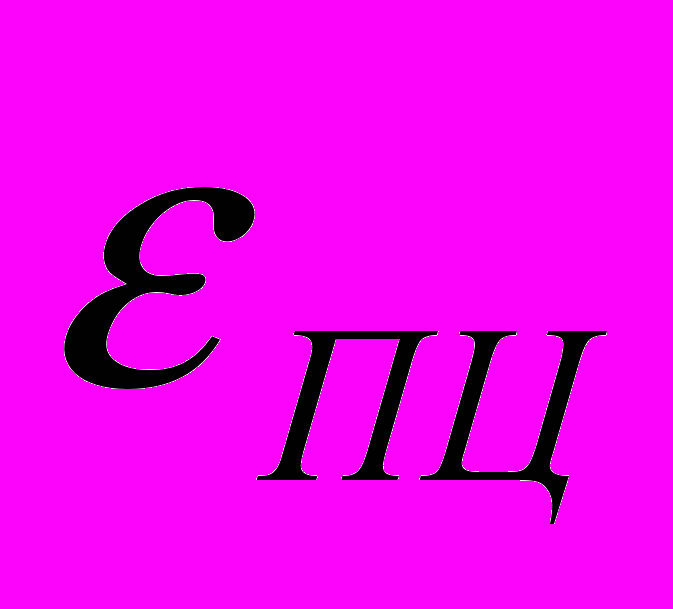для рельса равно 1,23, а для колеса - 2,17.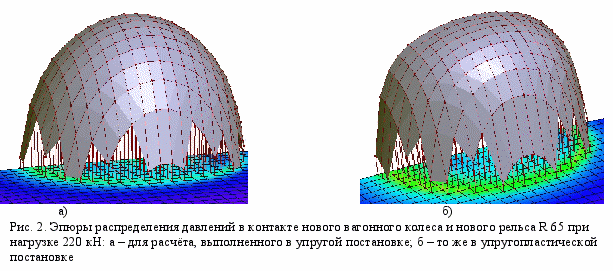
Максимальное контактное давление при расчете с учётом упругопластических деформаций меньше, оно составило 1013,13 МПа. Изменилась и форма эпюры распределения контактных давлений. Если при упругом решении она имела форму эллипсоида, то теперь эпюра приняла вид, представленный на рис. 2б.
Учёт упругопластических деформаций сказался на размере пятна контакта. Пятно контакта увеличилось как в направлении оси Х, так и в направлении оси Z (на 2 мм в каждом направлении). На рис. 3 приведены эпюры распределения контактных давлений для различных вариантов внешней нагрузки. На этих графиках видно, что чем больше нагрузка, тем больший эффект приносит учёт упругопластических деформаций в расчёте.
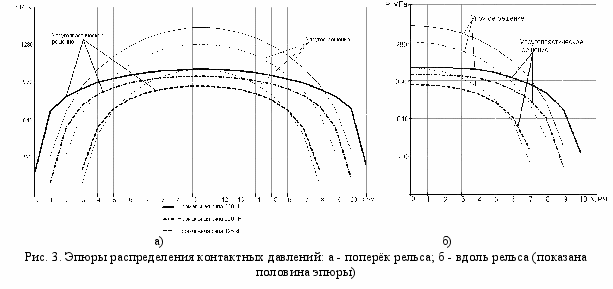
Упругопластический расчёт уточнил распределения напряжений и деформаций в области контакта. Максимальные напряжения и деформации, как и при упругом расчёте, залегают на некоторой глубине от поверхности контакта, но их величина уменьшилась. Максимальная интенсивность напряжений в рельсе теперь равна 666,28 МПа, а в колесе - 509,178 МПа. Отношение максимальной интенсивности деформаций
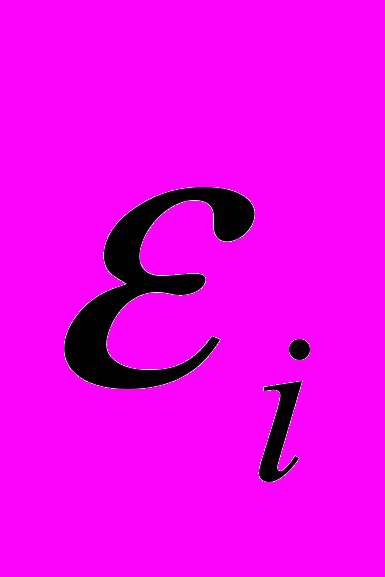к деформации начала текучести 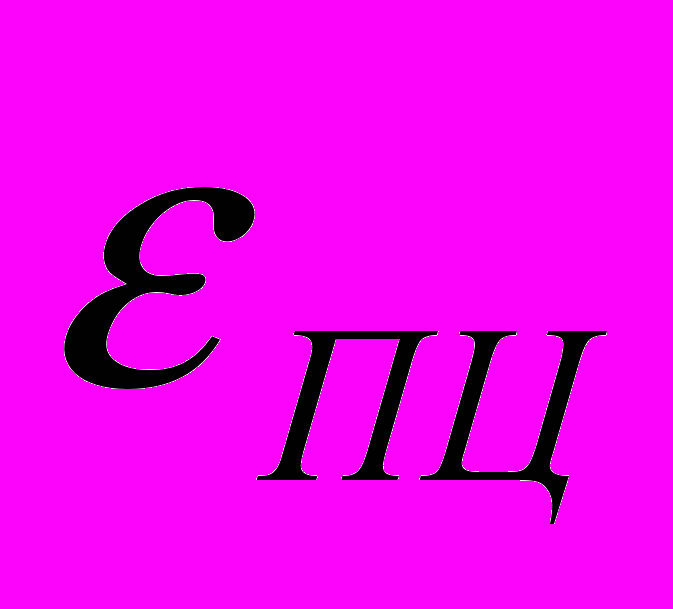для рельса равно 1,28, а для колеса - 2,96.Основные результаты решений этой задачи для разных нагрузок сопоставлены в табл. 1.
Таблица 1
Основные результаты решений задачи о контакте нового вагонного колеса и нового рельса R 65 для различных вариантов нагрузки
| Нагрузка, кН | Тип решения | P, МПа | Колесо | Рельс | ||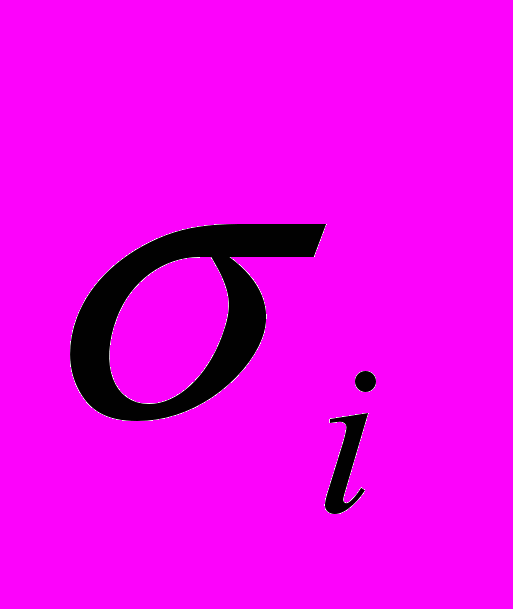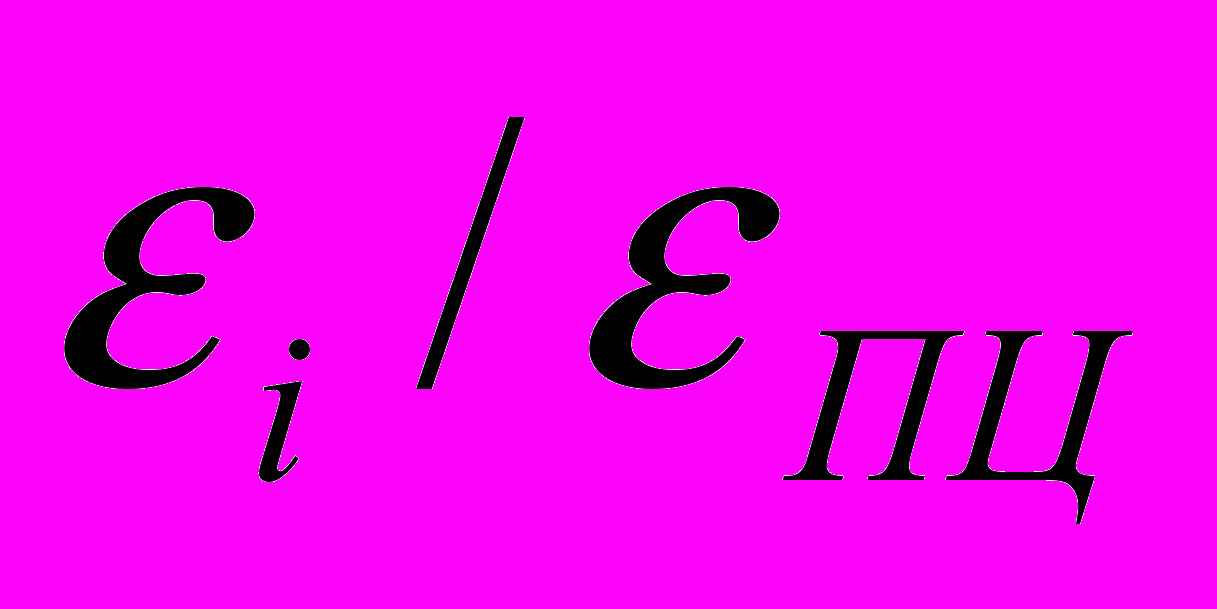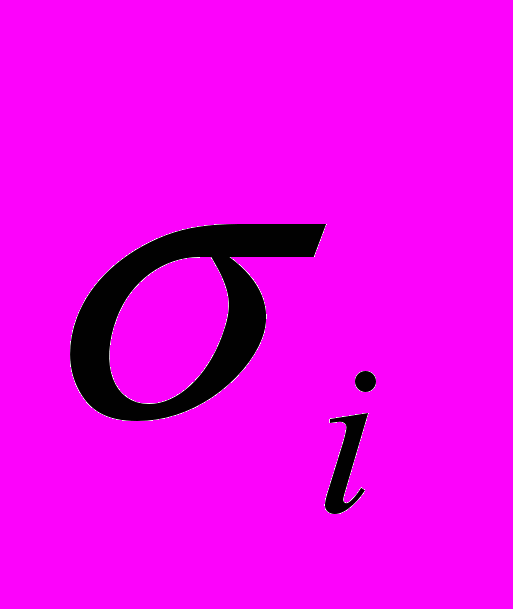
 , МПа |  | , МПа | | |||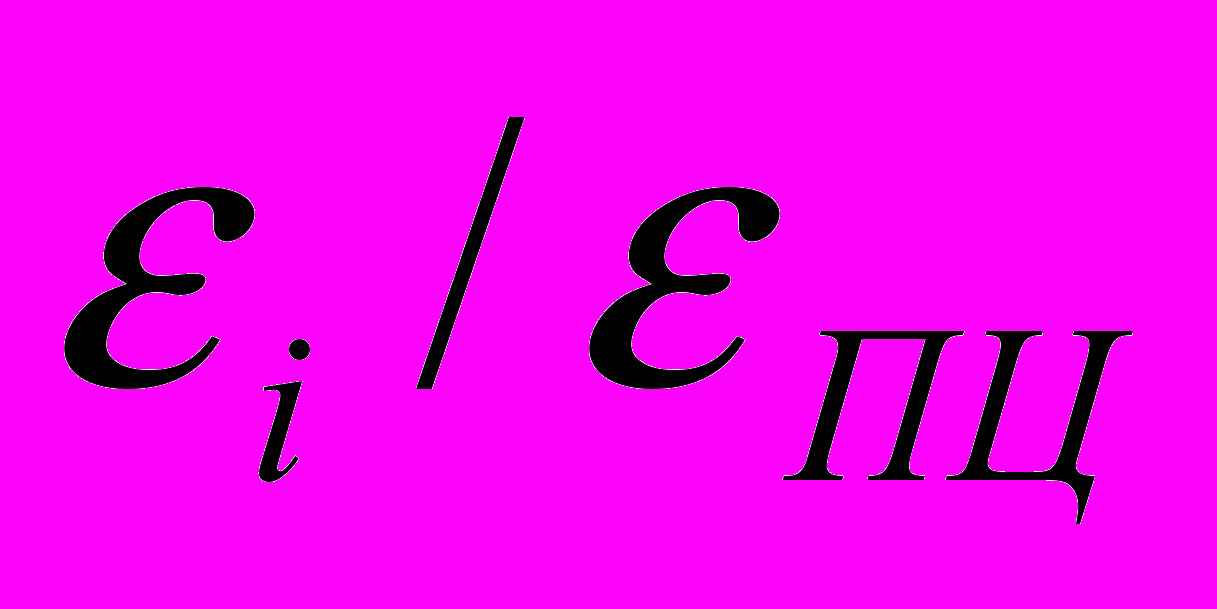
| 125 | Упругое | 1067,80 | 697,89 | 1,76 | 659,94 | 1,02 |
| Упругопластическое | 927,29 | 463,82 | 2,35 | 595,48 | 0,98 | |
| 220 | Упругое | 1287,21 | 863,20 | 2,17 | 796,12 | 1,23 |
| Упругопластическое | 1013,13 | 509,18 | 2,96 | 666,28 | 1,28 | |
| 300 | Упругое | 1426,68 | 969,88 | 2,44 | 878,82 | 1,35 |
| Упругопластическое | 1071,87 | 555,11 | 3,44 | 703,70 | 1,47 | |
У
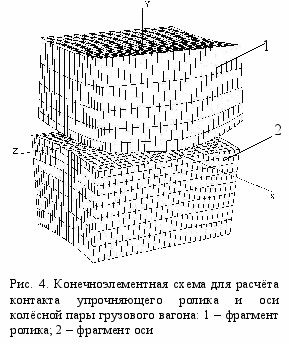пругопластический контакт упрочняющего ролика и оси грузового вагона. Для исследования напряжённо-деформирован-ного состояния в контакте упрочняющего ролика и оси вагона использовалась менее представительная расчётная модель (рис. 4). Моделировалось взаимодействие ролика диметром 
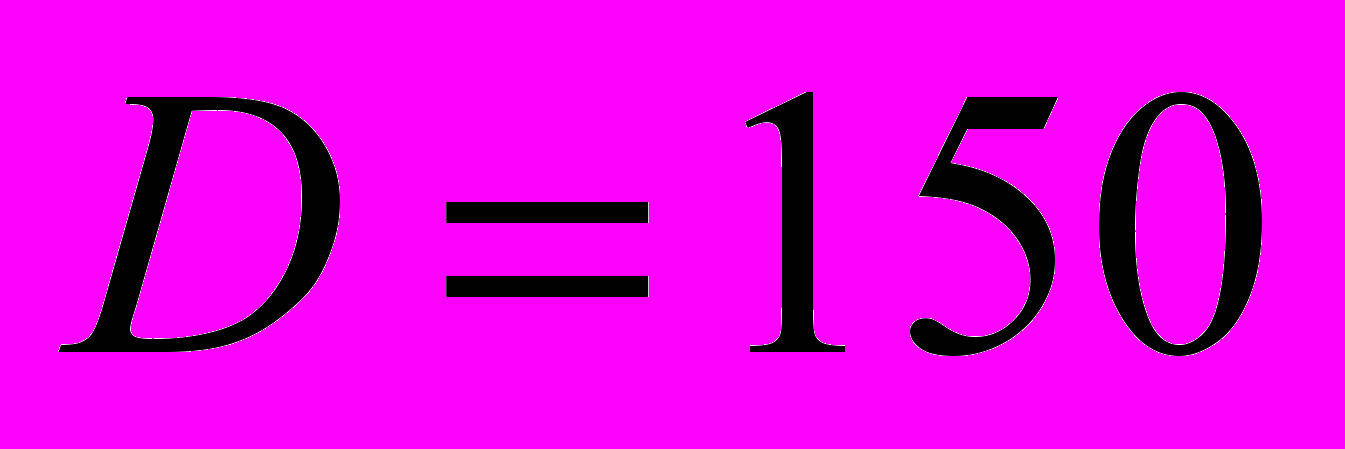мм и профильным радиусом 
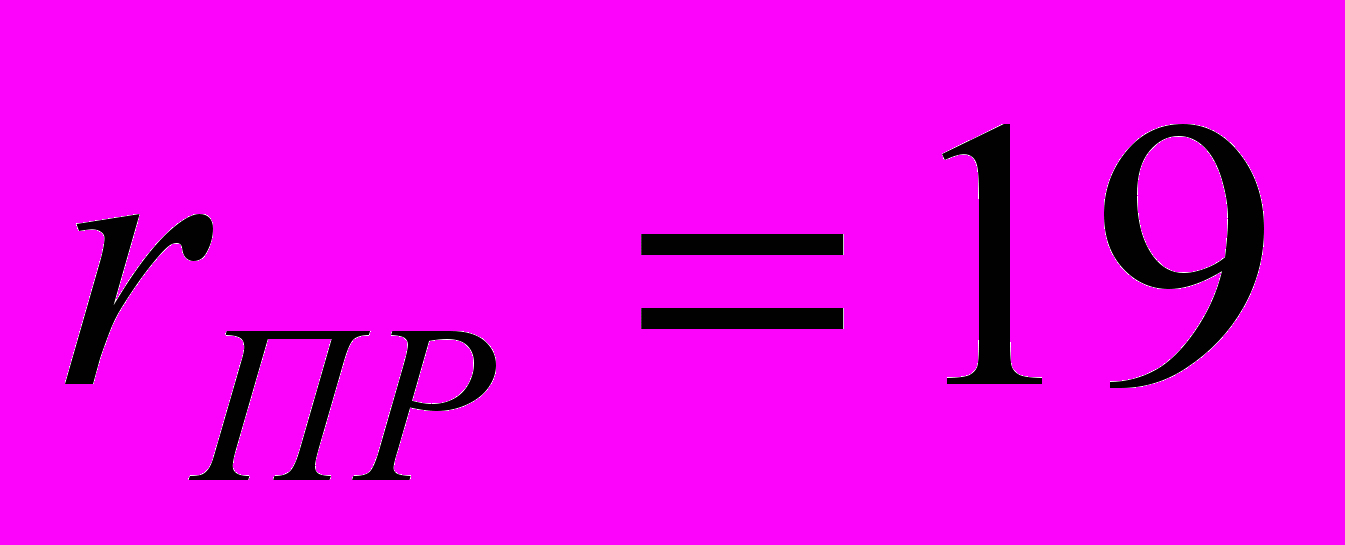мм с цилиндрическим участком (шейкой) оси РУ1Ш – 950 (ГОСТ 4835-80) грузового вагона. Диаметр рассматриваемого цилиндрического участка оси - 130 мм.Размер конечноэлементной схемы в направлении оси X - 16,8 мм, в направлении оси Y - 22,2 мм, в направлении оси Z - 16,8 мм. Модуль упругости и коэффициент Пуассона для ролика и оси приняты одинаковыми:
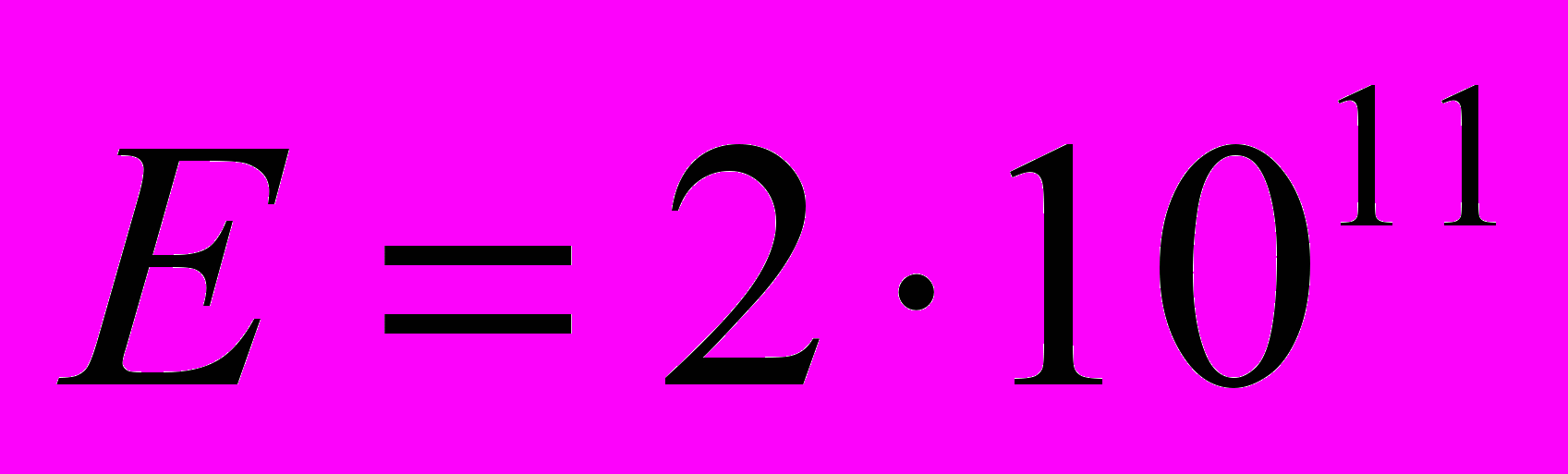Па, 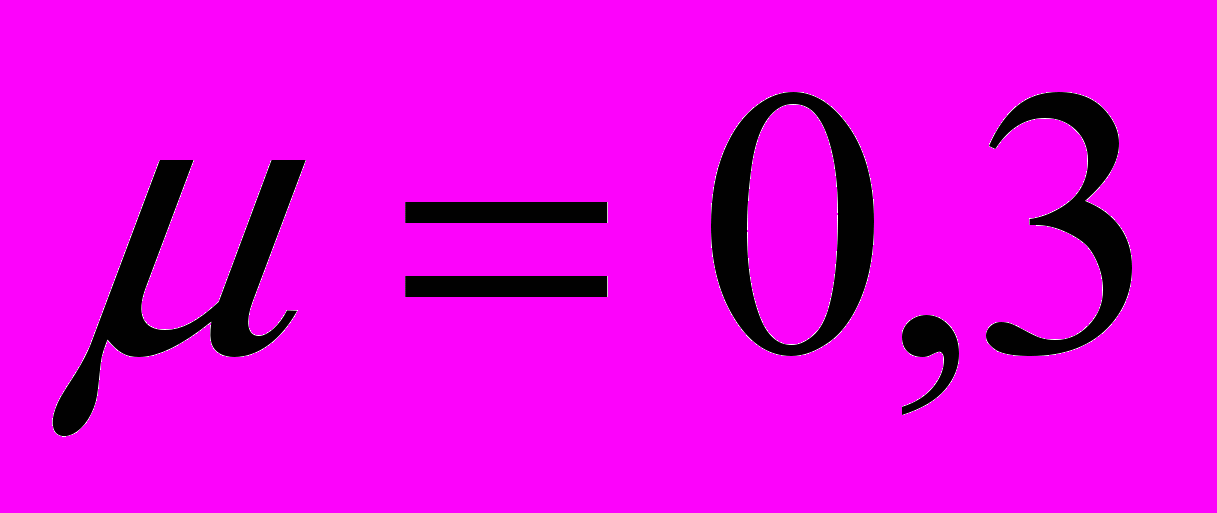. Так как поверхность оси при накатке роликами обильно смачивается машинным маслом, то коэффициент трения между роликом и осью принимался равным 0. К верхней грани фрагмента ролика в расчётной схеме прикладывалась равномерно распределенная вертикальная нагрузка. Расчёты выполнены для трёх вариантов нагрузок: 14,72 кН (1,5 т), 19,62 кН (2 т) и 24,53 кН (2,5 т).Для решения задачи в упругопластической постановке использовалась полигональная аппроксимация действительной диаграммы растяжения:
Здесь
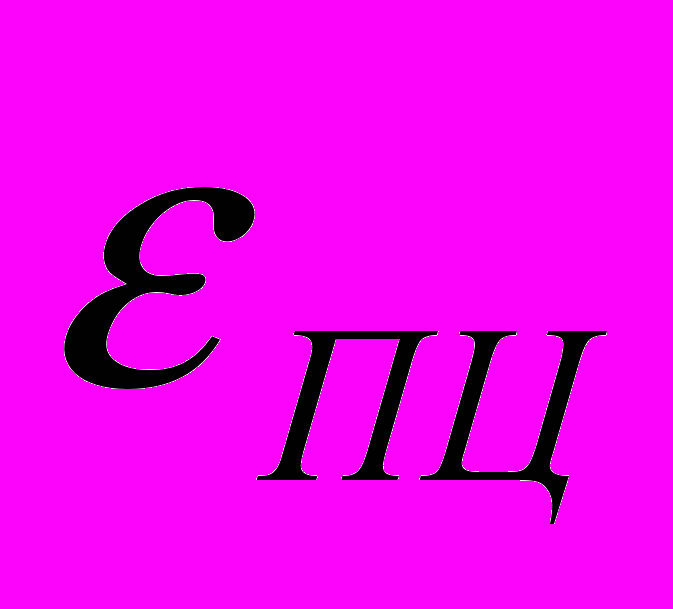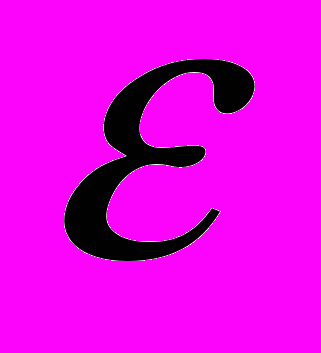- деформация, при которой нарушается прямая пропорциональность между напряжениями () и деформациями ();
и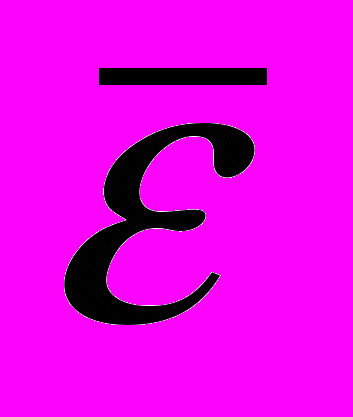 
вычисляются по следующим зависимостям: 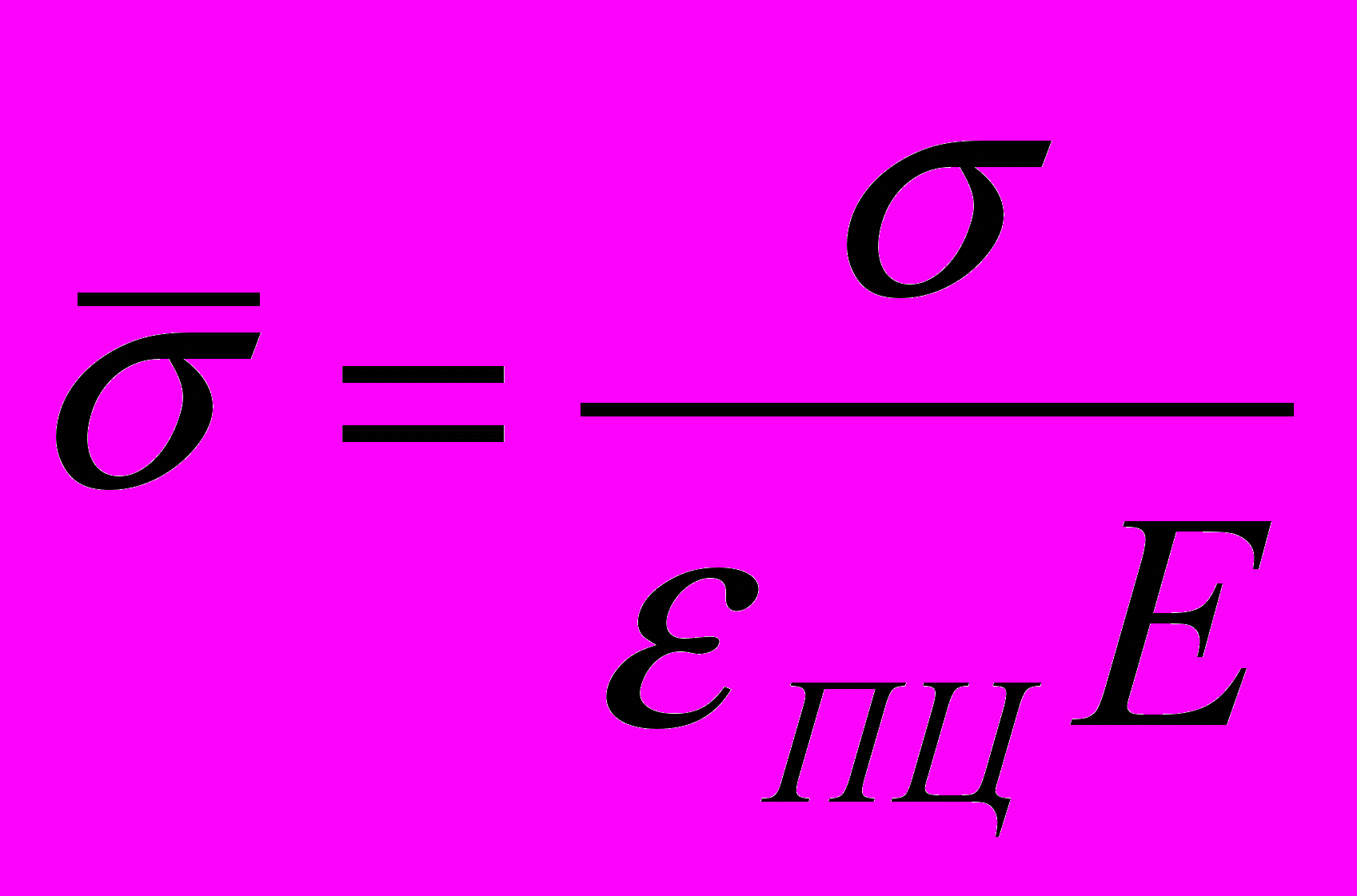, 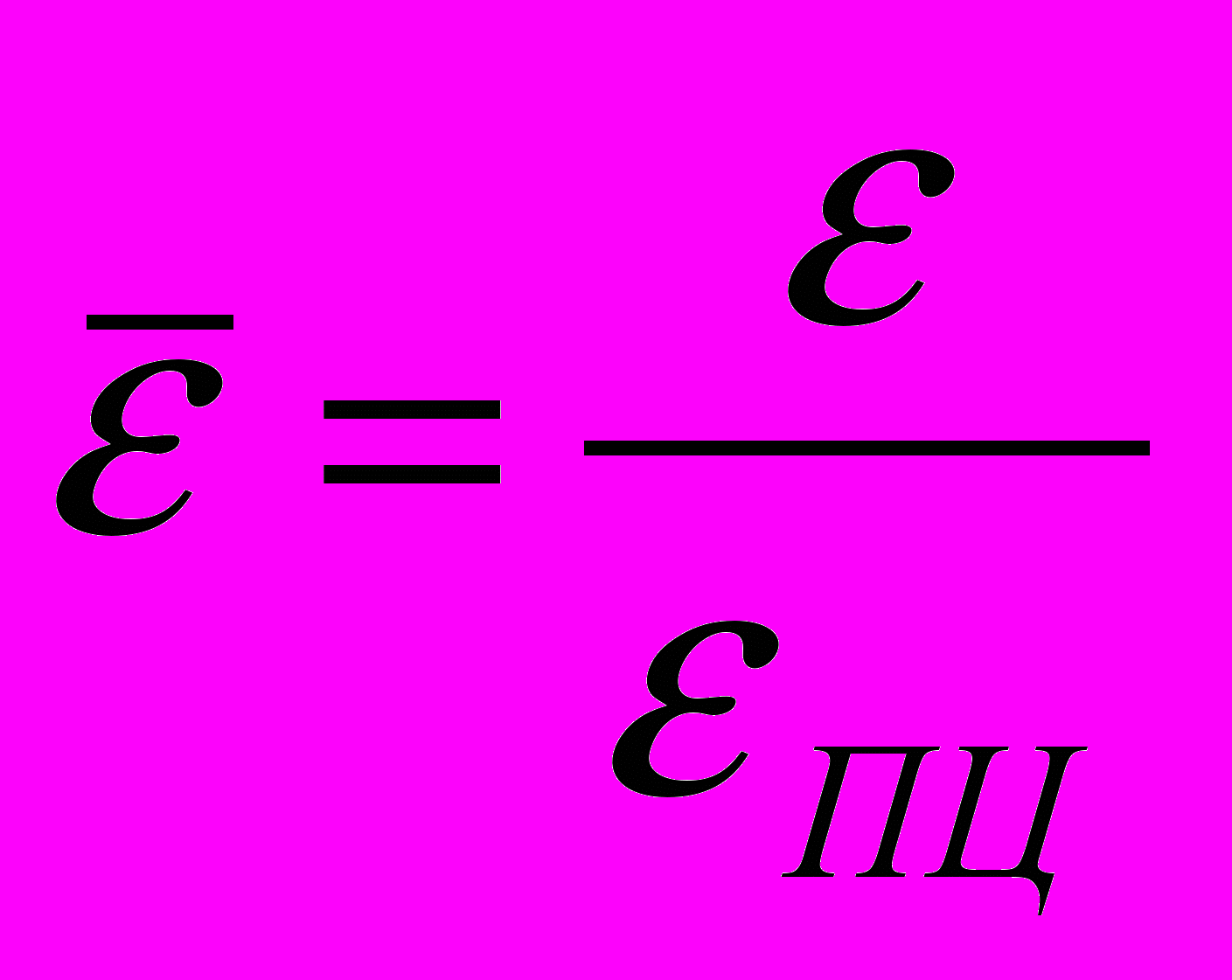.Диаграмма получена на образце, вырезанном из оси, забракованной на заводе-изготовителе по геометрическим параметрам. Ролики для накатки обычно выполняют из стали ШХ-15, которая после соответствующей термообработки имеет предел текучести порядка
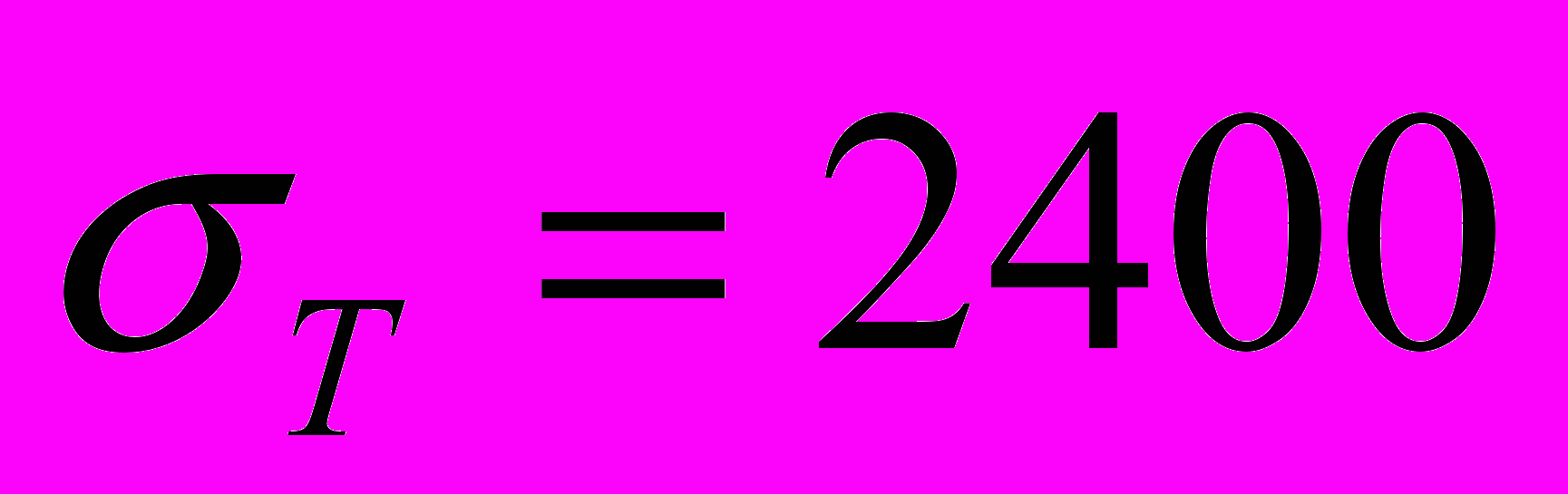МПа. Поэтому ролик представлен в расчётной схеме как упругое тело.Решение контактной задачи взаимодействия ролика и оси демонстрирует ещё большие различия между результатами, получаемыми в упругой и упругопластической постановках. На рис. 5а приведены эпюры распределения контактных давлений вдоль оси Х, а на рис. 5б - вдоль оси Z.
Максимальные контактные давления, вычисленные в упругой и упругопластической постановках, отличаются примерно в 2 раза. Так, при нагрузке на ролик 24,53 кН (2,5 т) максимальное контактное давление в упругом расчёте составляет 4167,96 МПа, а в упругопластическом - 2152,85 МПа. Значительные расхождения можно наблюдать и при рассмотрении напряжённо-деформированного состояния шейки оси (табл. 2).
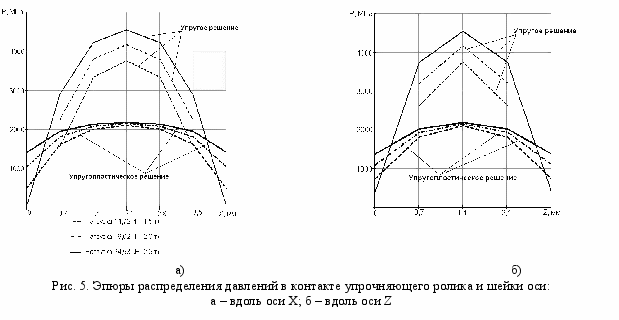
Таблица 2
Основные результаты решений задачи о контакте упрочняющего ролика и шейки оси грузового вагона для различных вариантов нагрузки
| Нагрузка, кН | Тип решения | P, МПа | Ось | Ролик | ||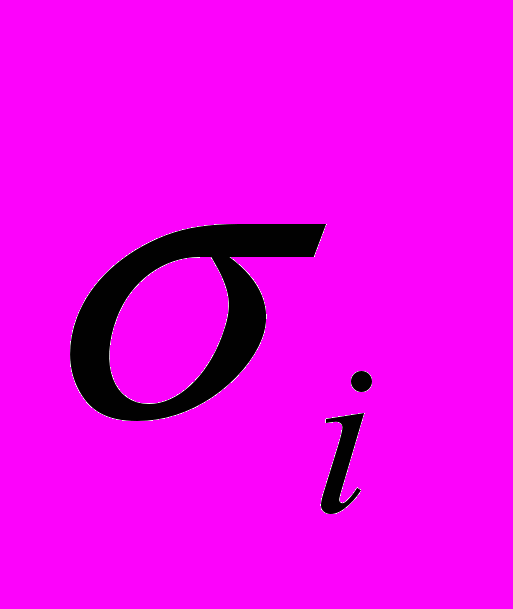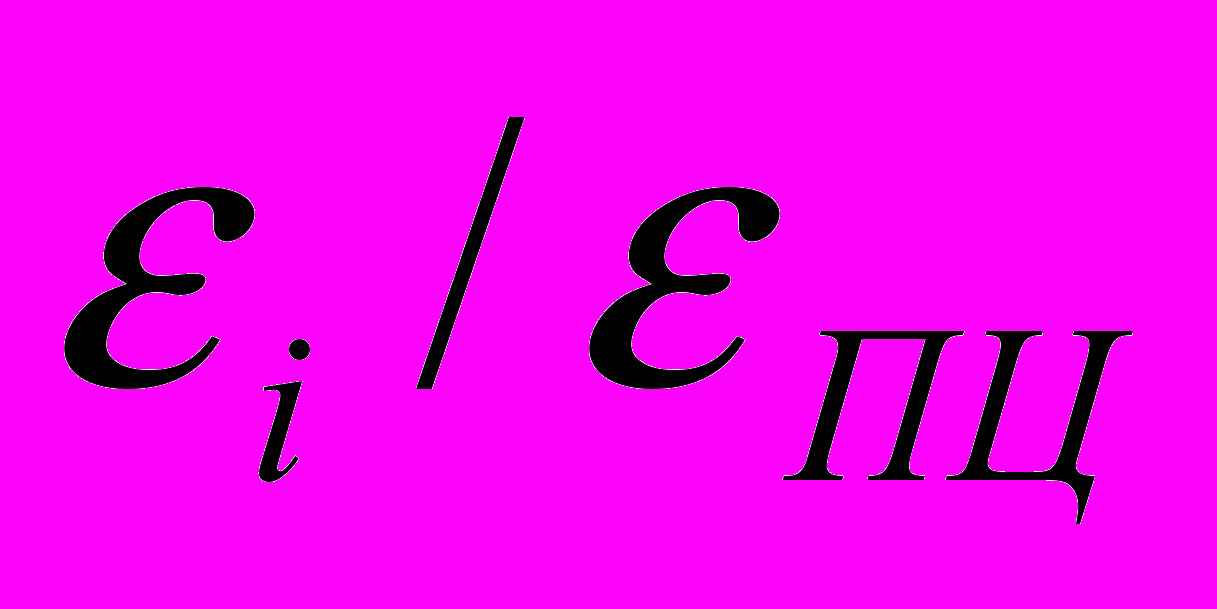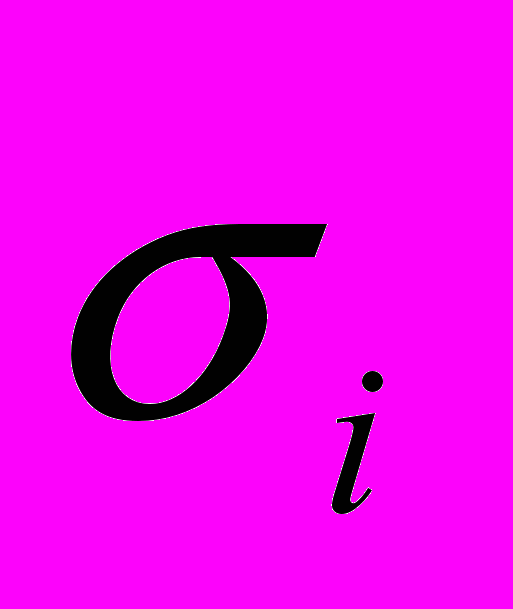
 , МПа | |  , МПа | | |||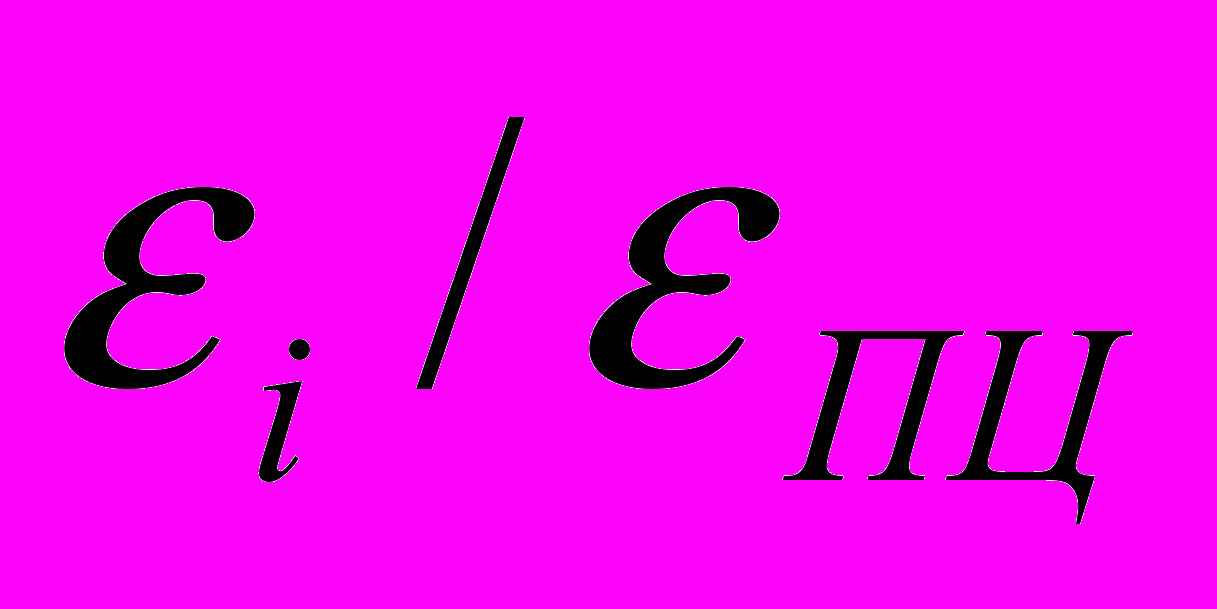
| 14,72 | Упругое | 3750,27 | 1905,20 | 5,40 | 1541,00 | 0,56 |
| Упругопластическое | 2101,64 | 644,07 | 12,24 | 1001,32 | 0,36 | |
| 19,62 | Упругое | 4167,96 | 2185,30 | 6,16 | 1808,60 | 0,65 |
| Упругопластическое | 2152,85 | 661,36 | 12,31 | 1070,54 | 0,39 | |
| 24,53 | Упругое | 4546,34 | 2432,60 | 6,85 | 2052,00 | 0,74 |
| Упругопластическое | 2185,47 | 673,95 | 17,30 | 1112,38 | 0,41 | |
Упругопластический расчёт распределений полей напряжений и давлений существенно уточнил результаты, полученные ранее в упругой постановке.
Возможно применение изложенной методики для моделирования процесса качения, анализа остаточных напряжений, возникающих в подповерхностном слое деталей. Решение контакной задачи качения даст возможность численными методами исследовать и оптимизировать технологии упрочнения деталей поверхностным пластическим деформированием, разрабатывать более экономичные конструкции железнодорожных колёс и рельсов.
СПИСОК ЛИТЕРАТУРЫ
- Малинин, Н.Н. Прикладная теория пластичности и ползучести: учеб. для студентов вузов / Н.Н. Малинин. - М.: Машиностроение, 1975. – 400 с.
- Мавлютов, Р.Р. Концентрация напряжений в элементах авиационных конструкций / Р.Р. Мавлютов. - М.: Наука, 1981. - 141 с.
- Сакало, В.И. Контактные задачи железнодорожного транспорта / В.И. Сакало, В.С. Коссов. - М.: Машиностроение, 2004. – 496 с.
- Zienkiewicz, O.C. The Finite Element Method. Fifth Edition. V. 2. Solid Mechanics / O.C. Zienkiewicz, R.L. Taylor. - Butterworth-Heinemann, 2000. - 459 p.
- Томашевский, С.Б. Создание трёхмерной конечноэлементной модели процесса упрочнения деталей машин поверхностным пластическим деформированием / С.Б. Томашевский// Вестн. БГТУ. – 2011. – №2. – С.55-61.
Материал поступил в редколлегию 11.03.11.