Методическое пособие для учащихся 9-11 классов средних общеобразовательных школ программирование на языке pascal

Вид материала

Содержание

Компьютерная графика
Краткие теоретические сведения.
Точка. Для выдачи точки на экран используется вызов процедуры PutPixel (x, у, номер_цвета)
Построение графика функции.
Задание цвета.
SetColor (цвет)
LineRel (dx, dy)
MoveRel (dx, dy)
Построение столбчатой диаграммы.
OutTextXY (х, у, ‘текст’)
Arc (х, у, начальный_угол, конечный_угол, радиус)
Вопросы к защите лабораторной работы

Подобный материал:

1 ... 6 7 8 9 10 11 12 13 14

КОМПЬЮТЕРНАЯ ГРАФИКА

Цель работы: приобрести навыки использования графического режима, закрепить знание графических операторов, научиться строить графики и диаграммы.

Краткие теоретические сведения.

Для построения изображения на экране дисплея используется специальная библиотека подпрограмм, называемая Graph. В нее входят графические процедуры и функции для выдачи различных по форме фигур и линий, а также средства организации графического режима. Эти средства предназначены для анализа возможностей используемого дисплея — разбиения поля экрана на различное число мелких квадратиков, каждый из которых считается отдельной точкой изображения и называется пикселем. Для дисплея типа VGA число точек может быть 640 * 480, а количество используемых цветов — 16. Однако более сложные, не рассматриваемые здесь средства Паскаля позволяют увеличить количество цветов до 256. Цвет, как и координаты экранной точки, задается целым числом. Начало координат экрана находится в левом верхнем углу (точка 0,0), ось Ох направлена вправо, Оу — вниз (рис.9).

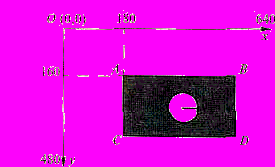
Рис. 9. Система координат экрана дисплея

Эту особенность направленности оси Оу следует учитывать при построении изображений, особенно графиков функций и диаграмм. Для построенной

Рис. 10.

Установление соответствия между точками отрезка [а, b] и осью Ох экрана дисплея

на рисунке 9 окружности необходимо отмечать координаты центра и радиус, для прямоугольника — координаты противоположных вершин (например, А и D). Координаты точки А (180, 160) заданы на рисунке. Каждое изображение можно также построить по точкам, указав для каждой точки ее координаты и цвет.

При построении изображений используются так называемые графические примитивы — базовые конструкции и их модификации. К графическим примитивам относятся: точка, отрезок, дуга.

Точка. Для выдачи точки на экран используется вызов процедуры

PutPixel (x, у, номер_цвета); где x, у — координаты точки.

С помощью этого оператора можно построить график функции.

Построение графика функции. Чтобы построить график, необходимо сначала задать отрезок области определения, на котором функция существует, и отобразить этот отрезок на ось Ох экрана дисплея. Точке х отрезка [а, b] из области определения функции должна соответствовать точка х экрана дисплея, а точке у = f(x) — значению функции — точка у1 экрана (рис. 10). Таким образом происходит масштабирование графика, что дает возможность отображать на экран любой отрезок области определения. Здесь, безусловно, надо учитывать разрешающую возможность экрана, чтобы масштаб позволил увидеть качественное поведение функции. Точки на экране, в отличие от точек геометрической прямой, имеют дискретные значения. Точки оси Ох нумеруются от 0 до 640, т. е. х1 = 0, 1,2,3, ...,640.

Из пропорции (х — а) / (b — а) = (х1 — 0) / (640 — 0) получим расчетную формулу вычисления аргумента функции, соответствующего заданной точке экрана: х = а + х1 * (b - а) / xmax

где хтax = 640, если дисплей типа VGA. Для найденного значения аргумента вычисляется значение функции: y=f(x)

Теперь необходимо умножить полученное значение функции на коэффициент масштабирования, показывающий, сколько пикселов (физических точек экрана) содержится в выбранной единице масштаба: k = xmax / (b - а)

Получаем значение у — координату для выдачи рассчитанной точки графика функции на экран: у1 = у * xmax / (b - а)

Теперь следует учесть особенность расположения оси Оу на экране и перевернуть график, предполагающий традиционное положение осей координат, а так- же добавить смещение, чтобы график располагался по центру экрана:

у1 = уmax / 2 - у1

С координатами х1 и у1 точка выводится на экран. Поскольку реальные координаты графика функции, по которым она вычисляется, вещественные числа, а координаты точек экрана — целые, то результат, полученный при использовании в программе формулы для вычисления у1, необходимо округлить до ближайшего целого числа. Округление производит функция trunc. аргумент которой — выражение вещественного типа: у1: = trunc (у * xmax / (b - а)).

Программа построения графических изображений должна начинаться с оператора подключения библиотеки графических процедур и специальной библиотеки, позволяющей использовать функции операционной системы (библиотеки Crt). Этот оператор располагается сразу за заголовком программы и имеет вид: uses Graph, Crt;

Сама программа состоит из описаний процедур построения изображений, описания функции, для которой строится график, и описания специальной процедуры установки графического режима. Главная программа при этом содержит операторы вызова этих процедур и оператор задержки изображения на экране (после построения последней точки изображение исчезает):

repeat until keypressed; {выполнять пустой цикл до нажатия любой клавиши}

Программа построения графика функции у = sin (х) на отрезке [—, ]:

program Р33;

uses Graph, Crt;

procedure Init; {установка графического режима}

var gr, gm: Integer;

begin

gr: = 0; {автоматическое распознавание типа дисплея}

InitGraph (gr, gm, ‘ ‘); {файл egavga.bgi находится в одном каталоге с turbo.ехе}

if GraphResult <> grOk then Halt (1); {обработка результата установки}

end;

function f (х: real): real; {вычисление функции f (х)}

begin

f: = sin (х)

end;

procedure grafic;

var xmax, ymax, х1, у1: integer; х, y, a, Ь: real;

begin

xmax: = 640; ymax: = 480; a: = - 3.14; b: = 3.14;

for х1: = 0 to xmax do

begin

х: = a + х1 * (b - a) / xmax;

y: = f (х); {вызов подпрограммы-функции}

у1: = trunc (y * xmax / (b - a));

у1: = ymax div 2 - у1;

PutPixel (х1, у1, 2); {выдача точки зеленым цветом}

end

end;

begin {главная программа}

Init; {вызов процедуры установки графического режима}

Grafic; {вызов процедуры построения графика функции}

repeat until keypressed

end.

				0	15	0	15
				15	0	15	0
				15	15	15	0

Рис. 11.

При построении сложных рисунков, выдаваемых по точкам, можно использовать прием мозаики: нарисовать рисунок по клеточкам и заполнить таблицу целых чисел, при этом каждое число соответствует номеру цвета определенной клеточки, а координаты клеточки соответствуют индексам элементов таблицы (рис. 11).

Задание цвета. Некоторые графические операторы, такие, как построение точки, включают в себя параметр цвета, но во многих других используется текущий цвет, определенный последним оператором задания цвета:

SetColor (цвет);

На рисунке 12 приведена таблица цветов, где каждый цвет может быть задан как номером, так и словом (на английском).

Отрезок. Для построения отрезка необходимо указать координаты его концов. Отрезок строится текущим цветом. Оператор построения отрезка:

Line(x1,y1,x2,y2);

При построении изображения компьютер как бы рисует лучом. Луч останавливается в последней точке изображения, координаты которой

черный	синий	зеленый	Бирюзовый
0	1	2	3
красный	малиновый	коричневый	серый-с
4	5	6	7
серый-т	голубой	зеленый-с	Бирюзовый-с
8	9	10	11
красный-с	малиновый-с	желтый	Белый
12	13	14	15

Рис. 12. Номера цветов (с-- светлый, т — темный)

запоминаются. Можно построить отрезок, указав либо смещение от этой точки по осям х и у, либо координаты конца отрезка (начало там, где остановился луч). Смещение задается в виде целого числа, причем положительное означает увеличение последней координаты на величину смещения, отрицательное — соответственное уменьшение координаты. Смещение удобно использовать для построения изображения в относительных координатах, когда достаточно указать координаты первой точки, а остальные будут пересчитаны. Таким образом можно перемещать картинку по экрану.

Оператор построения отрезка с указанием смещения: LineRel (dx, dy);

Оператор построения отрезка с указанием последней его точки: LineTo (x, у);

П

оследний оператор удобен для построения графика функции, которая либо резко возрастает, либо резко убывает. В этом случае изображение, построенное по точкам, терпит разрыв, так как для двух соседних аргументов два значения функции находятся далеко друг от друга. Первую точку графика надо выдать оператором Put Pixel, а остальные, вычисляемые и строящиеся в цикле, — оператором LineTo.

Луч, строящий изображения, может перемещаться без следа. Это позволяют делать операторы, аналогичные двум последним:

MoveRel (dx, dy);

MoveTo (x, у);

Прямоугольник строится подобно отрезку: необходимо указать координаты концов любой диагонали. Прямоугольник может быть построен в виде контура или в виде закрашенной фигуры. Для контурного изображения - оператор Rectangle (x1, у1, х2, у2); для закрашенного Ваг(х1,у1,х2,у2);

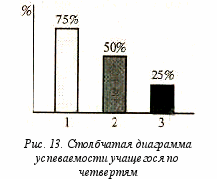
Построение столбчатой диаграммы. На рисунке 13 представлена столбчатая (линейная) диаграмма падения успеваемости некоторого учащегося по четвертям учебного года. В первой четверти успеваемость составила 75%, во второй — 50%, в третьей — 25%. Построим такую диаграмму с помощью программы, расположив самый высокий столбец в центральной части экрана

(его длина — 480 : 3 = 160 пикселов) и рассчитав остальные пропорционально их значениям относительно этого размера. По ширине вся диаграмма занимает также 1/3 часть, т. е. первоначальное значение координаты х равно 210 пикселов, ширина столбцов по 35 и расстояние между ними также 35 пикселов. Для расчета высоты второго столбца составим пропорцию 75 : 50 = 160 : х. Отсюда х = 106 (с округлением до целого). Высота третьего столбца 53 пик-

села. Поскольку нижние основания прямоугольников находятся на одно! уровне, для которого у = 320, расчет вторых координат (п оси у) производится вычитанием из 320 высоты соответствующего столбца.

Размещение текста на изображении производится с по мощью оператора:

OutTextXY (х, у, ‘текст’);

где х, у — координаты, начиная с которых будет выдан текст.

Программа построения столбчатой диаграммы имеет такую же структуру, как и программа РЗЗ.

program Р34;

uses Graph, Crt;

procedure Init; {установка графического режима}

var gr, gm: integer;

begin

gr: = 0; {автоматическое распознавание типа дисплея}

InitGraph (gr, gm, ‘ ‘); {файл egavga.bgi находится в одном каталоге с turbo.ехе}

if GraphResult <> grOk then Halt(1); {обработка результата установки} end;

procedure Diagram 1;

var х, у, х1, y1, x2, y2: integer;

begin

SetColor (14); Bar (210,160, 245, 320);

SetColor (10); Bar (210 + 2*35, 320 -106, 210 + 3-35, 320);

SetColor (2); Bar (210 + 4*35, 320 - 53, 210 + 5-35, 320);

OutTextXY(210, 320 + 30, ‘Успеваемость по четвертям’);

end;

begin

Init;

Diagram 1; repeat until keypressed

end.

Построение дуги. Для построения дуги. необходимо указать центр соответствующей окружности (х и у), начальный и конечный углы дуги и радиус. Углы отсчитываются против часовой стрелки, их значение указывается в градусах (от 0 до 359). Отсчет угла производится от направленного вправо по горизонтали радиуса. Оператор построения дуги имеет вид:

Arc (х, у, начальный_угол, конечный_угол, радиус);

Для закрашенного сектора используется следующий оператор с такими же параметрами:

PieSlice (х, у, начальный_угол, конечный_угол, радиус);

Если указать значения углов соответственно 0 и 359, то получится окружность или закрашенный текущим цветом круг. Окружность можно также изобразить оператором:

Circle (х, у, г);

Рассмотрим пример построения «рога изобилия», состоящего из окружностей. Центры окружностей перемещаются по окружности, представляющей собой траекторию точки, одна координата которой задается косинусом, а другая — синусом одного и того же угла x1/k. При k = 20 получается замкнутый круг, k = 10 — два круга, k = 30 — полукруг.

program Р35;

uses Graph, Crt;

procedure Init; {установка графического режима}

var gr, gm: integer;

begin

gr: = 0; {автоматическое распознавание типа дисплея}

InitGraph (gr, gm, ‘ ‘); {файл egavga.bgi находится в одном каталоге с turbo.ехе}

if GraphResult <> grOk then Halt(1); {обработка результата установки} end;

procedure Rog;

var xmax, ymax, х1, y1, х, у, r: integer;

begin

xmax: = 640; ymax: = 480;

for x1: = 1 to 125 do

begin

x: = trunc (xmax / 2 + ymax / 2 * cos (x1/20));

y: = trunc (ymax / 2 + xmax / 4 * sin (x1/20));

r: = trunc (ymax / 4 - x1);

Circle (x, y, r)

end

end;

begin

Init; Rog; repeat until keypressed

end

Построение круговой диаграммы

Диаграммы такого типа представляют собой круги, разделенные н. секторы разной площади (рис. 14) Площадь каждого сектора соответствует некоторой части, как правило, в процентном отношении, а за единицу (целое) принимается площадь всего круга. Вместо площади сектора можно рассчитать длину дуги. Построим круговую диаграмму изменения успеваемости, соответствующую линейной диаграмме на рисунке 13.

Программа имеет вид:

program Р38;

uses Graph, Crt;

procedure Init; {установка графического режима}

var gr, gm: integer;

begin

gr: == 0; {автоматическое распознавание типа дисплея}

InitGraph (gr, gm, ‘ ‘); {файл egavga.bgi находится в одном каталоге с turbo.exe}

if GraphResult <> grOk then Halt(1); {обработка результата установки} end;

procedure Diagram2;

var xmax, ymax, x1, y1, x, y, r: integer;

begin

xmax: = 640; ymax: = 480;

x: = 320; у: = 240; r: = 200; {координаты центра и радиус диаграммы}

x1: = trunc (75 * 36 / 15); {расчет длины первой дуги}

SetColor (14); PieSlice (x, у, 0, x1, r);

y1: = trunc (50’36/ 15) +x1;

SetColor (10); PieSlice (x, у, x1+1, y1, r); {вторая дуга + + первая}

SetColor (2); PieSlice (x, y, y1 +1, 359, r); {замыкание круга}

end;

begin

Init;

Diagram2;

repeat until keypressed

end.

Методические указания по работе и задания

№	Условие задачи
1	Построить семейство разноцветных окружностей, радиусы которых увеличиваются.
2	Написать программу, которая выводит на экран оцифрованную координатную сетку.
3	Написать программу, которая выводит на экран изображение шахматной доски.
4	Написать программу, которая рисует окружность движущуюся по экрану.
5	Написать программу, которая выводит на экран изображение часов, имеющих секундную и минутную стрелки.
6	Написать программу, которая выводит на экран круговую диаграмму, отображающую товарооборот (в процентах) книжного магазина (книги, журналы, открытки и канцтовары) и поместив необходимый текст в диаграмму.
7	Постройте концентрические окружности, закрасив каждую новым цветом.
8	Используя идею детской игры «мозаика», построить изображение разноцветной бабочки, сохранив предварительно в виде таблицы целых чисел (значений цветов) и выдав затем эту таблицу по точкам на экран, применяя двойной цикл.
9	Написать программу, которая выводит на экран изображение работающего светофора. Рекомендуемый вид светофора и алгоритм его работы приведены ниже.
10	С помощью программы построения графика функции постройте графики logx, tgx, cosx на различных участках областей определения этих функций.
11	Построить график функции cos x и при построения графика функции добавьте выдачу на экран координатных осей и отметку на них единицы измерения.
12	Написать программу, которая выводит на экран точечный график функции y=0,5x²+4x-3. Диапазон изменения аргумента – от –15 до 5, шаг аргумента – 0,1. График вывести на фоне координатных осей, точка пересечения которых должна находится в центре экрана.
13	Постройте елочку из п треугольников, определив ее предварительно рекурсивно и использовав в программе рекурсивную графическую процедуру.
14	Написать программу, которая выводит на экран гистограмму успеваемости учеников класса, например по итогам контрольной работы. Дополнить изображение так, чтобы на изображении были все подписи.
15	Напишите программу построения изображения произвольного рисунка, используя для проекта бумагу в клеточку (по теме транспорт, по теме моя любимая игрушка…).

ВОПРОСЫ К ЗАЩИТЕ ЛАБОРАТОРНОЙ РАБОТЫ

1. Как расположены оси координат на экране дисплея?

2. Что такое графические примитивы?

3. Как закрасить один пиксел экрана?

4. Как отобразить отрезок [a,b] на всю ширину экрана?

5. Сколько пикселов будет содержать единица измерения на отображаемом на экране отрезке [а, b]?

6. Как расположить график на экране с учетом направленности оси Оу в противоположную от традиционного направления сторону?

7. Какого типа данные соответствуют экранным координатам?

8. В какой библиотеке Паскаля содержатся графические подпрограммы и как подключить эту библиотеку при выполнении программы?

9. Как задержать изображение на экране после полного его построения?

10. Как задать цвет для построения линий, прямоугольников и дуг?

11. Какой оператор позволяет построить отрезок, используя только одну пару координат?

12. Как переместить рисующий луч по экрану так, чтобы не было следа?

13. Как построить график функции, которая резко возрастает или убывает?

14. Как построить изображение, которое можно перемещать по экрану, задавая координаты только первой его точки?

15. Какие операторы позволяют построить контурный и закрашенный прямоугольники?

16. Как построить линейную диаграмму?

17. Как подписать рисунок?

18. Как построить дугу окружности? Как с помощью оператора построения дуги построить окружность?

19. Как изобразить закрашенный сектор?

20. Для чего используется функция trunc?

21. Что такое круговая диаграмма?

Лабораторная работа № 12

Blog

Методическое пособие для учащихся 9-11 классов средних общеобразовательных школ программирование на языке pascal

Содержание

КОМПЬЮТЕРНАЯ ГРАФИКА