Ю. Ю. Галямов Кандидат экономических наук, профессор, зав каф. «Экономическая теория»

Вид материала

Содержание

Временная оценка денежных потоков
Дискретное непрерывное накопление
Правило 72-х.
3.2. Текущая стоимость единицы (кол. 4*)
Текущая стоимость единицы
3.3. Текущая стоимость аннуитета (кол. 5*)
Использование двух факторов.
3.4. Взнос на амортизацию единицы (кол. 6*)
3.5. Накопление (рост) единицы за период или фактор будущей стоимости аннуитета (кол. 2*)
3.6. Фактор фонда возмещения (кол. 3*)
3.7. Взаимосвязь функций

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 14

Глава 3

Временная оценка денежных потоков

Применение метода капитализации доходов в оценке требует знания таких понятий, как сложный процент, дисконтирование и аннуитеты.

Стоимость приносящей доход собственности определяется текущей стоимостью денежной единицы, которая будет получена в будущем. Для правильной оценки будущих поступлений необходимо провести временную корректировку, используя сложный процент и дисконтирование.

По теории стоимости денег во времени денежная единица, полученная сегодня, стоит дороже, чем полученная завтра. Это обусловлено, в основном, тем, что сегодняшняя денежная единица принесет доход больше, чем вложения будущих периодов.

Сложный процент означает, что уже полученный процент, будучи положенным на депозит вместе с первоначальными инвестициями, становится частью основной суммы. И в следующий период наряду с первоначальным депозитом полученный процент приносит новый процент.

Простой процент не предполагает данной процедуры - доход приносит только первоначально вложенная сумма.

Для определения роста сложного процента используется формула:

где:

- сумма после накопления в течение

временных периодов;

- периодическая ставка процента;

- число периодов.

Дисконтирование - это процесс приведения будущих доходов к их текущей стоимости.

Стоимость ожидаемых будущих доходов зависит от следующих элементов:

Суммы денежных средств, представленной наличными деньгами или их денежными эквивалентами, которые будут инвестированы или получены от инвестиций, что позволит рассчитать обеспечит ли данное вложение средств положительную ставку дохода (то есть приток денег превысит их отток).
Времени выплаты или получения сумм денежных средств, что важно для увеличения прибыли. Временной период может состоять из одного дня, месяца, квартала, полугодия или года.
Риска - неопределенности, связанной с инвестициями, то есть это вероятность того, что прогнозируемые доходы от инвестиций, окажутся больше или меньше предполагаемых величин.
Соответствующей ставки дохода на инвестиции - процентного соотношения между чистым доходом и вложенным капиталом, называемым конечной отдачей.

Естественно, что чем больше риск, тем выше должна быть ставка дохода, компенсирующая риск инвестора.

Для облегчения расчетов по формированию и оценке денежных потоков с заданными характеристиками (время и период поступления доходов от инвестиций, ставка процента) существуют таблицы, содержащие факторы сложного процента, которые отражают изменение стоимости одной денежной единицы во времени, часто используется специальный калькулятор.

Стандартные функции сложного процента:

1. накопленная сумма единицы (или будущая стоимость единицы);

2. накопление денежной единицы за период (или будущая стоимость аннуитета);

3. фактор фонда возмещения;

4. текущая стоимость единицы (реверсии);

5. текущая стоимость аннуитета;

6. взнос на амортизацию единицы.

Стоимость денег во времени.

Все шесть функции сложного процента строят, используя общую базовую формулу

, описывающую накопленную сумму единицы. Все факторы являются производными от этого базового уравнения.

Выделяют три основные функции, а остальные получают как обратные к ним величины:

функция	обратная величина
1. накопленная сумма единицы	4. текущая стоимость единицы
2. накопление денежной единицы за период	5. фактор фонда возмещения
3. текущая стоимость аннуитета	6. взнос на амортизацию единицы

Дальнейшее изложение функции предполагает рассмотрение их парами, то есть функции и ее обратной величины.

В основе оценки приносящей доход собственности лежит понятие текущей стоимости (present value - PV) денежного дохода, который может быть получен в ходе эксплуатации предприятия.

3.1. Накопленная сумма единицы (кол. 1*)

Рост основной суммы по сложному проценту проиллюстрирован на рисунке:

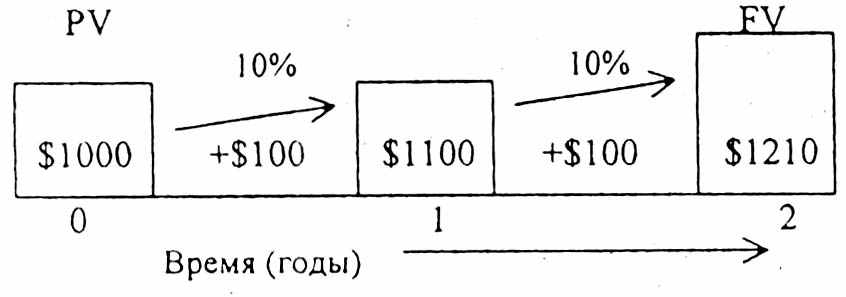
В таблицах сложного процента используется формула:

.

Расчет будущей стоимости текущего капитала проводят по формуле:

Где:

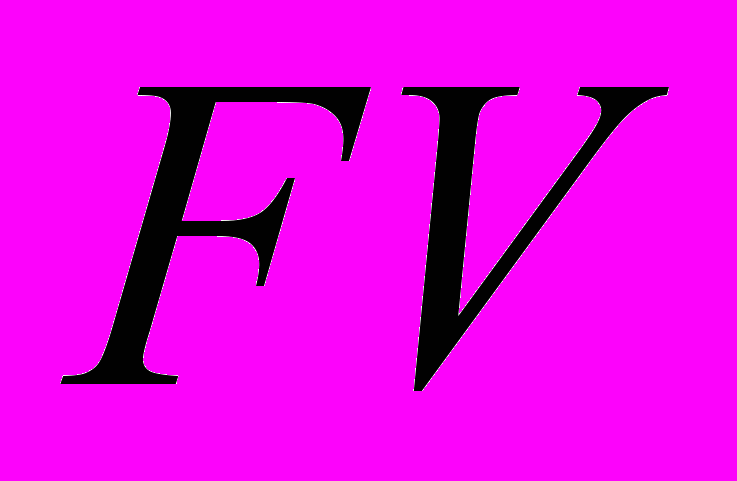- будущая стоимость капитала (future value)

- текущая стоимость капитала (present value).

Пример: Стоимость земельного участка 20000 долларов повышается на 12 процентов в год. Сколько она будет стоить через пять лет?

Будущую стоимость рассчитывают по выше указанной формуле, фактор накопления находят по колонке 1* в таблицах сложного процента в монографии Фридмана Дж. Ордуэйя «Анализ и оценка приносящей доход недвижимости» (Сводная таблица по шести функциям сложного процента).

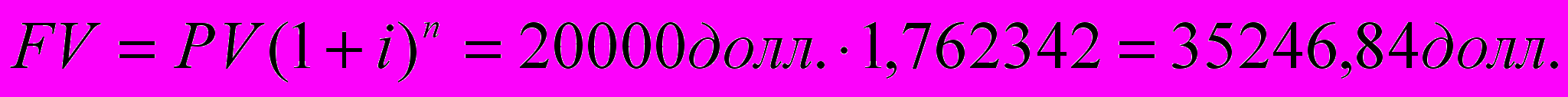
Дискретное непрерывное накопление

Период накопления может быть и более коротким, чем год, например, месяц, квартал, полугодие. Это фиксированное (дискретное) накопление. Расчет частного накопления проводят по формулам:

;

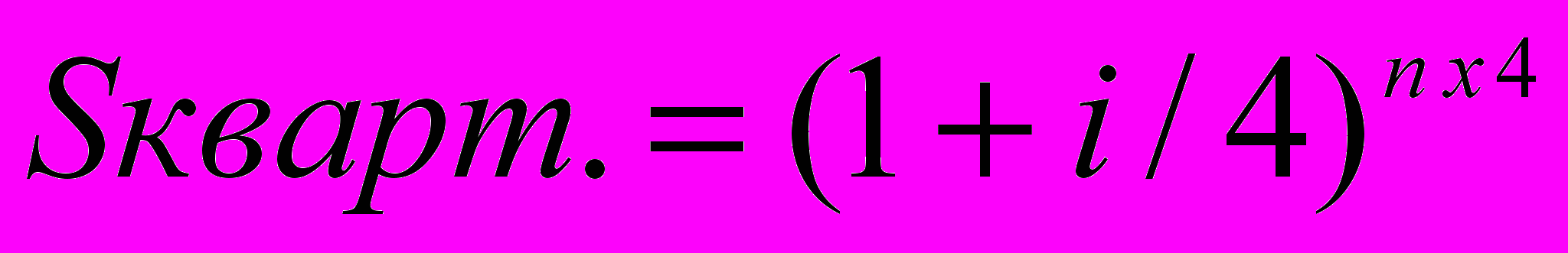Непрерывное накопление (приближением может быть ежедневное накопление) рассчитывают по формуле:

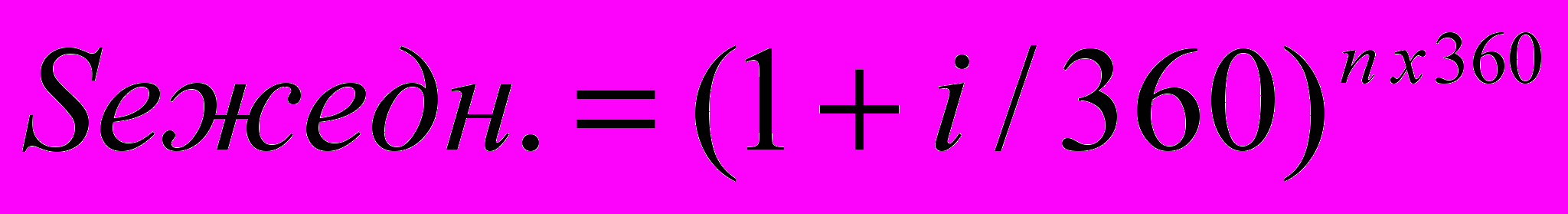
Если начисление процентов производится чаще одного раза в год, то есть сумма растет быстрее, чем при ежегодном начислении. Величина процентной ставки, которая позволила бы получить такую же величину основной суммы при ежегодном начислении, называется эффективной ставкой процента. В этом случае сама годовая ставка называется номинальной.

Пример: Банковская процентная ставка по вкладам составляет 10 процентов.

Начальная сумма 1000 долларов. Начисление процентов производится в конце года, квартала, месяца. Определить накопленные суммы через пять лет.

Решение:

1) годовое накопление расчет по таблицам:

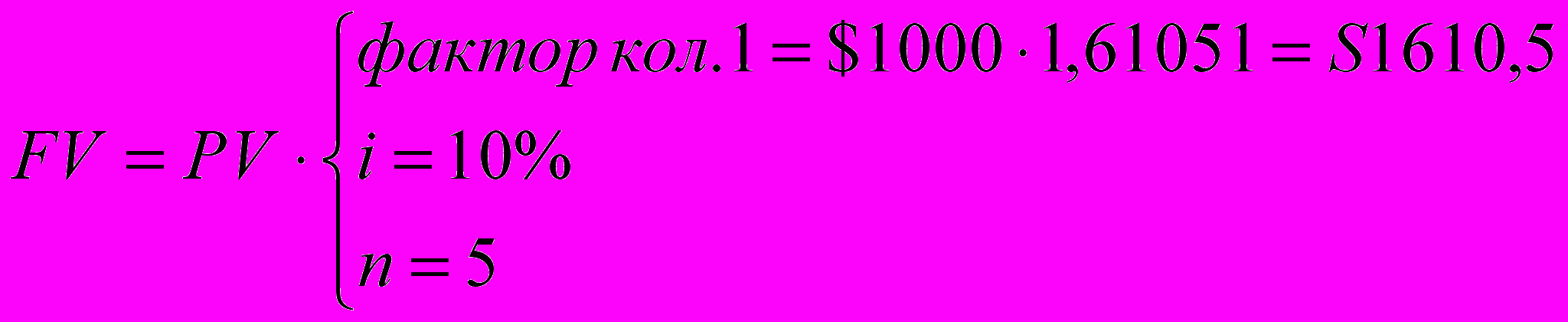
расчет по формуле:

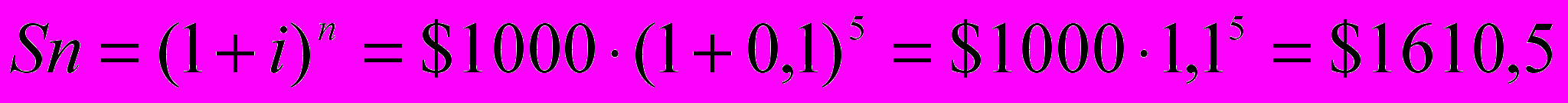
2) квартальное накопление расчет по формуле:

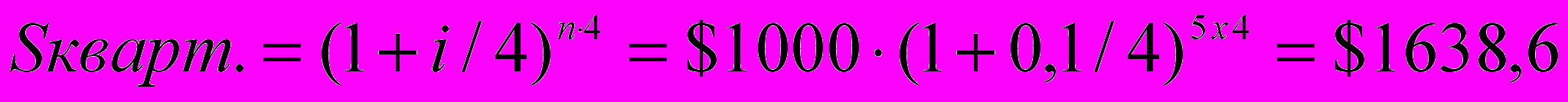
3) месячное накопление

расчет по формуле:

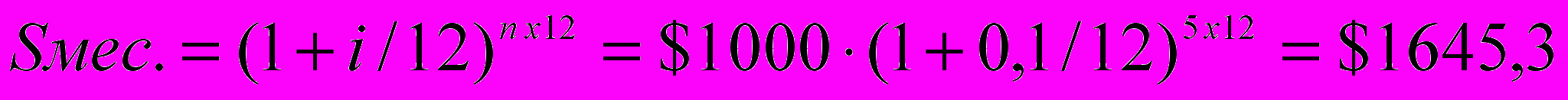
При номинальной ставке 10 процентов основная сумма через пять лет составит		Эффективная ставка. %
при годовом накоплении при квартальном при ежемесячном	1610,5 1638,6 1645,3	10 10,38 10,47

Таким образом, надо иметь в виду, что при одной и той же номинальной ставке и 10 процентов, более частое накопление приводит к более быстрому росту основной суммы и, следовательно, к большему значению эффективной ставки.

Правило 72-х.

Правило 72-х используется для примерного расчета количества лет, необходимых для увеличения наличной суммы в два раза при условии, что весь процент остается на депозите. Для расчёта необходимо разделить 72 на ставку процента (выраженную целым числом).

Например, при ставке сложного процента 3% денежная сумма удвоится примерно через 72:3 =24 года, при 3% ставке простого процента - за 33,5 лет, Правило 72-х можно применять и при обратной задаче, а именно, если известно, что за пять лет 10000 долларов превратились в 20000 долларов, то ставка сложного процента составляет примерно 72:5 = 14,4%.

Правило рекомендуется применять при ставке, изменяющейся от 3 до18 процентов.

3.2. Текущая стоимость единицы (кол. 4*)

Текущая стоимость единицы - это величина, обратная накопленной; сумме единицы. Это сегодняшняя стоимость единицы, которая должна быть получена в будущем. Текущая стоимость единицы графически изображена на рисунке:

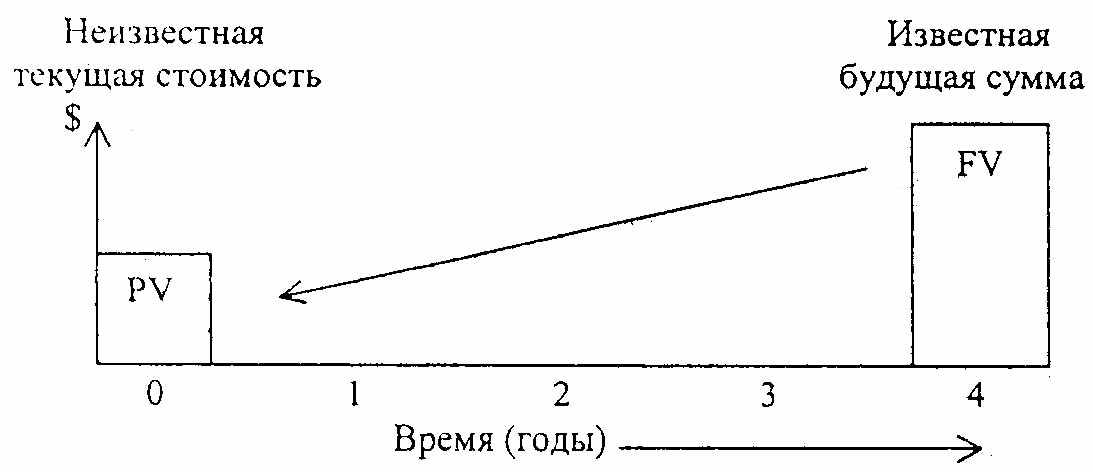
Расчет текущей стоимости единицы производится по формуле:

Эта функция является обратной величиной функции «накопленная сумма единицы».

Этот фактор используется для оценки текущей стоимости известной или прогнозируемой суммы будущего поступления денежных средств с учетом заданного сложного процента. При использовании фактора текущей стоимости появляется понятие дисконтирования, которое по смыслу противоположно накоплению.

Можно решить, какую сумму надо положить сегодня, чтобы получить заданную сумму в будущем.

Итак, будущая стоимость «дисконтируется» к текущей стоимости:

Год	Накопленная сумма $	Обратная величина	Текущая стоимость единицы $
1	1,1	1/1,1	0,909091
2	1,21	1/1,21	0,826446
3	1,331	1/1,331	0,751315
4	1,4641	1/1,4641	0,683013

Отсюда видно, что задача, которая должна быть решена с использованием фактора накопленной суммы единицы, может быть решена с применением фактора реверсии.

Интервалы между периодами дисконтирования могут быть более частыми, чем один год. При этом номинальная ставка дисконта делится на частоту интервалов, а число периодов умножается на число лет.

Расчет текущей стоимости капитала проводят по формуле:

Пример: Какую сумму следует сегодня депонировать в банке, начисляющем 11% годовых при ежегодном накоплении, для того чтобы через 4 года получить 10000 долл.? Решение:

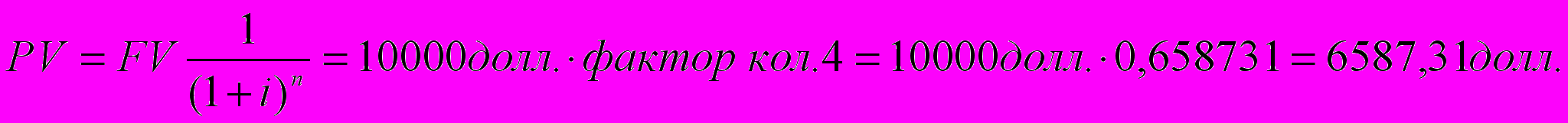
3.3. Текущая стоимость аннуитета (кол. 5*)

Под аннуитетом понимают серию равновеликих периодических платежей. Различают обычный и авансовый аннуитеты.

Платежом (payment - РМТ) п-ого периода называется единовременный денежный вклад в этом периоде.

Обычный аннуитет определяется как серия равновеликих платежей, осуществляемых в конце периода. Графическое изображение:

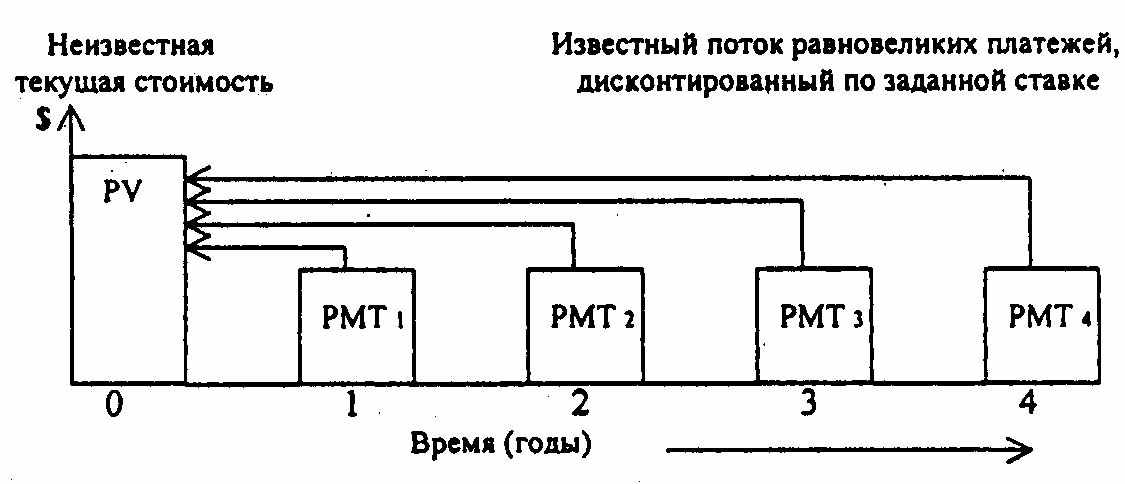
Текущая, стоимость аннуитета может быть рассчитана при заданной ставке дисконта через оценку каждого платежа по фактору текущей стоимости единицы:

$100 дохода в конце года при ставке 10% дисконта:

стоимость 1-го поступления - 90,91 (100 х 0,90909)

2-го - 82,64

3-го - 75,13

4

-го - 68,30

Сумма = 316,98 долл.

Итак, сегодняшние инвестиции в $316,98; являются обоснованной платой за право ежегодного получения $ 100 в течение 4-х лет:

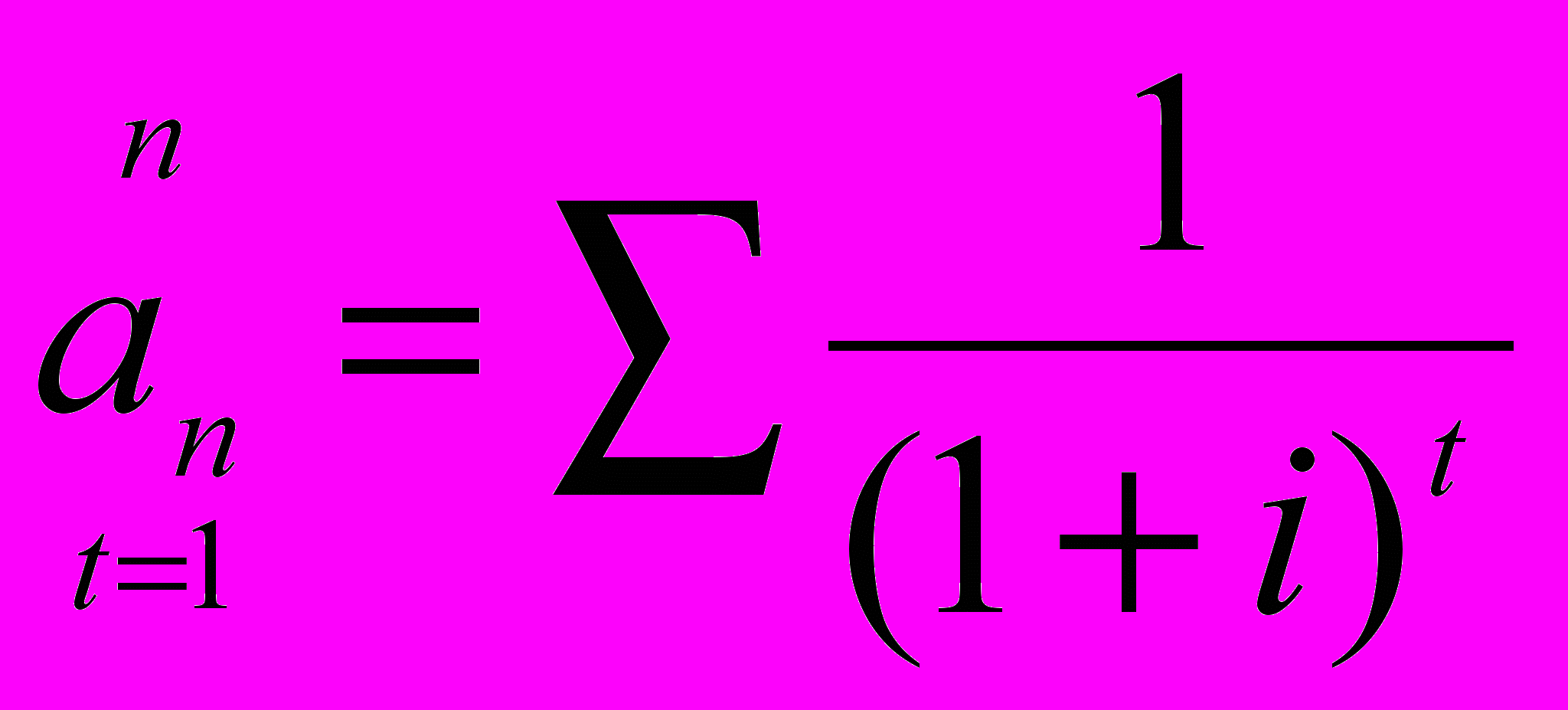
Второй способ предполагает использование фактора аннуитета или фактора Инвуда, который рассчитывается по следующей формуле:

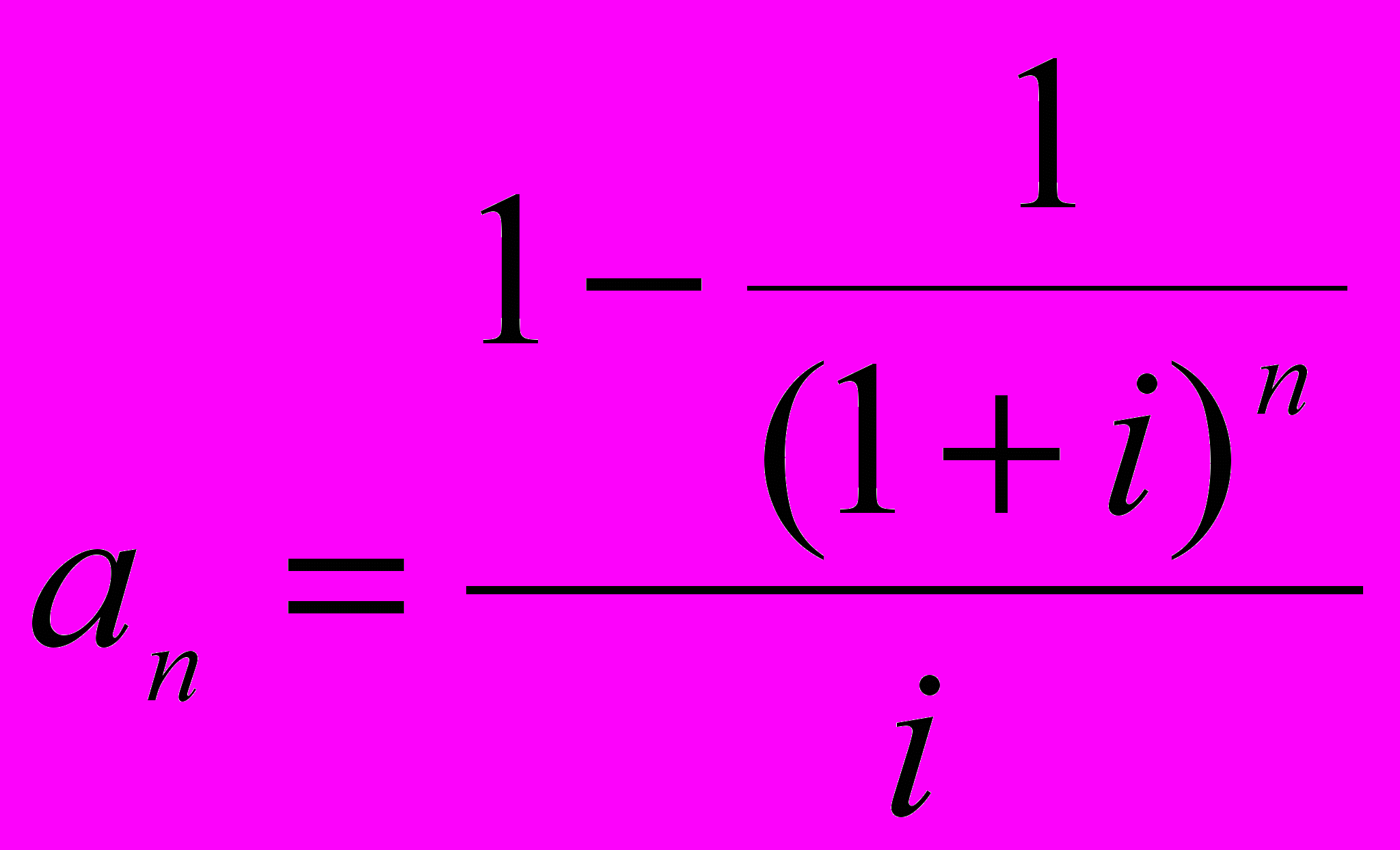
Для проверки правильности расчетов по второму способу рассмотрим метод «депозитной книжки». Депозит = $316,98, i = ,10%, п = 4 года при ежегодном изъятии 100 долл.

гг.	Остаток на начало года	+ 10% на остаток	- годовое изъятие	Остаток на конец года
1	316,98	+31,7	-100	=248,68
2	248,68	+24,87	-100	=173,55
3	173,55	+17,36	-100	=90,91
4	90,91	+9,09	-100	=0

Действительно, 316,98 долл. являются обоснованной платой за право ежегодного получения, 100 долл. в течение последующих 4-х лет. Расчеты текущей стоимости обычного аннуитета осуществляются по следующей формуле:

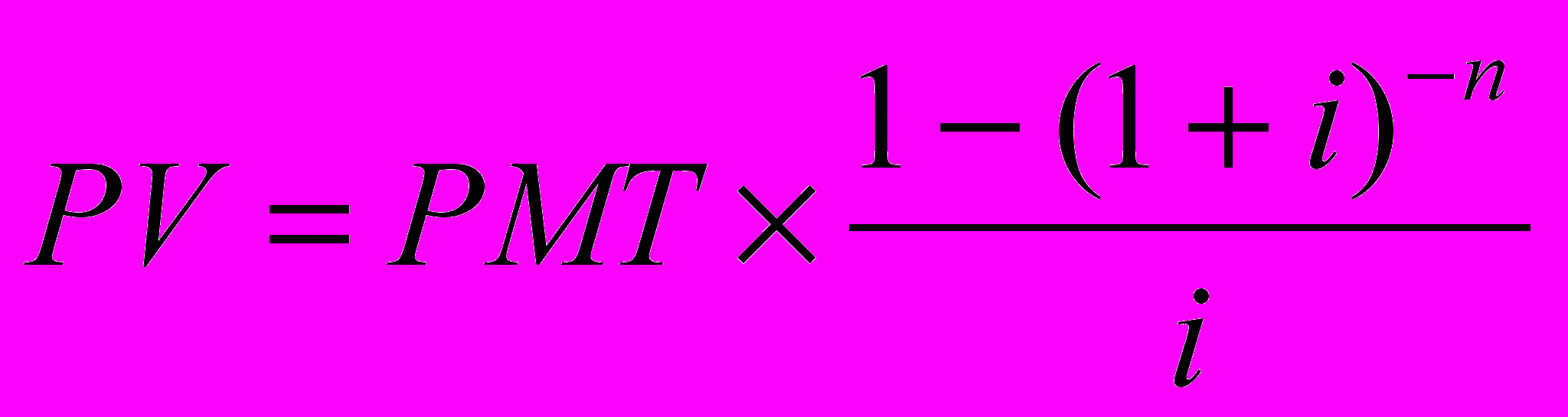
Авансовый аннуитет - поступление потоков платежей происходит в начале периода.

Так как первый платеж производится немедленно и поэтому не дисконтируется, то последующие поступления дисконтируются, по фактору обычного аннуитета укороченного на один период и добавляется к нему единица:

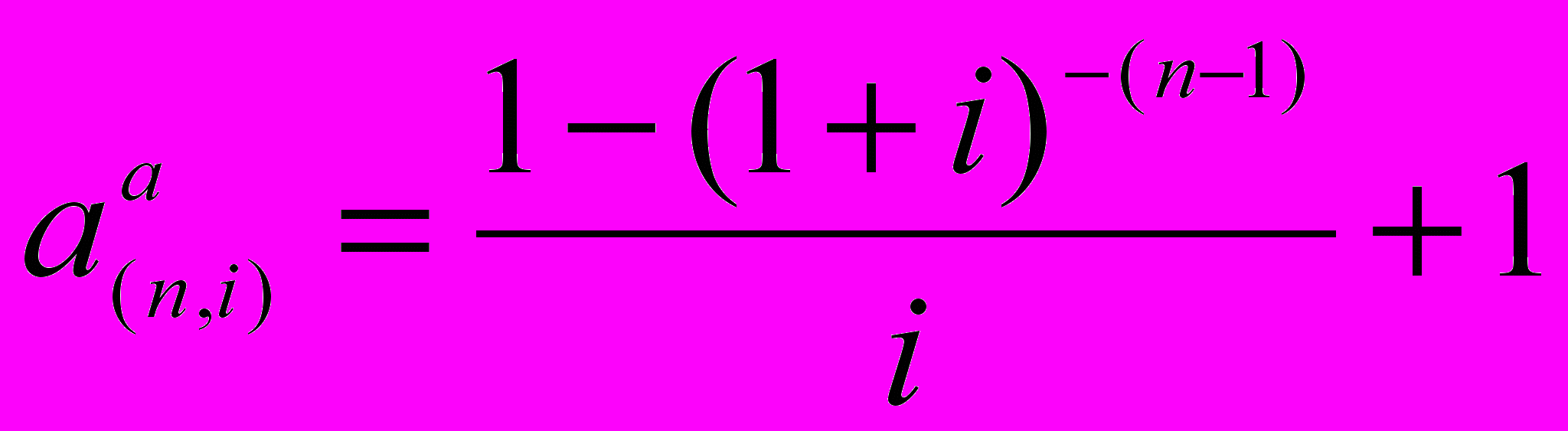
Для расчетов текущей стоимости авансового аннуитета используется формула:

Пример: Какова текущая стоимость арендных платежей, поступающих в конце каждого года в размере 1000 долл. на протяжении 7 лет при ставке дисконта 10%?

Решение:

Использование двух факторов.

Определение текущей стоимости предприятия методом дисконтирования будущих доходов предполагает использование двух факторов текущей стоимости единицы и текущей стоимости аннуитета.

Доход состоит из двух составных частей: потока доходов и единовременной суммы от перепродажи предприятия.

Рассмотрим пример:

В течение 8 лет недвижимость будет приносить доход в размере

20000 долл. Ставка доходности 14% годовых. В конце 8-го года предприятие будет продано за 110 000 долл. Определить текущую стоимость предприятия.

Решение:

рассчитаем текущую стоимость доходов:

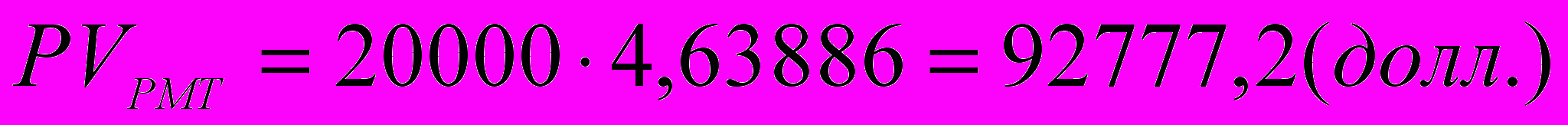
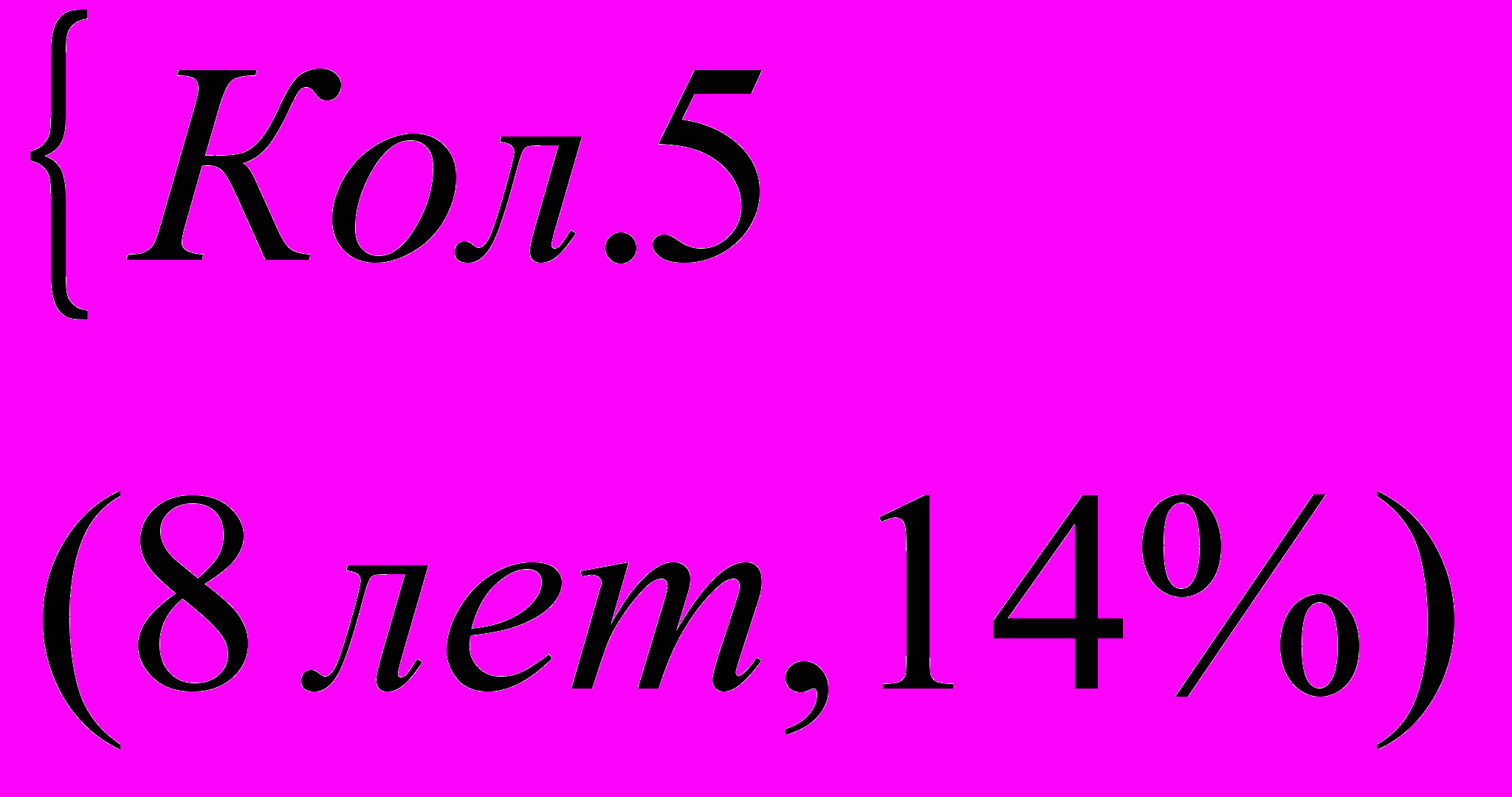
2) текущая стоимость реверсии составит:

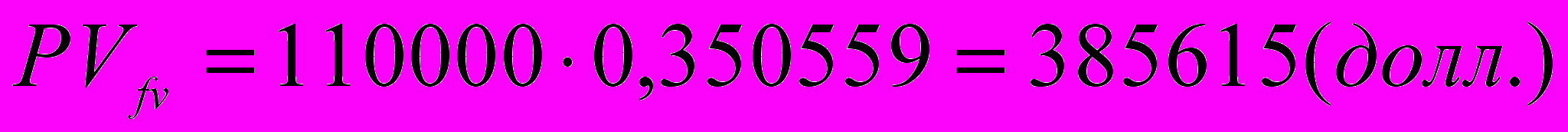
3.4. Взнос на амортизацию единицы (кол. 6*)

Амортизацией называется процесс погашения долга с течением времени. Взнос на амортизацию единицы - показывает, каким будет обязательный периодический платеж по кредиту, включающий процент и выплату части основной суммы и позволяющий погасить кредит в течение установленного срока. Он определяется как величина, обратная текущей стоимости аннуитета.

Каждый равновеликий взнос на амортизацию единицы включает:

процент - доход на инвестиции (on), выплату части первоначальной основной суммы кредита (of). Графическое изображение:

Взнос на амортизацию единицы определяется как: отношение одного платежа к первоначальной основной сумме кредита:

где: i - периодическая ставка процента, п - число периодов; а_п - текущая стоимость аннуитета.

Расчет п - периодного обычного взноса на амортизацию единицы осуществляется по формуле:

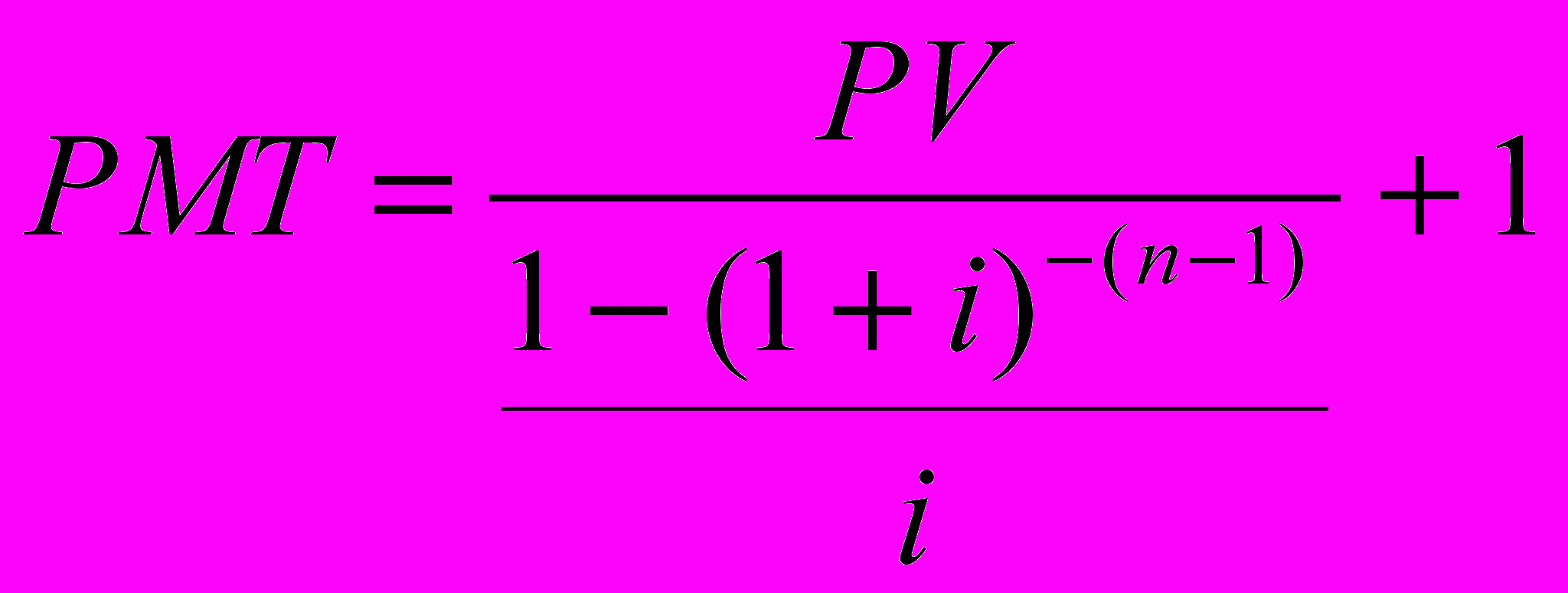
Пример: Какими должны быть ежемесячные выплаты по самоамортизирующемуся кредиту в 200000 долл., предоставленному на 25 лет при номинальной годовой ставке 12%?

Решение:

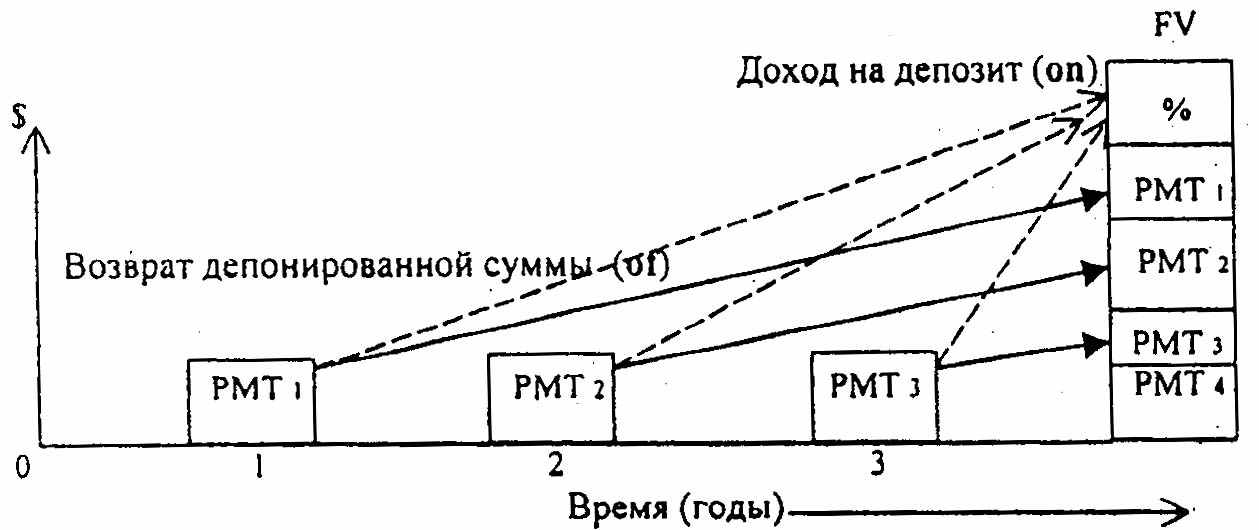
3.5. Накопление (рост) единицы за период или фактор будущей стоимости аннуитета (кол. 2*)

Фактор накопления единицы за период позволяет вычислить, какой по истечении всего установленного срока будет стоимость серии равных сумм, депонированных в конце каждого из периодических интервалов, по формуле:

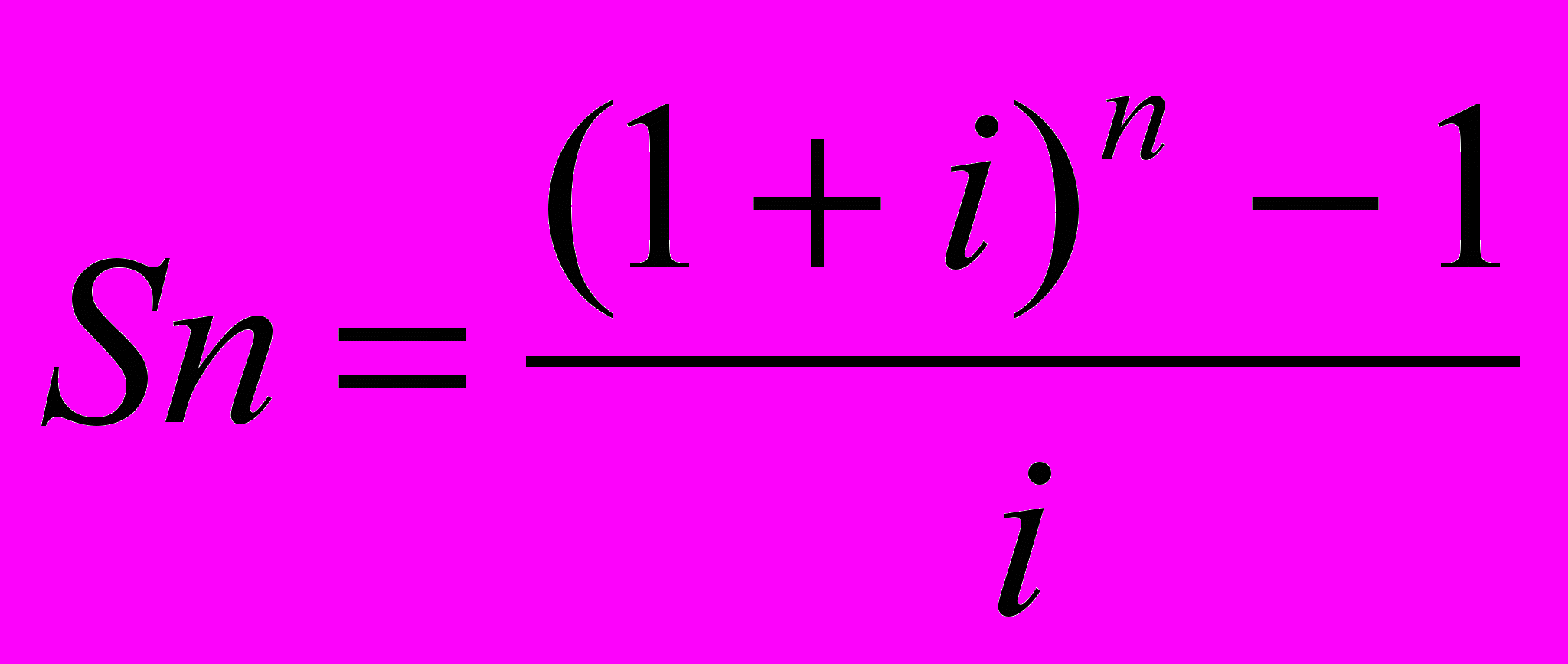
где: i - периодическая ставка процента;

п - число периодов;'

- текущая стоимость аннуитета.

Другой способ заключается в суммировании данных кол. 1, укороченной на один период. Например, при расчете 4-х летнего накопления показатели за 3 года суммируются, затем прибавляется 1. Графическое изображение функции накопления будущей стоимости аннуитета приведено на рисунке:

Расчет будущей стоимости обычного аннуитета осуществляется по формуле:

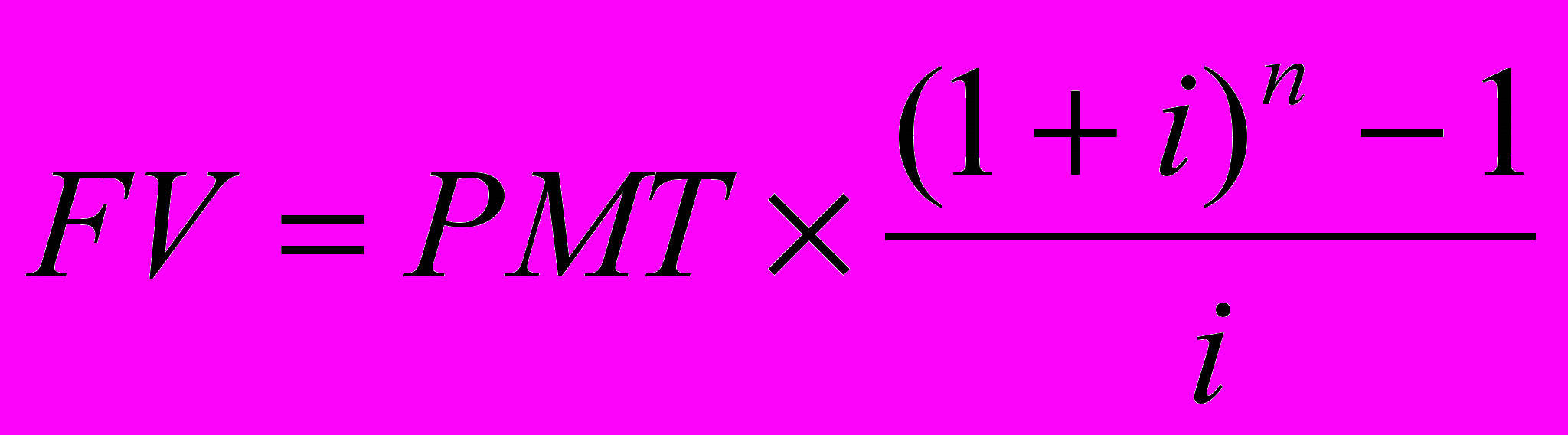
Если платежи осуществляются в начале периода (авансовый аннуитет), то применяется формула:

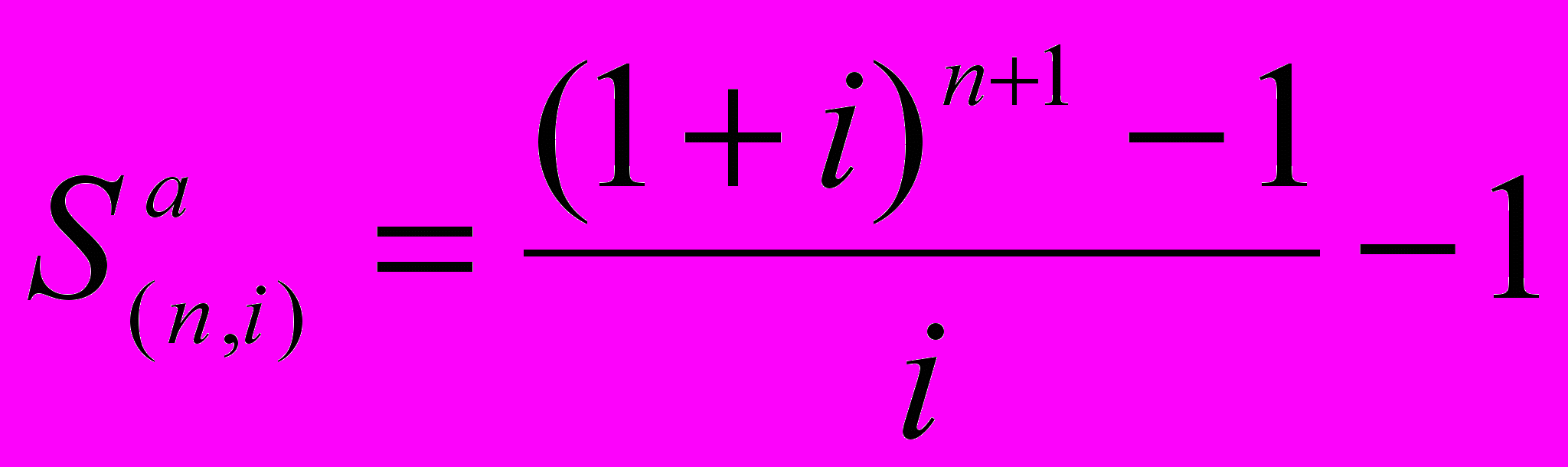
Расчет будущей стоимости авансового аннуитета проводят по следующей формуле:

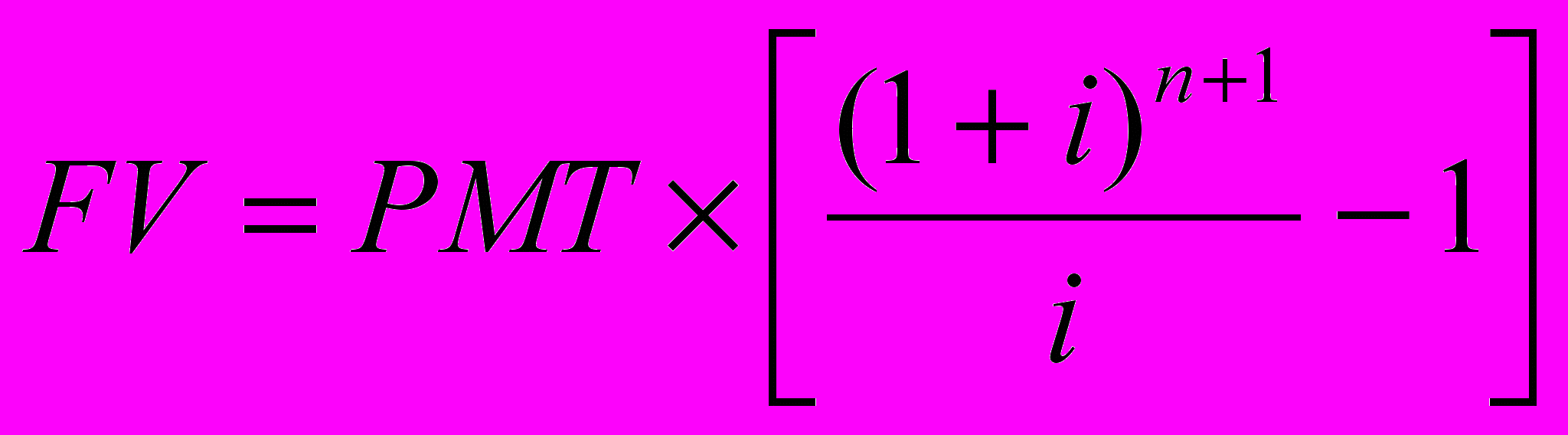
То есть, при использовании фактора кол.2* таблиц шести функций сложного процента, необходимо брать фактор за п+1 период, а затем вычесть 1.

Пример: Ежемесячные платежи по аренде поступают в начале каждого месяца в размере 2000 долл. Какова будущая стоимость платежей к концу 11 месяца при ставке дисконта 10%?

Решение:

3.6. Фактор фонда возмещения (кол. 3*)

Фактор фонда возмещения показывает денежную сумму, которую необходимо вносить в конце каждого периода для того, чтобы через заданное число периодов остаток составил один доллар. Эта величина, обратная фактору накопления единицы за период. Учитывает только возврат инвестированных средств (of), графическое изображение:

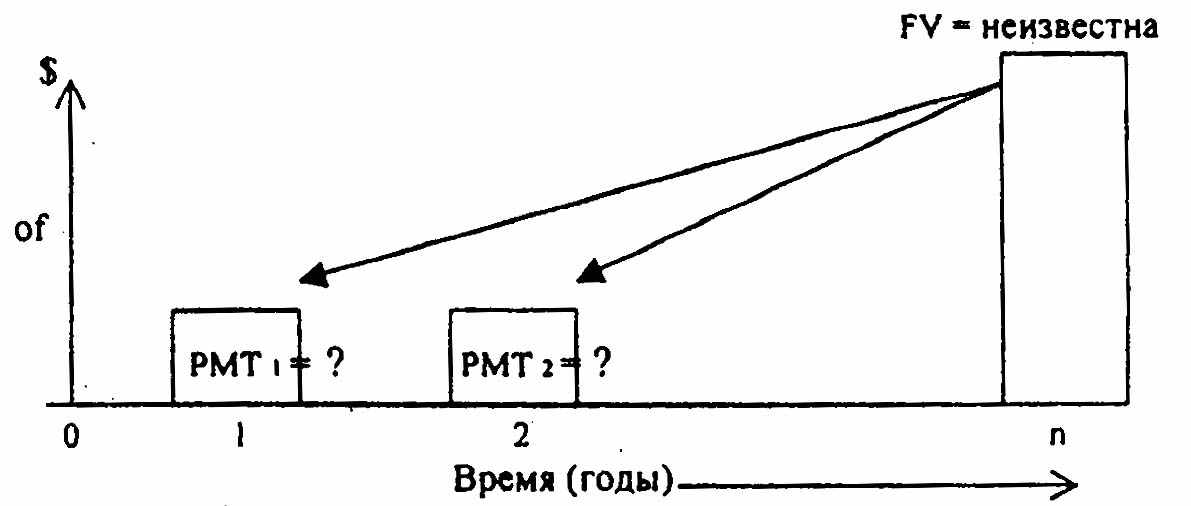
Рис. 6. Фактор фонда возмещения

При расчете фактора фонда обычного возмещения используется формула:

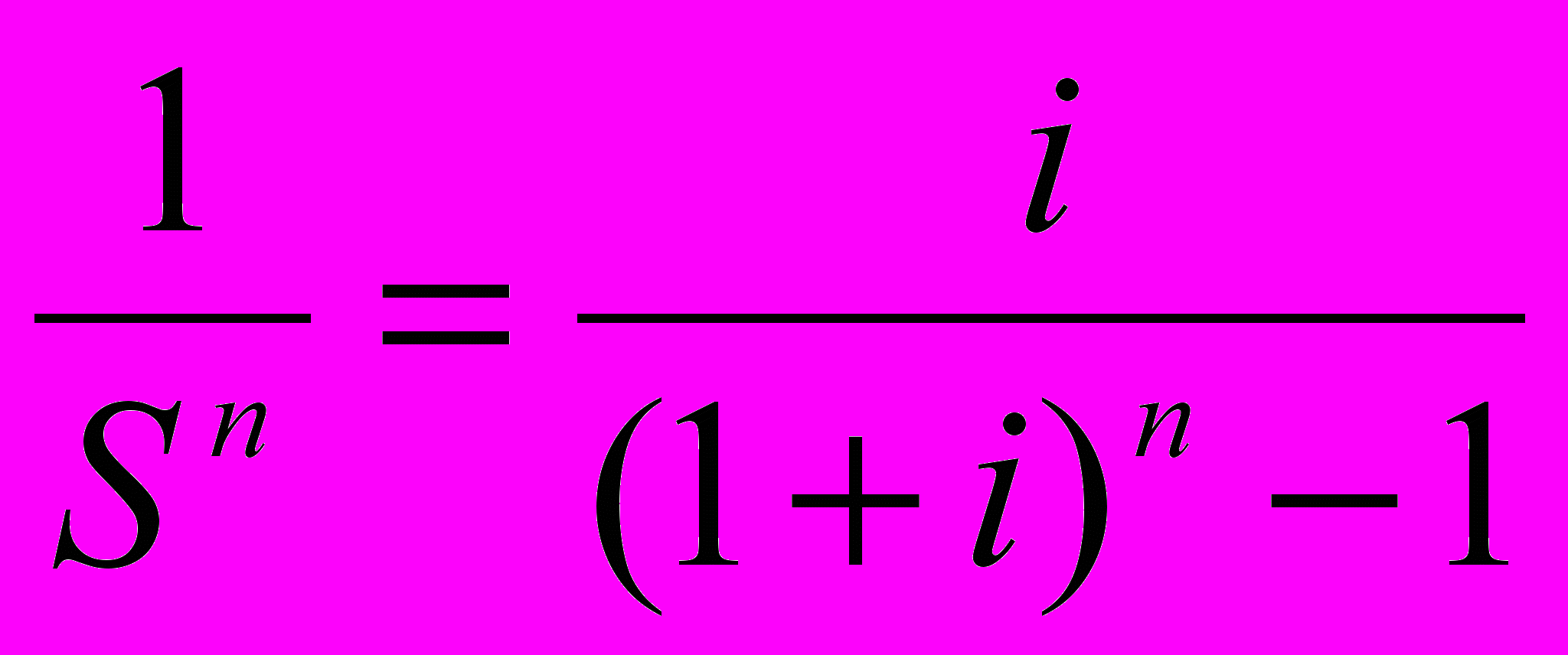
где: i - периодическая ставка процента;

п - число периодов;

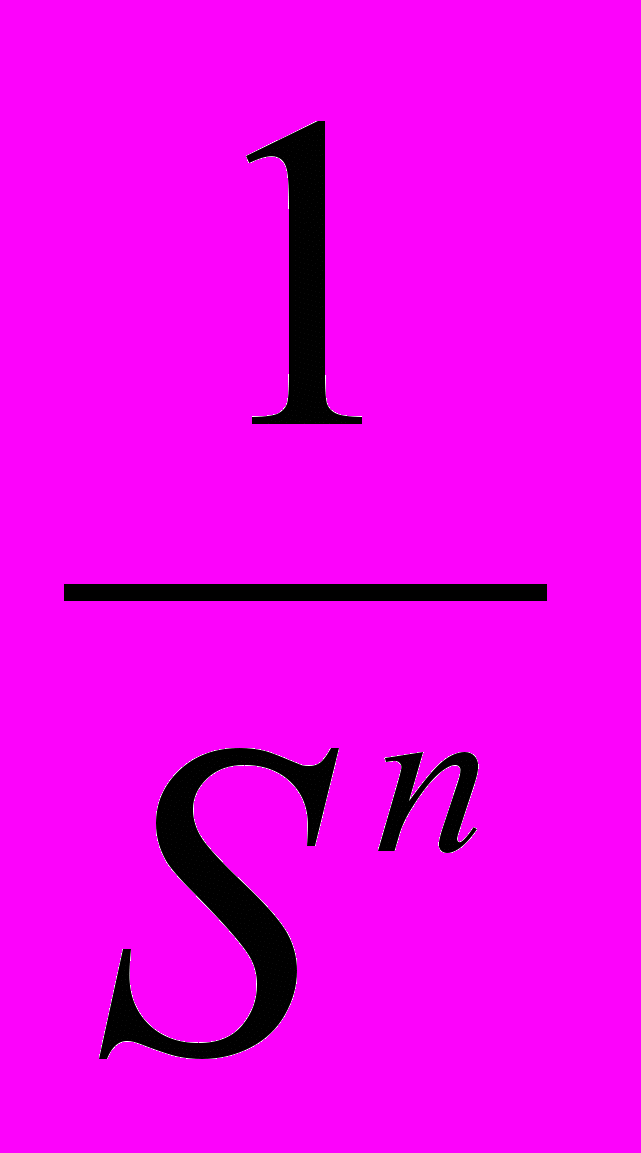- фактор фонда обычного возмещения.

Математическая запись соответствует формуле:

Если депонирование денежных сумм производится в начале периода, то следует воспользоваться формулой фактора фонда авансового возмещения:

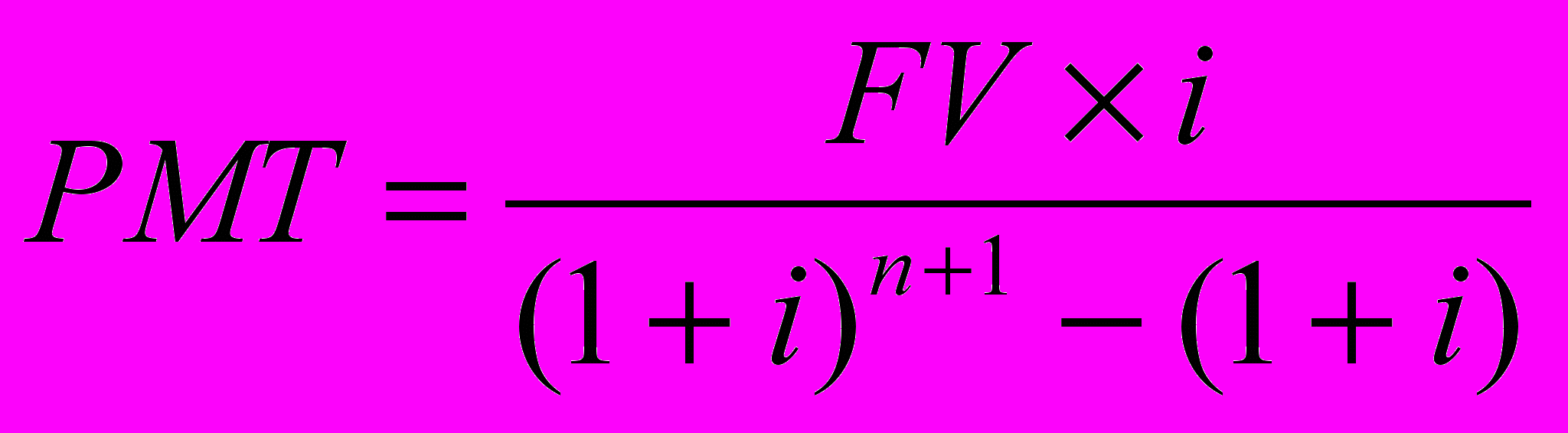
Пример: В течение 5 лет требуется накопить 15 000 долларов, депонируя ежемесячно равные денежные суммы. Ставка по вкладу составит 11%, процент будет начисляться каждый месяц. Каким должен быть месячный депозит?

Решение:

3.7. Взаимосвязь функций

Все шесть стандартных функций сложного процента строятся на основе базовой формулы (1+i)ⁿ, которая описывает накопленную сумму денежной единицы. Поэтому все- факторы являются производными от этого базового уравнения. Каждый из них предусматривает, что процент приносит деньги, находящиеся на депозитном счете, естественно, только до тех пор, пока они остаются на депозитном счете. Каждый из них учитывает эффект сложного процента. Три функции, как отмечалось выше, являются прямыми, три получают как обратные им величины. Расчеты, требующие умножения, выполняются и через деление на обратную величину и наоборот.

Сумма фактора фонда возмещения (кол.3) и ставки периодического процента равна взносу на амортизацию единицы (кол. 6). Таким образом, взнос на амортизацию единицы является суммой двух величин, то есть заемщики выплачивают в течение срока кредита первоначальную сумму кредита и процент за кредит. В том случае, когда основная сумма кредита не амортизируется до истечения срока кредита и выплачивается только процент, заемщик может вносить на отдельный счет периодические платежи, рассчитанные по фактору фонда возмещения. Если фонд возмещения приносит процент по той же ставке, что и полученный кредит, то по окончании срока накопленная сумма может погасить остаток долга.

Взнос на амортизацию единицы соотносится со ставкой процента так, чтобы взнос всегда превышал периодическую ставку процента вне зависимости от срока кредита.

Текущая стоимость обычного аннуитета никогда не может превысить фактор, равный частному от деления 1 денежной единицы на периодическую ставку процента. Например, если годовая ставка равна 10%, то максимальное значение рассчитывается: 1 д.е.: 0,1 = 10. Максимальное значение этого фактора при любой ставке процента показывает сумму, достаточную для генерирования 1 д.е. за период на протяжении неограниченного времени.

Остаток 10 д.е. при 10%-й ставке принесет за год 1 д.е. процента.

Сводная таблица по шести функциям сложного процента

функция	рисунок	формула	определение
Накопленная сумма единицы кол. 1*			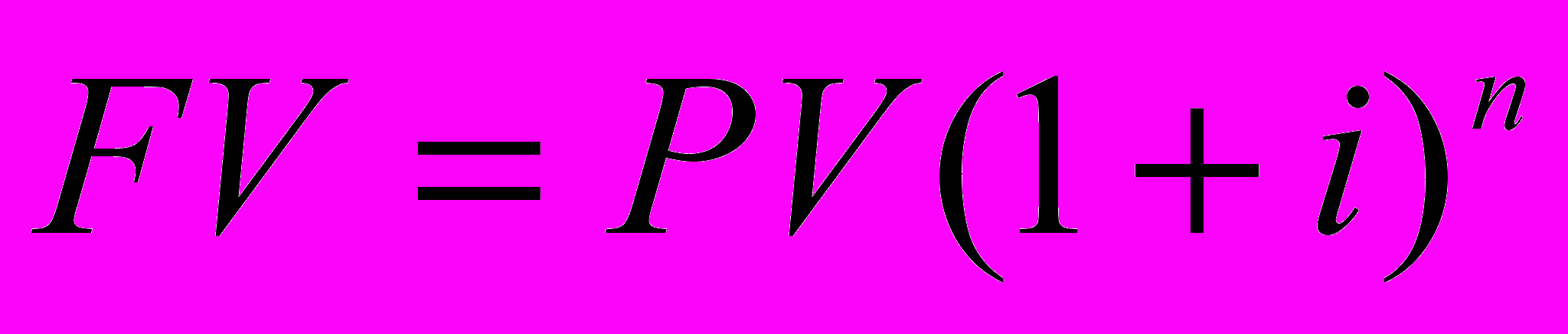Показывает рост $1, положенного на депозит, при накоплении по сложному проценту.
Накопление единиц за период кол. 2*			Показывает, какой по истечении всего срока будет стоимость серии равных сумм, депонированных в конце каждого из периодических интервалов.
Фактор фонда возмещения кол. З*		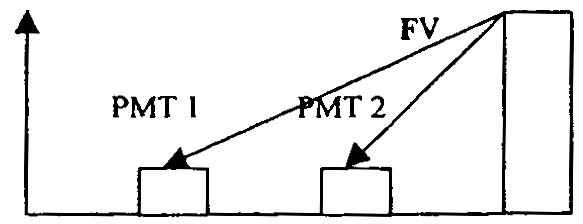	Показывает сумму равновеликого периодического взноса, который вместе с процентом необходим для того, чтобы к концу определенного периода накопить $1.
Текущая стоимость единицы кол. 4*		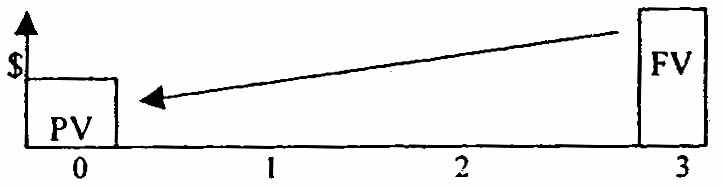	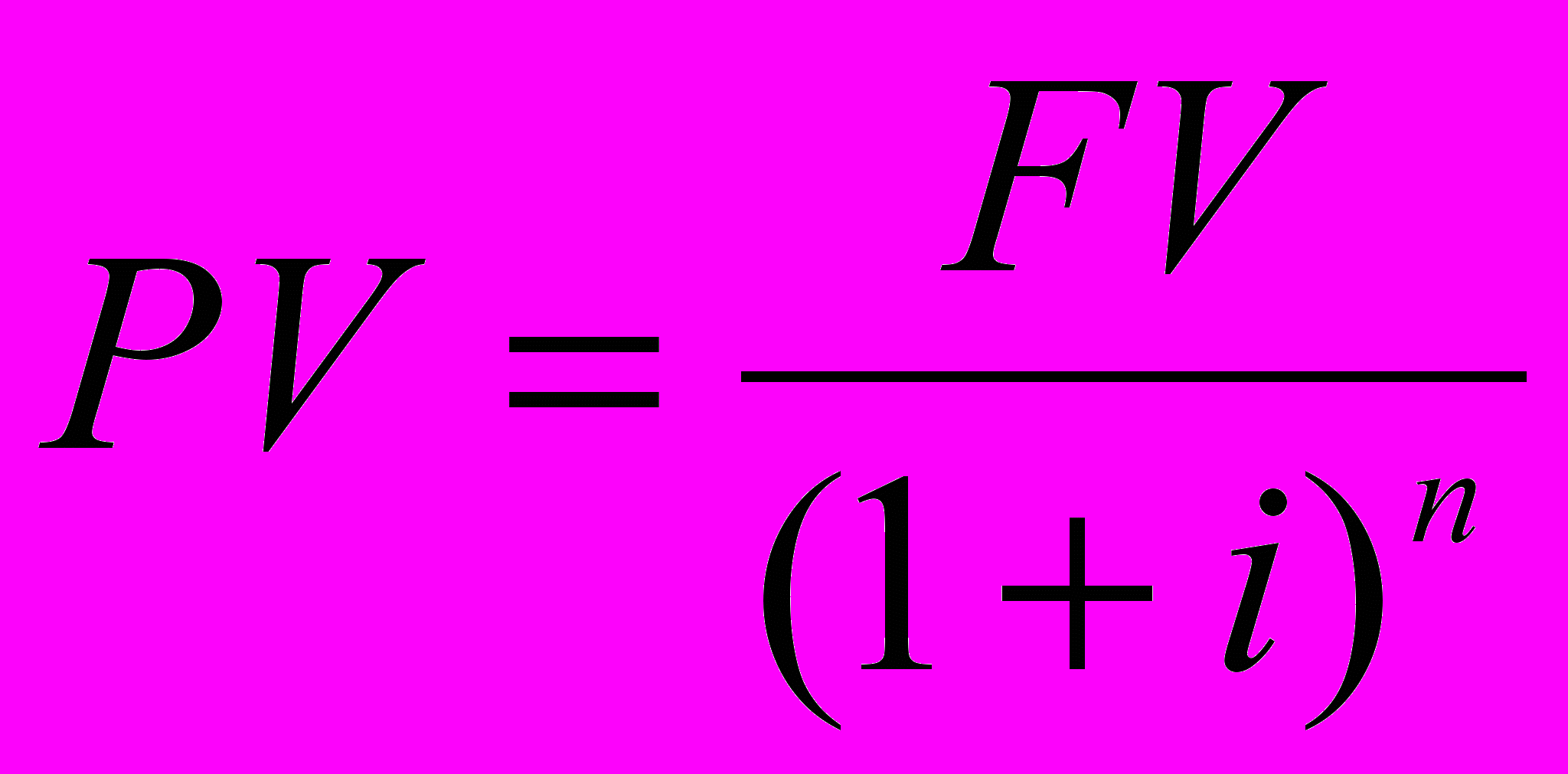Показывает текущую стоимость $1, который должен быть получен единовременно в будущем.
функция	рисунок	формула	определение
Текущая стоимость обычного аннуитета кол. 5*		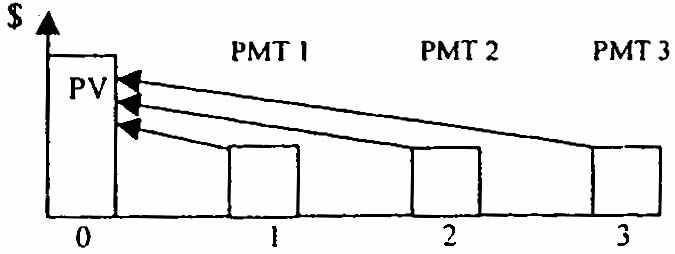	Показывает текущую стоимость равномерного потока доходов. Первое поступление происходит в конце первого периода; последующие - в конце каждого последующего периода.
Взнос на амортизацию единицы кол. 6*		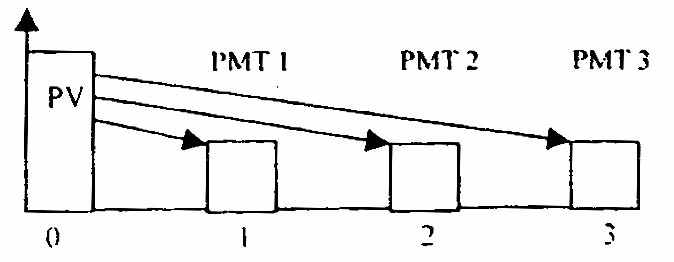	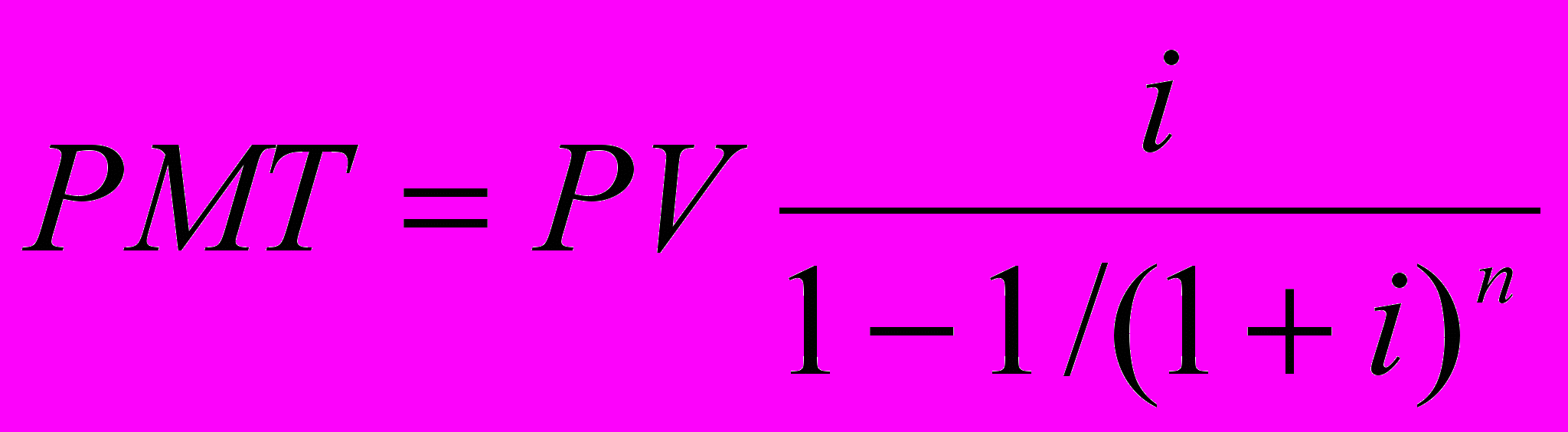Показывает равновеликий периодический платеж, необходимый для полной амортизации кредита

Вопросы и упражнения для самопроверки:

Назовите прямые и обратные функции сложного процента.
В чем заключается теория стоимости денег во времени?
Дайте определение процесса дисконтирования.
Что понимается под аннуитетными платежами? Приведите примеры.
Ежемесячные платежи по аренде поступают в начале каждого месяца в размере 12000 руб. Среднерыночная ставка дохода - 15%. Какова будущая стоимость платежей к концу 8-го месяца?
Кредит в размере 500000 руб. предоставлен по ставке 12% в год на 20 лет с ежемесячными выплатами. Определите величину ежегодных выплат по кредиту.
Владелец офисного помещения планирует провести ремонт через 5 лет. Это сегодня стоит 20000 руб., ежегодное удорожание ремонта составляет 6% в год. Какую сумму следует вносить в конце каждого года на счет, приносящий 10%, чтобы накопить достаточную сумму для ремонта?
N планирует приобрести новое оборудование для своей гостиницы через 5 лет. В настоящий момент это стоит 50000 руб. и будет дорожать на 7% в год. Достаточно ли будет средств на запланированное переоборудование, если N будет вносить в конце каждого месяца 1500 руб. на счет, приносящий 11% годовых?
Кредит в размере 7000 руб. выдан на 10 лет под 12% годовых. Определить сумму долга на конец 3-го года.
Определить число лет, необходимое для увеличения первоначального капитала в 2 раза, применяя сложные проценты по ставке 12% при годовом начислении?

Для практического освоения финансовых расчетов предлагается промежуточный контроль с использованием обобщающей сводной таблицы шести функций сложного процента.

Blog

Ю. Ю. Галямов Кандидат экономических наук, профессор, зав каф. «Экономическая теория»

Содержание