Оптимизационные модели и методы управления товарно-материальными запасами 08. 00. 13 Математические и инструментальные методы экономики

Вид материала

Содержание

Разработка оптимизационных моделей и алгоритмов управления товарно-материальными запасами
НЗ - неснижаемый запас, предназначенный для удовлетворения спроса рейсовых самолетов других государственных управлений авиапред
Экспериментальная реализация моделей и алгоритмов управления товарно-материальными запасами

Подобный материал:

1 2 3

Разработка оптимизационных моделей и алгоритмов управления товарно-материальными запасами

Под статическими моделями (задачами) управления запасами понимаются такие модели, все параметры которых на протяжении всего периода управления остаются неизменными или же их изменениями можно пренебречь. Существует определение других авторов, например: «Если все параметры модели не меняются во времени, то она называется статической, а в противном случае - динамической».

В статических задачах управления запасами плановый период управления представляет собой временной отрезок, в котором решение относительно уровня запаса принимается только один раз, в начале этого периода, с учетом всей предыстории и не зависит от времени.

Изучение статических моделей представляет интерес в случае, когда необходимо установить начальный уровень запасов новых продуктов, что и является отправным моментом для решения динамических задач управления запасами. В отличие от статических, динамические модели управления запасами возникают в ситуациях, когда значение параметров модели изменяется во времени.

В работе рассматривается широкий круг важных стохастических однопродуктовых и многопродуктовых задач управления запасами и анализируются преимущества применения предлагаемых алгоритмов по сравнению с традиционными методами классического анализа и математического программирования.

Предположим, что все запасаемые продукты в ТИК агрегированы в один продукт. Часть этих запасов можно использовать в процессе производства, а часть из них – для потребления. Исследование этих моделей представляет самостоятельный интерес и является исходным материалом при изучении многопродуктовых моделей запаса.

Однопродуктовая задача УЗ состоит в выборе решения, заключающегося в нахождении такого объема запаса продукции x, который минимизирует суммарные затраты, состоящие из стоимости запаса, а также ожидаемые затраты на хранение и потери от дефицита запасаемой продукции, т.е.

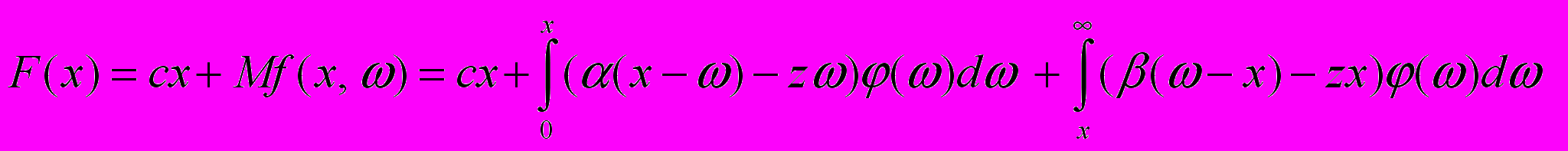(1)

при ограничениях

xX = {x: 0 ≤ x ≤ x ≤

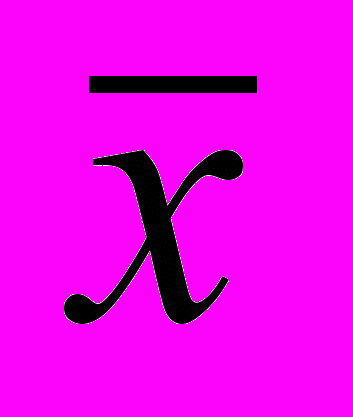}. (2)

Здесь стоимостная функция f(х, ω) задаётся следующим образом:

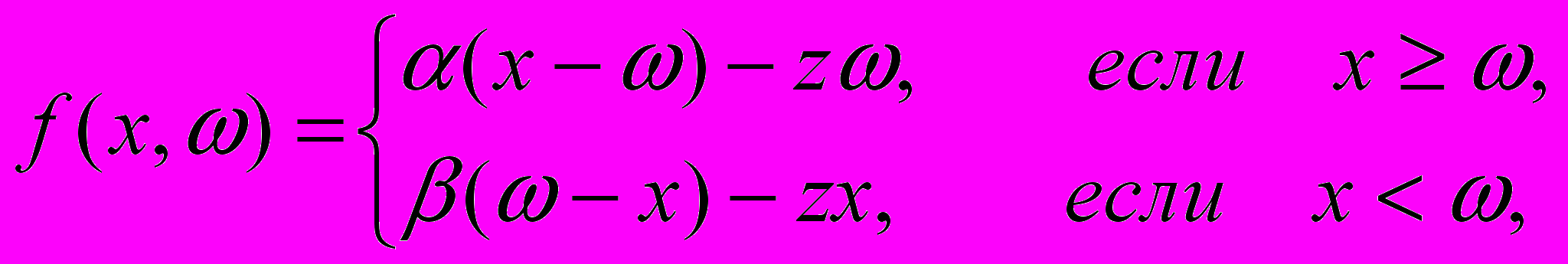
где сx – затраты на создание запаса;  – удельные издержки хранения, измеряются в денежных единицах;  - удельные издержки вследствие дефицита, измеряются в денежных единицах; z - реализационная цена единицы товара; x – вектор гарантированного спроса;

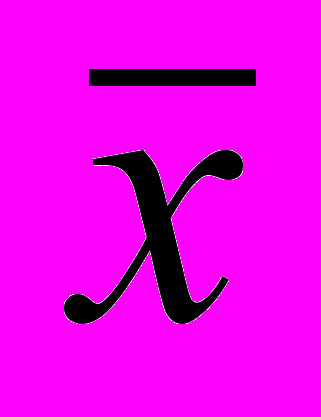- верхний уровень запасаeмой продукции на рассматриваемый период; φ(ω)dω – вероятность того, что спрос ω за рассматриваемый период находится в интервале (ω, ω + dω).

Задача (1) и (2) является частным случаем задачи стохастической оптимизации.

Методы решения. В работе для сравнения с предлагаемыми в работе алгоритмами приводится обычный - классический (или традиционный) - подход к решению задачи (1), (2) без ограничения. Тогда необходимым условием того, что x* является оптимальным уровнем запаса, будет

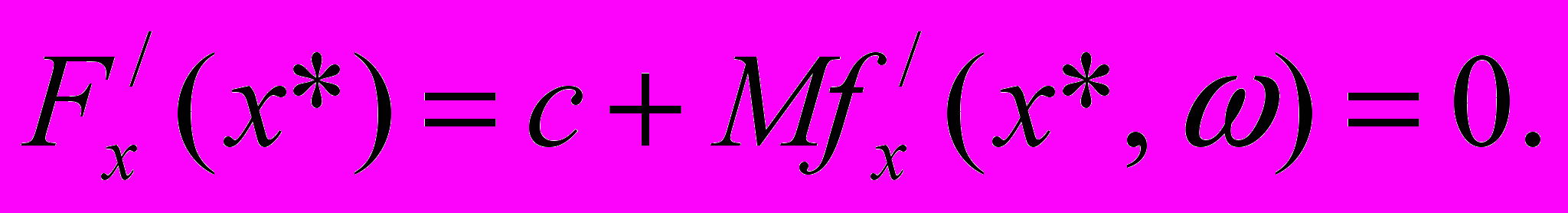( 3)

Здесь

– производная целевой функции F(x) в точке x*,

– производная стоимостной (подынтегральной) функции f(x, ) при оптимальном уровне запаса x* и спроса . Согласно (3)

F_x (x) = с + Р{ ≤ x}- (+z)(1-P{ ≤ x})= с + ( + +z) P{ ≤ x} – (+z) = 0,

так как

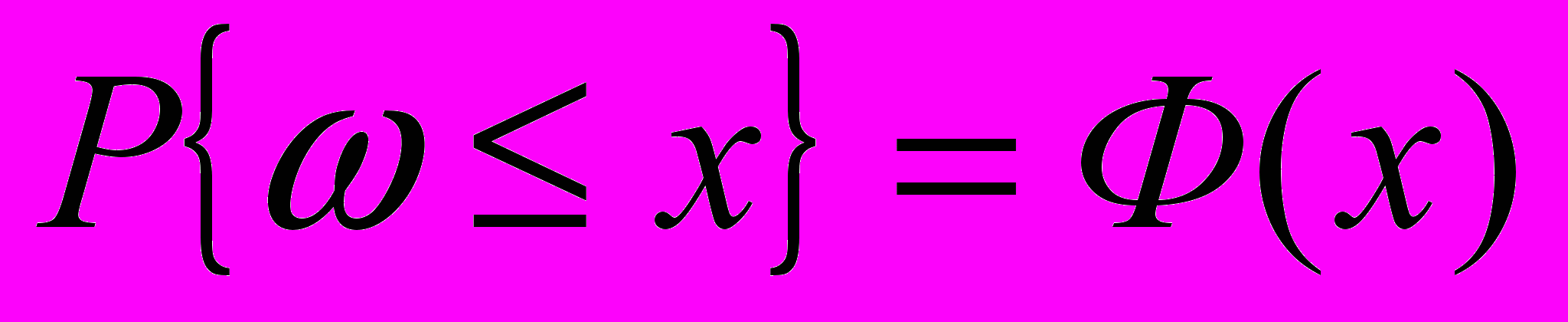- функция распределения , то

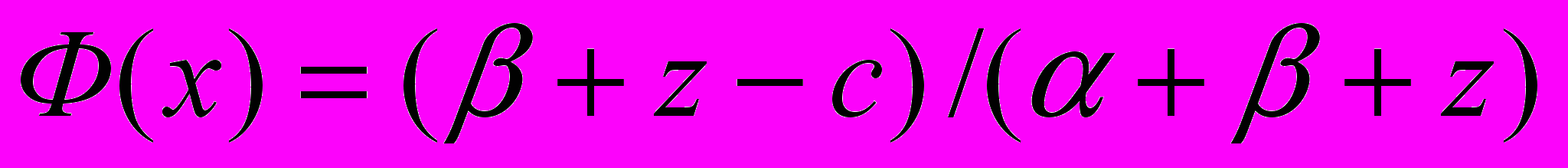. (4)

Следовательно, оптимальный уровень запаса

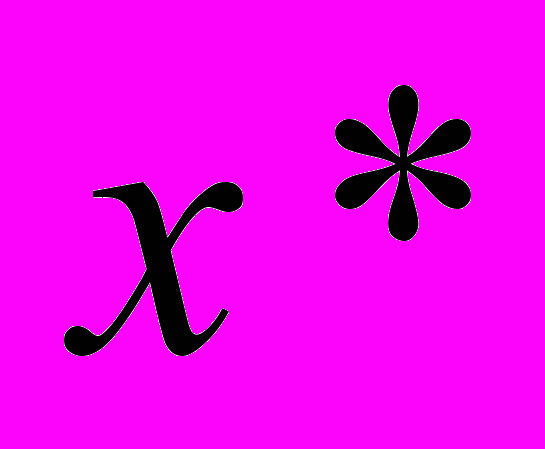, который соответствует минимуму целевой функции F(x), определяется с помощью обратной к функции (4), т. е.

.

Если, учитывать ограничение (2), то решение обычно находится следующим образом: если

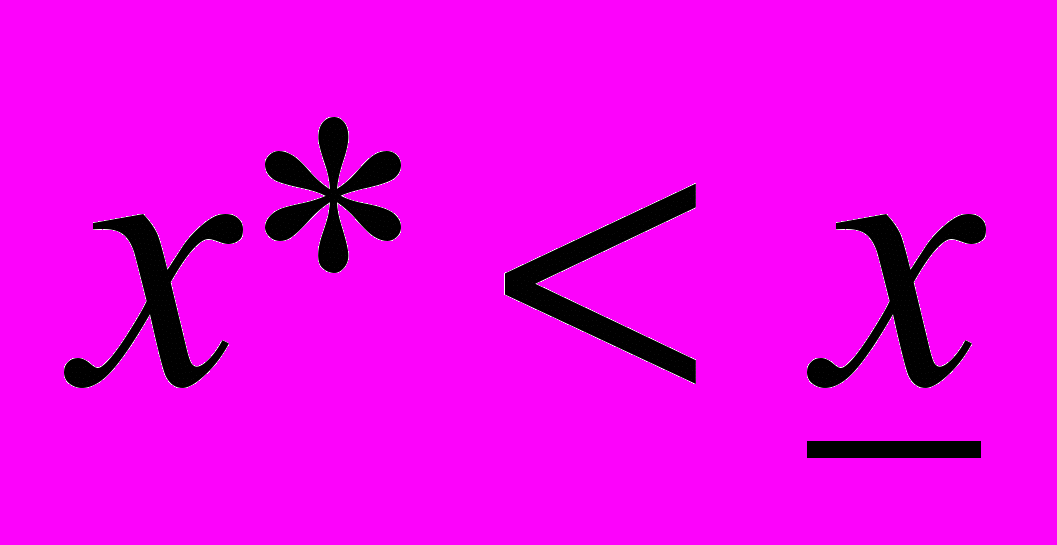, то примем

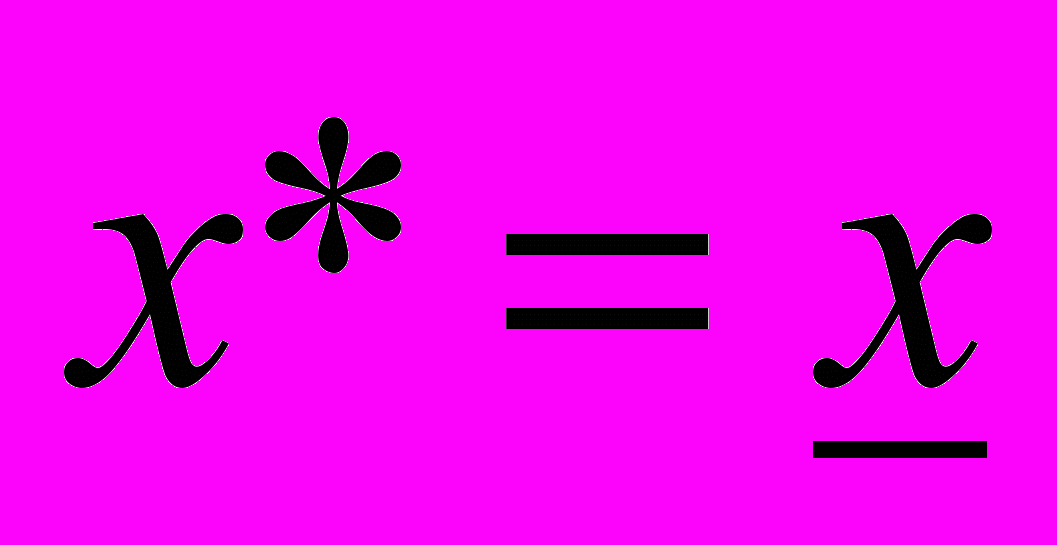; если

, примем

; если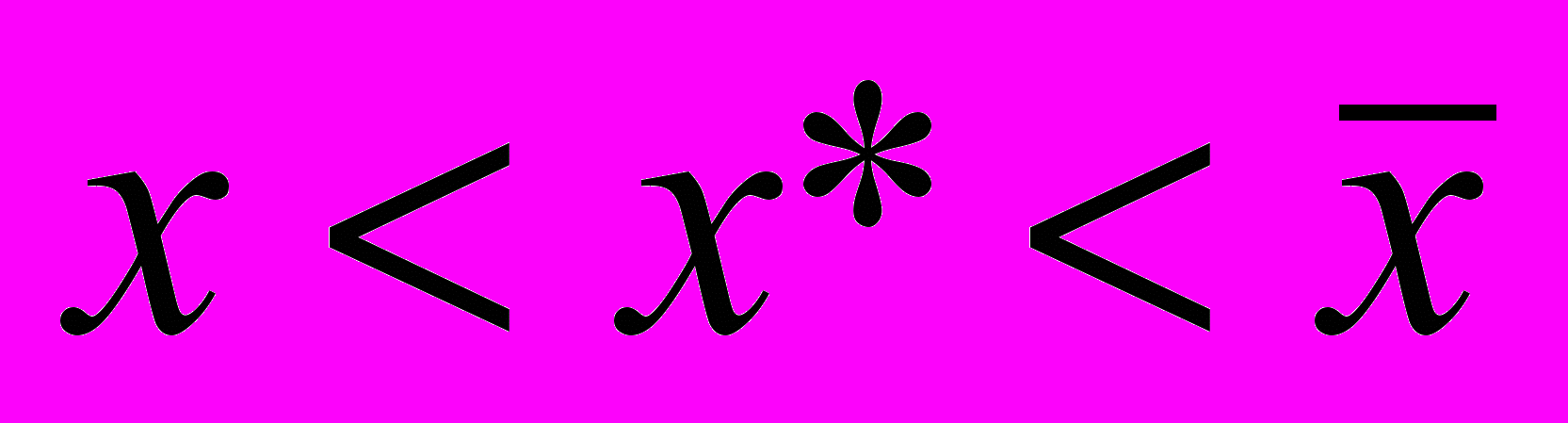

, то х* является истинным решением оптимального уровня запаса.

Таким образом, ТИК определяет объем инвестиции I в материально-технические запасы по формуле:

I = П_ц · х* , (5)

где П_ц – рыночная стоимость единицы запасаемой продукции, х* - оптимальный уровень запаса.

При решении задачи (1) и (2) классическим методом обычно возникает ряд трудностей, состоящих в следующем: определить функции (закона) распределения спроса не всегда удастся, т.е. решение уравнения (3) становится трудным.

Указанные особенности ограничивают применение классического подхода, поэтому необходимо создание специальных методов, ориентированных на решение задач УЗ вида (1) и (2), которые решаются с использованием доступной информации о наблюдениях (реализациях) значений спроса  и значении стоимостной функции f(x,) для фиксированного спроса  и уровня запаса х.

Алгоритм 1. Пусть на s-м итерации получено приближение x^s, s=0, 1, ..., к оптимальному уровню запаса х* (x⁰ – начальное приближение может быть выбрано произвольно равным 0). Тогда:

1. B соответствии с исходными данными о конкретных значениях спроса получаем наблюдение ^s над реализацией случайной величины  на s-м итерации. Заметим, что для этого может быть использована имитационная модель, спроса.

2. Построим вектор стохастического градиента функции F_x(x), определяемой (1):

,

где

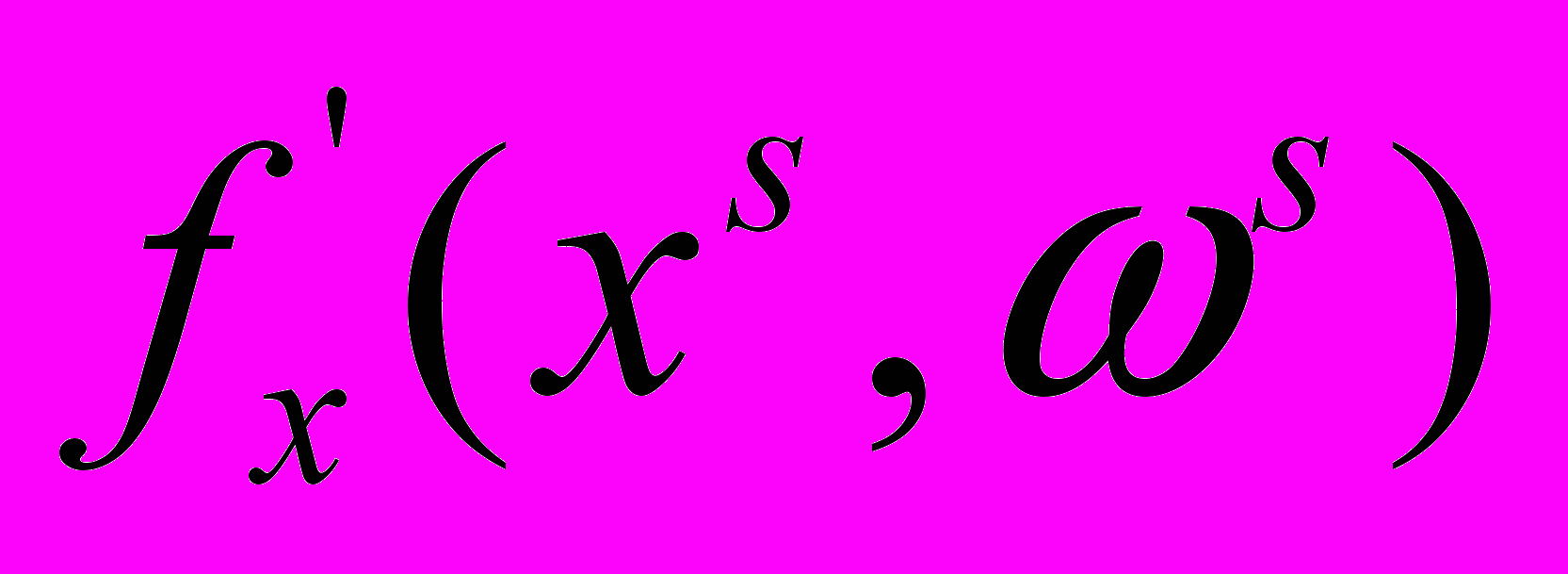- стохастический градиент функции f(x,) по х в точке (x^s,^s), определяется следующим образом:

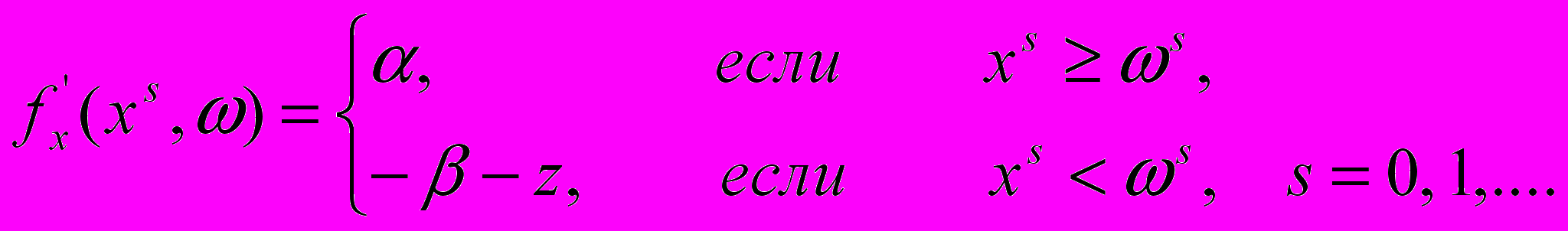(6)

3. Новое приближение определяем согласно рекуррентному правилу:

(7)

Здесь x⁰= 0; ρ_s - величина шага в направлении градиентного спуска на s-й итерации.

Эти условия необходимы для сходимости последовательности {x^s}, полученной согласно (7) к решению задачи х* вероятностью 1.

Алгоритмы не изменяются с изменением закона распределения спроса , не требуется знания этих законов в явном виде. Последнее означает, что алгоритм применим к решению более сложных задач, в которых спрос задается с помощью имитационной модели. Этот алгоритм легко реализуется на компьютере.

В отличие от однопродуктовых задач, ТИК организует запас m видов продукции. Задача состоит в нахождении такого объема запаса x = (x₁, ..., x_m), который минимизирует ожидаемые затраты, т. e.

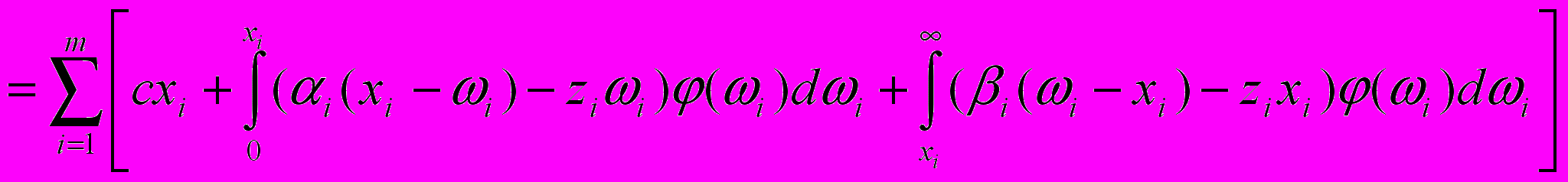, (8)

при ограничениях

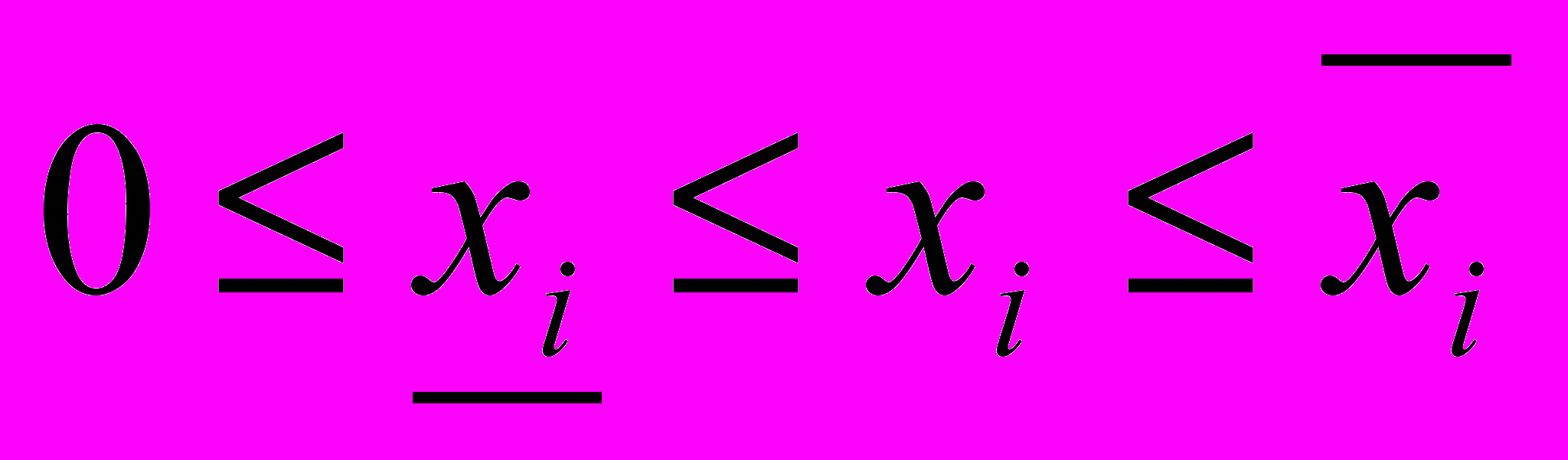. (9)

Здесь функция затрат f_i(x_i, ω_i), связанная с объемом запаса x_i и спросом ω_i, может быть представлена в следующем виде:

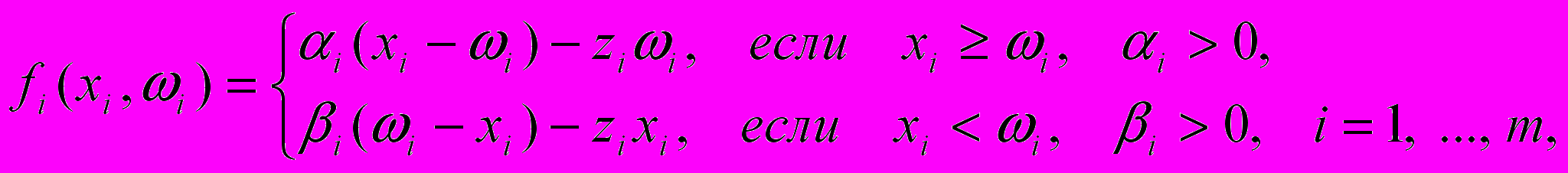(10)

где с_i – затраты, связанные с созданием запаса единицы товара i-ого вида (включая издержки выполнения заказа); α – удельные издержки, связанные с хранением излишнего запаса i-й продукции в единицу времени; β_i – удельные издержки, связанные с потерей от дефицита i-й продукции в единицу времени; z_i– реализационная цена i-ого вида продукц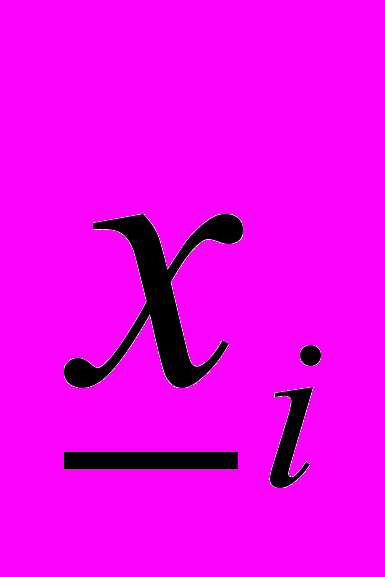ии;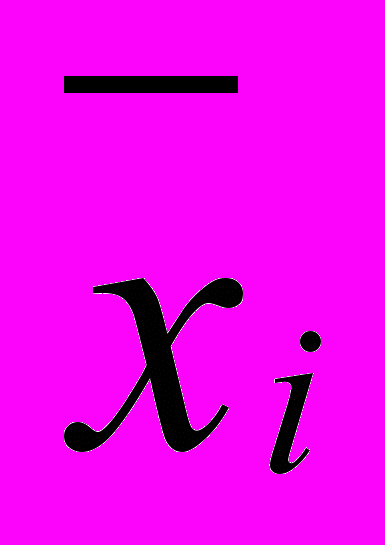

- соответственно нижние и верхние предельные объемы запасаемой продукции i-ого вида.

B частности, когда F(x) имеет непрерывные производные, ее минимум без учета ограничений (9) производится классическим методом, подобным (4), требуемое решение x_i^*, i=1,...,m находится из уравнения

, i= 1,2 …, m, где Ф_i(х_i) = P{ω_i < х_i} - функция распределения ω_i.

Если функция распределения известна, то

.

В случае, когда не известна функция Ф_i(х_i), применение метода стохастического градиента сводится к аналитическому алгоритму 1.

Алгоритм 2. Пусть на s-м итерации получено приближение

, s=0, 1, ..., к оптимальному уровню запаса

(

– начальное приближение может быть выбрано произвольно, например, равным 0). Тогда:

1. B соответствие с исходными данными о значениях спроса получаем наблюдение

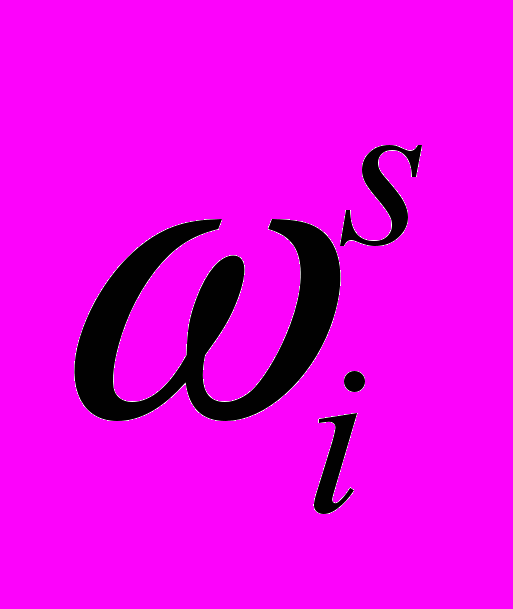над реализацией случайной величины  на s-м итерации. Заметим, что для этого может быть использована имитационная модель спроса.

2. Построим вектор стохастического градиента

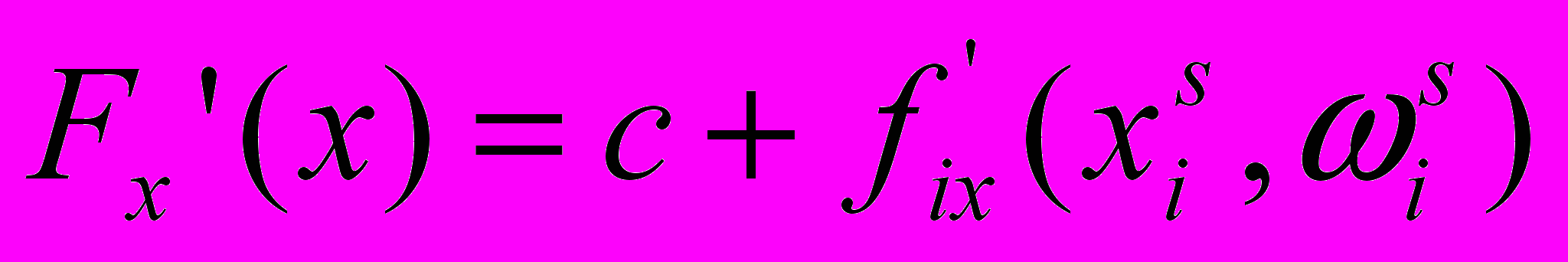, где

- стохастический градиент функции f_i (x_i,_i) в точке

- определяется следующим образом: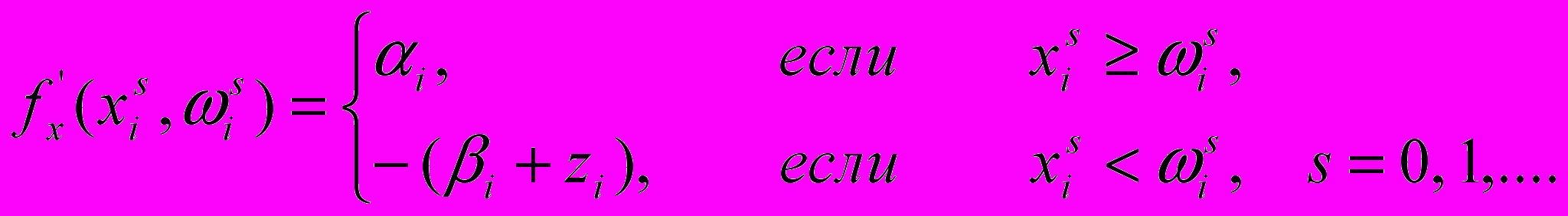

(11)

3. Новое приближение определяем согласно рекуррентному правилу:

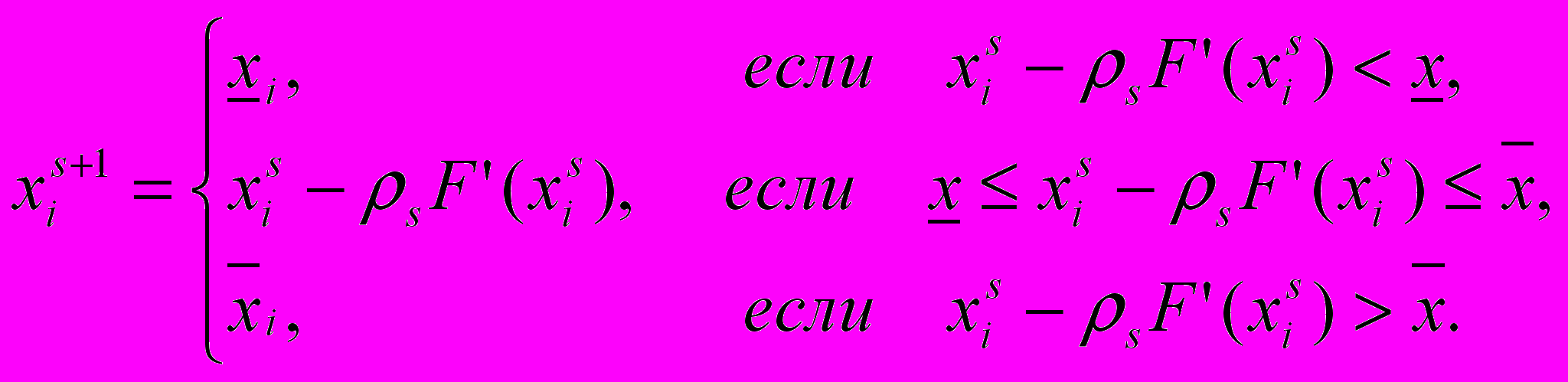(12)

Для сходимости последовательности {

} к решению задачи

достаточно аналогичных условий, приведенных в алгоритме 1 для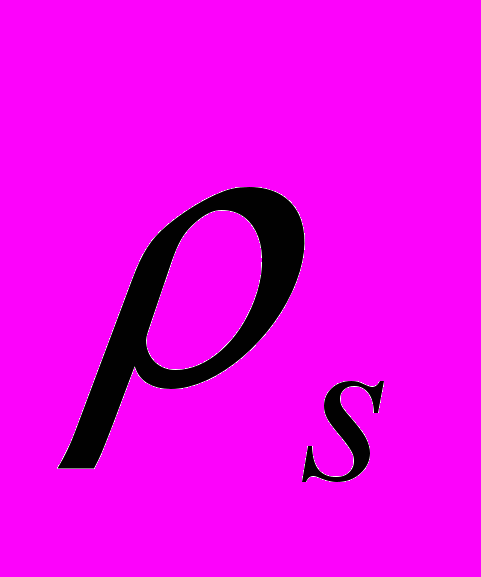

.

Решение задачи УЗ с корректировочными решениями заключается в том, что первоначально принятое (на основе имеющихся статистических данных о спросе) решение об объеме запасаемой продукции в условиях неточной информации и спросе впоследствии уточняется, корректируется по мере получения все более точной информации о них. Общая схема решения задачи УЗ с коррекцией следующая: решение (принятие исходного уровня запаса) - наблюдение (реализация спроса) - решение (определение оптимальной коррекции уровня запаса). Здесь основной целью задач управления запасами с коррекцией является выбор уровня запаса, минимизирующего ожидаемые затраты на его реализацию и коррекцию. Задачи УЗ с корректировочными решениями обладают адаптивными свойствами при принятии оптимального решения относительно уровня запасов.

Корректировка уровня запаса не является следствием недостатков функционирования ТИК, она органически присуща управлению запасами в вероятностных условиях.

В задаче управления запасами с учетом возможных перевозок, с учетом коррекции, в которой требуется минимизировать ожидаемые затраты на излишек, перевозку продукции и ожидаемые потери от дефицита, т.е.

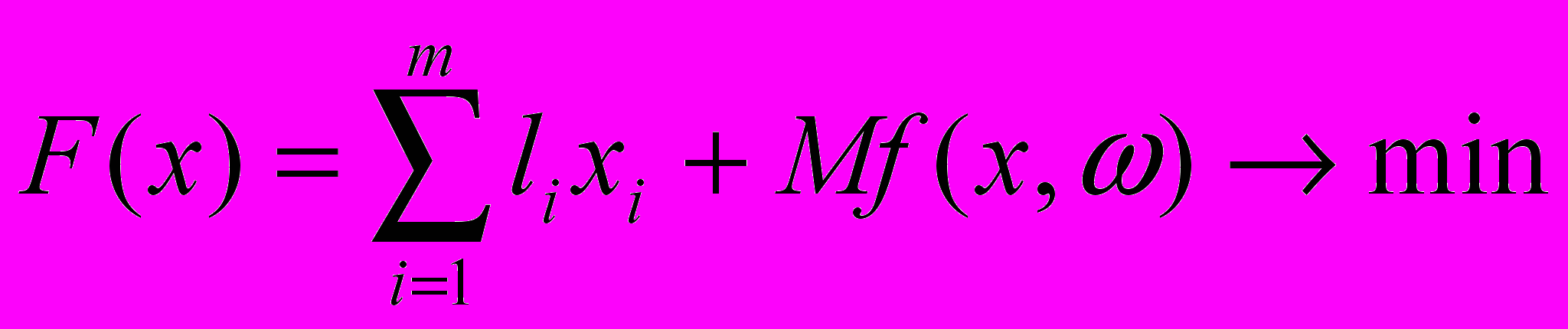, при х_i≥ 0, i= 1, ... , m. (13)

Здесь f(х,) - случайная величина, оптимальное значение целевой функции стохастической транспортной задачи определяется так минимум функции:

. (14)

На переменные y_ij, r_i, и h_i следующие полагаются ограничениями

;

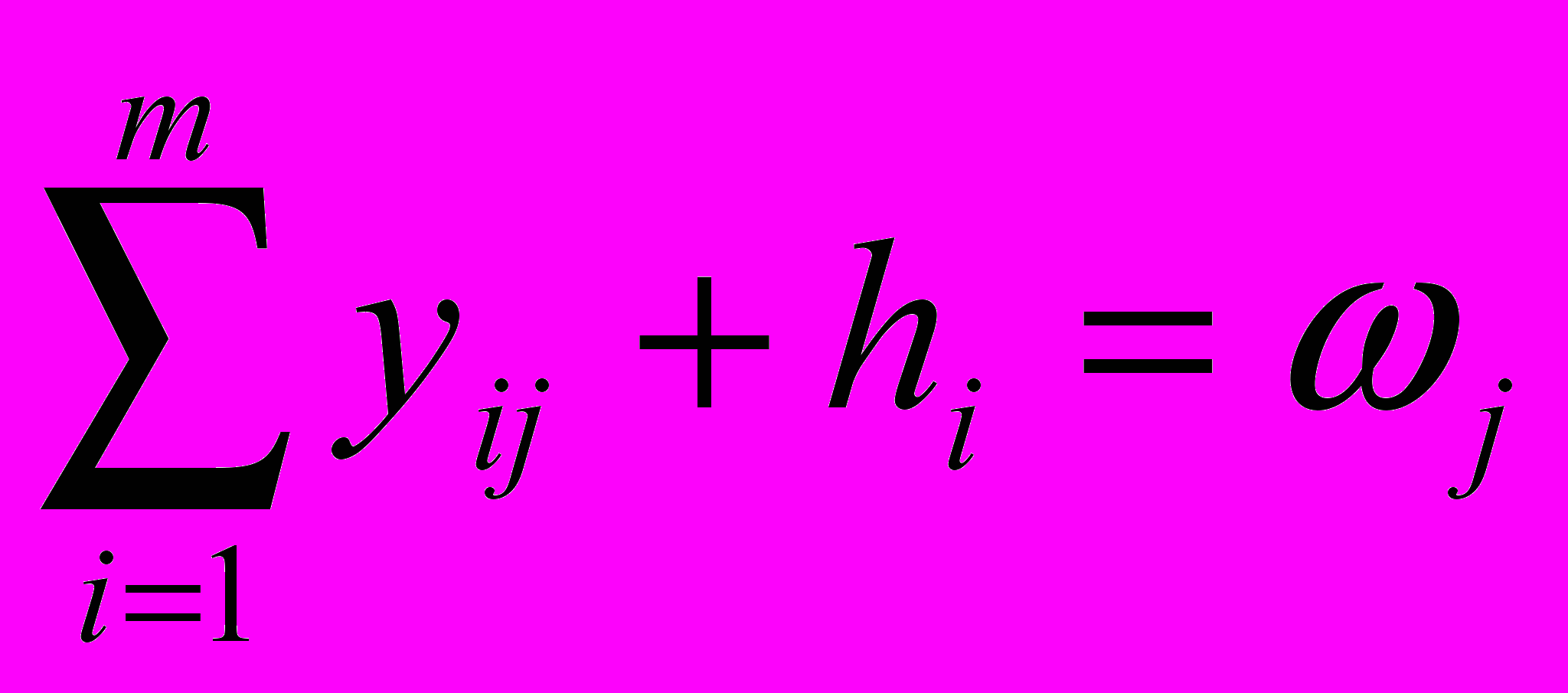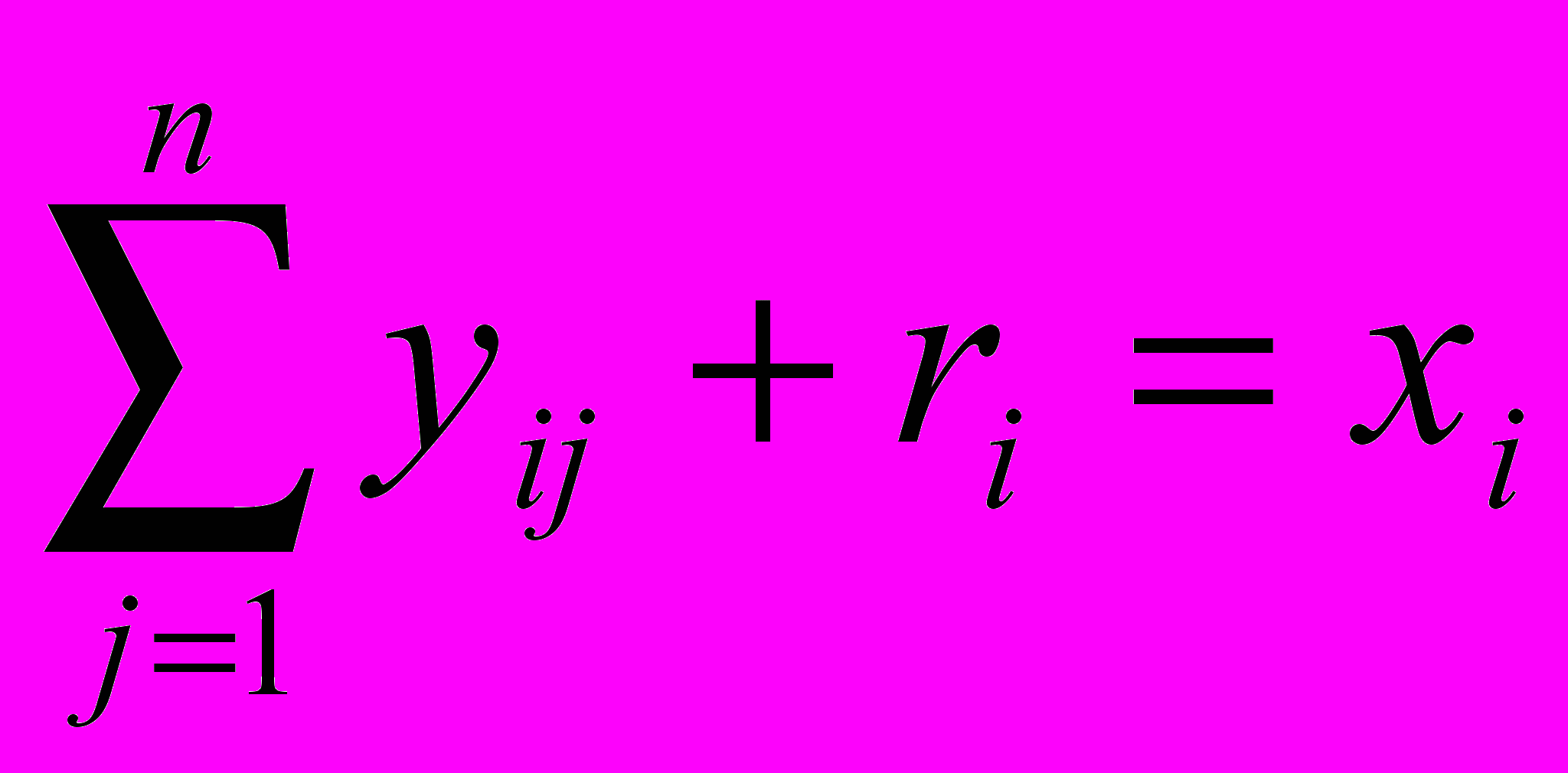; y_ij≥0_,h_j≥ 0, i=1, … , m; _.j =1, … , n. (15)

Задача (13) – (15) является задачей УЗ с коррекцией, где (13) коррекционная; (15) - коррекционная.

В указываемых задачах соответственно два этапа принятия решений: первый - принятие решения о первоначальном уровне запаса; второй - перераспределение запасов между рынками после того, как станет известна величина спроса.

Для решения поставленной задачи (13) - (15) предлагается алгоритм 3.

При рассмотрении и анализе практического применения задачи УЗ с коррекцией, делается вывод о том, какие переменные будут у задачи определения исходного уровня запаса, а какие - у коррекционной задачи.

Динамические задачи УЗ возникают в том случае, когда значения параметров модели изменяются на протяжении интервала управления. Такие изменения могут происходить непрерывно, в каждый момент времени, и тогда рассматривается динамическая модель с непрерывным временем или же в моменты перехода от одного подинтервала (периода) управления к другому - тогда рассматривается динамическая модель с дискретным временем.

Следует отметить, что в силу ряда причин (меньшей информационной сложности, более простого математического аппарата моделирования, дискретного характера получения информации и изменения управляющих воздействий и др.) чаще всего встречаются динамические модели с дискретным временем. Для решения этих задач предлагались методы, основанные на идеях динамического программирования и теории массового обслуживания. Успех применения указанных методов к задачам управления запасами является малоэффективным, поскольку эти методы налагают очень жесткие требования на размерность задач и на законы распределений случайных величин.

Динамические модели УЗ, в которых период управления подлежит дроблению, а продукт, оставшийся к концу предыдущего временного отрезка, может использоваться для удовлетворения спроса на следующем временном отрезке, т.е. управляющие воздействия являются функциями времени.

Изменениями параметров модели во времени далеко не всегда можно пренебречь. Это можно сделать, например, в случае относительно короткого интервала управления или в случае стационарного протекания процесса управления.

Детерминированные и стохастические задачи управления запасами динамического типа рассматривались в работах отечественных и зарубежных ученых. Для решения этих задач предлагались методы, основанные на идеях динамического программирования и теории массового обслуживания. Успех применения указанных методов к задачам управления запасами является малоэффективным, поскольку эти методы налагают очень жесткие требования на размерность задач и на законы распределений случайных величин.

Пусть функционирование ТИК рассматривается в течение t интервала [0, T], который разбивается на N период. В течение этих периодов ТИК должна удовлетворять случайный спрос _t на некоторый однородный продукт х_t в t-м периоде. Функция распределения спроса или ее реализации считается известной. Спрос _t удовлетворяется полностью или частично - в той степени, в какой это позволяет сделать имеющийся в наличии запас. Если спрос _t не удовлетворен полностью, то величина неудовлетворенного спроса y_t определяется по формуле

(16)

Предположим, что величина ранее не удовлетворенного спроса у_t не учитывается в (t + 1)-м периоде. В этом случае ТИК терпит убытки, прямо пропорциональные величине неудовлетворенного спроса ω_t. Стратегия управления запасами состоит в проверке, достигнут ли уровня запаса нижнего контрольного (критического) уровня

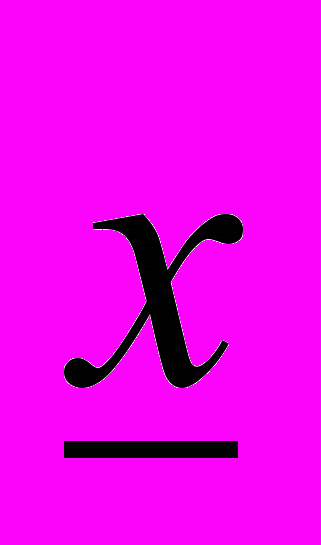, т.е. выполняется ли условие х_t ≤

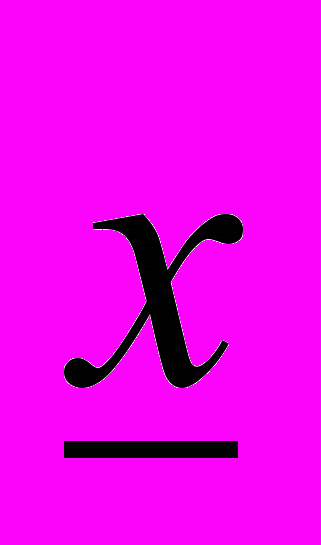. Если это так, и ранее посланная заявка для увеличения объема запаса удовлетворена, то подается новая заявка для увеличения объема запасаемой продукции. Объем одновременного увеличения запаса фиксирован и равен верхнему контрольному уровню

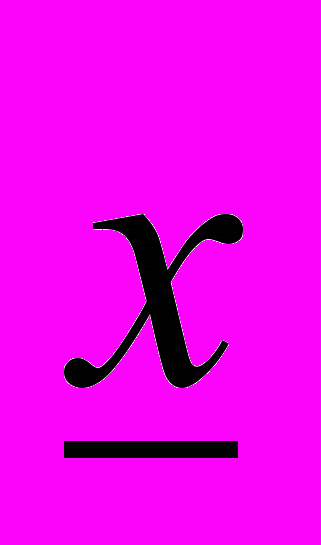. При этом объем запасаемой продукции проверяется только в дискретные моменты времени через равные интервалы, например, совпадающие с началом каждого периода. Срок поставки заказанной новой партии продукции равен l, l < N.

Математическая постановка задачи заключается в нахождении таких оптимальных параметров

, которые минимизируют ожидаемые затраты ТИК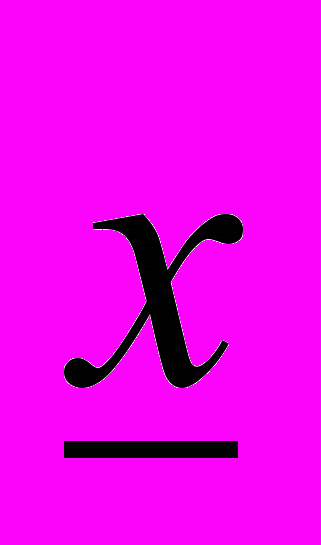 F(

) = Mf(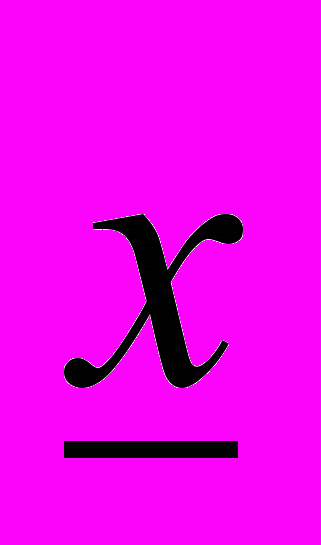

, ) при условии 0≤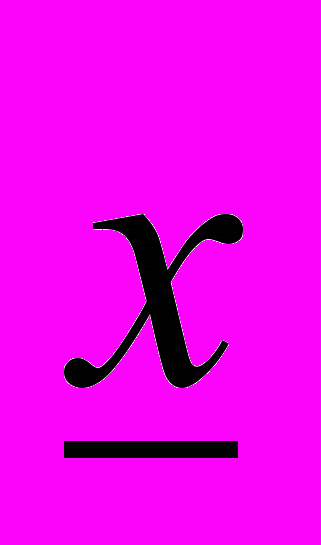

≤

.

Здесь f(

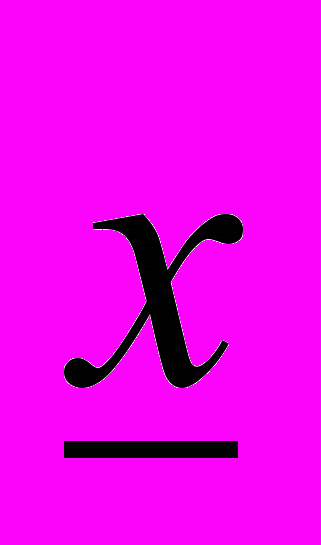, ) – стоимостная функция, выражает суммарные затраты, связанные с функционированием ТИК и определяется следующим образом:

. (17)

Здесь:

;

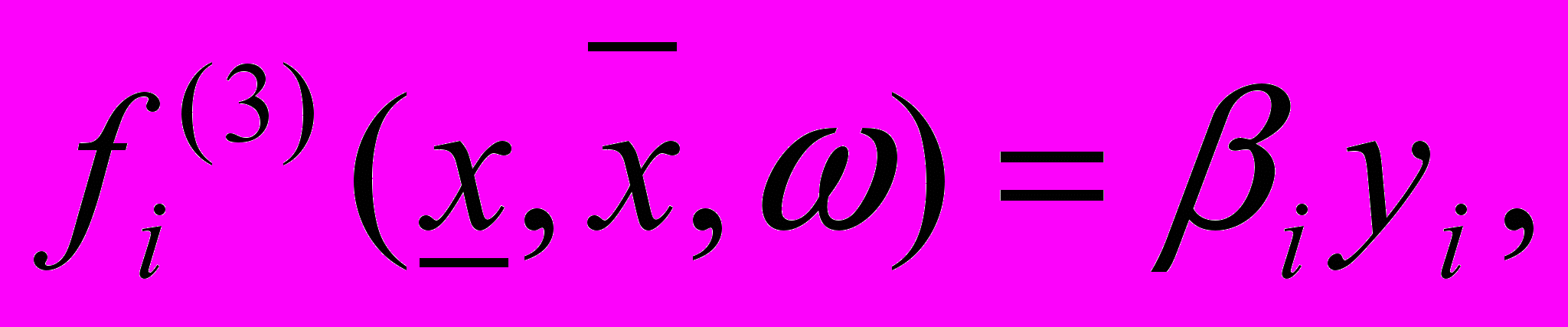соответственно являются затраты на создание, затраты на хранение излишнего и потери от дефицита запасаемой продукции.

На рисунке 4 приведена блок-схема функционирования имитационной модели рассматриваемой задачи управления запасами. В результате (проигрывания) эксперимента, на выходе, получаем числовое значение функции (17). Соответствующий этому цикл моделирования обведен за штриховым прямоугольником.

Алгоритм решения задачи принципиально не отличается от предыдущих.

Рассмотрение концептуальной постановки другой практической задачи УЗ заключается в следующем. Планирование в иерархических системах МТС объединенных авиаотрядов осуществляется ежегодно за определенный срок до окончания текущего года. Исходя из ожидаемого на конец года остатка данного материала, делается годовая заявка (потребность в ресурсах) П:

П = ПП +(НЗ + СЗ – О), (18)

где ПП - производственный запас для удовлетворения спроса приписного самолетно-вертолетного парка; О – остаток; НЗ - неснижаемый запас, предназначенный для удовлетворения спроса рейсовых самолетов других государственных управлений авиапредприятий (ГУАП); СЗ - страховой запас, рассчитанный на компенсацию срывов поставок.

Так как поставки авиатехнического имущества (АТИ) предусматриваются раз в квартал, то производится определение уровня запасов на каждый квартал (кроме СЗ, который является переходящим) и годовая заявка получается путем суммирования квартальных запасов с учетом остатков по формуле (18), что является недостаточным.

На самом деле уровни запасов АТИ каждого вида, а соответственно и потребность в ресурсах, определяются спросом имущества на планируемый период (год). В системе МТС ГУАП в связи с условиями эксплуатации - переходом на обслуживание авиатехники «по состоянию», спрос обусловлен многими факторами, имеющими случайный характер. Изучение расхода ряда запасных

частей, агрегатов и механизмов (на основе 5 летней статистики) подтвердило стохастический характер спроса АТИ. Сложность и ответственность планирования в иерархической многоэлементной системе снабжения со случайным спросом усугубляется необходимостью учета больших потерь от простоя самолетно-вертолетного парка в случае дефицита авиационно-технического имущества и значительных расходов на хранение и поддержание в нормальном состоянии излишков запаса в случае избытка авиационно-технического имущества.

Для нее, кроме введенных обозначений, введены следующие обозначения: x_i,

- начальный уровень запаса на i-м складе; _j,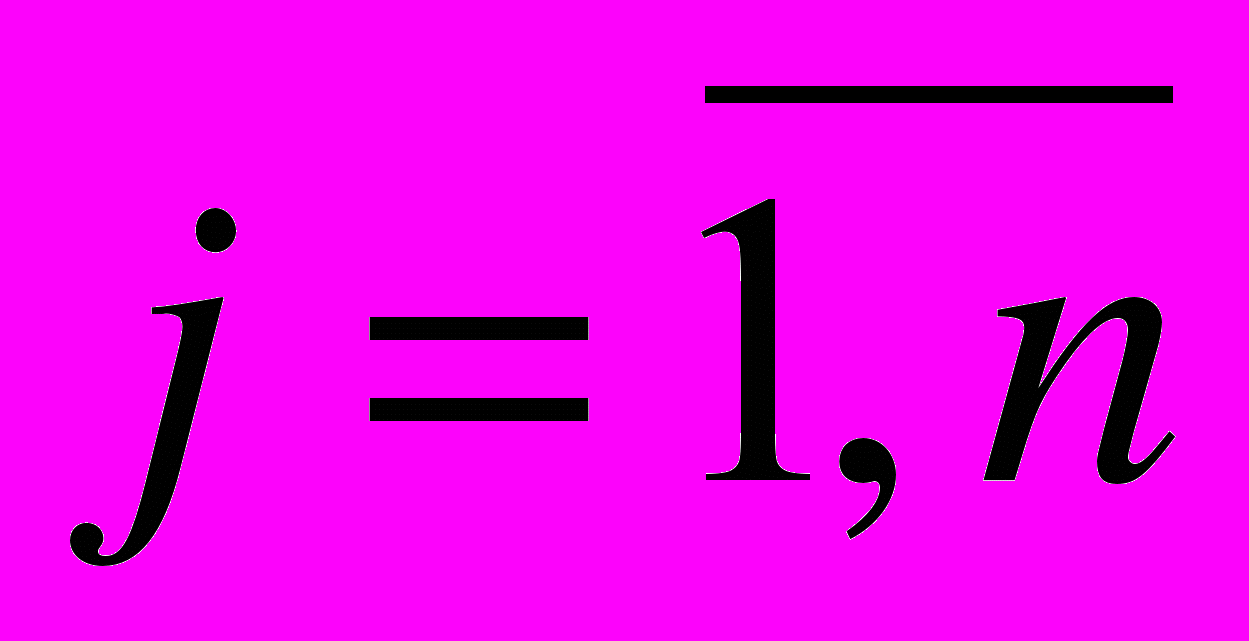

- случайные величины, характеризующие спрос на запасные части j-й авиационно-технической базы (АТБ); y_ij - объем поставок запасных частей из i-го склада на j-ю базу; c_ij - удельные затраты на перевозку запасных частей из i-го скла-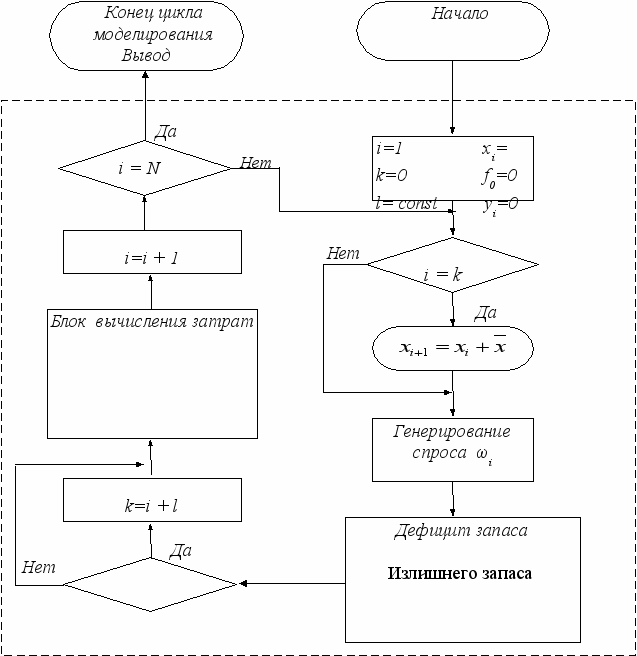

Примечание – составлен автором

Рисунок 5 - Блок-схема вычисления ожидаемых суммарных затрат

да на j-ю базу; α_i - удельные затраты на хранение запасных частей i-м складе; β_j - удельные потери, вызваные дефицитом запасных частей на j-й базе. Предполагается, что β_j≥ max c_ij, где максимум вычисляется для тех пунктов хранения i, перевозки из которых в пункт потребления j допустимы.

Задача состоит в выборе такого начального уровня запаса АТИ, который минимизирует ожидаемые суммарные затраты, связанные с хранением, дефицитом и перевозкой запасных частей.

Экспериментальная реализация моделей и алгоритмов управления товарно-материальными запасами

Основными характеристиками товарного потока как объекта торговой логистики является его количество, которое определяется: объемом и режимом потребления пользователя и мощностью производителя; пропускной способностью торгового посредника; характером производственного процесса поставщика-изготовителя продукции; эффективностью работы транспорта и средств связи; финансовыми возможностями субъектов торговой деятельности, их способностью своевременно и в полном объеме осуществлять поставку продукции.

Объектом реализации разработок является торговая компания (или торговая инвестиционная компания) ООО «КОМ», которая реализует строительные материалы. Компания имеет конгломерат - сеть магазинов. Эти магазины занимаются продажей строительных материалов. Имеется общий склад, куда поставляются материалы на временное хранение, и магазины, где осуществляется их розничная продажа. Одновременно с этим со склада товары продаются оптом. Магазины находятся на территории города Душанбе.

При решении задачи (1), (2), расчеты проводились для следующих значений её параметров: стоимость 1 м³ пилолесного материала к моменту доставки его на склад (включая издержки выполнения заказа) составляет с = 153 у.е.; издержки на хранение 1 м³ доски α = 3 у.е за год; потери от дефицита 1 м³ доски β = 44 у.е.; спрос ω – равномерно распределенный на интервале [3100; 3450], т.е. согласно классическому подходу, оптимальный уровень запаса будет x*= 3226,2 м³. При этом объем инвестиции ТИК составляет

I = 153 ·3226,2 = 493608,6 у.е.

Выполненный расчет показывает, что размер оптимальной партии поставки с целью создания запасов существенным образом зависит от расходов на издержки хранения и реализуемой цены. Так, если организация поставки и хранения одного вагона лесного материала по нашим расчетам составляет 9180 у.е., то издержки на хранение 60 м³леса в течение года определяются в размере 60 м³х 3 у.е. = 180 у.е.

Результат с использованием алгоритма 1 приведен в таблице 2 и на рисунке 6.

Как видно из третьей строки таблицы 2, значение ожидаемых затрат совпадает с его значением, найденным классическим методом, а уровень запаса x*=3229,137 м³не совпадает. Такая картина естественно возникает из-за неточности, априорной информации, относительно случайного спроса. При проведении расчетов нет необходимости в получении высокой точности решений.

Далее решается многопродуктовая задача УЗ для ООО «КОМ» по созданию пяти видов пилолесного материала для дальнейшей его реализации населению южных регионов Республики Таджикистана.

Расчеты проводились для следующих значений параметров модели: ω_i– случайные величины, равномерно распределенные на интервале [l_i, q_i], i = 1,...,5. Векторы l = (l_l, ..., l₅), q = (q₁, ..., q₅), = (α₁, ..., α₅); β = (β₁, ..., β₅), заданы в виде l = (9700, 9500, 7000, 6600, 4850), q = (10000, 10000, 7500, 6800, 5000),

Таблица 2. Расчет оптимального уровня запаса пилолесного материала при изменении расходов на издержки хранения и неизменности реализационной цены (z = 244 у.е.)

п\н	Издержки хранения - , (м³/у.е.)	Оптимальный уровень запаса х*, (м³)	Суммарные ожидаемые затраты - F(х), (у.е.)
1	1	3227,636	628045,993
2	2	3227,445	628040,627
3	3	3229,137	627781,795
4	4	3229,568	627759,130
5	5	3226,983	627706,900
6	6	3229,264	627740,569
7	7	3226,274	627630,122
8	8	3225,976	627464,159
9	9	3225,954	627308,898
10	10	3226,137	627294,557
Примечание – составлена автором на основе расчетных данных

α = (5, 5, 5, 5, 5), β = (50, 45, 45, 30, 39), с=(210, 200, 190, 185, 157), z=(260, 245, 235, 215, 196).

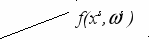
Рисунок 6 - График процесса оптимизации уровня запасов через каждые 10 итераций

Спрос ω – равномерно распределенный на интервале [l_i, q_i].

x* = (9780,7972; 9644,3672; 7168,0885; 6655,7884; 4880,9800),

F(х*) = 8949085,51.

В результате исследования алгоритма 2 получен оптимальный уровень запаса.

Blog

Оптимизационные модели и методы управления товарно-материальными запасами 08. 00. 13 Математические и инструментальные методы экономики

Содержание