Методические указания по практическим занятиям По дисциплине

Вид материала

Методические указания

Содержание Варианты индивидуальных заданий Номер варианта

Подобный материал:

• Методические указания к изучению курса и практическим занятиям для студентов спец., 914.85kb.
• Методические указания по практическим занятиям По дисциплине Математические методы, 129.27kb.
• Методические указания по практическим работам По дисциплине, 193.22kb.
• Методические указания к практическим работам по дисциплине «Экология», 365.02kb.
• Методические указания к практическим занятиям по дисциплине «Элементы и процессы архитектурного, 214.83kb.
• Методические указания для доаудиторной подготовки к практическим занятиям по эпидемиологии, 1893.8kb.
• Методические указания к лабораторно-практическим занятиям для студентов очного и заочного, 620.25kb.
• Методические указания к практическим занятиям и индивидуальные домашние задачи по физике, 635.57kb.
• Методические указания Задания к практическим занятиям Контрольные задания, 752.95kb.
• Методические указания к практическим занятиям для студентов нефилологических специальностей, 717.63kb.

Тема 7. Теория игр

Задание. Игры в чистых стратегиях.

Исполнение. Определить цену игры и стратегии игроков.

Оценка. Формирует необходимые представления о моделировании конфликтных ситуаций.

Время выполнения заданий: 2 часа.

Пример задачи. Для платежной матрицы определить: нижнюю и верхнюю цену игры; минимаксные и максиминые стратегии; наличие седловых точек; количество стратегий у каждого игрока; тип игры.

Решение задачи:

min max

j i




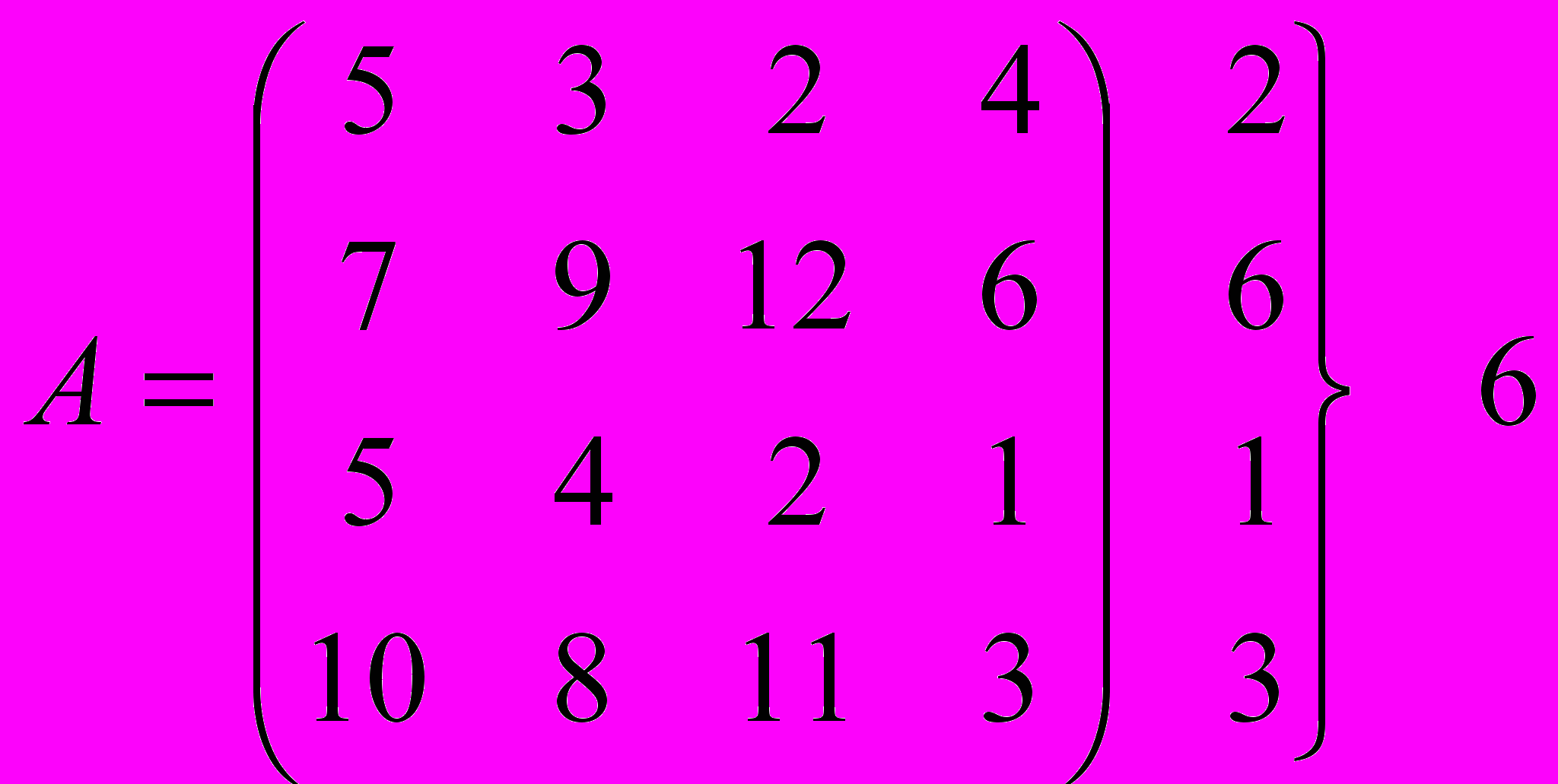
max 10 9 12 6

i

min 6

j

Нижняя цена игры 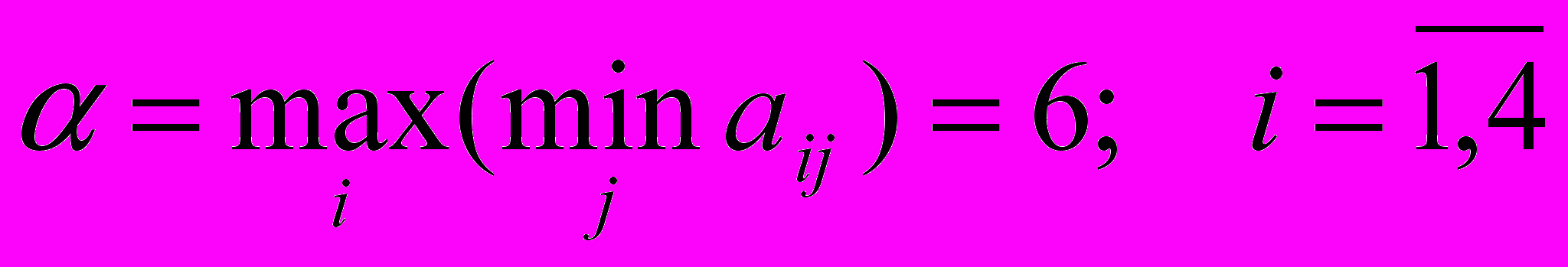- стратегия первого игрока (строки).

Верхняя цена игры 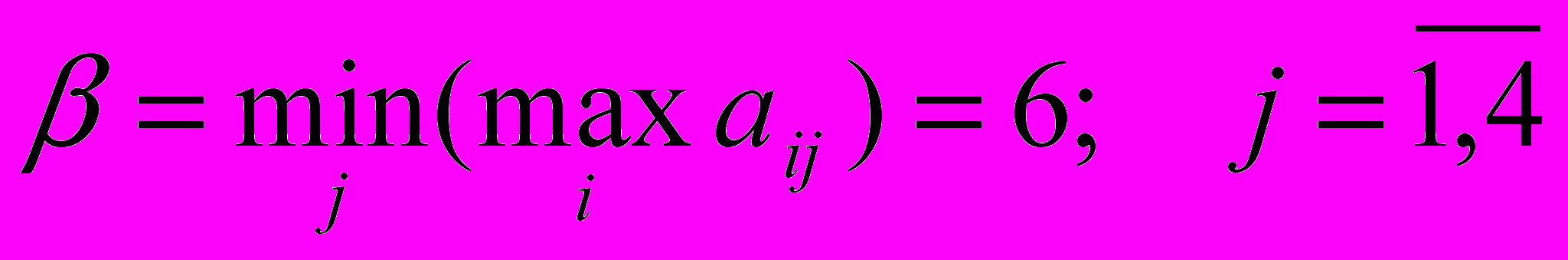- стратегия второго игрока (столбцы).

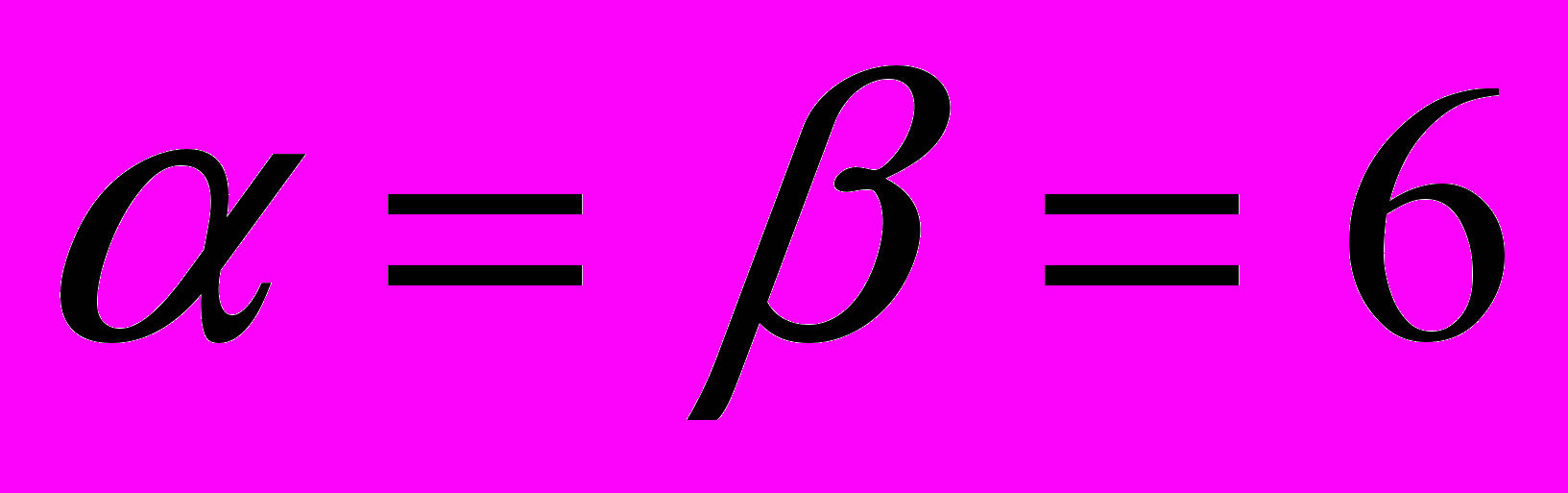- цена игры.

Таким образом, игра имеет седловую точку. Стратегия j = 4 – оптимальная для второго игрока (минимаксная стратегия), стратегия i =2 - для первого (максиминная стратегия). Имеем игру с чистыми стратегиями. Каждый из игроков имеет по 4 стратегии.

Варианты индивидуальных заданий

Задание. Для платежной матрицы определить: нижнюю и верхнюю цену игры; минимаксные и максиминые стратегии; наличие седловых точек; количество стратегий у каждого игрока; тип игры.

Номер варианта	Платежная матрица
1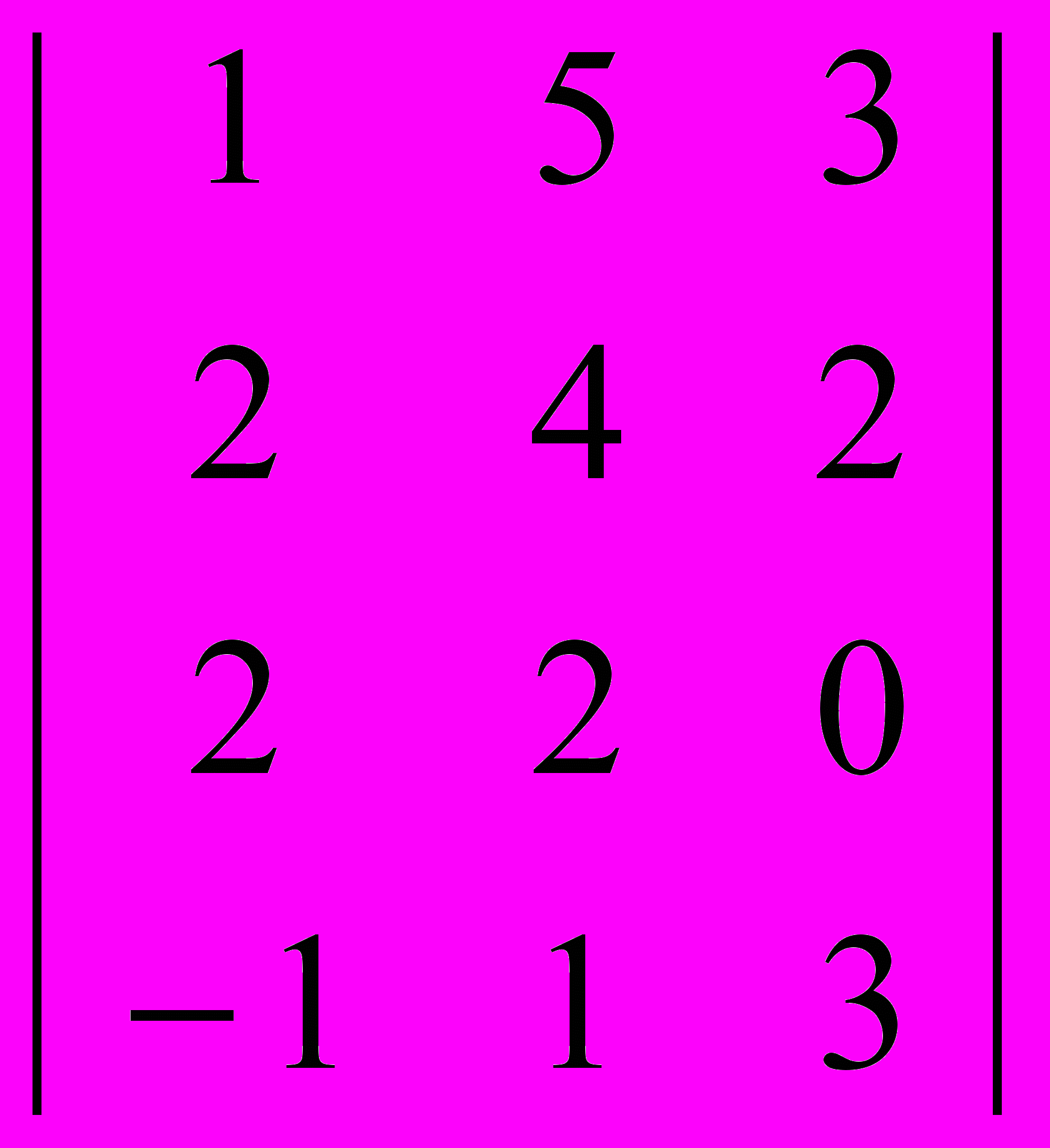
2
3
4
5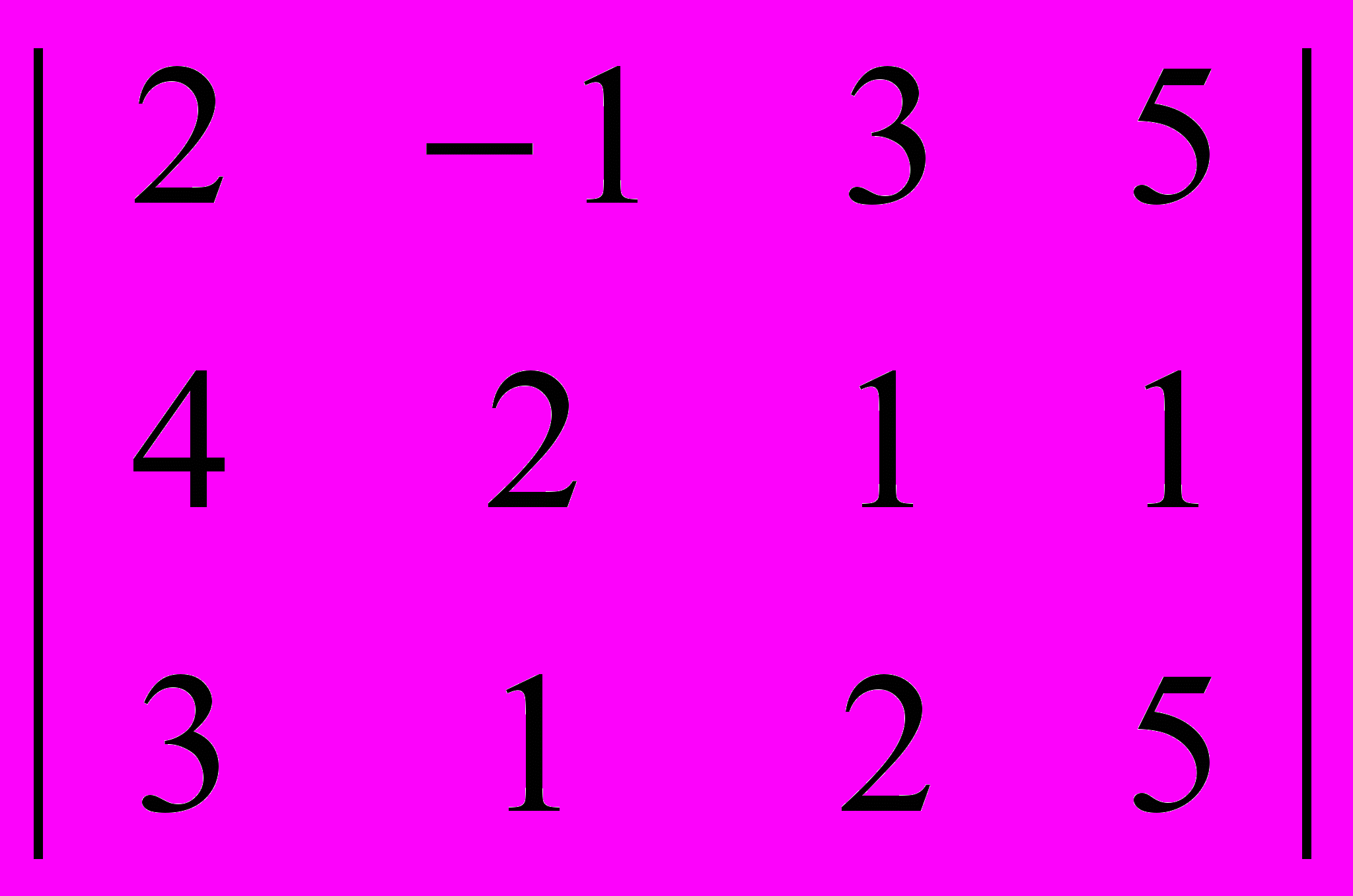
6
7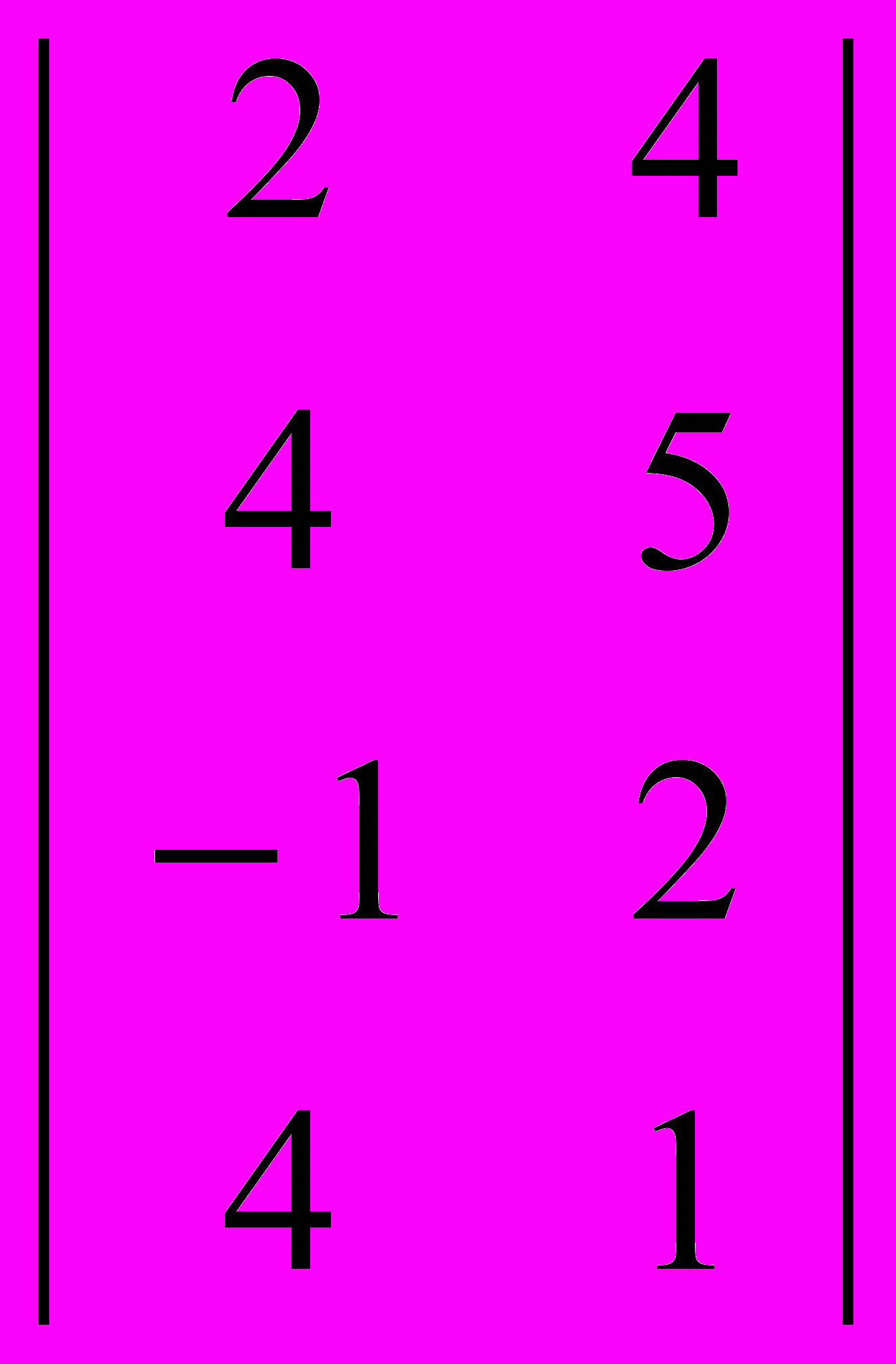
8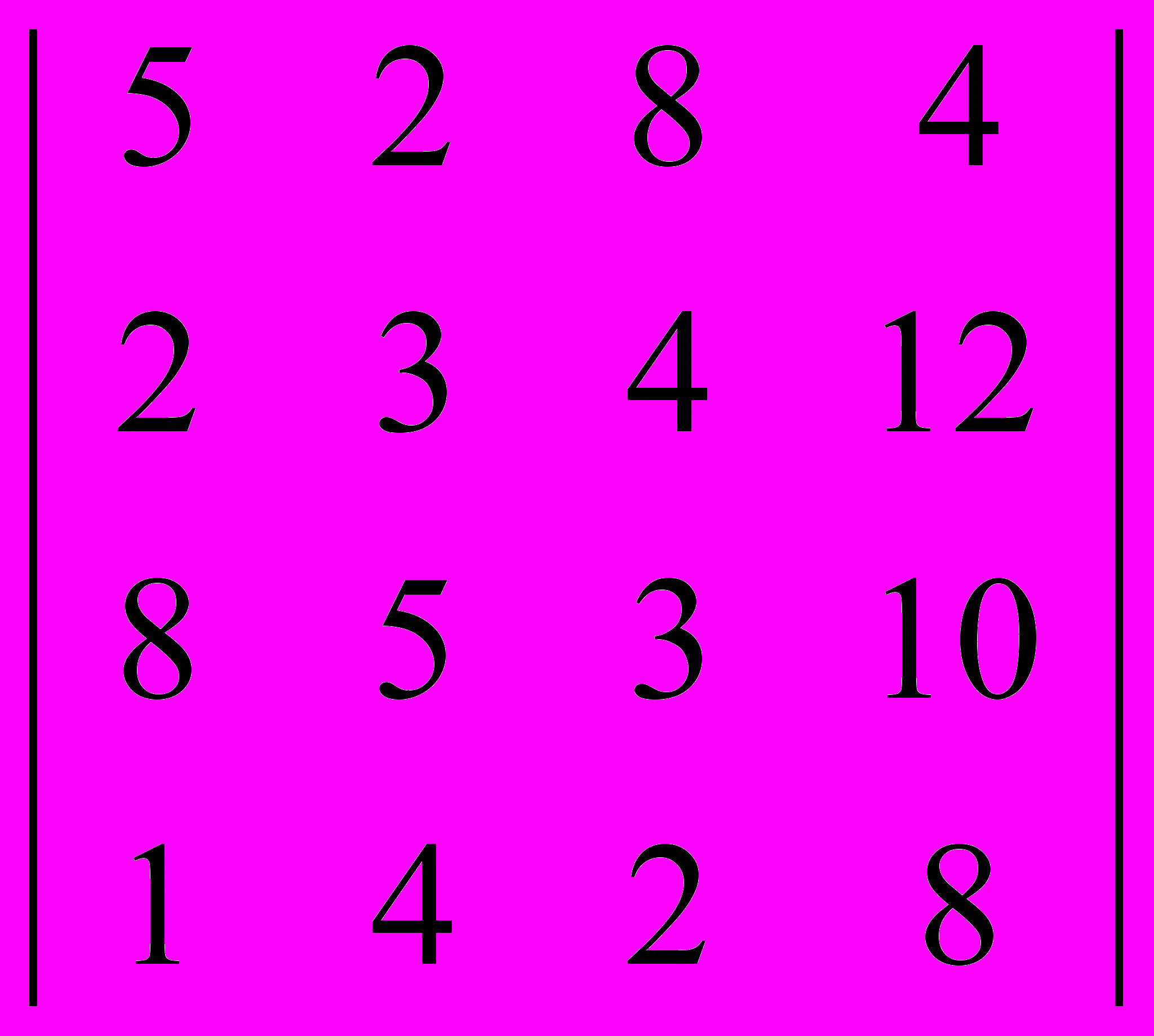
9
10

Тема 8. Динамическое программирование

Пример задачи. Дана схема маршрута движения (рисунок 1) с указанными на ней длинами l_ij маршрутов (км). Определить кратчайший маршрут движения из пункта А в В (где i – исходный пункт, j - входящий).

Решение задачи:

1. Определяются шаги оптимизации. Их всего четыре.

2. Присваиваем функцию длинны маршрута на последнем шаге F₄ = 0 и далее по шагам до начального (нулевого) шага.


Шаг 3. F₃ = l_3,4 + F₄ = 8 + 0 = 8.


Шаг 2. На этом шаге два пункта (2/1) и (2/2).





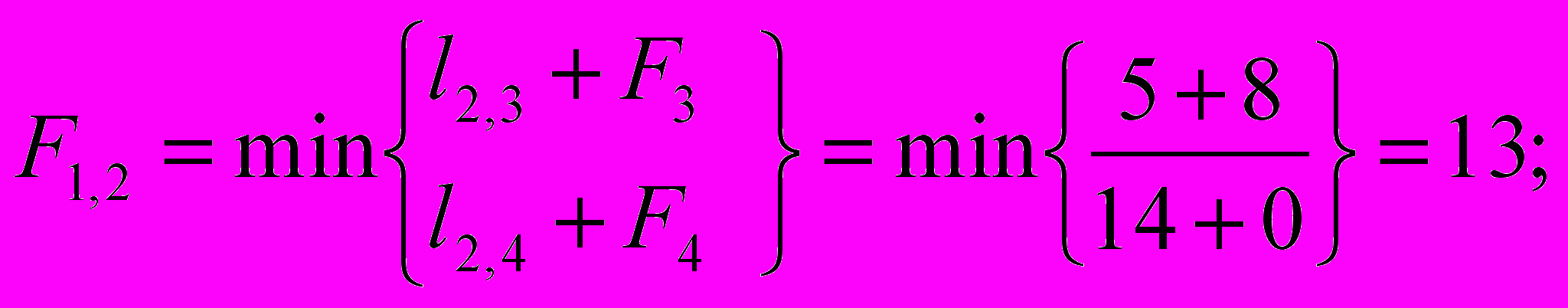
F_2,2 = l_{2 / 2,4} + F₄ = 5 + 0 = 5.


Шаг 1. На этом шаге также два пункта:








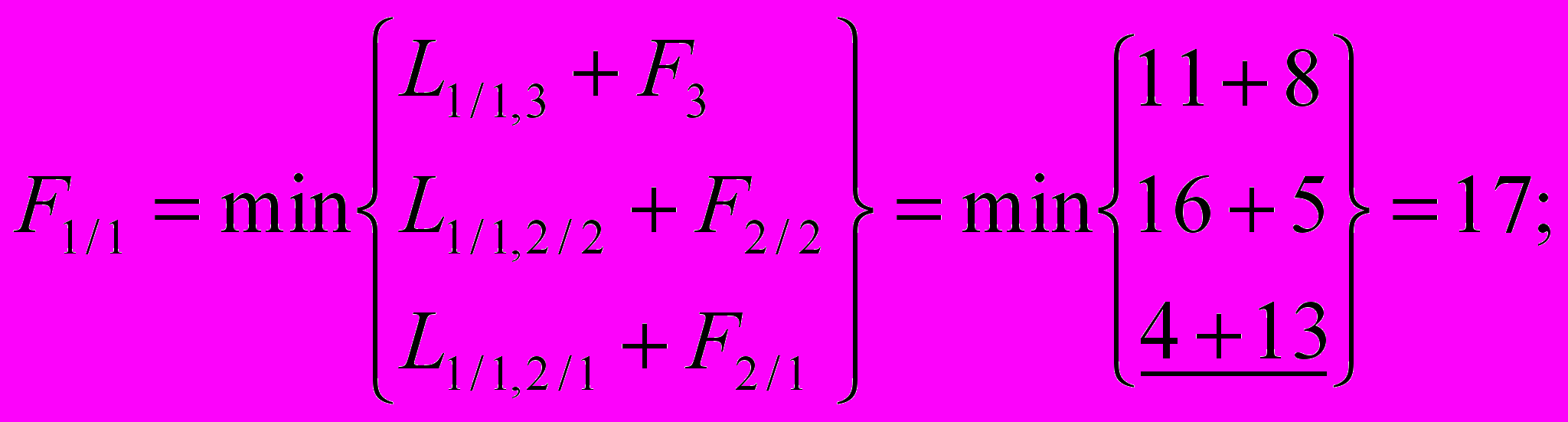
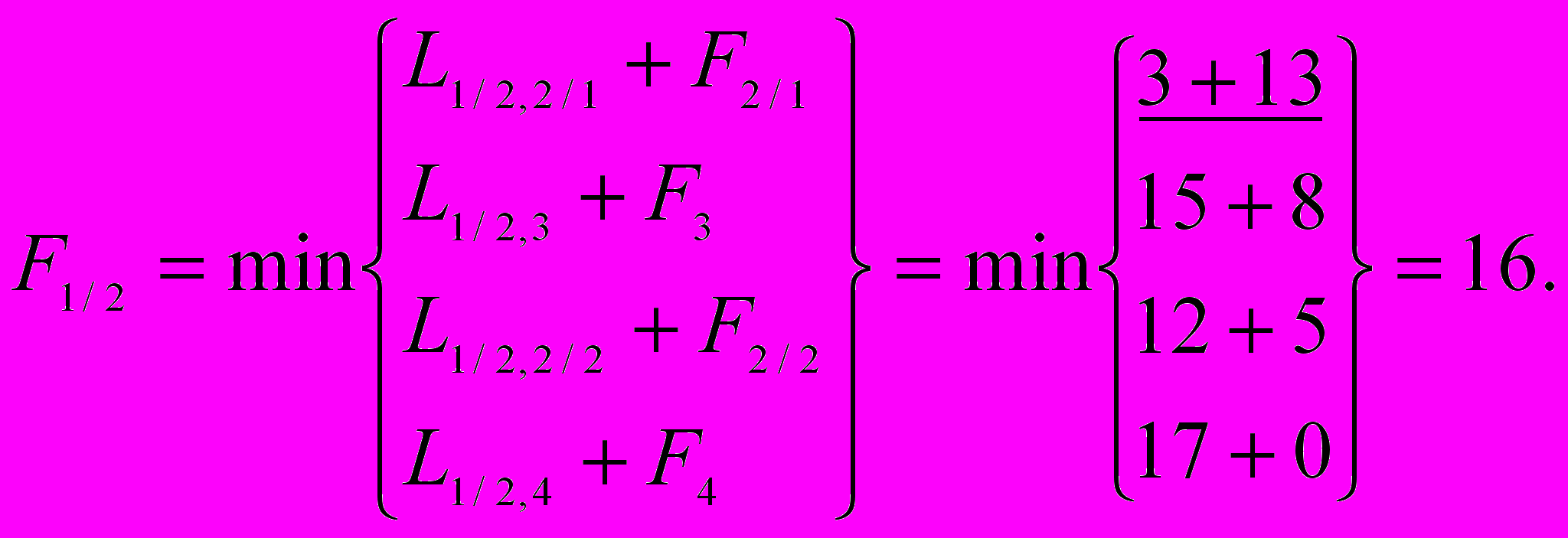
Шаг 0. Начало движения:






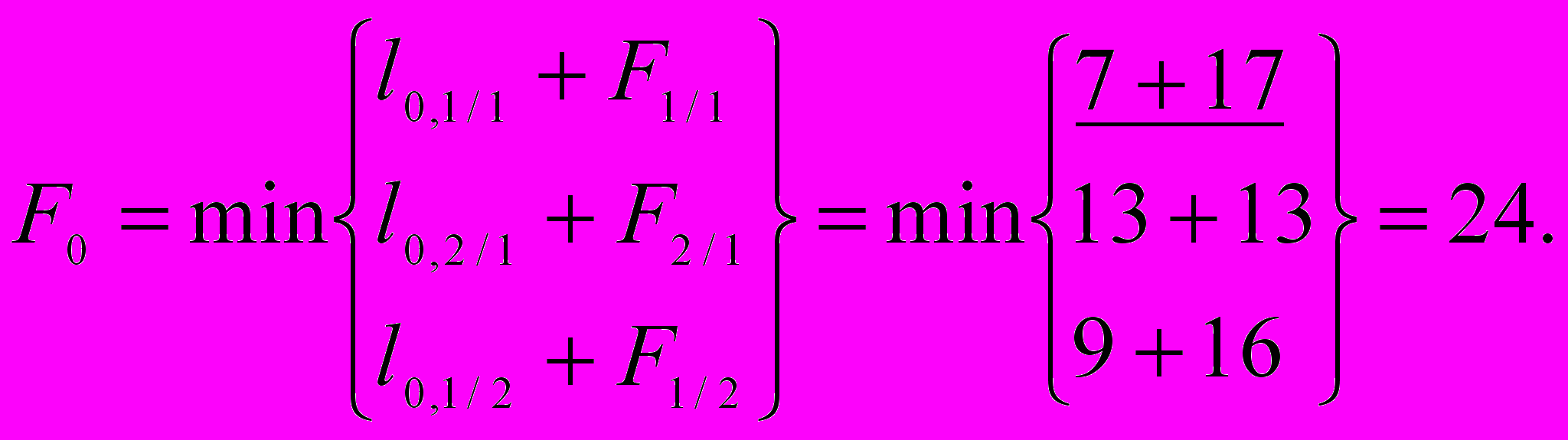
3. По выделенным на каждом шаге маршрутам (подчеркнуты линией) формируем кратчайший, составляющий целевую функцию F₀ = 24 (на рис. 8.2) он выделен жирной линией).





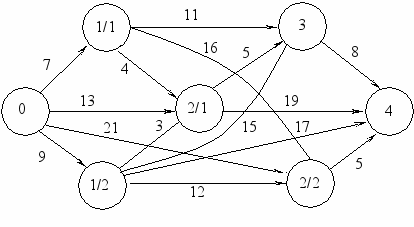
Метки на

маршрутах

Рисунок 1


2. Учебно-методическое обеспечение дисциплины

Основная литература:

1. Акулич И. Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993.

2. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. – М.: Финансы и статистика, 2001.

3. Монахов А.В. Математические методы анализа экономики. – СПб.: Питер, 2002.

4. Пазюк К.Т. Математические методы и модели в экономике. – Хабаровск, 2003.

5. Хазанова Л.Э. Математическое моделирование в экономике. – М.: Издательство БЕК, 1998 .

6. Экономико-математические методы и прикладные модели / под ред. В.В. Федосеева. – М.: ЮНИТИ, 2000.

7. Экономико-математические методы и модели / под ред. С.И. Макарова. – М.: КНОРУС, 2009.

8. Экономико-математические методы и модели. Задачник / под ред. С.И. Макарова, С.А. Севастьяновой – М.: КНОРУС, 2009.

9. Экономико-математические методы и модели / под ред. А.В. Кузнецова – Мн.: БГЭУ, 2000.


Дополнительная литература:

1. Афанасьев М.Ю., Суворов Б.П. Исследование операций в экономике: модели, задачи, решения. – М.: ИНФРА-М, 2003. – 444 с.

2. Вентцель Е.С. Исследование операций. – М.: Советское радио, 1972.

3. Красс М.С., Чупрынов Б.П. Математика для экономистов. – СПб.: Питер, 2005. – 464 с.

4. Кремер Н.М. Исследование операций в экономике. – М.: ЮНИТИ, 1997.

5. Калихман И.Л Сборник задач по математическому программированию. – М.: Высшая школа, 1975.

6. Таха Х. Введение в исследование операций: В 2 кн. – М.: Мир, 1985.