Методические указания по практическим работам По дисциплине
| Вид материала | Методические указания |
- Методические указания к практическим работам по дисциплине «Экология», 365.02kb.
- Методические указания по выполнению курсовой работы по дисциплине «Бухгалтерский учет», 1289.64kb.
- Методические указания по выполнению курсовой работы по дисциплине «Бухгалтерский учет», 1382.18kb.
- Методические указания по практическим занятиям По дисциплине Математические методы, 129.27kb.
- Методические указания по лабораторным работам По дисциплине, 929.67kb.
- Методические указания по лабораторным работам По дисциплине, 803.46kb.
- Методические указания по практическим занятиям По дисциплине, 519.54kb.
- Методические указания к лабораторным работам по дисциплине «Материаловедение и ткм», 215.09kb.
- Методические указания к изучению курса и практическим занятиям для студентов спец., 914.85kb.
- Методические указания к практическим занятиям по дисциплине «Элементы и процессы архитектурного, 214.83kb.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
Тихоокеанский государственный университет
Институт экономики и управления
Кафедра Экономическая кибернетика
Методические указания по практическим работам
По дисциплине Многомерные статистические методы
Для специальности
080116.65 «Математические методы в экономике»
Методические указания разработаны в соответствии с составом УМКД
Методические указания разработала Порошина Л.А. _____________
Методические указания утверждены на заседании кафедры,
протокол № ______ от «___» _______________ 200__ г.
Зав. кафедрой _________ «___» ______________ 200__ г. Пазюк К.Т.
Методические указания по практическим занятиям по дисциплине «Многомерные статистические методы» включают тематику вопросов, выносимых для самостоятельной подготовки, задачи, которые решаются студентами под контролем преподавателя или самостоятельно во время аудиторных занятий.
Методические указания рассмотрены и утверждены на заседании УМКС и рекомендованы к изданию
протокол № ______ от «___» _______________ 200__ г.
Председатель УМКС _______ «___» __________ 200__ г.
Директор института _________ «___» ____________ 200__ г. Зубарев А.Е.
Введение
Знание методов многомерной статистики сегодня необходимо не только для аналитической работы, но и для понимания новейших теорий по обработке данных массовых наблюдений.
Целью курса «Многомерные статистические методы» является ознакомление студентов с теоретико-методологическими основами использования в социально-экономических исследованиях количественных методов, конкретной математико-статистической методики сбора, обработки, анализа и системной интерпретации данных массовых источников.
К основным задачам дисциплины следует отнести:
- показать связь количественной и качественной стороны социально-экономических процессов как методологическую основу количественных методов;
- определить объективные социальные и научные, методологические и методические предпосылки включения в арсенал научной методики общенаучных, системных статистических методов;
- охарактеризовать основные принципы, направления и области применения многомерных статистических методов;
- опираясь на теорию моделирования ознакомить студентов с основными математико-статистическими методами, главными направлениями и возможностями их сущностно-содержательной интерпретации в рамках поставленной задачи;
- дать оценку роли методов математического моделирования в исследовании проблем экономического и социального развития страны.
Практические занятия по дисциплине проводятся в форме решения практических заданий по теме.
Завершается изучение дисциплины "Многомерные статистические методы" сдачей зачёта.
4. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
4.1. Разделы дисциплины и виды занятий и работ
Таблица 2. Разделы дисциплины и виды занятий и работ
| № | Раздел дисциплины | Л | ПЗ | С2 |
| 1 | Теоретические основы многомерного статистического анализа (МСА). Проверка статистических гипотез | 4 | 2 | 4 |
| 2 | Дисперсионный анализ | 2 | 2 | 7 |
| 3 | Многомерный регрессионный анализ | 4 | 1 | 7 |
| 4 | Кластерный анализ | 6 | 4 | 14 |
| 5 | Факторный анализ | 8 | 3 | 14 |
| 6 | Дискриминантный анализ | 6 | 3 | 11 |
| 7 | Многомерное шкалирование | 4 | 2 | 11 |
- Содержание разделов дисциплин
4.2.1. Теоретические основы многомерного статистического анализа. Проверка статистических гипотез.
Область применения и задачи многомерных методов. Методы МСА. Статистические гипотезы.
4.2.2. Дисперсионный анализ.
Содержание дисперсионного анализа. Однофакторный и двухфакторный дисперсионный анализ.
4.2.3. Многомерный регрессионный анализ.
Введение в множественный корреляционно-регрессионый анализ. Свойства статистических оценок параметров регрессионной модели. Статистическое оценивание методом наименьших квадратов – обобщения а случай матричного представления данных. Нелинейные регрессионные модели.
4.2.4. Кластерный анализ.
Общая характеристика методов кластерного анализа. Меры сходства. Иерархический кластерный анализ. Критерии качества классификации.
4.2.5 Факторный анализ.
Сущность методов факторного анализа и их классификация. Фундаментальная теорема факторного анализа Тэрстоуна. Общий алгоритм и и теоретические проблемы факторного анализа. Метод главных компонент. Вращение пространства общих факторов.
4.2.6. Дискриминантный анализ.
Основные положения дискриминантного анализа. Дискриминантные функции и их геометрическая интерпретация. Расчет коэффициентов дискриминантной функции.
4.2.7. Многомерное шкалирование.
Многомерное шкалирование в статистических исследованиях. Представление и первичная обработка статистических данных в многомерном шкалировании. Классическая модель многомерного шкалирования Торгерсоона.
Тема 1. Проверка статистических гипотез
Проверка статистических гипотез
Задание. Проверка гипотез о нормально распределенной совокупности, равенстве средний и дисперсий.
Исполнение. Решение задач.
Оценка. Формирует необходимые представления о возможности проверки статитисческих гипотез.
Время выполнения заданий: 2 часа.
Контрольные вопросы и задания
Задача 1.
Известна зависимость общих производственных затрат фирмы от ее выпуска:
| Выпуск, тыс.шт. | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
| Затраты, тыс.руб. | 700 | 800 | 880 | 940 | 980 | 1000 | 1120 | 1260 | 1420 | 1600 | 1800 | 2000 |
- Статистически проверить гипотезу о линейной зависимости затрат от выпуска с помощью критерия, основанного на группировке данных (данные разбить на 4 интервала в зависимости от объема выпуска). Уровень значимости принять равным 0,05.
- Подсчитать выбочный коэффициент корреляции. Проверить гипотезу о наличии линейной связи при уровне значимости 0,05. Найти интервальную оценку коэффициента корреляции с доверительной вероятностью 95%.
- Определить значение корреляционного отношения. Проверить гипотезу о наличии связи при уровне значимости 0,05. Группировать данные по 4 интервалам в зависимости от объема выпуска.
Задача 2.
В целях определения зависимости между уровнем образования и среднедушевым доходом был проведен опрос среди 2000 респондентов. Его результаты сведены в таблице:
| | <2тыс. | 2-5тыс. | 5-10тыс. | 10-30тыс. | >30тыс. |
| неполное среднее | 241 | 345 | 59 | 75 | 14 |
| среднее | 91 | 225 | 184 | 66 | 39 |
| высшее | 34 | 157 | 316 | 65 | 89 |
Вычислить значение характеристики Х2 квадратичной сопряженности и определить наличие связи при уровне значимости 0,001.
Контрольные вопросы и задания
- Что понимают под статистической гипотезой и какие характерные признаки для нее существуют?
- Что означает: простая и сложная, одномерная и многомерная статистические гипотезы?
- Какого рода ошибки могут допускаться и чем определяется достоверность вывод при проверке статистических гипотез?
Тема 2. Дисперсионный анализ
Дисперсионный анализ.
Задание. Двухфакторный дисперсионный анализ.
Исполнение. Решение задач по теме «Дисперсионный анализ».
Оценка. Формирует необходимые представления о применимости того или иного статистического инструментария к заданному классу задач.
Время выполнения заданий: 2 часа.
Контрольные вопросы и задания
Тема 3. Многомерная регрессия
Многомерная регрессия.
Задание. Построение уравнение множественной регрессии матричным методом.
Исполнение. Решение задач по теме «Многомерная регрессия».
Оценка. Формирует типологию множественной регрессии.
Время выполнения задания: 1 час.
Контрольные вопросы и задания
Тема 4. Кластерный анализ
Кластерный анализ.
Задание. Многомерная группировка посредством кластерного анализа.
Исполнение: решение задачи. Использование статистического инструментария подготовки исходных данных и метода решения. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях использования кластерного анализа.
Время выполнения заданий: 4 часа.
Задача 4.
Имеется набор из 50 точек на координатной плоскости:
3,40 65,21 49,30 60,38 50,37 43,10 63,44 78,30 40,45 20,45
25,14 2,26 52,27 70,45 65,14 30,21 51,6 75,35 35,42 25,47
26,19 14,35 7,27 4,34 59,11 35,18 54,3 32,45 30,48 23,48
7,20 12,45 32,10 40,10 50,12 75,46 20,11 30,43 28,48 23,44
13,48 15,29 50,20 42,14 42,8 55,47 13,15 `25,37 25,40 16,48
Разбить данный набор точек на некоторое количество кластеров, используя процедуру кластер-анализа любого типа.
Критерий качества:
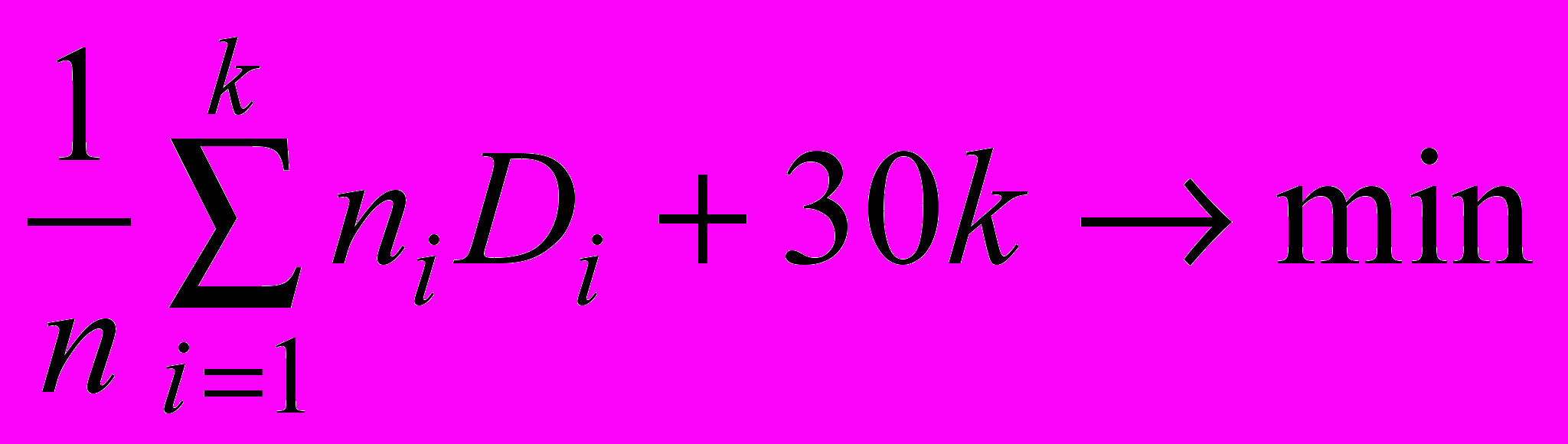, где k - количество кластеров, ni - число точек, попавших в i-кластер, Di-дисперсия в i-кластере.Контрольные вопросы и задания
- В чём состоит принципиальное отличие методов многомерных классификаций от комбинационных группировок?
- Перечислите задачи, решаемые при помощи методов кластерного анализа.
- Назовите две основные группы методов кластерного анализа и укажите их сходство и различие.
- Какие меры сходства используются при проведении многомерной классификации?
- Какие методы кластерного анализа могут привести к образованию пересекающихся кластеров?
- Перечислите основные вычислительные процедуры метода поиска сгущений.
- Как оценивается качество полученного разбиения совокупности на кластеры?
Тема 5. Факторный анализ
Задание. Используя метод главных компонент построить матрицу факторного отображения.
Исполнение: решение задачи. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях использования факторного анализа в экономическом анализе.
Время выполнения заданий: 2 часа.
Контрольные вопросы и задания
- В чём состоит различие понятий «общий фактор» и «элементарный признак»?
- Как определить достаточное число факторов для характеристики изучаемого явления или процесса?
- Какие особенности должны быть учтены, если для проведения анализа выбирается метод главных компонент?
- Что подразумевается под ортогональным и косоугольным факторными решениями?
- Какие алгоритмические шаги выполняются при реализации метода главных компонент?
- Чем объясняется возможность факторного отображения множества элементарных признаков?
- Что означает «простая структура» фактора?
Тема 6. Дискриминантный анализ
Задание. Построение дискриминантных функций и проведение классификации.
Исполнение: решение задачи. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях использования анализа.
Время выполнения заданий: 2 часа.
Контрольные вопросы и задания
- В чём заключается сущность дискриманантного анализа и его отличие от других методов многомерной классификации?
- Как определяется количество дискриминантных функций?
- Сформулируйте правило дискриминации
- В чём состоит сложность отбора дискриминантных переменных?
- Поясните, в каких случаях затруднена правильная классификация новых объектов.
Тема 7. Многомерное шкалирование
Задание. Построение симметричных матриц сходств.
Исполнение: решение задачи. Интерпретация результатов решения.
Оценка. Формирует необходимые представления о возможностях использования на практике методов многомерного шкалирования.
Время выполнения заданий: 2 часа.
Контрольные вопросы и задания
- Какие особенности в сравнении с другими статистическими методами отличают методы многомерного шкалирования?
- Перечислите основные виды многомерного шкалирования. Для решения каких типов задач они применимы?
- Покажите основные формальные модели, лежащие в основе алгоритмов многомерного шкалирования, в чём их различие?
6. Чему равны вклады общих факторов и специфического фактора в диспер-
сию случайной величины 1 2 i 0,5 0,9 i X F F = + +ε
��
, если Xi центрирована и нормирована.
Какова общность случайной величины Xi?
7. Найдите суммарную общность пяти случайных величин и долю этой общ-
ности, вносимую каждым из факторов, если матрица нагрузок
0,7 0,3
0,8 0,1
0,7 0,5
0,6 0,5
0,7 0,0
=
A
рассчитана по корреляционной матрице RХ (знаки нагрузок не указаны).
8. Продолжите итерационную процедуру метода максимального правдоподо-
бия в условиях факторного анализа производственной деятельности предприятий
(п. 1.4.4).
9. Проведите факторный анализ показателей мировой демографической ста-
тистики по данным табл. 1.4.1; при интерпретации общих факторов при необходимо-
сти используйте подходящую процедуру вращения факторного пространства.
10. Приведите алгоритм оценки общих факторов методом Бартлетта.
6. КОНТРОЛЬ ЗНАНИЙ СТУДЕНТА
6.1. Входной контроль
Входной контроль осуществляется в форме контрольного задания по разделам дисциплины базового курса «Матричная алгебра».
6.2. Тематика текущего контроля
Текущий контроль знаний осуществляется в процессе выполнения практических заданий путём индивидуального и группового опроса, собеседования и тестового контроля. Результаты текущего контроля знаний учитываются при промежуточной аттестации и на зачёте.
6.3. Выходной контроль
Выходной контроль осуществляется в форме зачёта по дисциплине.
В программу зачёта по дисциплине включены следующие вопросы:
1. Предмет МСА.
2. Особенности методов МСА. Их отличие от методов классической статистики.
3. Классификация методов МСА.
4. Задачи, решаемые при помощи методов МСА.
5. Сущность многомерной регрессии.
6. Понятие «общего фактора» и «элементарного признака».
7. Алгоритмические шаги при реализации метода главных компонент.
8. Алгоритмические шаги при реализации методов факторного анализа.
9. Понятие «простой структуры» факторов. Какими методами добиваются «простой структуры» факторов.
10. Особенности метода многомерного шкалирования.
11. основные методы многомерного шкалирования.
12. Задачи, решаемые при помощи методов многомерного шкалирования.
13. Основные формальные модели, лежащие в основе алгоритмов многомерного шкалирования. В чем их различие?
14. Принципиальное отличие методов многомерных классификаций от комбинированных группировок.
15. Задачи, решаемые при помощи методов кластерного анализа.
16. Меры сходства.
17. Методы кластерного анализа.
18. Основные вычислительные процедуры метода поиска сгущений.
19. Оценка качества разбиения совокупности на кластеры.
20. Сущность дискриминантного анализа.
21. Определение количества дискриминантных функций.
22. Правило дискриминации.
23. Отбор дискриминантных переменных.
Итоговый контроль знаний – зачет.
7 УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Рекомендуемая литература:
- Андерсон Т. В. Введение в многомерный статистический анализ. - М., 1983.
- Кендалл М. Дж., Стьюарт А. Многомерный статистический анализ и временные ряды. - М., 1976.
- Айвазян С. А. Прикладная статистика и эконометрика. - М., ЮНИТИ, 1999.
- Айвазян С. А. и др. Прикладная статистика. Т. 1-3. - М., 1989.
- Бородкин Л.И. Многомерный статистический анализ в исторических исследованиях. М., 1986.
- Бушин П.Я. Экономико-статистическое моделирование. Учеб. пособие.- Хаб. по литехнический институт, 1988. – 80 с.
- Глинский В.В. Ионин В.Г. Статистический анализ: Учеб. пособие.- М.: ИИД «Филинъ», 1998. – 264 с
- Дубров А. М., Мхитарян В. С., Трошин Л И. Многомерные статистические методы для экономистов и менеджеров. М. Финансы и статистика.
- Елисеева И.И. Статистические методы измерения связей. Л., 1982.
- Жуковская В.М., Мучник И.Е. Факторный анализ в социально-экономических исследованиях. М., 1976.
- Калинина В.Н., Соловьёв В.И. Введение в многомерный статистический анализ: Учебное пособие/ ГУУ. – М., 2003. – 66 с.
- Кендалл М. Дж., Стьюарт А. Многомерный статистический анализ и временные ряды. - М., 1976.
- Малюгин В. И., Степанова М. Д., Харин Ю. С. Методические указания к лабораторным работам ППП анализа данных. - Мн., 1992.
- Рябушкин Т.В. и др. Статистические методы и анализ социально-экономических процессов. – М.: Наука. 1990.- 296 с.
- Общая теория статистики: Учебник/ Под ред. Стерина А.А. М.: Финансы и стати
- стика, 1996.- 296 с.
- Сошникова Л. А., Томашевич В. Н. и др. Многомерный статистический анализ в экономике. М.: ЮНИТИ.
- Статистический анализ в экономике / Под ред. Громыко Г.Л. – М.: Изд. МГУ, 1992. – 134 с.
- Харин Ю.С., Хаткевич Л.А. Упражнения и методические указаня по спецкурсу “Многомерный статистический анализ”. – Мн., 1993.
10 СЛОВАРЬ ТЕРМИНОВ
Временной ряд - это последовательность измерений в последовательные моменты времени.
Дискриминантный анализ, используется для принятия решения о том, какие переменные дискриминируют или разделяют объекты на две или более естественно возникающих групп (его используют как метод проверки гипотез или как метод разведочного анализа
Дисперсионный анализ. Целью дисперсионного анализа (ANOVA) является проверка значимости различия между средними с помощью сравнения (т.е. анализа) дисперсий. А именно, разделение общей дисперсии на несколько источников (связанных с различными эффектами в плане), позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, с дисперсией, вызванной внутригрупповой изменчивостью. При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии.
Интервальная шкала. Эта шкала измерений позволяет не только упорядочить наблюдения, но и количественно выразить расстояния между ними (при этом на шкале не обязательно присутствует абсолютная нулевая отметка).
Интерполяция. Восстановление значения функции в промежуточной точке по известным ее значениям в соседних точках.
Канонический анализ. Каноническая корреляция позволяет исследовать зависимость между двумя наборами переменных (и применяется для проверки гипотез или как метод разведочного анализа).
Кластерный анализ. Термин кластерный анализ в действительности включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры, т.е. развернуть таксономии (обычно в разведочном анализе) или определить кластеры схожих объектов
Независимые и зависимые переменные. Термины зависимая и независимая переменная обычно применяются в экспериментальных исследованиях, где приходится манипулировать некоторыми переменными. В этом смысле "независимость" переменной определяется как независимость от реакции, свойств и намерений объектов эксперимента и т.п. Некоторые переменные предполагаются "зависимыми" от действий объекта эксперимента или условий эксперимента. Эти переменные, возможно в неявной форме, содержат некоторую информацию о поведении или реакции объекта в ходе эксперимента. Независимые переменные - это переменные, значениями которых можно управлять, а зависимые переменные - это переменные, которые можно только измерять или регистрировать.
Расстояния Махаланобиса. Независимые переменные в уравнении регрессии можно представлять точками в многомерном пространстве (каждое наблюдение изображается точкой). В этом пространстве можно построить точку центра. Эта "средняя точка" в многомерном пространстве называется центроидом, т.е. центром тяжести. Расстояние Махаланобиса определяется как расстояние от наблюдаемой точки до центра тяжести в многомерном пространстве, определяемом коррелированными (неортогональными) независимыми переменными (если независимые переменные некоррелированы, расстояние Махаланобиса совпадает с обычным евклидовым расстоянием). Эта мера позволяет, в частности, определить является ли данное наблюдение выбросом по отношению к остальным значениям независимых переменных.
Регрессия. Категория задач, где цель состоит в том, чтобы оценить значение непрерывной выходной переменной по значениям входных переменных.
Статистический анализ многомерный, в широком смысле — раздел математической статистики, объединяющий методы изучения статистических данных, относящихся к объектам, которые характеризуются несколькими качественными или количественными признаками.
Факторный анализ. Главными целями факторного анализа являются: (1) сокращение числа переменных (редукция данных) и (2) определение структуры взаимосвязей между переменными, т.е. классификация переменных. Поэтому факторный анализ используется либо как метод сокращения данных, либо как метод классификации.
Шкалирование. Приведение (с помощью специальной функции или алгоритма) значений переменных в диапазон, удовлетворяющий определенным требованиям (например: положительные, от нуля до единицы, не больше 10E12, с большой относительной дисперсией).
Экстраполяция. Прогнозирование неизвестных значений путем продолжения функций за границы области известных значений.