Рабочая программа по курсу «Математические методы в психологии» по специальности 030302 «клиническая психология»
| Вид материала | Рабочая программа |
- Рабочая учебная программа по курсу «Логика» для факультета клинической психологии для, 155.79kb.
- Рабочая учебная программа по дисциплине «Методологические основы психологии» для студентов, 177.86kb.
- Программа учебной дисциплины Математические методы в психологии федерального компонента, 278.34kb.
- Утверждено Цикловой Учебно-Методической комиссией по специальностям 040101 Социальная, 572.89kb.
- Рабочая программа дисциплины математические методы в психологии опд. Ф. 00 для специальности, 301.35kb.
- Рабочая программа по дисциплине «математические методы в психологии» Специальность, 179.84kb.
- Курса «Математические методы в психологии». Данный курс реализуется в рамках подготовки, 107.45kb.
- Программа для студентов, обучающихся по специальности «клиническая психология» «030302», 185.25kb.
- Программа по курссу психология развития и возрастная психология, 321.36kb.
- Рабочая программа по Психофармакотерапии для специальности 022700 клиническая психология, 246.12kb.
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ
ФЕДЕРАЛЬНОГО АГЕНТСТВА ПО ЗДРАВООХРАНЕНИЮ И СОЦИАЛЬНОМУ РАЗВИТИЮ»
| «СОГЛАСОВАНО» Декан факультета ФКППиСР профессор ________________ Н.А.Корнетов | «УТВЕРЖДАЮ» Проректор по учебной работе профессор ________________ А.И. Венгеровский |
РАБОЧАЯ ПРОГРАММА
по курсу «Математические методы в психологии»
по специальности 030302
«клиническая психология»
Курс − 4
Семестр − VII
Кафедра высшей математики
Учебные часы по Государственному образовательному стандарту Министерства образования и науки Российской Федерации и Министерства здравоохранения и социального развития − 100 ч.
Учебные часы по действующему учебному плану − 100 ч.
Лекции − 20 ч.
Практические занятия − 40 ч.
Самостоятельная работа − 40 ч.
ЦЕЛЬ И ЗАДАЧИ ИЗУЧЕНИЯ КУРСА
«МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ»
Основной целью изучения дисциплины «Математические методы в психологии» студентами, обучающимися по специальности «клиническая психология», является ознакомление студентов с основами современного математического аппарата, освоение математических методов для дальнейшего профессионального использования.
В процессе изучения дисциплины «Математические методы в психологии» решаются следующие задачи:
- Ознакомить студентов с основными математическими методами, используемыми в психологии.
- Сформировать положительную мотивацию использования математических методов как в фундаментальных, так и в прикладных исследованиях.
- Выработать навыки использования математических методов для решения профессиональных задач.
ТЕМАТИЧЕСКИЙ ПЛАН ЛЕКЦИЙ И ПРАКТИЧЕСКИХ ЗАНЯТИЙ
ПО КУРСУ «МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ»
| № п/п | Тема | Количество часов лекций | Количество часов практических занятий |
| | Основные понятия математической статистики (повторение) | 1 | 2 |
| | Представление экспериментальных данных | 1 | 2 |
| | Критерии согласия | 2 | 4 |
| | Параметрические критерии | 2 | 2 |
| | Непараметрические критерии | 4 | 8 |
| | Анализ номинативных данных | 2 | 4 |
| | Корреляционный анализ | 2 | 4 |
| | Дисперсионный анализ | 2 | 8 |
| | Многомерные методы | 4 | 6 |
| | Итого: | 20 | 40 |
СОДЕРЖАНИЕ КУРСА «МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ»
1. Основы математической статистики (повторение изученного в курсе «Математика»).
Измерительные шкалы. Виды организации эксперимента. Понятие генеральной и выборочной совокупности. Построение вариационных рядов. Расчет статистических характеристик.
Проверка статистических гипотез. Основные понятия. Понятие о статистической ошибке I и II рода. Параметрические и непараметрические критерии.
2. Способы представления экспериментальных данных.
Методы группировки экспериментальных данных. Представление данных в виде таблиц и графиков. Представление результатов статистической обработки данных.
3. Критерии согласия.
Понятие о критериях согласия. Основные критерии, используемые для проверки согласия экспериментальных данных с модельным распределением (– критерий Колмогорова, 2 – критерий Пирсона). Применение коэффициентов асимметрии и эксцесса для проверки нормальности распределения.
4. Параметрические критерии.
Проверка гипотезы о равенстве генеральных дисперсий (критерий Фишера – Снедекора, критерий Кочрена, критерий Барлетта, условия их применения). Проверка гипотезы о равенстве генеральных средних (
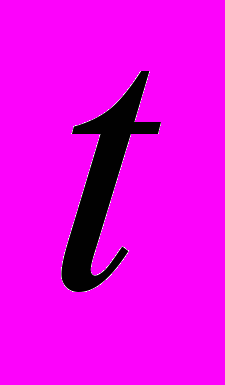 - критерий Стьюдента для зависимых и независимых выборок,
- критерий Стьюдента для зависимых и независимых выборок,  - критерий, условия их применения).
- критерий, условия их применения).5. Непараметрические критерии.
Непараметрические критерии для зависимых совокупностей (G – критерий знаков, Т – критерий Вилкоксона,
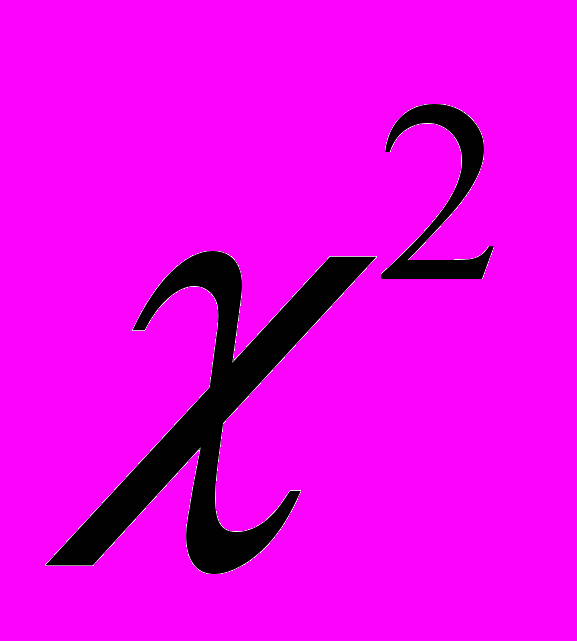 – критерий Фридмана, L – критерий тенденций Пейджа). Ограничения данных критериев и условия их применения.
– критерий Фридмана, L – критерий тенденций Пейджа). Ограничения данных критериев и условия их применения.Непараметрические критерии для независимых совокупностей (Q – критерий Розенбаума, U – критерий Манна-Уитни, Н – критерий Крускала-Уоллиса, S – критерий тенденций Джонкира, Х – критерий Ван-дер-Вардена, - критерий Колмогорова-Смирнова). Ограничения данных критериев и условия их применения.
6. Анализ номинативных данных.
Основные методы анализа номинативных данных. Сравнение эмпирического наблюдения с теоретическим (биномиальный критерий,
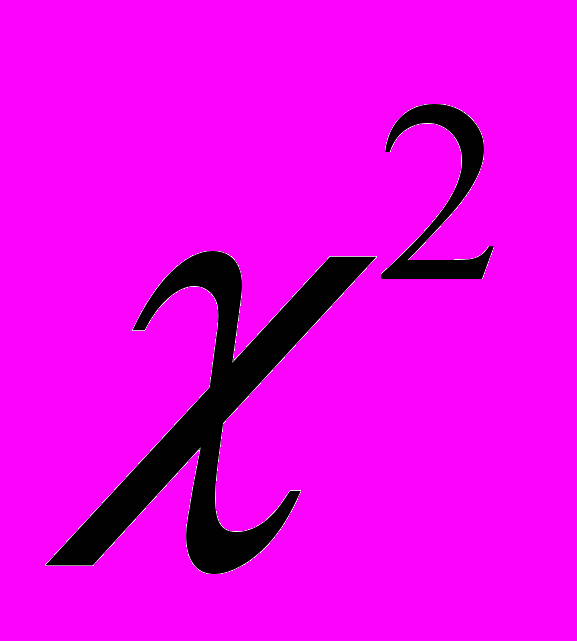 – критерий Пирсона). Сравнение двух эмпирических распределений (критерий
– критерий Пирсона). Сравнение двух эмпирических распределений (критерий  - угловое преобразование Фишера,
- угловое преобразование Фишера, 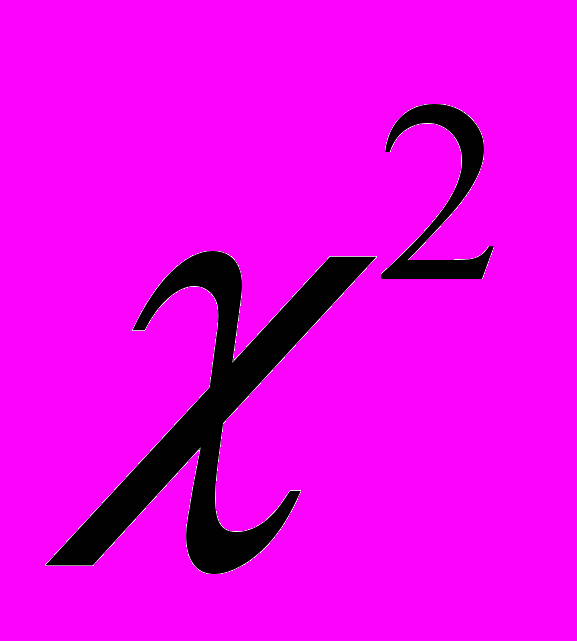 – критерий Пирсона, оценка разностей между долями, критерий Мак-Нимара).
– критерий Пирсона, оценка разностей между долями, критерий Мак-Нимара).7. Корреляционный анализ.
Понятие о корреляционной зависимости. Параметрический показатель связи – коэффициент линейной корреляции Пирсона. Построение уравнения регрессии.
Непараметрические показатели связи (коэффициент корреляции рангов Спирмена, коэффициент ассоциации, коэффициент взаимной сопряженности).
8. Дисперсионный анализ (ANOVA)
Понятие о дисперсионном анализе. Виды дисперсионного анализа (однофакторный, многофакторный, дисперсионный анализ с повторными измерениями, многомерный дисперсионный анализ). Математическая идея дисперсионного анализа, ограничения метода.
Однофакторный дисперсионный анализ в случае равномерного и неравномерного дисперсионного комплекса. Множественные сравнения в дисперсионном анализе.
Дисперсионный анализ с повторными измерениями.
Многофакторный дисперсионный анализ, математическая модель многофакторного дисперсионного анализа.
9. Многомерные методы.
Назначение многомерных методов. Классификация многомерных методов по назначению, по исходным предположениям о структуре данных, по виду исходных данных.
Множественный регрессионный анализ, математико-статистическая идея метода. Цели применения и основные методы множественного регрессионного анализа.
Факторный анализ, математическая идея метода. Понятие фактора, цель факторного анализа. Проблемы факторного анализа. Основные этапы факторного анализа.
Дискриминантный анализ, математическая идея метода. Цель дискриминантного анализа.
Многомерное шкалирование, математическая идея метода. Общая схема многомерного шкалирования.
Кластерный анализ, математическая идея метода. Виды кластерного анализа. Роль кластерного анализа в прикладном исследовании.
ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН ЛЕКЦИЙ
| №№ тем | Наименование тем и их содержание | Часы |
| 1 | Основные понятия математической статистики (повторение). Представление экспериментальных данных. | 2 |
| 2 | Критерии согласия (– критерий Колмогорова, 2 – критерий Пирсона, критерий асимметрии и эксцесса). | 2 |
| 3 | Параметрические критерии (критерий Фишера – Снедекора, критерий Кочрена, 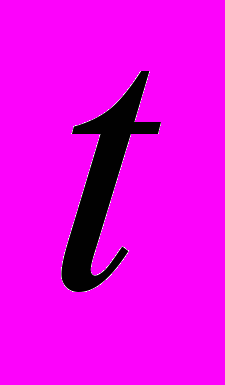 - критерий Стьюдента для зависимых и независимых выборок, - критерий Стьюдента для зависимых и независимых выборок,  - критерий). - критерий). | 2 |
| 4 | Непараметрические критерии для зависимых совокупностей (G – критерий знаков, Т – критерий Вилкоксона, 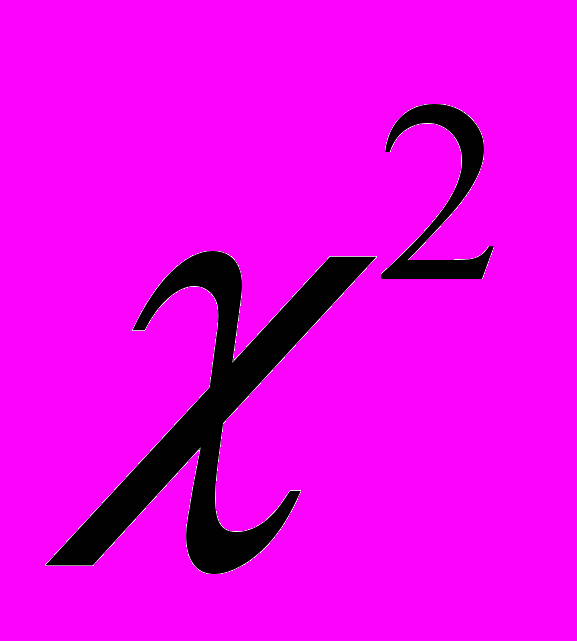 – критерий Фридмана, L – критерий тенденций Пейджа). – критерий Фридмана, L – критерий тенденций Пейджа). | 2 |
| Непараметрические критерии для независимых совокупностей (Q – критерий Розенбаума, U – критерий Манна-Уитни, Н – критерий Крускала-Уоллиса, S – критерий тенденций Джонкира, Х – критерий Ван-дер-Вардена, - критерий Колмогорова-Смирнова). | 2 | |
| 5 | Анализ номинативных данных (биномиальный критерий, 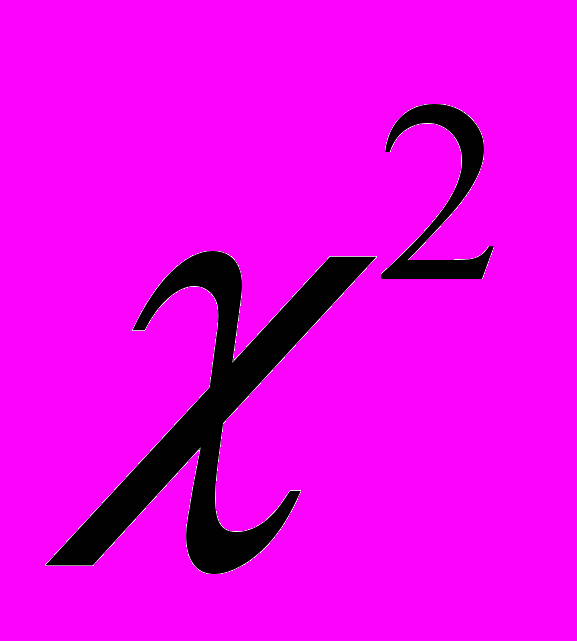 – критерий Пирсона, критерий – критерий Пирсона, критерий  - угловое преобразование Фишера, оценка разностей между долями, критерий Мак-Нимара). - угловое преобразование Фишера, оценка разностей между долями, критерий Мак-Нимара). | 2 |
| 6 | Корреляционный анализ. Понятие о корреляционной зависимости. Параметрические и непараметрические показатели связи (коэффициент линейной корреляции Пирсона, коэффициент корреляции рангов Спирмена, коэффициент ассоциации, коэффициент взаимной сопряженности). | 2 |
| 7 | Дисперсионный анализ. Виды дисперсионного анализа. Основные математические идеи метода. | 2 |
| 8 | Многомерные методы. Классификация многомерных методов. Множественный регрессионный анализ. Дискриминантный анализ. | 2 |
| Факторный анализ. Многомерное шкалирование. Кластерный анализ. | 2 |
Всего 20 часов.
ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН ПРАКТИЧЕСКИХ ЗАНЯТИЙ
| №№ занятий | Содержание занятий | Часы |
| 1 | Основные понятия математической статистики (повторение). Вычисление числовых характеристик выборочной совокупности. | 2 |
| 2 | Способы представления экспериментальных данных. | 2 |
| 3 | Критерии согласия (– критерий Колмогорова, критерий асимметрии и эксцесса). | 2 |
| 4 | Критерии согласия (2 – критерий Пирсона). | 2 |
| 5 | Параметрические критерии. | 2 |
| 6 | Непараметрические критерии для зависимых совокупностей (G – критерий знаков, Т – критерий Вилкоксона) | 2 |
| 7 | Непараметрические критерии для зависимых совокупностей ( 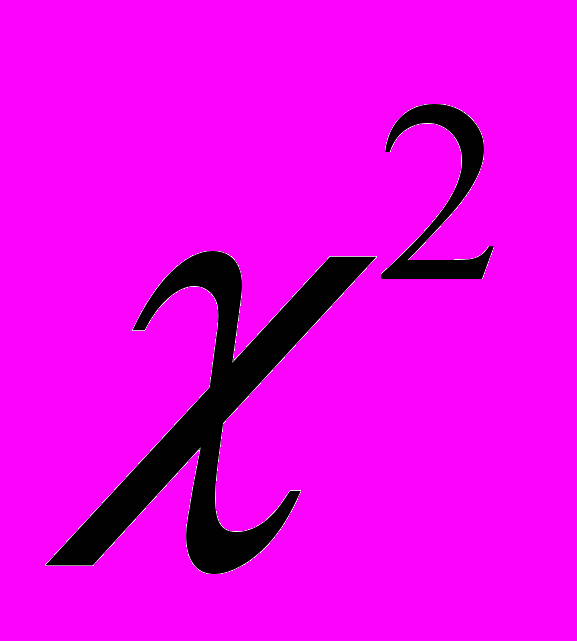 – критерий Фридмана, L – критерий тенденций Пейджа). – критерий Фридмана, L – критерий тенденций Пейджа). | 2 |
| 8 | Непараметрические критерии для независимых совокупностей (Q – критерий Розенбаума, U – критерий Манна-Уитни, Х – критерий Ван-дер-Вардена). | 2 |
| 9 | Непараметрические критерии для независимых совокупностей (Н – критерий Крускала-Уоллиса, S – критерий тенденций Джонкира, , - критерий Колмогорова-Смирнова). | 2 |
| 10 | Анализ номинативных данных (биномиальный критерий, 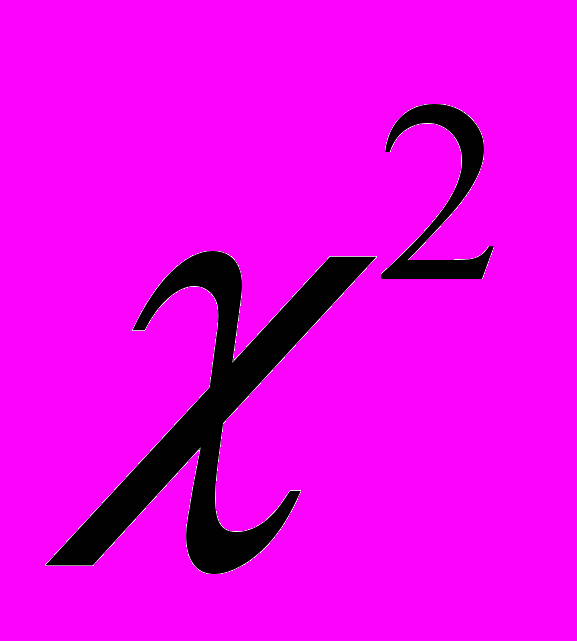 – критерий Пирсона). – критерий Пирсона). | 2 |
| 11 | Анализ номинативных данных (критерий  - угловое преобразование Фишера, оценка разностей между долями, критерий Мак-Нимара). - угловое преобразование Фишера, оценка разностей между долями, критерий Мак-Нимара). | 2 |
| 12 | Корреляционный анализ. Параметрический показатель корреляционной связи (коэффициент линейной корреляции Пирсона). Построение уравнения линейной регрессии. | 2 |
| 13 | Непараметрические показатели корреляционной связи (коэффициент корреляции рангов Спирмена, коэффициент ассоциации, коэффициент взаимной сопряженности). | 2 |
| 14 | Дисперсионный анализ. Однофакторный дисперсионный анализ равномерного дисперсионного комплекса. | 2 |
| 15 | Однофакторный дисперсионный анализ неравномерного дисперсионного комплекса. | 2 |
| 16 | Однофакторный дисперсионный анализ с повторными измерениями. | 2 |
| 17 | Многофакторный дисперсионный анализ (на примере двухфакторного). | 2 |
| 18 | Факторный анализ. | 2 |
| 19 | Кластерный анализ. | 2 |
| 20 | Зачетное занятие. | 2 |
Всего 40 часов.
ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ УМЕНИЙ ПО КУРСУ «МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ»
После окончания изучения дисциплины «Математические методы в психологии» студент должен:
1. Знать:
- измерительные шкалы, используемые в психологии, и особенности получаемых экспериментальных данных;
- параметрические и непараметрические критерии, используемые в психологии для обработки результатов исследований;
- методы анализа номинативных данных;
- основные методы корреляционного анализа;
- основные методы и математические идеи дисперсионного анализа.
2. Уметь:
- вычислять числовые характеристики выборочной совокупности;
- проверять согласие эмпирического распределения с теоретическим;
- применять параметрические и непараметрические критерии для обработки экспериментальных данных;
- анализировать номинативные данные;
- исследовать корреляционную связь между изучаемыми признаками;
- применять дисперсионный анализ.
3. Овладеть навыками:
- применения математических методов к решению профессиональных задач.
4. Иметь представления:
- о способах представления экспериментальных данных;
- об условиях применения различных критериев и их ограничениях;
- математической основе используемых методов;
- о многомерных методах и целях их применения.
Литература
по дисциплине «Математические методы в психологии».
Основная
1. Берестнева О.Г., Уразаев А.М., Муратова Е.А., Кубарев Е.Н., Воробьева Н.Г. Математические методы в психологии / под ред. О.Г. Берестневой, А.М. Уразаева. – Томск: Изд-во Томского государственного педагогического университета, 2001.
2. Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: ООО «Речь», 2003.
Дополнительная
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2000.
2. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2000.
3. Ермолаев О.Ю. Математическая статистика для психологов. – М.: Московский психолого-социальный институт: Флинта, 2003.
4. Наследов А.Д. Математические методы психологического исследования. Анализ и интерпретация данных. – СПб.: Речь, 2004.
Рабочая программа составлена старшим преподавателем кафедры высшей математики СибГМУ М.Б.Аржаник.
Рабочая программа обсуждена и утверждена на заседании кафедры высшей математики
"____"______________2006 г.
Заведующий кафедрой
профессор, доктор физ.-мат. наук В.В.Свищенко
