Geum.ru

Урок алгебры в 7 классе на тему «Действия с многочленами»

Вид материалаУрок

Содержание


2.Актуализация опорных знаний
Заседания ученого совета.
Лаборатория исследований.
Лаборатория открытий.
Лаборатория уравнений.
Лаборатория эрудитов.
Сообщение учащегося
Подобный материал:
Каменский муниципальный район

Воронежская область


Урок алгебры в 7 классе на тему «Действия с многочленами»


Разработала учитель математики:

Минайлова Г.С.-МОУ Ольховлогская ООШ,


Ольхов Лог

2011г.


Урок алгебры, 7 класс

Тема: «Действия с многочленами»


Цели урока:

Образовательные:
  • Обобщить и систематизировать знания по данной теме;
  • Провести диагностику усвоения знаний и умений применения их при выполнении практических заданий стандартного и более высокого уровня сложности.

Развивающие:
  • Развитие познавательной активности;
  • Развитие осмысленного отношения к своей деятельности;
  • Развитие самостоятельности мышления: видеть общую закономерность, делать обобщения и выводы.

Воспитательные:
  • Воспитание аккуратности;
  • Умение анализировать и адекватно оценивать свою деятельность.

Форма урока: деловая игра


Ход урока:


1.Организационный момент

Сегодня вы будете выступать в роли сотрудников научно-исследовательского института, участвовать в заседаниях ученого совета НИИ, чтобы обсудить тему «Действие с многочленами» (слайд №1)

Вы будете работать в различных лабораториях: лаборатории формул, лаборатории исследований, лаборатории выражений, лаборатории уравнений, лаборатории открытий.

В процессе работы в НИИ вы должны закрепить изученный материал, показать уровень усвоения темы, разобраться в непонятных ранее моментах

(слайд №2).

, проконтролировать и оценить свои знания .

У каждого на столе оценочный лист, где вы будете фиксировать свои достижения, и в конце оцените свою работу как сотрудники лаборатории

(слайд №3).




2.Актуализация опорных знаний


«Математическое домино»

У каждого учащегося карточка-домино. Карточка содержит вопрос-ответ.

Первым начинает ученик, у которого карточка содержит слова «старт и финиш». Он задает стартовый вопрос, он же дает финишный ответ. Каждый ученик должен быть внимательным, чтобы не пропустить ответ (карточка домино крепится магнитами на доску).


Финиш: Ответ: произведению суммы этих выражений на неполный квадрат их разности.

Старт. Вопрос: что называют многочленом?

Ответ: сумму одночленов.

Вопрос: что называют одночленом?


Ответ: произведение чисел, переменных и их степеней.

Вопрос: какие слагаемые называются подобными?


Ответ: слагаемые с одинаковой буквенной частью.

Вопрос: как привести подобные слагаемые?


Ответ: сложить их числовые коэффициенты, а результат умножить на общую буквенную часть.

Вопрос: как умножить одночлен на многочлен?


Ответ: одночлен умножить на каждый член многочлена, а результаты сложить.

Вопрос: как перемножить одночлены?


Ответ: перемножить числовые коэффициенты, затем перемножить степени с одинаковыми основаниями и результаты перемножить.

Вопрос: как умножить две степени с одинаковыми основаниями?


Ответ: основание оставить тем же, а показатели степеней сложить.

Вопрос: как возвести степень в степень?


Ответ: основание оставить тем же, а показатели степеней перемножить.

Вопрос: как умножить многочлен на многочлен?


Ответ: каждый член одного многочлена умножить на каждый член другого многочлена и результаты сложить.

Вопрос: чему равен квадрат суммы двух выражений?


Ответ: квадрату первого выражения плюс удвоенное произведение первого на второе плюс квадрат второго выражения.

Вопрос: чему равен квадрат разности?


Ответ: квадрату первого выражения минус удвоенное произведение первого на второе плюс квадрат второго выражения.

Вопрос: чему равно произведение разности и суммы двух выражений?


Ответ: разности квадратов этих выражений.

Вопрос: чему равно произведение разности двух выражений на неполный квадрат их суммы?


Ответ: разности кубов этих выражений.

Вопрос: чему равна сумма кубов двух выражений?


Вы получили пропуск в НИИ


Заседания ученого совета. Слайд №4


Лаборатория формул.




Выбрать пары равных выражений и с помощью стрелок составить верные формулы, например:





Проверка задания «Формулы сокращенного умножения» Слайд №5


Лаборатория выражений.


Выполнить тест по вариантам (слайд №6)


Слайд №7(проверка)


Лаборатория исследований.

Слайд №8


Найти ошибки и напротив каждого равенства написать верное или неверное.

Последующая проверка.


Лаборатория открытий. Слайд №9





Игра « Смотри, не ошибись» (три варианта, второй и третий немного сложнее, варианты на выбор).


Слайд №10

Проверка заданий игры «Смотри, не ошибись!»





Лаборатория уравнений. Слайд №11




Выполнить по вариантам по два уравнения. Затем нужно будет подойти к доске, отыскать полученный результат и прикрепить карточку- ответ буквой к своему уравнению. Если вашего результата нет, значит, уравнение решено неверно.

Слайд №12



Мы получили слово «АЛ-ДЖАБРА»


Алгебра-это раздел математики, где решаются уравнения, рассматриваются преобразования выражений, составленные из чисел и букв - не греческое.

А вот слово алгебра произошло от слова ал-джабра, взятого из названия книги узбекского математика, астронома и географа Мухаммеда АлХорезми «Краткая книга об исчислениях ал-джабры и ва-л-мукаблы». Арабское слово аль-джебр переводчик не стал переводить, а записал его латинскими буквами algebr. Так возникло название науки, которую мы изучаем. «Ал-джабра »-операция переноса отрицательных членов из одной части уравнения в другую, но уже с положительным знаком. По-русски это слово называется «восполнение».

Лаборатория эрудитов.

На формулах сокращенного умножения основаны некоторые математические фокусы, позволяющие производить вычисления в уме, например: (слайд №13)



Но самый элегантный фокус связан с возведением в квадрат чисел, оканчивающихся цифрой 5.

Сообщение учащегося

Проведем соответствующие рассуждения для возведения числа 85 в квадрат (слайд №11).

Замечаем, что для вычисления достаточно было умножить 8 на 9 и к полученному результату приписать справа 25.Аналогично можно поступать и в других случаях. Например, 35²= 1225 (3*4= 12 и к полученному числу приписать справа 25).

Чтобы целое число с половиной возвести в квадрат, нужно целое число умножить на соседнее, на единицу большее число и к полученному результату приписать одну четвертую (слайд №13).

Вопрос- изюминка: (слайд №13) Выполнить самостоятельно.


Проверка заданий (слайд №14)


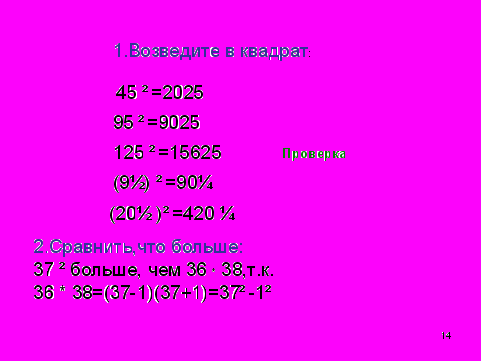
3.Подведение итогов урока, выставление оценок по критериям оценочного листа (слайд №3)


Слайд №15