Урок алгебры в 8 классе по теме «Решение квадратных уравнений»
| Вид материала | Урок |
- Урока алгебры и информатики «система счисления. Решение задач с помощью квадратных, 98.53kb.
- Урок алгебры в 8 классе с применением информационных технологий по теме «Решение квадратных, 94.17kb.
- Урок по теме «История развития общества, становление науки. Теорема Виета», 124.39kb.
- Урок по алгебре в 8-м классе "Решение квадратных уравнений, 54.09kb.
- «Решение квадратных уравнений» Обобщающий урок в 8 классе, 65.77kb.
- Тема: «Решение квадратных уравнений с помощью номограммы», 98.28kb.
- Урок повторения по алгебре и началам анализа 11 классе Тема: «Решение уравнений методом, 43.47kb.
- Урок по теме «Системы линейных уравнений», 8.64kb.
- Открытый урок по теме, 43.6kb.
- Методика изучения уравнений в курсе алгебры 7-9 классов Примерное содержание, 12.53kb.
Урок алгебры в 8 классе
по теме
«Решение квадратных уравнений».
Белоусова Наталья Николаевна
Учитель математики
ГОУ кадетская школа №1770
«Московский кадетский музыкальный корпус»
Урок разработан по учебнику «Алгебра – 8», авторы Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Издательство «Просвещение» 2005.
Цели урока:
Образовательные:
- Обобщение и систематизация основных знаний и умений по теме: отработка способов решения неполных квадратных уравнений, формирование навыков решения квадратных уравнений по формуле, решения приведенных квадратных уравнений.
Развивающие:
- Развивать логическое мышление учащихся, памяти, внимания, общеучебных умений, умения сравнивать и обобщать.
- Повышать интерес к изучаемой теме.
- Расширение кругозора учащихся.
Воспитательные:
- Воспитание трудолюбия, взаимопомощи, взаимоуважения и математической культуры.
- Воспитание общей культуры.
- Повышать интерес к изучаемой теме.
Данная работа может быть использована на обобщающем уроке по теме «Решение квадратных уравнений» с целью повторения и обобщения изученного материала (рассчитана на 2 часа).
Отдельные части работы могут быть использованы и на обучающих уроках или во внеклассной работе с целью ознакомления с дополнительными сведениями.
Данному уроку предшествовала поисковая и исследовательская работа.
Весь класс был разделен на группы (с учетом степени математической подготовки). Каждой группе были вручены карточки, где формулировались темы докладов.
Ход урока.
Учитель: Нам предстоит поработать над очень важной темой: “Решение квадратных уравнений”. Вы уже достаточно знаете и умеете по этой теме, поэтому наша с вами задача: обобщить и сложить в систему все те знания и умения, которыми вы владеете.
- Историческая справка (1 группа). (2, 3 слайды)
Необходимость решать уравнения не только первой, но и второй степени была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Уравнения второй степени умели решать еще в Древнем Вавилоне во ΙΙ тысячелетии до н. э. Математики Древней Греции решали квадратные уравнения геометрически; например Евклид – при помощи деления отрезка в среднем и крайнем отношениях. Приемы решения уравнений без обращений к геометрии дает Диофант Александрийский (ΙΙΙ в.). Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактатах.
Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте (около 598г.)
Среднеазиатский ученый ал-Хорезми (ΙΧ в.) в трактате «Китаб аль-джебр валь-мукабала» получил эту формулу методом выделения полного квадрата с помощью геометрической интерпретации. Общее правило решения квадратных уравнений было сформулировано немецким математиком М. Штифелем (1487 – 1567). После трудов нидерландского математика А. Жирара (1595 – 1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.
Евклид (28 слайд)
(3 в. до н.э.)
Древнегреческий математик, работал в Александрии. Главный труд «Начала»(15 книг), содержит основы античной математики, элементарной геометрии, теории чисел, общей теории отношений и метода определения площадей и объемов, включавшего элементы теории пределов, оказал огромное влияние на развитие математики.
Диофант Александрийский (29 слайд)
(около 3 в.).
Диофант - древнегреческий математик из Александрии (возможно, что он был эллинизированный вавилонянин). Мы очень мало знаем о нем. Автор трактата Арифметика в 13 книгах(сохранились 6 книг) посвященного главным образом исследованию неопределенных уравнений (т.н. диофантовых уравнений). Одним из первых Диофант стал использовать при записи алгебраических рассуждений специальные знаки. На результаты, полученные Диофантом, впоследствии опирались Ферма, Эйлер, Гаусс и др.
Брахмагупта (30 слайд)
(около 598 – 660 г. г.)
Последний и наиболее выдающийся из древних индийских математиков и астрономов. Родом из Удджайна в Средней Индии, где у него была астрономическая обсерватория. В 628 г. изложил четвертую индуистскую астрономическую систему в стихотворной форме в сочинении Открытие Вселенной (Брахма-спхута-сиддханта). Две его главы посвящены математике, в том числе арифметической прогрессии и доказательству различных геометрических теорем. Остальные 23 главы посвящены астрономии: в них описаны фазы Луны, соединения планет, солнечные и лунные затмения, даны расчеты положений планет. Труд Брахмагупты был переведен на арабский язык и таким образом попал в Египет, а оттуда в Европу. Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к форме ах2 + bх = с, а > 0. В данном уравнении коэффициенты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
Аль – Хорезми (31 – 32 слайды)
Мухаммад ибн Муса Хорезми (ок. 783 – ок. 850) – великий персидский математик, астроном и географ, основатель классической алгебры. Сведений о жизни ученого сохранилось крайне мало. Значительный период своей жизни он провел в Багдаде, возглавляя при халифе аль-Мамуне (сыне знаменитого Гаруна аль-Рашида) библиотеку «Дома мудрости». Согдиец Мухаммед ибн Муса аль-Хорезми (то есть, родом из Хорезма - с берегов Сыр-Дарьи) работал в первой половине 9 века. Главная книга Хорезми названа скромно: "Учение о переносах и сокращениях", то есть техника решения алгебраических уравнений. По-арабски это звучит «Китаб аль-джебр валь-мукабала"; отсюда произошло наше слово "алгебра".
Другое известное слово - "алгоритм", то есть четкое правило решения задач определенного типа - произошло от прозвания "аль-Хорезми". Третий известный термин, введенный в математику знаменитым согдийцем - это "синус".
В алгебраическом трактате аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
- «Квадраты равны корням», т. е. ах
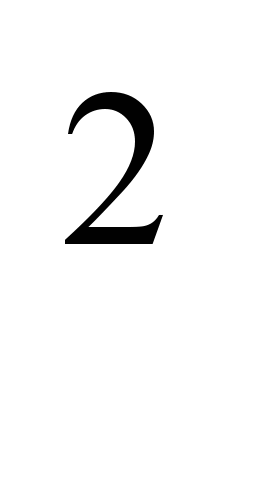 = bх.
= bх.
- «Квадраты равны числу», т. е. ах2 = с.
- «Корни равны числу», т. е. ах = с.
- «Квадраты и числа равны корням», т. е. ах2 + с = bх.
- «Квадраты и корни равны числу», т. е. ах2 + bх =с.
- «Корни и числа равны квадратам», т. е. bх + с = ах2.
- Для аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами аль-джабр и валь-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Учитель: Раз уж мы говорим об уравнениях, давайте вспомним – что это такое?
- Равенство, содержащее неизвестное.
Учитель: Является ли уравнением выражение (х + 1)(х – 4) = 0?
- Да
Учитель: Запишите его в тетрадях. Каким наиболее рациональным способом мы можем его решить?
- Приравнивая каждый множитель к нулю. Произведение равно нулю, когда один из множителей равен нулю, а другой при этом имеет смысл.
Учитель: Хорошо.
Решите, пожалуйста, это уравнение.
- х = -1 и х = 4.
Учитель: А можно ли его решить другим способом?
- Да, его можно привести к квадратному.
Учитель: Напомните, какие уравнения называются квадратными?
- Квадратным уравнением называется уравнение вида ах² + вх + с = 0, где х – переменная, а, в, с – некоторые числа, причем а ≠ 0.
Числа а, в, с – коэффициенты квадратного уравнения. Число а – первый коэффициент, в – второй коэффициент, с – свободный член. (4 слайд)
Учитель: Из предложенных уравнений выберите квадратные уравнения.(5 слайд).
5х² = 0 8х²- 4 +х² = 0 4х²-18х =4х²+5
16 - х² - 15 = 0 6 - 8х² =2х+9 25+х = 7х - 12
(х-1)(х+1) = х² 12х²+7х= - 7х²- 2х - 5х² = 9х -2
67х² - 95х = 0 6х(2х-3)=4х(3х+4) х² - 34х+289 = 0
х² + 6х + 8 = 0 10х²- 5 = 3х²-5 х² - 5х + 3 = 0
6х² + 7х = 5 х²- 5х +6 = 0 16 - х² = 0
Учитель: А какие виды квадратных уравнений вам известны?
- Полные, неполные, приведенные. (6 слайд).
- Неполные квадратные уравнения (2 группа). (7 – 8 слайды)
Полное квадратное уравнение имеет вид ах2 + bx + c = 0, а ≠ 0, в и с – любые числа.
Если в квадратном уравнении хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называется неполным
Рассматриваются следующие три случая неполных квадратных уравнений:
1) в ≠ 0, с = 0 (9 слайд)
ах2 + вх = 0
х(ах + в) = 0
х = 0 или ах + в = 0
х = -в/а
Пример: 18х
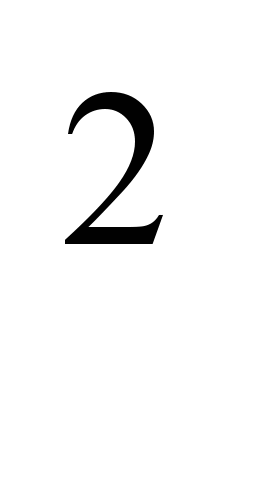 + 27х = 0
+ 27х = 09х(2х + 3) = 0
9х = 0 или 2х + 3 = 0
х = 0 или х = -1,5
2) в = 0, с ≠ 0, тогда имеем уравнение (10 слайд)
ах2 + с = 0
ах2 = - с
х2 = - с/а ( а≠0, по определению квадратного уравнения)
Решение данного уравнения имеет место при - с/а ≥0.
Пример: 4х
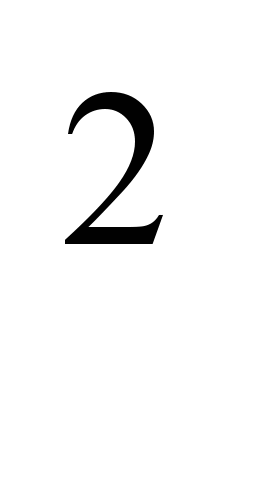 – 100 = 0
– 100 = 04х
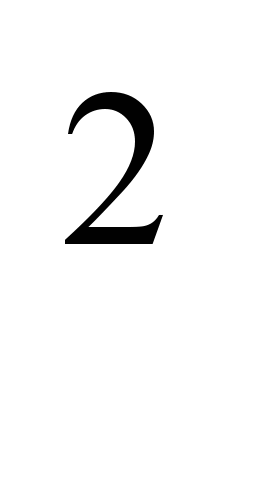 = 100
= 100х
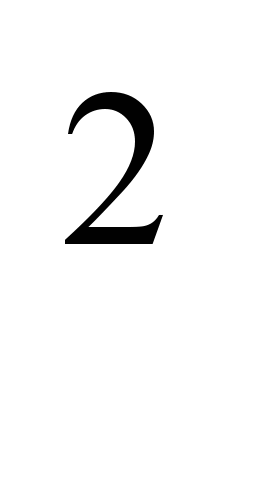 = 25
= 25х1 = 5, х2 = -5
3) в = 0, с = 0 (11 слайд)
ах2 = 0
х2 = 0
х = 0.
Примеры:
а) 157х
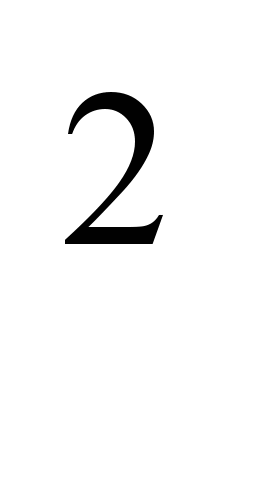 = 0
= 0х = 0
б) -298х
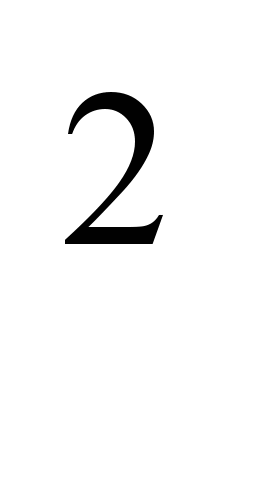 = 0
= 0 х = 0
в) 53,7х
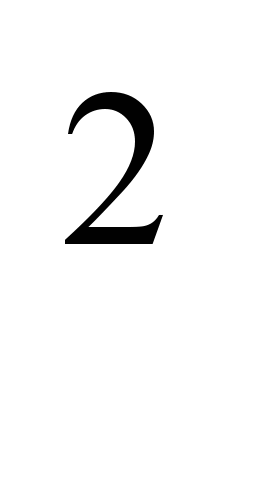 = 0
= 0 х = 0
Учитель: Из предложенных уравнений выберите неполные квадратные уравнения (12 слайд)
5х² = 0 - 5х² = 9х -28 х²- 4 +х² = 0
16 - х² - 15 = 0 6 - 8х² =2х+9 х² - 34х+289 = 0
67х² - 95х = 0 х² - 5х + 3 = 0 12х²+7х= - 7х²- 2х
х² + 6х + 8 = 0 х²- 5х +6 = 0 6х² + 7х = 5
10х²- 5 = 3х²-5 -16 + х² = 0
Учитель: Решить оставшиеся уравнения
3. Алгоритм решения квадратного уравнения (3 группа). (13 – 16 слайды)
В 3 и 4 группы вошли ребята со слабой математической подготовкой.
Целью выступления является обобщение теоретического материала, который полностью соответствует изложению в учебнике.
4. Приведенные квадратные уравнения (4 группа). (17 слайд)
Квадратное уравнение, у которого первый коэффициент равен 1, называется приведенным квадратным уравнением.
x
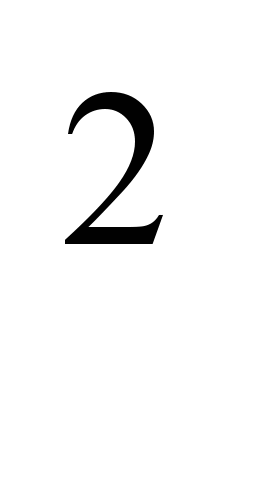 + px + q = 0
+ px + q = 0Теорема
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
(18 – 19 слайды):
Будущий преобразователь алгебры Франсуа Виет (1504 – 1603) появился на свет в маленьком французском городке. В 1560 году он окончил парижский университет и начал адвокатскую практику, через несколько лет перешел на государственную службу, став сначала советником короля Генриха ΙΙΙ, а затем рекетмейстером – докладчиком по ходатайствам. В 1569 году покровитель Виета – король – был убит, и Виет стал служить новому королю. Жизнь его проходила на фоне кровавых событий войны, которую вели две мощные религиозные группировки католиков и протестантов – гугенотов. Достаточно сказать, что он пережил Варфоломеевскую ночь. Но был небольшой промежуток времени, когда из-за происков врагов Виет был отстранен от военной службы и получил неожиданный досуг.
Сейчас нам трудно представить математику без формул и уравнений, но именно такой была она для Виета. Виет завершил создание буквенного исчисления, введя обозначения не только для неизвестного и его степени, но и для параметров. Это позволило записать целые классы задач, которые можно решать с помощью одного правила. Он встал у истоков создания новой науки – тригонометрии. Многие тригонометрические формулы, которые ныне изучают в курсе математики средней школы, впервые были записаны Виетом. В 1593 году он первым сформулировал теорему косинусов. Четыре года опалы оказались необычайно плодотворными для Виета. Он работал самозабвенно. По рассказам современником Виет мог просиживать за письменным столом по трое суток подряд. Только иногда забываясь сном на несколько минут. В тот период он начал большой труд, который назвал «Искусство анализа, или Новая алгебра». Книгу он не завершил, но главное, что определило развитие всей математики Нового времени, было написано.
Учитель: Из предложенных уравнений выберите приведенные квадратные уравнения (20 слайд)
5х² = 0 х² - 5х + 3 = 0
16 - х² - 15 = 0 х²- 5х +6 = 0
67х² - 95х = 0 8х²- 4 +х² = 0
х² + 6х + 8 = 0 х² - 34х + 289 = 0
10х²- 5 = 3х²-5 12х²+7х= - 7х²- 2х
- 5х² = 9х -2 6х² + 7х = 5
6 - 8х² =2х+9 -16 + х² = 0
Учитель: Решить оставшиеся уравнения
5. Выявление закономерностей между суммой коэффициентов а, в, с
и корнями уравнения (5 группа).
Для исследования были предложены следующие уравнения (21 слайд):
1) х2 + х – 2 = 0
2) х2 + 2х – 3 = 0
3) х2 – 3х + 2 = 0
4) 100х2 + 34х – 134 = 0
5) 200х2 – 23х – 177 = 0
6) х2 – х – 2 = 0
7) х2 – 2х – 3 = 0
8) 90х2– 25х -115 = 0
После решения уравнений, учащиеся должны были сделать вывод.
(22 слайд):
Если в квадратном уравнении ах² + вх + с = 0 сумма коэффициентов а + в + с = 0, то х1 = 1; х2 =
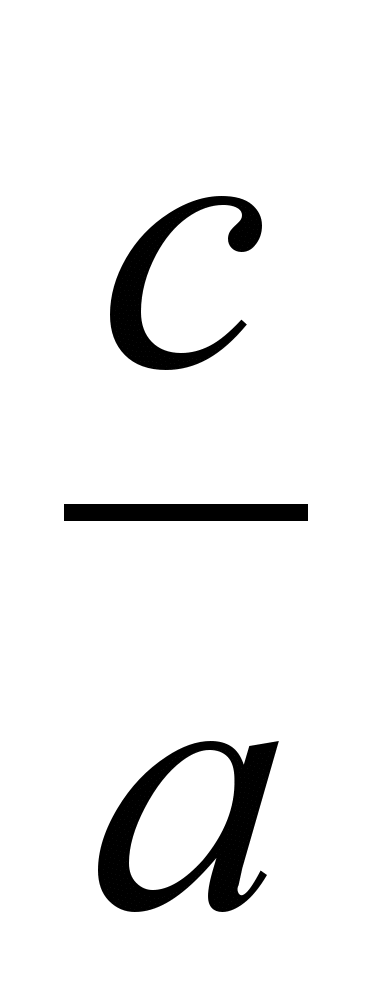 .
. Пример. 5х² - 8х +3 = 0
так как 5 – 8 + 3 = 0, то х1 = 1; х2 = 0,6
Если в квадратном уравнении ах² + вх + с = 0 выполняется равенство а + с = в, то х1 = -1; х2 = -
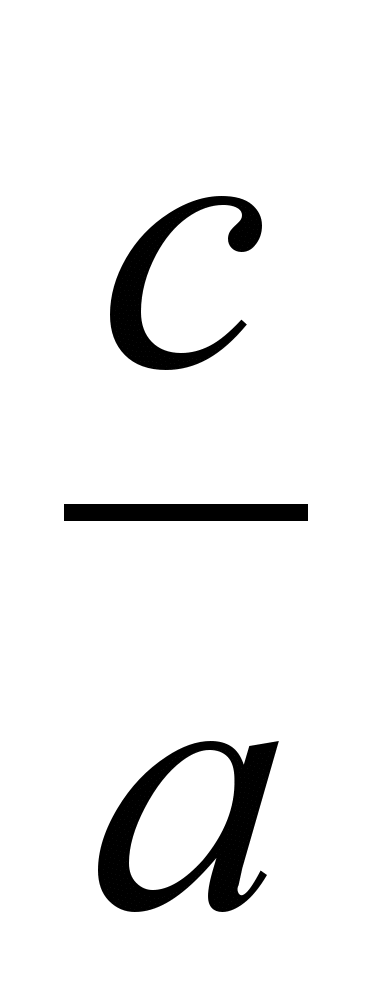 .
.Пример. 5х² + 8х +3 = 0
так как 5 + 3 = 8, то х1 = - 1; х2 = - 0,6
Учитель: Устно решить уравнения, применив «открытые» свойства. (23 слайд).
х2 – 17х - 18 = 0 100х2 – 97х – 197 = 0
2х2 – х – 3 = 0 5х2 – х – 6 = 0.
14х2 – 17х + 3 = 0
6. Решение квадратных уравнений с параметрами (6группа).
(24 слайд):
Для того чтобы познакомиться с понятием уравнения с параметром, рассмотрим следующее уравнение х
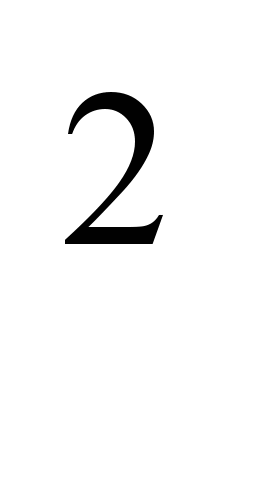 - (2а + 1)х + (а
- (2а + 1)х + (а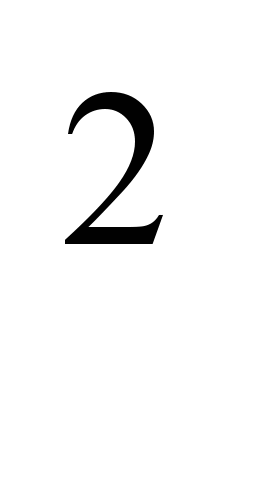 + а – 2) = 0.
+ а – 2) = 0.В заданном уравнении в роли коэффициентов выступают не конкретные числа, а буквенные выражения. Такие уравнения называют уравнениями с буквенными коэффициентами или уравнениями с параметрами.
Решить уравнение с параметром – это значит установить соответствие, позволяющее для любого значения параметра найти соответствующее множество корней.
(25 слайд):
Решить уравнение с параметром – это значит определить, при каких допустимых значениях параметров уравнение
- имеет решения;
- не имеет решения;
- установить количество решений;
- найти вид каждого решения при соответствующих ему значениях параметров.
Решим несколько уравнений.
1. При каком значении а уравнение 2х2 + ах + 8 = 0 имеет один корень? (26 слайд).
Решение. Квадратное уравнение имеет один корень, если D = 0.
D = а
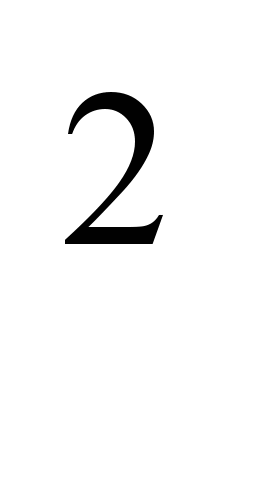 - 4·2·8
- 4·2·8 а2 – 4 · 2 · 8 = 0
a2 – 64 = 0
a2 = 64
a1= 8
a2 = - 8
Ответ: при а = 8, и при а = - 8 уравнение имеет один корень
2. В уравнении х2 + рх + 56 = 0 один из корней равен – 4, найдите другой корень этого уравнения и коэффициент р. (27 слайд)
Решение. Применим теорему Виета
х
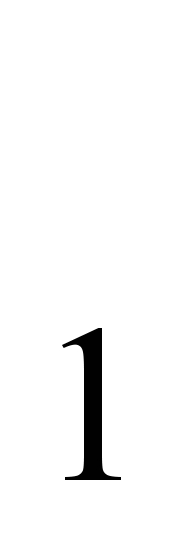 + х
+ х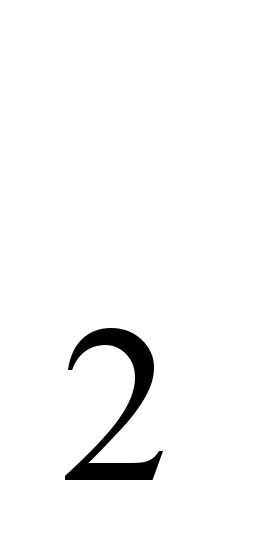 = - р
= - рх
 · х
· х = 56
= 56т. к. х
 = - 4, то найдем х
= - 4, то найдем х = 56 : (- 4)
= 56 : (- 4)х
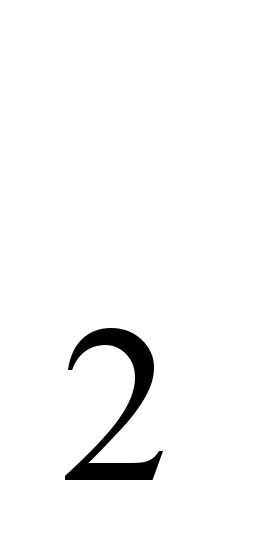 = - 14
= - 14- р = х
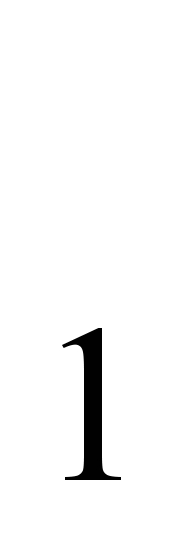 + х
+ х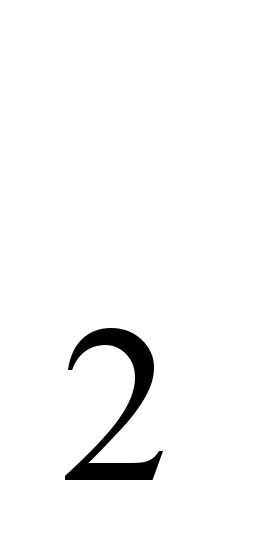 = - 4 + (-14) = - 18, значит р = 18.
= - 4 + (-14) = - 18, значит р = 18.Ответ: х
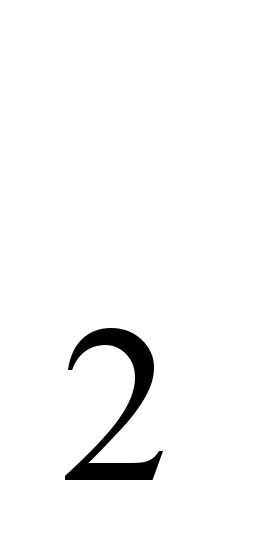 = - 14; р = 18.
= - 14; р = 18.7. Самостоятельная работа.
Учащимся предлагается трехуровневая работа.
Учитель: Если вы еще не уверены в своих силах и желаете закрепить решение уравнений, то выбираете уровень А.
Если считаете, что материал усвоен хорошо – В.
Если желаете испробовать свои силы на более сложных заданиях – уровень С.
Вариант 1.
Уровень А
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 3х2 + 6х – 6 = 0, б) х2 - 4х + 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 - 7х + 2 = 0, D = b2 - 4ac = (-7)2 – 4· 5 · 2 = …;
№3. Закончите решение уравнения 3х2 - 5х – 2 = 0.
D = b2 - 4ac = (-5)2- 4· 3·(-2) = 49; х1 = … х2=…
Уровень В
Решите уравнение: а) 6х2 – 4х + 32 = 0; б) х2 + 5х - 6 = 0.
Уровень С
Решите уравнение: а) -5х2 – 4х + 28 = 0; б) 2х2–8х–2=0.
Доп. задание. При каком значении а уравнение х2 - 2ах + 3 = 0 имеет один корень?
Вариант 2.
Уровень А
№1. Для каждого уравнения вида ax2 + bx + c = 0 укажите значения a, b, c.
а) 4х2 - 8х + 6 = 0, б) х2 + 2х - 4 = 0
№2. Продолжите вычисление дискриминанта D квадратного уравнения ax2 + bx + c = 0 по формуле D = b2 - 4ac.
5х2 + 8х - 4 = 0, D = b2 - 4ac = 82 – 4· 5 · (- 4) = …;
№3. Закончите решение уравнения х2 - 6х + 5 = 0.
D = b2 - 4ac = (-6 )2 - 4· 1·5 = 16; х1 = … х2=…
Уровень В
Решите уравнение: а) 3х2 – 2х + 16 = 0; б) 3х2 - 5х + 2 = 0.
Уровень С
Решите уравнение: а) 5х2 + 4х - 28 = 0; б) х2 – 6х + 7 = 0.
Доп.задание. При каком значении а уравнение х2 + 3ах + а = 0 имеет один корень.
8. Решение задач.
Последняя группа должна была подобрать задачи, приводящие к квадратным уравнениям, которые рассматриваются в древних математических рукописях и трактатах.
1. Индусская задача из Бхасхары (1114г.). (33 слайд)
Квадрат пятой части обезьян, уменьшенной на три, спрятался в гроте; одна обезьяна, влезшая на дерево, была видна. Сколько было обезьян?
Ответ: 50 обезьян.
2. Индусская задача из Бхасхары (1114г.). (34 слайд).
На две партии разбившись,
Забавлялись обезьяны.
Часть восьмая их в квадрате
В роще весело резвилась;
Криком радостным двенадцать
Воздух свежий оглашали.
Вместе сколько, ты мне скажешь,
Обезьян там было в роще?
Ответ: 48 или 16 обезьян.
3. Задача Безу (XVIII в.). (35 слайд)
Некто купил лошадь и спустя некоторое время продал ее за 24 пистоля. При этом он потерял столько процентов своих денег, сколько стоила ему лошадь. За какую сумму денег была куплена лошадь первоначально?
Ответ: 60 или 40 пистолей.
Учитель: Итак, мы проделали большую работу. Повторили всю теорию, касающуюся квадратных уравнений. Прорешали различные их виды.
Итог урока : выставление оценок
Домашнее задание.
Подготовиться к контрольной работе.
Задача из китайского трактата «Математика в девяти книгах» (примерно II в.до н.э)
«Имеется город с границей в виде квадрата со стороной неизвестного размера, в центре каждой стороны находятся ворота. На расстоянии 20 бу(1 бу=1,6 м) от северных ворот (вне города) стоит столб. Если пройти от южных ворот прямо 14 бу, затем повернуть на запад и пройти еще 1775 бу, то можно увидеть столб. Спрашивается: какова сторона границы города?»
