«Оптимизация кластерной системы на базе pvm компьютерной лаборатории физического факультета»

Вид материала

Курсовая

Содержание Процесс компиляции собственного программного обеспечения для работы с PVM. Тестирование новой конфигурации вычислительной системы. Нагрузочное тестирование сети. Kp - отношение количества расчетов на узле к количеству посылок данных по сети. Kt Kp – не меняется при данном тестировании по отношению к предыдущему. Коэффициент Kt Обычная связь Прямая связь Графическая консоль XPVM. Тест имитационной модели метода Монте-Карло.

Подобный материал:

• Физического воспитания; характеристика общих принципов системы физического воспитания,, 67.36kb.
• Название «Оптимизация многоэкстремальных функций на основе кластерной модификации генетического, 52.46kb.
• Международная китайская конференция по научным исследованиям и разработкам в области, 2320.87kb.
• Использование компьютерной датчиковой системы l-микро для организации научно-исследовательской, 100.74kb.
• Использование компьютерной датчиковой системы l-микро для организации научно-иссследовательской, 100.44kb.
• Название Предмет Направление, 567.87kb.
• Н. И. Лобачевского Физический факультет Кафедра физики полупроводников и оптоэлектроники, 109.99kb.
• Развитие физических качеств на уроках физической культуры методом круговой тренировки., 210.46kb.
• Методические указания по выполнению контрольных работ по курсу «Электродинамика сплошных, 35.47kb.
• Рабочая программа курса "симметрия и интегрируемые системы" (специальность физика 010400), 80.46kb.

Процесс компиляции собственного программного обеспечения для работы с PVM.

Для того, чтобы писать программы для исполнения в параллельной вычислительной машиной следует использовать стандартные вызовы библиотеки pvm3.h, необходимо указывать дополнительный набор ключей для осуществления процесса компиляции ПО. Компиляция ПО проводилась в Qt-creator. Дополнительный набор ключей указывался в *.pro файле проекта: QMAKE_LIBS += -lpvm3 -lrt .

Обязательным условием для гетерогенных установок является компиляция исходных кодов ПО для каждой системы в отдельности, в нашем случае LINUX64. Далее следует разослать на все узлы кластера исполняемый файл, т.е. скопировать его в каталог ~/pvm3/bin/LINUX64 на каждом узле.

1. Тестирование новой конфигурации вычислительной системы.
   

В этом разделе результаты теста новой конфигурации будут сравниваться с результатами теста предыдущей конфигурации, для выявления прироста или ухудшения производительности, в зависимости от тех или иных параметров.

1. Нагрузочное тестирование сети.
   

Сначала выполняется нагрузочного тестирования сети, как самого слабого звена в структуре кластера. Для этого был реализован параллельный алгоритм решения квадратного уравнения, коэффициентами которого являются случайные вещественные числа. Исходный текст программы был дополнен необходимыми изменениями, связанными с параметрами работы PVM, и представлен в Приложении к данной работе.

Для выявления участков работы кластера предлагается несколько коэффициентов. Kp - отношение количества расчетов на узле к количеству посылок данных по сети. Kt - отношение суммарного процессорного времени к астрономическому времени работы главного процесса.

Коэффициент Kp – не меняется при данном тестировании по отношению к предыдущему. Коэффициент Kt используется для анализа прироста производительности кластера с учетом новой конфигурации системы и новыми условиями работы тестовой программы. Под новыми условиями работы понимается следующее: в старой конфигурации кластера процессы на разных узлах кластера предавали сообщения друг другу обычным способом, через посредника – демон pvmd, в новой конфигурации кластера программа скомпилирована таким образом, чтобы механизм коммуникаций между задачами работал на прямую, минуя демон pvmd, т.е. каждая задача самостоятельно предает нужные данные другим задачам и соответственно делают также. Таким образом, достигается значительный выигрыш в производительности всей кластерной системы при расчете на ней сильно связанной задачи, требующей частой синхронизации процессов. Об этом свидетельствуют следующие факторы:

1. Скорость пересылки информации по сети увеличивается с 1,5 МБайт/с (10 Мбит/c) до 7,5 Мбайт/с (60 Мбит/с), данный показатель был зафиксирован в Системном мониторе Ubuntu, где отражается статистика загрузки сети.
   
2. В новой конфигурации коэффициент Kt значительно увеличивается в процентном отношении к старой конфигурации, о чем свидетельствуют приведенный ниже таблицы результатов тестирования и диаграммы, динамики прироста (рис.2) и общей динамики данного коэффициента (рис.3)
   

Обычная связь процессов старая конфигурация
Количество процессов		Посылок по сети, B	Расчетов на узле, С		Время работы главного процесса (астрономическое),D		Суммарное процессорное время кластера, Е		Kp = log(C/B)	Kt1 = E/D
18		1,00E+00	1,00E+09		99,10054		1186,258957		9	11,97026
18		1,00E+01	1,00E+08		112,6868		1058,926276		7	9,397075
18		1,00E+02	1,00E+07		107,7564		1038,060469		5	9,633397
18		1,00E+03	1,00E+06		113,0704		1033,268205		3	9,13827
18		1,00E+04	1,00E+05		144,8674		1038,608148		1	7,16937
18		1,00E+05	1,00E+04		341,0926		1115,252644		-1	3,269648
18		1,00E+06	1,00E+03		1592,878		1791,672389		-3	1,124802
18		1,00E+07	1,00E+02		14682,29		8547,911557		-5	0,582192
18		1,00E+08	1,00E+01		144365,1		74368,11773		-7	0,515139
Прямая связь процессов новая конфигурация
Количество процессов	Посылок по сети, B			Расчетов на узле, С		Время работы главного процесса (астрономическое),D		Суммарное процессорное время кластера, Е	Kp = log(C/B)	Kt2 = E/D
18	1			1000000000		119,7327823		1107,298489	9	9,248081
18	10			100000000		139,0967096		1058,176217	7	7,607486
18	100			10000000		127,1325296		1018,450738	5	8,010937
18	1000			1000000		147,4517699		1092,258965	3	7,407568
18	10000			100000		212,6682274		1212,215327	1	5,70003
18	100000			10000		387,8083071		1385,465934	-1	3,572554
18	1000000			1000		1702,352634		3398,62797	-3	1,99643
18	10000000			100		15483,53345		22804,68602	-5	1,472835
18	100000000			10		114135,2611		165196,0456	-7	1,447371

Обобщение результатов таблинчых значений:

№	Количество процессов	Посылок по сети, B	Расчетов на узле, С	Kt2/Kt1	Динамика Kt, %
1	18	1	1000000000	77%	-23
2	18	10	100000000	81%	-19
3	18	100	10000000	83%	-17
4	18	1000	1000000	81%	-19
5	18	10000	100000	80%	-20
6	18	100000	10000	109%	9
7	18	1000000	1000	177%	77
8	18	10000000	100	253%	153
9	18	100000000	10	281%	181

И


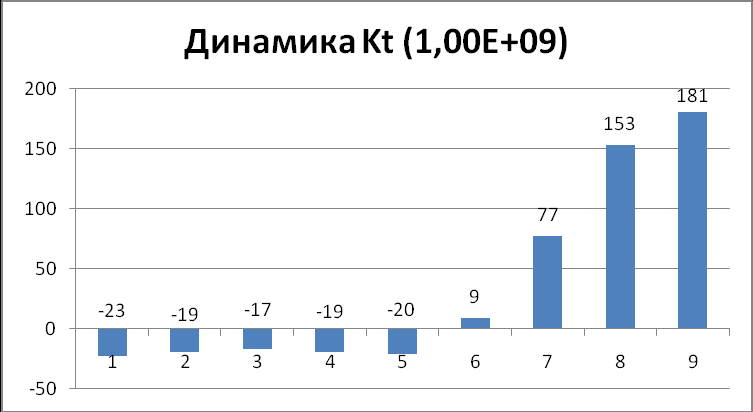
Диаграмма показывает на сколько процентов изменился коэффициент Kt в новой конфигурации относительно старой. (рис. 2)




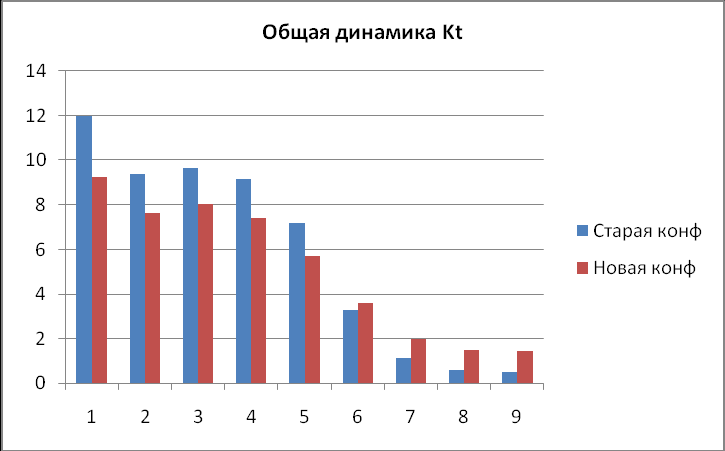
Общая динамика коэффициента производительности кластерной системы при двух конфигураций (рис.3).
з диаграммы видно, что при значении посылок сообщений по сети больше 100 тысяч, наблюдается значительный прирост коэффициента Kt. Таким образом, за счет прямой коммуникации задач в PVM эффективность кластерной системы возрастает при очень высокой связности вычислений. Небольшой снижение в динамике коэффициента Kt при малом количестве посылок по сети связано с тем, что время, затраченное на отправку сообщения: инициализация буфера передачи, упаковка сообщения, отсылка – приплюсовывается ко времени счета данной задачи, так как она сама выполняет эти действия, в то время как при старой конфигурации кластера эти действия за нее выполнял демон. Если оценивать такой показатель, как Астрономическое время работы главного процесс (D), то данный параметр также уменьшается при значительном увеличении количества посылок по сети, что видно из табличных значений. Также из них видно, что суммарное процессорное время кластера (Е) увеличивается при новой конфигурации, т.е. кластер считает дольше, но зато повышается эффективность его использования при сильно связанных вычислениях, так как значение коэффициента Kt стремится к значениям меньше 1 медленно, с ростом числа посылок по сети, по сравнению с предыдущей конфигурацией кластера, когда оно достигало их уже при миллионе пересылок по сети. Если значение коэффициента Kt становится меньшим 1, это говорит о том, что данную задачу затратно решать данным способом на кластере, так как скорость счета одной машины становиться больше скорости счета всей кластерной системы в целом, что видно из табличных значений старой конфигурации. Данный прирост производительности кластера не является предельным, зависит от коэффициента Kp, например, одном из тестирований он был равен log(100/10000) = -2 , то Kt возрос на 259% от старой конфигурации.

Графическая консоль XPVM.

Поначалу этого нагрузочного тестирования сети в работе использовалась графическая консоль (XPVM). Данная консоль содержит все те же самые наборы атрибутов и функций, что и обычна консоль PVM, только они представлены в графическом виде, в качестве кнопок и графиков.

Окно графической консоли разделено на две части. В верхней части сосредоточены кнопки управления кластером, а также наглядно представлена конфигурация кластерной системы в виде хостов. Когда они бездействуют, светятся белым, когда считают, зеленым. Нижняя часть она разделана на две взаимосвязанных части. Левая часть содержит номера TID запущенных задач, а правая иллюстрирует их поведение: пустая белая полоса задача запущена, зеленая - считается, красная – передает информацию, черные линии, отходящие от плоской задачи, свидельствуют об обмене информацией с другими задачами.

Данная графическая консоль достаточно хорошо иллюстрирует работу PVM. Значительным недостатком ее является то, что при большой связности задачи XPVM не эффективно использовать в виду того, что она каждое событие сохраняет в своей памяти и затем иллюстрирует на экране, с большой задержкой в силу, отсутствия возможности более быстрого способа иллюстрации, а также в виду того что при больших посылках по сети, она начинает использовать все больше и больше ресурсов компьютерной памяти (физической и виртуальной), когда они заканчивается на главном узле кластера, то локальные задачи теряют связь с главной задачей, они зависают в памяти узлов кластера, и все расчеты соответственно останавливаются. Ввиду этого негативного воздействия, данная графическая консоль более не использовалась, т.к. она очень затратная по компьютерным ресурсам.



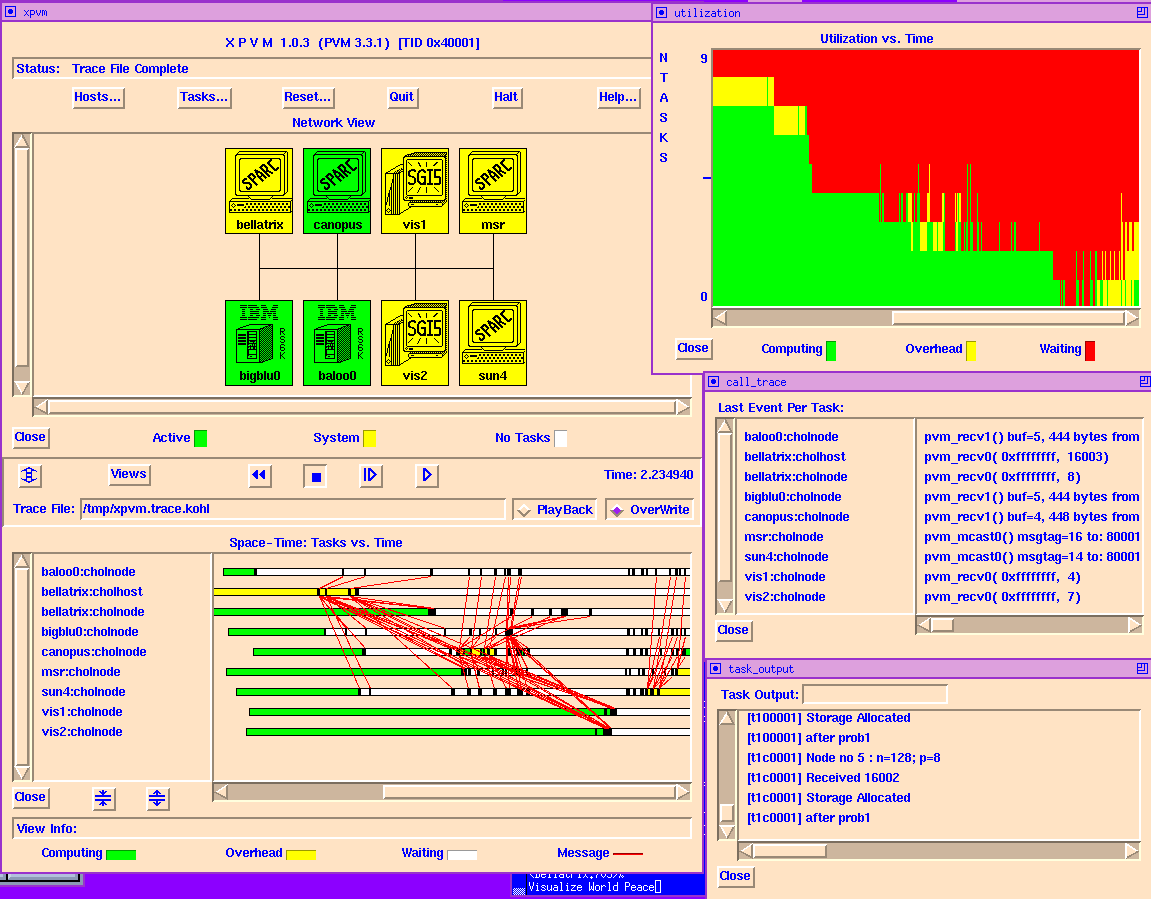
Иллюстрация графической консоли XPVM. (рис.4)

1. Тест имитационной модели метода Монте-Карло.
   

Имитационная модель метода Монте-Карло, широко применяющегося при решении задач математической физики. В качестве модельной задачи взяли последовательный алгоритм для нахождения числа Пи: случайным образом генерируем два числа из отрезка [0,1] — это координаты точки, проверяется, попадает ли эта точка в соответствующий сектор единичной окружности, если да — к счетчику прибавляется единица. Число Пи ищется как значение счетчика после проверки всех точек, умноженное на четыре и деленное на общее количество точек в опыте. Погрешность нахождения Пи уменьшается с ростом количества точек в опыте.

Данный алгоритм полностью подвергается распараллеливанию из-за того, что область данных можно разбить на не пересекающиеся отрезки, в него были добавлены те же изменения, что и в предыдущую программу нагрузочного тестирования сети. В опыте изменяется сразу две величины: первое - увеличивается количество точек, задействованных в эксперименте, с 10⁶ до 10¹⁰ и второе - увеличивается количество расчетных процессов в кластере с 9 до 90.

Для оценки новой конфигурации кластера использовались два значения выводимые программой:

1) Среднее процессорное время кластера (Е).

Кол-во процессов	Общее количество точек на кластер	Среднее Проц-Время кластера Старое, E1	Среднее Проц-Время кластера Новое, Е2	E1-E2
9	1000000	0,068295269	0,068040326	0,00
18	1000000	0,068048359	0,070339206	0,00
27	1000000	0,069430465	0,071388097	0,00
36	1000000	0,071551692	0,073252535	0,00
45	1000000	0,073866028	0,074620868	0,00
54	1000000	0,075496824	0,075872485	0,00
63	1000000	0,077019329	0,077618713	0,00
72	1000000	0,07928147	0,078803145	0,00
81	1000000	0,079825395	0,080585617	0,00
90	1000000	0,081010961	0,081267964	0,00
9	10000000	0,661045693	0,647701333	0,01
18	10000000	0,675413639	0,673377255	0,00
27	10000000	0,67726336	0,656369116	0,02
36	10000000	0,69438044	0,645981136	0,05
45	10000000	0,702692726	0,671263983	0,03
54	10000000	0,704552913	0,680988712	0,02
63	10000000	0,721303162	0,674876851	0,05
72	10000000	0,72625546	0,683088815	0,04
81	10000000	0,733851275	0,685225308	0,05
90	10000000	0,737615887	0,687342186	0,05
9	100000000	6,139807484	5,950953849	0,19
18	100000000	6,181287627	6,03603047	0,15
27	100000000	6,212874967	5,999045691	0,21
45	100000000	6,216053396	6,067578798	0,15
63	100000000	6,134568011	6,073195363	0,06
Кол-во процессов	Общее количество точек на кластер	Среднее Проц-Время кластера Старое, E1	Среднее Проц-Время кластера Новое, Е2	E1-E2
72	100000000	6,17565295	6,053301312	0,12
81	100000000	6,214479306	6,058565829	0,16
90	100000000	6,230372889	6,07777647	0,15
9	1000000000	62,19087335	59,38107455	2,81
18	1000000000	62,29993233	59,23171841	3,07
27	1000000000	63,43304354	59,28884506	4,14
36	1000000000	62,11486847	59,19742158	2,92
45	1000000000	64,15349547	59,19926148	4,95
54	1000000000	63,90943245	59,21409718	4,70
63	1000000000	61,92625735	59,39892504	2,53
72	1000000000	63,87289228	59,29861706	4,57
81	1000000000	63,78063174	59,28395371	4,50
90	1000000000	61,7612	59,28268173	2,48
9	10000000000	611,8024851	592,4171916	19,39
18	10000000000	625,3053222	592,4245721	32,88
27	10000000000	639,5959873	595,1258813	44,47
36	10000000000	637,4668521	591,0551191	46,41
45	10000000000	641,7515958	595,0374052	46,71
54	10000000000	639,0328503	594,7466575	44,29
63	10000000000	641,5984646	595,4592241	46,14
72	10000000000	640,4067908	594,5784957	45,83
81	10000000000	647,1050188	595,1500482	51,95
90	10000000000	649,7285772	595,5870165	54,14

Из данной таблицы видно, что среднее процессорное время старой конфигурации кластера (Е1) больше, чем новой (E2), при любом числе запущенных процессов. Это проиллюстрировано на диаграммах (рис.5). Следует также отметить тот факт, что при количестве точек большем 1 миллиарда, число запущенных процессов практически не влияет на время счета задачи на кластерной системе, т.е. сколько бы мы процессов счета не запустили, время счета всей кластерной системы останется практически неизменным, а если увеличить число точек (увеличилось в 10 раз), то время счета увеличится во столько раз, во сколько увеличилось число точек (с 59 до 590), об этом свидетельствуют последние две диаграммы (рис.5), такой явной, прямой зависимости при тестировании предыдущей конфигурации не наблюдалось.




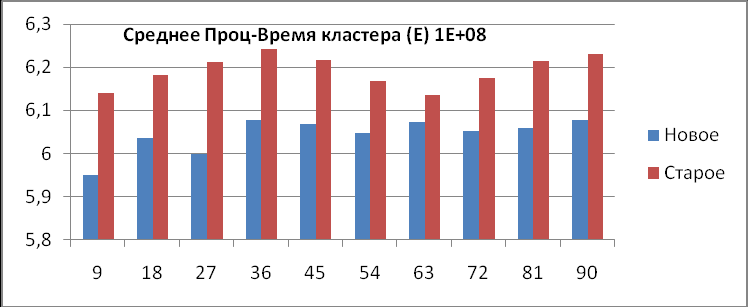
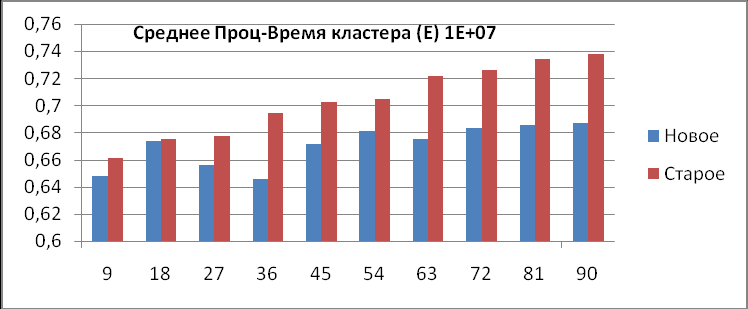
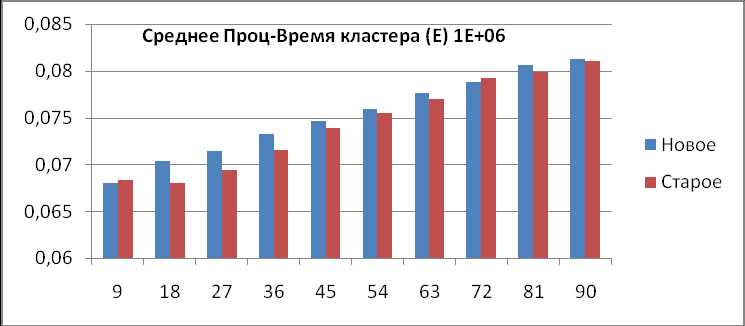
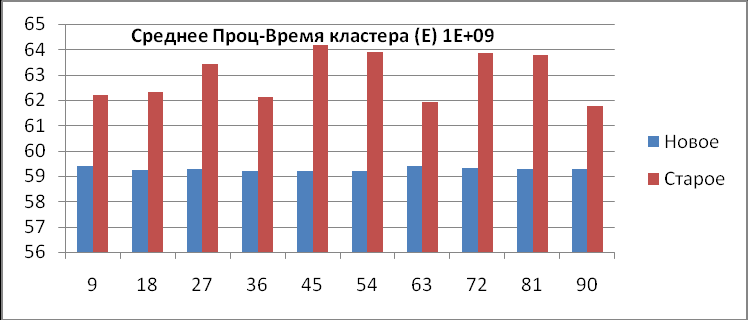
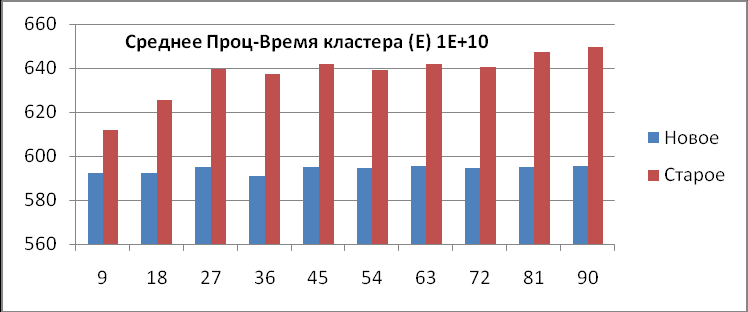
Диаграммы среднего процессорного времени работы кластера (рис.5).

2. Среднее астрономическое время мастера (D), т.е. время работы главной задачи.
   

Множитель числа процессов	Среднее Астро время мастера старое, D1	Среднее Астро время мастера старое, D2	Динамика D2/D1, %
1	0,022743768	0,032634701	43,49
2	0,019742664	0,03169092	60,52
3	0,021301948	0,034691644	62,86
4	0,024832952	0,040115372	61,54
5	0,028491408	0,045345944	59,16
6	0,029647164	0,051315045	73,09
7	0,033450504	0,05683616	69,91
8	0,036737372	0,063799631	73,66
9	0,042951404	0,068065941	58,47
10	0,043405036	0,075527723	74,01
1	0,103664444	0,202463692	95,31
2	0,11484904	0,165041815	43,70
3	0,127870064	0,159635056	24,84
4	0,134409268	0,164022045	22,03
5	0,12639482	0,17818776	40,98
6	0,116823392	0,180488963	54,50
7	0,130211992	0,173872781	33,53
8	0,12740668	0,18057806	41,73
9	0,140798348	0,175055627	24,33
10	0,142984988	0,176062221	23,13
1	0,700494568	0,88411162	26,21
2	0,547940688	0,675269863	23,24
3	0,5114647	0,611737833	19,61
4	0,488551472	0,54348774	11,24
5	0,518046152	0,584736824	12,87
6	0,551513784	0,535651952	-2,88
7	0,575195352	0,550129908	-4,36
8	0,610063008	0,549478912	-9,93
9	0,592967288	0,5678019	-4,24
10	0,564720308	0,539328296	-4,50
1	7,264334296	8,459022909	16,45
2	5,388554972	6,425114483	19,24
3	4,501883604	5,537003825	22,99
4	4,138298968	4,9413291	19,40
5	3,92861094	4,767840401	21,36
6	3,843623388	4,602281532	19,74
7	3,829017744	4,507728879	17,73
Множитель числа процессов	Среднее Астро время мастера старое, D1	Среднее Астро время мастера старое, D2	Динамика D2/D1, %
8	3,793960948	4,397511392	15,91
10	3,69318834	4,190045288	13,45
1	89,95403528	75,49142178	-16,08
2	46,51671818	57,16418391	22,89
3	48,92022383	51,29661245	4,86
4	46,58261083	47,41044204	1,78
5	47,46935875	50,82233079	7,06
6	47,406562	45,80383927	-3,38
7	48,7799673	43,59741354	-10,62
8	47,51148996	42,6926881	-10,14
9	48,393231	42,1579862	-12,88
10	47,43611276	41,95229874	-11,56

Данный показатель имеет значения хуже, чем в старой конфигурации, но стремится к ее значениям с ростом количества точек участвующих в расчетах (рис.6,7), т.е. данный показатель можно считать практически неизменившимся, если брать в расчет количество точек равное 10⁸, 10⁹, 10¹⁰.



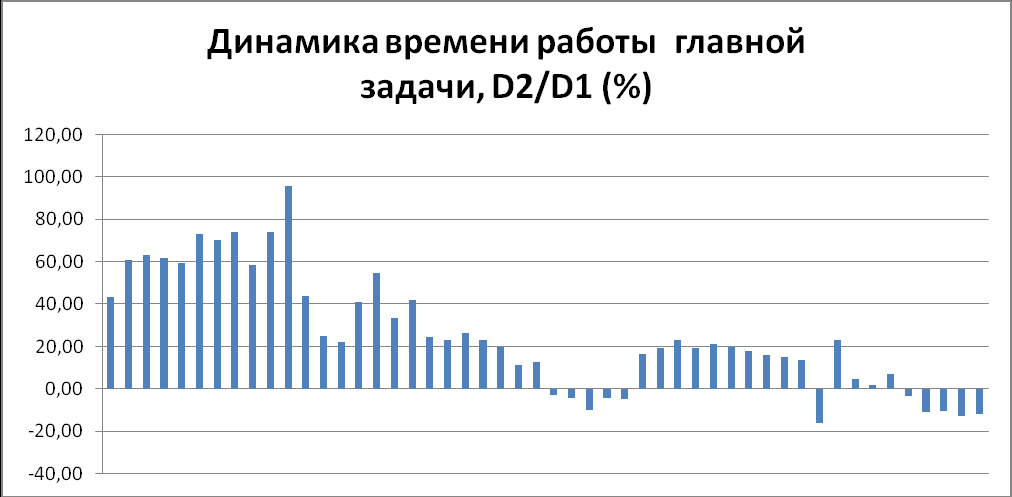
Динамика среднего астрономического времени работы главной задачи (рис.6).