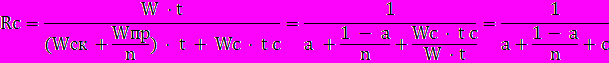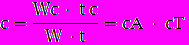Geum.ru

«Оптимизация кластерной системы на базе pvm компьютерной лаборатории физического факультета»

Вид материалаКурсовая

Содержание


1.4. Принципы построения кластера.
Производительность кластерной системы. Законы Амдала.
Подобный материал:
1   2   3   4   5   6   7

1.4. Принципы построения кластера.


Архитектура кластера должна обеспечивать масштабируемость ПО при увеличении количества узлов, т. е. прирост производительности при добавлении новых вычислительных модулей. Для этого важно правильно выбрать конфигурацию кластера в зависимости от профиля обмена данными между экземплярами программы, запущенными на разных узлах. Здесь нужно учитывать общий объем пересылаемых данных, распределение длин сообщений, использование групповых операций и т. п.

Каждый узел работает под управлением своей копии стандартной операционной системы, в большинстве случаев — Linux. Состав и мощность узлов могут быть разными в рамках одного кластера, однако чаще строятся однородные кластеры. Выбор конкретной коммуникационной среды (интерконнекта) определяется многими факторами: особенностями решаемых задач, доступным финансированием, требованиями к масштабируемости и т. п. В кластерных решениях применяются такие технологии интерконнекта, как Fast Ethernet, Gigabit Ethernet, SCI, Myrinet, QsNet, InfiniBand. Исходя из всего вышесказанного, можно утверждать, что использование кластера на физическом факультете позволит оптимизировать процесс расчета моделей сложных структур, таких как отдельные молекулы (в частности белки), смесей различных веществ, кристаллов и т.д.

Производительность кластерной системы. Законы Амдала.


Мерой измерения производительности любой вычислительной системы является Flops (floating point operations per second) — количество операций с плавающей точкой в секунду.
  1. Самым важным ограничением повышения производительности от распараллеливания алгоритма решения задачи являются законы Амдала, утверждающие:
  2. 1-ый закон Амдала. Производительность вычислительной системы, состоящей из связанных между собой устройств, в общем случае определяется самым непроизводительным ее устройством.
  3. Следствие. Пусть система состоит из простых устройств и граф системы связный. Асимптотическая производительность системы будет максимальной, если все устройства имеют одинаковые пиковые производительности.
  4. Предположим, что по каким-либо причинам n операций из N мы вынуждены выполнять последовательно. Причины могут быть разными. Например, операции могут быть последовательно связаны информационно. И тогда без изменения алгоритма их нельзя реализовать иначе. Но вполне возможно, что мы просто не распознали параллелизм, имеющийся в той части алгоритма, которая описывается этими операциями. Отношение β = n/N назовем долей последовательных вычислений.
  5. 2-й закон Амдала. Пусть система состоит из s одинаковых простых универсальных устройств. Предположим, что при выполнении параллельной части алгоритма все s устройств загружены полностью. Тогда максимально возможное ускорение равно:

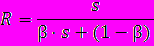
  7. 3-й закон Амдала. Пусть система состоит из простых одинаковых универсальных устройств. При любом режиме работы ее ускорение не может превзойти обратной величины доли последовательных вычислений.


Закон Амдала в сетевой форме.
  1. Одной из главных характеристик параллельных систем является ускорение R параллельной системы, которое определяется выражением:
  2. ,

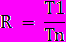где T1 − время решения задачи на однопроцессорной системе, а Tn − время решения той же задачи на n − процессорной системе.
  1. Пусть W = Wск + Wпр, где W − общее число операций в задаче, Wпр − число операций, которые можно выполнять параллельно, а Wcк − число скалярных (нераспараллеливаемых) операций.
  2. Обозначим также через t время выполнения одной операции. Тогда получаем закон Амдала:


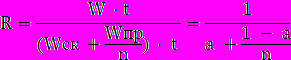
Здесь a = Wск/W − удельный вес скалярных операций.
  1. Закон Амдала определяет принципиально важные для параллельных вычислений положения:
  2. 1. Ускорение зависит от потенциального параллелизма задачи (величина 1–а) и параметров аппаратуры (числа процессоров n).
  3. 2. Предельное ускорение определяется свойствами задачи.
  4. Пусть, например, a = 0,2 (что является реальным значением), тогда ускорение не может превосходить 5 при любом числе процессоров, то есть максимальное ускорение определяется потенциальным параллелизмом задачи. Очевидной является чрезвычайно высокая чувствительность ускорения к изменению величины а.
  5. Основной вариант закона Амдала не отражает потерь времени на межпроцессорный обмен сообщениями. Эти потери могут не только снизить ускорение вычислений, но и замедлить вычисления по сравнению с однопроцессорным вариантом.

Поэтому необходима некоторая модернизация закона:


Здесь Wc − количество передач данных, tc − время одной передачи данных.

Выражение



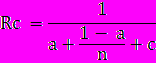
и является сетевым законом Амдала. Коэффициент сетевой деградации вычислений с:


определяет объем вычислений, приходящийся на одну передачу данных (по затратам времени). При этом сА определяет алгоритмическую составляющую коэффициента деградации, обусловленную свойствами алгоритма, а сТ − техническую составляющую, которая зависит от соотношения технического быстродействия процессора и аппаратуры сети.