Программа учебной дисциплины «Газодинамика» Специальность 010802 (опд в. 01)
| Вид материала | Программа |
- Программа учебной дисциплины опд. 03 "Математический анализ" специальность 010100, 101.48kb.
- Программа учебной дисциплины «Практический курс первого иностранного языка» (опд., 770.64kb.
- Программа учебной дисциплины " структуры повседневности и моральное сознание" специальность, 223.75kb.
- Рабочая программа учебной дисциплины судебная фотография и видеозапись Специальность, 90.44kb.
- Рабочая программа учебной дисциплины судебная адвокатура Специальность 030501. 65 «Юриспруденция», 148.98kb.
- Рабочая программа учебной дисциплины судебная психиатрия Специальность 030501. 65 «Юриспруденция», 141.66kb.
- А. И. Герцена программа учебной дисциплины опд. 04 Телекоммуникационные технологии, 58.37kb.
- Программа учебной дисциплины опд. "История немецкой классической философии" специальность, 240.38kb.
- Рабочая программа учебной дисциплины «Математика» Специальность «Прикладная информатика, 322.42kb.
- Программа дисциплины опд. Ф. 5 "Мировая экономика" для студентов, 127.06kb.
Министерство образования Российской Федерации
Санкт - Петербургский государственный университет
Физический факультет
| Рассмотрено и рекомендовано на заседании кафедры радиофизики | УТВЕРЖДАЮ декан факультета ________________ А.С. Чирцов |
| Протокол № от Заведующий кафедрой _____________________Н.Н.Зернов | |
ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
«Газодинамика»
Специальность 010802 (ОПД В.01)
Направление 010800 (ОПД В.03)
Разработчики:
доцент, канд. физ.-мат. наук ___________ ______ М.П. Базарова
доцент, канд. физ.-мат. наук ___________ ______ Т.Ю. Алехина
Рецензент:
профессор, докт.физ.-мат.наук ___________ ____В.А. Павлов
Санкт - Петербург
2006 г.
- Организационно-методический раздел
-
Цель изучения дисциплины:
- дать студентам общее представление о данной области физики и связи ее с различными прикладными задачами;
- ознакомить студентов с различными подходами к решению прикладных физических задач в данной области;
- обучить студентов макроскопическому подходу к выводу системы дифференциальных уравнений, описывающих процессы в нейтральных сплошных средах.
- Задачи курса:
- сформировать законченную систему знаний о макроскопическом подходе к выводу системы дифференциальных уравнений сплошной среды;
- ознакомить с различными аналитическими методами решения прикладных физических задач, связанных с интегрированием нелинейных дифференциальных уравнений в частных производных;
- содействовать формированию у слушателей интереса к современным проблемам и методам их решения в данной области знаний.
- Место курса в системе подготовки бакалавров по направлению «Радиофизика»:
Данная дисциплина является ознакомительной в подготовке бакалавра радиофизики и служит основой для изучения дисциплин «Нелинейная акустика», «Магнитная гидродинамика», «Ударные волны в неоднородных и ионизированных средах» и др., изучаемых в магистратуре на кафедре радиофизики.
- Требования к уровню освоения содержания курса.
В результате изучения курса студент должен:
- знать содержание дисциплины;
- иметь достаточно полное представление о подходах к решению прикладных физических задач, связанных с интегрированием нелинейных дифференциальных уравнений в частных производных;
- иметь четкое представление о связи математической постановки задачи и модели данного физического процесса.
- Объем и распределение часов курса по темам и видам занятий, форма итогового контроля
-
Изучение дисциплины по семестрам:
8 семестр: лекции - 42 ч., экзамен
- Содержание курса
- Основное содержание.
Раздел 1. Вывод замкнутой системы уравнений, описывающих движение газа.
- Модель сплошной среды. Тензор деформации. Тензор собственно деформации. Главные оси деформации. Субстанциальный и локальный способ описания движения среды. Тензор скорости деформации.
- Теорема переноса. Вывод уравнения неразрывности.
- Интегральная форма уравнений движения сплошной среды. Силы массовые и поверхностные. Тензор напряжений.
- Определяющее уравнение для тензора напряжений в случае изотропной сплошной среды. Коэффициент объемного расширения, коэффициент внутреннего трения, коэффициент объемной вязкости.
- Вывод уравнений Навье-Стокса в случае переменных коэффициентов вязкости. Уравнение движения идеального газа – уравнения Эйлера.
- Изменение кинетической энергии макроскопического движения сплошной среды. Необратимость движения вязкой среды. Диссипация механической энергии.
- Изменение кинетической энергии сплошной среды. Вывод уравнения для внутренней энергии сплошной среды.
- Вывод уравнения для удельной энтропии.
- Уравнение состояния, внутренняя энергия и удельные теплоемкости совершенного газа. Теплопроводность.
Раздел 2. Распространение волн бесконечно малой и конечной амплитуды в газообразной среде.
Тема 1. Распространение волн бесконечно малой амплитуды в газообразной среде.
- Распространение волн бесконечно малой амплитуды в идеальном газе. Линеаризация уравнений Эйлера. Уравнение для изменения давления в неоднородной среде. Распространение линейных звуковых волн в однородной среде.
- Распространение плоских монохроматических звуковых волн в однородном идеальном газе в линейном приближении. Распространение плоских монохроматических волн в вязком теплопроводном газе.
Тема 2. Распространение волн конечной амплитуды в газообразной среде.
- Распространение волн конечной амплитуды в идеальном газе. Простые волны Римана в баротропном случае. Физический смысл простой волны.
- Простые волны Римана в небаротропном случае. Скорость распространения простой волны. Искажение простой волны при распространении.
- Распространение волн конечной амплитуды в вязком теплопроводном газе. Квазипростые волны в вязком газе. Уравнение Бюргерса. Стационарная волна. Общее решение уравнения Бюргерса. Асимптотическое нестационарное решение уравнения Бюргерса.
Раздел 3. Ударные волны в идеальном газе.
- Понятие разрывного решения системы дифференциальных уравнений идеального газа. Уравнения движения сплошной среды в интегральной форме.
- Выводы соотношений на разрыве. Исследование соотношений на разрыве. Соотношение Гюгонио.
- Основные свойства ударных переходов. Изменение энтропии при ударных переходах.
- Соотношение на разрыве для совершенного газа. Предельные соотношения для сильных ударных волн.
- Однозначность разрывных решений системы дифференциальных уравнений идеального газа и возрастание энтропии при переходе через ударный фронт
Раздел 4. Задача о сильном взрыве в однородной атмосфере.
- Основные положения теории размерности. Теорема Ваши-Букингема (II теорема).
- Физическая постановка задачи о взрыве в однородной атмосфере. Постановка задачи о взрыве без противодавления (о сильном взрыве). Автомодельные решения.
- Определение скорости распространения фронта ударной волны.
- Исследование дифференциальных уравнений для автомодельных решений. Интеграл Седова. Качественное исследование решения.
- Перечень примерных контрольных вопросов и заданий для самостоятельной работы.
- Тензор деформации.
- Вывод уравнения неразрывности
- Интегральная форма уравнений движения сплошной среды.
- Тензор напряжений.
- Определяющее уравнение для тензора напряжений
- Уравнения Навье-Стокса.
- Уравнение для внутренней энергии.
- Уравнение для удельной энтропии.
- Вывод уравнения для удельной энтропии
- Относительная роль диссипативных (вязких и теплопроводных) членов в уравнениях газодинамики.
- Простые волны Римана в небаротропном случае.
- Решение нелинейных дифференциальных уравнений с помощью характеристик.
- Задача о потоке транспорта. Задача о светофоре.
- Распространение колебаний конечной амплитуды в вязком теплопроводном газе. Квазипростые волны.
- Уравнение Бюргерса. Стационарные решения уравнения Бюргерса.
- Общее решение уравнения Бюргерса. Асимптотическое решение уравнение Бюргерса.
- Общие свойства ударных переходов. Изменение энтропии при ударных переходах.
- Сильный взрыв в однородной атмосфере.
- Понятие автомодельности. Автомодельные решения.
- Примерный перечень вопросов к экзамену.
- Теорема переноса. Вывод уравнения неразрывности.
- Соотношение на разрыве для совершенного газа. Предельные соотношения для сильных ударных волн.
- Определяющее уравнение для тензора напряжений в случае изотропной сплошной среды. Коэффициент объемного расширения, коэффициент внутреннего трения, коэффициент объемной вязкости.
- Распространение волн бесконечно малой амплитуды в идеальном газе. Линеаризация уравнений Эйлера.
- Вывод уравнений Навье-Стокса в случае переменных коэффициентов вязкости. Уравнение движения идеального газа – уравнения Эйлера.
- Распространение плоских монохроматических звуковых волн в однородном идеальном газе в линейном приближении.
- Модель сплошной среды. Тензор деформации. Тензор собственно деформации.
- Распространение волн конечной амплитуды в идеальном газе. Простые волны Римана в баротропном случае. Физический смысл простой волны.
- Интегральная форма уравнений движения сплошной среды. Силы массовые и поверхностные. Тензор напряжений.
- Основные положения теории размерности. Теорема Ваши-Букингема (II теорема).
- Главные оси деформации. Субстанциальный и локальный способ описания движения среды. Тензор скорости деформации.
- Распространение линейных звуковых волн в однородной среде.
- Изменение кинетической энергии сплошной среды. Вывод уравнения для внутренней энергии сплошной среды.
- Понятие разрывного решения системы дифференциальных уравнений идеального газа. Уравнения движения сплошной среды в интегральной форме.
- Вывод уравнения для удельной энтропии. Теплопроводность.
- Выводы соотношений на разрыве. Исследование соотношений на разрыве.
- Изменение кинетической энергии макроскопического движения сплошной среды. Необратимость движения вязкой среды. Диссипация механической энергии.
- Исследование соотношений на разрыве. Соотношение Гюгонио.
- Распространение плоских монохроматических волн в вязком теплопроводном газе.
- Исследование соотношений на разрыве. Соотношение Гюгонио.
- Модель сплошной среды. Тензор деформации. Тензор собственно деформации.
- Простые волны Римана в баротропном случае.
Перечень примерных тестовых заданий по всему курсу (фрагмент).
- Что представляет собой модель сплошной среды?
- Вставьте пропущенное:
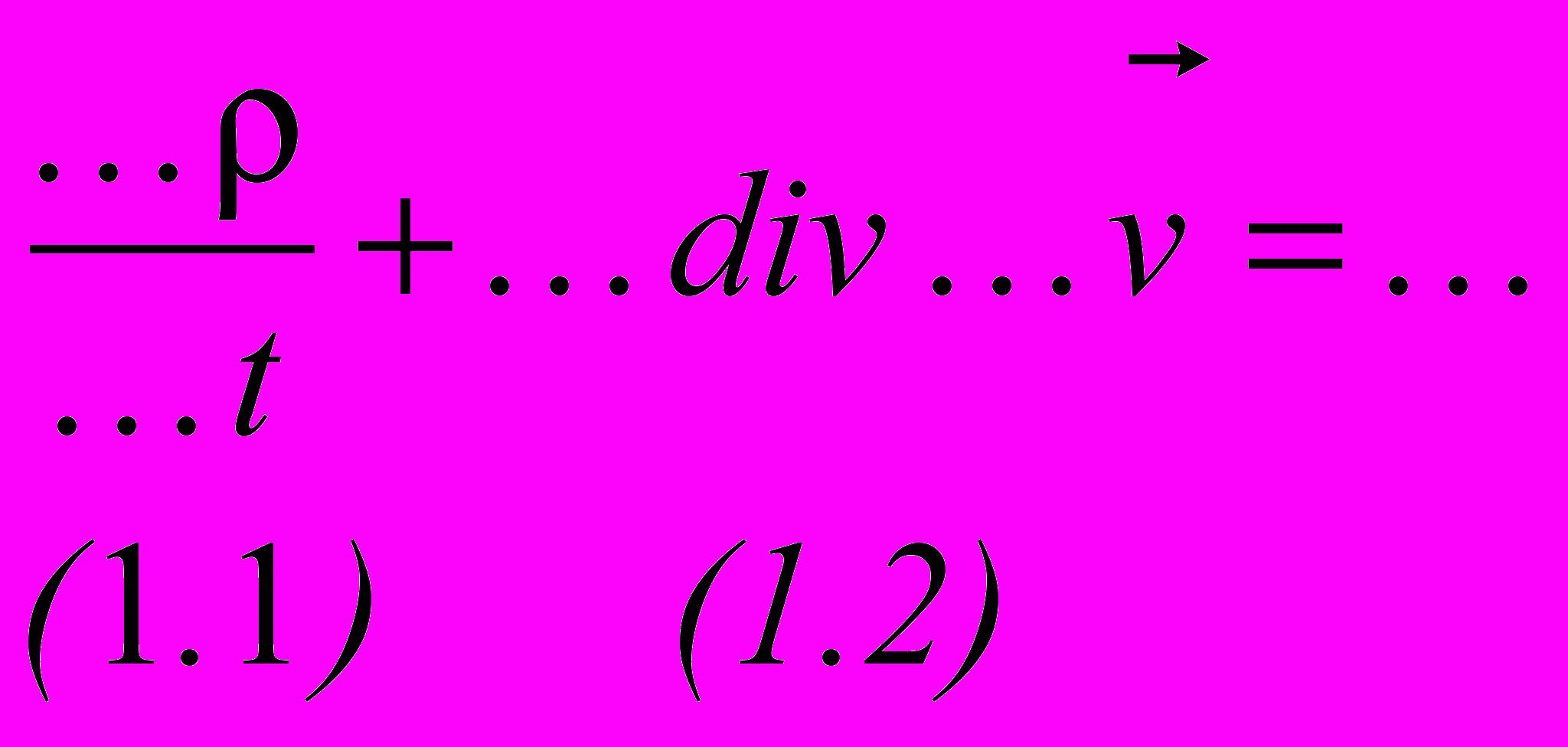 (1)
(1)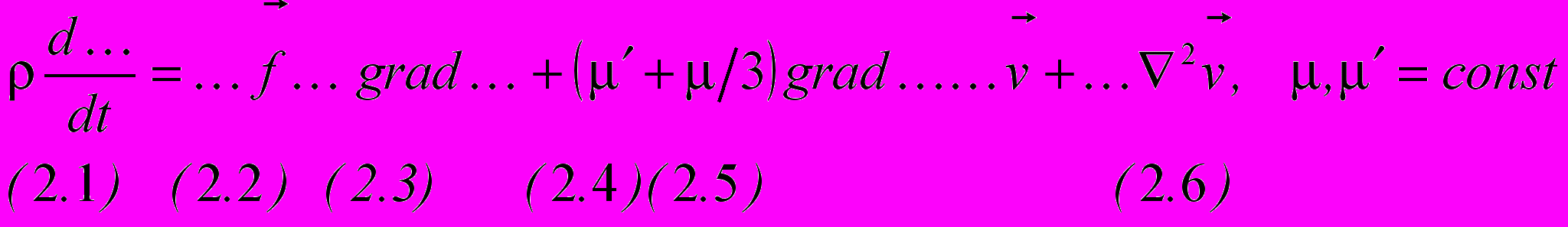 (2)
(2) (3)
(3)- Выпишите слагаемые, которые необходимо учитывать для построения решения уравнений газодинамики
а) в линейном приближении для однородного идеального газа:
в уравнении неразрывности - ;
в уравнениях Навье-Стокса - ;
б) в линейном приближении для однородного вязкого теплопроводного газа:
в уравнении для энтропии - ;
в) в нелинейном приближении для однородного идеального газа:
в уравнении для энтропии - ;
в уравнениях Навье-Стокса - ;
- Напишите формулу, определяющую скорость звука:
- Напишите дисперсионное соотношение для плоских монохроматических волн, распространяющихся в однородном идеальном газе:
- Дайте определение простой волны Римана
- Дайте определение ударной волны.
Примерный перечень задач к экзамену:
- Получить формулу зависимости удельной энтропии от давления для совершенного газа. (Воспользоваться соотношениями
 ,
, 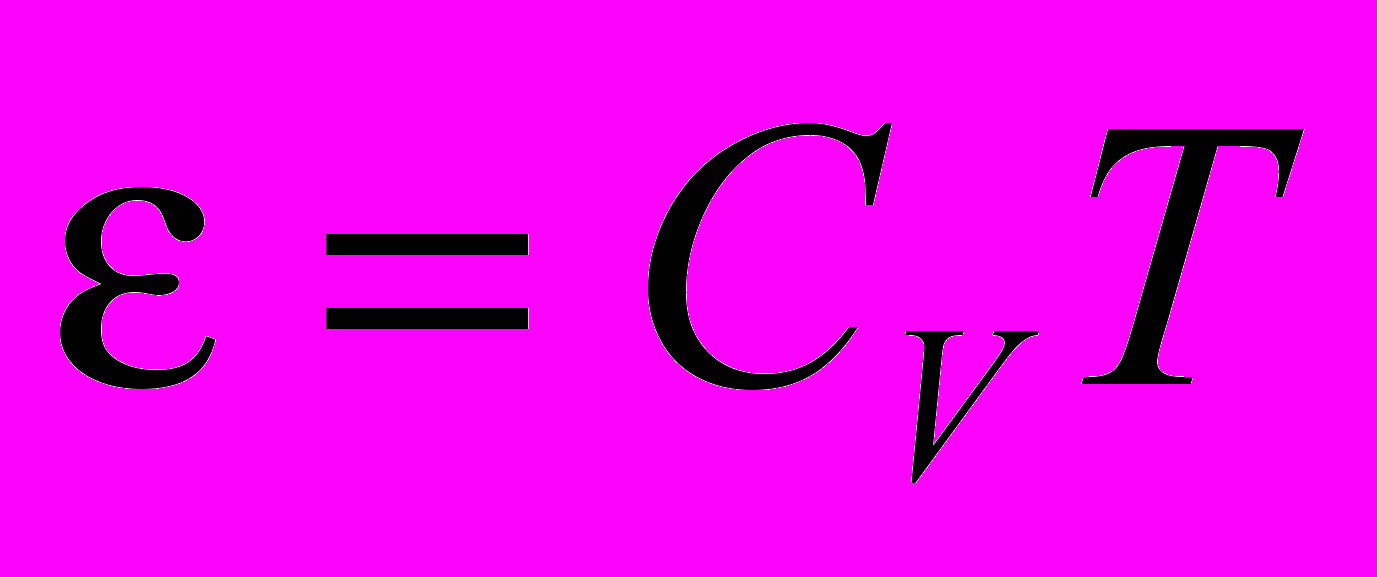 ,
, 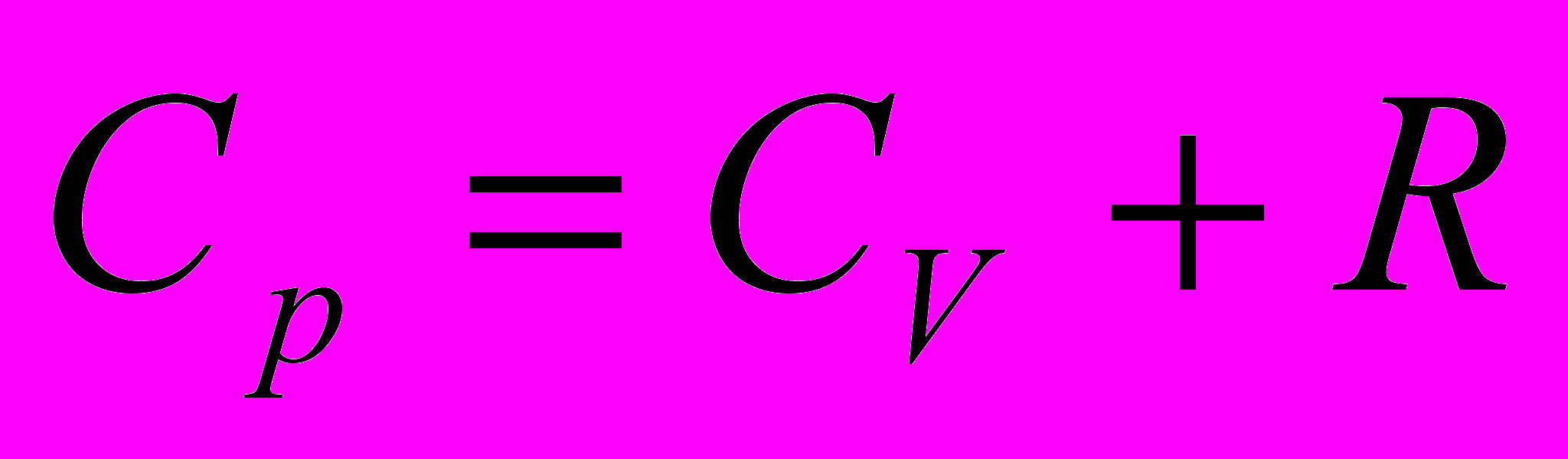 ,
, 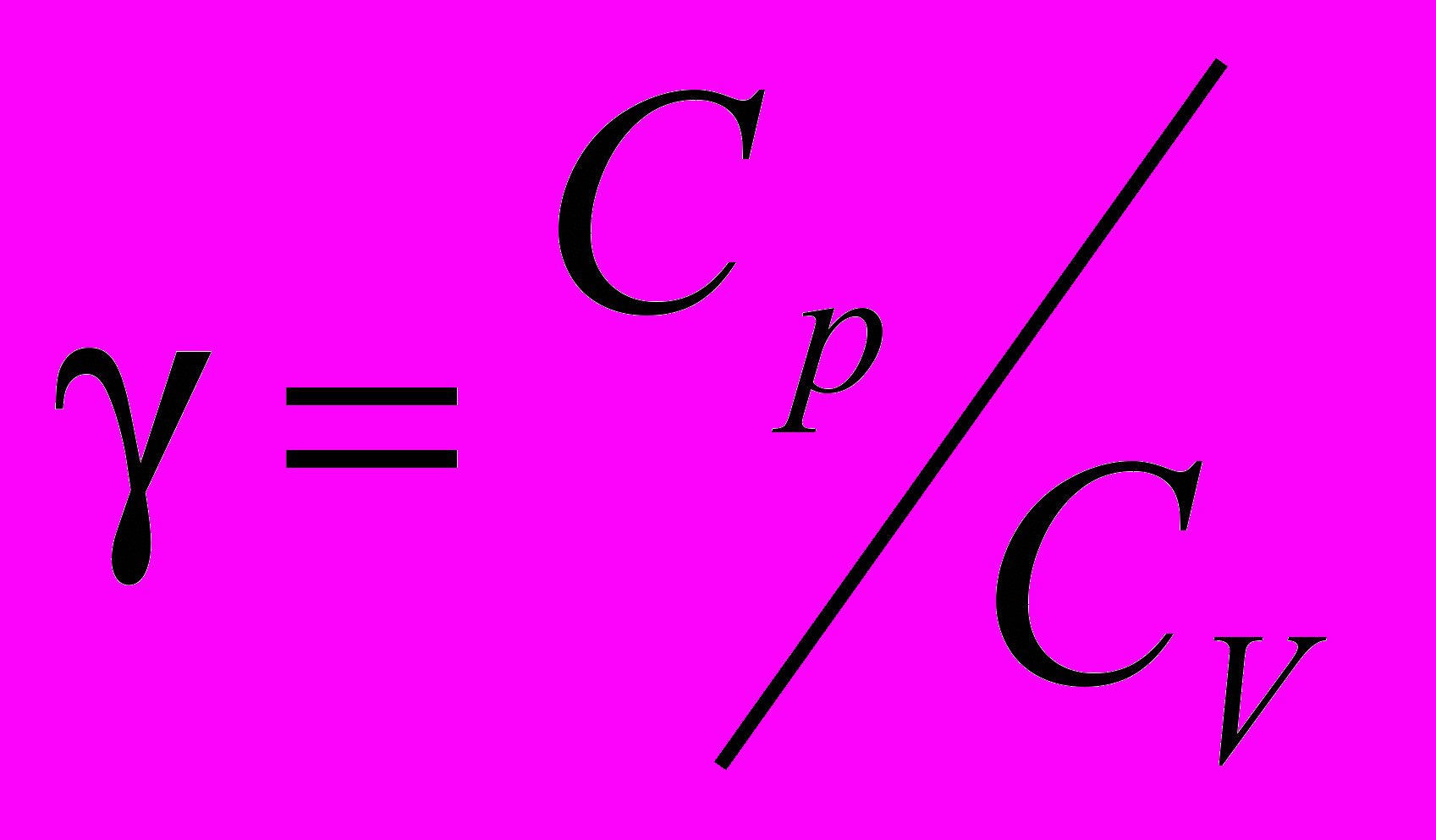 ).
).
- Получить формулу зависимости удельной энтропии от температуры для совершенного газа. (Воспользоваться соотношениями
 ,
, 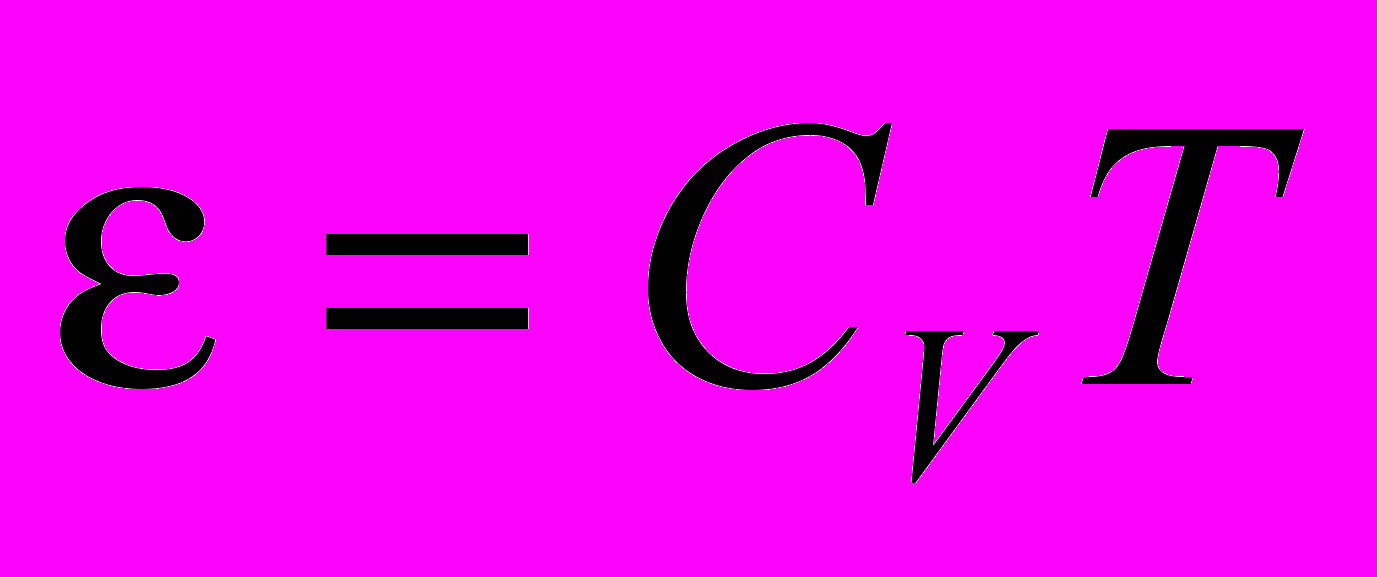 ,
, 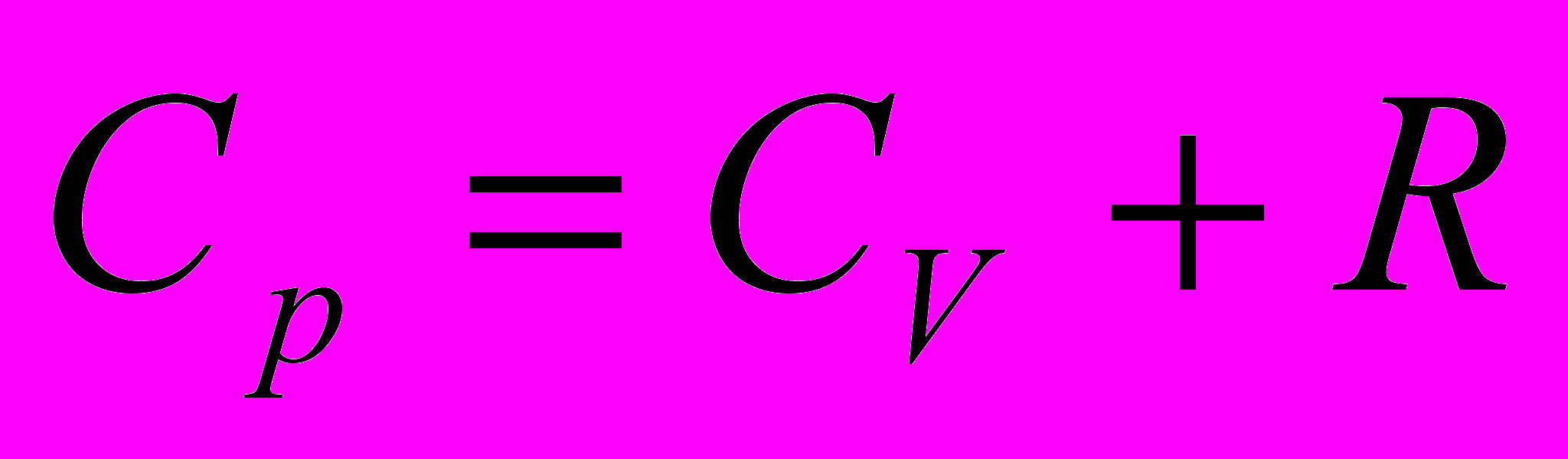 ,
, 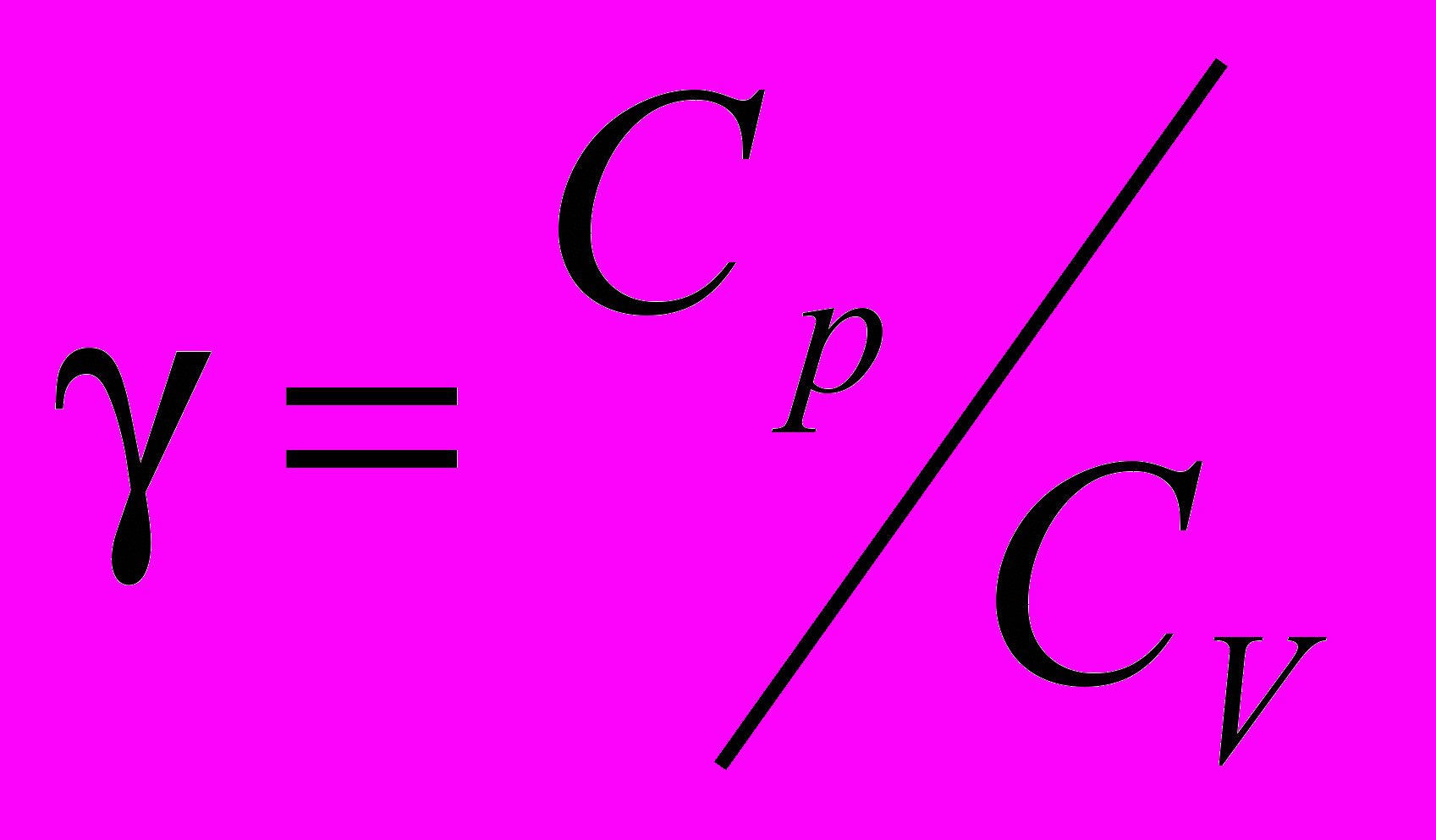 ).
).
- Получить формулу зависимости скорости звука с от температуры для совершенного газа. (Воспользоваться соотношениями
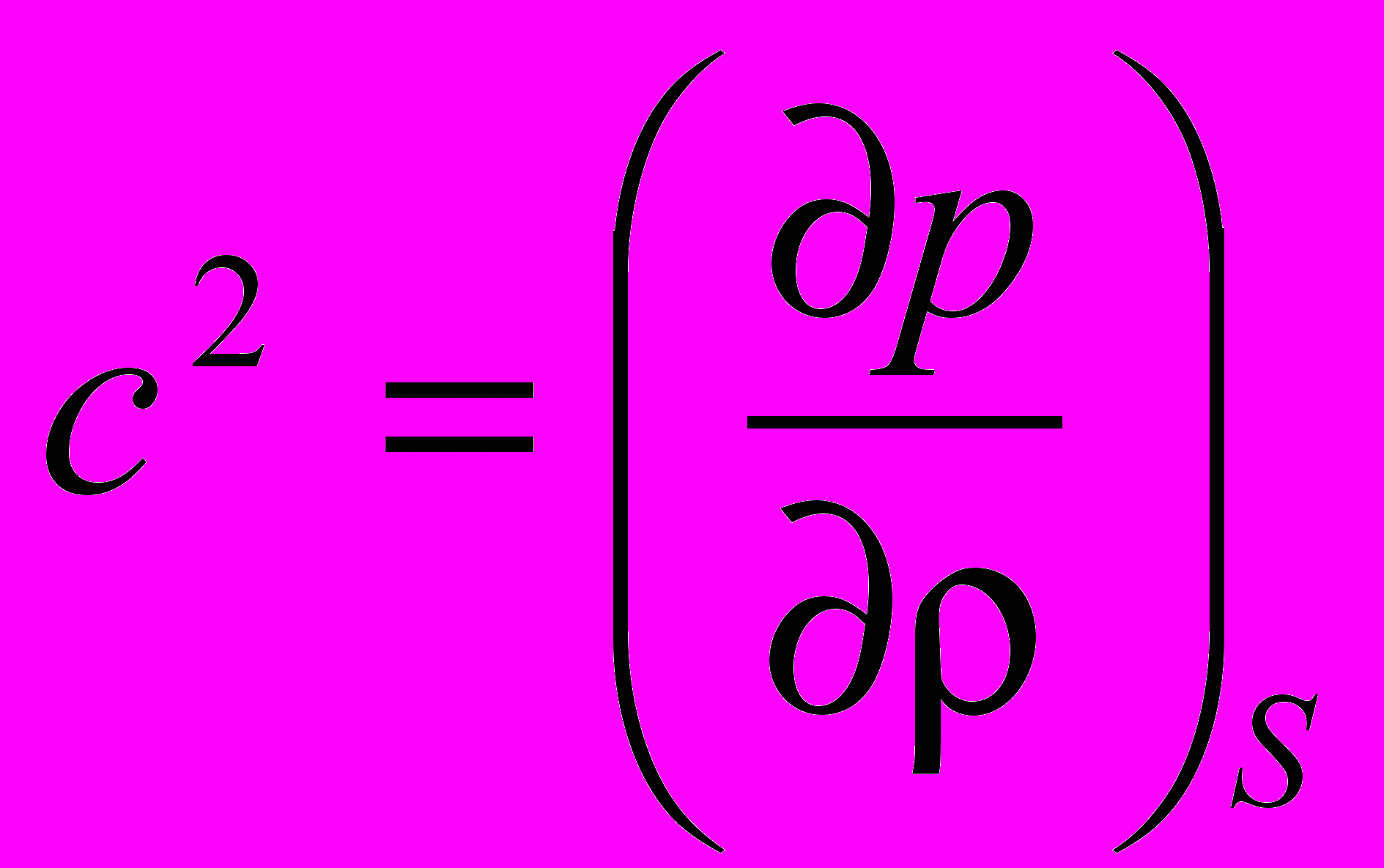 ,
,  ,
, 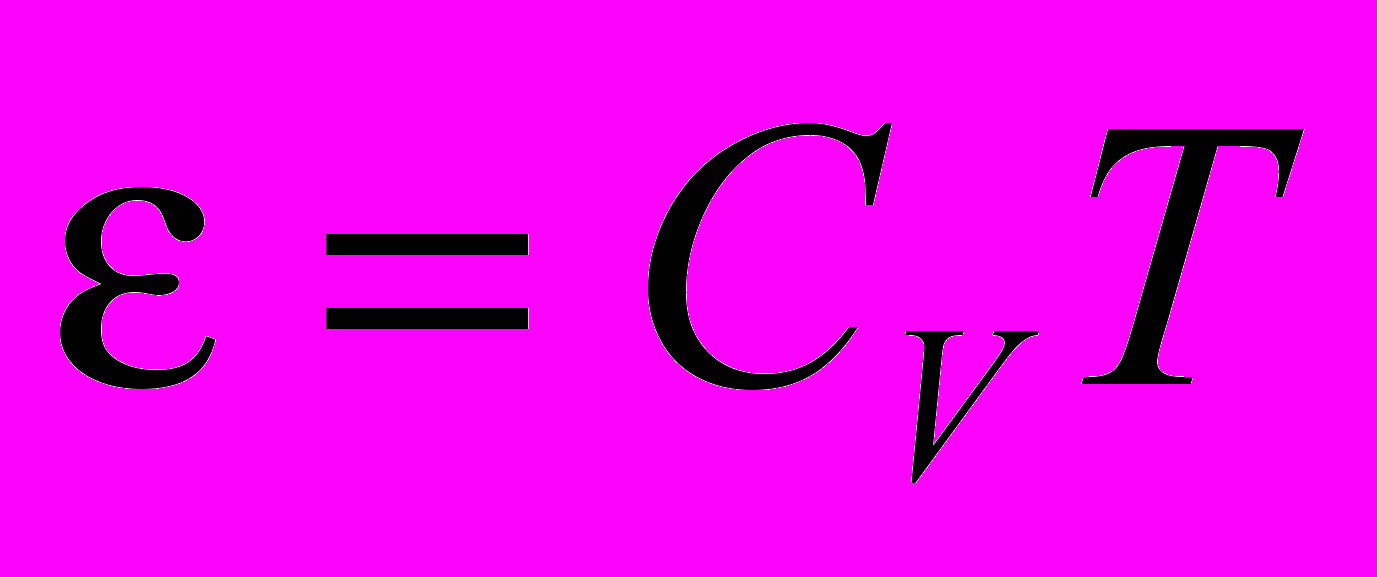 ,
, 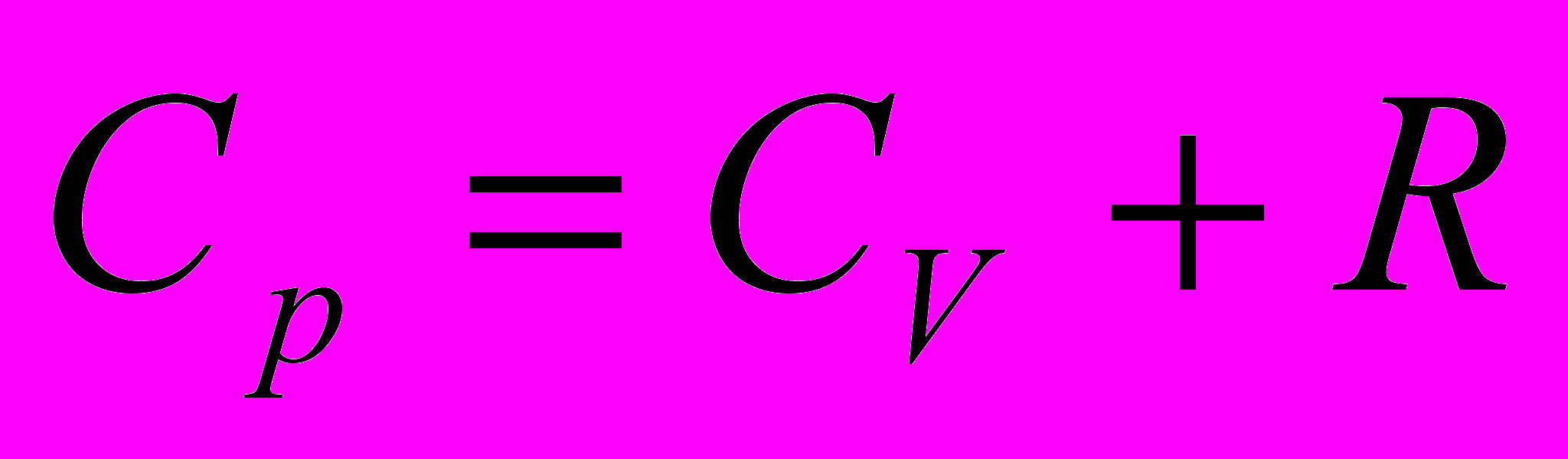 ,
, 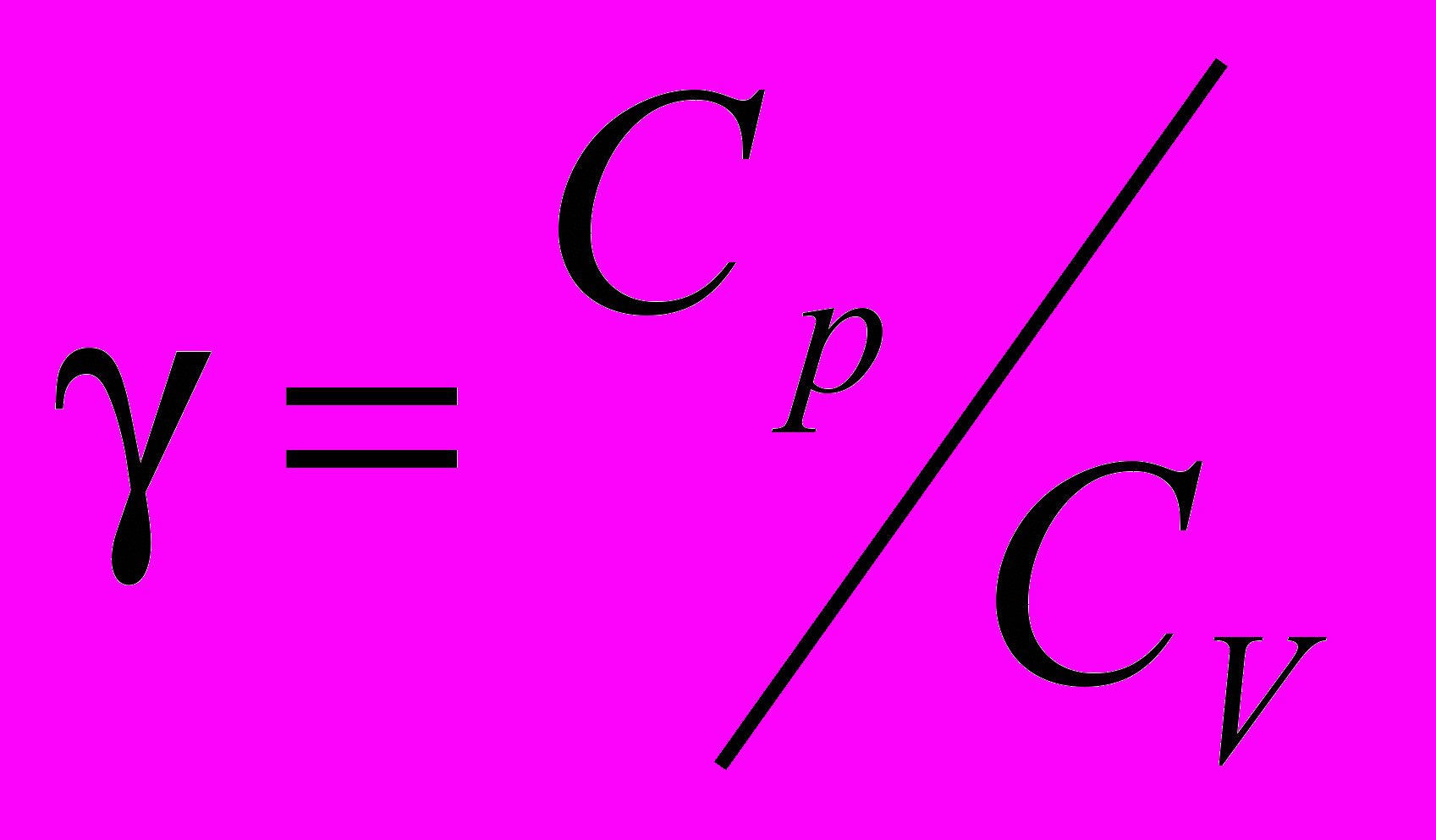 ).
).
- Найти отношение между абсолютными температурами для сильной ударной волны в совершенном газе.
- Найти отношение между плотностями для сильной ударной волны в совершенном газе.
- Из соображений размерности найти зависимость скорости звука в совершенном газе от абсолютной температуры.
- Найти зависимость коэффициента вязкости совершенного газа от абсолютной температуры на основании соображений размерности.
- Найти зависимость коэффициента теплопроводности совершенного газа от абсолютной температуры на основании соображений размерности.
- Учебно-методическое обеспечение курса
- Активные методы обучения
В данном курсе используются классические аудиторные методы чтения лекций.
- Материальное обеспечение курса, технические средства обучения и контроля
Стандартно оборудованные лекционные аудитории.
- Рекомендуемая литература (основная)
- Баренблатт. Подобие, автомодельность , промежуточные асимптотики. Л., 1978.
- Бриджмен. Теория размерности.
- Гинзбург И.П. Аэрогазодинамика. М., 1966.
- Карпман В И. Нелинейные волны в диспергирующих средах. М., 1973.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: в 10 –ти т. Т.VI. Гидродинамика. М., 1988.
- Невзглядов В.Г. Теоретическая механика. 1959.
- Нелинейные волны. Спец. выпуск «Радиофизика», Изв. ВУЗов, т.19, 5, 6, 1976.
- Овсянников Л.В. Лекции по основам газовой динамики. М., 2003.
- Прагер В. Введение в механику сплошных сред. 1963.
- Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их применение к газовой динамике. М., 1978.
- Седов Л.И. Методы подобия и размерности в механике. 1972.
- Серрин Дж. Математические основы классической механики жидкости. 1963.
- Уизем Дж. Линейные и нелинейные волны. 1977.
- Рекомендуемая литература (дополнительная)
- Абрамович Г.Н. Прикладная газовая динамика. М., 1976.
- Биркгоф Г. Гидродинамика. М., 1963.
- Виноградов Б.С. Прикладная газовая динамика. М., 1965.
- Гельфанд В.И. Некоторые задачи теории квазилинейных уравнений. УМН, Т.XIV, вып. 2., 1959, стр. 87.
- Гельфанд В.И. Нелинейные волны в диспергирующих средах. 1973.
- Зарембо Л.К., Красильноков В.А. Введение в нелинейную акустику. 1966.
- Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М., 1966.
- Зоммерфельд А. Дифференциальные уравнения в частных производных. 1950.
- Зоммерфельд А. Термодинамика и статистическая физика. 1955.
- Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика, М., 1963.
- Коган Б.Ю. Размерность физической величины. 1968.
- Крайко А.Н. Вариационные задачи газовой динамики. М., 1979.
- Курант Уравнения с частными производными.
- Леонтович М.А. Введение в термодинамику. 1952.
- Лойцянский Л.Г. Механика жидкости и газа. М., 1978.
- Мизес Р. Математическая теория сжимаемой жидкости. 1961.
- Олейник О.А. Разрывные решения нелинейных дифференциальных уравнений. УМН, Т. 12, № 3/75/, 1957, стр. 3-73.
- Руденко О.В., Солуян С.И. Теоретические основы нелинейной акустики. М., 1975
- Седов Л.И. Механика сплошной среды. Т.1-2., М., 1983-84.
- Соболев С.Л. Уравнения математической физики.
- Станюкович К.П. Неустановившиеся движения сплошной среды. М., 1955.
- Фок В.А. Механика сплошных сред. 1932.
- Черный Г.Г. Газовая динамика. М, 1988.
- Черный Г.Г. Течения газа с большой сверхзвуковой скоростью. М., 1959.
