Ических объектов и процессов в виде математических моделей, превращается тем самым в часть самой экономики, вернее, в сплав экономики, математики и кибернетики
| Вид материала | Документы |
Содержание1. Теоретические сведения. 2. Практическая часть. 2.5 Компьютерная реализация. |
- Эконометрические модели, 43.59kb.
- Рабочая программа спецкурса, 57.84kb.
- В. А. Гордин доктор физико-математических наук, ведущий научный сотрудник гидрометцентра, 86.79kb.
- Д э. н. М. В. Грачева, зав кафедрой «Математических методов анализа экономики», 20.32kb.
- Правительство Российской Федерации Государственный университет Высшая школа экономики, 91.67kb.
- Взаимосвязь миграционных процессов и инвестиций в человеческий капитал: информационный, 280.71kb.
- Методическая разработка устойчивость функционирования отраслей и объектов экономики, 248.03kb.
- Cols=2 gutter=66> Математическое моделирование и процесс создания математической модели, 130.19kb.
- М. В. Ломоносова Факультет вычислительной математики и кибернетики Кафедра математической, 6.81kb.
- Дик А. А., Егоров В. Ф. Современные подходы к оценке устойчивости функционирования, 350.78kb.
Ведение.
Экономико-математическое моделирование, явилось одним из эффективных методов описания сложных социально-экономических объектов и процессов в виде математических моделей, превращается тем самым в часть самой экономики, вернее, в сплав экономики, математики и кибернетики. Подтверждением положительной оценки этого явления стало присуждение Нобелевских премий в области экономики в последнее десятилетие в основном только за новые экономико-математические исследования.
Целью данной курсовой работы является рассмотрением двухэтапной транспортной задачи линейного программирования.
Транспортная задача — задача о наиболее экономном плане перевозок однородного или взаимозаменяемого продукта из пункта производства (станций отправления) в пункты потребления (станции назначения)— является важнейшей частной задачей линейного программирования, имеющей обширные практические приложения не только к проблемам транспорта.
Транспортная задача выделяется в линейном программировании определенностью экономической характеристики, особенностями математической модели, наличием специфических методов решения.
Простейшая формулировка транспортной задачи по критерию стоимости следующая: в m пунктах отправления (А1, ..., Аm) находится соответственно а1, ..., аm единиц однородного груза (ресурсы), который должен быть доставлен n потребителям (В1, ..., Вn) в количествах b1, ..., bn единиц (потребности). Известны транспортные издержки Cij перевозок единицы груза из i-гo пункта отправления в j-й пункт потребления.
Требуется составить план перевозок, т. е. найти, сколько единиц груза должно быть отправлено из i-го пункта отправления в j-й пункт потребления так, чтобы полностью удовлетворить потребности и чтобы суммарные издержки на перевозки были минимальными.
Данная работа состоит из двух глав. В первой главе рассматривается общий случай математической постановки задачи оптимизации и методы оптимизации транспортной задачи линейного программирования. Во второй главе приводится пример решения двухэтапной транспортной задачи двумя методами: метод сведения к классической форме задачи и метод раздельного прикрепления поставщиков. Так же во второй главе рассмотрена компьютерная реализация рассматриваемой задаче в Microsoft Excel.
Цели курсовой работы:
- показать, как разрабатываются математические модели двухэтапных транспортных задач линейного программирования;
- решить сформулированные математические задачи на ЭВМ с использованием пакетов прикладных программ линейного программирования.
1. Теоретические сведения.
Для экономических систем наиболее характерны задачи оптимизации и распределения ресурсов, решаемые методом линейного программирования, для которого разработаны надежные алгоритмы, реализованные в поставляемом с ЭВМ программном обеспечении; более сложные задачи (целочисленные, нелинейные) оптимизации можно свести к задачам линейного программирования.
Подобные методы широко применимы в производстве, транспорте, организации процессов, в обучении, руководстве персоналом и др. К числу наиболее известных задач, решаемых этим методом, относятся задача о назначениях, транспортная задача и др.
Задача о назначениях и распределении работ является частным случаем транспортной задачи, в которой приняты следующие допущения: число поставщиков m равно числу потребителей n; запасы каждого поставщика аi = 1; заявки каждого потребителя bj = 1; каждый поставщик может поставлять грузы только одному потребителю; каждый потребитель может получать грузы только от одного поставщика.
Если не учитывать направление оптимизации целевой функции (max или min), что не влияет на аналитические зависимости, то модель транспортной задачи при принятых выше допущениях получает вид модели задачи о назначениях. Если сумма всех запасов Аi у поставщика равняется сумме всех заявок Вj потребителей, то такую транспортную задачу называют сбалансированной; если А не равно В, то задача является несбалансированной, и её математическая модель может иметь вид:

Знак неравенства в ограничениях для запасов аi, означает, что объем груза, вывозимый от любого i-го поставщика по заявкам всех потребителей, не может превышать имеющегося у него запаса, при этом часть запаса груза может остаться невывезенной. Аналогично знак неравенства в ограничениях для заявок bj означает, что груз, получаемый j-м поставщиком, должен быть не меньше заявки, но превышение заявки при этом допускается.
Модель сбалансированной задачи является частным случаем модели несбалансированной задачи. Несбалансированная модель транспортной задачи является достаточно универсальной моделью, описывающей множество задач распределения однородных ресурсов — работ, назначений, материальных и трудовых ресурсов, транспортировки грузов, распределения инвестиций, финансовых средств и др., которые можно успешно решить, если знать ответы на вопросы:
- В каком смысле распределение средств должно быть наилучшим?
- Какой вклад дает каждый объект (субъект) в целевую
функцию?
Любая правильно составленная задача планирования имеет бесчисленное множество допустимых решений. Какое же из них выбрать? Мы уже знаем, чтобы ответить на этот вопрос, необходимо прежде всего сформулировать задачу оптимизации, при решении которой возможна лишь одна из двух взаимоисключаемых постановок: либо при заданных ресурсах максимизировать получаемый результат, либо при заданном результате минимизировать используемые ресурсы.
В различных отраслях народного хозяйства (материально-техническое снабжение, торговля) грузы могут доставляться через промежуточные пункты. Допустим, имеется m (
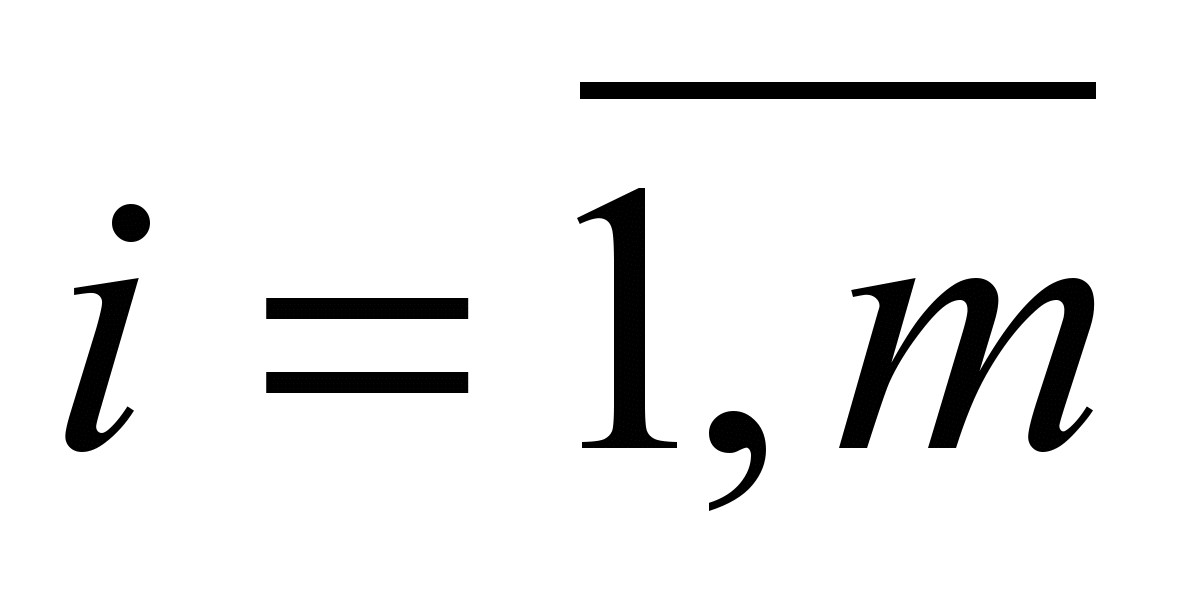 ) пунктов производства, n (
) пунктов производства, n (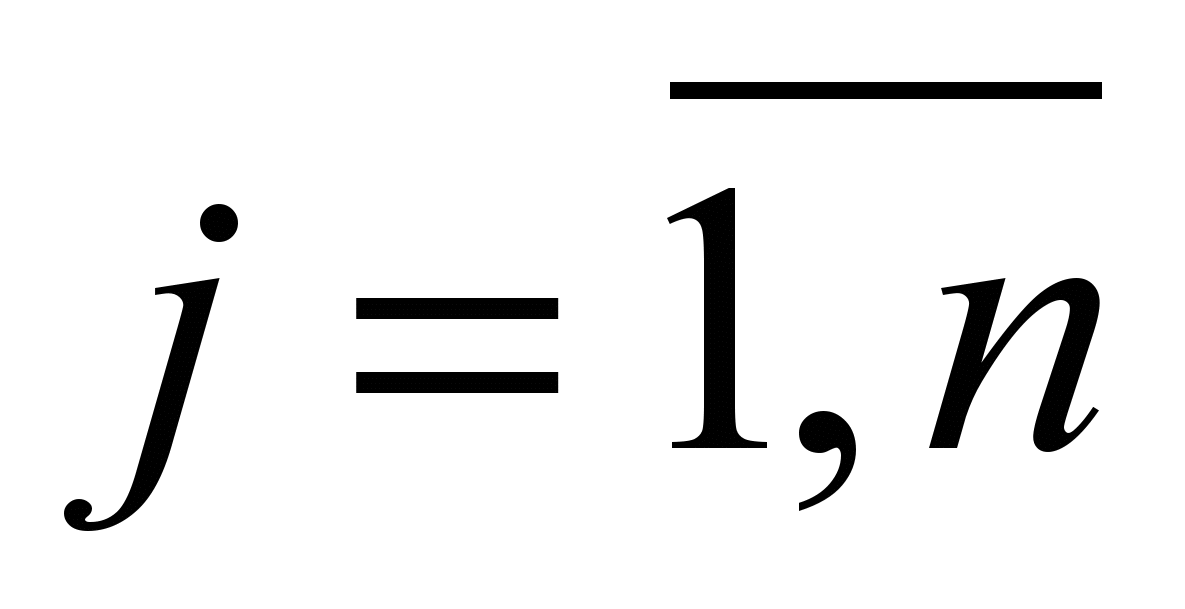 ) пунктов потребления и р (
) пунктов потребления и р (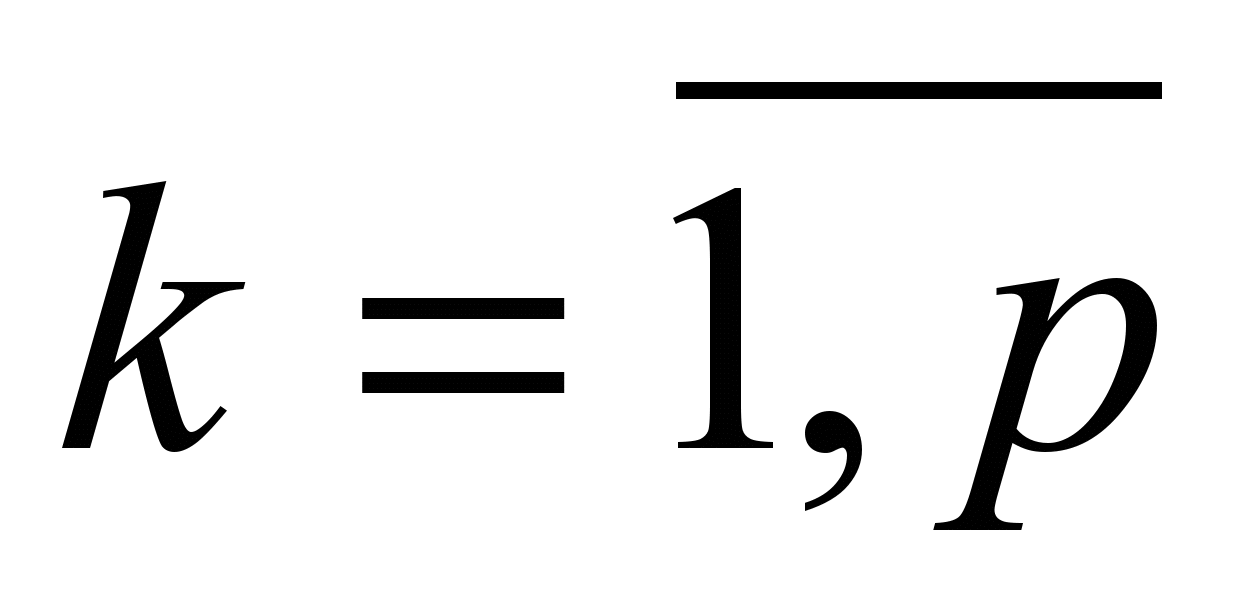 ) – промежуточных баз. Как в обычной транспортной задаче, обозначим через ai и bj соответственно объемы поставок и потребления. Пусть dk – мощность k-ой базы, cik и ckj – соответственно стоимость перевозки единицы продукции от поставщиков на базы и с баз к потребителям. Тогда модель задачи примет вид
) – промежуточных баз. Как в обычной транспортной задаче, обозначим через ai и bj соответственно объемы поставок и потребления. Пусть dk – мощность k-ой базы, cik и ckj – соответственно стоимость перевозки единицы продукции от поставщиков на базы и с баз к потребителям. Тогда модель задачи примет вид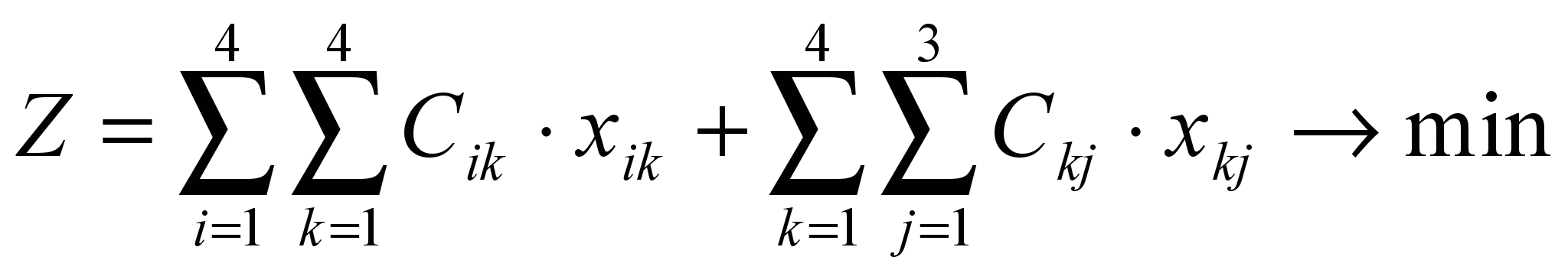
При ограничениях
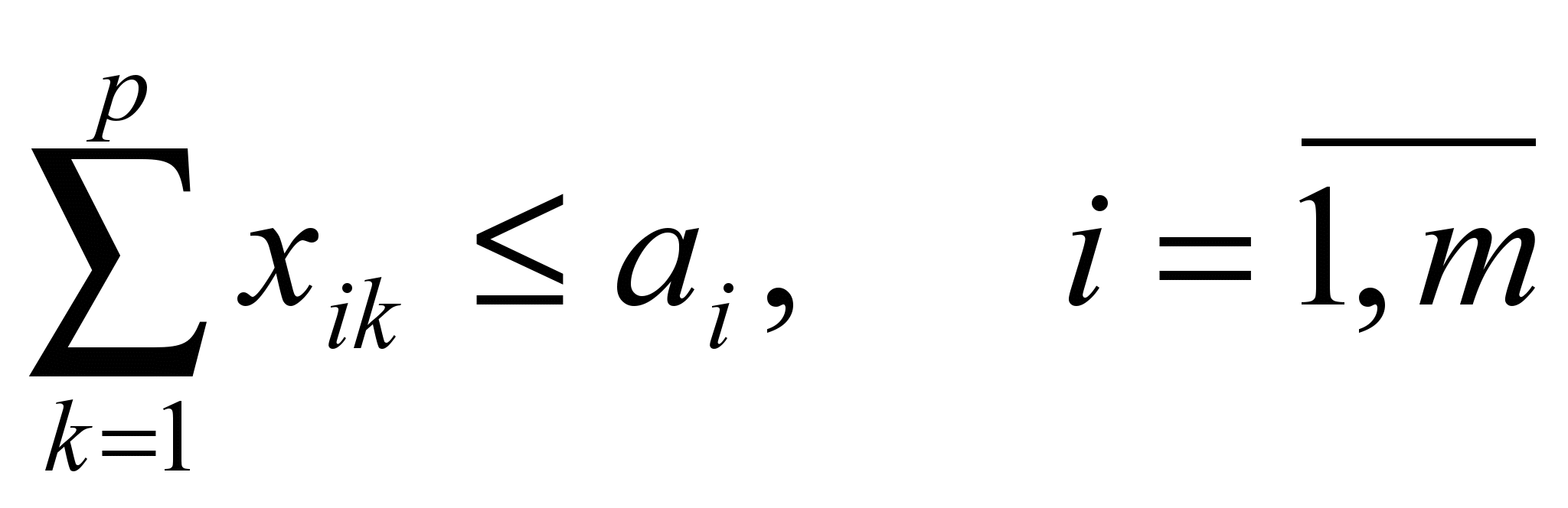 ;
;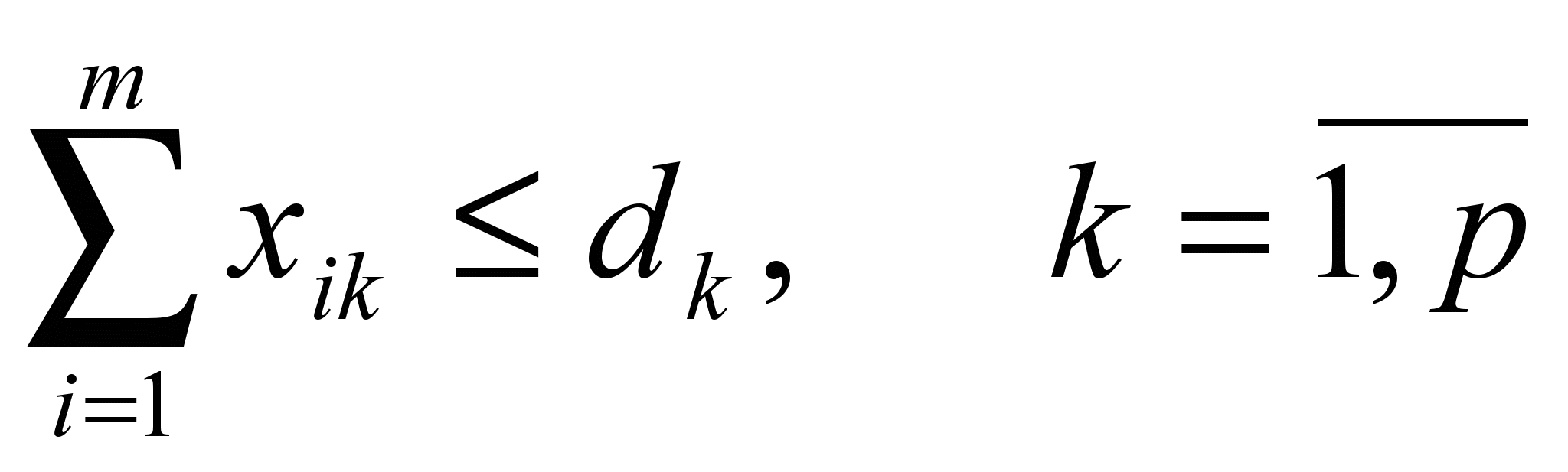 ;
;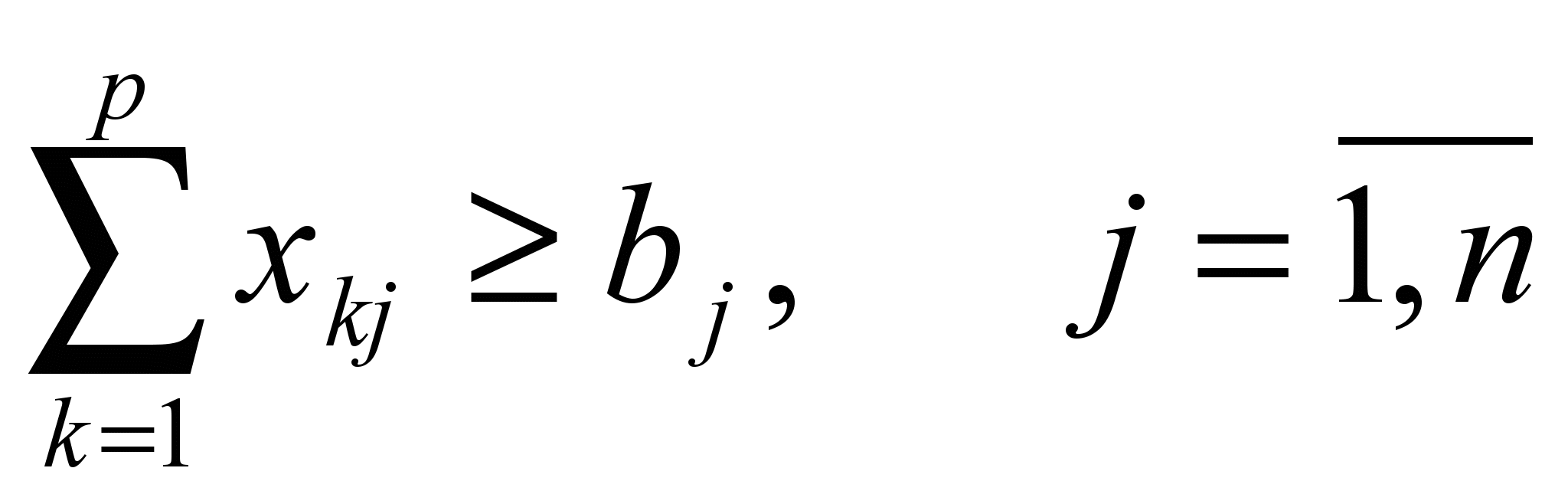 ;
;Xkj³0; Xik³0.
Если суммарная пропускная мощность баз равна суммарной мощности поставщиков и суммарному спросу потребителей, т. е. пропускные способности баз будут использованы полностью и, следовательно, схема перевозок с баз к потребителям не зависит от схемы перевозок от поставщиков на базы. В таких условиях задачу можно решать по частям. Оптимальный план можно составить объединением плана поставок от поставщиков к базам и плана поставок с баз к потребителям. Однако оптимальный план двухэтапной транспортной задачи, вообще говоря, отличен от плана, полученного объединением оптимальных планов решения транспортной задачи для каждого этапа в отдельности.
Двухэтапную транспортную задачу легко свести к классической транспортной задаче. Для этого базы будем считать одновременно поставщиками и потребителями. Для каждой базы в расширенной матрице (поставщики + базы) — (потребители + базы) отведем строку и столбец. Тогда матрица тарифов будет состоять из четырех блоков (табл. 1).
В первом — левом верхнем блоке будем отражать связи поставщиков с базами, в четвертом — связи баз с потребителями. Второй — правый верхний блок показывает связи поставщиков с потребителями. Поскольку по условию задачи непосредственные перевозки от поставщиков к потребителям запрещены, то в этом блоке все тарифы считают равными М (где М — большое число). Третий — левый нижний блок образуется по строкам и столбцам базами, имеет форму квадрата. Так как перевозки между базами запрещаются, то соответствующие показатели также считают равными М. В клетках третьего квадрата, в которых отражаются связи базы с самой собой, тарифы равны нулю. Поставки в этих клетках показывают величину неиспользованной мощности базы. Диагональ из нулевых тарифов, отражающая связи базы с самой собой, называется фиктивной.
Решение двухэтапной транспортной задачи имеет некоторые особенности. Основная из них – некоторое изменение нахождения базисного решения. Вначале необходимо распределить поставки в одном из блоков (первом или четвертом). Затем заполняется фиктивная диагональ, и только потом распределяются поставки в другом блоке (четвертом или первом). Вторая особенность заключается в том, что если цикл пересчета проходит через фиктивную диагональ, то он обязательно проходит через нее дважды; одна вершина цикла, находящаяся на диагонали, будет всегда положительной, а другая — отрицательной.
Таблица. 1.
| Потребители и их объемы | |||||||
| Поставщики | Мощности | D1 | …. | Dp | B1 | …. | Bn |
| d1 | …. | dp | b1 | …. | bn | ||
| A1 | a1 | I | II | ||||
| … | … | ||||||
| Am | am | ||||||
| D1 | D1 | III | IV | ||||
| … | … | ||||||
| Dp | dp | ||||||
2. Практическая часть.
Многоэтапная транспортная задача оптимального размещения и концентрации производства.
Транспортная система состоит из пяти пунктов производства, шести пунктов промежуточной переработки и шести пунктов потребления. Известны объемы производства каждого из пунктов Ai (1 тыс. ед. товаров), пропускные способности пунктов промежуточной переработки Dk(1 тыс. ед. товаров), а так же потребности по потребителям Bj (1 тыс. ед. товаров). Известна стоимость доставки 1 тыс. ед. товаров на склад и доставки 1 тыс. ед. товара со склада потребителю. Эти данные представлены в таблицах.
Таблица 1.
Поставки от производителей А1-А5 на склады D1-D6 и стоимость доставки партии товара на склад (тысячи денежных единиц).
| | D1=100 | D2 = 30 | D3 =70 | D4 =240 | D5 =160 | D6 =200 |
| A1 = 120 | 3 | 5 | 1 | 4 | 2 | 3 |
| A2 = 80 | 5 | 6 | 4 | 1 | 8 | 3 |
| A3 = 300 | 3 | 1 | 5 | 2 | 1 | 3 |
| A4 = 250 | 6 | 1 | 4 | 3 | 5 | 2 |
| A5 = 50 | 1 | 3 | 5 | 2 | 8 | 4 |
Таблица 2.
Поставки со складов потребителям и стоимость доставки партии товара со склада потребителям (тысячи денежных единиц).
| | B1 = 40 | B2 =160 | B3 =120 | B4 =150 | B5 =130 | B6 =200 |
| D1 =100 | 9 | 3 | 4 | 1 | 5 | 2 |
| D2 =30 | 1 | 6 | 2 | 5 | 3 | 8 |
| D3=70 | 3 | 5 | 2 | 1 | 3 | 4 |
| D4 =240 | 7 | 2 | 5 | 1 | 4 | 6 |
| D5 =160 | 2 | 3 | 1 | 4 | 2 | 8 |
| D6 =200 | 5 | 3 | 2 | 4 | 1 | 3 |
Определить объемы производства каждого поставщика, какие склады и с какой пропускной способностью требуется построить, направление и объемы поставки товаров на склады, а со складов к потребителям, которые удовлетворяли бы всем имеющимся условиям и обеспечивали минимальные суммарные затраты на поставку при условии, что все потребности будут удовлетворены.
1. Решить двухэтапную транспортную задачу
составить математическую модель
- изобразить задачу графически
- решить задачу методом потенциалов.
2. Решить эту же задачу путем раздельного прикрепления поставщиков к складам и складов к потребителям
составить математическую модель
- изобразить задачу графически
- решить задачу методом потенциалов.
Сравнить полученные результаты и сделать выводы.
- Решить двухэтапные транспортные задачи с учетом дополнительных ограничений:
Из А1 в Д1 можно перевезти не менее 80 единиц груза,
Из А3 в Д4 перевозки не осуществляются и из Д4 в В2 перевозки так же запрещены,
Из Д6 в В5 можно перевезти не более 50 единиц груза.
Оценить и проанализировать раздельное влияние этих ограничений и общее их влияние на затраты.
5. Решить задачи п.1, п.2 и п. 4 (4 задачи) с использованием ЭВМ.
2.1. Решим двухэтапную транспортную задачу.
Обозначим через Xik – количество продукции, поставляемое от i-го пункта производства на к-й промежуточный пункт (i=1, 2, 3, 4, 5; k= 1, 2, 3, 4, 5, 6), а через Xkj - количество продукции, поставляемое с к-го промежуточного пункта j-му потребителю (k= 1, 2, 3, 4, 5, 6; j=1, 2, 3,4, 5, 6). Тогда целевая функция, характеризующая суммарные транспортные расходы, запишется в виде:
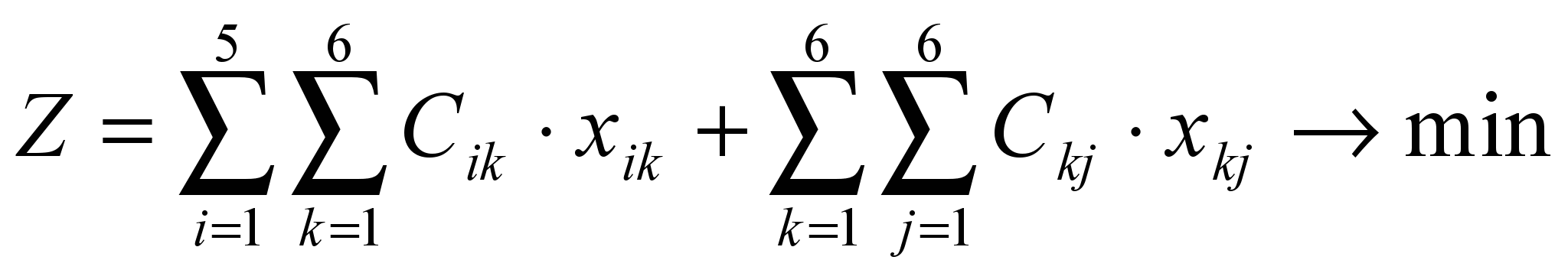
Ограничения запишутся в виде:
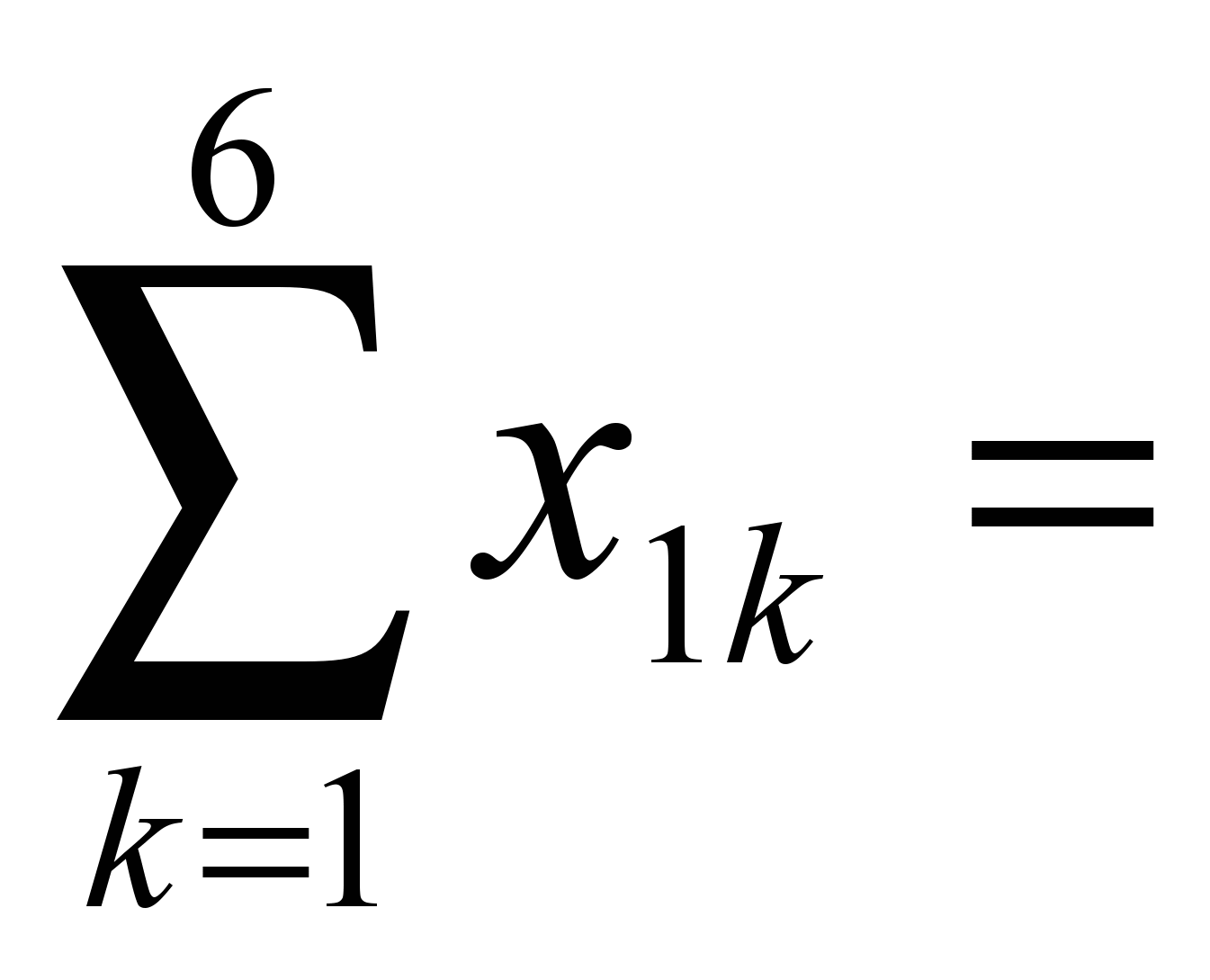 120,
120,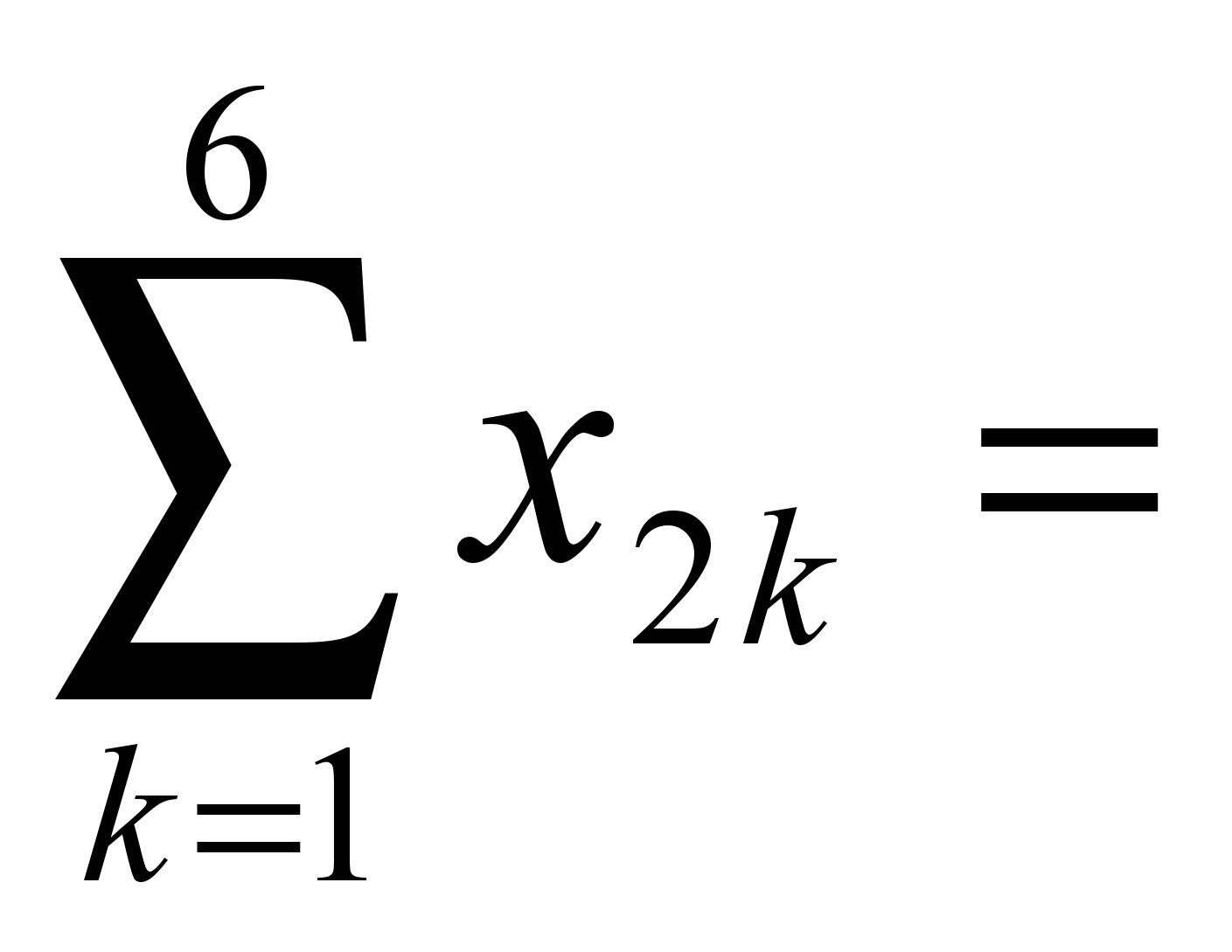 80,
80,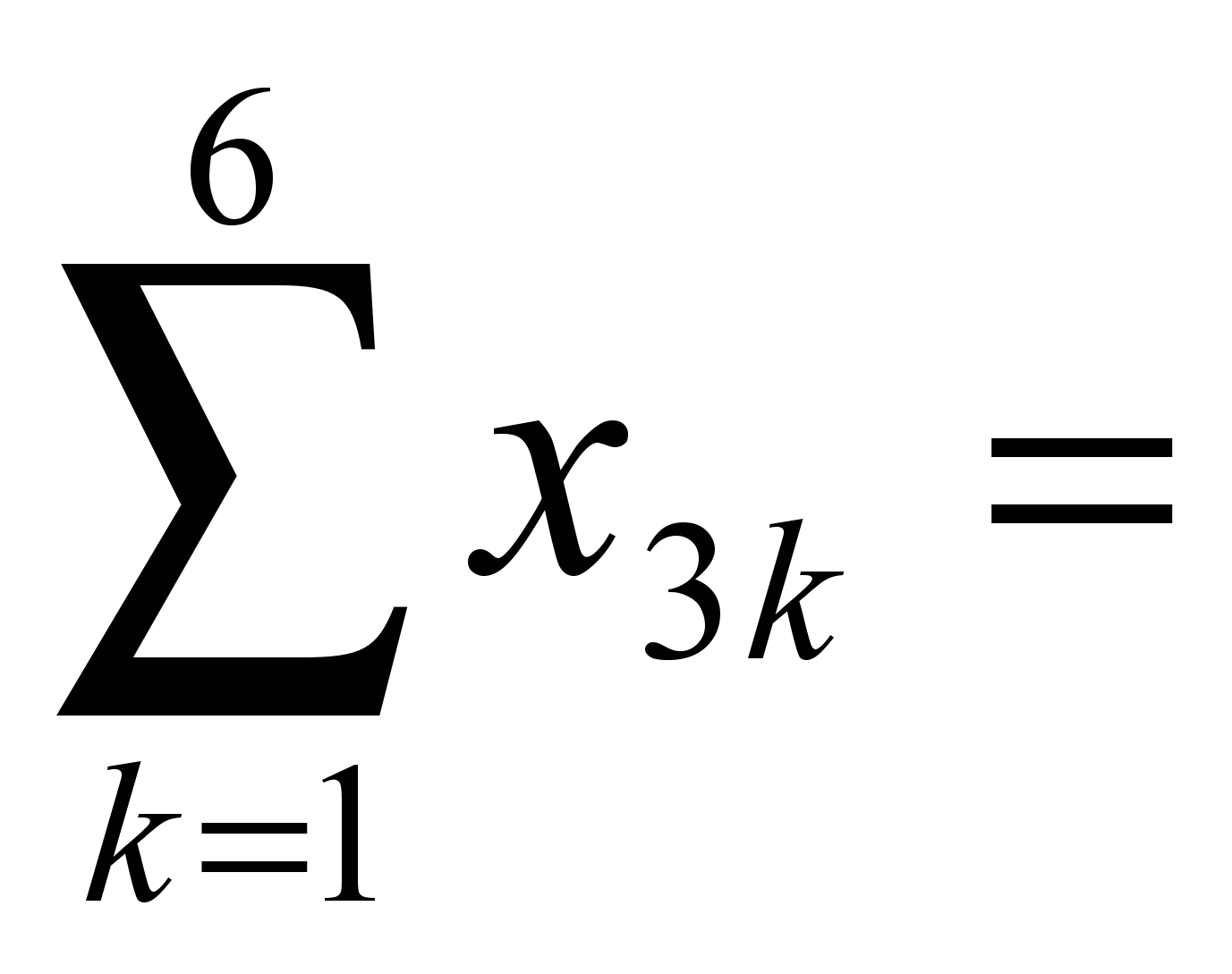 300,
300,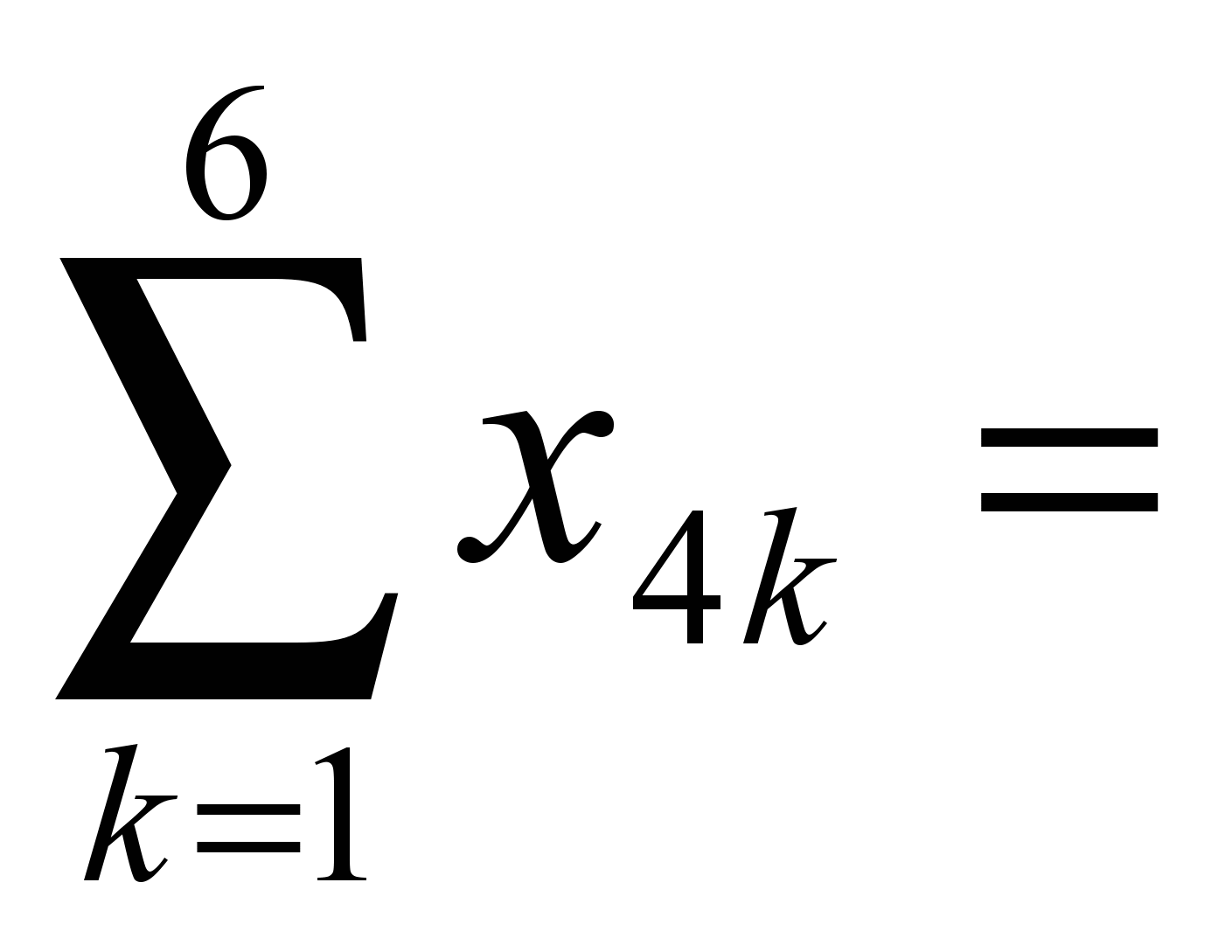 250,
250,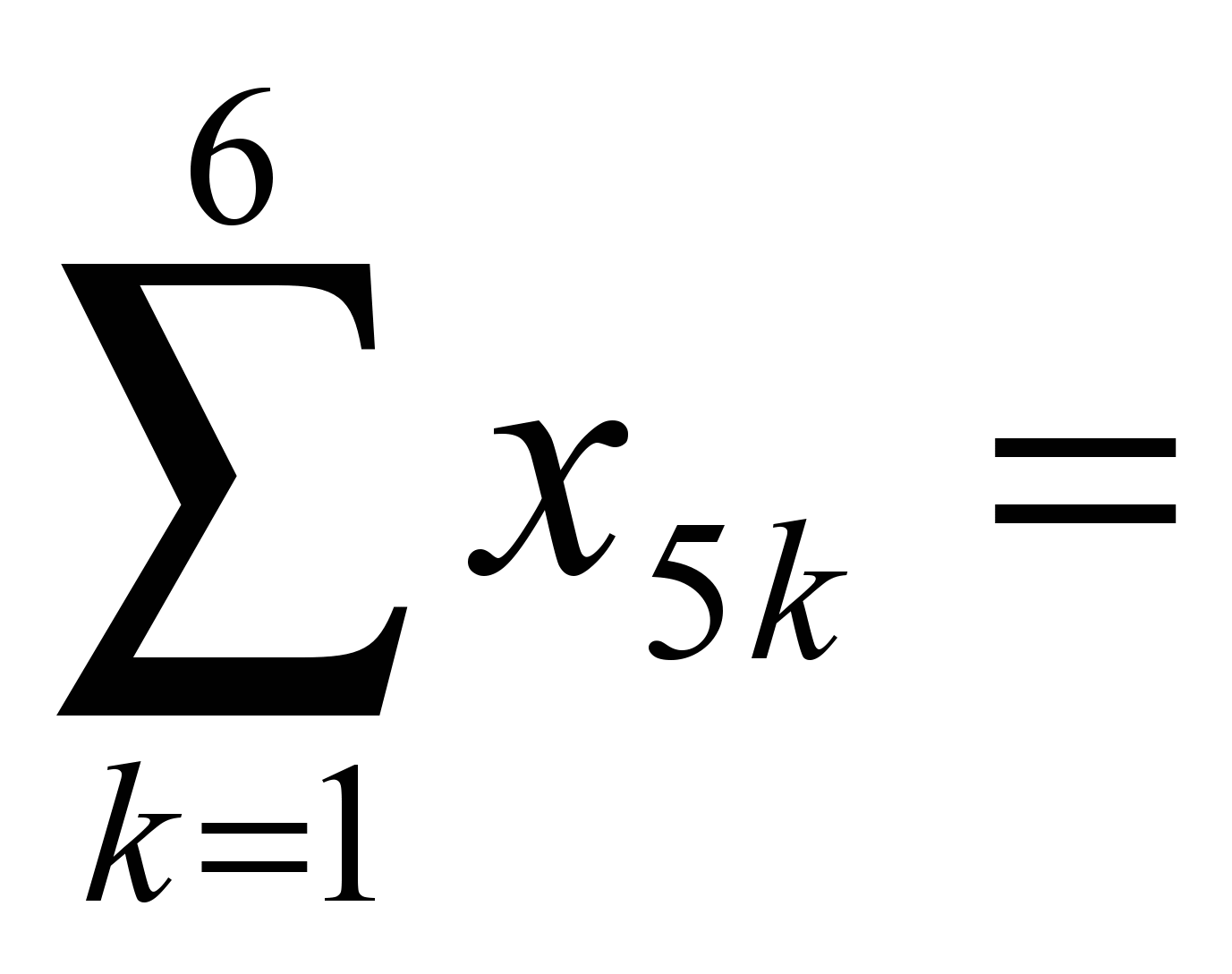 50.
50. 100,
100,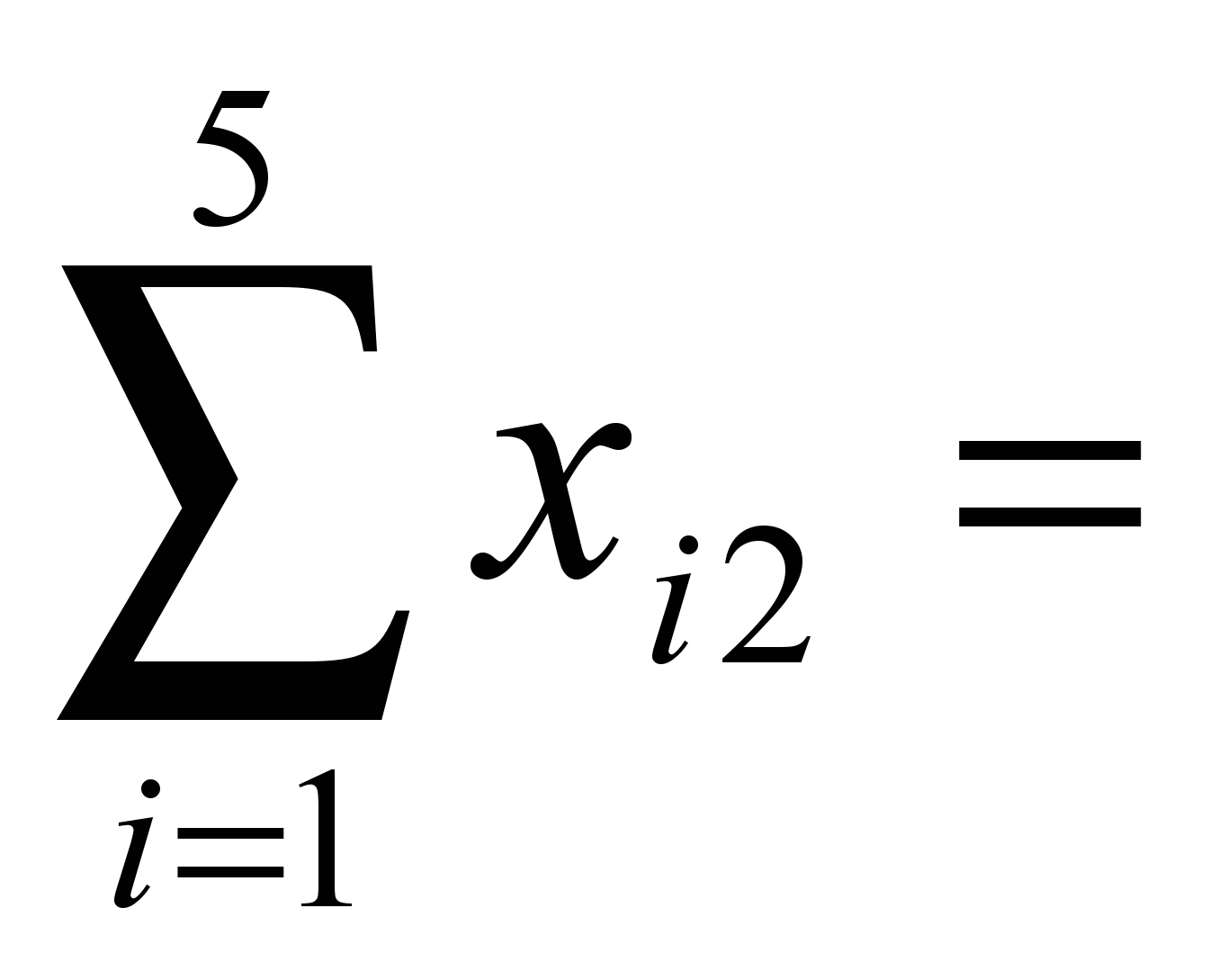 30,
30, 70,
70,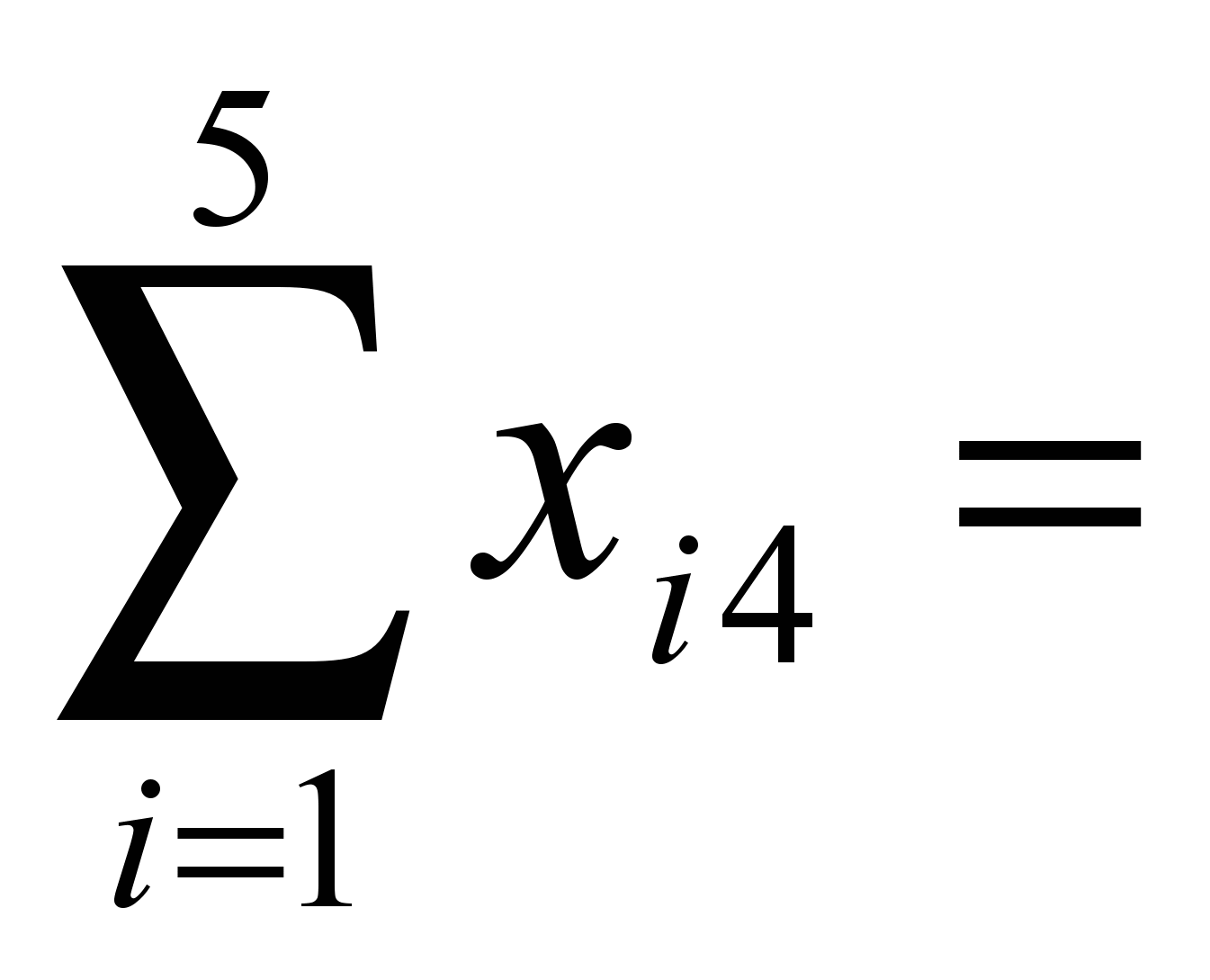 240,
240, 160,
160, 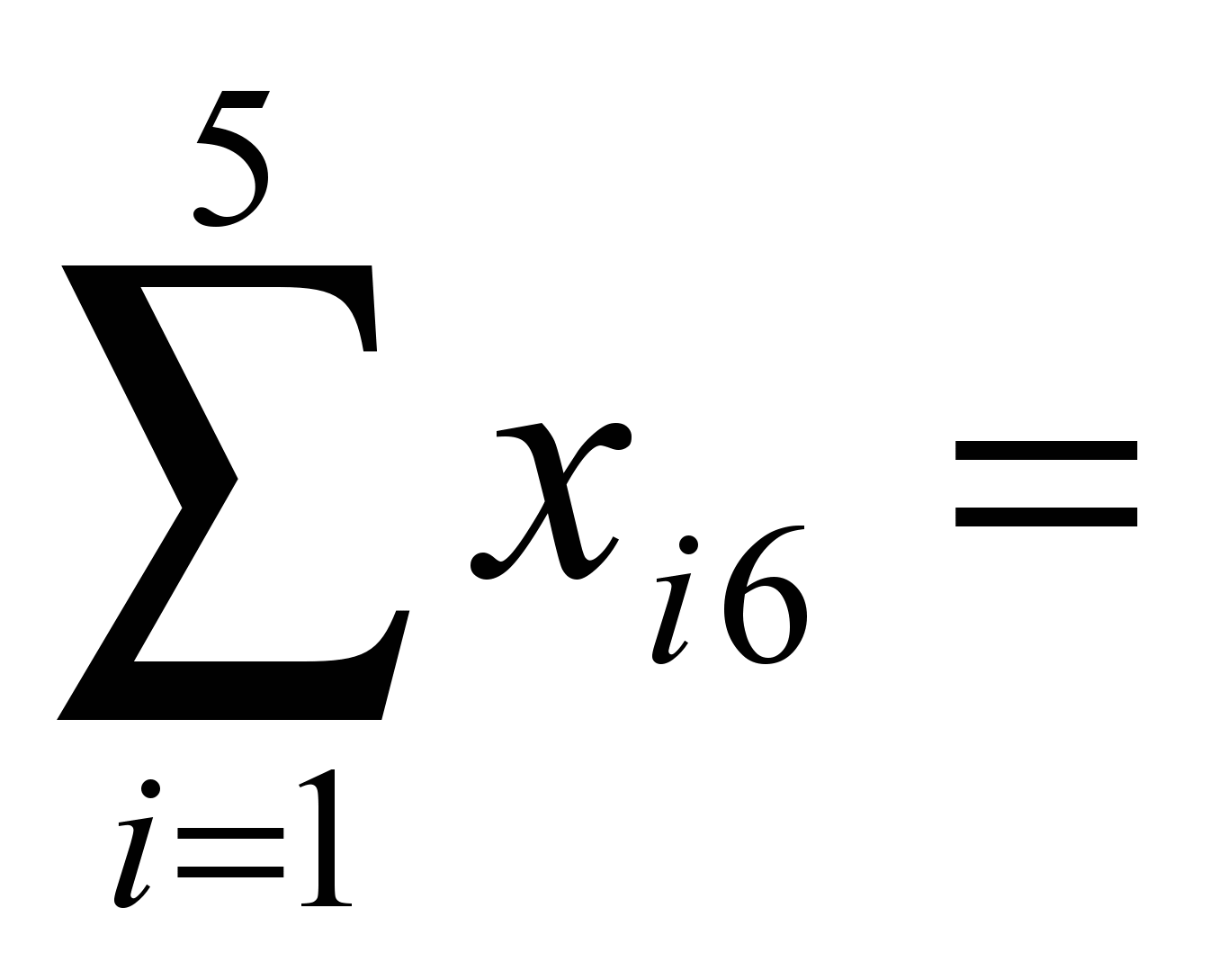 200.
200.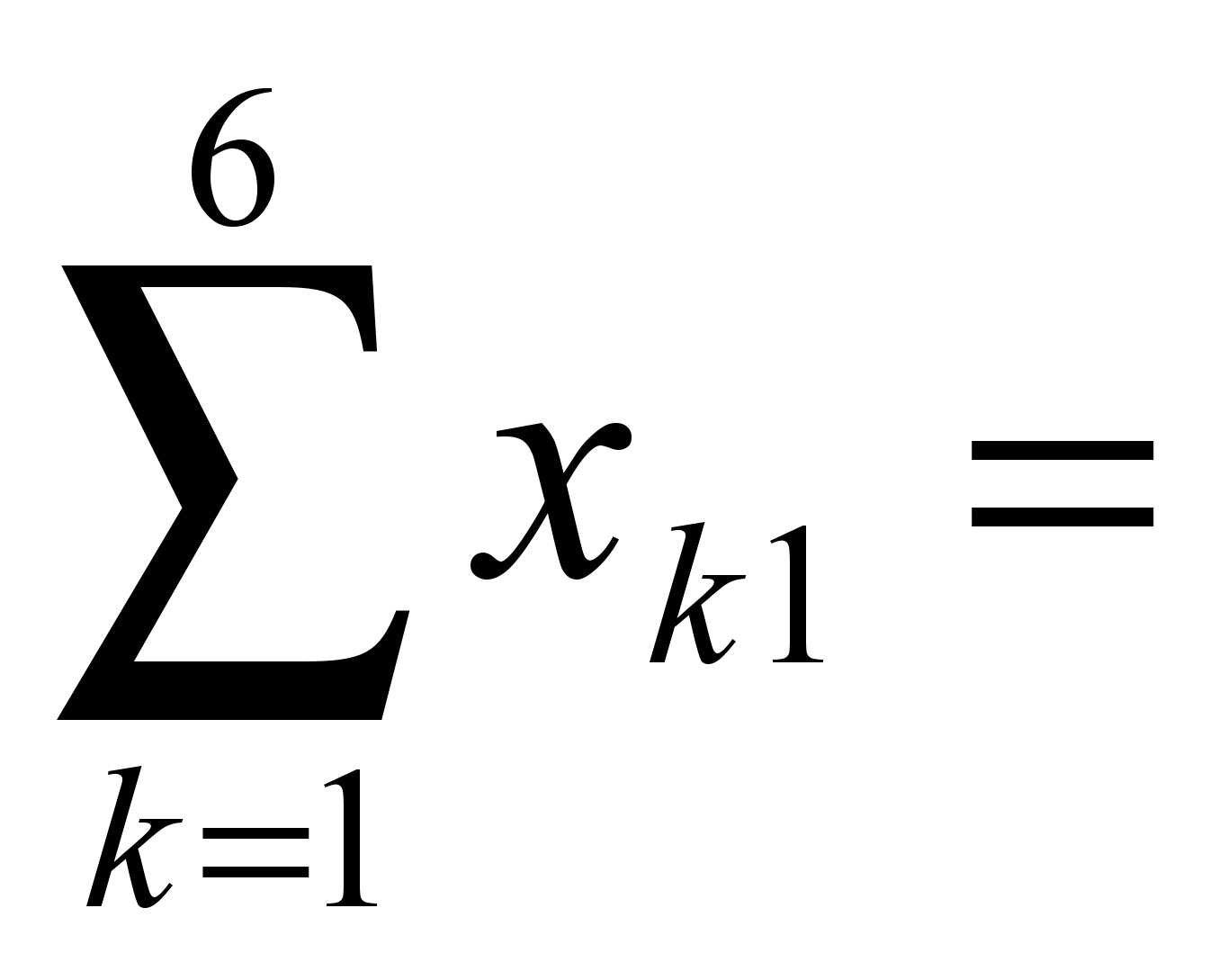 100,
100,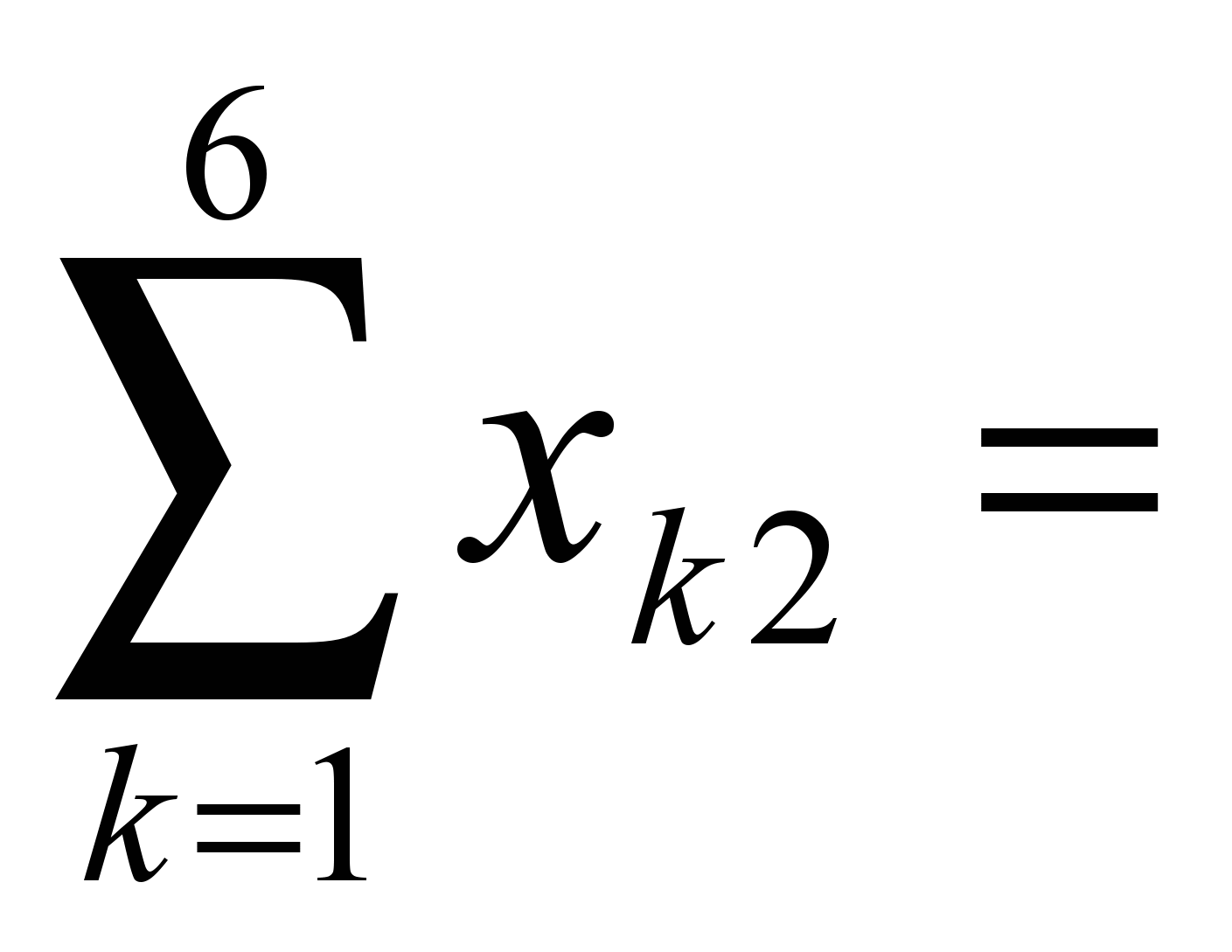 30,
30, 70,
70,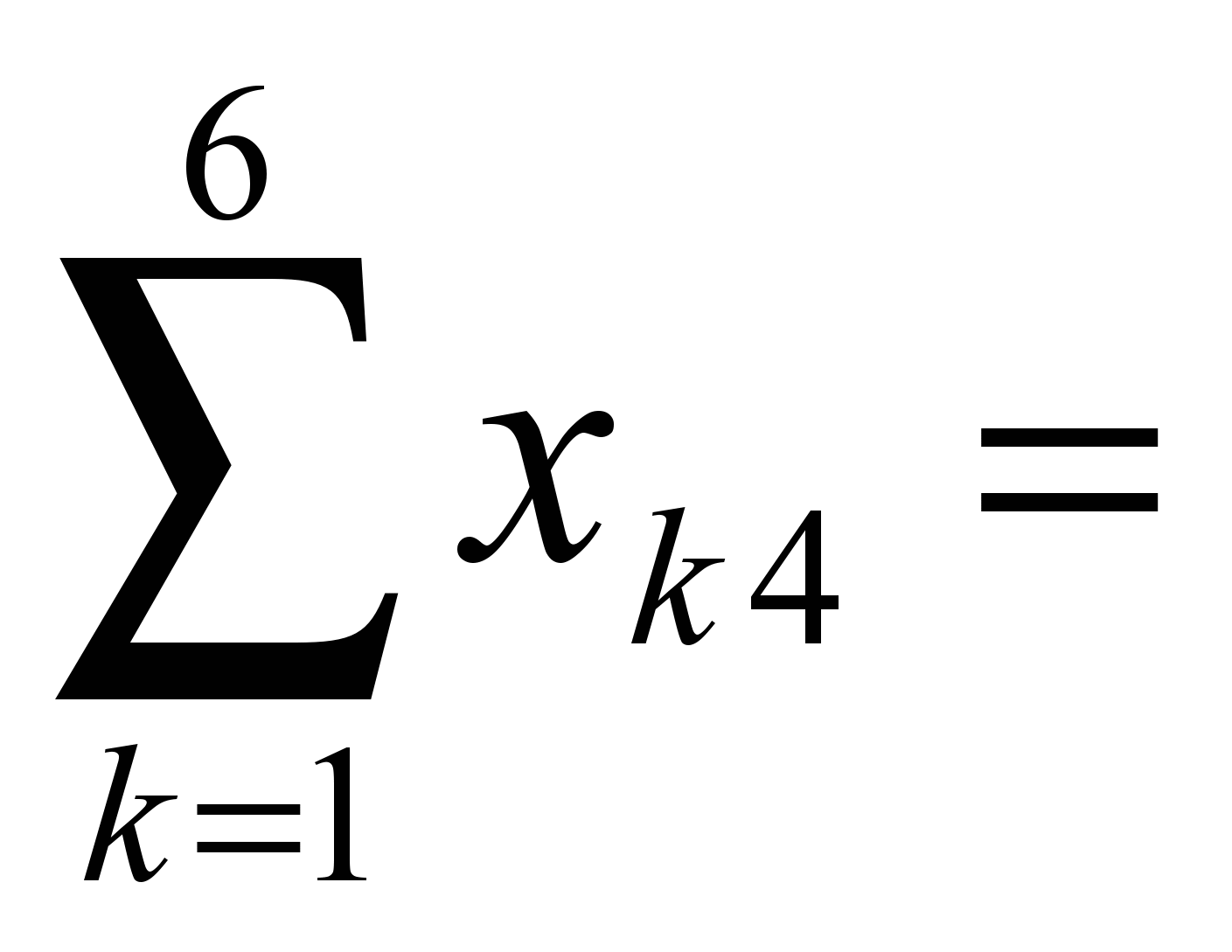 240,
240,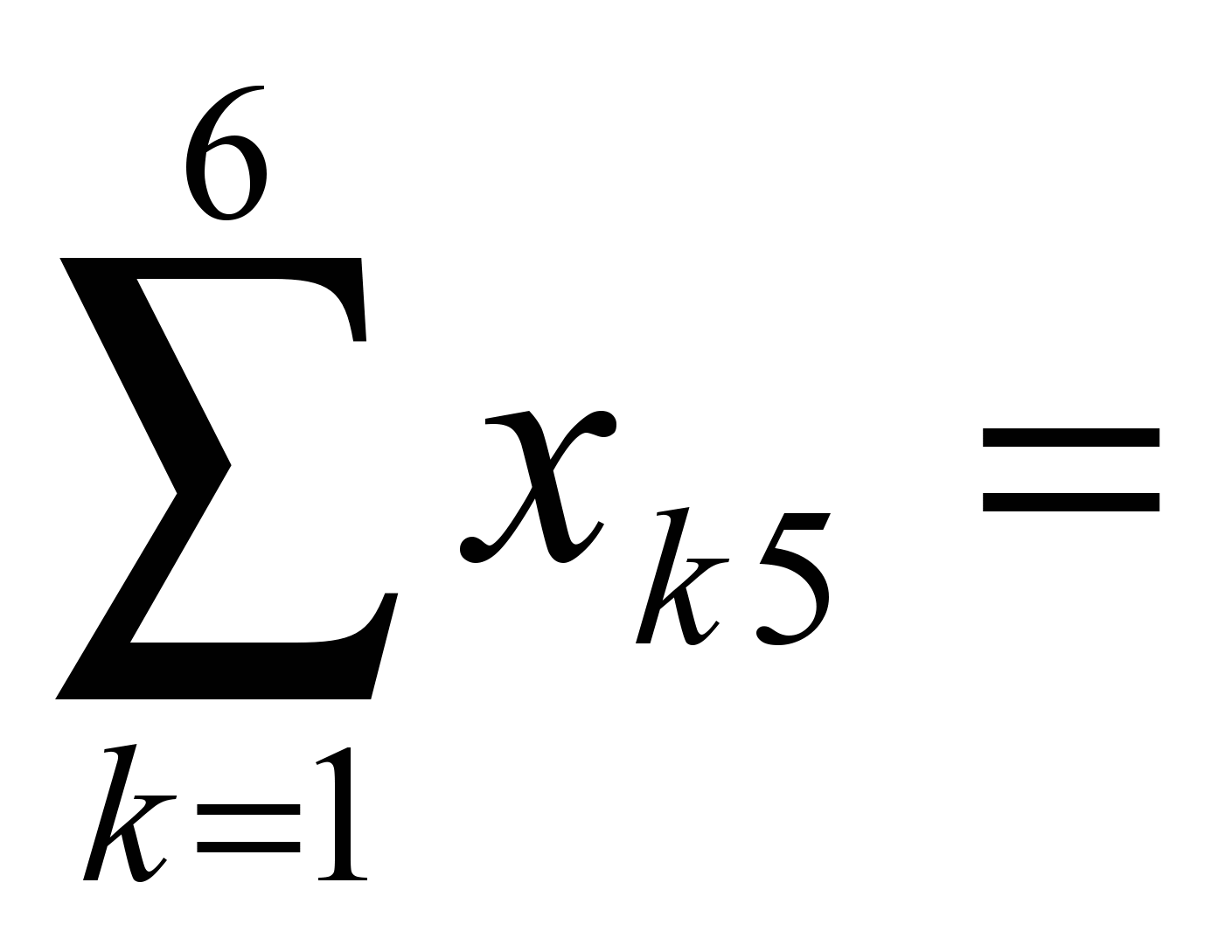 160,
160,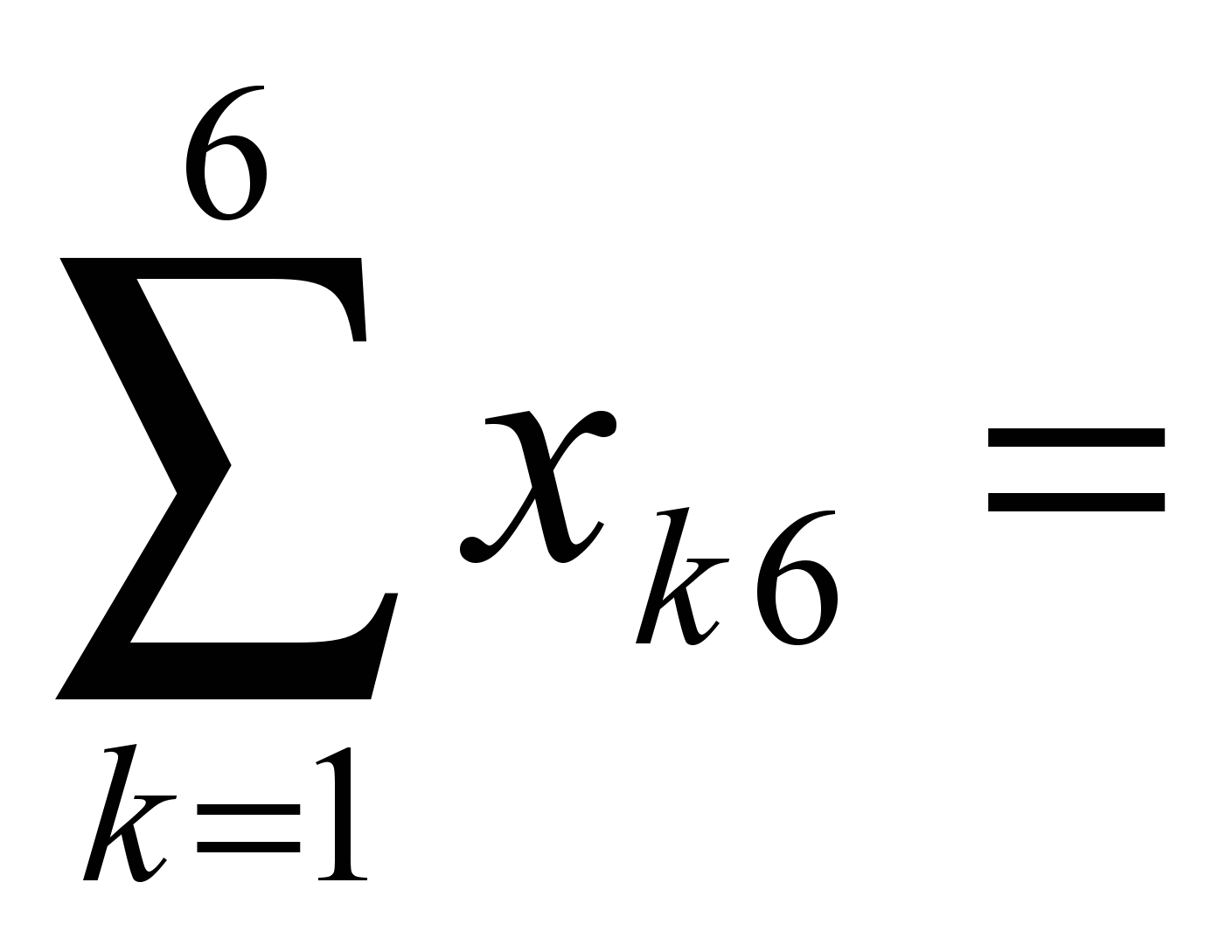 200.
200.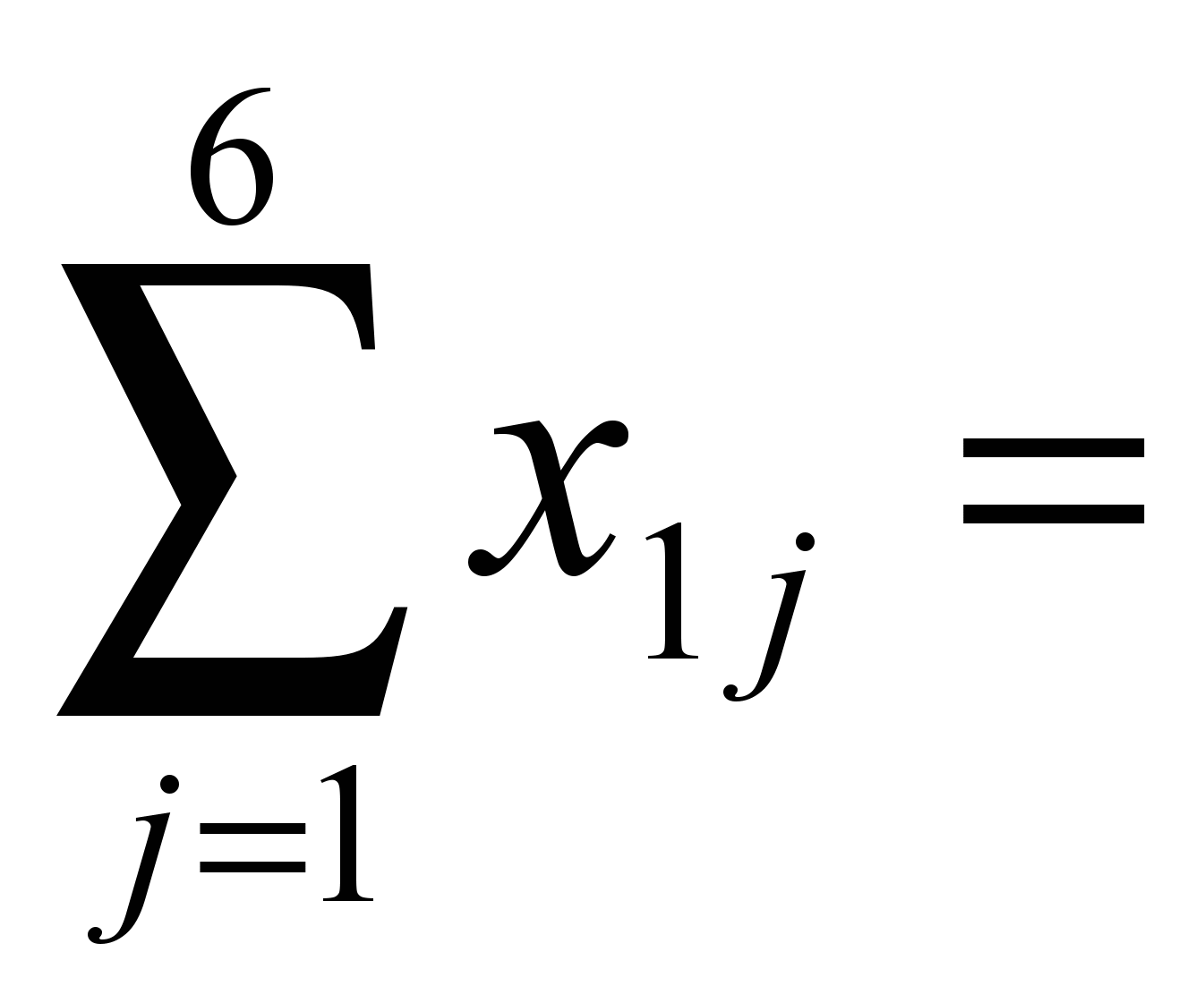 40,
40,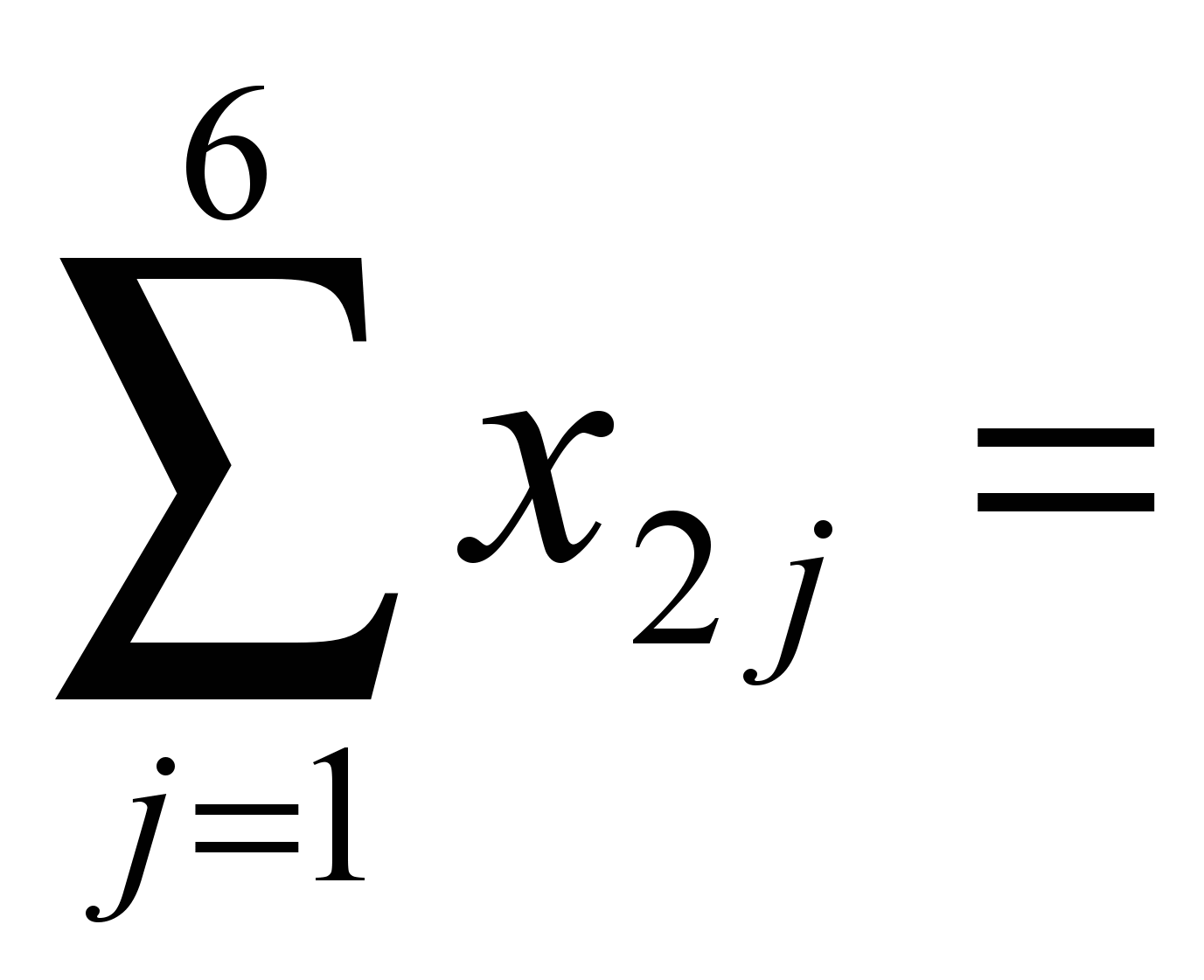 160,
160, 120,
120,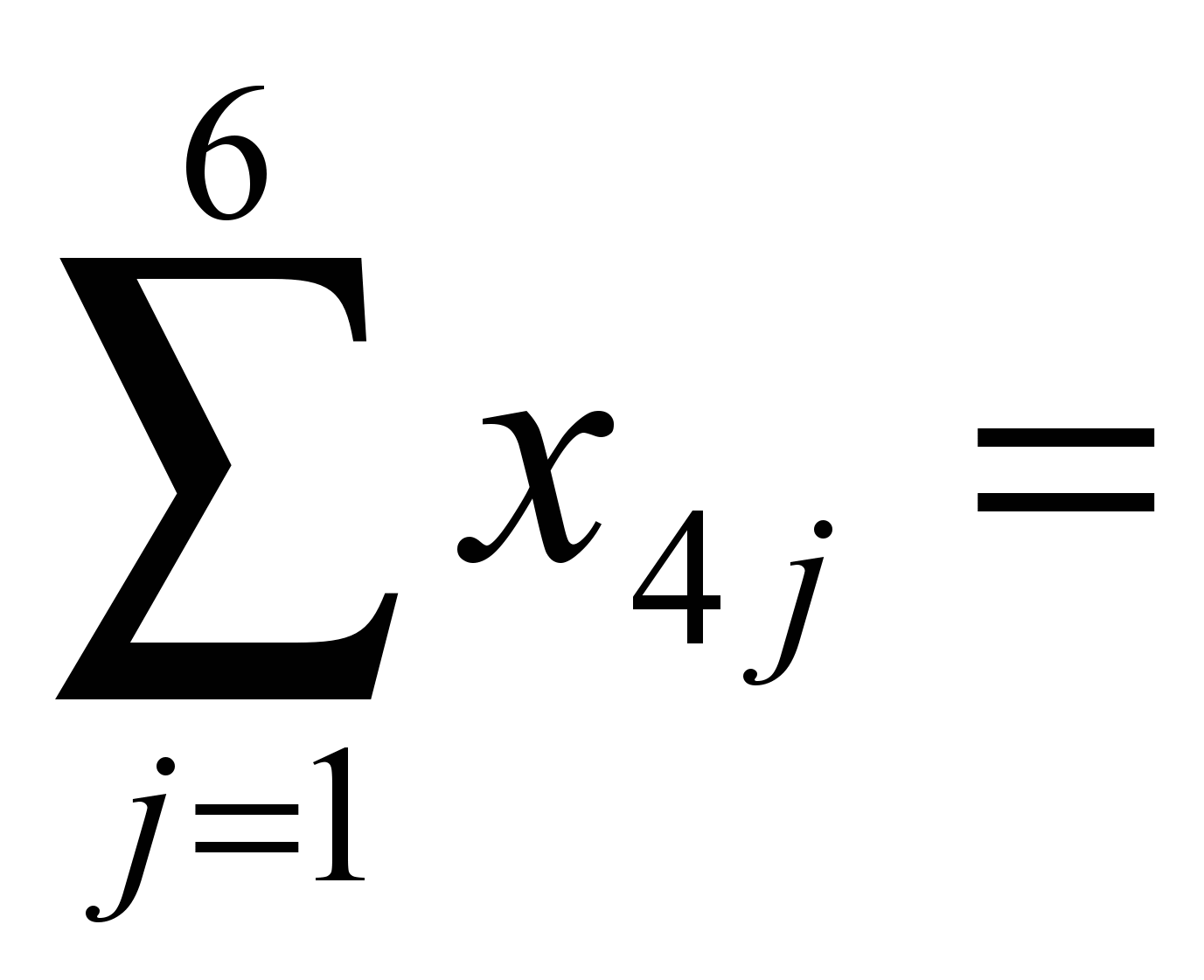 150.
150.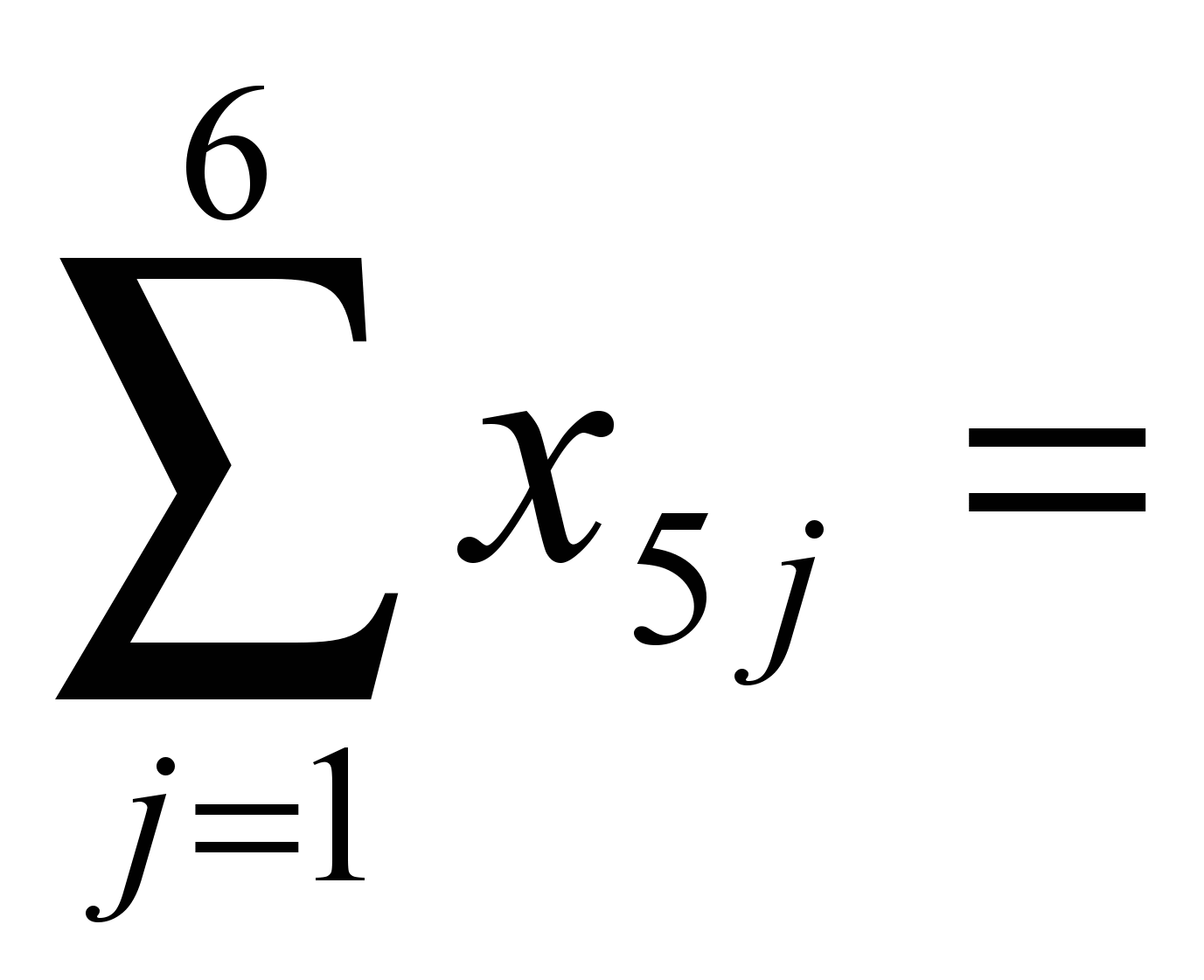 130
130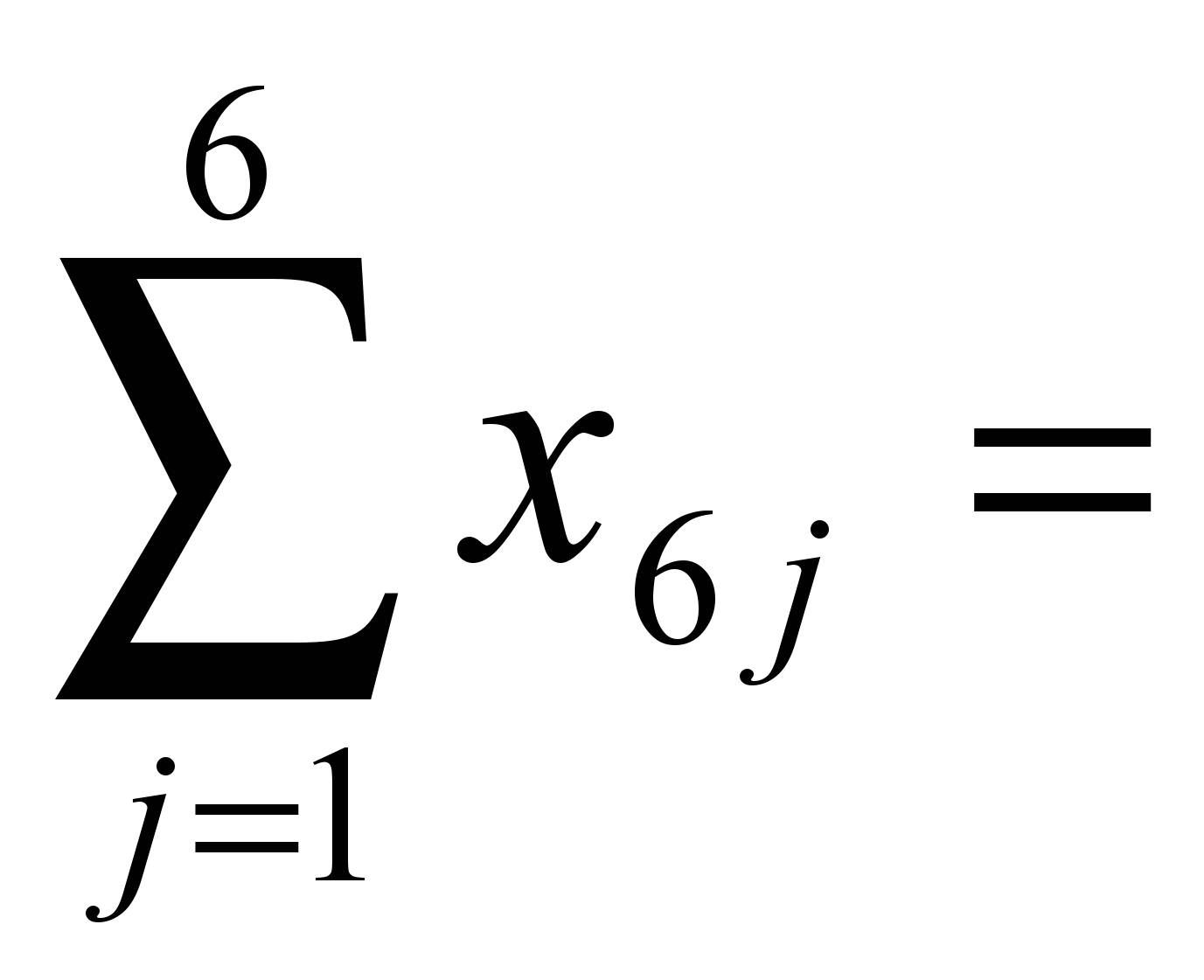 200.
200.Условия положительности переменных:
Xik³0 (i=1, 2, 3, 4, 5; k= 1, 2, 3, 4, 5, 6); Xkj³0 (k= 1, 2, 3, 4, 5, 6; j=1, 2, 3,4, 5, 6).
Так как
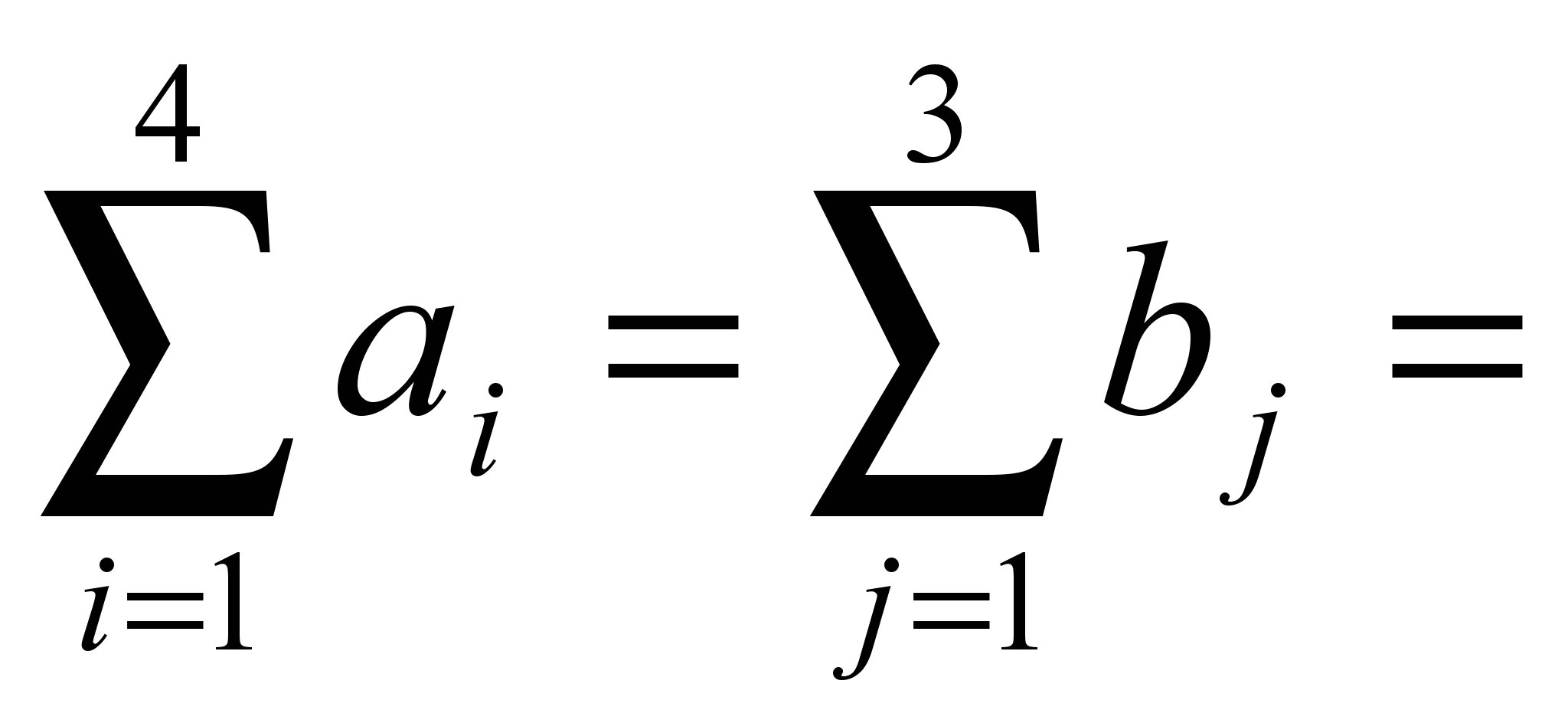 800, то можно решать двухэтапную транспортную задачу. Определяем число заполненных клеток первоначального опорного плана: 11 + 12 – 1 = 22.
800, то можно решать двухэтапную транспортную задачу. Определяем число заполненных клеток первоначального опорного плана: 11 + 12 – 1 = 22.Составляем начальный опорный план методом минимального элемента. Вначале заполняем первый или четвертый квадрант, затем третий, а затем оставшийся (первый или четвертый). В таблице 2.1 получен первоначальный опорный план. Проверим полученный план на оптимальность, для этого находим потенциалы Ui и Vj.
После того как мы определили потенциалы Ui и Vj, находим оценки свободных клеток:
S83 = 0 – (1+0) = -1; S8 10 = 1 – (1+2) = -2; и так далее.
 Полученный опорный план не оптимален, так как имеются отрицательные оценки, наибольшая по модулю из них S8 10. Строим для заданной клетки замкнутый контур и улучшаем, полученный опорный план.
Полученный опорный план не оптимален, так как имеются отрицательные оценки, наибольшая по модулю из них S8 10. Строим для заданной клетки замкнутый контур и улучшаем, полученный опорный план.В результате получаем таблицу 2.2.
После того как мы определили потенциалы Ui и Vj, находим оценки свободных клеток:
S83 = 0 – (1+0) = -1; S8 12 = 4 – (4+1) = -1; и так далее.
Полученный опорный план не оптимален, так как имеются отрицательные оценки, наибольшая по модулю из них S83 и S8 12. Строим для клетки S8 12 замкнутый контур и улучшаем, полученный опорный план.
В результате получаем таблицу 2.3.
Поскольку в таблице 2.3 нет свободных клеток с отрицательными оценками, то мы получили оптимальный план. В таблице 2.3 имеются нулевые оценки свободных клеток, следовательно, полученный нами оптимальный план не является единственным. Данному плану отвечают минимальные затраты, величина которых составляет:
f= (50∙3 + 70∙1 + 80∙1 + 140∙2 + 160∙1 + 30∙1+ 20∙3 + 200∙2 + 50∙1) + (100∙2 + 30∙1 + 70∙1 + 160∙2 + 80∙1+ 10∙2 + 120∙1 + 30∙2 + 100∙1 + 100∙3) = 1280 + 1300 = 2580 ден. ед.
2.2. Решим задачу путем раздельного прикрепления поставщиков к складам и складов к потребителям.
Запишем начальные условия первого этапа задачи в форме табл. 2.3.
Таблица.2.4
| Мощности поставщиков Аi | Промежуточные пункты и их спрос Dk | |||||
| D1 (100) | D2 (30) | D3 (70) | D4 (240) | D5 (160) | D6 (200) | |
| А1 (120) | 3 X11 | 5 X12 | 1 X13 | 4 X14 | 2 X15 | 3 X16 |
| А2 (80) | 5 X21 | 6 X22 | 4 X23 | 1 X24 | 8 X25 | 3 X26 |
| А3 (300) | 3 X31 | 1 X32 | 5 X33 | 2 X34 | 1 X35 | 3 X36 |
| А4 (250) | 6 X41 | 1 X42 | 4 X43 | 3 X44 | 5 X45 | 2 X46 |
| А5 (50) | 1 X51 | 3 X52 | 5 X53 | 2 X54 | 8 X55 | 4 X56 |
Составим математическую модель задачи.
Обозначим через Хik (i = 1,5; k = 1,6) объем продукции, который планируется перевезти от поставщика Аi, в промежуточный пункт Dk, а через f1 - общие затраты на первом этапе транспортировки.
Целевая функция задачи запишется в виде:
f1=3• X11 + 5 • X12 +...+ 4•X56 (min) (2.2.1)
Сравнивая суммарную мощность поставщиков 120 + 80 + 300 + 250 + 50 = 800 со спросом на промежуточных пунктах 100 + 30 + 70 + 240 + 160 + 200 = 800, видим, что эти суммы совпадают. Следовательно, данная транспортная задача обладает закрытой моделью.
Переходя к ограничениям на переменные Хik, следует учесть, что спрос на промежуточных пунктах Dk, не может превышать мощности поставщиков, т.е.
X11 + X12 + X13 + X14 + X15 + X16 =120
X21 + X22 + X23 + X24 + X25 + X26 = 80 (2.2.2)
X31 + X32+ X33 + X34+ X35 + X36 = 300
X41 + X42+ X43 + X44+ X45 + X46 = 250
X51 + X52+ X53 + X54+ X55 + X56 = 50
Условия удовлетворения спроса на промежуточных пунктах Dk:
X11 + X21 + X31+ X41+ X51 = 100
X12 + X22 + X32 + X42+ X52 = 30
X13 + X23+ X33+ X43+ X53 =70
X14 + X24+ X34+ X44 + X54 = 240 (2.2.3)
X15 + X25+ X35+ X45 + X55 = 160
X16 + X26+ X36+ X46 + X56 = 200
Условия неотрицательности переменных:
Хij ≥0 (i=1,5; k=1,6) (2.2.4)
Соотношения (2.2.1) - (2.2.4) образуют экономико-математическую модель рассматриваемой задачи. Таким образом, математическая модель задачи: целевая функция (2.2.1), описывающая суммарные затраты на первом этапе транспортировки, минимизируется при ограничениях (2.2.2) - (2.2.4).
Решим полученную задачу методом потенциалов.
Таблица 2.5
| | D1 (100) | D2 (30) | D3 (70) | D4 (240) | D5 (160) | D6 (200) | Ui |
| А1 (120) | 3 50 | 5 | 1 70 | 4 | 2 0 | 3 | 0 |
| А2 (80) | 5 | 6 | 4 | 1 80 | 8 | 3 | -2 |
| А3 (300) | 3 | 1 | 5 | 2 140 | 1 160 | 3 | -1 |
| А4 (250) | 6 | 1 30 | 4 | 3 20 | 5 | 2 200 | 0 |
| А5 (50) | 1 50 | 3 | 5 | 2 | 8 | 4 | -2 |
| Vj | 3 | 1 | 1 | 3 | 2 | 2 | |
Приступая к составлению исходного опорного плана, устанавливаем, что в нашем случае любой опорный план должен «загружать» m+n-1= 5+6-1=10 клеток.
Построим исходный опорный план методом минимального элемента.
Для исследования плана на оптимальность необходимо найти оценки свободных клеток. Для этого надо знать потенциалы Ui и Vj, которые определяются в результате решения системы уравнений
U
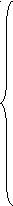 1 + V1 = 3
1 + V1 = 3U1 + V3 = 1
U1 + V5 = 2
U2 + V4 =1
U3 + V4 =2
U3 + V5 = 1
U4 + V2 = 1
U4 + V4 = 3
U4 + V6 = 2
U5 + V1 = 1
составленных по заполненным клеткам. Это неопределенная система, т.к. неизвестных на одно больше числа уравнений. Придадим одному из неизвестных определенное числовое значение, например, U4 = 0. Тогда остальные неизвестные находятся из системы.
Получаем
U1 = 0, U2 = -2, U3 = -1, U4 = 0, U5 = -2, V1 = 3, V2 = 1, V3 = 1, V4 = 3, V5 = 2, V6 = 2.
Теперь можно найти оценки свободных клеток: Δ12 = C12 - (U1 + V2) = 5-(1 + 0)= 4, Δ14= 1, Δ16 = 1, Δ21 = 4, Δ22 = 7, Δ23 = 5, Δ25 = 8, Δ26= 3, Δ31= 1, Δ32= 1, Δ33 = 5, Δ36= 2 и т. Д.
Поскольку в табл. 2.5 свободных клеток с отрицательными оценками нет, то опорный план является оптимальным. Итак, получен оптимальный план:

| | 50 | 0 | 70 | 0 | 0 | 0 |
| | 0 | 0 | 0 | 80 | 0 | 0 |
| X*= | 0 | 0 | 0 | 140 | 160 | 0 |
| | 0 | 30 | 0 | 20 | 0 | 200 |
| | 50 | 0 | 0 | 0 | 0 | 0 |
Этому плану соответствуют минимальные суммарные затраты в 1280 ден. ед.
(f1= 50∙3 + 70∙1 + 80∙1 + 140∙2 + 160∙1 + 30∙1+ 20∙3 + 200∙2 + 50∙1 = 1280)
Запишем начальные условия второго этапа задачи в форме таблицы 2.6.
Таблица 2.6
| Возможности промежуточных пунктов Dk | Пункты потребления и их спрос Вj | |||||
| В1 (40) | В2 (160) | В3 (120) | В4 (150) | В5 (130) | В6 (200) | |
| D1 (100) | 9 X11 | 3 X12 | 4 X13 | 1 X14 | 5 X15 | 2 X16 |
| D2 (30) | 1 X21 | 6 X22 | 2 X23 | 5 X24 | 3 X25 | 8 X26 |
| D3 (70) | 3 X31 | 5 X32 | 2 X33 | 1 X34 | 3 X35 | 4 X36 |
| D4 (240) | 7 X41 | 2 X42 | 5 X43 | 1 X44 | 4 X45 | 6 X46 |
| D5 (160) | 2 X51 | 3 X52 | 1 X53 | 4 X54 | 2 X55 | 8 X56 |
| D6 (200) | 5 X61 | 3 X62 | 2 X63 | 4 X64 | 1 X65 | 3 X66 |
Обозначим через Хkj (k = 1,6; j = 1,6) объем продукции, который планируется перевезти из промежуточного пункта Dk к потребителю bj, а через f2 - общие затраты на втором этапе транспортировки.
Целевая функция задачи запишется в виде:
f2 =9• X11 + 3 • X12 +...+ 3•X66 (min) (2.2.5)
Сравнивая суммарные возможности промежуточных пунктов 100 + 30 + 70 + 240 + 160 + 200 = 800 со спросом потребителей 40 + 160 + 120 + 150 + 130 + 200 = 800, видим, что эти суммы совпадают. Следовательно, данная транспортная задача обладает закрытой моделью.
Переходя к ограничениям на переменные Хkj, следует учесть, что спрос потребителей Вj, не может превышать возможности промежуточных пунктов, т.е.
X11 + X12 + X13 + X14 + X15 + X16 =100
X21 + X22 + X23 + X24 + X25 + X26 = 30 (2.2.6)
X31 + X32+ X33 + X34+ X35 + X36 = 70
X41 + X42+ X43 + X44+ X45 + X46 = 240
X51 + X52+ X53 + X54+ X55 + X56 = 160
X61 + X62+ X63 + X64+ X65 + X66 = 200
Условия удовлетворения спроса поставщиков Вj:
X11 + X21 + X31+ X41+ X51 + X61 = 40
X12 + X22 + X32 + X42+ X52 + X62 = 160
X13 + X23+ X33 + X43 + X53 + X63 = 120
X14 + X24+ X34+ X44 + X54 + X64 = 150 (2.2.7)
X15 + X25+ X35+ X45 + X55 + X65 = 130
X16 + X26+ X36+ X46 + X56 + X66 = 200
Условия неотрицательности переменных:
Хij ≥0 (j=1,6; k=1,6) (2.2.8)
Соотношения (2.2.5) - (2.2.8) образуют экономико-математическую модель рассматриваемой задачи.
Таким образом, математическая модель задачи: целевая функция (2.2.5), описывающая суммарные затраты на втором этапе транспортировки, минимизируется при ограничениях (2.2.6) - (2.2.8).
Решим полученную транспортную задачу методом потенциалов.
Таблица 2.7.
| | В1 (40) | В2 (160) | В3 (120) | В4 (150) | В5 (130) | В6 (200) | |
| D1 (100) | 9 | 3 | 4 | 1 | 5 | 2 100 | -2 |
| D2 (30) | 1 30 | 6 | 2 | 5 | 3 | 8 | -1 |
| D3 (70) | 3 | 5 | 2 | 1 70 | 3 | 4 0 | 0 |
| D4 (240) | 7 | 2 160 | 5 | 1 80 | 4 | 6 | 0 |
| D5 (160) | 2 10 | 3 | 1 120 | 4 | 2 30 | 8 | 0 |
| D6 (200) | 5 | 3 | 2 | 4 | 1 100 | 3 100 | -1 |
| Vj | 2 | 2 | 2 | 1 | 2 | 4 | |
Приступая к составлению исходного опорного плана, устанавливаем, что в нашем случае любой опорный план должен «загружать» m+n-1= 6+6-1=11 клеток.
Построим исходный опорный план методом минимального элемента.
Для исследования плана на оптимальность необходимо найти оценки свободных клеток. Для этого
надо знать потенциалы Ui и Vj, которые определяются в результате решения системы уравнений
U
 1 + V6 = 2
1 + V6 = 2U2 + V1 = 1
U3 + V4 = 1
U3 + V6 = 4
U4 + V2 = 2
U4 + V4 = 1
U5 + V1 = 2
U5 + V3 = 1
U5 + V5 = 2
U6 + V5 = 1
U6 + V6 = 3
составленных по заполненным клеткам. Это неопределенная система, т.к. неизвестных на одно больше числа уравнений. Придадим одному из неизвестных определенное числовое значение, например, U1 = 0. Тогда остальные неизвестные находятся из системы.
Получаем
U1 = 0-2 U2 = -1, U3 = 0, U4 = 0, U5 = 0, U6 = -1,V1 = 2, V2 = 2, V3 = 2, V4 = 1, V5 = 2, V6 = 4.
Теперь можно найти оценки свободных клеток: Δ11 = C11 - (U1 + V1) = 9-(2-2)= 9 и так далее. Поскольку в таблице 2.8 свободных клеток с отрицательными оценками нет, то опорный план является оптимальным.
Итак, получен оптимальный план:
 | 0 | 0 | 0 | 0 | 0 | 100 |
| | 30 | 0 | 0 | 0 | 0 | 0 |
| X*= | 0 | 0 | 0 | 70 | 0 | 0 |
| | 0 | 160 | 0 | 80 | 0 | 0 |
| | 10 | 0 | 120 | 0 | 30 | 0 |
| | 0 | 0 | 0 | 0 | 100 | 100 |
Этому плану соответствуют минимальные суммарные затраты в 1300 ден. ед.
( f2 = 100∙2 + 30∙1 + 70∙1 + 160∙2 + 80∙1+ 10∙2 + 120∙1 + 30∙2 + 100∙1 + 100∙3 = 1300)
Общие транспортные затраты в данном случае составят:
f = f1 + f2 = 1280 + 1300 = 2580 ден.ед.
Изобразим решение данной задачи на рисунке 2.2.
2.3. Сравнивая полученные результаты в пунктах 2.1 и 2.2, можем сделать вывод, что в нашем случае планы, полученные в пунктах 2.1 и 2.2 равнозначны. Так как суммарные транспортные затраты в обоих планах одинаковы и равны 2580 ден. ед.
2.4. Решим двухэтапные транспортные задачи с учетом дополнительных ограничений.
Все оценки свободных клеток в таблице 2.7. оказались положительными, следовательно, полученный нами опорный план, является оптимальным, и ему соответствуют минимальные транспортные затраты:
Zmin = (40∙1 + 80∙3 + 80∙1 + 30∙1 + 160∙1 + 110∙3+ 30∙4 + 130∙3 + 90∙2 + 20∙1 + 30∙2) + (100∙2 + 30∙1 + 70∙4 + 150∙1 + 10∙6+ 80∙4 + 10∙2 + 30∙3 + 120∙1 + 130∙3+ 50∙1+ 20∙3) = 3420 тыс. ден. ед.
Можем сделать вывод, что введение дополнительных ограничений, привело к повышению значения целевой функции на 3420 – 2580 = 840 ден. ед.
2.5 Компьютерная реализация.
2.5.1. Решим задачу пункта 2.1 в среде Microsoft Excel, используя надстройку поиск решения.
Создадим математическую форму и введем исходные данные.
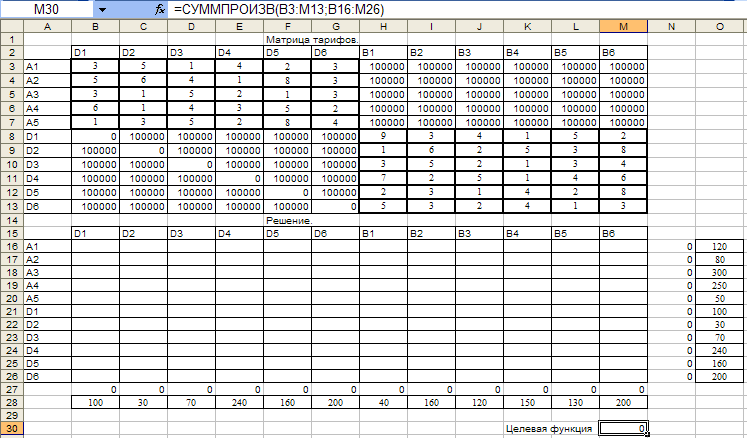
Заполним диалоговое окно поиск решения.
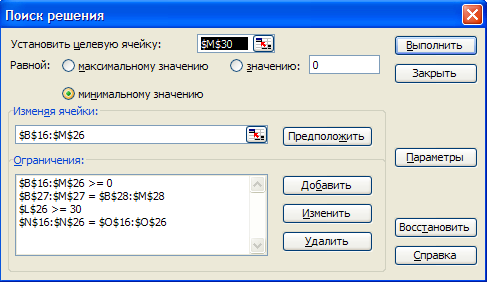
В результате получим:

Мы получили план перевозок c такими же суммарными затратами, что и в пункте 2.1. Следовательно, задача решена нами верно.
2.5.2. Решим задачу пункта 2.2 в среде Microsoft Excel, используя надстройку поиск решения.
Создадим математическую форму и введем исходные данные для первого этапа задачи.

В результате получим:
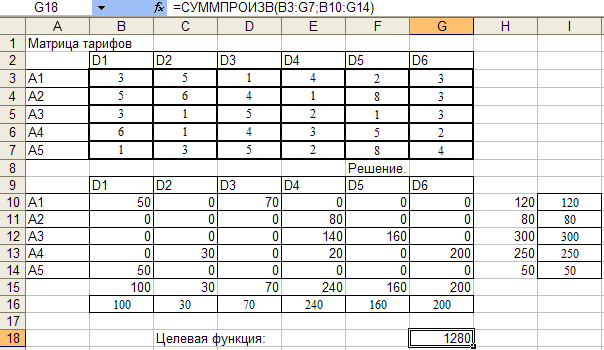
Создадим математическую форму и введем исходные данные для второго этапа задачи.
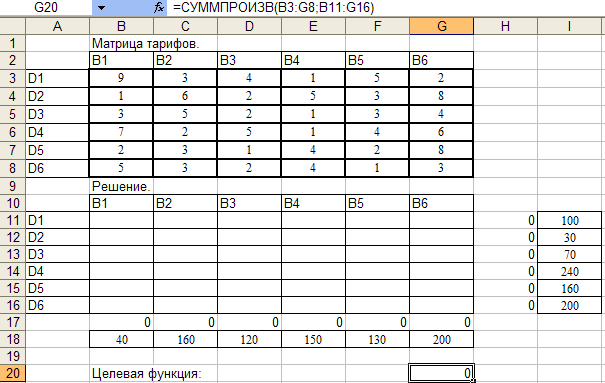
В результате получим:

Мы получили такое же решение, что и в пункте 2.2. Следовательно, в пункте 2.2 задача решена верно.
2.5.3. Решим двухэтапную транспортную задачу с учетом дополнительных ограничений:
- Из А1 в Д1 можно перевезти не менее 80 единиц груза,
Из А3 в Д4 перевозки не осуществляются и из Д4 в В2 перевозки так же запрещены,
Из Д6 в В5 можно перевезти не более 50 единиц груза.
Используя форму задачи пункта 2.5.1, дополним в диалоговое окно поиск решения заданные три ограничения, получим:
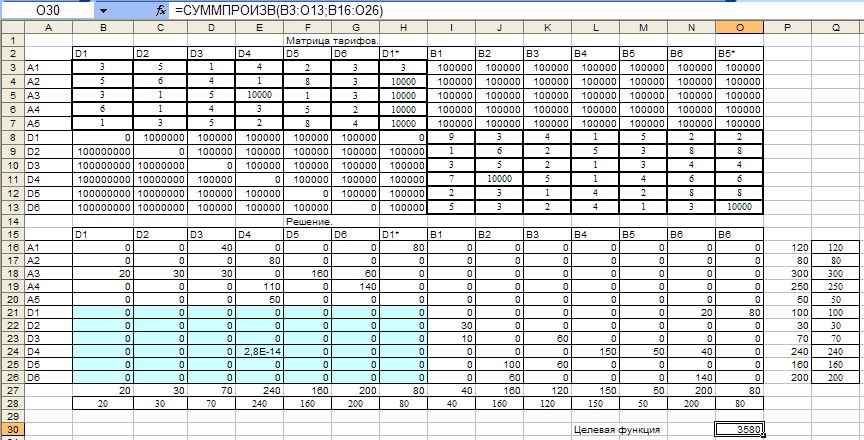
Можем сделать вывод, что введение дополнительных ограничений, привело к повышению значения целевой функции на 3420 – 2580 = 840 ден. ед.
Заключение.
Подводя итоги, проделанной нами работы, можем сделать вывод, что для рассматриваемого нами случая двухэтапной транспортной, когда возможности поставщиков равны потребностям потребителей, а вместимость промежуточных пунктов не превосходит по величине объем грузоперевозок, наиболее подходящим методом решения будет метод сведения двухэтапной транспортной задачи к классической задачи линейного программирования. Данный метод рассмотрен нами в пункте 2.1. главы 2. Значение целевой функции, полученное данным методом в нашем случае равно значению целевой функции, полученной в пункте 2.2. Обычно значение целевой функции, полученной при решении двухэтапной транспортной задачи выше значения целевой функции, полученной методом раздельного прикрепления. В нашем случае эти значения равны. Это объясняется тем, что данная задача имеет несколько оптимальных решений.
Анализируя влияние дополнительных ограничений, рассмотренное нами в пункте 2.4 главы 2, можем отметить, что при их введении значение целевой функции возрастает на 840 тыс. ден. ед.
Литература.
- Таха X. Введение в исследование операций. М: Издательский дом "Вильяме", 2001. -912с.
- Эддоус М., Стэнсфилд Р. Методы принятия решений. М.: Юнити, 1997. - 590 с.
- Кузнецов А.В., Сакович В.А., Холод II.И. Высшая математика: Математическое программирование. Мн.: Вышэйшая школа, 2001. - 351 с.
- Сборник задач и упражнений по высшей математике: Математическое программирование / Под общей ред. А.В.Кузнецова и Р.А.Рутковского. Мн.: Вышэйшая школа, 2002. - 447 с.
- Экономико-математические методы и модели / Под ред. А.В. Кузнецова. Мн.: БГЭУ,1999.-413с.
- Исследование операций в экономике / Под ред. НЛП. Кремера. М.: Банки и биржи -Юнити, 1997.-407с.
- Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.: Высшая школа, 2001. - 208 с.
- Смородинский С.С., Батин Н.В. Оптимизация решений на основе методов и моделей математического программирования. Мн.: БГУИР, 2003. - 136 с.
- Смородинский С.С., Батин Н.В. Методы анализа и принятия решений в слабоструктурированных задачах. Мн.: БГУИР, 2002. - 116с.
10. Смородинский С.С., Батин Н.В. Анализ и оптимизация систем на основе аналитических моделей. Мн.: БГУИР, 1997. - 77 с.
