Название "транспортная задача" объединяет широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом

Вид материала

Задача

Содержание Формулировка транспортной задачи Математическая модель транспортной задачи

Подобный материал:

• Под названием "транспортная задача" объединяется широкий круг задач с единой математической, 142.19kb.
• Задача линейного программирования состоит в том, что необходимо максимизировать или, 24.8kb.
• Задачи математического и линейного программирования. Математическая модель задачи использования, 25.82kb.
• Задачи линейного программирования Геометрическая интерпретация задач линейного программирования, 132.4kb.
• Краткий обзор моделей стохастического программирования и методов решения экономических, 59.55kb.
• Задачи линейного программирования Геометрическая интерпретация задач линейного программирования, 38.07kb.
• Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
• Название Лекция-семинар: Построение математических моделей целочисленного линейного, 64.42kb.
• Кафедра «Прикладная математика» Экономические приложения линейного программирования, 27.15kb.
• Темы курсовых работ «Методы оптимизации» Графический метод решения задачи линейного, 11.12kb.

Транспортная задача линейного программирования


Название “транспортная задача” объединяет широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом.

Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для её решения разработаны специальные методы.

Эти методы, как и симплексный метод, позволяют найти т.н. начальное опорное решение, а затем, улучшая его, получить оптимальное решение. К числу таких специальных, но принципиально новых, методов можно отнести и предлагаемый автором метод приоритетных связей.

1. Формулировка транспортной задачи
   

Однородный груз сосредоточен у m поставщиков в объёмах a₁, a₂, …, a_m. Данный груз необходимо доставить n потребителям в объёмах b₁, b₂, …, b_n. Известны c_ij, i = 1, 2, …, m, j = 1, 2, …, n – стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю.

Требуется составить такой план перевозок, при котором запасы всех поставщиков будут вывезены полностью, запросы всех потребителей полностью удовлетворены и суммарные затраты на перевозку всех грузов минимальны.

2. Математическая модель транспортной задачи
   

Переменными (неизвестными) транспортной задачи являются i = 1, 2, …, m, j = 1, 2, …, n – объёмы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные можно записать в виде матрицы перевозок





X =





Так как произведение c_ijx_ij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны




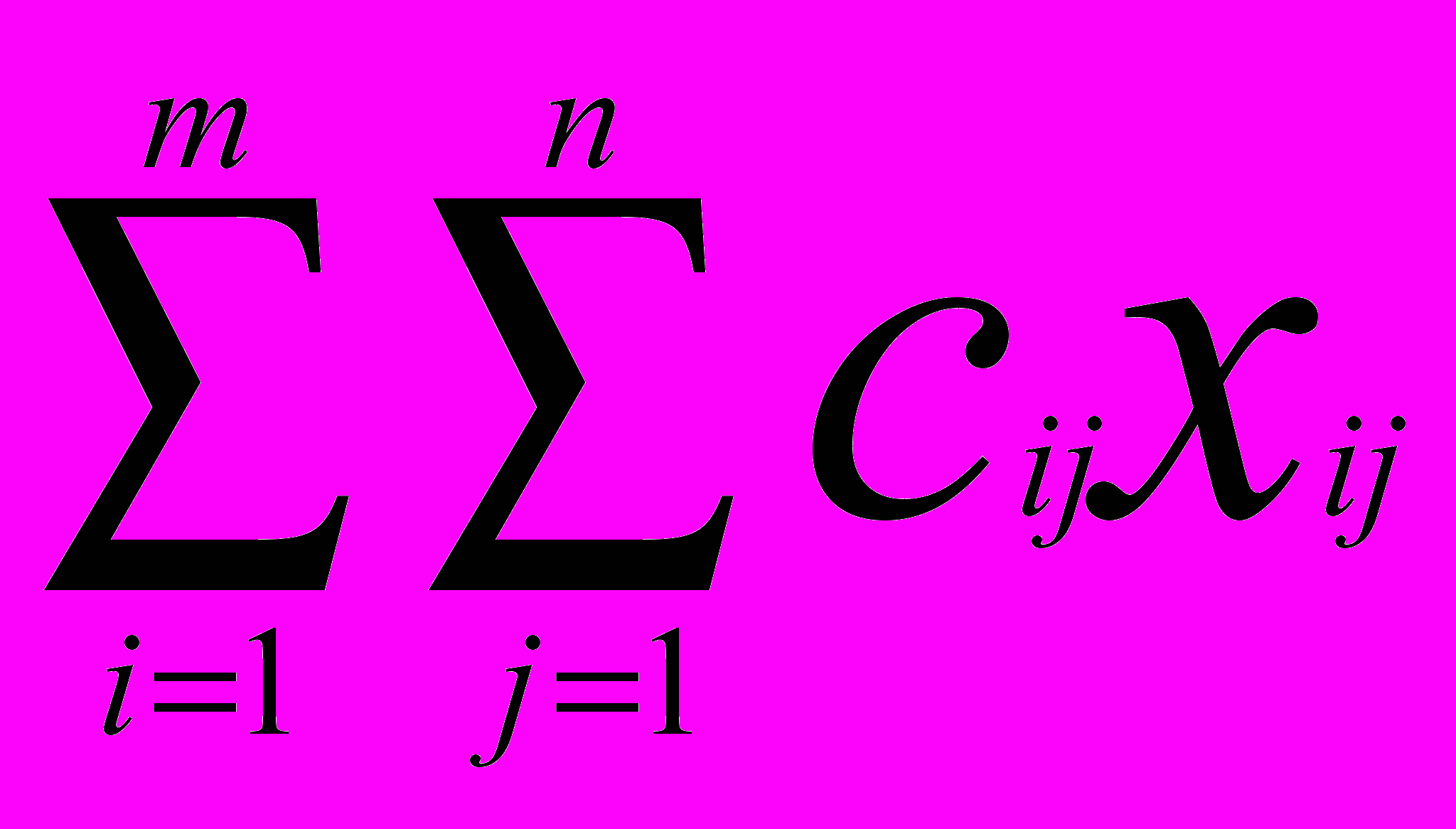
По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция имеет вид


(1.1)

Такой же вид с учётом условий неотрицательности объёмов перевозок имеет и математическая модель задачи.

Система ограничений задачи состоит из двух форм уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью:


= a_i, i = 1, 2, …, m. (1.2)


Вторая группа из n уравнений выражает требование полностью удовлетворить запросы всех n потребителей:


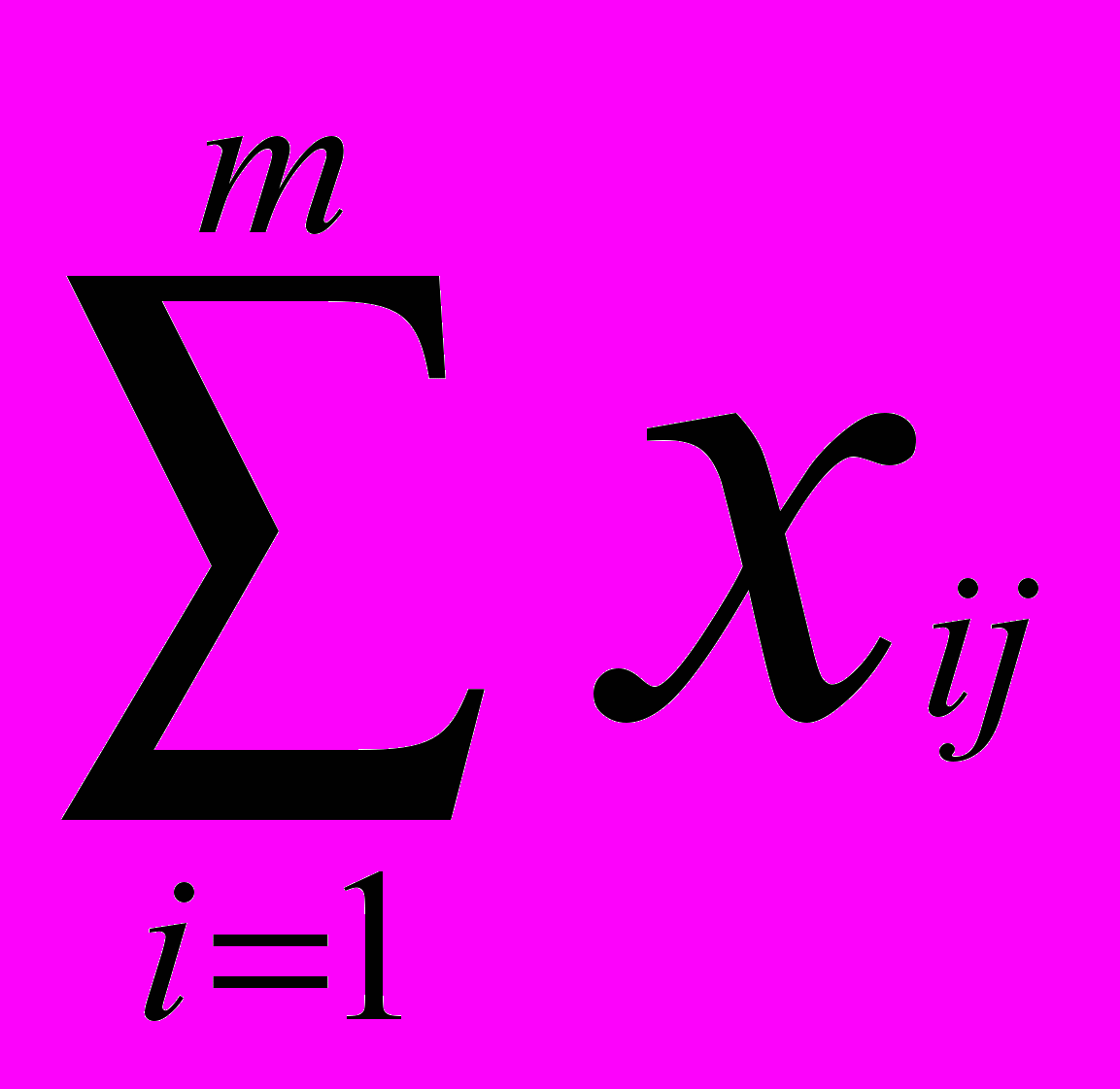= b_j, j = 1, 2, …, n. (1.3)


x_{ij 0,} i = 1, 2, …, m, j = 1, 2, …, n, (1.4)


В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.


= (1.5)

Такая задача называется задачей с правильным балансом, а её модель – закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а её модель – открытой.

Математическая формулировка транспортной задачи такова: найти переменные задачи


X = (x_ij), i = 1, 2, ,,,, m, j = 1, 2, …, n,


удовлетворяющие системе ограничений (1.2), (1.3), условиям неотрицательности (1.1) и обеспечивающие минимум целевой функции (1.1).


Конец постановки задачи