Конспект лекцій 2004 Загальна теорія систем. Конспект лекцій Для студентів денної І заочної форм навчання спеціальності 080200 "Інформатика"/Укл.
| Вид материала | Конспект |
- Конспект лекцій з дисципліни «теплоенергетика» для студентів за фахом мч, мс, лв, омт, 290.65kb.
- Конспект лекцій для студентів спеціальності "Економіка підприємства" денної й заочної, 882.83kb.
- Конспект лекцій по дисципліні Інформаційні моделі "великих" систем, 1986.92kb.
- Опорний конспект лекцій з дисципліни „ правознавство (для студентів денної І заочної, 1124.35kb.
- Конспект лекцій з курсу «Економіка підприємств електротранспорту», 2178.24kb.
- Конспект лекцій для студентів спеціальностей 030508 І 030508 "Фінанси І кредит" денної, 4154.08kb.
- Конспект лекцій з дисципліни «Оподаткування підприємств», 2062.58kb.
- Комп‘ютерні інформаційні технології в електроенергетиці тексти лекцій для студентів, 1076.06kb.
- Конспект лекцій для студентів спеціальності 8050201 Менеджмент підприємств та організацій, 203.46kb.
- Конспект лекцій з навчальної дисципліни «основи охорони праці» для студентів 3 курсу, 15.25kb.
Эмпирико – статистические модели используют кибернетическую идею «чёрного ящика», что не позволяет сделать выводы о структуре модели, причинно - следственных связях и механизмах её функционирования. Априорная информация относительно этих аспектов не используется.
В определении понятия система отсутствует конкретная информация о её внутреннем строении. Поэтому систему можно отобразить в виде чёрного не-прозрачного ящика, который выделен из среды. Эта максимально упрощенная
модель, отображает 2 важных свойства системы, а именно целостность и отделённость от среды. С другой стороны, хотя «чёрный ящик» и выделен из среды, тем не менее, он не изолирован от неё.
Название «чёрный ящик» образно подчёркивает полное отсутствие информации о внутреннем строении «ящика»: в этой модели заданы, фиксируются и пересчитываются только входные и выходные связи со средой. Во многих случаях, несмотря на внешнюю простоту и отсутствие данных о внутреннем строении системы, такая модель оказывается полезной.
Построение модели «чёрного ящика» не является тривиальной задачей, поскольку ответ на вопрос, какие из входов и выходов необходимо включить в модель в большинстве случаев не является простым и однозначным.
В процессе построения модели необходимо выбрать конечное число существенных входных параметров и выходных показателей. Критерием отбора при этом является целевое назначение модели, существенность тех или иных связей относительно этой цели. Именно на этом этапе возможно возникновение ошибок, поскольку во многих случаях априори не известно, какие пара- метры являются существенными, а какие нет. Во многих случаях оказывается, что те переменные и связи между ними, которые сначала казались несущественными, на самом деле существенны и должны быть учтены.
При идентификации сложных объектов, представленных в виде «чёрного ящика», возможны две базовые редукции:
1. К элементарным свойствам объекта - построение математической моде-ли зависимости выходного показателя от каждого из входных параметров - Y=F(Xi), i=1,n.
2. К системным свойствам объекта - построение математической модели зависимости выходного показателя от взаимного влияния входных параметров - Y=F(X1, X2, X3,…Xn).
Для осуществления редукции изучаемого объекта к его элементным свойс-твам разработан метод восстановления одномерных зависимостей (МВОЗ). С его помощью осуществляется разведочный анализ - построение качественных гипотез, определяющих характер зависимости (возрастающий, убывающий, экстремальный) между каждым входным параметром и выходным показате-лем в области значений, заданных таблицей исходного экспериментального материала.
5.1 Исходные данные для построения математической модели.
Начальный перечень входных параметров изучаемой системы (Xi, i=1,n) определяется с помощью экспертов. В некоторых случаях, например, при изучении технологических процессов, задача существенно упрощается, т.к. такой перечень содержится в технологическом регламенте каждого производства.
Перечень выходных показателей Ys, s=1,k и допустимые их значения за-даются при постановке задачи.
Исходным материалом для построения математической модели является таблица исходного экспериментального материала, каждая строка которой содержит значения всех контролируемых входных параметров и выходных показателей в одной реализации изучаемой системы.
Например, при изучении технологических процессов под реализацией по-нимается:
- для периодического (циклического) процесса - операция (информация о значениях входных параметров и выходных показателей в период времени от загрузки сырья до выгрузки готового продукта);
- для непрерывного процесса - информация о значениях входных параметров и выходных показателей в период времени больший времени пребывания при установившемся (стационарном режиме).
Необходимая для заполнения таблицы исходная экспериментальная инфор-мация фиксируется в режиме наблюдения за функционированием изучаемой системы.
Для составления таблицы может быть также использована ретроспектив-ная технологическая документация (диаграммы записывающих приборов, технологические журналы, операционные листы аппаратчиков, лабораторные журналы и т.п.). Однако в этом случае необходим предварительный анализ этих источников информации экспертами с целью оценки корректности зафиксированных в них данных.
Минимально необходимое количество реализаций (строк таблицы) 50. Очевидно, что с увеличением количества строк в исходной таблице растет адекватность модели и эффективность оптимизации. При количестве строк в таблице >100 высокая эффективность оптимизации может быть гарантирована.
Ниже в таблице 1 приведена форма представления исходных данных - таблица экспериментального материала, которая содержит информацию о значениях входных параметров и выходных показателей в m реализациях изучаемого процесса.
Таблица 1
| №№ | Значения входных параметров Xi | Значения выходных показателей Y1 | |||||||
| X1 | X2 | X3 | | Xn | Y1 | Y2 | … | Yk | |
| 1 | | | | | | | | | |
| 2 | | | | | | | | | |
| 3 | | | | | | | | | |
| … | | | | | | | | | |
| M | | | | | | | | | |
Принятые условные обозначения:
M - матрица (таблица) экспериментального материала размерности (n+k)*m;
{Xi} - вектор-столбец входных параметров размерности m;
{Xj} - вектор-строка входных параметров размерности n;
xij - значение i-ого входного параметра в j-ой строке матрицы M;
{Ys} - вектор-столбец выходных показателей размерности m;
{Yj} - вектор-строка выходных показателей размерности k;
ysj - значение s-ого выходного показателя в j-ой строке матрицы M;
[Ys] - допустимое (приемлемое) значение Ys;
n - размерность вектора входных параметров;
k - размерность вектора выходных показателей;
m - количество строк матрицы M;
5.2 Алгоритм построения зависимостей Y=F(Xi), i=1,n в случае, когда выходной показатель один.
Алгоритм построения одномерных моделей сводится к разделению диапазонов встречающихся в исходном экспериментальном материале значений каждого входного параметра Xi на 3 поддиапазона и вычислению средних значений Xi ср и соответствующих им средних значений Yср в каждом из поддиапазонов.
1. Таблицу исходных данных сортируют по возрастанию входного параметра X1.
2. Диапазон вариаций параметра Х1 делится на три поддиапазона из условия попадания в каждый поддиапазон одинакового количества опытов (примерно одинакового - если число опытов в таблице экспериментального материала не кратно трем или по разные стороны границы находятся одинаковые значения). Границы поддиапазонов определяются как среднее между значениями в последнем опыте предыдущего и первом опыте последующего поддиапазонов.
3. Для каждого поддиапазона определяются средние значения параметра Х1 и средние значения выходного показателя Y в строках, попавших в соответствующий поддиапазон при выполнении пп 1, 2 для строк .
4. По полученным по п.3 координатам трех точек (Х1 ср D1, Yср D1; Х1 ср D2, Yср D2; Х1ср D3, Yср D3) строят график зависимости выходного показателя от 1-ого входного параметра Y=F(X1).
5. Повторяют пп. 1-4 последовательно для каждого из n входных параметров и получают модель Y=Fi (Xi), i=1,n , описывающую зависимости выходного показателя от каждого из n входных параметров.
6. При необходимости по координатам трех точек кроме графика можно построить для каждого параметра аналитические выражение зависимости Y=Fi (Xi).
В построении модели Y=Fi (Xi) участвуют два вектор - столбца таблицы экспериментального материала - {Xi} и {Y}. Однако значение выходного по-казателя Y определяется всеми входными параметрами. Если бы зависимость выходного показателя от входного параметра Xi была слабой, то в каждом поддиапазоне средние значения Y были бы очень близкими, т.е. зависимость Y=Fi (Xi) практически не проявилась бы на фоне влияния остальных параметров.
При построении модели значения параметра Xi проранжированы по возрастанию и усредняются в каждом поддиапазоне, значения же остальных параметров случайным образом «размазаны» по всему диапазону их возможных значений. Это позволяет выделять влияние i-ого параметра на фоне шумов остальных параметров.
Полученные с помощью МВОЗ одномерные модели представляют собой как бы рентгеновский снимок изучаемой системы и позволяют специалистам наглядно увидеть все существующие зависимости. Во многих случаях эти зависимости тривиальны, т.е. соответствуют априорным знаниям специалистов. Этот факт является подтверждением корректности полученных с помощью формальных процедур моделей.
В некоторых случаях одномерные модели даже при одном выходном по-казателе несут новую, нетрививиальную, неизвестную ранее специалистам ин-формацию о закономерностях изучаемого процесса.
Поскольку при построении одномерной модели Y= F(Xi) из таблицы экспериментального материала используются только два вектор - столбца {Xi} и
{Y}, а значение Y зависит также и от значений остальных входных парамет-ров, в том числе и ненаблюдаемых, одномерная модель учитывает контекст задачи - область вариаций значений остальных входных параметров.
Поэтому:
- Полученные зависимости интерпретируются как формальные гипотезы о характере изменения выходного показателя (возрастающий, убывающий, экстремальный) при изменении соответствующего входного параметра от Xmin до Xmax.
- Апостериорная информация о полученных зависимостях во многих случаях является новой, ранее неизвестной;
- При изменении контекста задачи (изменении диапазонов варьирования других параметров), зависимость Y=F(Xi) для i-ого параметра также соот-ветствующим образом изменяется ;
- Полученные зависимости инвариантны к пропускам в экспериментальном материале отдельных значений и вектор - столбцов любых (в том числе и не наблюдаемых) параметров.
- Алгоритм построения зависимостей Yоб=F(Xi), i=1,n в случае, когда входных показателей более одного.
Эффективность функционирования большинства реальных систем определяется не одним, а несколькими выходными показателями. Например, качество работы любого технологического процесса определяется: качеством продукции и её себестоимостью, производительностью, количеством токсичных и загрязняющих окружающую среду отходов и др.
Однако для решения задачи оптимизации известными континуальными методами необходимо иметь один критерий оптимизации.
- “Различные методы решения многокритериальной задачи отличаются видом и способом получения дополнительной информации, а также алгоритмом "сворачивания" исходных критериев в один глобальный критерий.- «Свертка частных критериев оптимизации всегда является субъективным неформальным актом» (Расстригин Л.А. Современные принципы управления сложными объектами. - М.:"Советское радио", 1980, с.232.)
Эта проблема была бы легко разрешима, если бы удалось найти корректный метод свертки множества выходных показателей в обобщенный критерий,
измеряемый в континуальных шкалах. К сожалению, все известные методы свертки основаны на экспертных оценках, т.е. субъективны.
Между тем требования к отдельным выходным показателям реальных систем задаются либо директивными документами (для технологических процессов ГОСТами, техническими условиями, регламентами, технологическими инструкциями и т.п.) в виде соответствующих ограничений на допустимые значения по каждому из них, либо задаются из каких - либо соображений при постановке задачи исследования.
Например, в соответствии с технологической инструкцией по доменному производству, химический состав чугуна, направляемого в конвертерный цех, должен соответствовать следующим ограничениям: кремний 0.6-1.1%, марганец 0.45-0.8%, сера < 0.05%, фосфор < 0.1%.
Наличие допустимых ограничений позволяет осуществить объективную свертку множества выходных показателей в обобщенный критерий Yоб, измеряемый в дискретных шкалах. Обобщенный критерий Yоб принимает два значения: Yоб=1, если все частные критерии (выходные показатели) удовлетворяют заданным ограничениям, и Yоб=0, если хотя бы один частный критерий не удовлетворяет этим ограничениям.
Однако методы построения математических моделей по экспериментальному материалу, в котором входные переменные представлены в континуальных, а выходные в дискретных шкалах, неизвестны.
Для решения задачи восстановления зависимостей между обобщенным критерием Yоб и каждым из входных параметров Xi по экспериментальному материалу, полученному в режиме наблюдения за изучаемым технологическим процессом ("пассивный" эксперимент), используется новый метод разведочного анализа, сущность которого сводится к:
- формальной свертке множества выходных показателей в обобщенный критерий, измеряемый в дискретных бинарных шкалах и принимающий два значения (0 или 1);
- обратному переходу к оценке обобщенного критерия в континуальных шкалах за счет разбиения диапазона вариаций значений каждого входного параметра Xi на три поддиапазона и определения в каждом поддиапазоне отношения количества точек, соответствующих "хорошим" реализациям, к общему их количеству. ("Хорошими" являются реализации, в которых Yoб=1). Эти отношения и являются континуальной оценкой обобщенного критерия.
Ниже представлен алгоритм реализации метода восстановления одномерных зависимостей обобщенного критерия от входных параметров Yoб=F(Xi), i=1,n. по экспериментальным данным, полученным в результате наблюдения за изучаемым процессом.
1. Осуществляется свертка комплекса выходных показателей в обобщенный критерий Yoб. В j-ой строке исходной матрицы М вектор - строка выходных показателей {Yj} принимает значение: Yj oб =1 ("хорошо"), если каждый показатель удовлетворяет заданным ограничениям и Yj oб= 0 ("плохо"), если хотя бы один показатель не удовлетворяет заданным ограничениям.
2. Таблицу исходных данных сортируют по возрастанию входного пара-метра X1.
3. Диапазон вариаций значений параметра Х1 делится на три поддиапазона из условия попадания в каждый поддиапазон примерно одинакового количество точек (m1» m2» m3; m1+m2+m3= m).
4. Для каждого поддиапазона определяются средние значения параметра Х1.
5. В каждом поддиапазоне определяют соотношения: R1= m1х/m1; R2= m2х/m2; R3= m3x/m3, где m1х, m2х,... m3x, соответственно, количество "хороших" точек в первом, втором и третьем поддиапазонах.
6. По полученным по пп.4,5 координатам трех точек (Х1 ср D1, R1;
Х1 ср D2, R2; Х1 ср D3 , R3) строят график зависимости обобщенного критерия от первого входного параметра Yоб=F1(X1).
7. Повторяют пп. 2-6 последовательно для каждого из n входных параметров и получают модель Yоб=Fi(Xi), i=1,n, описывающую зависимости об-общенного критерия от каждого из n входных параметров.
Различие в построении одномерных моделей с одним выходным показателем и комплексом выходных показателей заключается лишь в том, что в первом случае рассчитываются средние значения выходного показателя, а во втором - отношения R1, R2 и R3, оценивающие значения обобщённого критерия Yоб в численных шкалах (чем больше - тем “лучше”).
Далее будут рассматриваться одномерные модели с одним выходным пока-зателем, однако все, сказанное про них, справедливо и для моделей с комплек-сом выходных показателей.
Поскольку психофизиологические ограничения человека в распознавании абстрактных образов не позволяют ему на интуитивном уровне оценить влияние одного входного параметра более чем на один выходной показатель, то при изучении таких объектов с помощью МВОЗ получаемые формальные гипотезы в подавляющем большинстве случаев несут новую, неизвестную ранее специалистам информацию о закономерностях изучаемого технологического процесса.
5.4 Анализ одномерных зависимостей.
5.4.1 Оценка характера зависимости выходного показателя (комплекса вы-ходных показателей) от каждого из входных параметров.
Возможны 4 вида одномерных зависимостей (см. Рис.1):
I - монотонно убывающая - с увеличением значения параметра Xi значение выходного показателя уменьшаются;
II - монотонно возрастающая - с увеличением значения параметра Xi значение выходного показателя растёт;
III - экстремальная - экстремум, соответствующий «лучшему» значению выходного показателя;
IV - экстремальная - экстремум, соответствующий «худшему» значению выходного показателя.
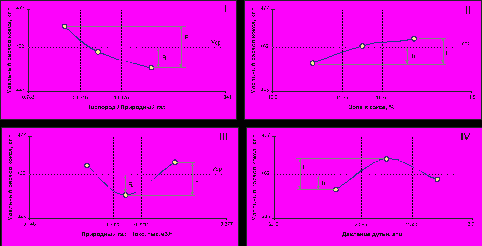
Рис. 1 Примеры одномерных зависимостей, полученных при изучении влияния параметров доменного процесса на удельный расход кокса. (Чем меньше удельный расход кокса - тем лучше).
Обозначения, принятые на графиках:
F - сила параметра Xi, которая определяется как разность между максимальным и минимальным средними значениями выходного показателя в поддиапазонах.
R - резерв выходного показателя по каждому из входных параметров, который определяется как разность между средними значениями выходного показателя в «лучшем» поддиапазоне и во всей таблице исходных данных.
Модель, приведенная на рисунке 1, получена при идентификации доменной печи 5 на Криворожском горнометаллургическом комбинате.
Анализируя приведенные зависимости (Рис.1), можно утверждать:
Зависимость I - имеется определенный резерв по улучшению выходного показателя, который может быть реализован за счет увеличения значений входного параметра до максимальных, приведенных в таблице экспериментальных данных. При дальнейшем изучении процесса имеет смысл исследовать область со значениями параметров Xi, большими, чем имеются в исходном экспериментальном материале.
Зависимость II - имеется определенный резерв по улучшению выходного показателя, который может быть реализован за счет уменьшения значений входного параметра до минимальных, приведенных в таблице экспериментальных данных. При дальнейшем изучении процесса имеет смысл исследовать область со значениями параметра Xi, меньшими, чем имеются в исходном экспериментальном материале.
Зависимость III - имеется определенный резерв по улучшению выходного показателя, который может быть реализован за счет поддержания значений параметра во втором поддиапазоне. При дальнейшем изучении процесса имеет смысл более подробно исследовать область значений параметра, соответствующую второму поддиапазону, с целью выявления возможности дальнейшего повышения эффективности процесса.
Зависимость IV – система (в данном случае доменный процесс) работает не оптимально. Поиск оптимальных значений необходимо вести в областях ниже минимального и выше максимального значений параметра Xi, чем в исходном экспериментальном материале.
Следствия:
1. Если каждая из зависимостей Y=F(xi), i=1,n имеет экстремум, соответствующий «лучшему» значению выходного показателя, то оптимум изучаемого процесса находится внутри исследуемой области.
2. Если каждая из зависимостей Y=F(xi), i=1,n имеет экстремум, соответствующий «худшему» значению выходного показателя, то оптимум изучаемого процесса находится вне исследуемой области.
3. Если некоторые из зависимостей Y=F(xi), i=1,n монотонны (возрастающие или убывающие) или имеют экстремум, соответствующий «худшему» значению выходного показателя, то оптимум изучаемого процесса находится вне области исследования. В этом случае поиск глобального оптимума системы должен осуществляться по каждому из таких параметров в направлениях повышения эффективности по выходному показателю в каждой из этих зависимостей.
4. Результаты разведочного анализа, осуществляемого с помощью метода восстановления одномерных зависимостей, могут быть использованы для корректной оценки эффективности работы изучаемой системы и в качестве рекомендаций по повышению эффективности её функционирования.
5.4.2 Оценка силы зависимости выходного показателя (комплекса выход-ных показателей) от каждого из входных параметров.
Сила параметра Xi определяется как разность между максимальным и минимальным средними значениями выходного показателя в поддиапазонах.
Например, сила параметра Xi на рис.1 определяется как разность между средними значениями выходного показателя Y в 1-ом и 3-ем поддиапазонах.
5.4.3 Оценка резерва повышения значения выходного показателя (комплекса выходных показателей) от каждого из входных параметров.
Резерв возможного «улучшения» выходного показателя за счёт выбора оптимального диапазона значений параметра Xi определяется как разность меж -
ду средними значениями выходного показателя в «лучшем» поддиапазоне и во всей таблице исходных данных.
5.5. Оптимизация изучаемой системы с помощью одномерных моделей.
Синтез оптимального управления изучаемой системой заключается в по-строении модели, в которой для каждого параметра задаётся тот поддиапазон его значений, которому соответствует наилучшее (максимальное или мини-мальное по условиям задачи) среднее значение выходного показателя (обобщенного критерия).
В случае, когда изучаемая система представляет собой технологический процесс, с помощью МВОЗ корректно решается одна из самых сложных задач управления – определение требований к неуправляемым параметрам.
Практически в любом технологическом процессе помимо управляемых имеются так же неуправляемые параметры (например, показатели качества сырья). Обычно требования к этим показателям задаются директивными документами (ГОСТами, техническими условиями, технологическими регламентами). Однако из-за того, что зачастую одно и то же сырье применяется в различных технологических процессах, возникают существенные расхождения между требованиями к показателям качества сырья, задаваемых директивными документами, и конкретными технологическими процессами.
При наличии в таблице исходного материала неуправляемых параметров оптимизация условий проведения конкретного технологического процесса с помощью его одномерной модели Y=F(Xi), i=1,n позволяет технологически обоснованно определить необходимые для данного процесса требования к показателям качества сырья.
Практически все созданные человеком «большие системы» работают неоптимально и имеют существенные резервы для повышения эффективности.
Например, все действующие технологические процессы в химии, метал-лургии, нефтепереработке и других отраслях промышленности работают в неоптимальных режимах и имеют значительные резервы для повышения эффективности работы по экономическим, экологическим и потребительским критериям.
Качественной оценкой эффективности работы действующего техноло-гического процесса является вид графиков, полученных при построении одномерных моделей зависимости выходного показателя (заданного комплекса выходных показателей) от каждого из входных параметров. Очевидно, чем больше экстремальных зависимостей с экстремумами, соответствующими требованиям к выходному показателю, тем выше эффективность работы процесса.
Предельной количественной оценкой резерва изучаемого производства по заданному критерию является суммарная оценка резервов по каждому из вход-ных параметров.
Использование метода восстановления одномерных зависимостей для оптимизации «больших» систем позволяет без дополнительных капитальных затрат, только на основании анализа информации, фиксируемой в режиме на-блюдения существенно повышать эффективность их функционирования.
Например, для химических, металлургических, нефтеперерабатывающих и других технологических процессов появляется возможность на существую-щем оборудовании, с использованием существующих систем информацион-ного обеспечения и управления, т.е. практически без дополнительных затрат решать задачи повышения качества продукта, сокращения расходных норм по сырью, полупродуктам, энергетике, снижению себестоимости продукции и т.п.
Сопоставление результатов оптимизации с действующим регламентом позволяет внести соответствующие корректировки в технологический регламент производства.
В случае, если эти корректировки не выходят за рамки патента по данному производству, по результатам оптимизации следует оформить рационализаторское предложение, если выходят - заявку на патент.
5.6 Область использования одномерных моделей.
Методы одномерной идентификации и оптимизации корректны при изучении отдельных производств и полученные результаты ни в коем случае не могут переноситься на другие аналогичные агрегаты, технологические схемы, производства. Известно, что технологические агрегаты (например, домны, конвертеры, мартены, электропечи, ректификационные колонны и т.п.), даже имеющие одинаковое конструктивное исполнение и размеры, обладают высокой степенью индивидуальности
Кроме того, известно:
- «Характер зависимости конкретной выходной переменной от учитываемых входных переменных не является постоянным и меняется в зависимости от состояния технологического процесса».
- «Структура и параметры технологического процесса меняются со временем и во многих случаях предугадать закономерности этих изменений довольно трудно».
- «В различных режимах работы объекта степень влияния одних и тех же переменных на ход процесса может быть совершенно различной. Если в одном режиме некоторая входная переменная является определяющей, то в другом - она может практически не влиять на ход процесса».
(Основы управления технологическими процессами. Под ред. Н.С. Райбмана. - М.:"Наука", 1978.-с.440).
Следовательно, даже при работе на одном объекте в случае изменения состава и показателей качества сырья необходимо соответственно заново строить математическую модель, проводить оптимизацию и вносить соответствующие изменения в управление процессом.
Выводы
1 Метод восстановления одномерных зависимостей (МВОЗ) предназначен для изучения индивидуальных систем.
2. С помощью МВОЗ можно по экспериментальным данным, фиксируемым в режиме наблюдения за изучаемой системой, решить задачу её идентифика-ции.
3. С помощью математической модели, полученной при идентификации, могут быть решены задачи анализа характеристик изучаемой системы и её оптимизации.
4. Математические модели, постронные с помощью МВОЗ, обладают сле-дующими свойствами. Они:
- объективны - процедура построения модели полностью формализована – ап-риорная информация экспертов не используется;
- информативны - содержат зависимости выходного показателя (комплекса вы-ходных показателей) от каждого из входных параметров изучаемой системы;
- наглядны - формулируются в виде формальных непротиворечивых на дан-ном экспериментальном материале гипотез, легко интерпретируемых на языке соответствующей предметной области;
- не чувствительны к коррелированности переменных;
- конструктивны - позволяют оценить силу влияния каждого входного пара-метра на выходной показатель (комплекс выходных показателей) и величину резерва по выходному показателю от каждого из входных параметров.
Известно, что лучшим способом адаптации модели при изменении условий функционирования изучаемой системы является повторное построение мате-матической модели по новым данным. Очевидно, что при таком подходе при прочих равных условиях преимуществом обладает тот метод моделирования, который требует для своей реализации минимальных затрат и позволяет пос-троить модель в кратчайшие сроки. Такими достоинствами обладает МВОЗ.
5. На основании математической модели, построенной с помощью МВОЗ, решаются следующие задачи:
- Оценка резервов системы по выходным показателям, которые могут быть реализованы за счёт оптимизации технологического режима на существующем оборудовании и с использованием существующих систем информационного обеспечения и управления (т.е. без дополнительных затрат).
- Оценка силы влияния каждого входного параметра на выходной пока-затель (комплекс заданных выходных показателей).
- Оценка резерва повышения эффективности работы системы в зависимос-ти от каждого их входных параметров изучаемой системы.
- Определение оптимальных условий проведения технологического режи-ма, при которых обеспечивается заданное качество его работы.
6. Поскольку ни один специалист не может себе представить зависимость комплекса выходных показателей от какого либо входного параметра, то если
такая зависимость получена с помощью МВОЗ, можно утверждать, что с по-мощью этого метода решается одна из важнейших задач искусственного ин-теллекта – «получение новых знаний из экспериментальных данных».
