Элементы математической логики
| Вид материала | Документы |
- Курс, специальность: «Прикладная информатика (в экономике)» 1 семестр (лекции 36 часов;, 84.15kb.
- Контрольная работа по теме «Элементы математической логики», 36.88kb.
- Лекции по математической логике и теории алгоритмов для студентов 2 курса специальности, 769.24kb.
- Элективный курс "Системы счисления и элементы математической логики" для учащихся, 49.65kb.
- Отличия человеческой логики от математической логики, 139.86kb.
- Дипломных работ элементы математической логики в начальном курсе математики, 29.99kb.
- 1. Введение в алгебру логики Прямое произведение множеств. Соответствия и функции., 38.38kb.
- Программа элективного курса «Элементы математической логики», 56kb.
- Программа по дисциплине дискретная математика, 32.4kb.
- Учебно-методический комплекс для специальности, 395.26kb.
Элементы математической логики
Математическая логика - это анализ методом рассуждений, при этом в первую очередь исследуются формы рассуждений, а не их содержание, т. е. математическая логика, исследует соотношения между основными понятиями математики, на базе которых доказываются математические утверждения. Простейшую из формальных логических теорий называют алгеброй высказываний, поэтому начнем знакомство с элементами математической логики с такого понятия, как высказывание, которое лежит в основе логико-математической теории дискретной математики.
1. Составные высказывания
Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.
Приведем примеры высказываний.
Пример 1. Волга впадает в Каспийское море.
Пример 2. Два больше трех.
Первое высказывание является истинным, а второе - ложным.
Таким образом, высказывание обладает свойством представлять истину или ложь, поэтому на высказывание можно смотреть как на величину, которая может принимать только одно из двух значений: «истина», «ложь».
Поставим в соответствие высказыванию логическую переменную х, которая принимает значение 1, если высказывание истинно, и 0, если высказывание ложно.
Мы не будем исследовать внутреннюю структуру высказываний, потому что такое исследование оказывается достаточно трудным и относится скорее к лингвистике, чем к математике. Поэтому мы будем поступать так, как если бы мы знали все о простых высказываниях, и будем изучать лишь их сочетания, т. е. как различными способами из отдельных высказываний можно построить новое высказывание.
Это новое высказывание называется составным, в то время как высказывания, из которых оно образовано; называются его простыми составляющими или компонентами. Любое высказывание, даже такое, которое на самом деле является сложным, может быть использовано в качестве одного из простых составляющих какого-то другого составного высказывания.
2. Простейшие связки
Значение истинности составного высказывания определяется значениями истинности его компонент.
Высказывания будем обозначать прописными буквами латинского алфавита Х, У, Z ... .
Составные высказывания будем получать из простых с помощью логических операций: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность, которые осуществляются при помощи логических связок:
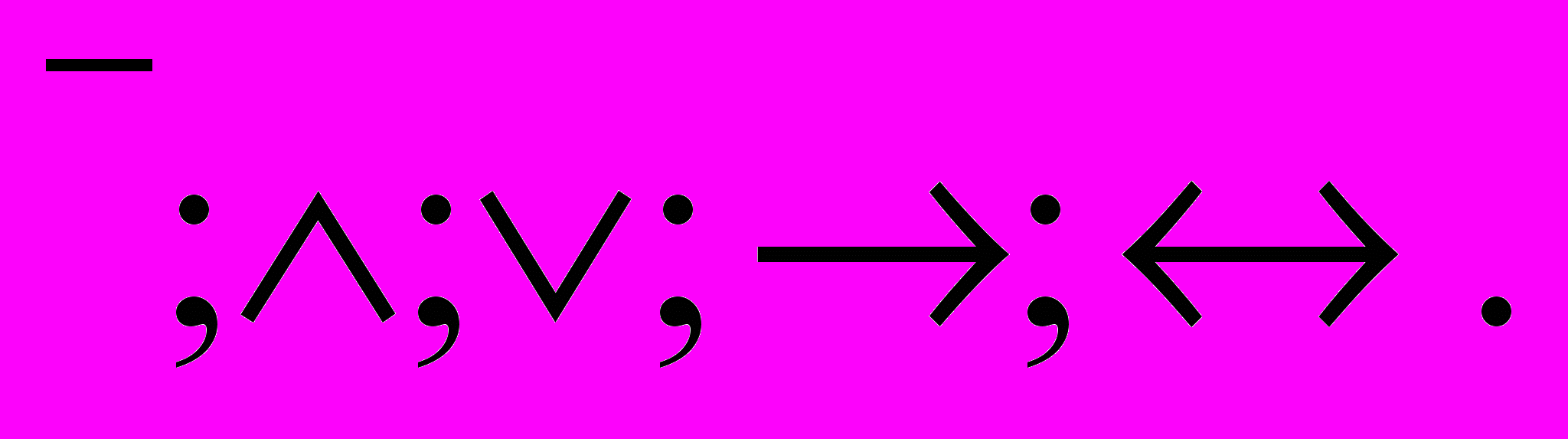
| Название | Прочтение | Обозначение |
| Отрицание | не | - |
| Конъюнкция | и |  |
| Дизъюнкция | или |  |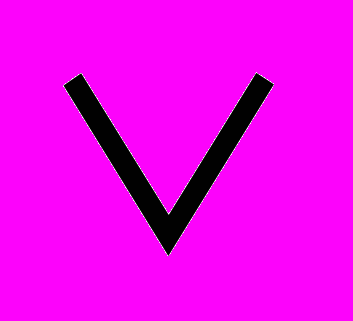
| Импликация | если ... то |  |
| Эквивалентность | тогда и только тогда, когда |  |
При рассмотрении той или иной связки мы хотим знать, каким именно образом истинность составного высказывания, порожденного этой связкой, зависит от истинности его компонент. Очень удобно изображать эту зависимость, пользуясь таблицами истинности, которые называются также интерпретациями логических операций. Каждой строке таблицы истинности взаимно однозначно соответствует набор составляющих высказываний и соответствующее значение составного высказывания. Наборы из нулей и единиц, соответствующих составляющим высказываниям, в каждой строке таблицы истинности имеют стандартное расположение, т. е. расположены в лексикографическом порядке (порядке возрастания).
Пусть даны два произвольных высказывания Х и У.
Отрицанием высказывания Х называется высказывание
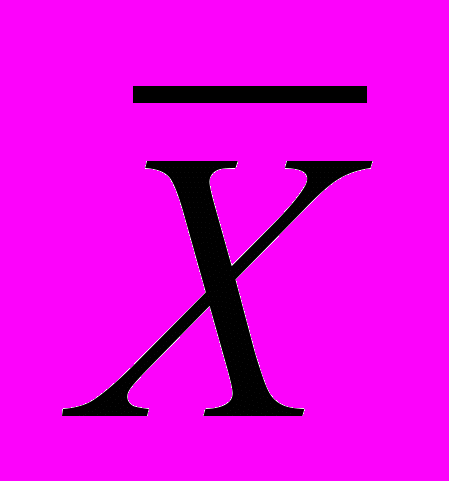, которое истинно, когда Х ложно, и ложно, когда Х истинно.Таблица истинности для отрицания.
| Х | |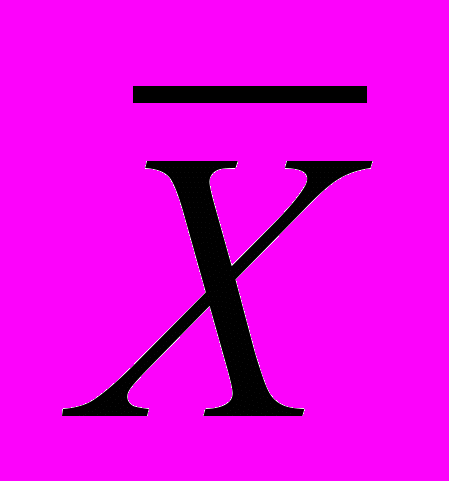
| 0 | 1 |
| 1 | 0 |
Конъюнкцией двух высказываний Х и У называется высказывание
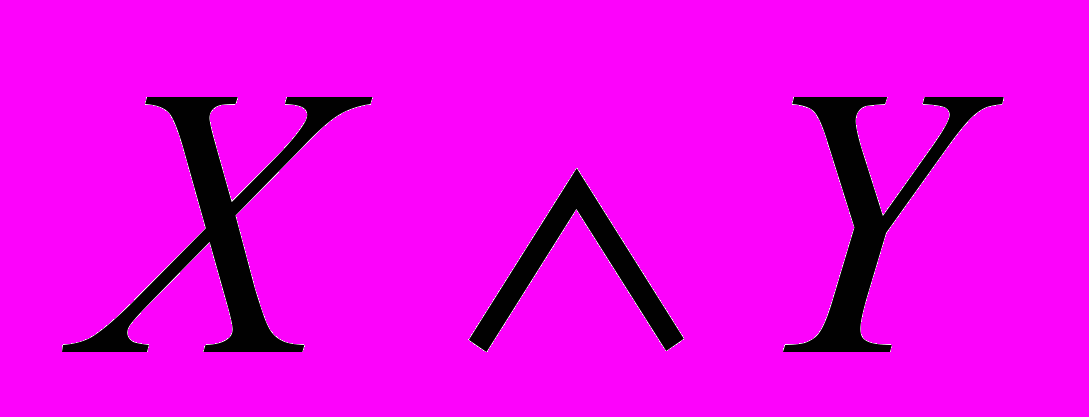, которое истинно только в том случае, когда Х и У оба истинны.Таблица истинности для конъюнкций.
| Х | Y | |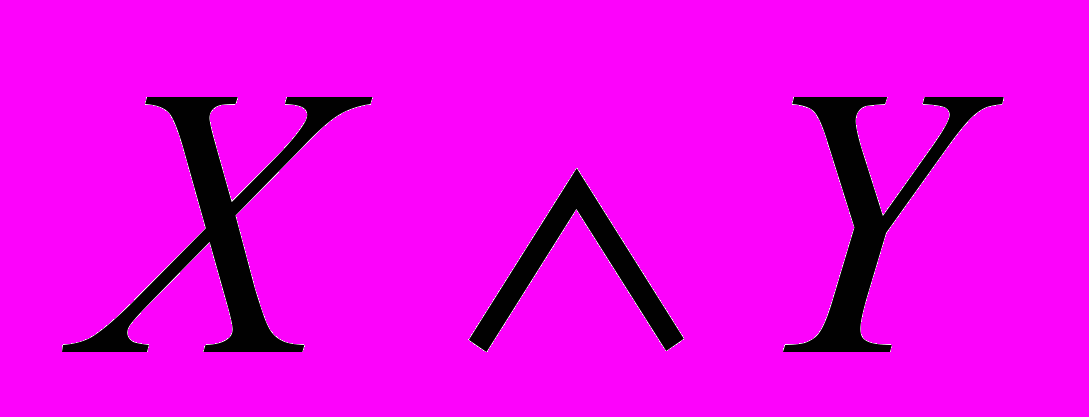
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Дизъюнкцией двух высказываний Х и У называется высказывание
, которое истинно, когда хотя бы одно из них истинно.Таблица истинности дизъюнкций.
| Х | Y | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Импликацией двух высказываний Х и У. называется высказывание
, которое ложно тогда и только тогда, когда Х истинно, а У ложно.Таблица истинности для импликации.
| Х | Y | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Эквивалентностью высказываний Х и У называется высказывание
, которое истинно тогда и только тогда, когда Х и У оба истинны или ложны.Таблица истинности для эквивалентности.
| Х | Y | |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Для образования составных высказываний наряду с единичным использованием каждой основной связки можно пользоваться основными связками многократно, получая более сложные составные высказывания - аналогично тому, как с помощью основных арифметических операций образуются сложные алгебраические выражения.
Например, составными будут высказывания:
; 
; 
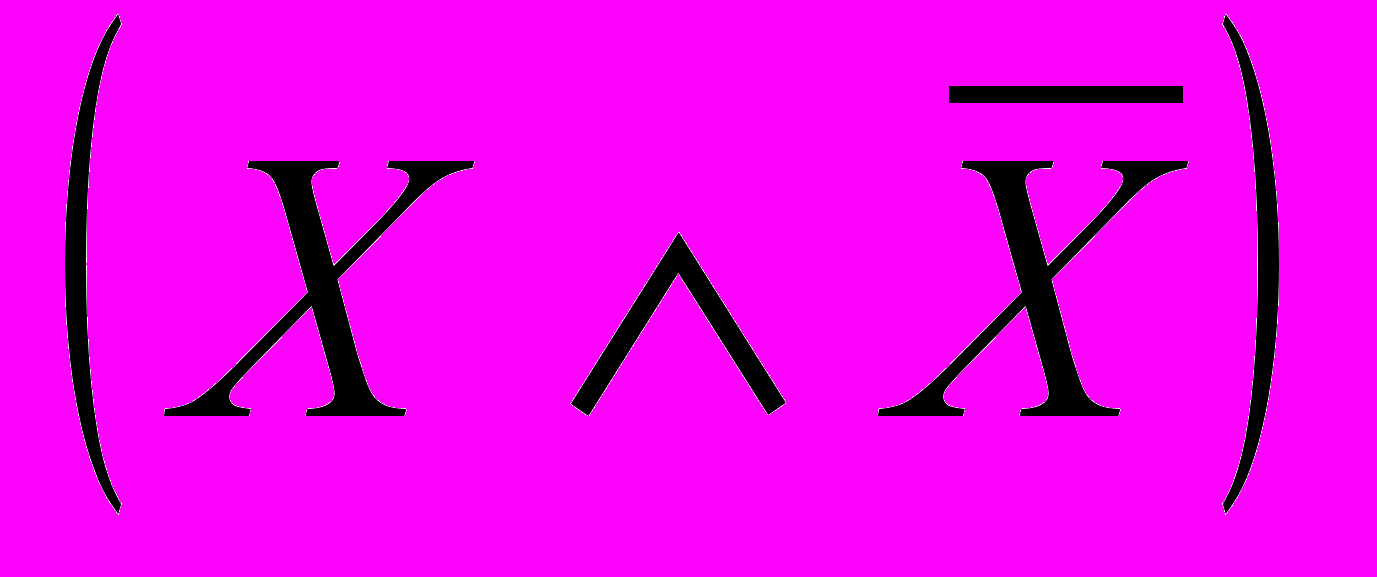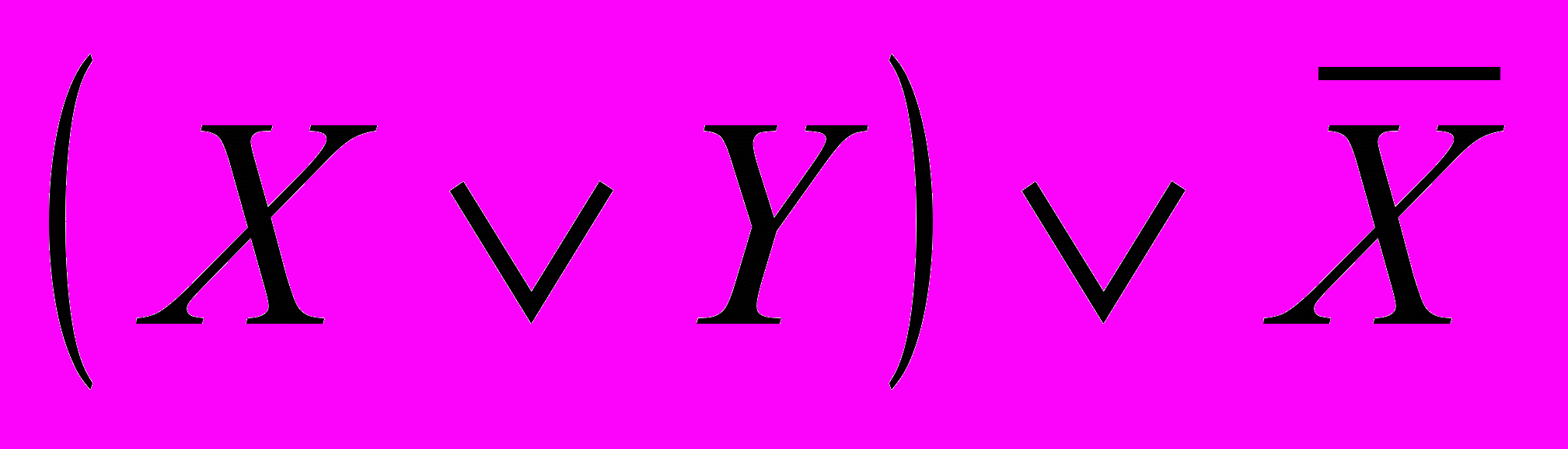.Их следует читать «изнутри наружу», подобно алгебраическим выражениям, в которых сначала группируются величины, заключенные в самые внутренние скобки, затем эти скобки в свою очередь группируются и т. д. Если скобок нет, то операции надо выполнять в следующем порядке: конъюнкция, дизъюнкция, импликация, эквивалентность, отрицание. Каждое составное высказывание имеет свою таблицу истинности, которая может быть построена стандартным образом.
3. Другие связки
Новые высказывания могут быть образованы при помощи нескольких логических операций и составлять формулы, некоторые из которых рассматриваются как логические операции, осуществляемые при помощи других логических связок: | ; ↓ ;
.| Название | Прочтение | Обозначение |
| Штрих Шеффера | Антиконъюнкция | | |
| Стрелка Пирса | Антидизъюнкция | ↓ |
| Сумма по модулю два | Антиэквивалентноеть | |
Штрих Шеффера,
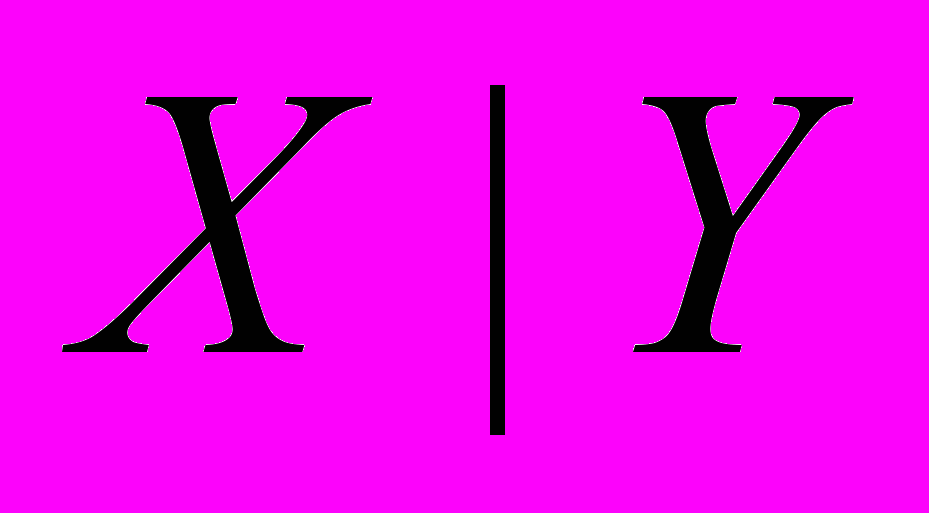или антиконъюнкция, по определению 
.Таблица истинности штриха Шеффера.
| Х | Y | |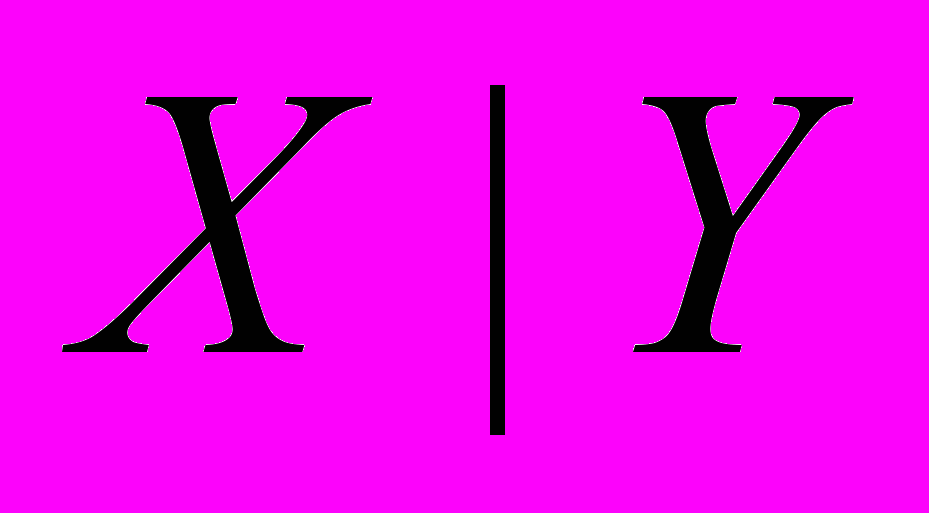
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Стрелка Пирса,
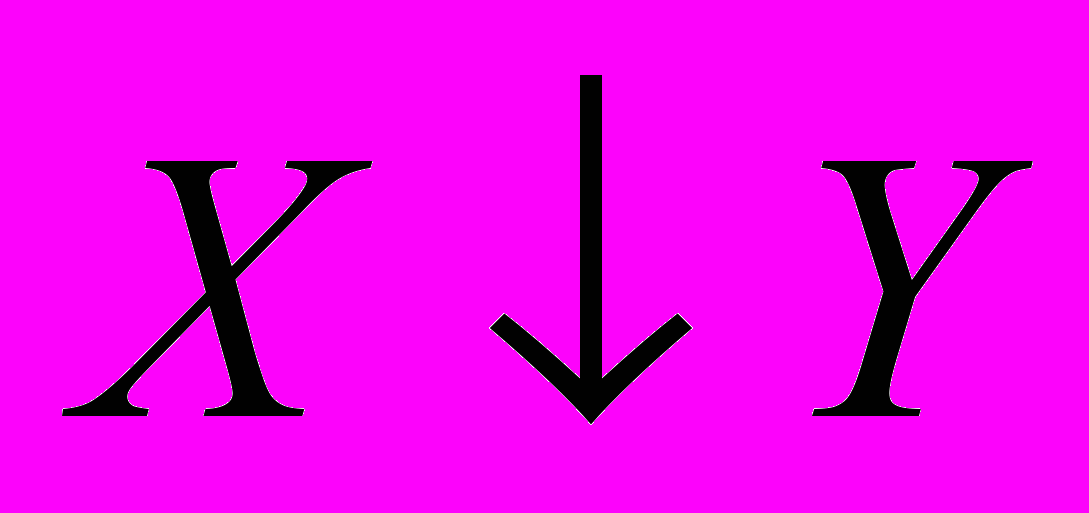или антидизъюнкция, по определению 
.| Х | Y | |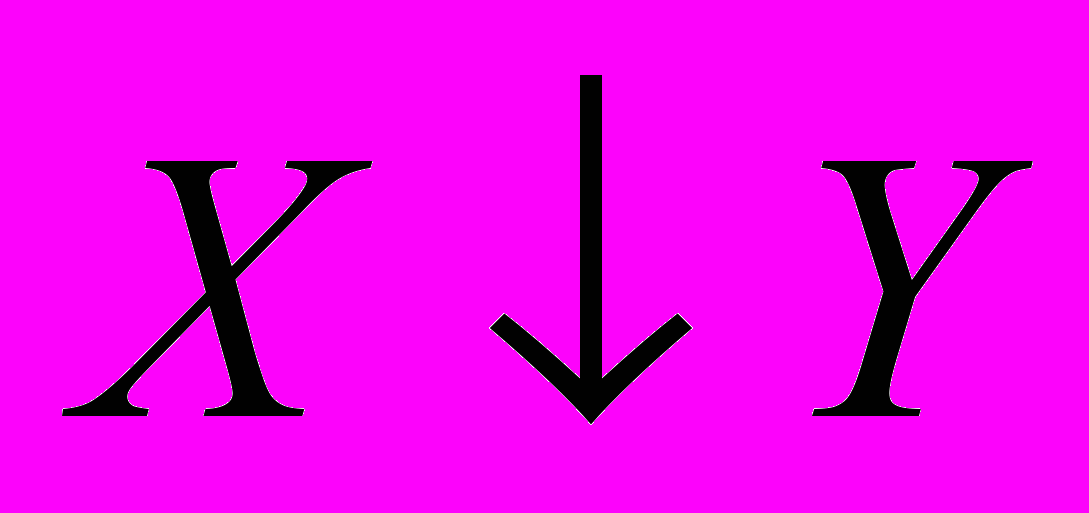
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Сумма по модулю два,
или антиэквивалентность, по определению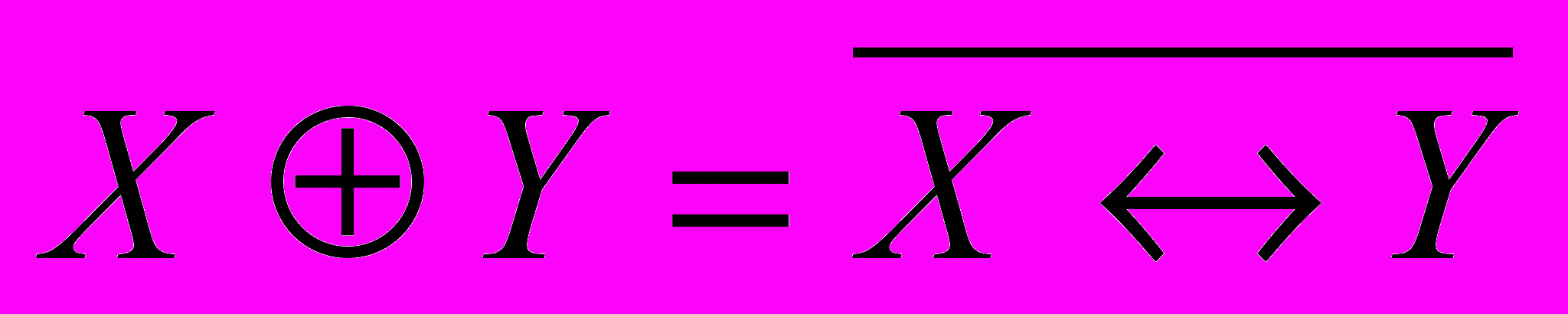 
.Таблица истинности суммы по модулю два.
| Х | Y | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Заметим, что таблицы истинности логических операций содержат 2n строк, где п - число простых высказываний.
4. Логические отношения
Иногда бывает желательно рассмотреть взаимоотношение двух высказываний. Наиболее интересное из таких отношений имеет место, когда из одного высказывания логически следует другое. Если из Х следует У, мы говорим также, что У является следствием Х или что У логически выводимо из Х. Исходя из анализа логических возможностей для пары высказываний Х и У, отношение следствия можно охарактеризовать таким образом: из Х следует У, если У истинно всякий раз, когда истинно Х, т. е. если У истинно во всех логически возможных случаях, в которых Х истинно.
В случаях составных высказываний, имеющих одни и те же компоненты, таблицы истинности дают удобный метод для проверки того, имеет ли место отношение следствия.
Следующая таблица иллюстрирует этот метод:
| Х | Y | | | |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Высказывание
истинно в первом и четвертом случаях и в обоих этих случаях истинно также высказывание . Мы видим, что из следует высказывание . Сравнение двух последних столбцов показывает, что из высказывания не следует , из не следует .При помощи таблиц истинности удобно осуществлять проверку эквивалентности двух составных высказываний, имеющих одни и те же компоненты. Для этого достаточно лишь посмотреть, одинаковы ли таблицы истинности у этих составных высказываний.
Из следующей таблицы истинности видно, что
эквивалентно 
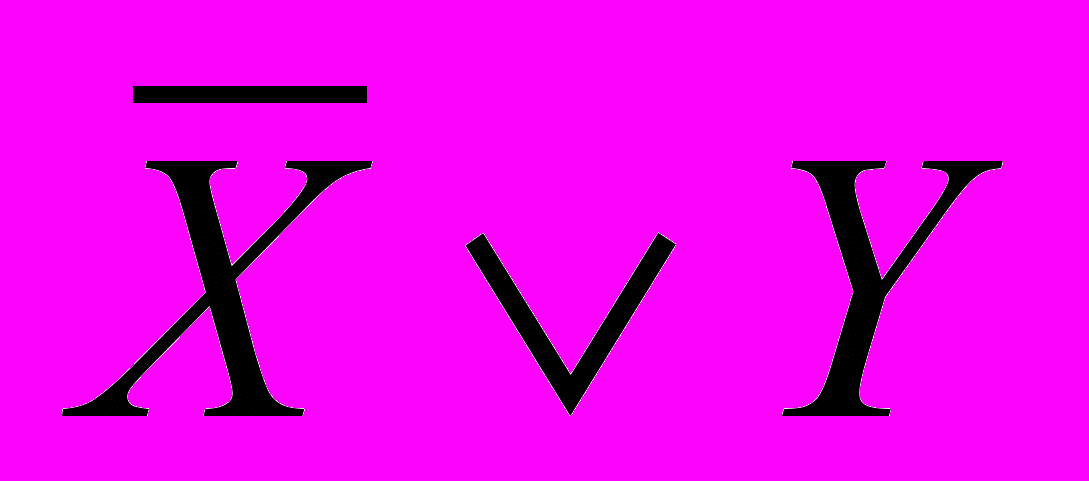.| Х | Y |  | | |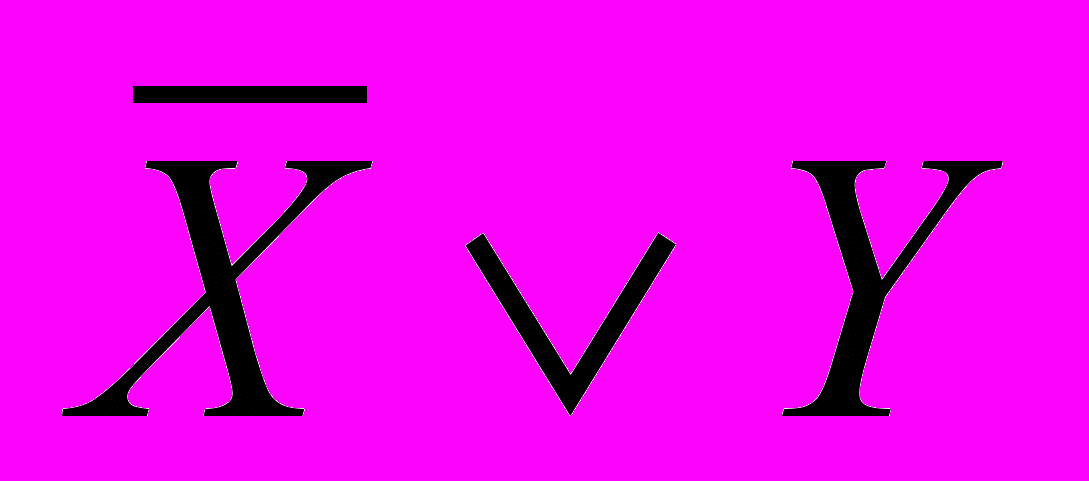
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
Два высказывания называются логически несовместимыми, если из истинности одного из них необходимо следует ложность другого. Другими словами, несовместимость высказываний Х и У означает, что они никогда не могут оказаться одновременно истинными. Если несколько составных высказываний построены из одних и тех же простых составляющих, то для проверки их совместимости нужно построить таблицы истинности для каждого из высказываний. Если среди всех строк найдется, по крайней мере, одна, в которой все составные высказывания истинны, то составные высказывания совместимы. В противном случае они оказываются несовместимыми.
5. Основные законы, определяющие свойства введенных логических операций
1) Идемпотентность дизъюнкции и конъюнкции:
, 
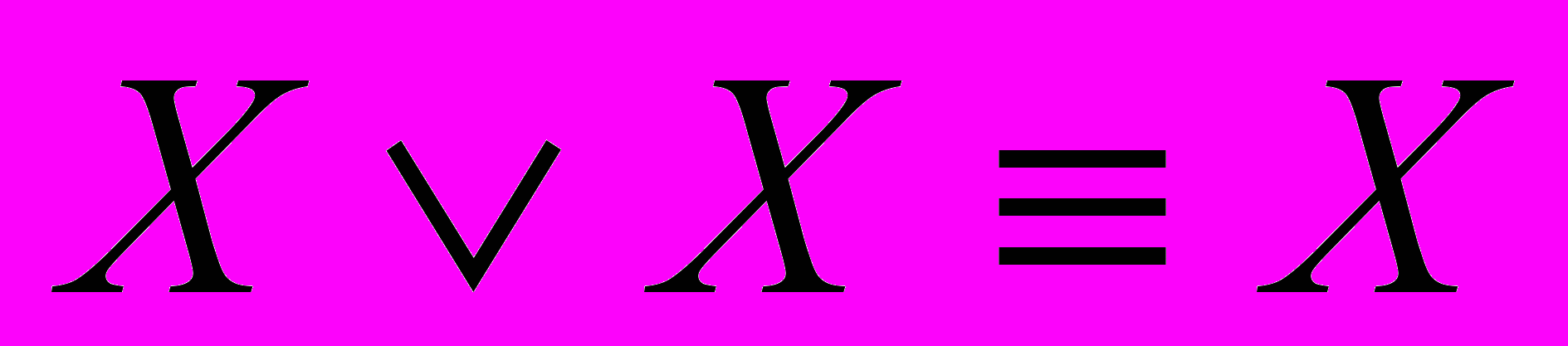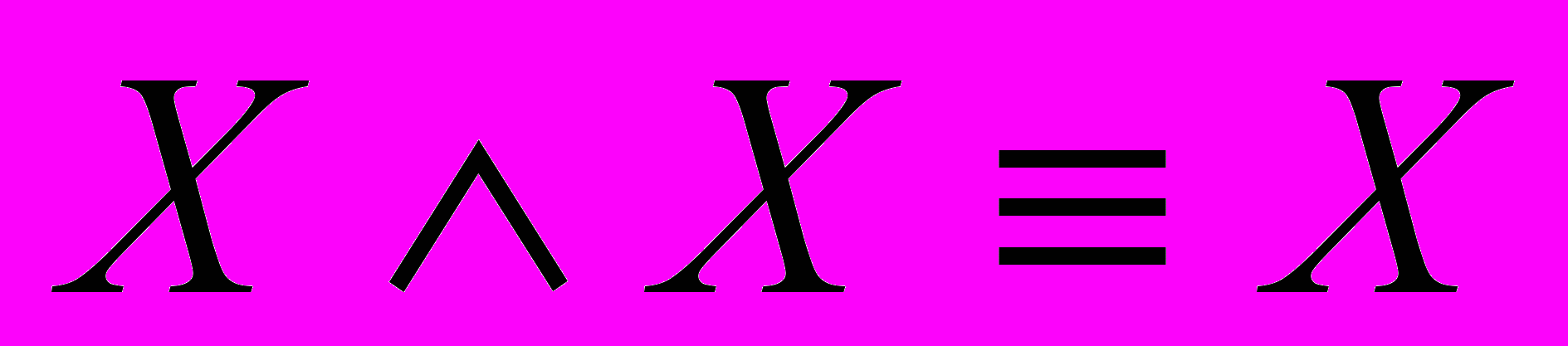.2) Коммутативность дизъюнкции и конъюнкции:
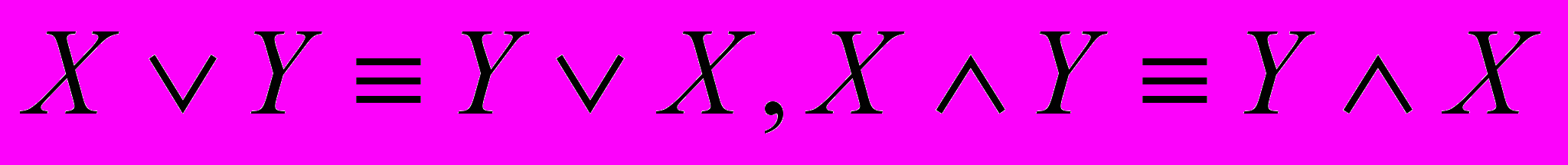.3) Ассоциативность дизъюнкции и конъюнкции:
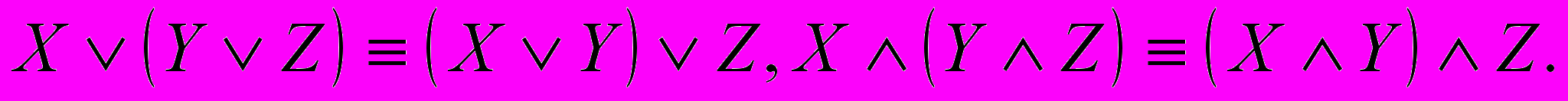
4) Дистрибутивность операций дизъюнкции и конъюнкции относительно друг друга:
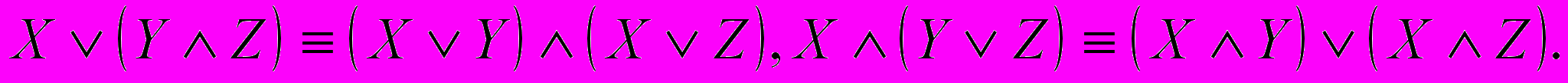
5) Двойное отрицание:
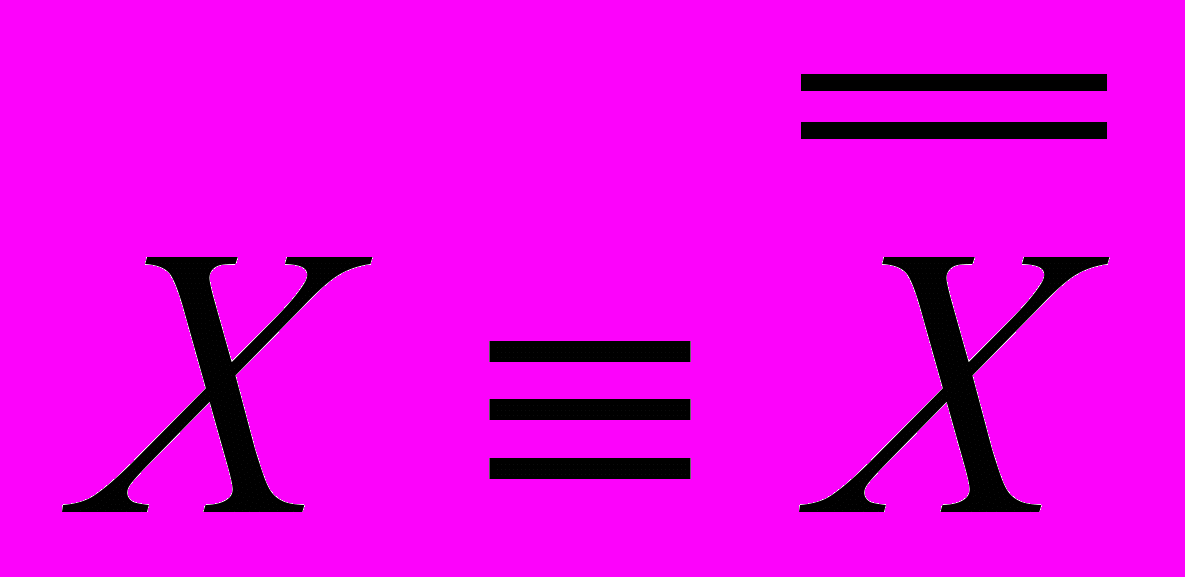.6) Закон де Моргана:
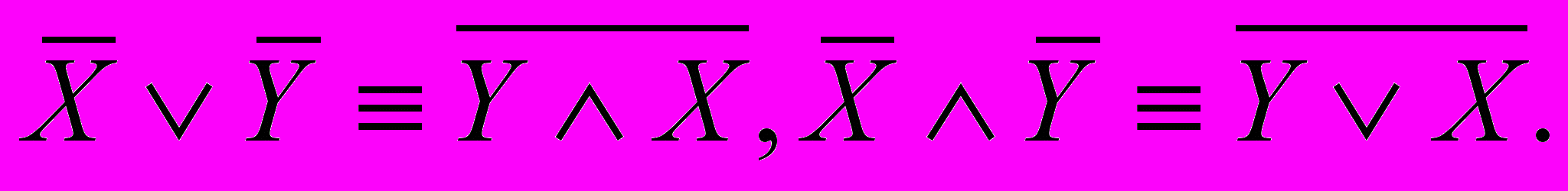
7) Склеивание:
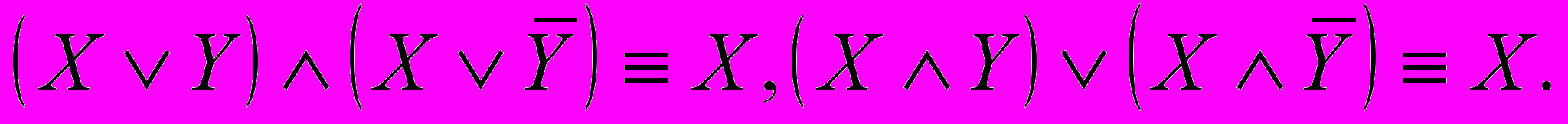
8) Поглощение:
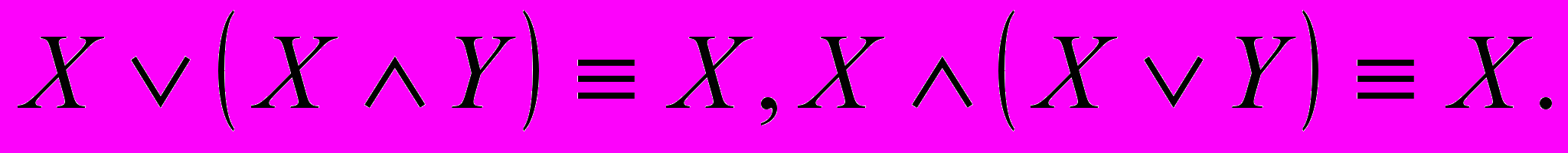
9) Действие с логическими константами 0 и 1:
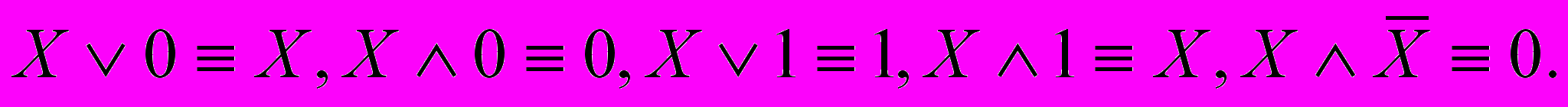
10) Закон исключения третьего:
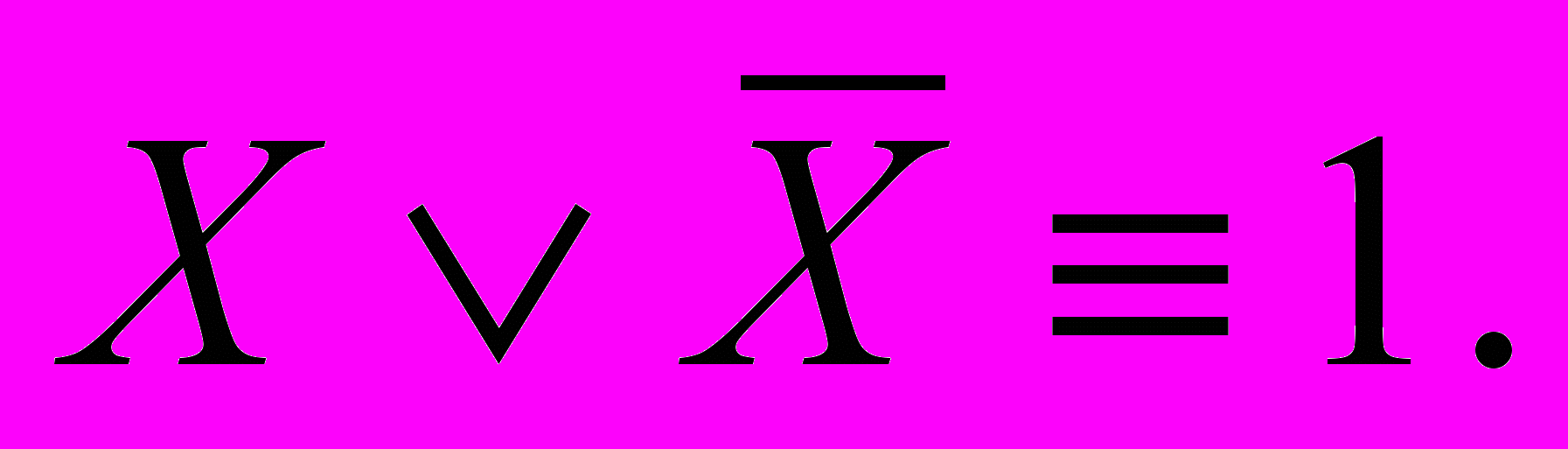
11) Тождество:
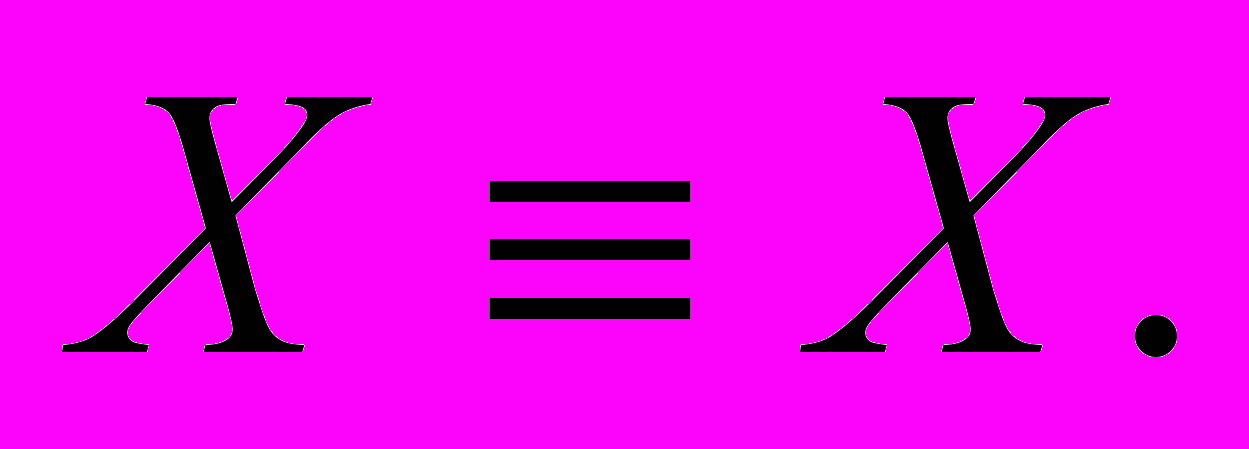
12) Отрицание противоречия:
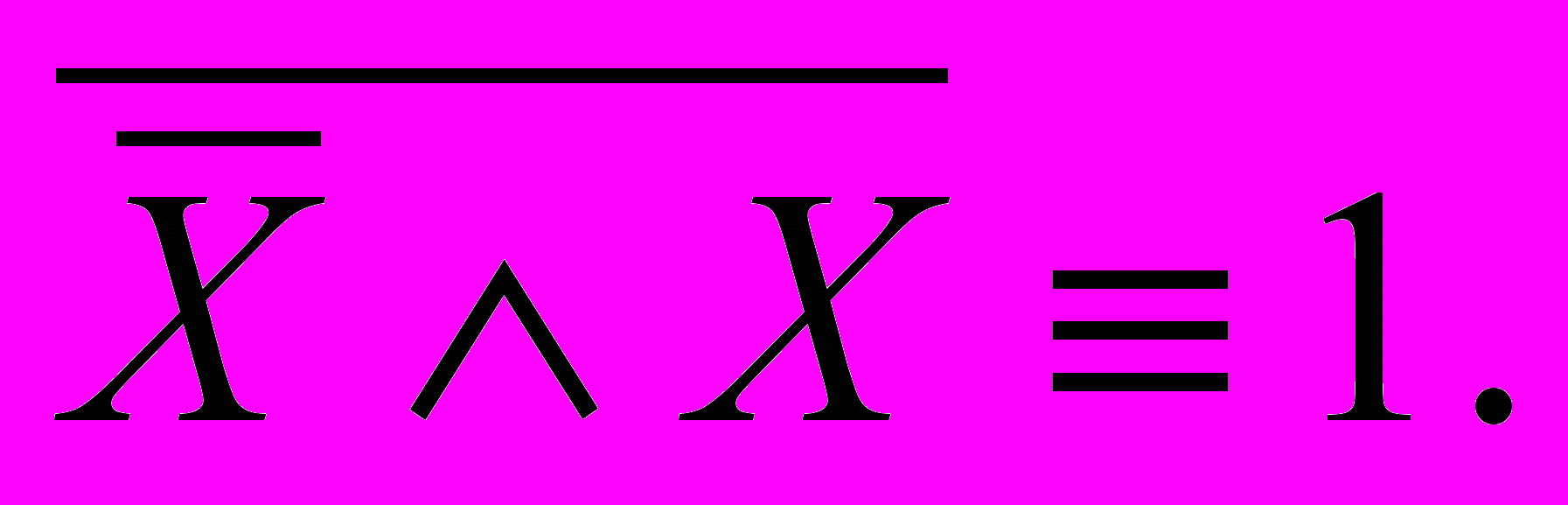
13) Контрапозиция:
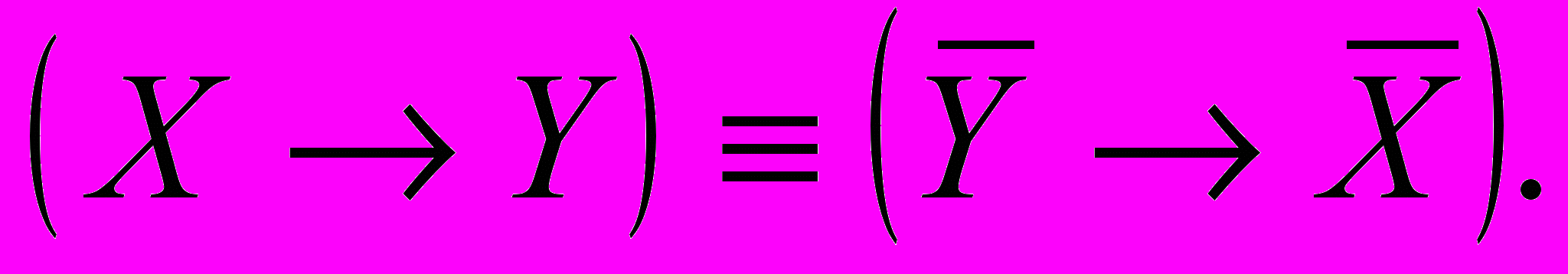
14) Цепное заключение:
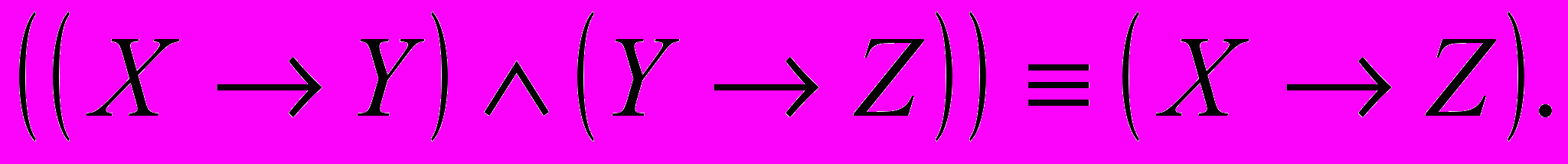
15) Противоположность:
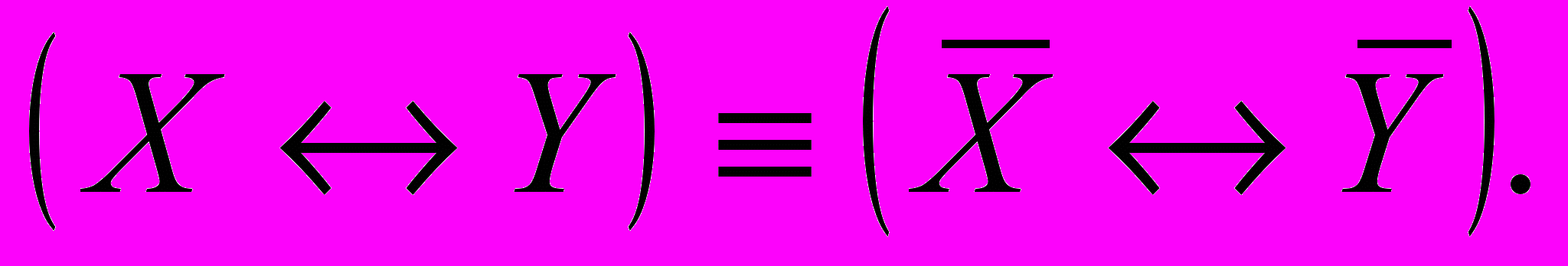
16) Модус поненс (modus ponens):
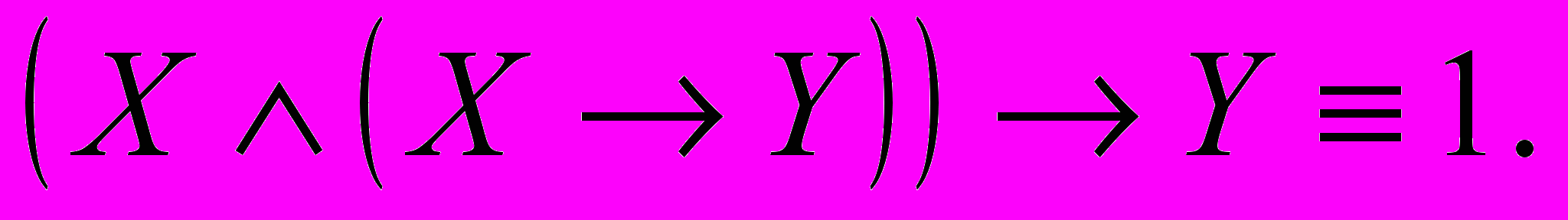
Сформулированные законы легко проверить с помощью таблицы истинности.
4. Булевы функции
Булева функция, или функция алгебры логики, является одним из основных объектов дискретной математики.
Булевы функции названы в честь Дж. Буля, положившего начало применению математики в логике.
Функцию
, принимающую одно из двух значений 0 или 1, от n переменных, каждая из которых принимает одно из двух значений 0 или 1, будем называть булевой функцией от n переменных.Булева функция от п переменных сопоставляет. каждому упорядоченному набору (кортежу), составленному из п элементов, 0 и 1, либо 1, либо 0.
Две булевы функции называются равными, если для любых одинаковых наборов значений переменных обе функции принимают одинаковые значения. Булевых функций одной переменной четыре, а двух переменных - шестнадцать и т. д. Число булевых функций от п переменных равно
.Рассмотрим функции одной и двух переменных, которые называются «элементарными» функциями и С помощью которых можно определить функции большего количества переменных.
Рассмотрим таблицы истинности таких функций.
Таблица истинности булевой функции одной переменной:
 |  |  |  |  |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Функции
и называются константами - соответственно 0 и 1.Функция
совпадает с переменной x и называется тождественной 
.Функция
принимает значения, противоположные значениям аргумента x, и называется отрицанием x, обозначается 
.Таблица истинности булевой функции двух переменных:
 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Следует отметить, что здесь к функциям двух переменных относятся и такие, которые в действительности зависят от одной переменной.
Функции
и представляют собой константы 0 и 1.Функции
, , , существенно зависят только от одной переменной: 
, 
, 
, 
.Остальные функции существенно зависят от двух переменных, и для них есть названия и обозначения:
а) функция
и называется конъюнкцией,б) функция
называется дизъюнкцией,в) функция
и называется эквивалентностью,г) функция
и называется суммой по модулю два, или суммой Жегалкина,д) функция
и называется конверсией,е) функция
называется импликацией,ж) функция
и называется штрих Шеффера,з) функция
называется стрелкой Пирса,и) функции
и логически несовместимы с импликацией и конверсией и называются функциями запрета.8. Свойства элементарных булевых функций
Для булевых функций справедливы равенства, аналогичные формулам, сформулированным для высказываний.
1. Функции: конъюнкция, дизъюнкция, сумма по модулю два, стрелка Пирса, штрих Шеффера обладают свойством коммутативности.
2. Функции: конъюнкция, дизъюнкция, сумма по модулю два·обладают свойством ассоциативности и свойством дистрибутивности.
3. Закон де Моргана:
; 
.4. Закон двойного отрицания:
.5. Выражение дизъюнкции через конъюнкцию и суммы по модулю два:
.6. Выражение дизъюнкции через импликацию:
.7. Выражение отрицания через штрих Шеффера, стрелку Пирса, сумму по модулю два и эквивалентность:
.8. Выражение конъюнкции через штрих Шеффера:
.9. Выражение дизъюнкции через стрелку Пирса:
.10. Закон поглощения:
; 
.11. Закон склеивания:
.12. Для функций: конъюнкция, дизъюнкция и сумма по модулю два справедливы следующие тождества:
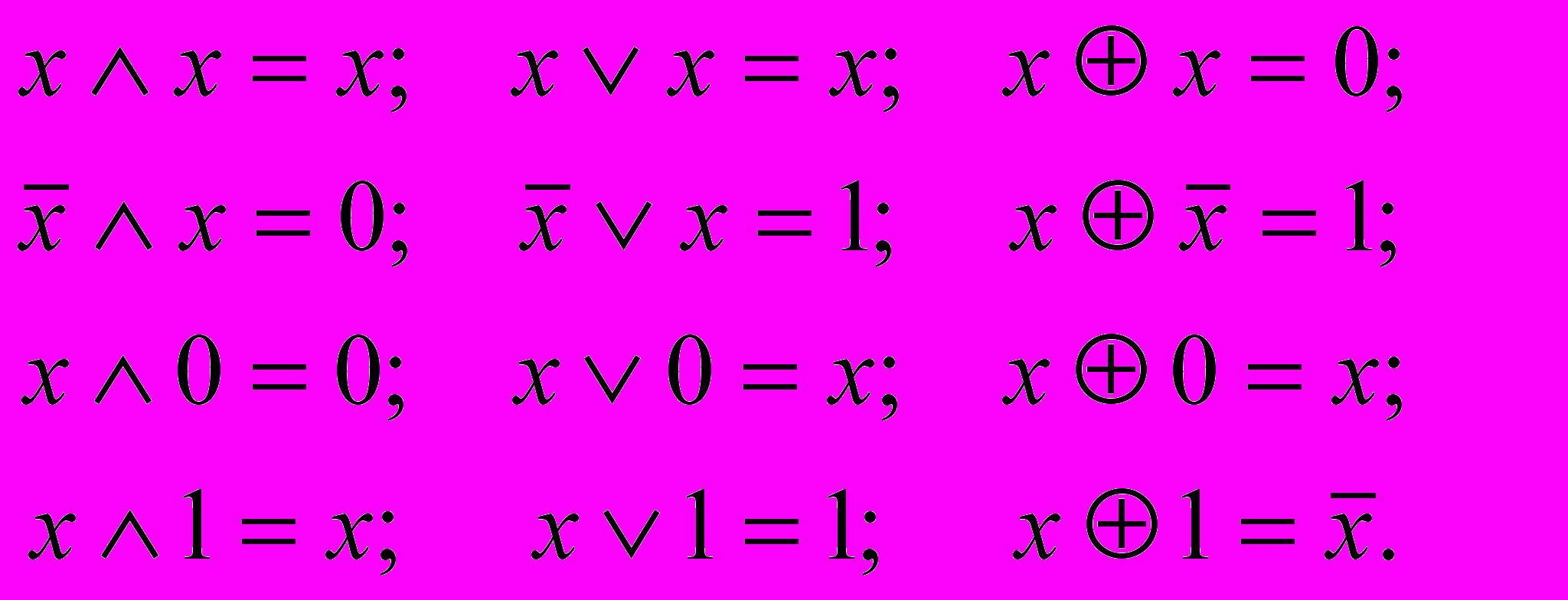
13. Для функций конъюнкция и дизъюнкция справедливы тождества:
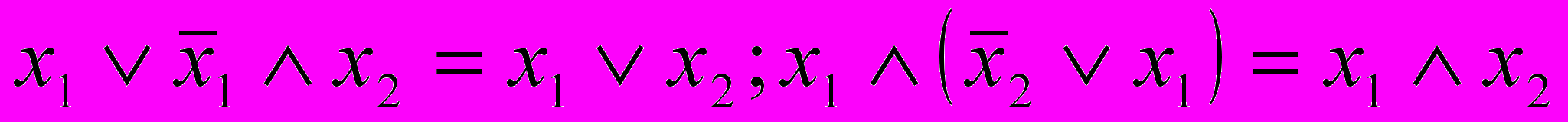.Для доказательства справедливости любых из приведенных тождеств нужно составить таблицы истинности для булевых функций.
Булеву функцию любого числа переменных можно задать формулой, содержащей функции одной и двух переменных посредством подстановки одних булевых функций вместо переменных в другие булевы функции, т. е. посредством суперпозиции булевых функций.